扩展功能
文章信息
- 杨达, 陈玉婷, 文成, 赵新朋
- YANG Da, CHEN Yu-ting, WEN Cheng, ZHAO Xin-peng
- 基于CPT-UE模型的城市道路施工顺序优化
- Scheduling Optimization of Urban Road Work Zones Based on CPT-UE Model
- 公路交通科技, 2018, 35(9): 78-84
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(9): 78-84
- 10.3969/j.issn.1002-0268.2018.09.012
-
文章历史
- 收稿日期: 2017-07-07
近年来,为了有效缓解城市交通拥堵,国家对地铁、轻轨等交通基础设施建设的投入也不断加大,但在这些交通基础设施建设的同时,也使得城市道路网络上出现了大量的施工区,当下,对有关施工区[1-2]的研究已经成为交通领域的热点研究之一。这些施工区的存在通常会伴随着车道封闭,从而引起道路通行能力下降,交通事故增加等诸多弊端。当路网上有多个施工区时,不同的施工顺序可能会使网络上总旅行时间和旅行费用有着显著的差异。尽管无法消除城市道路施工造成的不利影响,但政府决策者却可以选择对交通网络影响较小的施工顺序。因此,科学合理地对施工顺序进行优化在城市道路施工中就显得尤为重要。
现有对城市道路施工顺序优化问题的研究主要集中在施工周期为数个小时的短时范畴[3-10],很少有研究关注施工周期为数个月甚至是数年的长期施工范畴[11-13]。早期的研究者[14-15]用基于排队理论演化出的一系列公式对一天或一周的交通延误进行计算,从而确定不同施工队的施工任务以及施工区先后施工顺序。这种延误计算方法假设交通网络中的路段是孤立的,并没有从交通网络层面考虑交通流之间的相互影响,如相邻路段的拥堵扩散等,因此,它不能评估施工对整个道路交通网络造成的影响。2000年以来,为了克服这一缺陷,部分研究者[4-5, 8, 10]直接采用VISSIM,PARAMICS等交通仿真工具对整个网络层面的交通延误进行计算,从而确定最优的施工顺序。这些研究关注的都是施工周期为数个小时,所有施工项目在一天之内完成的短期施工顺序优化问题。在长期施工顺序优化问题研究方面,Lee[11]采用问卷调查的方法对未来数天内交叉口不同流向的交通转移比例进行调查,并利用VISSIM仿真来确定最优施工顺序,这种方法工作量巨大,网络适用范围有限,当施工区数量较多时将变得相当复杂。Zheng等[12-13]虽然采用UE分配的方法对网络上的总交通延误进行计算,但他们是以月为单位来进行交通分配的,实际上并非所有施工区的施工周期都是月的整数倍,在实际应用中这种方法具有一定的局限性。另外,由于出行者对实际旅行时间的认知存在一定的主观性,因此,网络上的交通分布是基于出行者对实际旅行时间的主观感知值而达到最终平衡态的,并非是基于实际的旅行时间。
考虑到目前城市道路施工周期都相对较长,仅通过交通仿真方法来确定最优的施工顺序无法满足实际需要,而现有对长期施工顺序优化问题的研究方法在精确性、适用性等方面还有一定的局限性,且所使用的交通分配方法也无法体现出行者对道路实际旅行时间的主观感知特征。因此,在国内外已有大量学者将累积前景理论[16-18](CPT)应用到交通领域的基础上,本研究利用基于该理论的用户平衡(UE)分配模型,提出了一个对城市道路施工顺序优化的双层规划模型,该模型能够评估不同施工顺序的优劣,对以天为单位且施工周期较长的施工顺序优化问题具有良好的适用性。最后利用遗传算法对所提出的模型进行求解,从而得到最优的施工顺序,并通过一个算例进行了仿真分析。
1 路段累积前景累积前景理论作为经济学领域的重要研究成果,它可以描述有限理性人在不确定状态下寻求效益时的一系列主观决策过程。由于交通系统中的出行者大多都是有限理性的,因此,在路径选择时影响决策的主要因素是实际旅行时间t相对于参考点t0的主观感知变化,而并非真实的旅行时间本身,决策前,出行者自身会根据实际旅行时间t判断自身决策的感知价值。根据参考点t0,出行者的主观价值可以分为收益(t≤t0)和损失(t>t0)两部分,价值函数g(t)可表示为下述形式:
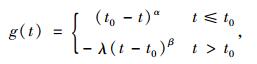
|
(1) |
式中,α, β为风险态度系数,其取值越大说明决策者越倾向于冒险0 < α, β≤1;λ为损失规避系数,当λ≥1时,损失部分的价值函数要比收益部分的价值函数更加陡峭,即决策者对损失更加敏感。
在决策时,出行者往往会对路径选择概率的判断带有一定的主观性,它是出行者对客观事件的主观判断,体现了出行者自身的经验和期望。这里采用Prelec等人[19]在1998年提出的主观概率函数的形式:
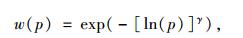
|
(2) |
式中,p为真实的概率值;w(p)为主观概率权重;γ(0 < γ < 1)为参数。
假定路段实际旅行时间由两部分构成,一部分是确定项tr,由真实的交通量来决定,即与道路的拥挤效应有关;另一部分是随机项ε,它不受道路拥挤效应的影响并服从一定的概率分布,在实际的交通出行中主要由人的出行认知、道路环境等因素来决定。出行者在路段上实际的旅行时间可表示为式(3):
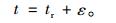
|
(3) |
这里假定随机项ε服从相关离散型概率分布,因为虽然连续性随机变量分布(即较小的旅行时间间隔)能使计算出的累积前景值更加精确,但在实际中出行者对较小的出行时间间隔并不敏感,他们难以区分这种时间间隔下旅行时间的差异[20]。因此,对于一个离散型的旅行时间的分布结果,其累积前景值由式(4)算得:
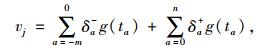
|
(4) |
式中,vj为路段j的累积前景值;δa为相应可能结果的主观概率权重值(δa+为收益,δa-为损失):
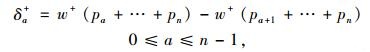
|
(5) |

|
(6) |
对于端点处采用式(7)、式(8)计算:
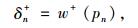
|
(7) |
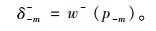
|
(8) |
假设交通网络G(N, L)是一个充分连接的有向图,由一系列节点N和路段L组成。同时,用W表示任一OD对r, s的集合,且r, s之间的交通需求是固定的,p(k)为某一施工顺序k造成的网络总旅行时间增加量。一般来说,施工队和施工区的数量对最优施工顺序有着重要的影响,因此,有必要建立一个适用于任意多个施工队和施工区的场景一般化模型。对于有施工区存在的城市道路网而言,其最明显的特征是网络总旅行时间较无施工区存在时有着明显的增加,而决策者总是希望因施工引起的网络总旅行时间增加量最小,本研究提出的城市道路施工顺序优化模型中的上层规划模型如式(9)所示:
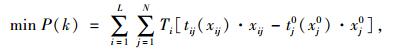
|
(9) |
约束为:
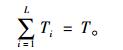
|
(10) |
实际上,在各个施工阶段,网络上的出行者总是试图选择累积前景值最大的路径出行,其流量分布应符合CPT-UE交通分配模型,下层规划模型如式(11)所示:
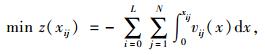
|
(11) |
约束为:
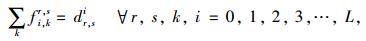
|
(12) |
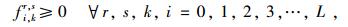
|
(13) |
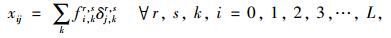
|
(14) |
式中,i为施工阶段数(i=0, 1, 2, 3,…, L, 当i=0时表示网络上无施工),对于多个施工队来说,当任意一个施工队有新的施工任务开始或者结束时,即路网中有路段通行能力发生变化时,施工由当前阶段转变为下一阶段;Ti为第i个施工阶段的施工周期;T为总施工周期;xij为第i个施工阶段路段j的流量;xj0为无施工背景下路段j的流量;vij(x)为第i个施工阶段路段j的累积前景计算公式;tij(xij)为第i个施工阶段路段j的平均旅行时间;tj0(xj0)为无施工背景下的路段j的平均旅行时间;dr, si为在第i个施工阶段任意OD对r, s之间的交通需求,为固定值;fi, kr, s为在第i个施工阶段任意OD对r, s之间路径k上的流量;δj, kr, s为若路段j在连接OD对r, s之间的路径k上,其取值为1,否则为0。
2.2 求解算法由于交通系统的复杂性,施工顺序优化通常是一个复杂的非线性规划问题,实际中会受到多种因素的约束,如施工周期、施工队数量、施工成本等。即便可以在一定程度上简化问题,但当施工队和施工区的数量都较多时,可行的施工顺序数量也将呈几何式增长,穷举所有可行的施工顺序,从而确定最优解往往是不现实的。近年来,研究者大多采用启发式算法对施工顺序优化问题进行求解[3-5, 8],在这些启发式算法中,由于遗传算法在求解的过程中具有全局搜索能力,模型解陷入局部最优的可能性相对较小,收敛速度较快,比较适合求解整数规划问题。因此,本研究也采用遗传算法对上述双层规划模型进行求解。
3 算例分析 3.1 试验设计如图 1所示,测试网络是一个充分连接的有向图,包括9个节点,12个路段,1个OD对1至9。假定测试网络上有6个施工区,每个施工区位于一个路段上,OD对1至9之间的交通需求为固定值2 000,参数α,β,λ,γ分别取0.8,0.8,2.25和0.74,路段阻抗函数采用常用的BPR函数。当随机项ε取1,2,3,4,5 min时,其对应概率分别为0.05,0.2,0.5,0.2和0.05。路段自由行驶时间(min)、初始路段通行能力(veh/min)、有施工路段的通行能力(veh/min)以及施工周期(d)设置如表 1所示。
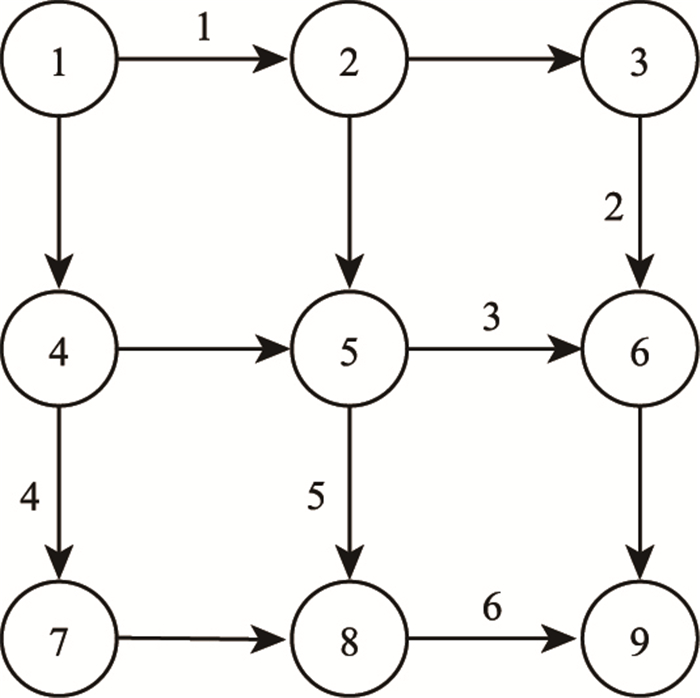
|
| 图 1 测试网络 Fig. 1 Text network |
| |
| 路段 | 自由行驶时间/min | 初始路段通行能力/(veh·min-1) | 有施工路段的通行能力/(veh·min-1) | 施工周期/d |
| 1→2 | 13 | 1 500 | 800 | 100 |
| 2→3 | 13 | 1 200 | — | — |
| 1→4 | 13 | 1 200 | — | — |
| 2→5 | 14 | 800 | — | — |
| 3→6 | 14 | 900 | 450 | 120 |
| 4→5 | 13 | 900 | — | — |
| 5→6 | 13.5 | 1 300 | 650 | 130 |
| 4→7 | 13 | 1 200 | 600 | 150 |
| 5→8 | 13.5 | 1 200 | 600 | 180 |
| 6→9 | 13.5 | 900 | — | — |
| 7→8 | 14 | 900 | — | — |
| 8→9 | 14 | 2 000 | 1 100 | 200 |
3.2 参考点影响分析
参考点对累积前景值的认知有着重要的影响,不同的参考点会使路网上的交通分布发生变化,从而引起网络总旅行时间增加量的改变。因此,有必要对不同参考点设置下的最优施工顺序及任务分配变化情况进行仿真分析。图 2 (a)~(h)给出了不同参考点设置(13~20)下3个施工队的最优施工顺序及任务分配变化情况。
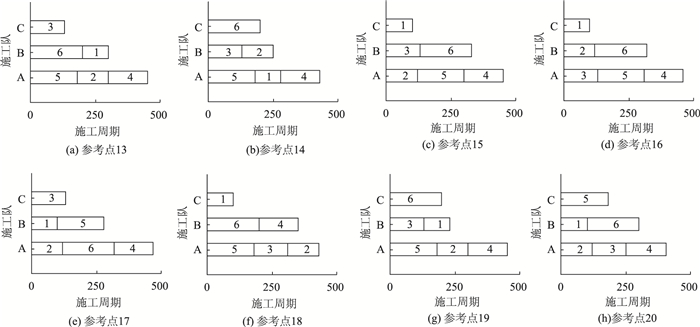
|
| 图 2 不同参考点下最优施工顺序及任务分配 Fig. 2 Best scheduling of work zones and task assignment in different reference point settings |
| |
由图 2可知,在施工队数量固定的前提下,不同的参考点取值会使最优的施工顺序及各个施工队的任务分配发生变化,同时也会改变总施工周期。当参考点取17时,总施工周期最长,为470 d;当参考点取20时,总施工周期最短,为400 d。实际中,虽然参考点的选取会随出行者自身出行经验的变化而变化,但不同的参考点取值对网络总旅行时间增加量的影响并不明显,如图 3所示,网络总旅行时间增加量在参考点取14时达到最大,在参考点取18时达到最小,两者仅相差2.79%。但对于出行者而言,不同的参考点取值会改变自身对实际旅行时间的认知,在本研究的算例中,参考点17是一个临界值,即当参考点取值在17以下时,网络总累积前景值减少量会随着参考点取值的增加而增加;当参考点大于17时,网络总累积前景值减少量会随着参考点取值的增加而减少。可见,虽然不同的参考点取值对整个交通网络的影响不大,但对出行者在出行时的主观认知有着重要的影响。
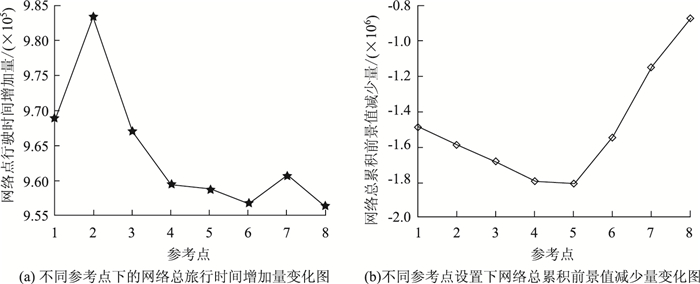
|
| 图 3 不同参考点下相关指标的变化情况 Fig. 3 Variation of concerned index in different reference points |
| |
3.3 施工队数量分析
不同的施工队数量设置会使网络上总旅行时间的增加幅度不同,因此,本节分别分析了1~6个施工队设置下各个施工队的任务分配及最优施工顺序的变化情况。由于本研究假定各个施工队具有相同的工作能力,因此,当网络上只有1个施工队时,虽然有36种可行的施工顺序,但所有可行施工顺序所引起的网络总旅行时间增加量是相同的;当网络上有6个施工队时,仅有1种施工顺序。在此仅给出这两种情形下的网络总旅行时间增加量及总累积前景值变化量,2~5个施工队下的最优施工顺序及各个施工队的任务分配如图 4所示。
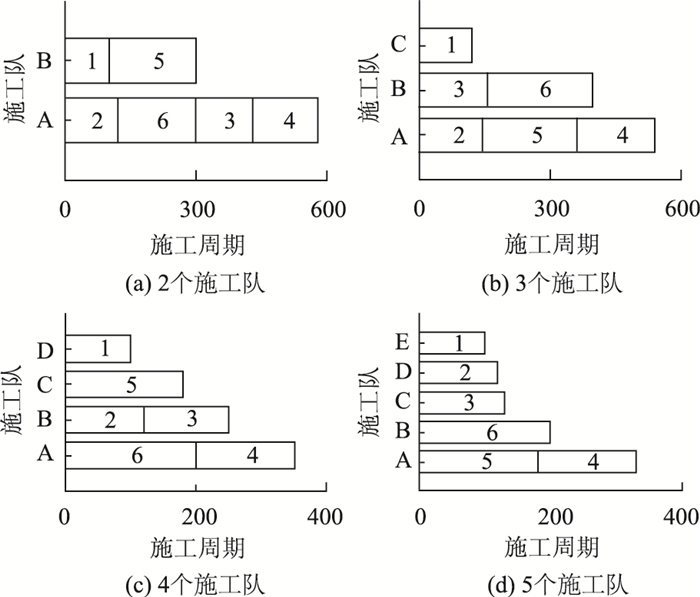
|
| 图 4 不同施工队数量下最优施工顺序及任务分配 Fig. 4 Best scheduling of work zones and task assignment in different numbers of construction teams |
| |
由图 4可以发现,增加施工队的数量可以在一定程度上缩短总施工周期,但并不意味着对整个网络的影响最小。如图 5所示,当网络上有1个和6个施工队时,因施工引起的网络总旅行时间增加量都相对较大。这是因为虽然施工队数量较少,单日的网络总旅行时间增加量也较小,但由于其施工周期较长,使得对整个施工期间的影响变大;而当施工队数量较多时,整个周期相对较短,但由于施工引起的单日网络总旅行时间增加量较大,从而对整个施工期间的影响较大。因此,过多和过少的施工队数量设置都不利于缓解施工期间的交通拥堵,在实际中有必要对施工队数量进行计算。另外,网络总累积前景值的变化规律与网络总旅行时间增加量类似,即当网络上有1个和6个施工队时,因施工引起的网络总累积前景值减少量都相对较大。
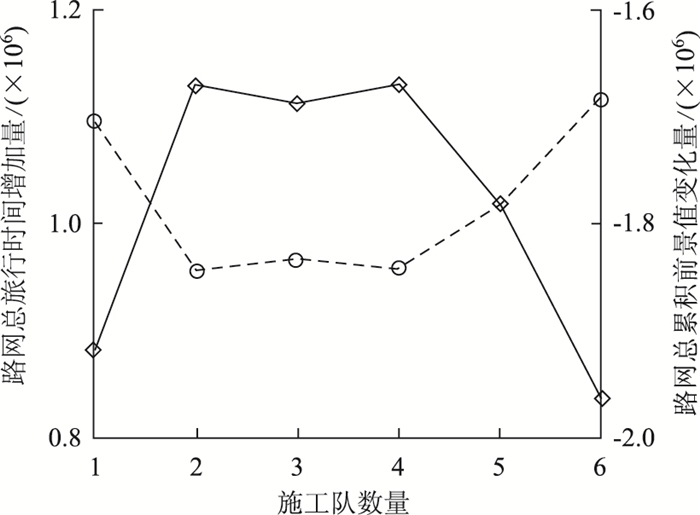
|
| 图 5 不同施工队数量下相关指标的变化情况 Fig. 5 Variation of concerned index in different numbers of construction teams |
| |
4 结论
在城市交通基础设施建设的过程中,合理的道路施工顺序对缓解城市交通拥堵有着重要的影响。现有对城市道路施工顺序优化的研究主要集中在短时施工范畴,相关研究手段并不适合对长期施工顺序优化问题的研究,而现有对长期施工顺序优化问题的研究在适用性、精确性等方面还有一定的不足。因此本研究利用基于累积前景理论的用户平衡交通分配模型,提出了一个对长期施工顺序进行优化的双层规划模型,该模型可适用于任意多个施工队和施工区的场景,随后利用经典的遗传算法对该双层规划模型进行求解,并通过一个算例进行了分析、总结,得到了以下新的结论:
(1) 在本算例中,不同的参考点取值会使最优的施工顺序及各个施工队的任务分配发生变化,同时也会改变总施工周期,但不同的参考点取值对整个交通网络的影响并不明显,网络总旅行时间增加量在参考点分别取14和18时仅相差2.79%。
(2) 增加施工队的数量可以在一定程度上缩短总施工周期,但并不意味着对整个网络的影响最小。在本算例中,当网络上的施工队有1个和6个时,对网络的影响相对较大;当网络上的施工队有3~5个时,对网络的影响相对较小,网络总累积前景值的变化规律与网络总旅行时间增加量类似,因此,在实际中有必要对网络上的施工队数量进行计算。
(3) 在实际中,由于城市道路交通网络规模较大,施工区往往数量较多,不同的施工顺序可能会使网络总旅行时间的增加量有着显著的差异,因此,政府决策者应提前对城市道路施工顺序进行优化,以减少施工期间的交通拥堵。
由于研究的局限性,文中仅从出行者交通成本的角度对施工顺序优化问题展开了分析,并没有考虑政府成本,实际中,网络交通流达到平衡态需要一定的演化时间,这些都可能会影响城市道路施工顺序优化,今后的研究也将围绕这些方面进行展开。
| [1] |
李玉洁, 陈玲娟, 张光德. 基于元胞自动机的施工区道路车辆换道点研究[J]. 武汉科技大学学报, 2016, 39(3): 231-235. LI Yu-jie, CHEN Ling-juan, ZHANG Guang-de. Research of Vehicle Lane Changing Point on the Construction Area Road Based on Cellular Automata[J]. Journal of Wuhan University of Science and Technology, 2016, 39(3): 231-235. |
| [2] |
邱小平, 孙若晓, 马丽娜, 等. 基于社会力的信号交叉口施工区交通流建模[J]. 交通运输系统工程与信息, 2015, 16(1): 99-104. QIU Xiao-ping, SUN Ruo-xiao, MA Li-na, et al. Modeling and Analyzing of Traffic Flow on the Work Zone of Urban Signalized Intersection Based on Social Force[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 16(1): 99-104. |
| [3] |
CHANG Y Y, SAWAYA O B, ZILIASKOPOULOS A K. A Tabu Search Based Approach for Work Zone Scheduling[C]//Proceedings of the 80th Annual Meeting of the Transportation Research Board. Washington, D.C.: Transportation Research Board, 2001.
|
| [4] |
CHEU R L, MA W. An Improved Genetic Algorithm-simulation Methodology for Lane Closure Scheduling[C]//Proceedings of the 81st Annual Meeting of the Transportation Research Board. Washington, D.C.: Transportation Research Board, 2001.
|
| [5] |
CHEU R L, WANG Y, FWA T F. Genetic Algorithm-simulation Methodology for Pavement Maintenance Scheduling[J]. Computer-aided Civil and Infrastructure Engineering, 2004, 19(6): 446-455. |
| [6] |
CHIEN S, TANG Y, SCHONFELD P. Optimizing Work Zones for Two-lane Highway Maintenance Projects[J]. Journal of Transportation Engineering, 2002, 128(2): 145-155. |
| [7] |
CHIEN S, TANG Y. Scheduling Highway Work Zones with Genetic Algorithm Considering the Impact of Traffic Diversion[J]. Journal of Advanced Transportation, 2014, 48(4): 287-303. |
| [8] |
MA W T, CHEU R L, LEE D H. Scheduling of Lane Closures Using Genetic Algorithms with Traffic Assignments and Distributed Simulations[J]. Journal of Transportation Engineering, 2004, 130(3): 322-329. |
| [9] |
TANG Y, CHIEN S. Optimization of Work Zone Schedule Considering Time-varying Traffic Diversion[C]//Proceedings of the 89th Annual Meeting of the Transportation Research Board. Washington, D.C.: Transportation Research Board, 2009.
|
| [10] |
WANG Y, CHEU R L, FWA T F. Highway Maintenance Scheduling Using Genetic Algorithm with Microscopic Traffic Simulation[C]//Proceedings of the 81st Annual Meeting of the Transportation Research Board. Washington, D.C.: Transportation Research Board, 2002.
|
| [11] |
LEE H Y. Optimizing Schedule for Improving the Traffic Impact of Work Zone on Roads[J]. Automation in Construction, 2009, 18(8): 1034-1044. |
| [12] |
ZHENG H, CAI C D, NAVA E J, et al. Optimization of Renewal-based Project Scheduling in an Urban Network[C]//Proceedings of the 91st Annual Meeting of the Transportation Research Board. Washington, D.C.: Transportation Research Board, 2012.
|
| [13] |
ZHENG H, NAVA E, CHIU Y C. Measuring Networkwide Traffic Delay in Schedule Optimization for Work-zone Planning in Urban Networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(6): 2595-2604. |
| [14] |
FWA T F, CHEU R L, MUNTASIR A. Scheduling of Pavement Maintenance to Minimize Traffic Delays[J]. Transportation Research Record, 1998, 1650: 28-35. |
| [15] |
MUNTASIR A. Scheduling of Pavement Maintenance Activities[D]. Singapore: National University of Singapore, 1998.
|
| [16] |
TVERSKY A, KAHNEMAN D. Advances in Prospect Theory:Cumulative Representation of Uncertainty[J]. Journal of Risk and Uncertainty, 1992, 5(4): 297-323. |
| [17] |
李晓伟, 陈红, 邵海鹏, 等. 基于累积前景理论的公路建设项目灰关联排序模型[J]. 公路交通科技, 2011, 28(10): 130-135. LI Xiao-wei, CHEN Hong, SHAO Hai-peng, et al. Grey Correlation Priority Decision Model of Highway Construction Project Based on Cumulative Prospect Theory[J]. Journal of Highway and Transportation Research and Development, 2011, 28(10): 130-135. |
| [18] |
刘玉印, 刘伟铭, 田世艳. 出行者有限理性条件下混合策略网络均衡模型[J]. 公路交通科技, 2011, 28(7): 136-141. LIU Yu-yin, LIU Wei-ming, TIAN Shi-yan. Network Equilibrium Model with Mixed Strategies under Bounded Rationality[J]. Journal of Highway and Transportation Research and Development, 2011, 28(7): 136-141. |
| [19] |
PRELEC D. The Probability Weighting Function[J]. Econometrica, 1998, 66(3): 497-527. |
| [20] |
AVINERI E. The Effect of Reference Point on Stochastic Network Equilibrium[J]. Transportation Science, 2006, 40(4): 409-420. |
 2018, Vol. 35
2018, Vol. 35
