扩展功能
文章信息
- 智路平, 周溪召
- ZHI Lu-ping, ZHOU Xi-zhao
- 基于动态行程时间可靠性的单车辆路径选择算法研究
- Study on Single Vehicle Routing Algorithm Based on Dynamic Travel Time Reliability
- 公路交通科技, 2018, 35(9): 71-77, 84
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(9): 71-77, 84
- 10.3969/j.issn.1002-0268.2018.09.011
-
文章历史
- 收稿日期: 2017-04-23
2. 上海理工大学 管理学院, 上海 200093
2. School of Management, University of Shanghai for Science and Technology, Shanghai 200093, China
随着交通拥堵程度的日益增加,车辆行程时间的不可控程度日趋严重。在此背景下,车辆最优路径选择问题的重要性受到出行者及管理者的极大关注。
车辆路径选择问题[1],自提出以后得到快速发展,演变出众多子问题[2-4],而对其分析一般归结于求解最短路径。在有时间窗限制及随机动态路网条件下进行最短路选择,为受限的动态最短路问题,难点在于此时车辆的路段行程时间具有明显的波动性,不再适于作为最短路问题的求解指标。
关于动态最短路问题,Hall[5]研究了交通网络中随时间变化的动态最短路径问题;Michael等[6]对单个车辆动态路径选择问题的模型进行了研究和分析;Chabini等[7]发现设定车辆在路径上的驾驶行为满足先进先出准则时,可以使用Dijkstra算法对动态路径规划问题进行求解,且不会增加问题求解的复杂程度;Fu等[8]研究了动态随机网络中的最短路径问题;Chai等[9]对自适应信号控制网络中的动态交通路径问题进行了研究;Tilk等[10]在有界双向动态规划约束的最短路径问题求解变量加速技术的基础上,引入动态中途点来减少最短路径问题求解整体计算量;石小法等[11]考虑交通信息对出行者选择出行路径的动态影响,建立了一种动态路径选择模型;张安英等[12]建立了动态路阻下的出行时间预测和路径选择模型,将路径选择范围从最优路径扩大到随机路径;张梦颖[13]研究了旅行时间不确定的车辆路径问题;任小聪等[14]建立了基于事故信息的车辆路径选择模型;苏贞旅等[15]构建了基于出发时刻的带有时间窗的动态最短路模型。
然而此类研究并未对随机动态路网条件下单一车辆的路径选择问题进行深入分析,且对路径构成单元路段的行程时间的研究多将路口延误固化,得到固定的行程时间预测值,或者是对时变的行程时间进行理论性描述,难于进行实时计算,最终导致路径选择时对路网的动态波动性考虑不足,影响路径选择方案的有效性。
基于此,本研究将信号转换时刻目标车辆位置与车流排队队尾之间的相对位置关系的可能状态进行分类,根据排队长度、车流消散速度及信号周期长度的不同,按照集散波原理进行相应的行程时间预测,获得可列的行程时间预测值集,并求对应的行程时间可靠性,将最短时间路径问题转化为最可靠路径问题。然后对单车辆简单网络路径选择问题和单车辆复杂网络路径选择问题分别提出对应的求解算法:针对单车辆简单网络路径选择,将期望行程时间、预测行程时间、行程时间可靠性与时间窗进行比对,生成3段路径优化选择算法;针对单车辆复杂网络路径选择问题,提出一个全新的权值异化型Dijkstra算法进行求解,并验证可行。
1 随机动态行程时间预测模型根据集散波理论[16],将t时刻路段a及下游信号交叉口的行程时间Ta(t)分为两段[17-18]:路段非拥挤区段的行程时间ra(t)及排队区段的行程时间da(t)。
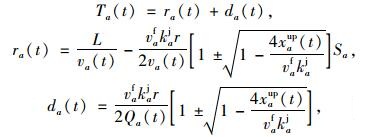
|
(1) |
式中,L为路段长度;r为红灯时长;Sa为标准小汽车的平均空间长度;Qa(t)为交叉口通行能力;vfa为自由流速度;kaj为阻塞密度;xaup(t)为上游驶入流量。
1.1 动态路段行程时间预测如图 1所示,O点为路段起点, D点为含下游交叉口的路段终点。目标车辆在路段下游红灯信号亮起时进入路段,根据第n次红灯信号结束时,该车辆位置(T点、K点或L点)与下游排队队尾(K点)的相对位置关系,分析后续车辆及车流运行状态,进行行程时间分情况预测。各状态预测行程时间见表 1。
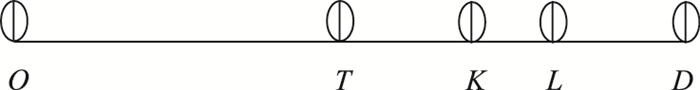
|
| 图 1 路段关键点相对位置图示 Fig. 1 Relative positions of key points of section |
| |
| 序号 | 位置 | 车辆状态 | 行为分析 | 预测行程时间 |
| 1 | T | 车队消散,直接通过 | 以速度va(t)两兼通过全程 | 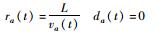 |
| 2 | T | 车队消散,处于停车线 | 等待一次红灯后通过 | 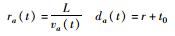 |
| 3 | T | 部分消散,位于队尾L | 下一次绿灯时排队通过 | 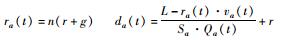 |
| 4 | T | 部分消散,位于队尾L | 接下来第m次绿灯时通过 | 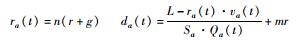 |
| 5 | K | 车队消散,位于队尾K | 绿灯结束刚好通过 | ra(t)=nr+(n-1)g da(t)=g |
| 6 | K | 车队消散, 位于队尾K | 绿灯结束前通过 | 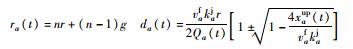 |
| 7 | K | 部分消散,位于队尾L | n=1,下m次绿灯时通过 |  |
| 8 | K | 部分消散,位于队尾K | n>1,下m次绿灯时通过 | 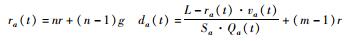 |
| 9 | L | 车队消散,位于L | n=1,直接通过 | 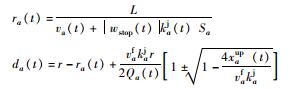 |
| 10 | L | 部分消散,位于L | n=1,下m次绿灯时通过 | 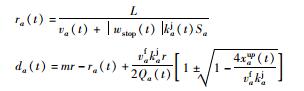 |
| 11 | L | 车队消散,位于L | n>1,直接通过 | 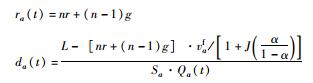 |
| 12 | L | 部分消散,位于L | n>1,下m次绿灯时通过 | 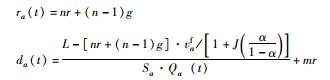 |
注:va(t)为非拥挤状态下t时刻的车辆行驶速度, 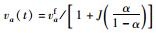 ,其中α为服务水平; J为服务水平参数;t0为车辆停车、启动后通过下游交叉口的延误时间; g为绿灯时长; wstop(t)为t时刻的停车波波速。 ,其中α为服务水平; J为服务水平参数;t0为车辆停车、启动后通过下游交叉口的延误时间; g为绿灯时长; wstop(t)为t时刻的停车波波速。 |
||||
1.2 动态路径行程时间及可靠性预测
设路径行程时间Ti(t)为路径上各路段行程时间之和。
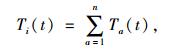
|
(2) |
式中a为构成路径i的各条路段编号。
预测行程时间为考虑路网及交通流随机性的与时刻t相关的行程时间,将该预测行程时间与期望行程时间之比在可接受水平之内的概率称为随机动态行程时间可靠性。
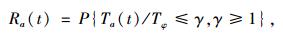
|
(3) |
式中,Ra(t)为随机动态路段行程时间可靠性;Tφ为期望行程时间;γ为可接受水平。对于可接受水平γ的取值,根据本研究对期望行程时间、预测行程时间的设定,由于预测行程时间需要考虑路网的随机动态特征,相关变量多达28个,而期望行程时间的约束条件较少,对期望行程时间的估计值偏小,因此设定γ取值范围为γ∈[2, 3]。
路径行程时间可靠性为各构成路段行程时间可靠性之积:
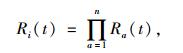
|
(4) |
式中a为构成路径i的各条路段编号。
2 单车辆简单网络路径选择算法对于单车辆简单网络路径选择,已有算法[2, 6, 9-10]多将行程时间作为路径选择的关键变量,然而在拥挤网络条件下,出行者关注的重点除了行程时间,还有行程时间可靠性。基于此,提出以下算法:将行程时间及行程时间可靠性综合考虑,同时作为路径选择的依据。步骤如下:
路径集合表示为PS,且PS={i|i=1, 2, …, n},其中i表示第i条路径;“∨i”、“∧i”为扎德算子,其中“∨i”表示各元素中取大值、“∧i”表示各元素中取小值。
2.1 预判阶段比较各路径期望行程时间Tφi与时间窗上界Tmax(一般根据历史经验设定,为预期中通过该路径的最大行程时间与根据工作计划留给完成该路径的行程时间的权衡值),按照以下规则进行路径选择:
(1) 若期望行程时间都在时间窗内,则选择期望行程时间较短的路径为选择方案;
(2) 若某一条路径的期望行程时间在时间窗内,其他皆在时间窗外,则选择期望行程时间在时间窗内的路径;
(3) 若期望行程时间都在时间窗外,则认为没有可选方案,需重新界定时间窗。
算法如下:
(1) 若Tφi<Tmax, i=1, 2, …, n, 则PS={i|∧i=1nTφi};
(2) 若Tφi<Tmax, Tφj>Tmax, i, j=1, 2, …, n, i≠j,则PS={i};
(3) 若Tφi>Tmax, i=1, 2, …, n,则PS={φ}。
2.2 初选阶段预测行程时间Ti(t)为一预测值组,取其中的最大值Timax(t)、最小值Timin(t)为预测行程时间取值区间的上下界,即Ti(t)∈[Timin(t), Timax(t)],将预测行程时间最大值Timax(t)与时间窗上界Tmax进行比对,按照以下规则进行路径选择:
(1) 若预测行程时间最大值都在时间窗内,则选择期望行程时间最大值较小的路径为选择方案;
(2) 若某一条路径的预测行程时间最大值在时间窗内,其他皆大于时间窗上界,则选择预测行程时间最大值在时间窗内的路径;
(3) 若预测行程时间最大值都在时间窗外,则比较各条路径的预测行程时间集,选择集合中值在时间窗内的样本数占组内总样本数的比例大的路径。
算法如下:
(1) 若Timax(t)≤Tmax, i, j=1, 2, …, n,则PS={i|∧i-12Timax(t)};
(2) 若Timax(t)≤Tmax, Tjmax(t)>Tmax, i, j=1, 2, …, n, i≠j, 则PS={i};
(3) 若Timax(t)>Tmax, i=1, 2, …, n,则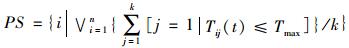
使用行程时间可靠性Ra(t)对路径选择方案的校核是在初选阶段的基础上进行的。
(1) 当预测行程时间最大值都在时间窗内,若预测行程时间最大值小的路径行程时间可靠性高,则选择该路径;若预测行程时间最大值大的路径行程时间可靠性高,对行程时间可靠性定义进行形式变换,得:Ra(t)=P{Ta(t)≤γTφ, γ≥1},可知,行程时间可靠性越高,预测行程时间小于期望行程时间的可接受倍数的可能性越高,即行程时间取得较小值的可能性越大。依据安全的前提下追求效率的原则,可以选择预测行程时间最大值大但行程时间可靠性高的路径。总之,若预测行程时间最大值都在时间窗内,则选择行程时间可靠性高的路径。
(2) 若某一条路径的预测行程时间最大值在时间窗内,其他皆在时间窗外,无论该路径的行程时间可靠性是否最高,根据优先满足时间窗的安全限制原则,皆选择该路径。
(3) 若预测行程时间最大值都在时间窗外,进一步检查各路径期望行程时间的某一可接受倍数是否都在时间窗,若均在时间窗内,则选择对应行程时间可靠性高的路径;若只有一条路径的该值在时间窗内,则选择该路径;若各路径的该值均超过时间窗上界,则需对时间窗修正后重新计算。
算法如下:
(1) 若Timax(t)≤Tmax, i=1, 2, …, n,则:PS={i|∧i=1nRa(t)};
(2) 若Timax(t)≤Tmax, Tjmax(t)>Tmax, i, j=1, 2, …, n, i≠j,则:PS={i};
(3) 若Timax(t)>Tmax, i=1, 2, …, n,则: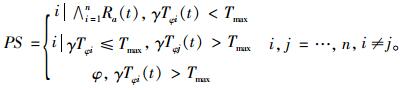
总之:3段选择模型,重点都在各路径行程时间均在时间窗内的选择问题上;一内一外情况下的选择很明确,皆选内;均在外的情况暂时可以进行路径选择,未来需调整时间窗。时间窗的调整需要结合预测行程时间与工作计划,保证调整后的时间窗上界大于预测的行程时间最大值。
3个阶段是递进关系,也是循序验证过程,最终路径的选择由修正阶段的结果确定。
2.4 案例分析两条路径选择案例,如图 2所示:LINE1:O-A-B-D;LINE2:O-C-D。
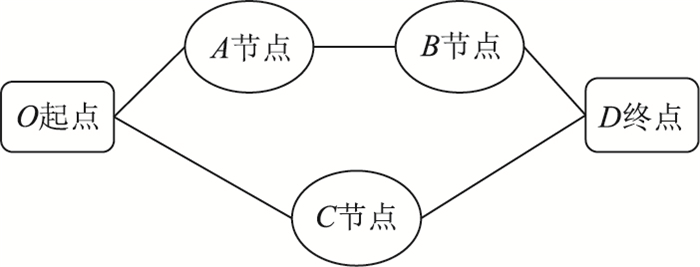
|
| 图 2 双路径数学模型 Fig. 2 Two-path mathematical model |
| |
假设D处未形成排队入场的情况。路径中各关键节点情况如表 2所示。
| 节点A | 节点B | 节点C |
| 无信号控制。虚拟周期30 s,东西向15 s,南北向15 s | 周期57 s,南北向绿灯30 s,东西向绿灯27 s | 周期73 s,南北向绿灯44 s,东西向绿灯29 s |
根据预测行程时间算法,给出各路段的预测行程时间集,如表 3所示。然后计算各路径行程参数,见表 4。
| 分类 | n | m | 预测行程时间/s | ||||
| OA | AB | BD | OC | CD | |||
| 1 | 1 | 1 | 27 | 78 | 42 | 67 | 88 |
| 2 | 1 | 1 | 42 | 105 | 42 | 96 | 88 |
| 3 | 1 | 1 | 29 | 131 | 42 | 80 | 88 |
| 4 | 1 | 2 | 44 | 158 | 42 | 109 | 88 |
| 5 | 2 | 1 | 60 | 114 | 42 | 146 | 88 |
| 6 | 2 | 1 | 57 | 125 | 42 | 129 | 88 |
| 7 | 1 | 1 | 42 | 95 | 42 | 85 | 88 |
| 1 | 2 | 57 | 122 | 42 | 114 | 88 | |
| 8 | 2 | 2 | 72 | 152 | 42 | 158 | 88 |
| 9 | 1 | 1 | 27 | 68 | 42 | 56 | 88 |
| 10 | 1 | 2 | 42 | 95 | 42 | 85 | 88 |
| 1 | 3 | 57 | 122 | 42 | 114 | 88 | |
| 11 | 2 | 1 | 57 | 125 | 42 | 128 | 88 |
| 12 | 2 | 2 | 87 | 179 | 42 | 186 | 88 |
| 路径 | 路段 | Tmax/s | Tφ/s | Ta(t)区间/s | Ra(t) |
| 1 | OA | [0, 350] | 27 | [27, 87] | 0.5 |
| AB | 78+27 | [68, 179] | 0.86 | ||
| BD | 42 | 42 | 1 | ||
| 2 | OC | 67+29 | [56, 186] | 0.79 | |
| CD | 88 | 88 | 1 |
| 路径 | Tmax/s | Tφ/s | 对比 | 判断 | 方案 |
| 1 | [0, 350] | 174 | Tφ1 < Tmax | Tφ1 < Tφ2 | √ |
| 2 | 184 | Tφ2 < Tmax | × |
| 路径 | Tmax/s | Ti(t)/s | 对比 | 判断 | 方案 |
| 1 | [0, 350] | 308 | T1max(t) < Tmax | T1max(t)> T2max(t) |
× |
| 2 | 274 | T2max(t) < Tmax | √ |
| 路径 | Tmax/s | Ti(t)/s | 对比 | Ri(t) | 判断 | 方案 |
| 1 | [0, 350] | 308 | T1max(t) < Tmax | 0.5 | R1(t)> R2(t) |
× |
| 2 | 274 | T2max(t) < Tmax | 0.79 | √ |
案例最终结果为各路径期望行程时间、预测行程时间均在时间窗内的情况。
在预判阶段,两条路径的期望行程时间均小于时间窗上界,而LINE1的期望行程时间较小,依据模型,本阶段路径选择为LINE1;
在初选阶段,两条路径的预测行程时间最大值均小于时间窗上界,而LINE2的预测行程时间最大值较小,依据模型,本阶段路径选择为LINE2;
在修正阶段,LINE2的行程时间可靠性更高,则依据模型,最终确认路径选择方案为LINE2。
3 单车辆复杂网络路径选择算法根据复杂网络的特性,设定车辆在路网中满足先进先出的运行规则,且车辆行驶在没有环路的路径上。
如图 3所示的复杂路网模型中用各路段的行程时间可靠性值作为路网模型中各边的权值,车辆由起点O点到达终点D点,点A,B,C,E代表交叉口,寻找最可靠路径。
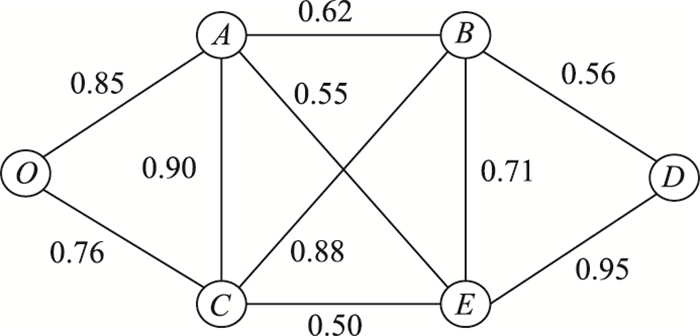
|
| 图 3 复杂路网模型 Fig. 3 Complex road network model |
| |
3.1 权值异化的Dijkstra算法
根据对数函数运算规则:正数积的对数,等于同一底数的这几个正数的对数和,而路径可靠性等于各组成路段的可靠性之积,则可转换为路径可靠性的对数值等于各路段可靠性的对数值之和。同时根据对数的单调性,求各路径可靠性中的最大值等价于求以小于1的正数为底的路径可靠性对数值中的最小值,从而将原问题变换为满足传统的最短路问题设定的模式,然后即可使用Dijkstra算法求解。将模型中各边权值以0.1为底进行对数变换后各边的权值如图 4所示。
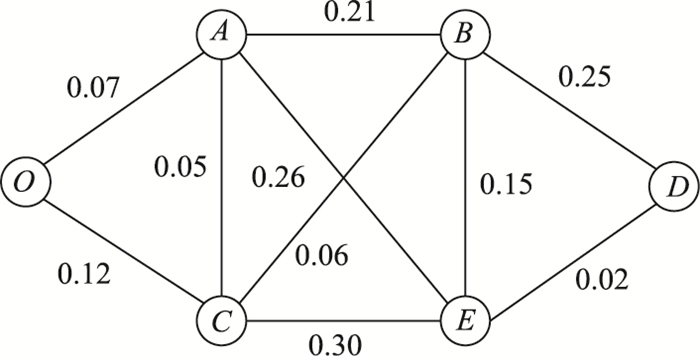
|
| 图 4 权值对数化复杂路网 Fig. 4 Weight value logarithmic complex road network |
| |
应用Dijkstra算法,求从O点到D点权值之和最小的路径,即最可靠路径,标号结果如图 5所示。由图 5可知,从O点到D点的路径可靠性对数值为0.35,根据标号过程逆推最可靠路径。
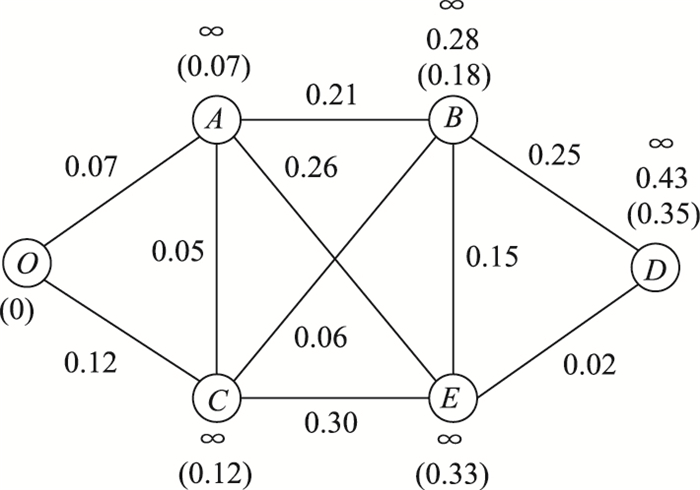
|
| 图 5 权值对数化复杂路网标号结果图 Fig. 5 Weight value logarithmic complex road network marking result |
| |
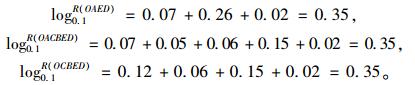
|
可见可靠性最高的路径有3条:OAED,OACBED,OCBED。
3.2 路径枚举法为了验证权值异化算法的有效性,对图 3所示路网用路径枚举法罗列出全部的路径,用构成路径的各路段可靠性之积作为路径行程时间可靠性,见表 8。
| 序号 | 路径 | 路段可靠性 | 路径可靠性 |
| 1 | OABD | 0.85×0.62×0.56 | 0.30 |
| 2 | OABED | 0.85×0.62×0.71×0.95 | 0.36 |
| 3 | OABCED | 0.85×0.62×0.88×0.5×0.95 | 0.22 |
| 4 | OAED | 0.85×0.55×0.95 | 0.45 |
| 5 | OAEBD | 0.85×0.55×0.71×0.56 | 0.19 |
| 6 | OACED | 0.85×0.9×0.5×0.95 | 0.36 |
| 7 | OACBD | 0.85×0.9×0.88×0.56 | 0.38 |
| 8 | OACBED | 0.85×0.9×0.88×0.71×0.95 | 0.45 |
| 9 | OCED | 0.76×0.5×0.95 | 0.36 |
| 10 | OCEBD | 0.76×0.5×0.71×0.56 | 0.15 |
| 11 | OCEABD | 0.76×0.62×0.55×0.5×0.56 | 0.07 |
| 12 | OCBD | 0.76×0.88×0.56 | 0.37 |
| 13 | OCBED | 0.76×0.88×0.71×0.95 | 0.45 |
| 14 | OCABD | 0.76×0.9×0.62×0.56 | 0.24 |
| 15 | OCAED | 0.76×0.9×0.55×0.95 | 0.36 |
| 16 | OCAEBD | 0.76×0.9×0.55×0.71×0.56 | 0.15 |
分析表 8,各路径中可靠性最大者为0.45,对应的路径有3条:OAED,OACBED,OCBED,取此可靠性值的对数,得log0.10.45=0.35。对比第3.1节的结果可知,由枚举法取得的最可靠路径与由权值异化的Dijkstra算法取得的最可靠路径结果一致。由此可见,本研究将权值异化后使用Dijkstra算法进行路径选择问题的求解是可行的。
同时,随着路网复杂度的增加,本算法在执行速度上呈现出明显的优势:当全连通的路网节点数达到20以上时,本算法运算耗时就远远低于枚举法;当节点数达到50以上,使用枚举法的执行时间就让人难以承受,而本算法依然可行。
因此,本研究提出的权值异化的Dijkstra算法是单车辆复杂网络路径选择问题求解的优化算法。
4 结论对于随机动态路网中单车辆的路径选择问题,综合考虑道路服务水平、随机动态路网的特性等道路信息,避免由于信息利用不全产生错误判断,本研究将随机动态行程时间可靠性纳入路径选择的判断标准中。
对于单车辆简单网络路径选择问题,本研究建立的3段选择算法,可以确保选取的路径在行程时间及行程时间可靠性两方面均达到最优。通过案例分析表明,本算法在保证取得高随机动态行程时间可靠性的同时,将行程时间限定在时间窗内,可有效降低出行时间损耗、提高出行效率。
对于单车辆复杂路网路径选择问题,本研究建立了权值异化的Dijkstra算法,为物流配送提供了一种高可靠性路径选择的优化算法,该算法方便高效。
由于随机动态复杂网络中,出行者对行程时间可靠性的要求高于对行程时间的要求,使用权值为行程时间可靠性的Dijkstra算法,一定程度上降低了对出行时间指标的要求。若在简单网络中使用权值异化的Dijkstra算法,无法针对时间窗的限制进行分析,可能将行程时间可靠性高但期望行程时间或预测行程时间过长的路径作为最优路径,与实际简单网络出行者对行程时间及行程时间可靠性的双重最优要求相悖。故在简单网络中使用3段选择算法更有效。
总之,基于随机动态行程时间可靠性,本研究建立的3段路径选择算法,对于结构简单的随机动态拥挤网络十分有效;本研究建立的权值异化Dijkstra算法,既考虑了复杂网络的随机动态性,又提高了路径选择算法的运行效率。
| [1] |
SIMON H A. Rational Decision Making in Business Organizations[J]. American Economic Review, 1979, 69(4): 493-513. |
| [2] |
GRANGIER P, GENDREAU M, LEHUÉDÉ F, et al. A Matheuristic Based on Large Neighborhood Search for the Vehicle Routing Problem with Cross-docking[J]. Computers & Operations Research, 2017, 84(C): 116-126. |
| [3] |
DU J, LI X, YU L, et al. Multi-depot Vehicle Routing Problem for Hazardous Materials Transportation:A Fuzzy Bilevel Programming[J]. Information Sciences, 2017, 399: 201-218. |
| [4] |
ALVAREZ A, MUNARI P. An Exact Hybrid Method for the Vehicle Routing Problem with Time Windows and Multiple Deliverymen[J]. Computers & Operations Research, 2017, 83: 1-12. |
| [5] |
HALL R W. The Fastest Path through a Network with Random Time-dependent Travel Times[J]. Transportation Science, 1986, 20(3): 182-188. |
| [6] |
SWIHART M R, PAPASTAVROU J D. A Stochastic and Dynamic Model for the Single-vehicle Pick-up and Delivery Problem[J]. European Journal of Operational Research, 1999, 114(3): 447-464. |
| [7] |
CHABINI I, LAN S. Adaptations of the A* Algorithm for the Computation of Fastest Paths in Deterministic Discrete-time Dynamic Networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2002, 3(1): 60-74. |
| [8] |
FU L, RILETT L R. Expected Shortest Paths in Dynamic and Stochastic Traffic Networks[J]. Transportation Research Part B:Methodological, 2008, 32(7): 499-516. |
| [9] |
CHAI H, ZHANG H M, GHOSAL D, et al. Dynamic Traffic Routing in a Network with Adaptive Signal Control[J]. Transportation Research Part C:Emerging Technologies, 2017, 85: 64-85. |
| [10] |
TILK C, ROTHENBÄCHER A K, GSCHWIND T, et al. Asymmetry Matters:Dynamic Half-way Points in Bidirectional Labeling for Solving Shortest Path Problems with Resource Constraints Faster[J]. European Journal of Operational Research, 2017, 261(2): 530-539. |
| [11] |
石小法, 王炜, 卢林, 等. 交通信息影响下的动态路径选择模型研究[J]. 公路交通科技, 2000, 17(4): 35-37. SHI Xiao-fa, WANG Wei, LU Lin, et al. Study on Dynamic Route Choice Model with Travel Information[J]. Journal of Highway and Transportation Research and Development, 2000, 17(4): 35-37. |
| [12] |
张安英, 孙全欣, 韦伟, 等. 动态路阻下的出行时间预测和路径选择模型[J]. 公路与汽运, 2014(2): 48-52. ZHANG An-ying, SUN Quan-xin, WEI Wei, et al. Travel Time Prediction and Route Choice Model under Dynamic Path Obstruction[J]. Highways & Automotive Applications, 2014(2): 48-52. |
| [13] |
张梦颖.不确定因素下路径规划问题研究[D].合肥: 中国科学技术大学, 2016. ZHANG Meng-ying. Vehicle Routing Problems with Uncertain Factors[D]. Hefei: University of Science and Technology of China, 2016. |
| [14] |
任小聪, 向红艳, 陈坚. 交通事故信息对路径选择行为的影响建模与分析[J]. 公路交通科技, 2016, 33(7): 103-107. REN Xiao-cong, XIANG Hong-yan, CHEN Jian. Modeling and Analysis of Influence of Traffic Accident Information on Route Choice Behavior[J]. Journal of Highway and Transportation Research and Development, 2016, 33(7): 103-107. |
| [15] |
苏贞旅, 周和平, 陶亭. 大数据下基于出发时刻的动态最短路[J]. 长沙理工大学学报:自然科学版, 2017, 14(3): 35-40. SU Zhen-lü, ZHOU He-ping, TAO Ting. Dynamic Shortest Path Based on Departure Time under Big Data[J]. Journal of Changsha University of Science and Technology:Nature Science Edition, 2017, 14(3): 35-40. |
| [16] |
王殿海. 交通流理论[M]. 北京: 人民交通出版社, 2002. WANG Dian-hai. Traffic Flow Theory[M]. Beijing: China Communications Press, 2002. |
| [17] |
宋博文, 张俊友, 李庆印, 等. 基于交通波理论的改进动态路阻函数[J]. 重庆交通大学学报:自然科学版, 2014, 33(1): 106-110. SONG Bo-wen, ZHANG Jun-you, LI Qing-yin, et al. Improved Dynamic Road Impedance Function Based on Traffic Wave Theory[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2014, 33(1): 106-110. |
| [18] |
王荣彦.城市交通流诱导系统动态路阻函数及最优路径算法研究[D].西安: 长安大学, 2008. WANG Rong-yan. Study on Dynamic Impedance Functions and Routing Optimizing Methods for City Traffic Flow Guidance System[D]. Xi'an: Chang'an University, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1527015 |
 2018, Vol. 35
2018, Vol. 35
