扩展功能
文章信息
- 温廷新, 于凤娥, 邵良杉, 田煜晨
- WEN Ting-xin, YU Feng-e, SHAO Liang-shan, TAN Yu-chen
- 基于GA-SVM的隧道围岩分类研究
- Study on Classification of Tunnel Surrounding Rock Based on GA-SVM
- 公路交通科技, 2018, 35(9): 63-70
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(9): 63-70
- 10.3969/j.issn.1002-0268.2018.09.010
-
文章历史
- 收稿日期: 2017-03-08
2. 辽宁工程技术大学 工商管理学院, 辽宁 葫芦岛 125105
2. School of Business Administration, Liaoning Technical University, Huludao Liaoning 125105, China
随着国内外岩体工程的迅速发展,深部采矿工程、隧道工程、城市地下工程以及各类水利水电工程等大量工程项目正在建设或即将开工建设[1]。在地下岩体施工过程中,围岩类别的确定既有利于采取合理的设计和工程处理措施,又对地下工程的稳定性、安全性起着至关重要的作用。
随着地下洞室工程建设的增多,复杂地质条件及动力条件下的围岩稳定性分类问题受到了国内外众多学者的高度关注[2]。国外的围岩分类方法有很多种,如Barton的Q分类体系[3]和Bieniawski的岩体质量指标分类(RMR)[4]等。Q分类体系基本上是一个定性的分类方法,而RMR是一个半定量、半定性方法,二者使用参数较多,并用数学公式来表达,且均需要有经验的地质人员参与,主观随意性较大。我国在工程实践中主要是采用《水利水电工程地质勘察规范》(GB50287—99)中的T系统分类[5]及《工程岩体分级标准》(GB 50218—94)的BQ分级[6]。然而,在施工过程中常常需要迅速判别岩体类型以便采用合理的工程处理措施,若根据分级标准和规范来判别岩体类型会降低施工效率,故其使用具有一定的局限性。近些年,诸多学者采用多种地质因素组合来判别岩体类型,如BP神经网络法[7]、模糊综合评判法[8]、特尔菲-理想点法[9]、非线性耦合分类技术[10]、Bayes判别分析法[11]、Fisher判别分析法[12]、距离判别分析[13]等多个指标的综合判别方法。上述方法都有较高的工程应用价值,同时也存在一定的局限性,如BP神经网络结构不易确定,算法存在易陷入局部极小值的缺陷,对解决小样本问题能力有限;模糊综合评判法在确定各指标权重时,主要依靠经验判断或专家评定,具有较大的波动性、随意性;Fisher判别分析法虽然对总体的分布不做任何要求,但对于线性不可分的样本很难确定分类。此外,围岩分类是一个受多种因素影响的复杂非线性系统,且研究样本数量有限,因此有必要建立一种适用于多影响因素、小样本、非线性的综合预测模型。
基于此,笔者采用因子分析对围岩类别评价指标进行降维处理,提取公共因子,从而简化预测模型的输入,提高围岩分类的效率。针对支持向量机(SVM)核函数受Mercer条件限制,且存在核函数构建及参数选择较为困难等不足,结合遗传算法的高效、并行、全局寻优能力强等优势,对SVM的惩罚函数C和核函数参数σ进行寻优,并将提取出的公共因子作为GA-SVM模型的输入变量,由此建立基于因子分析的GA-SVM隧道围岩分类模型,并将其进行实际应用,证明该模型的安全性与可靠性。
1 相关理论基础 1.1 因子分析因子分析(Factor Analysis,FA)是多元统计分析中对高维数据进行降维的一种统计方法,即将研究对象中多个具有相关关系的变量浓缩成少数几个具有不相关关系的指标变量,也称公共因子。将彼此相关的意义单一的指标变量转变为彼此不相关的意义综合的少数几个指标变量,主要运用正交变换思想,保留有显著贡献的特征向量。原始观测变量被分解为公因子的线性组合,即:
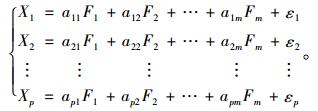
|
(1) |
由式(1)可得该数学模型的矩阵形式:

|
(2) |
式中,X=(X1, X2, …, Xp)T为可实测的随机向量;F=(F1, F2, …, Fm)T为公共因子,且公因子F1, F2, …, Fm相互独立且不可观测;A=(aij)p×m为因子载荷矩阵,因子载荷aij为在各个因子变量不相关的情况下,第i个原始观测变量与第j个因子变量的相关系数,反映了第i个原始观测变量在第j个因子变量上的重要性,aij的绝对值越大,说明原始观测变量Xi与因子变量Fj的关系就越强;ε=(ε1, ε2, …, εp)T为特殊因子,即表示原始观测变量不能被因子变量解释的部分,且彼此之间互不相关。
1.2 遗传算法遗传算法(Genetic Algorithm,GA)是美国J. Holland教授1975年提出的一种基于生物界进化规律进行计算机模拟而发展起来的随机搜索的优化方法[14]。不同于传统优化算法,它是借鉴生物学的自然选择和遗传机制,以种群搜索和种群中个体(染色体)之间的信息交换为策略的高效随机搜索方法。其主要特点是采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,而不需要确定规则。
1.3 支持向量机支持向量机(SVM)是由Vapnik等提出的一种研究小样本、小概率事件的神经网络模型[15],其基本思想是通过一个非线性映射,把输入空间的数据映射到一个高维特征空间,将实际问题转化为一个带不等式约束的二次规划问题[16]。通过有限样本学习训练,采用结构风险最小化原则,保证获得全局最优解,能较好地解决非线性、高维数等小样本问题。
若训练样本集为(x, y),φ(°),Rd,其中x={xi|i=1,2,…,n}为输入样本集,xi表示第i个输入样本;y={yj|j=1,2,…,n}为输出样本集,yj表示第j个输出样本;Rd为输入空间,R为输出空间。用一非线性映射ϕ(°)将样本的输入空间Rd映射到特征空间ϕ(x)=[ϕ(x1), ϕ(x2),…,ϕ(xn)], 然后在高维特征空间中构造最优决策函数:
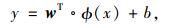
|
(3) |
式中,w为权值向量;b为偏置量。
根据结构风险最小化原则,SVM的优化问题可表示为:

|
(4) |

|
(5) |
式中,C>0为惩罚参数;ξi为松弛变量。
用Lagrange方法求解这个优化问题,即:

|
(6) |

|
(7) |
式中,α={α1,α2,…,αm}为解向量; αi和αj为解向量的元素;K(xi, xj)为核函数,若K为正定核函数,则一定存在最优解α*={α1*, α2*, …, αm*},使得:
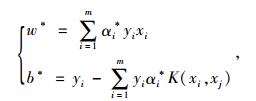
|
(8) |
式中w*, b*为式(8)的最优解。
将最优解带到分类函数式:
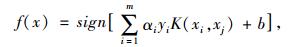
|
(9) |
便可实现对样本的分类。
1.4 GA优化SVM根据遗传算法优化原理和SVM分类模型,提出GA优化SVM惩罚函数C和核函数参数σ的方法。具体步骤如下:
Step 1:数据预处理。对训练样本和测试样本进行归一化处理,消除原始变量之间的量纲差异。
Step 2:染色体编码与种群初始化。对SVM的惩罚函数C和核函数参数σ进行二进制编码,并随机产生初始化种群。
Step 3:解码与适应度函数的确定。对种群中的各染色体解码,获取C及σ的值,再用训练样本对SVM进行训练,并用训练好的SVM计算测试样本集的预测精度E,由预测精度E构造种群个体的适应度函数。
Step 4:判断优化过程是否满足遗传算法的终止条件(最大进化代数),若满足终止条件,则停止计算,输出最优参数组合,转向Step 5;否则进行选择、交叉、变异等操作以产生新一代种群,并开始新一代遗传。
Step 5:将得到的最优参数惩罚因子C和核函数参数σ代入SVM模型中,对训练集进行训练。
Step 6:对测试集进行分类预测,得出预测分类准确率。
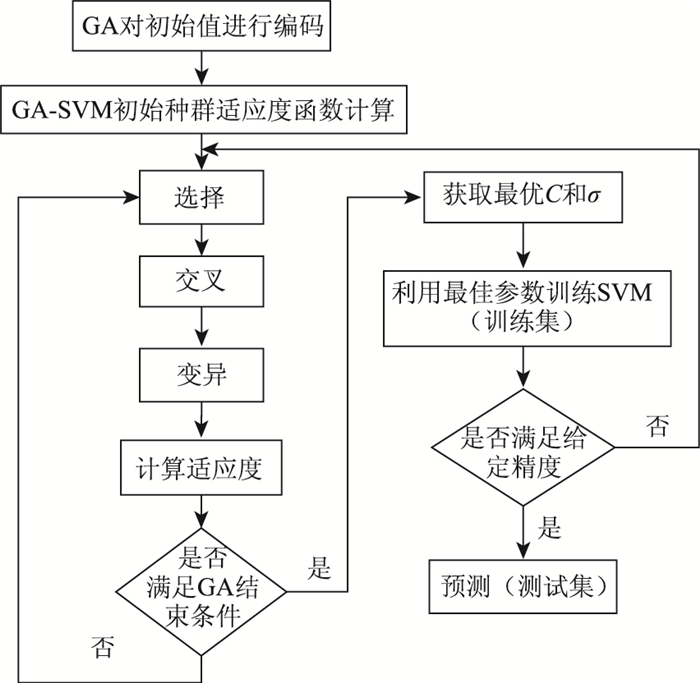
遗传算法优化SVM的具体流程见图 1。
|
| 图 1 GA优化SVM的流程 Fig. 1 Flowchart of SVM optimization by GA |
| |
2 基于因子分析的GA-SVM隧道围岩分类模型及应用 2.1 判别因子的选取
围岩稳定性分类是受诸多不确定因素影响与控制的复杂非线性问题。影响围岩稳定性的因素众多,大致可以概括为岩石性质、地质构造和岩体结构3类。根据《工程岩体分级标准》(GB 50218—94)及相关研究成果[17-18],遵循指标选取的重要性、独立性和易测性原则,选取岩石质量指标RQD(X1)、完整性系数Kv(X2)、单轴饱和抗压强度Rc(X3)、纵波波速Vp(X4)、弹性抗力系数Ko(X5)、结构面摩擦系数f(X6)6个判别指标作为分类影响因素。
(1) 岩石质量指标RQD是综合反映岩石完整程度和岩块大小的指标,该指标是利用钻孔的修正岩芯采取率来评价岩石质量的优劣。
(2) 完整性系数Kv反映了岩体结构特征,即岩体完整性程度。该指标一般可用弹性波探测岩体波速与岩块波速之比的平方表示,即:Kv=(Vpm/Vpr)2, 或采用岩体体积节理数Jv值根据表 1确定相应的Kv值[19]。
| Jv/(条·m-3) | Kv |
| < 3 | >0.75 |
| 3~10 | 0.75~0.55 |
| 10~20 | 0.55~0.35 |
| 20~35 | 0.35~0.15 |
| >35 | < 0.15 |
(3) 单轴饱和抗压强度Rc是基本力学属性之一,反映了岩块软硬特性及岩性特征,且点荷载试验是一种快速、经济并且有效的现场测定岩石强度的方法。
(4) 纵波波速Vp在一定程度上反映了岩体的完整程度及刚度特征。
(5) 弹性抗力系数Ko反映了围岩的综合物理力学性质,一般采用查表或者利用弹性公式来确定。
(6) 结构面摩擦系数f反映了结构面粗糙程度、蚀变及充填情况,是影响围岩稳定性的主要因素之一。
2.2 因子分析以广东省东江-深圳供水改造工程为研究背景,模型所用36组数据引自文献[18]。运用SPSS19.0统计软件对选取的6个指标变量进行Pearson相关性分析和因子分析检验。根据相关系数矩阵得出这6个指标变量间存在显著的相关关系,指标之间隐含着信息重叠。由KMO检验和Bartlett球度检验结果(见表 2)可知,样本的KMO值为0.844,Bartlett球度检验给出的Sig.值为0.000,小于显著性水平0.01,通过统计检验,认为适合做因子分析。以上两个检验结果都表明这6个指标变量可通过因子分析处理以实现降维的目的。
| KMO样本测度 | 0.844 | |
| Bartlett球形检验 | 卡方值 | 217.871 |
| 自由度 | 15 | |
| Sig.值 | 0.000 | |
根据实际需要,将RQD,Kv,Rc,Vp,Ko和f这6个指标做因子分析处理,得到公共因子总方差解释表(见表 3)、因子载荷矩阵(见表 4)。
| 序号 | 特征值 | 贡献率/% | 累计贡献率/% |
| 1 | 5.116 | 85.261 | 85.261 |
| 2 | 0.403 | 6.718 | 91.979 |
| 3 | 0.191 | 3.192 | 95.171 |
| 4 | 0.188 | 3.127 | 98.298 |
| 5 | 0.067 | 1.119 | 99.418 |
| 6 | 0.035 | 0.582 | 100.000 |
| 指标 | F1 | F2 |
| 岩石质量指标RQD | 0.892 | 0.338 |
| 完整性系数Kv | 0.770 | 0.555 |
| 单轴饱和抗压强度Rc | 0.416 | 0.873 |
| 纵波波速Vp | 0.786 | 0.573 |
| 弹性抗力系数Ko | 0.433 | 0.879 |
| 结构面摩擦系数f | 0.652 | 0.663 |
由表 3可知,若采用主成分抽取方法提取特征根大于1的公因子,只能提取出1个公因子,累计方差贡献率为85.261%。为了降低信息损失的程度,提取前两个公因子可使累计方差贡献率达到91.979%,即前2个公因子可解释原始指标变量91.979%的信息,并将2个公因子分别记为F1和F2。
由于初始因子综合性太强,难以凸显实际意义,故对因子载荷矩阵进行方差最大化旋转,使得每个因子上具有的最高载荷变量数最小,从而降低因子的综合性,并得到旋转后的因子载荷矩阵(表 4)。表 4中的数值绝对值的大小表明了公共因子变量与原始变量的相关程度,公共因子F1很好地解释了岩石质量指标RQD、完整性系数Kv、纵波波速Vp,公共因子F2充分地解释了单轴饱和抗压强度Rc、弹性抗力系数Ko、结构面摩擦系数f。最后运用Regression法计算各因子得分并列入表 5。
| 序号 | 评价指标 | 公共因子得分 | 实际结果 | 回判结果 | |||||||
| X1 | X2 | X3 | X4 | X5 | X6 | F1 | F2 | ||||
| 1 | 58 | 0.59 | 85 | 4 207 | 18 | 5 | -0.275 60 | 1.698 06 | Ⅱ | Ⅱ | |
| 2 | 75 | 0.55 | 55 | 3 700 | 5 | 3 | 1.127 33 | -0.868 19 | Ⅲ | Ⅲ | |
| 3 | 44.5 | 0.5 | 20 | 3 000 | 1 | 1.5 | 0.353 14 | -1.350 98 | Ⅳ | Ⅳ | |
| | | | | | | | | | | | |
| 27 | 66 | 0.42 | 68.5 | 3 580 | 8 | 4 | 0.197 16 | 0.161 37 | Ⅲ | Ⅲ | |
| 28 | 42 | 0.24 | 62.7 | 2 690 | 2.5 | 1.75 | -1.045 64 | -0.001 83 | Ⅳ | Ⅳ | |
| 29 | 25 | 0.27 | 18.5 | 2 500 | 3 | 2 | -1.063 06 | -0.427 58 | Ⅳ | Ⅳ | |
2.3 GA-SVM隧道围岩分类模型的构建
根据相关围岩分类标准及工程经验,将隧道围岩类型分为5类,即Ⅰ级、Ⅱ级、Ⅲ级、Ⅳ级、Ⅴ级,GA-SVM隧道围岩分类模型所用的数据源自文献[18]。选取表 5中的29组隧道围岩样本数据作为该模型的训练样本,另7组样本数据作为该模型的测试样本(见表 6)。在隧道围岩类型判别中,对岩体的6个判别指标进行因子分析,得到2个主要的判别指标F1和F2作为GA-SVM围岩分类模型的输入向量,将5个围岩类型作为输出向量,建立基于因子分析的GA-SVM隧道围岩分类模型。
| 序号 | RQD | Kv | Rc | Vp | Ko | f | 因子分析结果 | 预测结果 | ||||||
| F1 | F2 | 实际类别 | 本文方法 | SVM模型 | BPNN模型 | Fisher判别法 | ||||||||
| 1 | 25 | 0.17 | 6.3 | 2 300 | 1 | 0.75 | -1.082 44 | -1.455 52 | Ⅴ | Ⅴ | Ⅴ | Ⅴ | Ⅴ | |
| 2 | 42 | 0.45 | 62.4 | 3 681 | 10 | 4 | -0.408 26 | 0.175 36 | Ⅲ | Ⅲ | Ⅲ | Ⅲ | Ⅲ | |
| 3 | 75 | 0.57 | 82.9 | 4 145 | 10 | 4 | 0.45936 | 0.010 44 | Ⅲ | Ⅲ | Ⅲ | Ⅲ | Ⅲ | |
| 4 | 94 | 0.71 | 81.5 | 4 631 | 18 | 5.5 | 1.194 76 | 0.332 05 | Ⅱ | Ⅱ | Ⅱ | Ⅲ* | Ⅱ | |
| 5 | 68 | 0.52 | 120 | 3 980 | 18 | 5.5 | -0.538 56 | 1.775 84 | Ⅱ | Ⅱ | Ⅱ | Ⅱ | Ⅱ | |
| 6 | 80 | 0.69 | 60 | 4 567 | 10 | 4 | 1.341 43 | -0.762 20 | Ⅲ | Ⅲ | Ⅱ* | Ⅲ | Ⅲ | |
| 7 | 25 | 0.36 | 62.4 | 3 300 | 3.5 | 3 | -0.966 29 | -0.075 97 | Ⅳ | Ⅳ | Ⅳ | Ⅳ | Ⅳ | |
| 注:*代表误判的样本。 | ||||||||||||||
根据GA-SVM的计算原理,利用LIBSVM工具箱,基于Matlab 2012b平台编程训练。首先将核函数K设置为径向基(Radial Basis Function,RBF)类型,为降低整个模型的计算复杂度,采用RBF核函数将2个输入向量投影到一个高维空间进行分析。为使GA-SVM模型的预测精度更高,需要对RBF核函数的参数σ和惩罚函数C进行优化选取。将这两个参数代入遗传算法中,同时,以所得到的2个公共因子F1和F2作为输入层的行向量对应于GA算法中一个染色体。为消除原始变量之间的量纲差异,要对原始数据进行预处理,即通过实数编码的方式将所有的染色体整体归一化到[0, 1]范围。同时,相关参数设置为:初始化种群规模sizepop=20,种群中个体的交叉概率Γ=0.7,变异概率φ=0.01,将GA模型优化后的参数σ和惩罚项C代入SVM模型,并选择其预测精度作为GA模型的适应度函数E。为保证GA算法的收敛性,将遗传算法的终止条件设定为最大进化代数,最大进化代数设置为maxgen=200。通过不同种群之间的选择交叉和种群内个体之间的交叉变异,所有数据向全局最优解迭代进化,最终得到全局最优解。
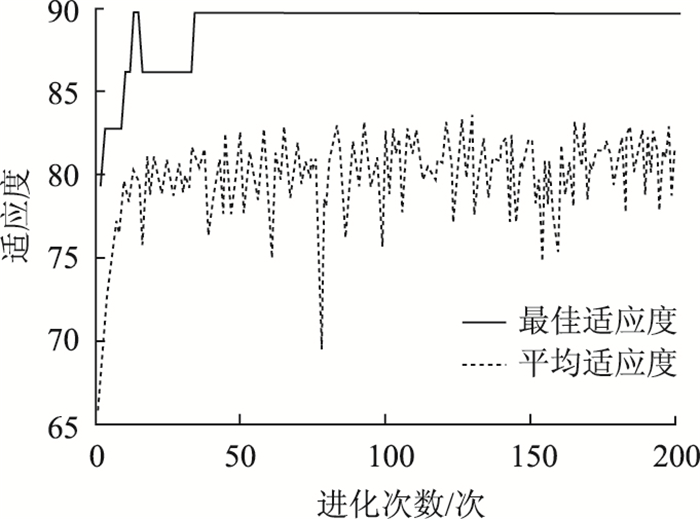
在模型的训练过程中,随着迭代次数的增加,GA优化SVM预测模型的参数经过200次进化,逐渐得到一个最佳适应度的稳定迭代值,见图 2。
|
| 图 2 遗传算法适应度曲线 Fig. 2 Fitness curve of genetic algorithm |
| |
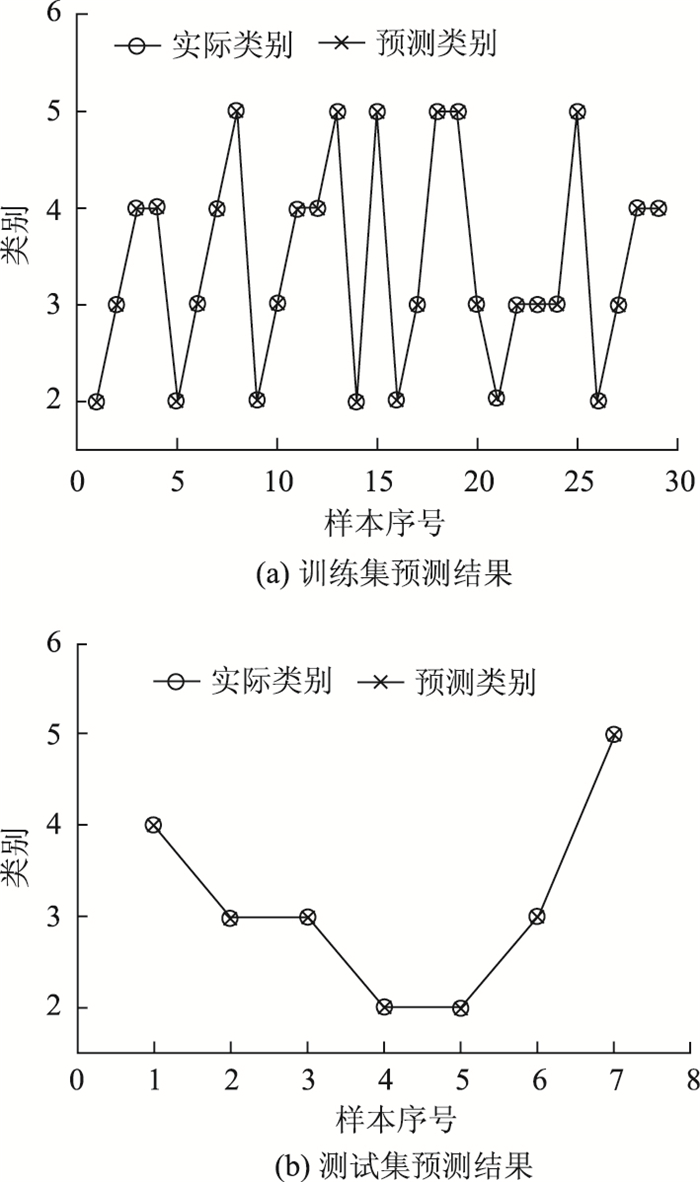
由图 2可知,GA-SVM模型的最优惩罚函数和核函数参数的值分别为C=10.729 8和σ=1.935。将得到的最优参数C和σ代入SVM模型,用29组训练样本数据进行训练,得到训练集的预测结果如图 3(a)所示。利用训练好的GA-SVM模型对测试集(表 6)进行预测分类,预测结果如图 3(b)所示。
|
| 图 3 训练集和测试集预测结果 Fig. 3 Prediction results of training set and testing set |
| |
由图 3可知,训练集预测结果与围岩实际类型完全一致,其回代误判率为0,证明GA-SVM模型在隧道围岩分类问题上具有较高的准确率和较好的稳定性。由此可见,可将该模型运用到实际的工程项目中。
2.4 不同模型预测效果对比为验证GA-SVM模型是否较其他智能算法模型在隧道围岩分类方面具有优越性,将常用的SVM模型、BP神经网络(BPNN)的预测结果与之进行比较,比较结果见表 6。其中,SVM模型、BPNN模型的输入是未经过因子分析处理的原始数据,并设置BP神经网络的输入层节点数为6,代表 6个判别指标的输入,隐含层的节点数设为10,输出层的节点数设为5,表示含义分别为:1-0-0-0-0(Ⅰ级)、0-1-0-0-0(Ⅱ级)、0-0-1-0-0(Ⅲ级)、0-0-0-1-0(Ⅳ级)、0-0-0-0-1(Ⅴ级),由此构建结构为6-10-5的BP神经网络。SVM模型相关参数设置为:kernel_type=’RBF_kernel’,cost=1,eps=10-3,degree=3。
根据对比结果(见表 6)可知,GA-SVM模型的预测结果与实际围岩类型完全吻合,但另两个模型预测结果与围岩实际类型存在一定的出入。在BPNN模型中,将4号围岩样本错判为Ⅲ级;在SVM模型中,将6号样本错判为Ⅱ级。从整体的预测精度分析,GA-SVM的误判率为0,低于其他2种预测模型的误判率。由此证明GA-SVM预测模型在隧道围岩分类方面具有较强的适用性。同时,将GA-SVM模型的预测结果与文献[18]中所用Fisher判别方法的判别结果进行比较,其判别结果与实际类别也完全吻合,准确率为100%。然而对于线性不可分的样本,Fisher判别分析很难具有普遍性的优异分类效应。由此可证,基于因子分析建立的GA-SVM隧道围岩分类模型安全可靠,能够实现对隧道围岩快速、有效的分类。
3 结论(1) 将统计学理论及机器学习算法应用于隧道围岩分类问题中,提出了基于因子分析的GA-SVM隧道围岩分类模型。应用因子分析理论对隧道围岩类别的6个判别指标进行分析得到2个公共因子,减少了指标间的冗余信息,简化了GA-SVM模型预测过程的工作量,提高了预测的效率。同时,由判别指标的相关性分析可知,岩石质量指标RQD、完整性系数Kv、单轴饱和抗压强度Rc、纵波波速Vp、弹性抗力系数Ko和结构面摩擦系数f这6个指标间相关性较强。
(2) 经因子分析得到的公共因子F1和F2作为GA-SVM模型的输入向量,构建了基于因子分析的GA-SVM隧道围岩分类模型。训练及测试对比结果显示,该模型在判别隧道围岩类型中具有较好的稳定性和较高的准确率,能较快找到全局最优解,泛化能力强,能够快速、有效地判别围岩类别。因此,该模型适用于隧道围岩分类问题。
(3) 笔者只是初步尝试了将基于因子分析的GA-SVM模型应用于隧道围岩分类问题中,有些问题还需进一步深入研究。在后续工作中,将更加全面地收集岩体的物理指标参数,分析提取出更为有效的判别因子,并对遗传算法的更新策略提出改进,使GA-SVM隧道围岩分类模型能有更快的收敛速度和更强的预测能力。
| [1] |
邢猛, 李连崇. 隧洞围岩损伤演化与时效破坏过程的模拟分析[J]. 地下空间与工程学报, 2017, 13(3): 703-710. XING Meng, LI Lian-chong. Numerical Analysis on Damage Evolution and Time-dependent Failure of Rock Surrounding Underground Tunnel[J]. Chinese Journal of Underground Space and Engineering, 2017, 13(3): 703-710. |
| [2] |
刘耀儒, 武哲书, 何柱, 等. 基于非线性动力分析的隧洞稳定性评价[J]. 岩石力学与工程学报, 2017, 36(增1): 3156-3163. LIU Yao-ru, WU Zhe-shu, HE Zhu, et al. Stability Evaluation of the Tunnels Based on Nonlinear Dynamic Analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(S1): 3156-3163. |
| [3] |
BARTON N, LIEN R, LUNDE J. Engineering Classification of Rock Masses for the Design of Tunnel Support[J]. Rock Mechanics, 1974, 6(4): 189-236. |
| [4] |
BIENIAWSKI Z T. Engineering Rock Mass Classifications:A Complete Manual for Engineers and Geologists in Mining, Civil and Petroleum Engineering[J]. Petroleum, 1976, 251(3): 357-365. |
| [5] |
GB 50287-99, 水利水电工程地质勘察规范[S]. GB 50287-99, Code for Water Resources and Hydropower Engineering Geological Investigation[S]. |
| [6] |
GB50218-94, 工程岩体分级标准[S]. GB50218-94, Standard for Engineering Classification of Rock Masses[S]. |
| [7] |
段林娣, 宋成辉. 应用BP神经网络进行隧道围岩快速分级[J]. 中国安全科学学报, 2010, 20(2): 41-45. DUAN Lin-di, SONG Cheng-hui. Application of BP Neural Network in the Rapid Classification of Surrounding Rock[J]. China Safety Science Journal, 2010, 20(2): 41-45. |
| [8] |
吴相金, 龚建平. 公路隧道围岩分类模糊综合评判[J]. 公路交通科技, 2007, 24(1): 118-125. WU Xiang-jin, GONG Jian-ping. Fuzzy Comprehensive Assessment for Highway Tunnel Surrounding Rock Classification[J]. Journal of Highway and Transportation Research and Development, 2007, 24(1): 118-125. |
| [9] |
王迎超, 孙红月, 尚岳全, 等. 基于特尔菲-理想点法的隧道围岩分类研究[J]. 岩土工程学报, 2010, 32(4): 651-656. WANG Ying-chao, SUN Hong-yue, SHANG Yue-quan, et al. Classification of Surrounding Rock Based on Delphi Method and Ideal Point Method[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(4): 651-656. |
| [10] |
余伟健, 高谦, 韩阳, 等. 非线性耦合围岩分类技术及其在金川矿区的应用[J]. 岩土工程学报, 2008, 30(5): 663-669. YU Wei-jian, GAO Qian, HAN Yang, et al. Non-linear Coupling Classification Technique of Surrounding Rock Mass and Its Application in Jingchuan Mine[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(5): 663-669. |
| [11] |
李春萍, 郝会兵. 煤巷围岩分类的Bayes判别分析法[J]. 煤炭学报, 2011, 36(2): 304-307. LI Chun-ping, HAO Hui-bing. Method of Bayes Discriminant Analysis for Classifying Mine-lane Surrounding Rocks[J]. Journal of China Coal Society, 2011, 36(2): 304-307. |
| [12] |
姜春露, 姜振泉, 孙强. 基于Fisher判别分析法的隧洞围岩分类[J]. 煤炭学报, 2012, 37(10): 1665-1670. JIANG Chun-lu, JIANG Zhen-quan, SUN Qiang. Classification of Rocks Surrounding Tunnel Using Fisher Discriminant Analysis Method[J]. Journal of China Coal Society, 2012, 37(10): 1665-1670. |
| [13] |
宫凤强, 李夕兵. 距离判别分析法在岩体质量等级分类中的应用[J]. 岩石力学与工程学报, 2007, 26(1): 190-194. GONG Feng-qiang, LI Xi-bing. Application of Distance Discriminant Analysis Method to Classification of Engineering Quality of Rock Masses[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(1): 190-194. |
| [14] |
刘希亮, 赵学胜, 陆锋, 等. 基于GA-SVM的露天矿抛掷爆破抛掷率预测[J]. 煤炭学报, 2012, 37(12): 1999-2005. LIU Xi-liang, ZHAO Xue-sheng, LU Feng, et al. A GA-SVM Based Model for Throwing Rate Prediction in the Open-pit Cast Blasting[J]. Journal of China Coal Society, 2012, 37(12): 1999-2005. |
| [15] |
温廷新, 孙红娟, 徐波, 等. 矿区采空塌陷危险性预测的RS-SVM模型[J]. 中国安全科学学报, 2015, 25(10): 16-21. WEN Ting-xin, SUN Hong-juan, XU Bo, et al. RS-SVM Model for Predicting Underground Goaf Collapse Risk[J]. China Safety Science Journal, 2015, 25(10): 16-21. |
| [16] |
龙文, 梁昔明, 龙祖强, 等. PSO-LSSVM灰色组合模型在地下水埋深预测中的应用[J]. 系统工程理论与实践, 2013, 33(1): 243-248. LONG Wen, LIANG Xi-ming, LONG Zu-qiang, et al. LSSVM Grey Combined Forecasting Model Based on PSO and Its Application in Groundwater Dynamic Prediction[J]. Systems Engineering-Theory & Practice, 2013, 33(1): 243-248. |
| [17] |
周翠英, 张亮, 黄显艺. 基于改进BP网络算法的隧洞围岩分类[J]. 地球科学-中国地质大学学报, 2005, 30(4): 480-486. ZHOU Cui-ying, ZHANG Liang, HUANG Xian-yi. Classification of Rocks Surrounding Tunnel Based on Improved BP Network Algorithm[J]. Earth Science-Journal of China University of Geosciences, 2005, 30(4): 480-486. |
| [18] |
邵良杉, 徐波. 基于因子分析与Fisher判别分析法的隧洞围岩分类研究[J]. 公路交通科技, 2015, 32(7): 98-119. SHAO Liang-shan, XU Bo. Research on Research on Classification of Tunnel Surrounding Rock Based on Factor Analysis and Fisher Discriminant Analysis[J]. Journal of Highway and Transportation Research and Development, 2015, 32(7): 98-119. |
| [19] |
李鹏远, 姜谙男. 公路隧道施工期围岩快速分类极限学习机模型研究[J]. 城市勘测, 2016(1): 149-153. LI Peng-yuan, JIANG An-nan. Study on the Extreme Learning Machine Model of Highway Tunnel Rapid Surrounding Rock Classification in Construction Phase[J]. Urban Geotechnical Investigation & Surveying, 2016(1): 149-153. |
 2018, Vol. 35
2018, Vol. 35
