扩展功能
文章信息
- 沈翔, 王达磊
- SHEN Xiang, WANG Da-lei
- 风障对平行梁桥面风环境的改善作用研究
- Effect of Wind Barrier on Improvement of Wind Environment above Parallel Girders
- 公路交通科技, 2018, 35(9): 49-55
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(9): 49-55
- 10.3969/j.issn.1002-0268.2018.09.008
-
文章历史
- 收稿日期: 2017-05-10
侧风往往对车辆的行驶安全影响较大,基于社会效益与经济效益的双重考量,越来越多的车道两侧加装了风障。桥梁由于高于地面风环境更为复杂[1-4],因此桥面车辆行驶的安全性尤其需要得到重视。
桥面侧风对桥面行车安全造成了严重的影响,基于社会效益与经济效益的双重考量,越来越多的桥梁已经加装了风障[5-7]。侧风能导致车辆偏离其正常行驶轨迹甚至能够导致车辆侧翻[8-13]。作为主要应对手段, 风障被广泛运用在桥面以减小桥面侧风,改善桥面行车环境[13]。通过设置风障,大部分桥面行驶车辆的风环境安全能够得到满足[14-15]。
然而大部分学者的研究都集中在单梁[16],如果将平行梁当做两个单独的单梁,在每片梁的两侧都安装风障,这是不经济的。如果仅仅在两片平行梁的外侧安装风障,当两片梁的间距过大,桥面风环境的安全性就得不到保障。因此必然存在一个距离,如果平行梁间距超过了这个距离则应当在平行梁的两侧都安装风障。
为了研究这个距离,本研究基于大型流体计算通用软件FLUENT建立了单梁及不同间距平行梁的计算流体力学(CFD)模型。基于这些模型,针对平行梁间距展开了参数研究。通过研究找到了一个临界距离,间距超过这个临界距离的平行梁建议在每片梁的两边都安装风障。
1 数学模型及计算域 1.1 数学模型计算流体力学模型(CFD)需要满足一定的基本控制方程即质量守恒方程与动量守恒方程。由于环境风速远低于200 km/h,对应的马赫数远小于0.3,因此梁周围的流场可以简化为不可压缩流场。本研究采用三维大涡模型(LES)模拟梁周围的流场,这是由于LES能够有效地捕捉流场的非稳态特征[17]。LES的质量守恒及动量守恒方程如下:
质量守恒方程:
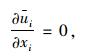
|
(1) |
动量守恒方程:
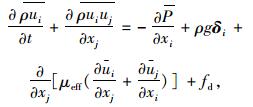
|
(2) |
式中,i, j=1, 2, 3分别为x,y,z方向;t为时间;u为网格过滤速度;P为网格过滤压力; ρ为空气密度; g为重力加速度; δi为应变张量; μeff为湍流黏性系数; fd为源顶。
1.2 计算域和边界条件对于深山峡谷中的连续梁桥,桥梁跨中位置往往位于峡谷中央,其风速也往往是最大的。因此研究针对此位置的梁段展开。本研究针对的梁为四车道梁,梁宽17 m,高3.6 m,采用风障的透风率为50%,高度为2.2 m,安装在1 m高防撞墙上。为了减少计算量,我们对桥面铺装、雨水口、排水管等细部构造进行了简化,并忽略了风障的细微振动。
计算域如图 1所示。计算域越大,桥面风环境的模拟就越真实。然而考虑到计算机计算能力的限制,应选用一个大小适当的计算域以平衡计算效率与模拟真实性。计算域的设置必须保证计算域入口到梁的距离;梁到计算域出口的距离; 梁顶到计算域顶的距离; 梁底到计算域底的距离与梁高的比值大于一定的值,研究中该值依据文献[10]确定。为了验证计算域的有效性,研究中将该值扩大一倍后比较两种计算域大小条件下梁的升力系数与阻力系数的变化情况。变化率须小于1%以确保所选用的计算域的有效性。速度入口的风速被设置为10 m/s。压力出口的压力被设置为一个标准大气压。研究采用的单梁模型及其上风障的安装形式如图 2所示。研究采用的平行梁模型及其上风障的安装形式如图 3所示,平行梁间间距为1~136 m。
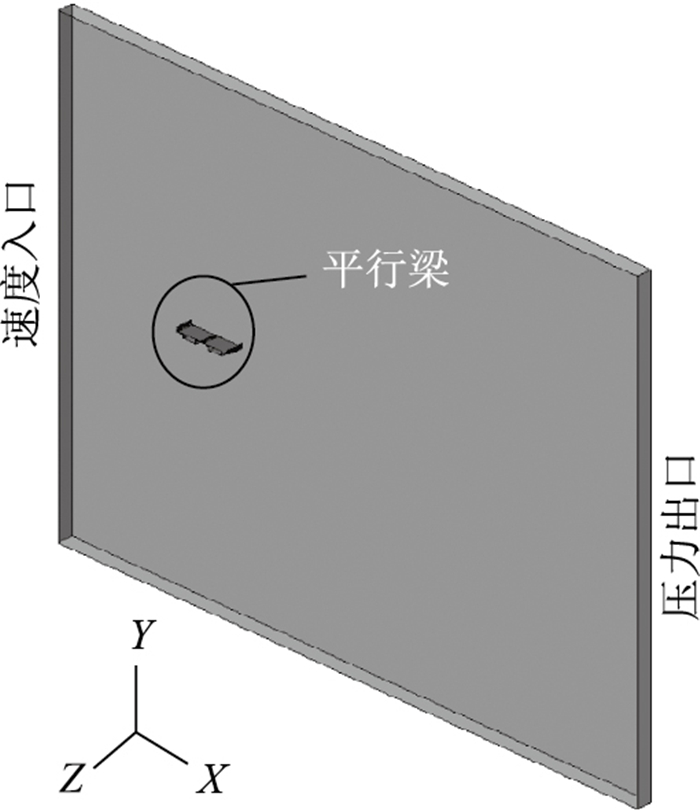
|
| 图 1 计算域及边界条件设置 Fig. 1 Computational domain and boundary setting |
| |
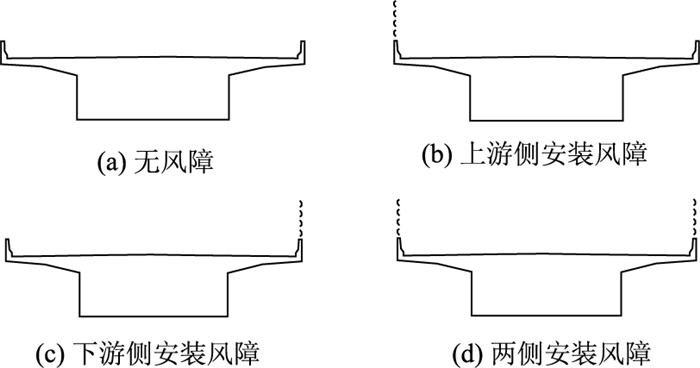
|
| 图 2 梁及梁上风障安装形式 Fig. 2 Girder and wind barrier layout on girder |
| |

|
| 图 3 平行梁间距示意图 Fig. 3 Gap of parallel girders |
| |
ICEM-CFD软件被用来对计算域进行网格划分。梁和风障表面采用三棱柱网格作为边界层,靠近梁和风障的位置设置四面体网格以更好地适应梁和风障外形。而在远离梁和风障的位置采用六面体网格以减少网格数量。最终各模型的总网格数量均在120万到200万之间。在计算过程中通过网格自适应使Y+小于2,以满足大涡模拟对边界层网格的要求。计算中待迭代残差小于0.000 1时认为计算收敛,计算时间步长设置为0.001 s。
2 计算结果与讨论 2.1 数值模拟方法验证文献[8]提供了钢箱梁上风障挡风风洞试验。为了验证LES方法对桥面风环境模拟的有效性,研究对该风洞试验进行了数值模拟,得到的钢梁断面风速比如图 4所示。
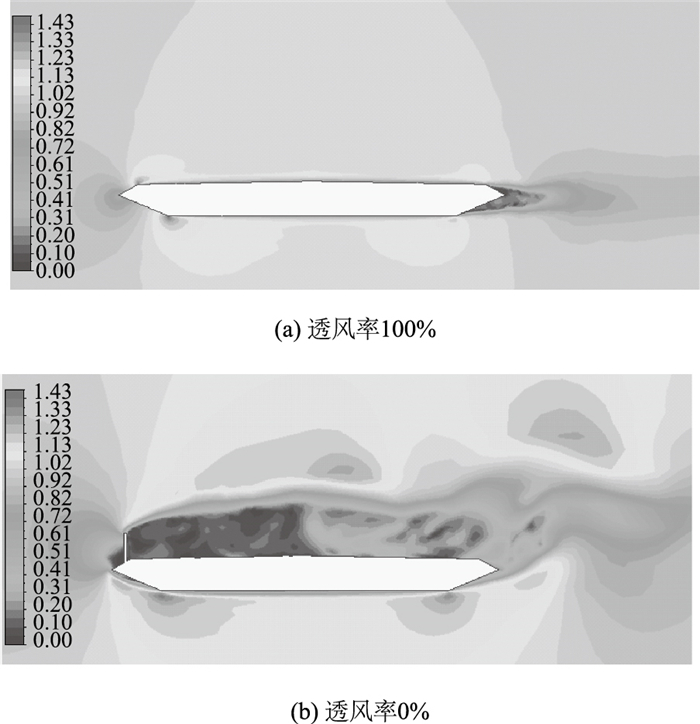
|
| 图 4 风速比云图 Fig. 4 Nephograms of ratio of wind velocity |
| |
将风洞试验得到的第3车道风剖面与数值模拟得到的第3车道风剖面进行比较如图 5所示。可以看出数值模拟与风洞试验结果相近,差异可能是由于入口风湍流度设置上的差异造成的。因此该数值模拟方法的有效性得到了验证。
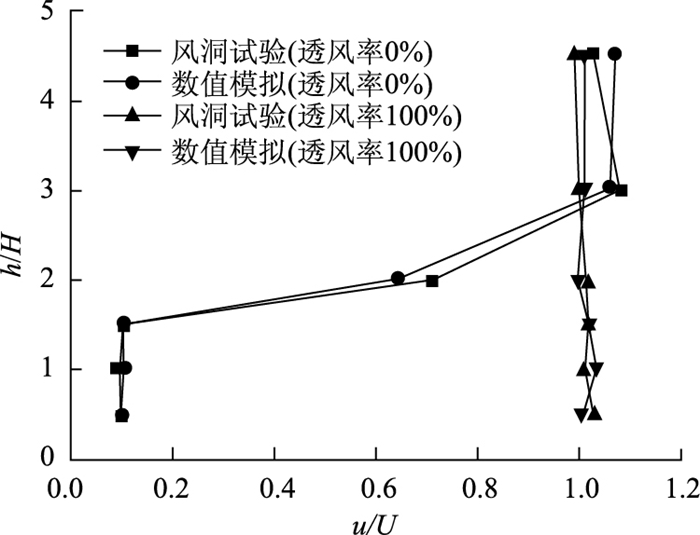
|
| 图 5 第3车道风速比 Fig. 5 Ratio of wind velocity on the third lane |
| |
2.2 单梁桥面风环境计算结果与讨论
在没有风障保护的情况下,单梁桥面风环境见图 6(来流风速为10 m/s)。由于上游侧防撞墙的阻塞,上游防撞墙后的风速较低,并在之后形成了回流。4条车道(相对于来风方向,从上游到下游分别为车道1,车道2,车道3,车道4)上的风剖面如图 7所示。比较4个车道可以看出1号车道行车风环境最为恶劣。根据《中华人民共和国道路交通安全条例》,重型货车从地面起不超过4 m,集装箱货车不超过4.2 m[18]。可知只要在4.2 m高度范围内风环境安全,则不必要安装风障。对图 7进行统计可以发现4条车道恢复到来流风速80%的高度分别为:2.3,3.3,4,4.1 m,均小于4.2 m高度。因此如果将防撞墙看做是一种风障,那么防撞墙对桥面行车风环境的保护作用不足。
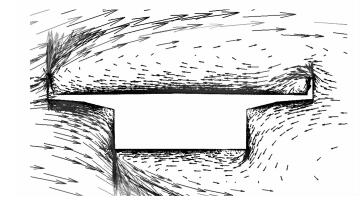
|
| 图 6 桥面风场环境分布 Fig. 6 Wind field distribution on girder deck |
| |
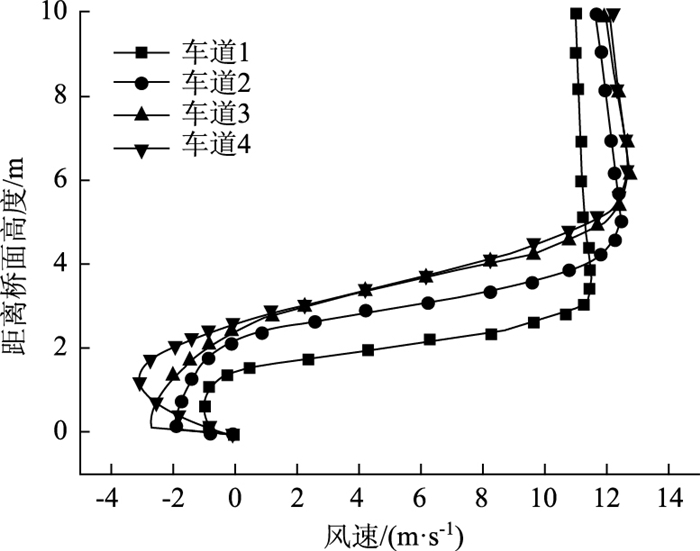
|
| 图 7 桥面以上各车道风剖面 Fig. 7 Wind speed profile above each lanes on girder deck |
| |
与不安装风障的单梁对比,图 2中各梁上车道的风剖面如图 8所示。比较图 8(a)与图 8(b)可以看出,上游侧加装风障一方面可以抑制桥面风回流,另一方面可以使风速达到或者超过来流风速的位置提高。比较图 8(a)与图 8(c)可以看出下游侧安装的风障对改善桥面风环境没有帮助,甚至由于在下游风障前产生了强烈的回流,劣化了最下游车道的风环境。比较图 8(b)与图 8(d)可以看出在上游侧已经安装风障的情况下,在下游侧加装风障并不能改善桥面风环境。然而考虑到风向的可变性,通常将风障安装于梁的两侧。以上研究已经指出,在未安装风障的情况下,1号车道的风环境最为恶劣,因此研究针对最上游车道(1号车道)进行。图 8所示各梁的1号车道风剖面如图 9所示。在无风障的情况下,1号车道2.3 m高度处已经达到来流风速的80%,可以认为防撞墙的影响高度为2.3 m。在上游侧加装透风率为50%的风障后,风速随桥面高度增加而增加的趋势在2.2~3.8 m高度范围内受到了抑制。这是由于透风率为50%的风障相当于多孔介质,阻塞了防撞墙上一定高度范围内气流的通过。对于仅在上游侧安装风障和两侧安装风障的梁,1号车道恢复到来流风速80%的高度大约为4 m。虽然没能达到4.2 m高度,但已经能满足绝大多数车辆的通行要求了。而如果仅在下游侧安装风障,则1号车道的风环境并未得到提高。这是由于在未安装风障的梁上,距离下游挡风墙顶2.2 m高度处的风速仅为3.1 m/s,仅相当于来流风速的31%。因此在此高度范围内安装风障并不会对上游流场产生太大的影响。
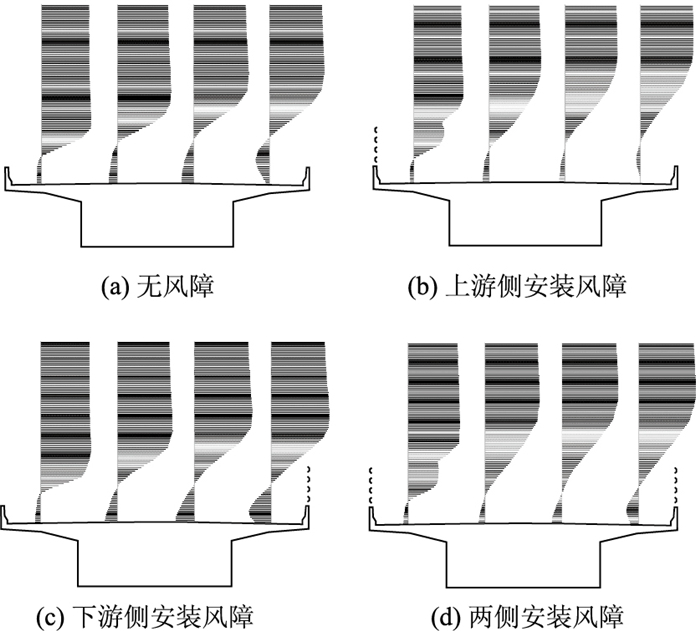
|
| 图 8 桥面以上各车道风剖面 Fig. 8 Wind speed profile on each lane on girder deck |
| |
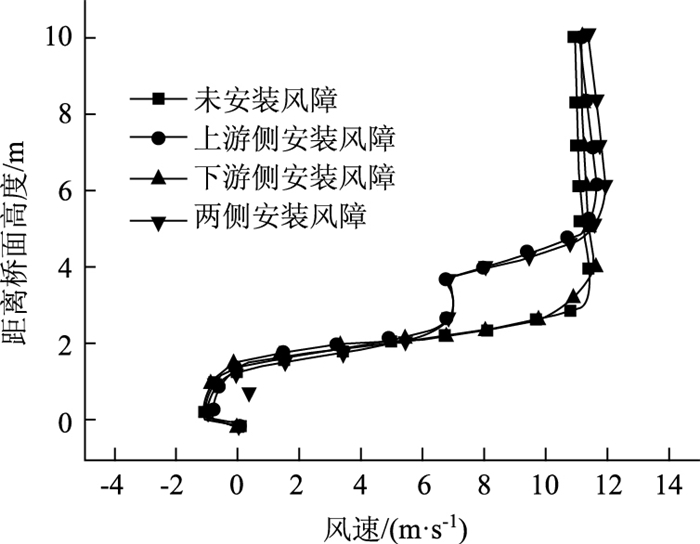
|
| 图 9 1号车道上风剖面图 Fig. 9 Wind speed profile on the first lane |
| |
为了量化各车道的桥面风环境,本研究引入了风环境折减系数λs来评价桥面风环境的安全性。桥面风环境折减系数定义如下[10]:
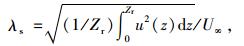
|
(3) |
式中,Zr为桥面以上λs的计算高度范围。这里取Zr为4 m,因为大部分车辆的高度都小于4 m;u(z)为桥面以上z高度处的风速;U∞为来流风速。事实上,λs为桥面以上一定高度范围内风速的均方平均值与来流风速的比值, λs越小桥面风环境就越安全。
图 8中各车道的λs如表 1所示。可以看出上游侧风障对桥面风环境的改善有积极作用,而下游侧安装的风障不仅不能改善桥面风环境,还会在下游车道产生湍流,劣化行车环境。
| 风障布置类型 | 车道1 | 车道2 | 车道3 | 车道4 |
| 无风障 | 0.84 | 0.72 | 0.58 | 0.56 |
| 上游侧安装风障 | 0.70 | 0.55 | 0.44 | 0.35 |
| 下游侧安装风障 | 0.83 | 0.70 | 0.61 | 0.66 |
| 两侧安装风障 | 0.70 | 0.54 | 0.45 | 0.47 |
因此如果两幅之间的距离太远,仅仅在平行梁的外侧安装风障不足以保证车辆的行驶安全,需要在平行梁的内侧也加装风障。本研究中,平行梁间距(如图 3所示)被用来做参数分析。
2.3 平行梁桥面风环境计算结果与讨论图 10所示为平行梁局部流场横桥向风速与来流风速的比值。与单梁周围风场类似,当平行梁间距为1 m及0.5倍桥宽时,风场平顺地经过平行梁位置。当平行梁间距增加到1倍梁宽时,下游侧梁开始受到上游梁段导致的不稳定流场的影响。但由于1倍梁宽距离并不是太远,上游侧梁产生的尾流发育不完善,并没有严重的湍流在下游侧桥面出现。随着平行梁间距的不断增加,上游侧梁周围的流场越来越近似于单梁周围的流场,下游侧梁也逐渐进入了上游侧梁产生的尾流充分发展区。由于湍流的影响,下游梁表面开始出现强烈的湍流。以图 10(g)为例,下游侧桥面回流的风速达到了来流风速的47%,而桥面以上4 m高度风速达到了来流风速的90%。
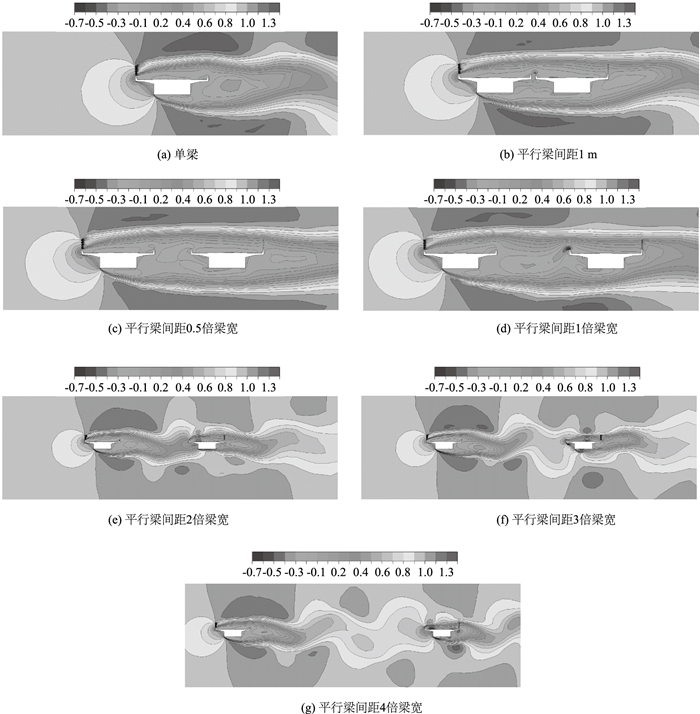
|
| 图 10 风速比分布 Fig. 10 Distribution of ratio of wind velocity |
| |
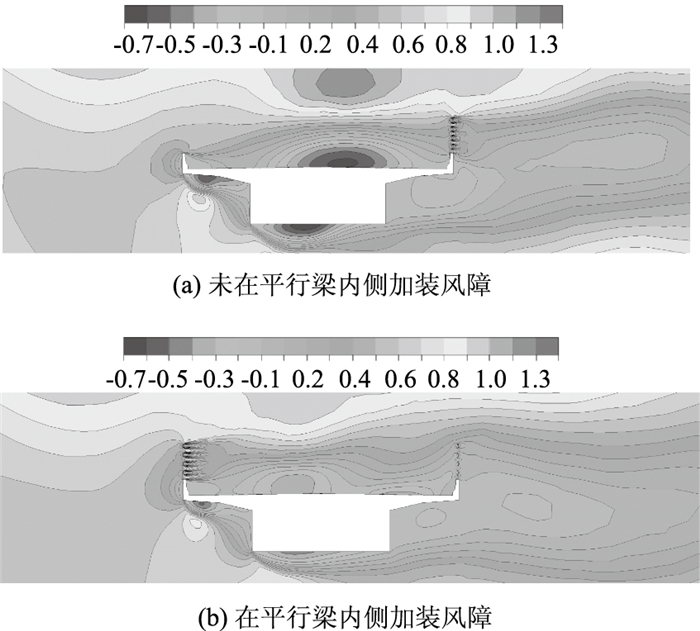
下游侧梁表面的风环境折减系数λs如表 2所示。由于上游侧梁的遮挡效应,表 2中的数值远小于单梁仅在下游侧设置风障时的情况。当平行梁间距增大到两倍梁宽后,下游侧桥面会产生强烈的回流,因此如果平行梁间距达到一定值,应当考虑在平行梁内侧加装风障。以间距为3倍梁宽的平行梁为例,在平行梁内侧加装风障后,桥面上风环境的改善如图 11所示。可以看出加装风障后桥面风回流明显减轻,风环境得到了改善。如表 2所示,可以发现,当平行梁间距由1.5倍梁宽增长到2倍梁宽时,λs有一个明显的增长。因此本研究建议当平行梁间距大于等于2倍梁宽时,在平行梁内侧加装风障。
| 平行梁间距 | 最大λs |
| 1 m | 0.55 |
| 0.5倍梁宽 | 0.57 |
| 1倍梁宽 | 0.55 |
| 1.5倍梁宽 | 0.60 |
| 2倍梁宽 | 0.67 |
| 3倍梁宽 | 0.66 |
| 5倍梁宽 | 0.72 |
| 8倍梁宽 | 0.71 |
|
| 图 11 风速比分布(间距为3倍梁宽) Fig. 11 Distribution of ratio of wind velocity |
| |
3 结论
本研究通过计算流体力学模型(CFD)研究了平行梁桥面风环境,对单梁与平行梁上布置风障的减风效果进行了分析。研究重点分析了风障的不同布置形式以及平行梁间距对桥面风环境的影响。得到以下结论:
(1) 采用三维大涡模拟可以对桥梁表面风环境进行模拟,计算得到了车道中心线处风剖面以及减风系数,对LES模拟桥面风环境的可靠性进行了验证。
(2) 仅靠防撞墙不能保证桥面行车高度范围内风环境满足行车安全要求,因此在桥面安装风障对于保证桥面行车安全十分必要。风障安装位置对桥面风环境有着显著的影响。上游侧安装的风障能够有效地改善桥面风环境而下游侧安装的风障对桥面风环境没有改善作用。
(3) 对于分体式桥梁,如果左右两幅之间的间距超过了一定范围,下游侧梁将受到上游侧梁漩涡脱落的影响,桥面风环境将十分复杂。通过一系列的参数研究,本研究建议如果平行梁间距达到两倍梁宽,就应该在平行梁内侧加装风障。
| [1] |
薛亚飞, 刘志文. 复杂地形桥位风场空间分布特性数值模拟[J]. 公路交通科技, 2016, 33(5): 66-72. XUE Ya-fei, LIU Zhi-wen. Numerical Simulation of Spatial Distribution Feature of Wind Field over Bridge Site at Complex Terrain[J]. Journal of Highway and Transportation Research and Development, 2016, 33(5): 66-72. |
| [2] |
王润建, 李海光. 基于CFD方法的大跨高墩刚构桥梁风荷载数值识别[J]. 公路交通科技, 2010, 28(10): 72-76, 88. WANG Run-jian, LI Hai-guang. Numerical Simulation of Spatial Distribution Feature of Wind Field over Bridge Site at Complex Terrain[J]. Journal of Highway and Transportation Research and Development, 2010, 28(10): 72-76, 88. |
| [3] |
金磊, 王修勇, 廖建宏, 等. 矮寨悬索桥桥址风环境观测系统及数据分析[J]. 湖南工程学院学报:自然科学版, 2011, 21(3): 65-67. JIN Lei, WANG Xiu-yong, LIAO Jian-hong, et al. Wind Monitoring System and Data Analysis for Aizhai Suspension Bridge[J]. Journal of Hunan Institute of Engineering:Natural Science Edition, 2011, 21(3): 65-67. |
| [4] |
张征文. 基于CFD模拟的大跨度桥梁静风稳定性风偏角影响分析[J]. 公路交通科技, 2013, 30(10): 74-79. ZHANG Zheng-wen. Analysis of Influence of Windage Yaw Angle of Aerostatic Stability on Long Span Bridge Based on CFD Simulation[J]. Journal of Highway and Transportation Research and Development, 2013, 30(10): 74-79. |
| [5] |
阮欣, 陈艾荣, 王达磊. 杭州湾跨海大桥风障设置风险评估[J]. 桥梁建设, 2007, 1(1): 78-80. RUAN Xin, CHEN Ai-rong, WANG Da-lei. Risk Assessment of Installing of Wind Shielding Screens for Hangzhou Bay Sea-crossing Bridge[J]. Bridge Construction, 2007, 1(1): 78-80. |
| [6] |
王玉倩, 阮欣, 陈艾荣. 全寿命成本分析法在侧风影响下桥梁行车安全决策中的应用[J]. 公路交通科技, 2008, 26(10): 94-98. WANG Yu-qian, RUAN Xin, CHEN Ai-rong. Application of Life-cycle Cost Analysis in Decision Making of Vehicle Driving Safety on Bridges under Crosswind[J]. Journal of Highway and Transportation Research and Development, 2008, 26(10): 94-98. |
| [7] |
白璐, 申爱琴, 韦振勋. 公路防风结构物实测效果比较与优化设置模拟研究[J]. 公路交通科技, 2016, 33(2): 39-45, 53. BAI Lu, SHEN Ai-qin, WEI Zhen-xun. Comparison of In-situ Observation Effect of Highway Windbreak Structures and Simulation of Installation Optimization[J]. Journal of Highway and Transportation Research and Development, 2016, 33(2): 39-45, 53. |
| [8] |
GAO G J, DUAN L L, MIAO X J. Overturning Stability of Box-car on Qinghai-Tibet Railway Line with Strong Cross Wind[J]. Journal of Central South University, 2011, 42(4): 1150-1155. |
| [9] |
KRAMER C, GRUNDMANN R, GERHARDT H J. Testing of Road Vehicles under Cross Wind Conditions[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1991, 38(1): 59-69. |
| [10] |
陈晓冬.大跨桥梁侧风行车安全分析[D].上海: 同济大学, 2007. CHEN Xiao-dong. Analysis of Vehicle Driving Safety on Bridges under Crosswind[D]. Shanghai: Tongji University, 2007. |
| [11] |
周记国, 胡兆同, 薛晓锋, 等. 侧向风作用下车辆荷载突变效应的CFD模拟研究[J]. 公路交通科技, 2015, 32(1): 145-152. ZHOU Ji-guo, HU Zhao-tong, XUE Xiao-feng, et al. Simulation of Effect of Sudden Change of Vehicle Loads under Cross Wind by CFD Method[J]. Journal of Highway and Transportation Research and Development, 2015, 32(1): 145-152. |
| [12] |
李岩, 盛洪飞, 陈彦江, 等. 强风环境下斜拉桥车桥系统动力响应分析研究[J]. 公路交通科技, 2008, 25(7): 59-64. LI Yan, SHENG Hong-fei, CHEN Yan-jiang, et al. Dynamic Response Analysis of Vehicle-bridge System for Cable-stayed Bridge in Strong Windy Environment[J]. Journal of Highway and Transportation Research and Development, 2008, 25(7): 59-64. |
| [13] |
CHU C R, CHANG C Y, HUANG C J, et al. Windbreak Protection for Road Vehicles Against Crosswind[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 116(5): 61-69. |
| [14] |
项超群, 郭文华, 张佳文. 强侧风下桥上高速列车倾覆稳定性及最优风障高度的研究[J]. 振动与冲击, 2014, 33(12): 80-86. XIANG Chao-qun, GUO Wen-hua, ZHANG Jia-wen. Overturning Stability of a High-speed Train Running on a Bridge and Optimal Height of Wind Barriers under Strong Crosswind[J]. Journal of Vibration and Shock, 2014, 33(12): 80-86. |
| [15] |
李波, 张剑, 杨庆山. 桥梁风障挡风性能的试验研究[J]. 振动与冲击, 2016, 35(8): 78-82. LI Bo, ZHANG Jian, YANG Qing-shan. Experimental Study on Windbreak Performance of Wind Barriers on Bridge[J]. Journal of Vibration and Shock, 2016, 35(8): 78-82. |
| [16] |
KOZMAR H, PROCINO L, BORSANI A, et al. Sheltering Efficiency of Wind Barriers on Bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012(107-108): 274-284. |
| [17] |
WEI Q, CHEN H, MA Z. An Hybrid RANS/LES Model for Simulation of Complex Turbulent Flow[J]. Journal of Hydrodynamics, 2016, 28(5): 811-820. |
| [18] |
胡朋, 王长中, 潘晓东. 基于行车安全的侧风多发区路堤风障形式研究[J]. 中外公路, 2013, 33(4): 9-13. HU Peng, WANG Chang-zhong, PAN Xiao-dong. Study on Wind-barrier Form at Cross-wind-prone Area for Roadway Safety[J]. Journal of China & Foreign Highway, 2013, 33(4): 9-13. |
 2018, Vol. 35
2018, Vol. 35
