扩展功能
文章信息
- 李华强, 刘浩学, 韩言虎
- LI Hua-qiang, LIU Hao-xue, HAN Yan-hu
- 多式联运联盟合作伙伴选择
- Selection of Partner in Multimodal Transport Alliance
- 公路交通科技, 2018, 35(8): 152-158
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(8): 152-158
- 10.3969/j.issn.1002-0268.2018.08.020
-
文章历史
- 收稿日期: 2018-04-16
2. 长安大学 经济与管理学院, 陕西 西安 710064
2. School of Economics and Management, Chang'an University, Xi'an Shaanxi 710064, China
《物流术语》(GB/T18354—2006)对多式联运的定义:联运经营者受托运人、收货人或旅客的委托,为委托人实现2种或2种以上运输方式的全程运输,以及提供相关运输物流辅助服务的活动。联运经营者即为多式联运经营人,由多式联运经营人对货物运输全程负责,是与货物托运人签订全程运输服务合同的当事人[1]。多式联运经营人要为全程运输的全部或若干区段寻找承运人,并与之订立合同,形成多式联运联盟。在多式联运经营人的统一管理下,各区间多样的运输方式及服务、全程运输中所涉及的实际承运人、代理人、有关机构有机地衔接,各个运输过程及环节构成不间断的、一体化的国际货物运输体系[2]。已有研究表明,糟糕的合作伙伴选择是联盟失败最重要的原因[3], 以及联盟保持成功合作的关键因素是选择正确的合作伙伴[4],因此多式联运经营人能否选择合适的联盟合作伙伴,即区段承运人,关系到多式联运成本、时间、风险以及经营人的综合服务质量等。
多式联运联盟合作伙伴选择问题已得到研究者的关注。王凤洲等分析基于系统整合观的多式联运系统特征[5]。马彩雯提出将Agent技术应用于多式联运各区段承运人的选择[6],但仅设计出分运承运人选择系统结构,并未给出具体的算法。陈宇等认为多式联运动态联盟合作伙伴的选择是一个运营成本、时间和风险目标组合优化过程[7]。刘舰等建立了基于综合运输成本最小、运输风险最小和合作强度最大的多目标优化选择模型[8];进一步运用决策和博弈理论对核心企业与候选企业、候选企业之间进行博弈分析[9],该研究丰富了承运人选择分运人的理论研究。郭琴等建立复合信息熵权的多式联运型物流网络协同度模型[10]。东方基于各类承运人多式联运多属性指标,采用混合集合规划确定出多式联运承运人的最佳组合,考虑的是托运人选择承运人的问题[11]。陈岩提出联盟界面管理评价指标体系[12],但未明确多式联运企业的性质。黄慧琼等运用PROMETHEEⅡ方法选择联盟合作伙伴[13],该研究一方面未明确选择物流企业的主体,另一方面在合作伙伴评价指标体系中没有考虑战略层面的因素。张德超把集装箱多式联运看作是一种特殊的动态企业联盟,构建一个综合影响因子以改进经典Shapley收益分配模型[14]。段华薇等将基于增量利润和基于系统贡献度的收益共享契约应用于公铁联运物流服务供应链协调问题中[15]。夏新海构建基于合作博弈的集装箱港口联盟模型[16],论证了多式联运中港口联盟的重要性,并未涉及联盟合作伙伴的选择研究。
综合已有研究成果不足之处以及多式联运发展实际,本研究在构建多式联运联盟承运人评价指标体系时既要从战略维度考虑、又要从业务运营维度考虑;将多式联运经营人对联盟承运人选择的过程视为一个信息具有灰色特征、复杂多因素的动态综合决策过程,构建基于层次分析法和信息熵组合赋权的灰色关联度评价模型,针对具体实例进行应用分析,确保多式联运联盟承运人选择具有科学性和实用性。
1 承运人选择的影响因素及评价指标体系构建 1.1 承运人选择的影响因素分析多式联运联盟承运人选择涉及到的影响因素很多,本研究主要遵循战略相容、实力优先、成本可控、风险最小等原则,从战略维度、业务运营维度2个方面分析承运人选择的影响因素。
(1) 战略维度。多式联运运行具有牵涉主体多、资金投入大、集聚要素多等复杂性特征,决定了多式联运经营人与承运人之间不是一次性的短期合作关系,而是一种长期的战略联盟关系,这种关系具有排他性、强链接性。如果不能形成战略上的合作关系,对企业之间的合作稳定性产生极大影响,且关系一旦破裂,可能会造成不可估量的损失。因此在战略目标、企业家精神、企业文化、合作关系认同等方面达到一定的统一性,才能从根本上保证多式联运联盟顺利运转。
(2) 业务运营维度。经过长期实践总结,多式联运有一套比较成熟的业务流程:①多式联运经营人与托运人、分承运人签订合同,约定货物交接时间和地点、运费标准、单证形式、相关责任等内容;②多式联运经营人办理货物运输和进出口的报关、报检等相关手续;③多式联运经营人负责货物全程运输计划和衔接安排以及分区段运输之间的货物仓储、搬运、中转等,分承运人负责相应区段的具体运输任务,共同将货物运抵目的地;④收货人凭多式联运单证取货,完成一个多式联运循环。由多式联运经营人对货物联运整个流程进行把控,负责外部关系协调处理和内部分承运人的管理,分承运人对相应区段运输任务,可见分承运人的选择至关重要。从承运人自身实力角度看,货物运输、装卸、搬运、中转等环节需要强大的资金实力、专业的装备、标准化的作业流程、熟练的人工、健全的组织体系、先进的信息技术应用,这些因素对运输成本和运输时间产生直接影响;从承运人之间转换的角度看,承运人的交叉作业能力、技术设备的兼容程度、企业沟通协调等会影响多式联运中转效率,继而产生不同的中转成本;从风险防范的角度看,多式联运面临复杂多变的外部环境,在联运过程中会遇到不同属性的风险因素。通过加强技术创新和应用、提高企业管理水平等手段,提高风险防范能力,减少风险损失,提高顾客满意度。
1.2 承运人选择的评价指标体系构建基于承运人选择的影响因素分析,结合对西安某集团、太原某物流等多式联运企业的调研资料,征询数位有代表性的从事多式联运高校、研究机构的学者和管理部门的专家,从战略维度、业务运营维度2个方面最终确定了13个评价指标,其中3个定量指标、10个定性指标,共同构成多式联运联盟承运人选择评价指标体系,如表 1所示。
| 评价维度 | 评价指标 | 指标描述 |
| 战略维度 | 战略目标相似度(I1) | 企业在发展多式联运具有相同的追求目标 |
| 企业文化兼容性(I2) | 对彼此企业文化认同 | |
| 合作认同度和稳定性(I3) | 对未来合作认可并可期待,确保稳定和可持续 | |
| 业务运营维度 | 注册资本金(I4) | 通过注册资本金以反映企业的资金实力 |
| 专业的装备及良好的兼容程度(I5) | 多式联运需要专业的载运工具和设备,并能适应不同企业和区段的互补要求 | |
| 作业流程标准化水平(I6) | 多式联运作业环节多,标准化空间大 | |
| 健全的组织体系(I7) | 多式联运运作程序多,需要完善的规章制度、机构设置和规范管理等 | |
| 先进的信息技术应用(I8) | 物联网、RFID等信息技术将提高企业效率,规避风险 | |
| 运输成本(I9) | 成本是选择多式联运联盟承运人的重要指标 | |
| 运输时间(I10) | 时间要求是多式联运的重要指标,对有时间窗运输要求的尤其如此 | |
| 交叉作业能力(I11) | 货物不同区段运输的中转、搬运、装卸的交叉作业 | |
| 企业沟通协调(I12) | 企业沟通协调能力关系到额外成本的产生 | |
| 风险防范能力(I13) | 企业具有规避、防范等众多不同属性风险因素的能力 |
2 基于组合赋权的承运人灰色关联评价模型 2.1 熵值法确定权重
考虑多式联运经营人的选择空间包括m个潜在承运人(合作伙伴),表示为Q=(q1, q2, …, qm),指标体系包括n个评价指标,表示为P=(p1, p2, …, pn),从而可以得到初始评价矩阵Aij=(aij)m×n,aij为第i个承运人在第j个指标上的评价值。为了消除量纲对决策矩阵的影响,对原始矩阵指标进行归一化处理,得到规范化矩阵Xij=(xij)m×n,i=1, 2, …, m;j=1, 2, …, n。
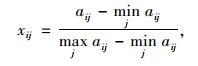
|
(1) |
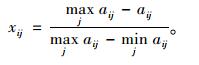
|
(2) |
评价指标pj的熵值Hj为:
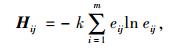
|
(3) |
式中,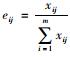
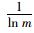
评价指标pj的差异度系数dj为:
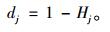
|
(4) |
评价指标pj的客观权重wj为:
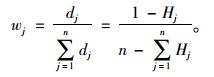
|
(5) |
得到客观权重向量Wk=(wk1, wk2, …, wkn)T,其中0 < wkj < 1,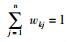
针对多目标决策问题确定权重的最常用的方法是层次分析法,该方法发展得比较成熟,下面简要梳理其应用步骤[18]。
第一步,根据系统的总目标进行目标分解,建立递阶层次结构;
第二步,采用一定的标度方法,对不同层次的元素进行定量化,构造判断矩阵;
第三步,求解判断矩阵的特征根及其对应的特征向量进行重要性排序;
第四步,对判断矩阵进行一致性检验,判断权重分配的合理性。根据层次分析法确定的主观权重向量Wz =(wz1, wz2, …, wzn)T,其中0 < wzj < 1,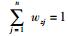
(1) 组合赋权过程将2.1和2.2确定的权重进行线性组合,其权重系数分别为α和β,α和β可以取不同的[0, 1]区间值。
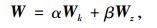
|
(6) |
式中0≤α, β≤1,α+β=1。
(2) 灰色关联系数计算
记规范化矩阵Xij=(xij)m×n中的相对最优评价值组成参考数列X*=(x1*, x2*, …, xn*),Xi=(xi1, xi2, …, xin)为规范化矩阵Xij=(xij)m×n中的比较数列,则X*(j)与Xi(j)的关联系数为:
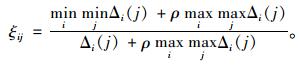
|
(7) |
式中,j=1, 2, …, n;Δi(j)=|X*(j)-Xi(j)|;ρ为分辨系数,其值越小,分辨力越大,一般ρ的取值区间为(0, 1),具体取值可视情况而定。通常取ρ=0.5。
(3) 灰色关联度计算和排序
对于包含m个承运人和n个评价指标的评价系统,通过式(7)计算可得到关联系数矩阵n=(ξij)m×n,关联系数矩阵n与权重向量W相乘得到决策向量L,即:
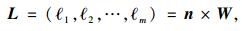
|
(8) |
式中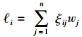
根据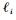
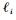
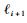
吉林省某公司正在大力开拓商品车集装箱多式联运业务,以商品车运输为主营业务,以长春为起点,构建全国范围的多式联运网络。以长春—佛山线路的商品车集装箱公水联运为例,在起点采用集装箱装运,通过公路运输到达大连港,经水路运输到达广州港以后拆箱,采用轿笼车装运运达4S店。从长春到大连的公路运输中有4家物流企业甲、乙、丙、丁作为潜在备选分承运人,采用基于组合赋权的承运人灰色关联评价模型对备选分承运人进行评价排序,为企业多式联运联盟合作伙伴选择和网络构建提供决策依据。
3.1 初始评价矩阵根据文献[19]对某一定性指标而言各方案的相对优劣程度进行标度,标度规则如表 2所示,得到定性指标的基础评价数据;定量指标的原始数据通过调研获取,通过式(1)、式(2)计算得到定量指标的基础评价数据。
| 语气算子 | 同样 | 稍稍 | 略为 | 较为 | 明显 | 显著 | 十分 | 非常 | 极其 | 极端 | 无可比拟 | |||||||||
| 模糊标度值 | 0.50 | 0.53 | 0.55 | 0.58 | 0.60 | 0.63 | 0.65 | 0.68 | 0.70 | 0.73 | 0.75 | 0.78 | 0.80 | 0.83 | 0.85 | 0.88 | 0.90 | 0.93 | 0.95 | 1.0 |
| 相对隶属度 | 1.0 | 0.91 | 0.82 | 0.74 | 0.67 | 0.60 | 0.54 | 0.50 | 0.43 | 0.38 | 0.33 | 0.29 | 0.25 | 0.21 | 0.18 | 0.14 | 0.11 | 0.08 | 0.05 | 0 |
就多式联运联盟潜在承运人甲、乙、丙、丁的战略目标相似度(I1)指标而言,承运人丙强于乙,乙强于甲,甲强于丁,其强弱顺序为丙、乙、甲、丁。以承运人丙作为比较标准,丙比乙处于同样和稍稍优越之间,丙比甲处于稍稍和略微之间,丙比丁处于较为优越,由表 2可知,乙、甲、丁的相对隶属度分别为0.91,0.74,0.54。由此得到多式联运潜在承运人甲、乙、丙、丁关于指标I1的相对隶属度向量为a1=(0.74, 0.91, 1, 0.54)。同理,得到其他定性指标的相对隶属度向量,分别为a2=(0.82, 1, 0.91, 0.74),a3=(0.74, 1, 0.82, 0.60),a5 =(0.74, 0.82, 1, 0.43),a6=(0.67, 0.74, 1, 0.38),a7=(0.82, 1, 0.91, 0.33), a8=(1, 0.74, 0.91, 0.43),a11=(0.60, 0.82, 1, 0.54),a12=(0.82, 1, 0.91, 0.74),a13=(0.67, 0.74, 1, 0.33)。
根据表 3中的数据以及式(1)、式(2)可得到指标注册资本金(I4)、运输成本(I9)、运输时间(I10)的相对隶属度向量分别为a4=(0.23, 0.77, 1, 0),a9=(0.47, 0.67, 0, 1),a10=(0.17, 0.58, 1, 0)。
| 经济指标 | 备选承运人 | |||
| 甲 | 乙 | 丙 | 丁 | |
| 注册资本金/万元 | 10 000 | 24 000 | 30 000 | 4 000 |
| 承运运费/[元·(veh·km)-1] | 0.98 | 0.95 | 1.05 | 0.90 |
| 运输时间/小时 | 7 | 6.5 | 6 | 7.2 |
多式联运联盟承运人选择的初始评价矩阵:
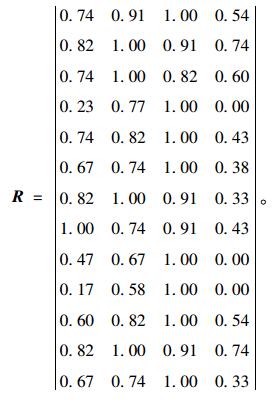
|
(1) 按照式(3)~式(5)计算得到评价指标的客观权重:
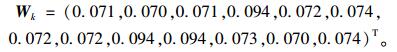
|
(2) 按照2.2所列步骤进行计算得到评价指标的主观权重:
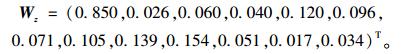
|
(3) 式(6)中的α, β取值为0.5,得到各指标的组合权重:
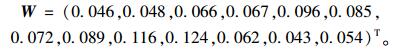
|
由式(7)计算得到关联系数矩阵:
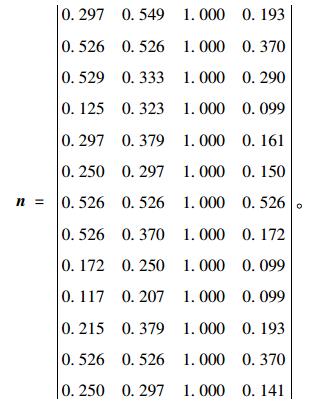
|
由式(8)计算得到决策向量L=(0.971, 1.031, 2.484, 0.582)T,由此可见4个多式联运承运人选择顺序为丙、乙、甲、丁。
该计算结果与4个多式联运联盟潜在承运人的发展实际一致,验证了基于组合赋权的承运人灰色关联评价模型具有科学性、实用性和可操作性,为多式联运经营人选择承运人形成联盟提供了科学的比选方法。
4 结论多式联运的高度复杂性决定了多主体集成特征,承运人选择是多式联运经营人构建联盟过程中的一项重要内容。本研究从战略维度、业务运营维度2个方面构建多式联运联盟承运人选择评价指标体系,采用熵值法和层次分析法组合设置指标权重,建立具有模糊特征的灰色关联度评价模型,并进行模型应用。
(1) 从战略和业务运营维度构建多式联运联盟承运人选择评价指标体系,既考虑联盟企业的长期合作性,减少选择成本,又考虑多式联运实际业务流程及其衔接性和交叉性特点,保障业务合作顺利开展,减少合作过程成本。同时集成研究学者、一线人员和政策制定者的观点,综合考虑确定评价指标。
(2) 通过基于信息熵和层次分析法的组合赋权设置指标权重,层次分析法是应用广泛的主观赋权方法,对定性指标进行赋权时实用性较强;基于信息熵原理的客观赋权能够减少主观依赖性,充分发挥客观数据的作用。将二者进行组合,大大提高了权重设置的科学性和合理性。
(3) 充分考虑多式联运行业处于发展初期时的特点,建立具有模糊特征的灰色关联度评价模型,实际案例验证表明,模型方法适合当前我国多式联运企业发展实际,评价结果客观合理,具有可操作性和实用性。
| [1] |
曾永长. 多式联运流程设计与路径优化[D]. 重庆: 重庆大学, 2009. ZENG Yong-chang. Multimodal Transport Process Design and Path Optimization[D]. Chongqing: Chongqing University, 2009. |
| [2] |
李丹凝. 多式联运下的集装箱供应链合作伙伴选择研究[D]. 北京: 北京交通大学, 2016. LI Dan-ning. Research on Partner Selection of Container Supply Chain under Multimodal Transport[D]. Beijing: Beijing Jiaotong University, 2016. |
| [3] |
RACKHAM N. Getting Partnering Right[M]. New York: McGraw-Hill Inc., 1955.
|
| [4] |
福克纳D, 鲍曼C. 竞争战略[M]. 北京: 中信出版社, 1997. FAULKNER D, BOWMAN C. Competitive Strategy[M]. Beijing: CITIC Press, 1997. |
| [5] |
王凤洲, 陆晓倩, 吴秋明. 基于系统整合观的多式联运系统特征分析[J]. 系统辩证学学报, 2005, 13(4): 74-78. WANG Feng-zhou, LU Xiao-qian, WU Qiu-ming. The Analysis of Modern Multi-modal Transportation System Feature Based on System Integration Concept[J]. Journal of Systemic Dialectics, 2005, 13(4): 74-78. |
| [6] |
马彩雯. 基于多Agent的多式联运各区段分运承运人选择[J]. 哈尔滨工业大学学报, 2007, 39(12): 1989-1992. MA Cai-wen. Carrier Selection in Various Sections of Multi-modal Transport Based on Multi-agent[J]. Journal of Harbin Institute of Technology, 2007, 39(12): 1989-1992. |
| [7] |
陈宇, 任建伟, 刘盾, 等. 基于遗传算法的集装箱多式联运联盟合作伙伴的选择[J]. 铁道运输与经济, 2007, 29(2): 79-81. CHEN Yu, REN Jian-wei, LIU Dun, et al. Partner Selection in AVE of the Container Intermodal Transportation Based on Genetic Algorithm[J]. Railway Transportation and Economy, 2007, 29(2): 79-81. |
| [8] |
刘舰, 俞建宁, 董鹏. 多式联运分运人选择的模型和算法[J]. 运筹与管理, 2010, 19(5): 160-166. LIU Jian, YU Jian-ning, DONG Peng. Optimization Model and Algorithm for Intermodal Carrier Selection in Various Sections[J]. Operations Research and Management Science, 2010, 19(5): 160-166. |
| [9] |
刘舰. 多式联运分运人选择的博弈模型[J]. 兰州交通大学学报, 2015, 34(6): 65-69. LIU Jian. Game Model for Sub-carrier Selection in Intermodal Freight Market[J]. Journal of Lanzhou Jiaotong University, 2015, 34(6): 65-69. |
| [10] |
郭琴, 刘海静, 张秋生, 等. 基于复合信息熵权的多式联运型物流网络协同度模型研究[J]. 物流技术, 2011, 30(1): 35-38. GUO Qin, LIU Hai-jing, ZHANG Qiu-sheng, et al. Model of Level of Collaboration for Multi-modal Logistics Networks Based on Composite Information Entropy Weighing[J]. Logistics Technology, 2011, 30(1): 35-38. |
| [11] |
东方. 基于混合集合规划的多式联运承运人选择问题研究[J]. 中国物流与采购, 2011(16): 70-71. DONG Fang. Research on Choice of Multimodal Carrier Based on Hybrid Set Planning[J]. China Logistics & Purchasing, 2011(16): 70-71. |
| [12] |
陈岩. 基于多层次灰色评价法的多式联运企业联盟界面管理研究[J]. 北方交通, 2011(3): 89-92. CHEN Yan. Interface Management Study of Multimodal Transportation Business Alliance Based on Multi-level Grey Evaluation Method[J]. Northern Communications, 2011(3): 89-92. |
| [13] |
黄慧琼, 伍转青. 物流企业多式联运合作伙伴的优选研究[J]. 铁路采购与物流, 2015(1): 52-55. HUANG Hui-qiong, WU Zhuan-qing. Study on Optimization of Multimodal Transport Partners in Logistics Enterprises[J]. Railway Purchasing and Logistics, 2015(1): 52-55. |
| [14] |
张德超. 基于Shapley值的多式联运收益分配研究[J]. 交通科技与经济, 2015, 17(6): 35-40. ZHANG De-chao. The Benefit Assignment Mechanism Research on Multimodal Transport Based on Shapley Value[J]. Technology & Economy in Areas of Communications, 2015, 17(6): 35-40. |
| [15] |
段华薇, 戴玥, 严余松. 铁路物流中心参与的公铁联运物流服务供应链协调[J]. 计算机集成制造系统, 2016, 22(6): 1590-1598. DUAN Hua-wei, DAI Yue, YAN Yu-song. Contracts for Road and Railway Intermodal Transportation Logistics Service Supply Chain in Railway Logistics Park[J]. Computer Integrated Manufacturing Systems, 2016, 22(6): 1590-1598. |
| [16] |
夏新海. 基于博弈论的集装箱港口联盟模型构建与应用[J]. 武汉理工大学学报:社会科学版, 2017, 30(2): 39-45. XIA Xin-hai. Construction and Application of Container Port Alliance Model Based on Game Theory[J]. Journal of Wuhan University of Technology:Social Science Edition, 2017, 30(2): 39-45. |
| [17] |
王媛, 程曦, 殷培红, 等. 影响中国碳排放绩效的区域特征研究:基于熵值法的聚类分析[J]. 自然资源学报, 2013, 28(7): 1106-1116. WANG Yuan, CHENG Xi, YIN Pei-hong, et al. Research on Regional Characteristics of China's Carbon Emission Performance Based on Entropy Method and Cluster Analysis[J]. Journal of Natural Resources, 2013, 28(7): 1106-1116. |
| [18] |
常建娥, 蒋太立. 层次分析法确定权重的研究[J]. 武汉理工大学学报:信息与管理工程版, 2007, 29(1): 153-156. CHANG Jian-e, JIANG Tai-li. Research on the Weight of Coefficient through Analytic Hierarchy Process[J]. Journal of Wuhan University of Technology:Information and Management Engineering Edition, 2007, 29(1): 153-156. |
| [19] |
王广月, 刘健. 基于组合权重的灰色关联度方案决策模型及其应用[J]. 工业建筑, 2004, 34(4): 61-65. WANG Guang-yue, LIU Jian. Grey Relative Degree Decision Making Model Based on Combinatorial Weight and Its Application[J]. Industrial Construction, 2004, 34(4): 61-65. |
 2018, Vol. 35
2018, Vol. 35
