扩展功能
文章信息
- 李伟瀚, 张彬, 介玉新, 耿招, 马培
- LI Wei-han, ZHANG Bin, JIE Yu-xin, GENG Zhao, MA Pei
- Mohr-Coulomb与Hoek-Brown强度准则在浅埋偏压隧道数值模拟中的对比
- Comparison of Mohr-Coulomb and Hoek-Brown Criteria in Numerical Simulation of Shallow Unsymmetrial Loading Tunnel
- 公路交通科技, 2018, 35(8): 112-122
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(8): 112-122
- 10.3969/j.issn.1002-0268.2018.08.016
-
文章历史
- 收稿日期: 2017-05-18
2. 清华大学 水沙科学与水利水电工程国家重点实验室, 北京 100084;
3. 北京中安质环技术评价中心有限公司, 北京 100022
2. State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing 100084, China;
3. Beijing Zhongan Quality Environmental Technology Assessment Center, Co., Ltd., Beijing 100022, China
隧道作为地下通道的工程建筑物,具有某些其他工程无法比拟的优势,在公路、铁路的建设中尤其如此。随着对公路通行能力要求的不断提高,公路隧道更趋向于大跨度、小净高的方向发展[1]。在城市快速道路或高速公路中,由于地形限制,常常出现浅埋偏压的情况,加大了设计、施工的难度,并且非常容易引起结构的变形破坏问题。因此,浅埋偏压隧道的问题受到了众多学者的关注。
理论分析、数值模拟、模型试验以及现场监测等方法是目前研究隧道工程问题的主要手段,通过这些方法部分学者研究了在浅埋、偏压、破碎岩体等不同或复合的地质条件下,大跨或连拱隧道的修建技术、施工优化以及开挖方案[2-7]。另一些学者结合数值模拟和现场监测,对支护结构受力进行了深入分析,并研究了支护结构优化问题,为支护方案提出了建议[8-11]。
随着计算机技术的迅速发展,数值模拟成为了研究各类工程问题的重要手段,而在数值模拟研究中,强度准则的选择对模拟的结果影响很大。目前,对隧道模拟比较常用的强度准则是Mohr-Coulomb强度准则和Hoek-Brown强度准则。对于这两种强度准则的选择,赵坚、李海波基于对花岗岩的一系列动力试验,研究了Mohr-Coulomb和Hoek-Brown强度准则用于评估脆性岩石动态强度的适用性[12];Mohr-Coulomb强度准则作为岩土工程中应用最为广泛的强度理论,很多学者选择它作为数值模拟的强度准则[13-16];Hoek-Brown强度准则是以大量试验数据为依据的经验准则,它综合考虑了岩体结构面特征、岩块强度、施工扰动等影响因素。Hoek-Brown强度准则自1980年E. Hoek和E. T. Brown提出后[17],经过30 a的发展,已经得到了广泛的认可,大量学者对其进行了研究[18-21]及应用[12-24]。Durcker-Prager屈服准则也广泛应用于隧道数值模拟中,最初于1952年由Durcker-Prager提出。Durcker-Prager准则在π平面上为圆形,在主应力空间的屈服面为光滑曲面,形式简单物理意义明确,并且考虑了静水压力和中间主应力的影响[25]。许多学者对其展开了有益的研究[26]。但本研究限于篇幅,暂且只讨论Mohr-Coulomb和Hoek-Brown强度准则在隧道数值模拟中的对比。
本研究以贵阳市黔春大道七冲村二号隧道为例,基于有限差分软件FLAC3D,分别采用Mohr-Coulomb和Hoek-Brown强度准则,对浅埋偏压大跨隧道的施工全过程进行了数值模拟,并结合现场监测数据,研究在该类问题的数值模拟中两个强度准则的适用性。
1 工程概况黔春大道七冲村二号隧道设计行车速度40 km/h,为双向8车道城市主干道隧道,隧道为小净距隧道。隧道起止里程K2+680~K3+040,长360 m。隧道开挖采用钻爆法施工,结构形式选用单线单洞四心圆断面,拱半径10.5 m,曲墙半径6.25 m,内轮廓净宽19.4 m,净高9.4 m。初衬采用钢拱架、锚杆、钢筋网、喷射混凝土组合衬砌,二衬采用C35防水钢筋混凝土,厚0.6 m。
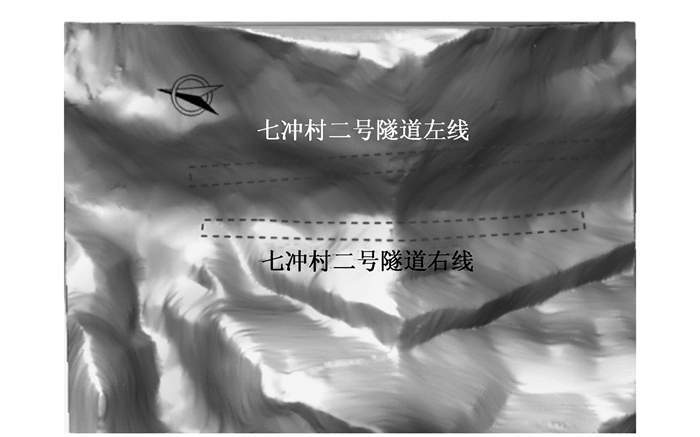
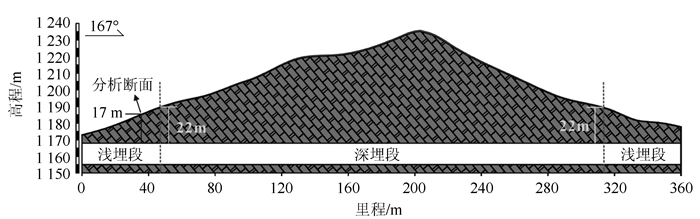
隧道洞口处采用明挖法,后过渡至暗挖。由于地形原因(见图 1),隧道进口端和出口端各有一段浅埋偏压地段,如图 2所示。根据隧道宽度、围岩级别等因素,确定浅埋临界深度为22 m,隧道上方地形坡度约为30°。
|
| 图 1 七冲村二号隧道地形云图 Fig. 1 Nephogram of Tunnel No. 2 in Qichong Village |
| |
|
| 图 2 七冲村二号隧道左洞纵剖面 Fig. 2 Longitudinal section of left tunnel of Tunnel No. 2 in Qichong Village |
| |
拟建场区主要受黔灵湖向斜影响,岩层产状87°~103°,倾角54°~73°,岩体节理裂隙较发育,岩体较破碎。
根据区域地质资料及钻探揭示,场地上覆土层主要为耕植土(少量堆积体),下覆基岩为侏罗系中下统自流井组(J1-2zl)泥砂岩夹白云质灰岩,对岩土层分述如下:
泥质砂岩(J1-2zl):紫红色,灰绿色,薄至中厚层泥质砂岩,强~中风化,细晶结构,节理裂隙较发育。白云质灰岩(J1-2zl):灰白色,薄至中厚层中白云质灰岩,强~中风化,细晶结构,节理裂隙较发育。
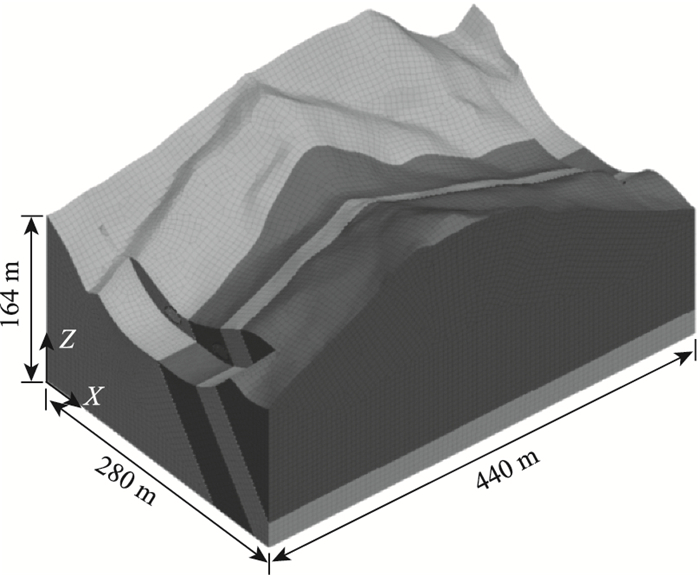
2 计算模型 2.1 模型介绍按实际地形建立三维模型。计算模型长440 m,宽280 m,隧道底部距模型底部96 m。由于隧道进出口处埋深较浅,采用明挖法,建立模型时挖掉了这两处。隧道暗挖段长360 m,两隧道中心距60.5 m,隧道高宽等参数与工程概况中所介绍的相同。
初衬中的锚杆采用cable单元,钢拱架采用beam单元,喷射混凝土及钢筋网根据实际设计资料,结合相关数值模拟经验,等效成shell单元进行模拟;二衬采用实体单元。
模型的地层根据钻探资料简化为白云质灰岩(灰白色)及泥砂岩(灰绿色)互层,共4层,如图 3所示。地表为自由边界,四周为辊支撑,底面设固定约束。
|
| 图 3 计算模型 Fig. 3 Computation model |
| |
2.2 岩体及支护结构力学参数
隧道围岩分别采用FLAC3D中基于Mohr-Coulomb强度准则的本构模型和基于Hoek-Brown强度准则的本构模型。支护结构采用弹性模型。
2.2.1 Mohr-Coulomb强度准则力学参数根据室内试验得出泥砂岩及白云质灰岩的弹性模量、黏聚力、内摩擦角等物理力学参数,见表 1。
| 参数 | 密度/ (g·cm-3) |
弹性模量/GPa | 泊松比 | 黏聚力/ MPa |
内摩擦角/(°) |
| 泥砂岩 | 2.6 | 20 | 0.3 | 2.1 | 31 |
| 白云质灰岩 | 2.7 | 30 | 0.26 | 3.4 | 35 |
2.2.2 Hoek-Brown强度准则力学参数
根据E-Hoek等提出的基于GSI的岩体参数mb,s,a的取值方法[27]:
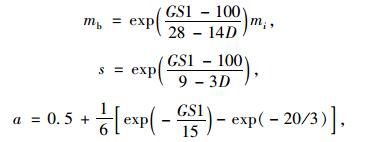
|
式中D为考虑爆破影响和应力释放的扰动参数,实际施工过程中采用钻爆法施工,为小规模光面爆破,根据表 2,取D=0.1。
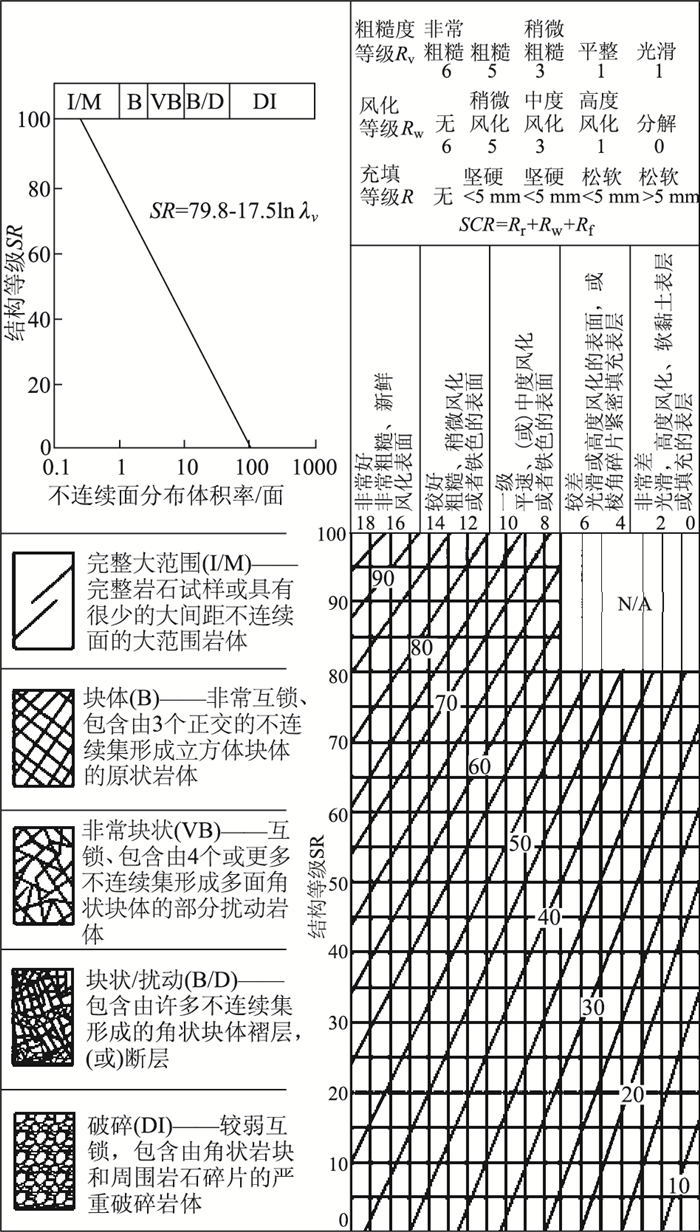
GSI是地质强度指标的简称,通过岩体结构和结构面特征对岩体强度进行量化。本研究根据1999年H. Sonmez等提出的GSI定量评价方法,通过线性拟合和综合打分的方法对岩体结构和结构面参数进行量化,根据图 4可查得GSI值。根据现场调查分析可知,泥砂岩不连续面分布体积率约为7,不连续面稍微粗糙,中风化,含松软填充物 < 5 mm,综合结构面等级SR及结构面参数Rf,Rw,Rc,量化地质强度指标为45。白云质灰岩不连续面分布体积率约为2,不连续面稍微粗糙,中风化,含松软填充物 < 5 mm,综合结构面等级SR及结构面参数Rf,Rw,Rc,量化地质强度指标为55。
mi为岩石量纲统一的经验参数,反应岩石的软硬程度,取值范围为0.001~25.0,可根据表 3得出,泥砂岩mi可取7,白云质灰岩可取9。
| 岩石类型 | 分类 | 小类 | 不同质地岩石及其mi值 | |||
| 粗糙的 | 中等的 | 精细的 | 非常精细的 | |||
| 沉积岩 | 碎屑 | 砾岩(21±3)*角砾岩(19±5) | 砂岩17±4 | 粉砂岩7±2硬砂岩(18±3) | 黏土岩4±2页岩(6±2)泥灰岩(7±2) | |
| 非碎屑 | 碳酸盐 | 结晶灰岩(12±3) | 粉晶灰岩(10±2) | 微晶灰岩(9±2) | 白云石(9±3) | |
| 蒸发盐 | 石膏8±2 | 硬石膏12±2 | ||||
| 有机物 | 白垩7±2 | |||||
| 变质岩 | 非片理化 | 大理岩9±3 | 角页岩(19±4)变质砂岩(19±3) | 石英岩20±3 | ||
| 轻微片理化 | 混合岩(29±3) | 闪岩26±6 | 片麻岩28±5 | |||
| 片理化* | 片岩12±3 | 千枚岩(7±3) | 板岩7±4 | |||
| 火成岩 | 深成类 | 浅色 | 花岗岩32±3花岗闪长岩(29±3) | 闪长岩25±5 | ||
| 深色 | 辉长岩27±3苏长岩20±5 | 粗粒玄武岩(16±5) | ||||
| 半深成类 | 斑岩(20±5) | 辉绿岩(15±5) | 橄榄岩(25±5) | |||
| 火山类 | 熔岩 | 流纹岩(25±5)安山岩25±5 | 英安岩(15±3)玄武岩(25±5) | 黑曜岩(19±3) | ||
| 火山碎屑 | 集块岩(19±3) | 角砾岩(19±5) | 凝灰岩(13±5) | |||
| 注:括号内的数值均为估计值; “*”表示该行中的值为垂直于片理层状面的岩样测试所得;当沿着弱面破坏时mi值将会明显不同。 | ||||||
将D,GSI,mi的值代入公式可得出mb,s,a共3个参数。对岩石进行点荷载试验,可整理得岩石单轴抗压强度σc。综上所述,Hoek-Brown强度准则参数见表 4。
| 参数 | σc/MPa | GSI | D | mi | mb | s | a |
| 泥灰岩 | 33 | 45 | 0.1 | 7 | 0.885 4 | 0.001 8 | 0.508 1 |
| 白云质灰岩 | 60 | 55 | 0.1 | 9 | 1.657 8 | 0.005 7 | 0.504 0 |
| 注:σc为岩石单轴抗压强度;a为针对不同岩体的量纲统一的经验参数;s反映岩体破碎程度。 | |||||||
2.3 初始应力场及开挖工序
在进行开挖模拟前,对整个模型进行初始应力平衡,以获得初始应力场。形成应力场后,位移清零。
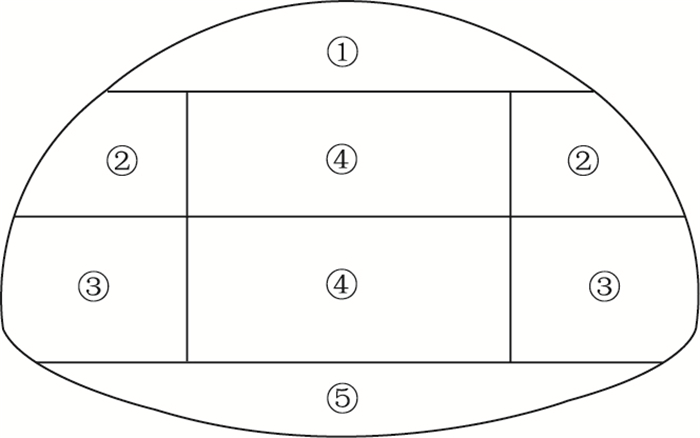
隧道施工采用三台阶法开挖,如图 5所示,首先开挖隧道顶部①作为第1台阶;然后依次开挖②、③作为第2、3台阶;预留中部核心土④保持掌子面稳定,并作为①的施工便道;台阶完成后再依次开挖核心土④及仰拱⑤。
|
| 图 5 隧道开挖顺序 Fig. 5 Sequence of tunnel excavation |
| |
模拟开挖时,按图 5所示的开挖顺序,以2 m为一个循环向前掘进。
3 模拟结果分析分别基于Mohr-Coulomb强度准则和Hoek-Brown强度准则,模拟隧道开挖全过程。选取隧道K3+005为典型断面,即开挖进尺35 m处,该断面上,隧道最大埋深17 m,属于浅埋段,断面位置如图 2所示。主要从围岩位移和应力两方面分析两种模拟结果的差异。
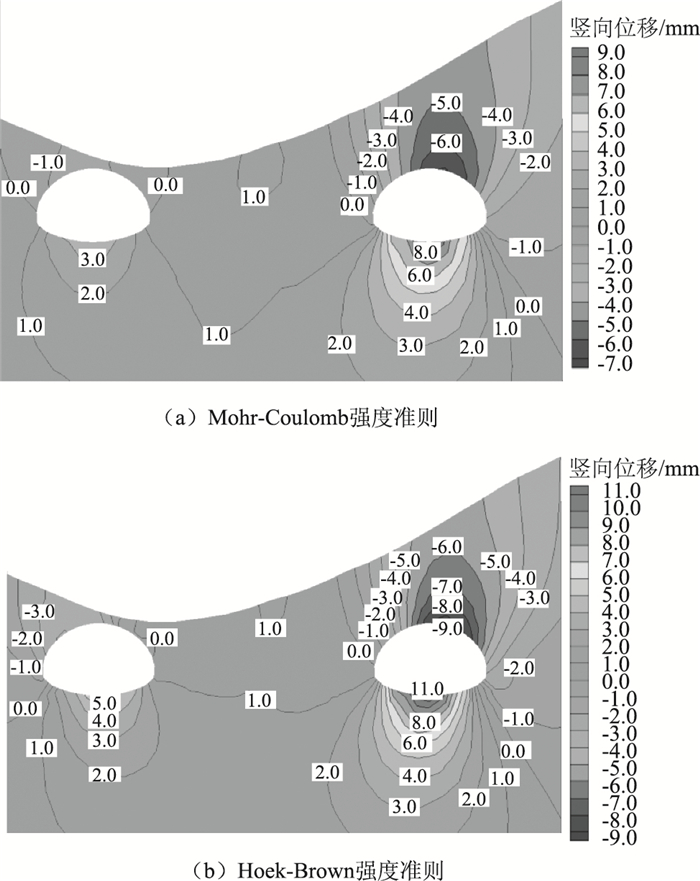
3.1 位移结果分析基于两种不同强度准则的模拟结果的隧道位移云图如图 6、图 7所示。
|
| 图 6 竖向位移 Fig. 6 Vertical displacement |
| |
|
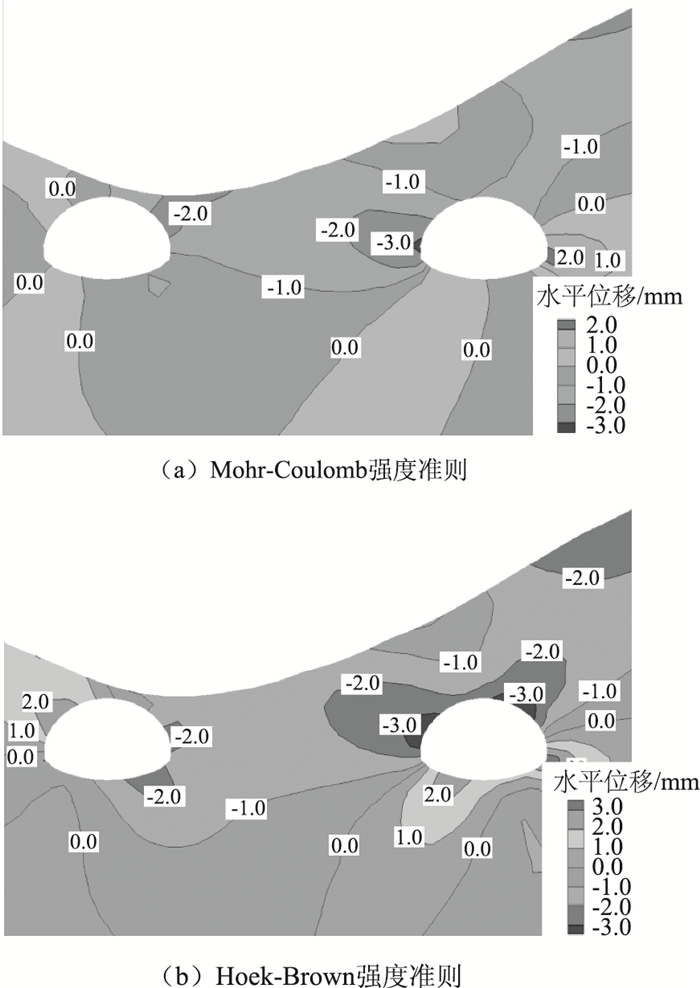
| 图 7 水平位移 Fig. 7 Level displacement |
| |
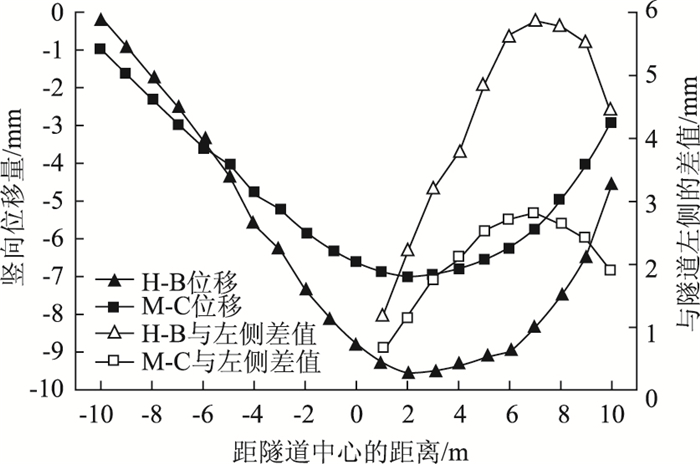
为更清晰地观察隧道受到的偏压影响,比较隧道左右两侧的位移差值。以隧道中心为零点,每隔1 m取一次右线隧道拱顶的竖向、水平位移值,并比较隧道左右两侧的位移差值,绘制成曲线,如图 8、图 9所示。
|
| 图 8 右线隧道顶部沉降曲线 Fig. 8 Settlement curves of right tunnel top |
| |
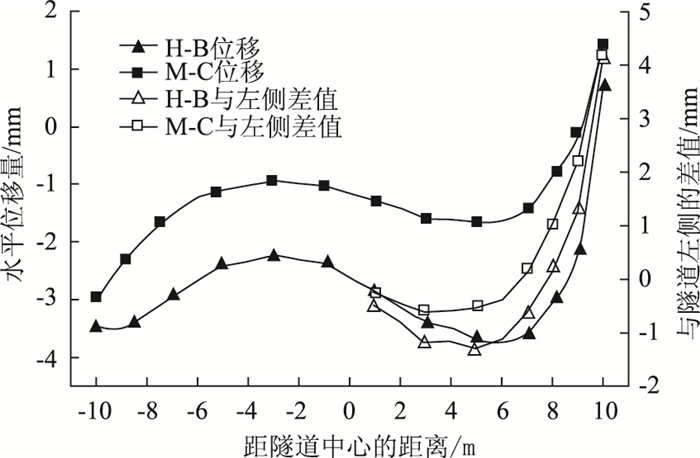
|
| 图 9 右线隧道顶部水平收敛曲线 Fig. 9 Horizontal convergence curves of right tunnel top |
| |
右线隧道中,基于Mohr-Coulomb强度准则的模拟结果中,最大竖向位移出现在距隧道中心向右约2 m处,最大值为7.13 mm。隧道右侧与左侧的竖向位移最大差值出现在距隧道中心约7 m处,最大差值为2.82 mm。最大水平位移出现在距隧道中心向左约10 m处,最大值为3.29 mm。隧道右侧与左侧的水平位移最大差值出现在距隧道中心约10 m处,最大差值为4.39 mm。
基于Hoek-Brown强度准则的模拟结果中,最大竖向位移也出现在距隧道中心向右约2 m处,最大值为9.81 mm。隧道右侧与左侧的最大差值出现在距隧道中心约7 m处,最大差值为5.88 mm。最大水平位移也出现在距隧道中心向右约6 m处,最大值为3.82 mm。隧道右侧与左侧的最大差值出现在距隧道中心约10 m处,最大差值为4.16 mm。
两种模拟结果的位移具有相似的规律,而基于Hoek-Brown强度准则模拟结果的位移值明显大于基于Mohr-Coulomb强度准则的模拟结果。
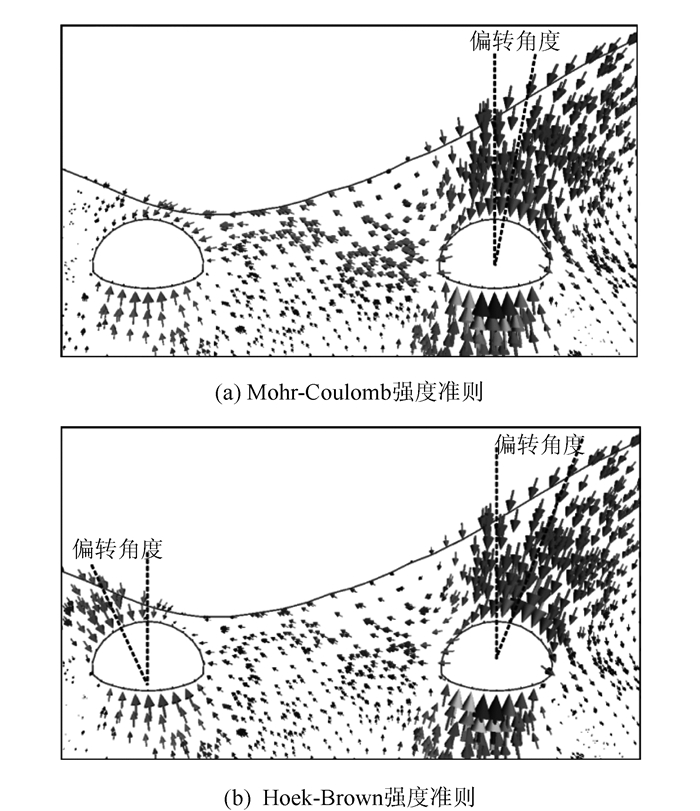
在没有偏压的情况下,隧道的最大竖向位移通常产生于拱顶和拱底,最大水平位移则产生于两侧的拱脚处。而在偏压情况下,最大竖向位移发生偏转,且与基于Mohr-Coulomb强度准则模拟结果相比,基于Hoek-Brown强度准则模拟结果的右线隧道竖向位移偏转角度更大,既偏压效果更明显,如图 10所示。
|
| 图 10 位移矢量 Fig. 10 Displacement vectors |
| |
右线隧道中,两种模拟结果的拱顶拱底围岩表现为向隧道内挤入,左右两侧则表现为向外挤出。
但在左线隧道中,基于Mohr-Coulomb强度准则模拟结果的变形较为异常,由于受到右线隧道变形的影响,并没有表现出偏压的影响,反而浅埋侧位移比深埋侧更大,且左右两侧围岩均向隧道内挤入。而基于Hoek-Brown强度准则模拟结果仍然表现出了偏压的影响,但同样受到右线隧道变形的影响,与右线隧道不同的是,它的左右两侧围岩表现为向内挤入。
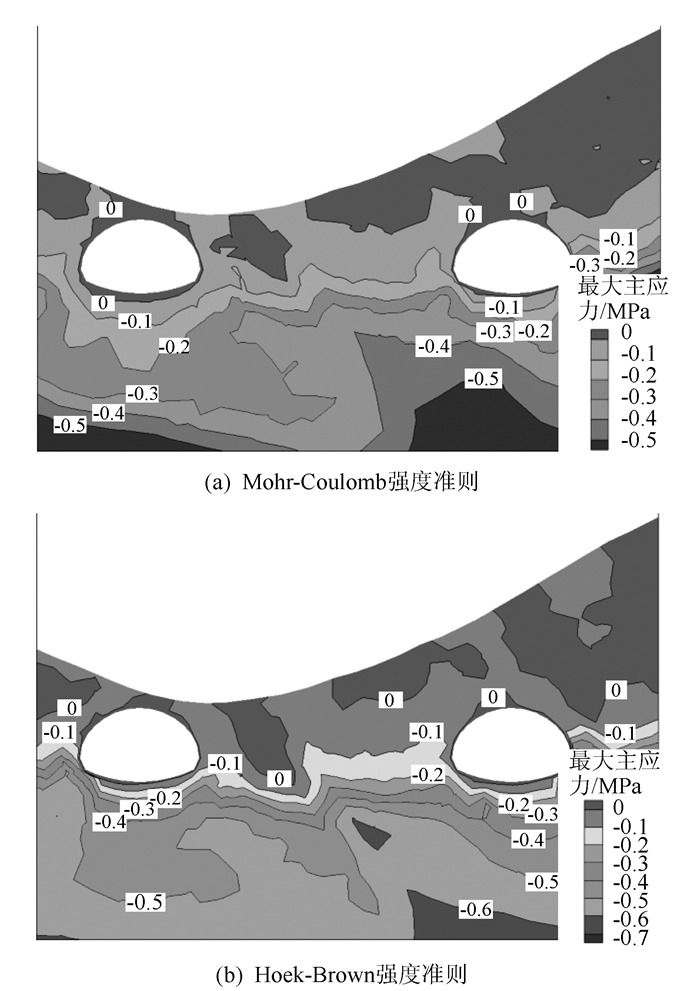
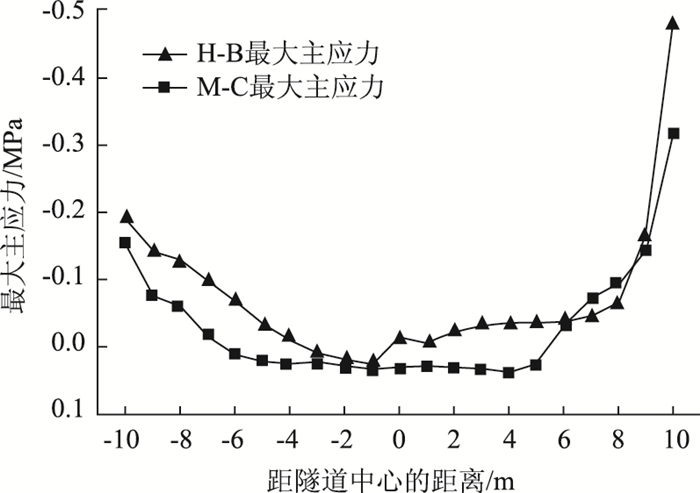
3.2 应力结果分析基于两种不同强度准则的模拟结果的最大主应力云图如图 11所示。以隧道中心为零点,每隔1 m取一次右线隧道拱顶的最大主应力值,绘制成曲线,如图 12所示。
|
| 图 11 最大主应力 Fig. 11 Maximum principal stresses |
| |
|
| 图 12 右线隧道顶部最大主应力曲线 Fig. 12 Minimum principal stress curves of right tunnel top |
| |
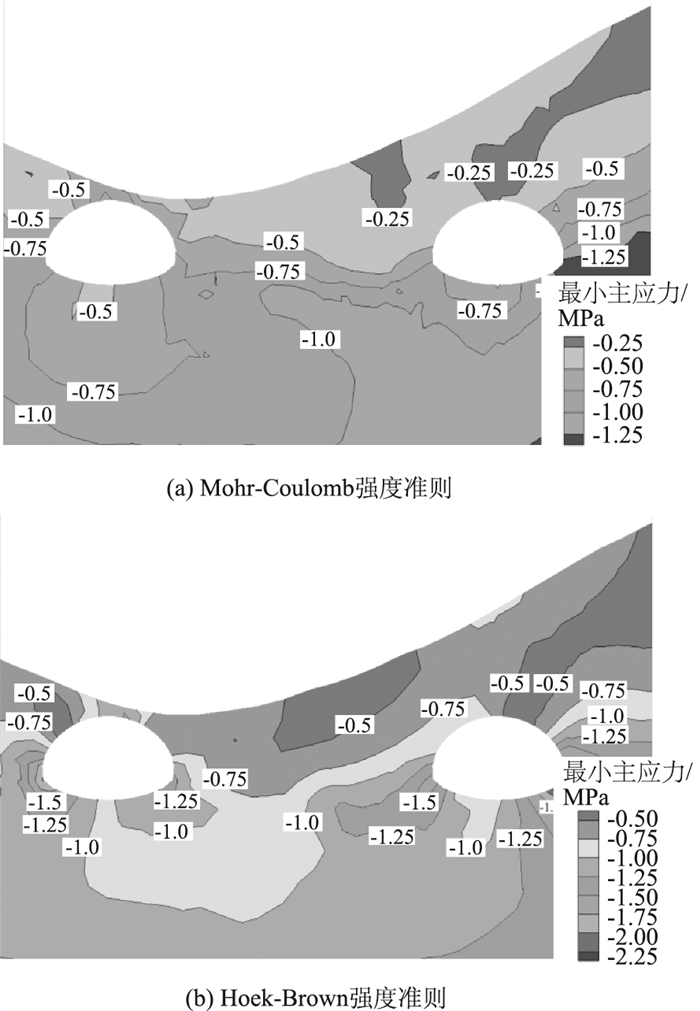
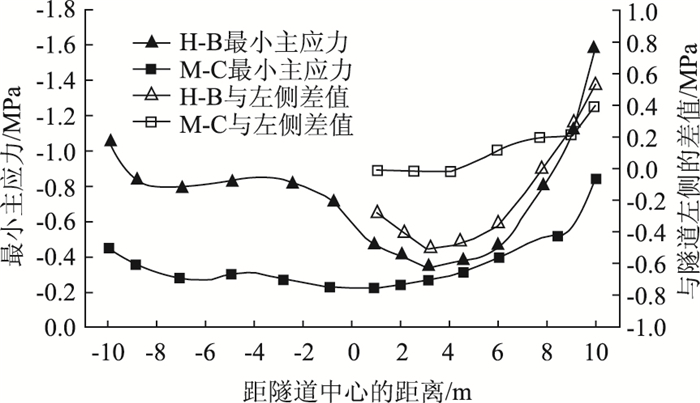
基于两种不同强度准则的模拟结果的最小主应力云图如图 13所示。以隧道中心为零点,每隔1 m取一次右线隧道拱顶的最小主应力值,为了更清晰地观察隧道受到的偏压影响,比较隧道左右两侧的最小主应力差值,比较左右两侧的最小主应力差值,绘制成曲线,如图 14所示。
|
| 图 13 最小主应力 Fig. 13 Minimum principal stresses |
| |
|
| 图 14 右线隧道顶部最小主应力曲线 Fig. 14 Minimum principal stress curves of right tunnel top |
| |
右线隧道中,基于Mohr-Coulomb强度准则的模拟结果中,最大主应力的最大值为0.04 MPa,出现在距隧道中心向右约4 m处;最小主应力的最大值为0.85 MPa,出现在距隧道中心向右约10 m处。隧道右侧与左侧的最小主应力最大差值出现在距隧道中心约10 m处,最大差值为0.40 MPa。
基于Hoek-Brown强度准则的模拟结果中,最大主应力的最大值为0.03 MPa,出现在距隧道中心向左约1m处;最小主应力的最大值为1.59 MPa,出现在距隧道中心向右约10 m处。隧道右侧与左侧的最小主应力最大差值出现在距隧道中心约10 m处,最大差值为0.53 MPa。
两种模拟结果的最大主应力最大值均为正,都位于隧道顶部,也就是说隧道顶部都出现了拉应力。但基于Mohr-Coulomb强度准则模拟结果的隧道顶部出现拉应力的范围更大,数值也更大。两种模拟结果中的最大主应力都受到了偏压的影响,但影响不大。最大主应力在隧道右拱脚出现最小值。
两种模拟结果的最小主应力均为压应力,从隧道中心向两边逐渐减小,深埋侧边墙比浅埋侧边墙的应力集中更明显,承受更大的应力;至拱脚处,最小主应力达到最小值,且深埋深侧拱脚的最小主应力大于浅埋深侧。
在偏压影响下,基于Hoek-Brown强度准则模拟结果的最小主应力以及主应力迹线偏转角度明显大于基于Mohr-Coulomb强度准则的模拟结果,如图 14和15所示。

|
| 图 15 右线隧道主应力迹线 Fig. 15 Main stress traces of right tunnel |
| |
3.3 与监测结果的比较
隧道由大里程向小里程开挖,当右线隧道开挖至里程K2+779,即开挖进尺259 m时,在初衬施作完毕后,在侧壁上钻孔安装多点位移计,位移计安装在隧道左右两侧的拱脚部位。在模拟时,对该处进行水平位移监测,可获得围岩水平位移随开挖进尺变化的曲线图。
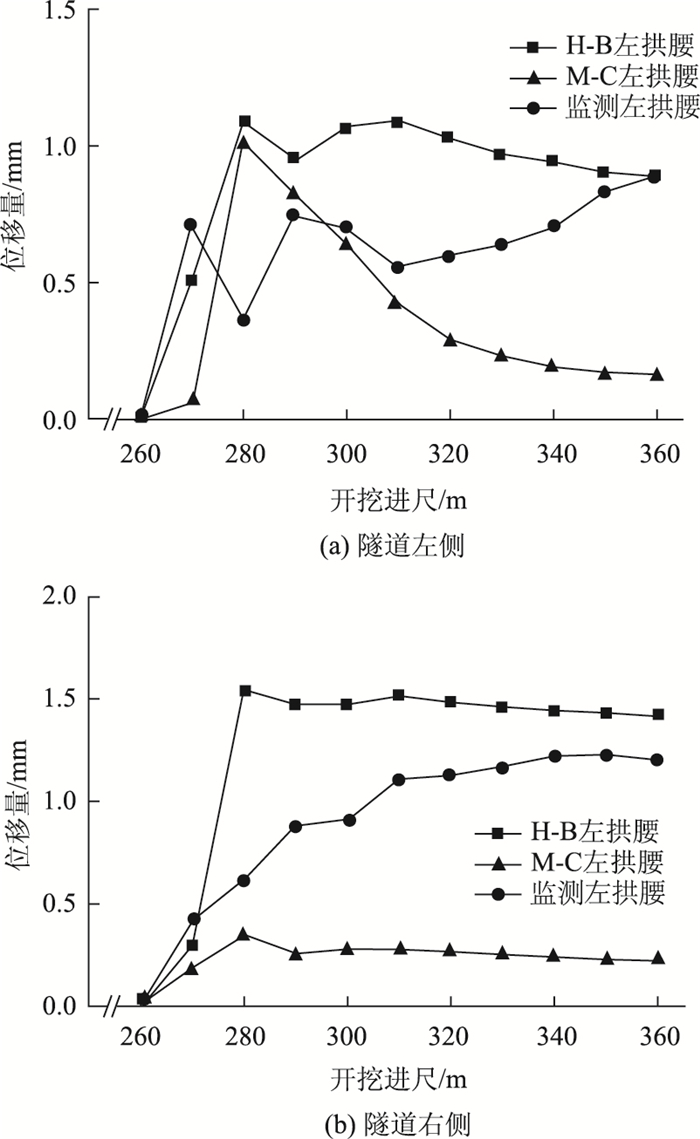
将监测数据与两种模拟结果所得的水平位移曲线进行比较,如图 16所示。
|
| 图 16 围岩水平位移变化曲线 Fig. 16 Horizontal displacement curves of surrounding rock |
| |
在该断面上,隧道埋深早已超过临界深度,属于深埋段,两种模拟结果的水平位移变化与监测结果的趋势大致相同,相比之下,基于Hoek-Brown强度准则模拟结果的水平位移变化曲线与监测结果的相关性更好。
隧道两侧拱脚处的水平位移均为正,是由于受到偏压影响,位移矢量发生偏转,右侧拱脚处的变形表现为向隧道外挤出,与之对称的变形出现在左侧拱脚偏上处,而左侧拱脚表现为向隧道内挤入,因此位移为正。
同样由于偏压的影响,隧道右侧的位移比左侧的略大,基于Hoek-Brown强度准则模拟结果左侧的最终位移为0.88 mm,右侧为1.41 mm;基于Mohr-Coulomb的左侧最终位移为0.16 mm,右侧为0.22 mm;监测结果的左侧最终位移为0.89 mm,右侧为1.20 mm。两种模拟结果与监测结果均有此特点。
4 结论根据Mohr-Coulomb强度准则和Hoek-Brown强度准则各自的特点,从竖向位移、水平位移、最小主应力等方面对比分析两种模拟结果,得出以下结论:
(1) Mohr-Coulomb强度准则将围岩视为连续介质,其破坏模式为线性破坏,而Hoek-Brown强度准则将围岩视为非连续介质,反映了岩体非线性破坏的特点,考虑了岩体中的结构面等因素对强度的影响。因此,在位移及应力分析中,基于Hoek-Brown强度准则模拟结果的竖向位移、水平位移及应力值都更大。
(2) 由于受到偏压的影响,两种模拟结果的位移矢量及主应力迹线与正常情况下不同,发生了一定角度的偏转。右线隧道中,相比基于Mohr-Coulomb强度准则的模拟结果,基于Hoek-Brown强度准则模拟结果的偏转角度更大,受到偏压的影响更大。
在左线隧道中,基于Mohr-Coulomb强度准则模拟结果的变形较为异常,由于受到右线隧道变形的影响,左线隧道并没有表现出偏压的影响,反而浅埋侧位移比深埋侧更大。
(3) 但是在低应力状态下,Mohr-Coulomb强度准则的适用性仍较好,因此在浅埋段中,基于两种强度准则的模拟结果在变形的发展趋势上以及应力重分布的情况都大致吻合。
右线隧道中,最大沉降出现在隧道中心偏深埋侧,最大水平位移出现在深埋侧拱脚及浅埋侧拱腰。最大主应力在隧道顶部出现的最大值为正值(拉应力),最大主应力从隧道中心向两侧逐渐减小,变为负值,在深埋侧拱脚出现最小值。但基于Mohr-Coulomb强度准则模拟结果的隧道顶部出现拉应力的范围更大,数值也更大。最小主应力的最大值出现在隧道中心偏深埋侧,从拱顶向两侧逐渐减小,在深埋侧拱脚处达到最小值;相比于浅埋侧,深埋侧的边墙及拱脚承受更大的应力。
(4) 两种模拟结果的水平位移变化与监测结果的趋势大致相同,相比之下,基于Hoek-Brown强度准则模拟结果的水平位移变化曲线与监测结果的相关性更好。
| [1] |
康勇, 杨春和, 何正, 等. 煤系地层大跨度隧道围岩结构稳定性研究[J]. 岩土力学, 2010, 31(增1): 266-278. KANG Yong, YANG Chun-he, HE Zheng, et al. Stability Analysis of Surrounding Rock Structure of Large-span Tunnel Passing through Coal Seams[J]. Rock and Soil Mechanics, 2010, 31(S1): 266-278. |
| [2] |
张顶立, 王梦恕, 高军, 等. 复杂围岩条件下大跨隧道修建技术研究[J]. 岩土力学与工程学报, 2003, 22(2): 290-296. ZHANG Ding-li, WANG Meng-shu, GAO Jun, et al. Construction Technique of Large-span Tunnel under Condition of Complicated Surrounding Rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2): 290-296. |
| [3] |
汤劲松, 刘松玉, 童立元, 等. 破碎岩体浅埋大跨公路隧道开挖方案对比研究[J]. 岩土力学, 2007, 28(S1): 469-473. TANG Jin-song, LIU Song-yu, TONG Li-yuan, et al. Comparative Study on Tunneling Scheme of Shallow Overburden and Large-span Highway Tunnel in Cracked Rock Mass[J]. Rock and Soil Mechanics, 2007, 28(S1): 469-473. |
| [4] |
朱正国, 乔春生, 高保彬. 浅埋偏压连拱隧道的施工优化及支护受力特征分析[J]. 岩土力学, 2008, 29(10): 2747-2758. ZHU Zheng-guo, QIAO Chun-sheng, GAO Bao-bin. Analysis of Construction Optimization and Supporting Structure under Load of Shallow Multi-arch Tunnel under Unsymmetrical Pressure[J]. Rock and Soil Mechanics, 2008, 29(10): 2747-2758. |
| [5] |
王更峰, 熊晓晖, 张永兴, 等. 大跨小净距隧道合理开挖方法与支护参数对比研究[J]. 公路交通科技, 2011, 28(3): 101-107. WANG Geng-feng, XIONG Xiao-hui, ZHANG Yong-xing, et al. Comparative Study of Rational Excavation Method and Support Parameter for Large-span Small-spacing Tunnel[J]. Journal of Highway and Transportation Research and Development, 2011, 28(3): 101-107. |
| [6] |
王军, 曹平, 林杭. 受偏压隧道影响边坡加固的数值分析[J]. 公路交通科技, 2009, 26(9): 102-106. WANG Jun, CAO Ping, LIN Hang. Numerical Analysis of Slope Reinforcement with Effect of Bias Tunnel[J]. Journal of Highway and Transportation Research and Development, 2009, 26(9): 102-106. |
| [7] |
安永林, 史胜利, 彭立敏, 等. 隧道浅埋软弱围岩段双下侧导坑施工性态[J]. 公路交通科技, 2009, 26(1): 114-119. AN Yong-lin, SHI Sheng-li, PENG Li-min, et al. Construction Behavior of Double Down-side Drifts in a Weak Tunnel with Shallow Cover[J]. Journal of Highway and Transportation Research and Development, 2009, 26(1): 114-119. |
| [8] |
伍国军, 陈卫忠, 戴永浩, 等. 浅埋大跨公路隧道施工过程和支护优化的研究[J]. 岩土工程学报, 2006, 28(9): 1118-1123. WU Guo-jun, CHEN Wei-zhong, DAI Yong-hao, et al. Study on Excavation Sequences and Support Optimization for Shallow-buried and Large-spanned Tunnels[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1118-1123. |
| [9] |
高世军, 张学民. 地形与地质构造偏压隧道结构受力分析[J]. 中外公路, 2009, 29(5): 204-207. GAO Shi-jun, ZHANG Xue-min. Analysis of Structure under Load of Bias Tunnel Caused by Terrain and Geological Structure[J]. Journal of China and Foreign Highway, 2009, 29(5): 204-207. |
| [10] |
张成平, 张顶立, 王梦恕. 大断面隧道施工引起的上覆地铁隧道结构变形分析[J]. 岩土工程学报, 2009, 31(5): 805-810. ZHANG Cheng-ping, ZHANG Ding-li, WANG Meng-shu. Structural Deformation of Overlying Subway Tunnels Induced by Tunneling[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(5): 805-810. |
| [11] |
王亚琼, 张少兵, 谢永利, 等. 浅埋偏压连拱隧道非对称支护结构受力性状分析[J]. 岩石力学与工程学报, 2010, 29(增1): 3265-3272. WANG Ya-qiong, ZHANG Shao-bing, XIE Yong-li, et al. Mechanical Characteristics of Unsymmetrical Support Structure of Shallow-buried Bias Multi-arch Tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 3265-3272. |
| [12] |
赵坚, 李海波. 摩尔-库伦和霍克-布朗强度准则用于评估脆性岩石动态强度的适用性[J]. 岩石力学与工程学报, 2003, 22(2): 171-176. ZHAO Jian, LI Hai-bo. Estimating the Dynamic Strength of Rock Using Mohr-Coulomb and Hoek-Brown Criteria[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2): 171-176. |
| [13] |
安永林, 黄戡, 彭立敏, 等. 强度折减法分析隧道整体稳定性[J]. 公路交通科技, 2011, 28(4): 91-95. AN Yong-lin, HUANG Kan, PENG Li-min, et al. Analysis of Tunnel Stability Based on Strength Reduction Method[J]. Journal of Highway and Transportation Research and Development, 2011, 28(4): 91-95. |
| [14] |
王伟峰, 毕俊丽. 软岩浅埋隧道施工工法比选[J]. 岩土力学, 2007, 28(增1): 430-436. WANG Wei-feng, BI Jun-li. Construction Project Optimizing of Soft Rock and Shallow Buried Tunnel[J]. Rock and Soil Mechanics, 2007, 28(S1): 430-436. |
| [15] |
王绍君, 刘宗仁, 陶夏新. 浅埋暗挖隧道施工性态的数值模拟与分析[J]. 土木工程学报, 2007, 40(6): 75-79. WANG Shao-jun, LIU Zong-ren, TAO Xia-xin. Numerical Simulation and Analysis of Construction Behavior of Shallow Tunneling by Excavation[J]. China Civil Engineering Journal, 2007, 40(6): 75-79. |
| [16] |
王清标, 蒋金泉, 路林海, 等. 不同开挖方式对近距离交叠隧道影响模拟研究[J]. 岩石力学与工程学报, 2013, 32(10): 75-79. WANG Qing-biao, JIANG Jin-quan, LU Lin-hai, et al. Numerical Simulation for Influence Law of Different Excavation Methods on Adjacent Overlapping Tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(10): 75-79. |
| [17] |
HOEK E, BROWN E T. Underground Excavations in Rocks[M]. London: Institution of Mining and Metallurgy, 1980.
|
| [18] |
朱合华, 张琦, 章连洋. Hoek-Brown强度准则研究进展与应用综述[J]. 岩石力学与工程学报, 2013, 32(10): 1945-1963. ZHU He-hua, ZHANG Qi, ZHANG Lian-yang. Review of Research Progresses and Applications of Hoek-Brown Strength Criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(10): 1945-1963. |
| [19] |
张良刚, 吴立, 徐昌茂, 等. 基于模糊综合评判的Hoek-Brown强度准则修正及应用[J]. 岩土力学, 2013, 34(增2): 88-99. ZHANG Liang-gang, WU Li, XU Chang-mao, et al. Modification of Hoek-Brown Criterion and Its Application Based on Fuzzy Synthetic Evaluation[J]. Rock and Soil Mechanics, 2013, 34(S2): 88-99. |
| [20] |
何江达, 张建海, 范景伟. 霍克-布朗强度准则中m, s参数的断裂分析[J]. 岩石力学与工程学报, 2001, 20(4): 432-435. HE Jiang-da, ZHANG Jian-hai, FANG Jing-wei. Fracture Analysis on the Parameters m, s in Hoek-Brown Strength Criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(4): 432-435. |
| [21] |
EBERHARDT E. The Hoek-Brown Failure Criterion[J]. Rock Mechanics and Rock Engineering, 2012, 45(6): 981-988. |
| [22] |
段群苗, 白浪峰, 任辉龙. 基于Hoek-Brown强度准则的大跨连拱隧道围岩稳定性分析[J]. 现代隧道技术, 2013, 50(6): 94-100. DUAN Qun-miao, BAI Lang-feng, REN Hui-long. Stability Analysis of the Surrounding Rock of Large-Span Multi-Arch Tunnels Based on the Hoek-Brown Criterion[J]. Modern Tunneling Technology, 2013, 50(6): 94-100. |
| [23] |
刘立鹏, 姚磊华, 陈洁, 等. 基于Hoek-Brown强度准则的岩质边坡稳定性分析[J]. 岩石力学与工程学报, 2010, 29(增1): 2879-2886. LIU Li-peng, YAO Lei-hua, CHEN Jie, et al. Rock Slope Stability Analysis Based on Hoek-Brown Failure Criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 2879-2886. |
| [24] |
谷拴成, 张磊. 基于霍克-布朗准则的巷道围岩塑性区估计[J]. 煤炭工程, 2012, 9(9): 70-73. GU Shuan-cheng, ZHANG Lei. Estimation on Plastic Zone of Surrounding Rock in Mine Roadway Based on Hock-Brown Criterion[J]. Coal Engineering, 2012, 9: 70-73. |
| [25] |
郑颖人, 沈珠江, 龚晓南. 广义塑性力学-岩土塑性力学原理[M]. 北京: 中国建筑工业出版社, 2002. ZHENG Ying-ren, SHEN Zhu-jiang, GONG Xiao-nan. Generalized Plastic Mechanics:The Principles of Geotechnical Plastic Mechanics[M]. Beijing: China Architecture and Building Press, 2002, 51-61. |
| [26] |
邓楚键, 何国杰, 郑颖人. 基于M-C准则的D-P系列准则在岩土工程中的应用研究[J]. 岩土工程学报, 2006, 28(6): 735-739. DENG Chu-jian, HE Guo-jie, ZHENG Ying-ren. Studies on Drucker-Prager Yield Criterions Based on M-C Yield Criterion and Application in Geotechnical Engineering[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 735-739. |
| [27] |
HOEK E, CARRANZA-TORRES C, CORKUM B. Hoek-Brown Failure Criterion-2002 Edition[C]//Proceedings of the North American Rock Mechanics Society NARMS-TAC 2003. Toronto: University of Toronto Press, 2002: 267-273.
|
| [28] |
SONMEZ H, ULUSAY R. Modifications to the Geological Strength Index (GSI) and Their Applicability to Stability of Slopes[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(6): 743-760. |
| [29] |
HOEK E, BROWN E T. Practical Estimates of Rock Mass Strength[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165-1186. |
 2018, Vol. 35
2018, Vol. 35