扩展功能
文章信息
- 赵明华, 吴文, 陈言章
- ZHAO Ming-hua, WU Wen, CHEN Yan-zhang
- 考虑嵌岩段侧摩阻力的溶洞顶板稳定性研究
- Study on Stability of Karst Cave Roof Considering Side Friction Resistance of Rock-socketed Section
- 公路交通科技, 2018, 35(8): 73-79
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(8): 73-79
- 10.3969/j.issn.1002-0268.2018.08.011
-
文章历史
- 收稿日期: 2017-02-21
我国疆域辽阔,岩溶地质分布广泛,约占国土面积的1/3[1-2]。在岩溶区进行桥梁桩基设计和施工时,溶洞顶板安全厚度的计算是工程设计的关键技术之一。
目前,众多学者对该课题进行了研究,主要从试验、数值、理论3方面展开。试验研究方面,刘铁雄[3]、王革立[4]探讨了不同厚度、跨度对溶洞顶板极限承载力的影响,并给出了经验计算公式。张慧乐[5]、张智浩等[6]研究了不同形状、大小、位置的溶洞极限破坏模式,并给出了不同破坏模式下的理论计算方法。在数值研究方面,阳军生等[7]利用ABAQUS对溶洞上方圆形地基极限承载力进行了探讨。尹凯丽等[8]基于ANSYS有限元软件,研究了溶洞高度顶板厚度顶板跨度和岩体强度对桩基承载力的影响。在理论研究方面,刘之葵等[9]在弹性力学的基础上,结合格里菲斯准则对溶洞稳定性进行了评价。赵明华等[10-12]将桩端持力岩层视为刚性板,分别从抗冲切、抗剪切、抗弯拉3方面对溶洞稳定性进行了验算。在此基础上,柏华军[13]考虑溶洞顶板自重的影响,对溶洞顶板抗冲切、抗剪切、抗弯拉验算方法进行了完善。
在工程实践中,溶洞的形态分布比较复杂,将溶洞视为梁板结构能较好地满足工程的需求。现有的理论研究计算模型简单,能较好地指导工程实践,但未考虑桩岩侧阻力对顶板承载力的影响。史佩栋等[14]、明可前[15]的研究成果表明,嵌岩桩侧阻力占总极限承载力的比例较大,且桩土侧阻力较小,桩岩侧阻力较大。A. Serran等[16]对嵌岩桩侧摩阻力的研究也表明嵌岩段侧摩阻力能提供较大的承载力。因此,嵌岩桩作用在溶洞顶板上时,桩岩侧阻力对溶洞顶板的影响一般不能忽略,而目前尚缺乏考虑嵌岩段侧阻力对溶洞稳定性影响的研究。
鉴于此,本研究拟考虑桩岩侧阻力对溶洞顶板稳定性的影响,建立能考虑桩岩侧阻力影响的简化计算模型,分别对溶洞顶板的抗冲切、抗剪切、抗弯拉验算方法进行完善,以期为工程实践提供参考。
1 计算模型及基本假定为便于分析,本研究结合岩溶区桩基工程特点,将计算模型简化(见图 1),并作如下假定。

|
| 图 1 简化计算模型 Fig. 1 Simplified calculation model |
| |
(1) 溶洞顶板为周边固支的圆板。
(2) 基桩作用在溶洞顶板几何中心,不考虑桩土摩阻力。
(3) 溶洞天然状态下处于稳定状态,不考虑地下水和时间效应的影响,且不计软弱下卧层对溶洞顶板的顶托力。
图 1中,D为桩径,h为嵌岩深度,H为顶板厚度,L为顶板跨度。
2 溶洞顶板安全厚度验算溶洞顶板在嵌岩桩荷载作用下可能出现冲切破坏、剪切破坏、弯拉破坏,为保证工程的安全性,溶洞顶板须符合抗冲切、抗剪切、抗弯拉验算的要求。下面将分别给出3种破坏模式的验算方法。
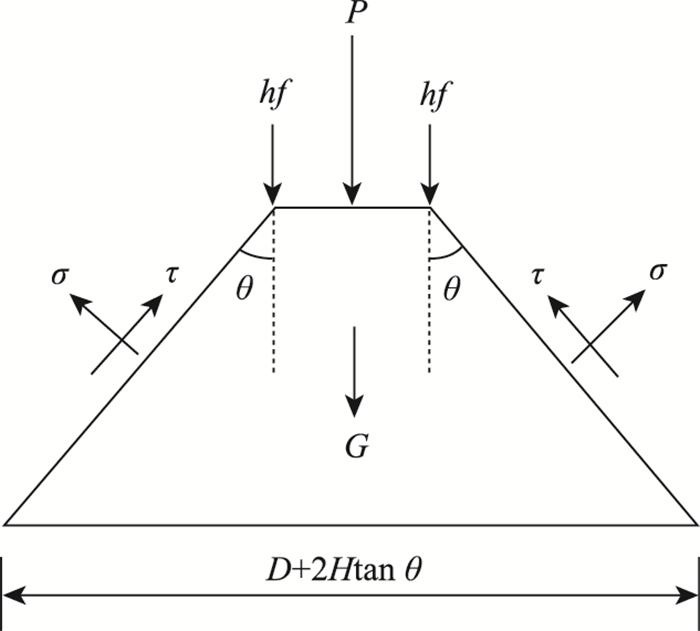
2.1 抗冲切验算溶洞顶板发生冲切破坏时,会产生一个冲切圆锥台,取该圆锥台作为分析对象,其受力情况如图 2所示。
|
| 图 2 冲切破坏模式 Fig. 2 Punching failure model |
| |
图 2中,P为嵌岩桩桩端荷载,f为桩岩侧摩阻力,根据《公路桥涵地基基础设计规范》(JTG D63—2007)[17],可取f=0.05σc(σc为岩石抗压强度),σ和τ分别为冲切破坏面上的正应力、切应力,G为冲切锥台的自重,θ为冲切破坏角,通常可取θ=45°-φ/2(φ为岩石的内摩擦角)。
假定冲切破坏面的应力均匀分布,由静力平衡条件可得冲切面上的平均应力σl为:

|
(1) |
式中,A为冲切破坏面的面积,可由式(2)确定:
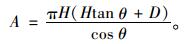
|
(2) |
锥台的自重G为:

|
(3) |
式中γ为岩石的重度。
将σl沿冲切面分解,可得冲切面的正应力、切应力为:

|
(4) |

|
(5) |
通过大、小主应力转换公式:

|
(6) |
可得冲切面上大、小主应力为:

|
(7) |
式中,
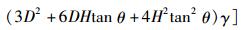
本研究采用格里菲斯[17]判据来判断溶洞顶板是否破坏,其表达式如下:

|
(8) |
式中σt为岩石的抗拉强度。
式(8)中规定压应力为正,拉应力为负,与式(7)中符号规定相反。因此,对溶洞顶板进行抗冲切验算时,需要对式(7)进行符号变换。
本研究所提抗冲切验算方法相对已有研究具有以下创新:(1)考虑了嵌岩段岩层侧阻力的影响;(2)考虑了冲切锥台及顶板上覆地层自重的影响。
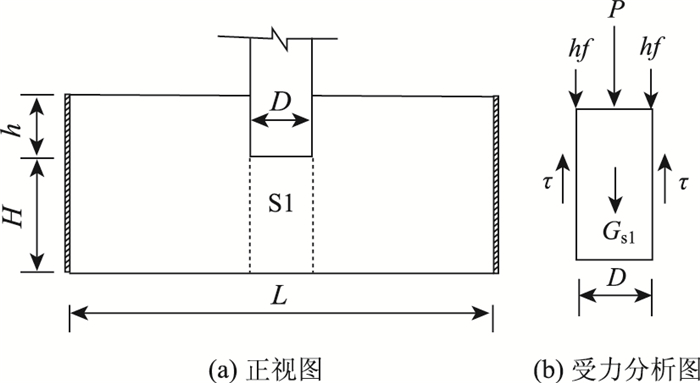
2.2 抗剪切验算溶洞顶板在嵌岩桩荷载作用下发生剪切破坏时,可分两种情况:(1)桩端岩层发生剪切破坏,如图 3(a)所示;(2)顶板边缘岩层发生剪切破坏,如图 4所示。下面将分别讨论两种情况的验算方法。
|
| 图 3 桩端岩层的剪切破坏 Fig. 3 Shear failure mechanism of rock stratum under pile tip |
| |
|
| 图 4 顶板边缘岩层的剪切破坏 Fig. 4 Shear failure mechanism of rock stratum at the edge of roof |
| |
(1) 桩端岩层发生剪切破坏
假定剪切面上应力分布均匀,取剪切体S1作为研究对象,受力分析如图 3(b)所示。
根据图 3(b),由静力平衡条件可得:

|
(9) |
式中Gs1为剪切体S1的自重,如式(10)所示:

|
(10) |
溶洞顶板岩石类别多为石灰岩,因此对岩石的剪切破坏用双曲线型莫尔判据[18]比较合适,其表达式为:

|
(11) |
式中, 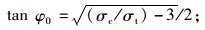
将式(9)代入式(11),则可判断桩端岩层是否会发生剪切破坏。
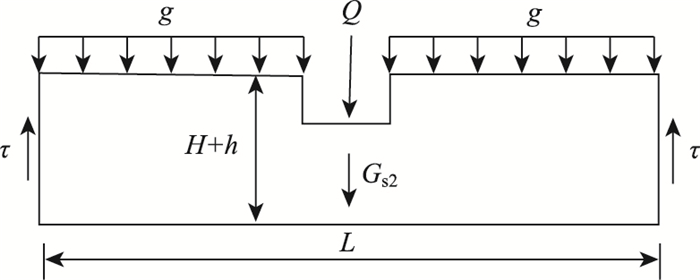
(2) 顶板边缘岩层发生剪切破坏
受力分析如图 4所示。
同样假定剪切面上应力分布均匀,取整个顶板作为研究对象,受力分析如图 4所示。
根据图 4,由静力平衡条件可得:

|
(12) |
式中,Q=P+πDhf;g为上覆土层的荷载;Gs2为顶板重度,由式(13)确定:

|
(13) |
将式(12)代入式(11),则可判断溶洞顶板边缘岩层是否会发生剪切破坏。
本研究所提抗剪切验算方法可以考虑嵌岩段岩层侧阻力、岩层自重的影响,并全面分析顶板发生剪切破坏的两种情况,能弥补已有方法在这方面的不足。
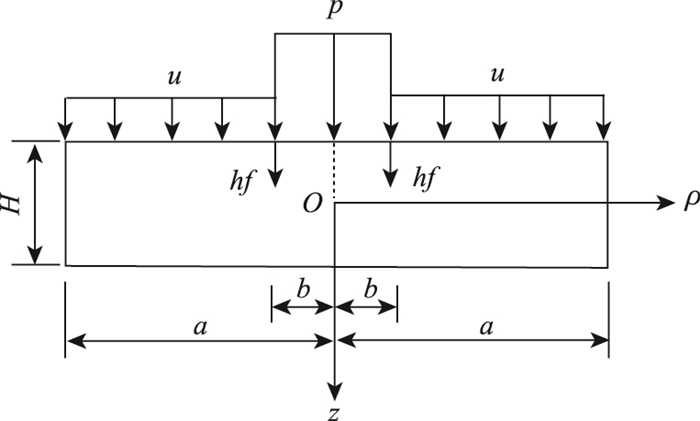
2.3 抗弯拉验算根据工程实际情况,常见的溶洞顶板跨度远大于板厚,且变形破坏时挠度变形远小于溶洞顶板厚度,因此,本研究将溶洞顶板视为周边固支圆板的小挠度弯曲问题。
抗弯验算模型如图 5所示,以O点作为坐标原点,ρ为横坐标,z为纵坐标,建立坐标系。将桩端荷载视为均布荷载p,O为顶板几何中心点,u=g+γh, a=L/2,b=D/2。
|
| 图 5 抗弯验算模型 Fig. 5 Bending check model |
| |
溶洞顶板底面中心处拉应力最大,因此,根据弹性力学的变分法[19]对溶洞顶板底面中心处拉应力进行求解。
由图 5可知,该问题为轴对称问题。根据边界条件:

|
(14) |
式中w为顶板的挠度。
因此可取挠度w的表达式为:

|
(15) |
式中C1,C2,C3为待定系数。
在式(15)中只取一个待定系数,则:

|
(16) |
式中w1为w的一个特解。
由变分法可得圆板的形变势能Vε为:

|
(17) |
式中N为薄板的弯曲刚度,如式(18)所示:

|
(18) |
式中,μ为泊松比;E为弹性模量。
根据式(16)可得:

|
(19) |
将式(19)代入式(17),并积分得:

|
(20) |
另一方面,圆板上荷载在位移w1上所做的功可表示为:

|
(21) |
将w1代入式(21),并积分可得:

|
(22) |
根据变分原理有:

|
(23) |
将式(20)、式(22)代入式(23)可求得C1为:

|
(24) |
溶洞顶板弯矩Mρ可表示为:

|
(25) |
将式(16)代入式(25)可得:

|
(26) |
相对应的拉应力σρ可表示为:

|
(27) |
当ρ=0时,溶洞顶板挠度w最大,且当z=H/2时,其相应的拉应力σρ也达到最大值,则溶洞顶板底面中心为最危险点,因此,以该点作为验算点来判断溶洞顶板是否满足抗拉要求。
将ρ=0和z=H/2代入式(26)、式(27),可得溶洞顶板最大拉应力σmax为:

|
(28) |
假如σmax < σt,则溶洞顶板满足抗弯要求。
本研究所提的溶洞顶板抗弯拉验算方法是基于变分法求得,适用于较为复杂荷载条件下溶洞顶板的抗弯拉验算。该方法与现有方法相比,更为全面地分析了各应力对溶洞顶板弯拉破坏的影响。
2.4 安全储备的讨论实际工程中,溶洞顶板与理论计算假定的情况有差别,如地下水、节理裂隙的影响等。为了保证工程设计的安全,设计时需有一定的安全储备,工程中一般采用安全系数的方法。
根据文献[10],安全系数K一般可取3~4。在实际工程设计时,可根据具体的工况调整选用。
3 工程算例 3.1 工程概况银家庄大桥为新建洞口至新化高速公路一座跨越岩溶区的桥梁,本研究选取银家庄大桥0#桥台右的一根桩进行验算,其基本工程概况如图 6所示,该桩作用在圆柱形溶洞正上方,计

|
| 图 6 工程概况(单位:m) Fig. 6 Engineering overview(unit:m) |
| |
算参数取值如表 1所示。
| 参数 | 数值 |
| 桩长l/m | 14.7 |
| 嵌岩深度h/m | 1 |
| 桩径D/m | 1.5 |
| 溶洞跨径L/m | 18 |
| 设计荷载P0/kN | 9 186 |
| 中风化石灰岩抗拉强度σt/MPa | 2.8 |
| 中风化石灰岩内摩擦角φ/(°) | 32 |
| 中风化石灰岩泊松比μ | 0.25 |
| 中风化石灰岩单轴饱和抗压强度σc/MPa | 18 |
| 中风化石灰岩重度γ/(kN·m-3) | 28 |
| 桩的重度γ1/(kN·m-3) | 25 |
| 填筑土重度γ2/(kN·m-3) | 17 |
| 亚黏土、黏土重度γ2/(kN·m-3) | 18 |
| 砂砾重度γ2/(kN·m-3) | 20 |
3.2 考虑嵌岩段侧摩阻力验算
下面分别对溶洞顶板进行抗冲切、抗剪切、抗弯拉的验算。
(1) 抗冲切验算
根据规范,嵌岩段摩阻力f=0.05σc=0.9 MPa,桩的自重G0=π(D/2)2lγ1=972 kN,P=G0+P0-πDhf=5 916 kN,锥台自重G=1 033 kN。取安全系数4,则大、小主应力σ1 =390 kPa, σ3=-1 284 kPa,代入式(8),可知溶洞顶板满足抗冲切要求。
(2) 抗剪切验算
① 桩端岩层发生剪切破坏,剪切体自重Gs1=175 kN,安全系数取4,则破坏面剪应力τ=2 446 kN,将τ代入式(11),可知满足要求。②溶洞顶板边缘岩层发生剪切破坏,剪切体自重Gs2=32 298 kN,取安全系数4,则τ=284 kN,将其代入式(11),同样满足抗剪要求。
(3) 抗弯拉验算
取安全系数4,可求得σmax=2.56 MPa < σt=2.8 MPa, 因此,满足抗弯要求。
3.3 与传统方法的对比文献[10]提出了基于梁板结构的溶洞顶板抗冲切、抗剪切、抗弯拉验算方法,随后文献[11]引入破坏准则,完善了文献[10]的研究,但文献[10-11]都未考虑自重的影响,因此,文献[13]完善了考虑自重影响的溶洞顶板稳定性分析,并认为顶板自重对稳定性有较大影响。
在本研究的工程算例中,采用文献[10-11, 13]的方法都可以证明工程的可靠性,但是都忽略了嵌岩段侧摩阻力的影响,这些方法在实际工程中偏于保守,为了方便对比,定义系数ξ为嵌岩段侧摩阻力与嵌岩桩设计荷载的比值。
本例中安全系数取4,则可得嵌岩桩安全荷载为36 744 kN,而嵌岩段提供的承载力为4 241.2 kN,求得ξ=11.542%。这说明嵌岩段侧摩阻力占承载力比例较大。当实际工程中嵌岩深度较长、岩石质量较好时,ξ会增大,此时忽略嵌岩段侧摩阻力的设计将过于保守。
综上所述,溶洞顶板在嵌岩桩荷载作用下满足抗冲切、抗剪切、抗弯拉要求,处于稳定状态,与工程实际吻合良好。通过对比分析可知,在实际工程设计中应适当考虑嵌岩段侧摩阻力的影响。
4 结论(1) 通过对嵌岩桩承载机理及溶洞顶板性能的分析,提出了考虑桩岩侧阻力的溶洞顶板抗冲切、抗剪切、抗弯拉计算模型。
(2) 在溶洞顶板的抗冲切、抗剪切验算中分别引入格里菲斯判据和莫尔判据,根据变分原理求得溶洞顶板最大拉应力,并对溶洞顶板的抗弯拉进行了验算。本研究方法综合考虑了桩岩侧阻力、溶洞顶板自重、拉应力、切应力共同作用的影响,使计算模型能更符合工程实际情况。
(3) 工程算例表明了本研究理论方法的合理性、可行性。与传统方法对比分析表明,不考虑嵌岩段侧摩阻力影响的设计偏于保守,建议在实际工程中可以适当考虑嵌岩段侧摩阻力的有利作用。
| [1] |
刘之葵, 梁金城, 朱寿增, 等. 岩溶区土洞地基稳定性分析[J]. 水文地质工程地质, 2003, 30(3): 24-28. LIU Zhi-kui, LIANG Jin-cheng, ZHU Shou-zeng, et al. Stability Analysis of Soil Cave Foundation in Karst Area[J]. Hydrogeology & Engineering Geology, 2003, 30(3): 24-28. |
| [2] |
赵明华, 邱志博, 张锐. 岩溶区地基极限承载力上限有限元数值模拟分析[J]. 水文地质工程地质, 2014, 41(6): 57-62. ZHAO Ming-hua, QIU Zhi-bo, ZHANG Rui. Numerical Simulation Analysis of Foundation Ultimate Bearing Capacity in Karst Area Using Upper Bound Finite Element Method[J]. Hydrogeology & Engineering Geology, 2014, 41(6): 57-62. |
| [3] |
王革力. 岩溶地基嵌岩桩桩基特性分析与试验研究[D]. 长沙: 中南大学, 2002. WANG Ge-li. Analysis and Experiment Research of Rock-socketed Pile Foundation in Karst Area[D]. Changsha: Central South University, 2002. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y627124 |
| [4] |
刘铁雄. 岩溶桩基与顶板作用机理分析与模拟试验研究[D]. 长沙: 中南大学, 2003. LIU Tie-xiong. Mechanism Analysis and Simulation Experiment Research of Interaction of Karst Pile Foundation with Cave Roof[D]. Changsha: Central South University, 2003. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y501833 |
| [5] |
张慧乐, 张智浩, 王述红, 等. 岩溶区嵌岩桩的试验研究与分析[J]. 土木工程学报, 2013, 46(1): 92-103. ZHANG Hui-le, ZHANG Zhi-hao, WANG Shu-hong, et al. Experimental Study and Analysis of Rock-socketed Pile in Karst Area[J]. China Civil Engineering Journal, 2013, 46(1): 92-103. |
| [6] |
张智浩, 张慧乐, 马凛, 等. 岩溶区嵌岩桩的破坏模式与工程设计探讨[J]. 岩石力学与工程学报, 2013, 32(增2): 4130-4138. ZHANG Zhi-hao, ZHANG Hui-le, MA Lin, et al. Discussion on Failure Mode and Engineering Design of Rock-socketed Pile in Karst Area[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 4130-4138. |
| [7] |
阳军生, 张军, 张起森, 等. 溶洞上方圆形基础地基极限承载力有限元分析[J]. 岩石力学与工程学报, 2005, 24(2): 296-301. YANG Jun-sheng, ZHANG Jun, ZHANG Qi-sen, et al. Finite Element Analysis of Ultimate Bearing Capacity of Circular Footing above Karst Cave[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(2): 296-301. |
| [8] |
尹凯丽, 郝世龙. 武汉地区岩溶对桩基承载力影响数值模拟研究[J]. 水文地质工程地质, 2015, 42(6): 96-102. YIN Kai-li, HAO Shi-long. Study of the Effect of Karst on the Bearing Capacity of Pile Foundation in Wuhan District Based on Numerical Simulation[J]. Hydrogeology & Engineering Geology, 2015, 42(6): 96-102. |
| [9] |
刘之葵, 梁金城, 朱寿增, 等. 岩溶区含溶洞岩石地基稳定性分析[J]. 岩土工程学报, 2003, 25(5): 629-633. LIU Zhi-kui, LIANG Jin-cheng, ZHU Shou-zeng, et al. Stability Analysis of Rock Foundation with Cave in Karst Area[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(5): 629-633. |
| [10] |
赵明华, 曹文贵, 何鹏祥, 等. 岩溶及采空区桥梁桩基桩端岩层安全厚度研究[J]. 岩土力学, 2004, 25(1): 64-68. ZHAO Ming-hua, CAO Wen-gui, HE Peng-xiang, et al. Study on Safe Thickness of Rock Mass at End of Bridge Foundation's Pile in Karst and Worked-out Mine Area[J]. Rock and Soil Mechanics, 2004, 25(1): 64-68. |
| [11] |
赵明华, 张锐, 胡柏学, 等. 岩溶区桩端下伏溶洞顶板稳定性分析研究[J]. 公路交通科技, 2009, 26(9): 13-16, 31. ZHAO Ming-hua, ZHANG Rui, HU Bo-xue, et al. Analysis of Stability of Cave Roof under Pile Tip in Karst Area[J]. Journal of Highway and Transportation Research and Development, 2009, 26(9): 13-16, 31. |
| [12] |
赵明华, 肖尧, 徐卓君, 等. 基于莫尔破坏判据的溶洞顶板冲切破坏研究[J]. 公路交通科技, 2016, 33(9): 58-63. ZHAO Ming-hua, XIAO Yao, XU Zhuo-jun, et al. Study on Punching Shear Failure of Cave Roof in Karst Area Based on Mohr Failure Criterion[J]. Journal of Highway and Transportation Research and Development, 2016, 33(9): 58-63. |
| [13] |
柏华军. 考虑溶洞顶板自重时桩端持力岩层安全厚度计算方法[J]. 岩土力学, 2016, 37(10): 2945-2952. BAI Hua-jun. A Method for Calculating the Safety Rock Thickness of Pile Bearing Strata with Considering Deadweight of Karst Cave Roof[J]. Rock and Soil Mechanics, 2016, 37(10): 2945-2952. |
| [14] |
史佩栋, 梁晋渝. 嵌岩桩竖向承载力的研究[J]. 岩土工程学报, 1994, 16(4): 32-39. SHI Pei-dong, LIANG Jin-yu. Vertical Bearing Capacity of Rock-socketed Piles[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(4): 32-39. |
| [15] |
明可前. 嵌岩桩受力机理分析[J]. 岩土力学, 1998, 19(1): 65-69. MING Ke-qian. Analysis of Bearing Mechanism of Socketed Pile[J]. Rock and Soil Mechanics, 1998, 19(1): 65-69. |
| [16] |
SERRANO A, OLALLA C. Shaft Resistance of a Pile Embedded in Rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(1): 21-35. |
| [17] |
JTG D63-2007, 公路桥涵地基基础设计规范[S]. JTG D63-2007, Code for Design of Ground Base and Foundation of Highway Bridges and Culverts[S]. |
| [18] |
刘佑荣, 唐辉明. 岩体力学[M]. 北京: 中国地质大学出版社, 1999. LIU You-rong, TANG Hui-ming. Rock Mechanics[M]. Beijing: China University of Geosciences Press, 1999. |
| [19] |
徐芝纶. 弹性力学[M]. 北京: 高等教育出版社, 2006. XU Zhi-lun. Elasticity[M]. Beijing: Higher Education Press, 2006. |
 2018, Vol. 35
2018, Vol. 35
