扩展功能
文章信息
- 余郁, 熊文, 薛玉波, 叶见曙
- YU Yu, XIONG Wen, XUE Yu-bo, YE Jian-shu
- 单塔单索面钢箱梁宽体斜拉桥空间效应分析
- Analysis on Spatial Effect of Cable-stayed Bridge with Wide Steel-box Girder, Single Pylon and Single Cable Plane
- 公路交通科技, 2018, 35(8): 64-72
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(8): 64-72
- 10.3969/j.issn.1002-0268.2018.08.010
-
文章历史
- 收稿日期: 2017-03-22
2. 东南大学 交通学院, 江苏 南京 210096
2. School of Transportation, Southeast University, Nanjing Jiangsu 210096, China
随着社会经济的发展,我国城市的交通量迅速增加,市政桥梁的宽度越来越大,而市政桥梁在满足通行需求的同时还要兼顾美观的效果,这使得城市桥梁的结构形式更加复杂。为确保桥梁宽度的有效增加,单线悬吊体系是该类超宽桥梁的优选结构形式,一旦悬吊体系设计为单线支撑,利用与其他构造合并的设计而不占用桥梁宽度,可以进一步增大桥面的有效宽度,更加适合在交通流量较大的市政桥梁中的大规模应用[1-6]。由于桥梁宽度的不断增加和单索面悬吊体系结构的复杂性,使得该类桥梁结构力学行为分析工作的难度大幅度提高,特别是在现阶段城市交通量不断增长的社会背景与需求下,对该类桥型空间力学行为特征的研究显得尤为及时与必要[7-9]。
单塔单索面钢箱梁斜拉桥是市政桥梁单线悬吊体系的典型结构代表,由于其形式非常适合于超宽桥梁设计,逐渐在交通量较大的城市中得到应用,在高效满足复杂的社会通行需求的同时,还具有美观效果,更适合作为城市的地标建筑物。但是从结构特性来看,无论是构造本身还是在设计、施工、运营阶段的受力均异常复杂,需要充分考虑其空间力学行为特征才能在结构安全的前提下发挥其功能与景观的特性[10-11]。
从单塔单索面斜拉桥的结构形式来看,主梁宽度与其长度相比明显较宽。以扬州市开发路东延跨京杭运河大桥为例,该桥桥宽39 m,主跨长135 m,宽跨比为0.289,显然结构受力空间效应非常突出。特别当采用钢箱梁作为主梁的截面形式时,横向受力特征、顶板的第3体系受力均会对结构设计、施工及运营阶段的力学行为产生较大影响。为增大桥宽,采用单索面作为主梁的支撑体系,主梁在偏载作用下的扭转受力行为(包括扭转对主梁纵、横向受力的耦合影响)更值得深入分析。因此,首先将精细化三维空间模型与传统杆系梁格模型进行对比,并给出推荐分析方法,进而针对单塔单索面宽体斜拉桥的空间应力分布、局部构件受力特性及偏载效应等空间力学效应进行分析,最终对此类结构的安全性与合理性给出更明确的理论解释与优化依据。
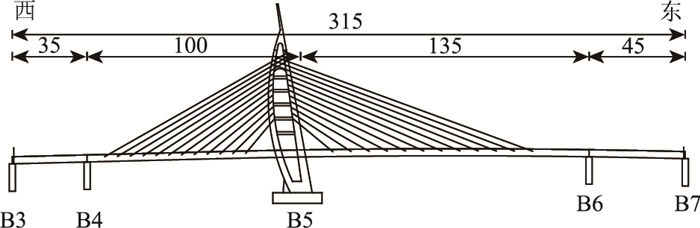
1 背景桥梁简介扬州市开发路东延跨京杭运河大桥采用单塔单索面不对称斜拉桥,为墩、塔、梁固结体系。主梁、主塔为钢结构,主墩为混凝土结构,跨径布置为:35 m(西边跨)+100 m(副跨)+135 m(主跨)+45 m(东边跨)=315 m,见图 1。主桥总宽39 m,中间单索面区域为4 m,主塔向副跨侧倾斜79.7°左右,桥面以上主塔高68.238 m,顺桥向为双柱帆式造型,横桥向为竖一字形变截面塔。全桥共设置12对拉索,主跨侧梁上拉索间距为8.5 m,副跨侧梁上拉索间距为6.0 m,拉索均锚固于主梁横隔板处。
|
| 图 1 桥梁立面图(单位:m) Fig. 1 Elevation view of bridge (unit: m) |
| |
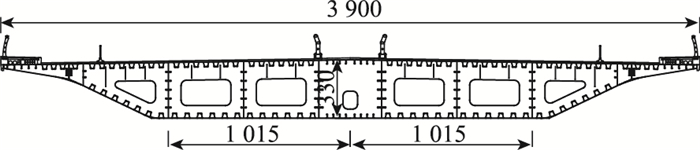
主梁采用封闭钢箱梁,梁高3.3 m,底板采用流线型。钢箱梁材质选用Q345qD桥梁结构用钢,顶板按正交异性板设计,板厚一般采用14 mm,顶板的加劲纵肋采用6 mm钢板压制成的梯形闭口肋,闭口肋顶宽300 mm,高260 mm,底宽184 mm,顶板闭口肋的间距为550 mm,底板闭口肋的间距为700 mm。该钢箱梁横断面示意见图 2。
|
| 图 2 主梁断面图(单位:cm) Fig. 2 Cross-section of main girder (unit: cm) |
| |
上塔柱为索塔桥面以上部分,总高度68.238 m,为焊接钢结构。塔身外缘角隅采用圆弧进行美化,塔身及塔根部分纵桥向分为两个塔柱,上塔身接主梁处横桥向宽3.5 m,纵桥向长分别为3.0 m及3.50 m,塔顶区域两塔柱合二为一。为增加上塔柱的刚度,塔身部分采用钢结构内灌C50微膨胀混凝土,两个塔柱伸入钢箱梁并灌注C50混凝土。两塔柱间共设置5对钢横梁,其中最下一对横梁高1.2 m,宽0.6 m。下塔柱(主墩身)为钢箱梁以下及承台以上部分。下塔柱采用C50混凝土异形框架结构,顺桥向为双柱结构,外形为主塔结构向下的延伸,双柱下塔柱在承台顶面合二为一。
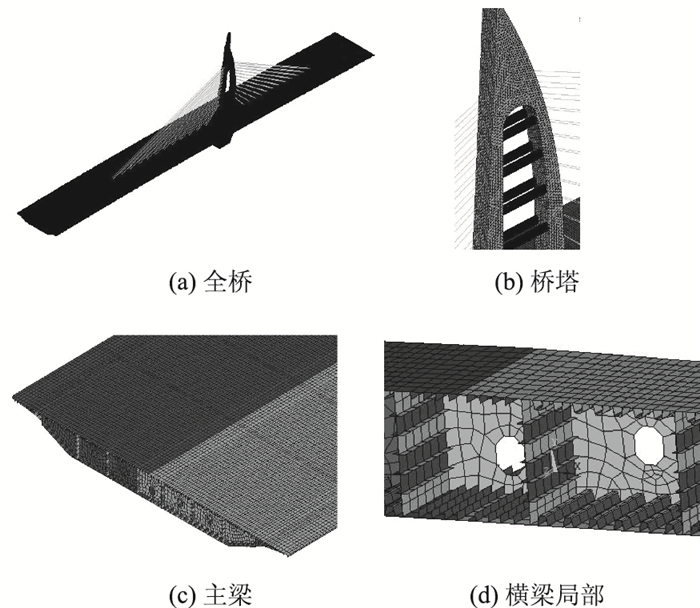
2 数值模型 2.1 模型建立考虑到该结构空间效应较为显著,因此采用大型有限元软件ANSYS建立全桥的精细化空间模型进行数值分析。其中钢箱梁和桥塔钢板采用Shell63壳单元模拟,加劲U肋及钢横梁均采用壳单元Shell63按图纸尺寸与形态进行建模,U肋沿纵向穿过横梁,两者在交叉处并未固结。混凝土塔身采用Solid45实体单元模拟,拉索采用Link8杆单元模拟。参考钢管混凝土建模方法,内灌注混凝土仅考虑其重量,并不计入承受荷载的能力[12-14]。全桥边界条件为:B3,B4,B6,B7为竖向与横向支承,B5为全固结。考虑到桥梁尺寸较大,综合考虑计算精度与效率,横桥向单元尺寸为0.2~0.4 m,纵向单元尺寸为0.3~0.5 m,模型具有100万个单元,70万个节点,见图 3。
|
| 图 3 有限元模型 Fig. 3 Finite element model |
| |
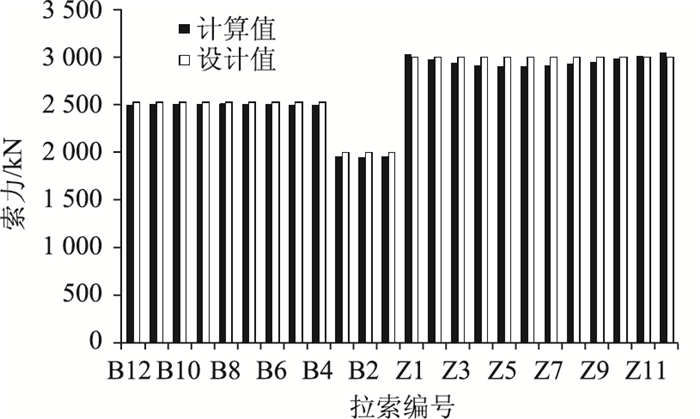
为保证成桥状态下的索力与设计值一致,通过迭代分析,不断更新索单元的初始应变,将成桥计算索力与目标设计值进行对比更新,直至得出可以接受的与目标设计索力相近的结果[15-18]。按施工过程施加各拉索的初始张拉力,最终计算成桥索力与设计索力差别较小,最大的误差仅为3%,见图 4。其中,B1-B12代表边跨拉索,Z1-Z12代表主跨拉索。另外,该桥结构的安全性、稳定性及疲劳性能均已由设计部门完成设计验算,在此不再赘述。
|
| 图 4 索力对比 Fig. 4 Comparison of stay cable forces |
| |
2.2 模型比较与必要性分析
采用杆系有限元软件MIDAS建立梁格模型,该梁格模型依据汉勃利提出的原则进行纵梁划分,即划分以后各工字型截面形心大致在同一高度。从此纵向分割成10道纵梁,横向联系位置按真实横隔板位置布置,无法在梁格模型中体现的质量将采用外荷载的形式计入。将该模型的计算结果与ANSYS建立的精细化空间模型计算结果进行对比。其中,梁格模型采用Block Lanczos方法进行动力分析,桥面铺装等二期恒载用质量单元模拟。
(1) 动力特性对比
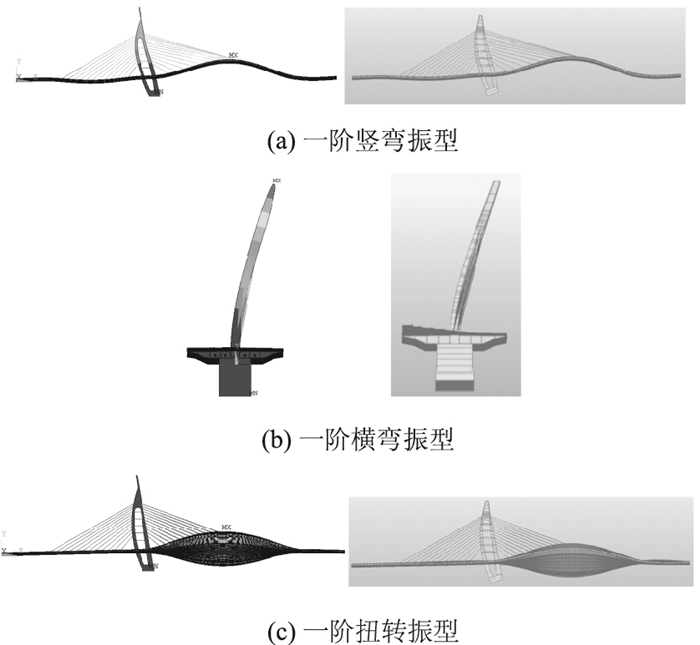
表 1与图 5分别给出基于ANSYS精细化空间模型与MIDAS梁格模型计算得到的自振频率与振型。
| 振型 | ANSYS精细化模型 | Midas梁格模型 |
| 一阶竖弯 | 0.863 | 0.891 |
| 一阶横弯 | 0.711 | 0.898 |
| 一阶扭转 | 1.540 | 0.988 |
|
| 图 5 振型对比(左:精细三维模型;右:梁格模型) Fig. 5 Comparison of mode shapes (left: refined 3D model; right: grillage beam model) |
| |
通过对比可以发现,两种模型一阶竖弯频率及相应振型的差异很小,验证了两模型整体竖向刚度的一致性。一阶横弯振型为桥塔的侧向弯曲,由于精细化三维空间模型采用实体单元布尔运算切割,较为精确地模拟塔顶弧线的渐变及桥塔的变截面特性,而梁格模型不能精确模拟该渐变段,因此两者横向动力特性存在一定的差异。而对于一阶扭转振型,两者具有较为明显的差异,这主要是因为梁格模型无法准确模拟闭口钢箱梁的扭转刚度,导致其频率计算值远小于采用壳-实体单位建立的精细三维空间模型计算结果。因此,从动力特性来看,采用更为精细的壳-实体三维空间模型进行该类单索面超宽体钢箱梁斜拉桥是非常必要的。
(2) 剪力滞效应对比
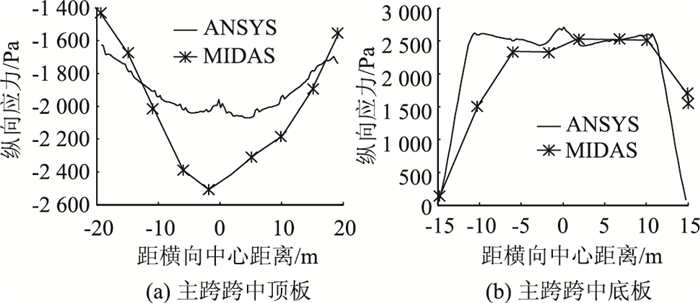
图 6给出了ANSYS精细化三维空间模型与MIDAS杆系梁格模型在均布荷载作用下主跨跨中截面顶、底板的纵向应力剪力滞效应对比,其中原点设置在桥梁横向中心位置。按剪力滞系数的定义,图 6(a)对应的剪力滞系数分别为1.22(MIDAS)和1.08(ANSYS);图 6(b)对应的剪力滞系数分别为1.38(MIDAS)和1.17(ANSYS)。
|
| 图 6 纵向应力剪力滞效应对比 Fig. 6 Comparison of shear lag effects of longitudinal stress |
| |
通过对比可以发现,虽然梁格模型将主梁分割成多个纵梁,一定程度上能考虑纵向应力的横向分布,可反映出部分剪力滞效应,但是与精细化三维空间模型的计算结果相比,缺乏局部细节的应力分布,横向应力分布的对称性也不强,某些位置的应力值相差较大。这主要是由于梁格模型仅能给出纵梁单元的平均应力,无法精确模拟第2、第3体系的受力特性。因此,从应力的空间分布来看,采用更为精细的壳-实体三维空间模型分析该类单索面超宽体钢箱梁斜拉桥亦是非常必要的。
3 空间效应分析 3.1 应力空间分布(1) 空间变形
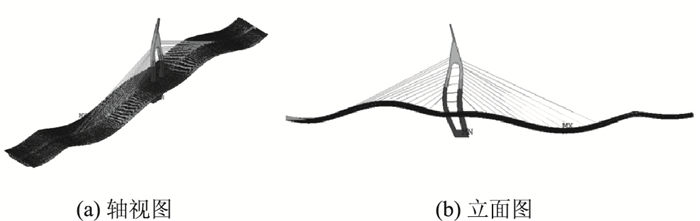
在成桥索力以及自重、二期恒载作用下,全桥(包括塔梁固接区、有索区,无索区等,下同)整体空间变形见图 7。桥梁边跨上拱,边跨跨中附近最大上拱为0.048 9 m;主跨下挠,最大值出现在主跨跨中附近,为0.081 m。
|
| 图 7 空间变形图 Fig. 7 Spatial deformation |
| |
(2) 正向应力空间分布
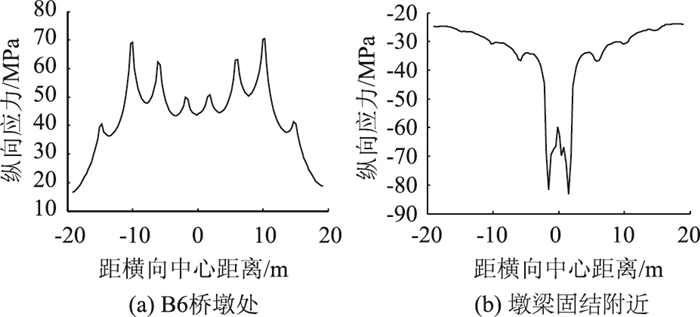
图 8为全桥顶板纵向应力分布图,最大拉应力出现在B6桥墩位置(编号见图 1),约79.5 MPa,最大压应力出现在主梁与桥塔固结处附近,约86 MPa。图 9(a)给出了B6桥墩处顶板纵向应力横桥向分布,由于结构和荷载沿横向对称,纵向应力沿横桥向亦对称分布。纵向应力在各腹板位置出现峰值,尤其在离桥梁横向中心10 m左右的腹板处应力水平最高。图 9(b)给出了墩梁固结附近顶板的纵向应力横桥向分布,在腹板与桥塔固结处出现较大应力集中,使得固结段应力水平较高,而其余位置应力水平相对较低。

|
| 图 8 顶板空间变形图 Fig. 8 Spatial deformation of top plate |
| |
|
| 图 9 顶板纵向应力横桥向分布 Fig. 9 Longitudinal stress distribution of top plate along transverse direction |
| |
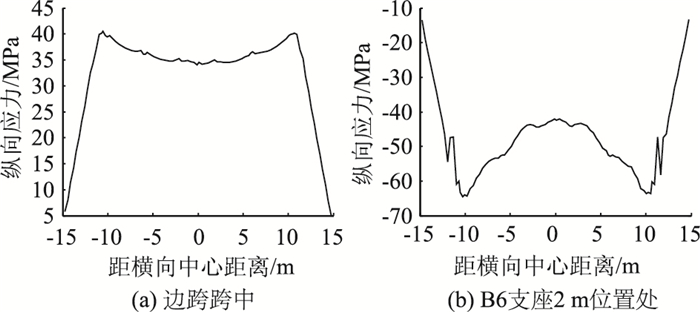
图 10为全桥底板纵向应力分布图,最大拉应力出现在墩梁固结位置,约53.3 MPa,最大压应力出现在B6桥墩支座位置,约152 MPa,该数值主要是由于支座模拟耦合效应的局部应力集中所引起的。图 11(a)给出了边跨跨中底板纵向应力的横向分布,可见其在离桥梁中心横向10 m左右应力稍大,向中心位置逐渐降低,底板两侧倾斜段应力水平较低。图 11(b)给出了离B6支座2 m位置处的纵向应力分布,类似地,在离桥梁中心横向10 m位置处应力水平比其他位置高,而中心位置应力水平低。

|
| 图 10 底板空间变形图 Fig. 10 Spatial deformation of bottom plate |
| |
|
| 图 11 底板纵向应力横桥向分布 Fig. 11 Longitudinal stress distribution of bottom plate along transverse direction |
| |
上述应力分布规律说明,单塔单索面超宽钢箱梁的截面正应力分布存在非常显著的剪力滞现象,采用单梁,甚至梁格模型,均不能确保得到准确的计算结果。
(3) 横向应力空间分布
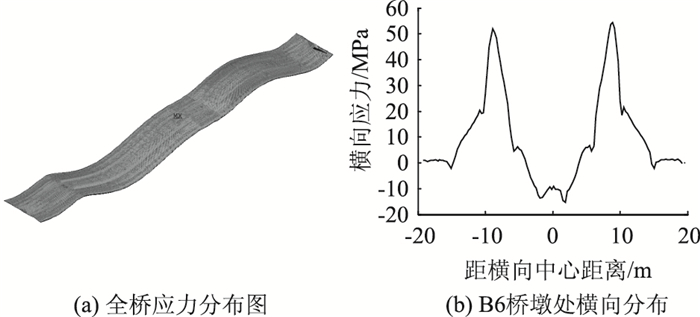
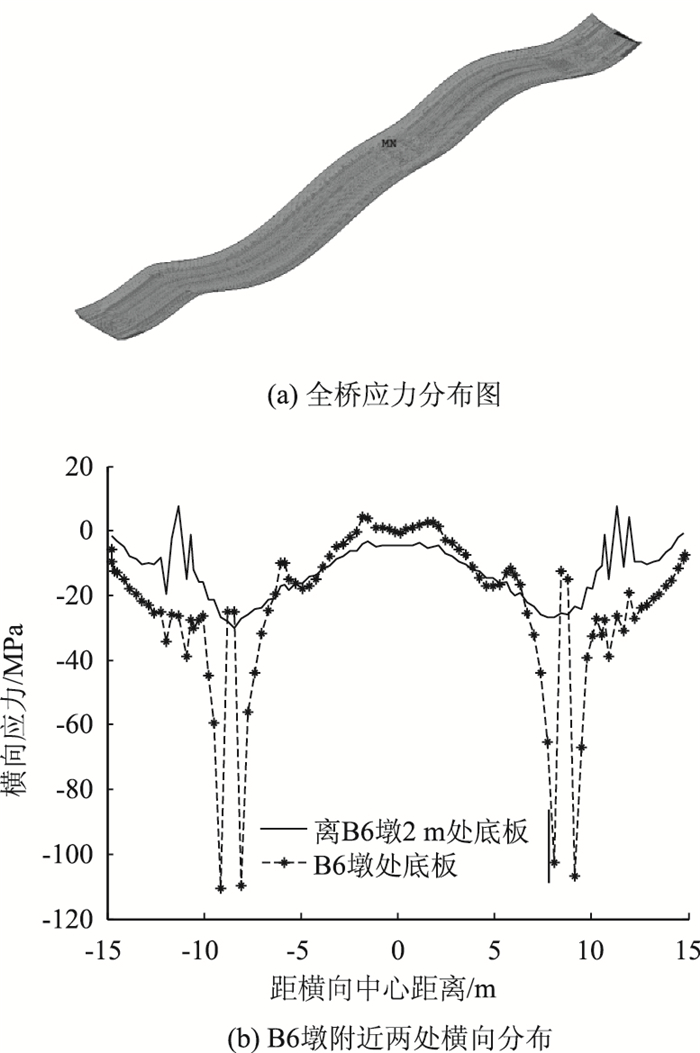
图 12(a)为全桥顶板横向应力分布,最大拉应力出现在墩梁固结位置,约65 MPa,最小压应力出现在边跨支座位置,约30 MPa。图 12(b)为B6墩处顶板横向应力横向分布,在支座位置出现较大峰值,而其余位置应力水平较低。图 13(a)为底板横向应力分布,由于墩梁固结段构造较为复杂,不考虑局部节点应力集中现象,底板最大压应力为117 MPa(B6桥墩),而绝大部分位置应力水平约40 MPa左右。图 13(b)为B6桥墩附近不同断面位置的横向应力分布,可见,在支座位置存在较大的应力集中现象,而稍微离开支座一段距离则应力分布较为平缓,应力值也大幅度降低。
|
| 图 12 顶板横向应力分布 Fig. 12 Transverse stress distribution of top plate |
| |
|
| 图 13 底板横向应力分布 Fig. 13 Transverse stress distribution of bottom plate |
| |
可以看出,对于单塔单索面超宽钢箱梁,除了纵向正应力,其横向正应力沿截面横向也具有非常明显的分布不均匀现象,特别在一些复杂构造处,不均匀性更加明显。所以必须进行三维实体空间分析。
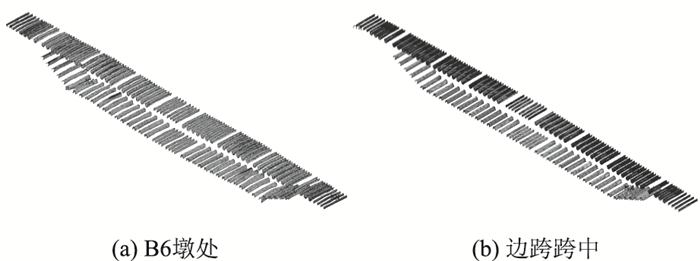
3.2 局部构件受力分析图 14(a)给出了B6桥墩位置附近U肋的Von Mises应力分布图。由于底板支座位置附近有较显著的应力集中现象,因此其附近的U肋应力水平较高,而顶板应力水平相对较低。图 14(b)给出了边跨跨中位置附近U肋的Von Mises应力分布,类似地,底板U肋应力水平要高于顶板的应力水平,但总体应力水平不高。实际上,U肋与横隔板连接时,其3条边中有1条边在横隔板上开口穿过,另外2条边则在穿过后与横隔板焊接。本研究偏于安全起见,未考虑U肋与横隔板的连接,使得计算结果偏于保守。另外,从U肋整体来看,其应力分布规律与顶、底板的正应力分布是一致的。
|
| 图 14 U肋Von Mises应力 Fig. 14 Von Mises stresses of U-ribs |
| |
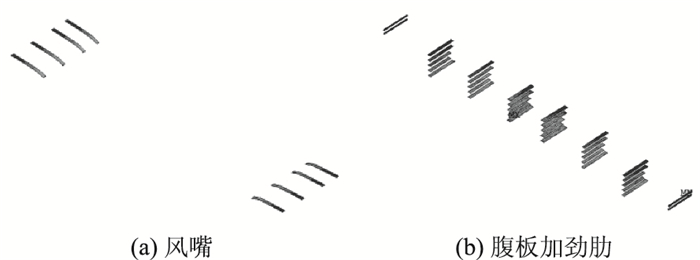
除U肋外,侧封板(风嘴)的Von Mises应力分布也不均匀,但总体水平不高,最大值为56 MPa,出现在塔梁固结位置附近,风嘴应力在靠近主梁横向中心的位置较高,而在远离主梁横向中心侧的应力值较低,见图 15(a)。腹板加劲肋同样具有不均匀的Von Mises应力分布,总体水平也不高,最大值为63 MPa,出现在塔梁固结段位置附近,见图 15(b)。
|
| 图 15 塔梁固结位置构件Von Mises应力 Fig. 15 Von Mises stresses of components of girder crossing pylon |
| |
可以看出,局部构件的应力计算结果同样具有强烈的空间性,最大值与最小值均分布在不同位置,需要分别进行验算。
3.3 偏载受力特性(1) 偏载工况1
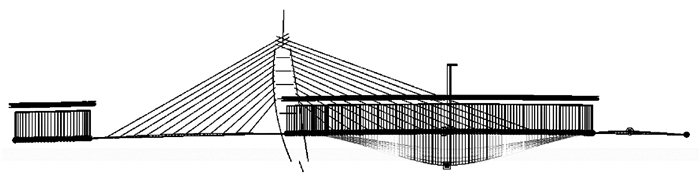
以主跨跨中竖向挠度最大进行荷载纵向最不利布置,进而进行横向最不利的偏载布置,作为本研究的最不利偏载工况1,研究结构的偏载受力特性。首先通过影响线分析得到最不利纵向布载位置(以工况1为例,图 16给出了其纵向布载),进而依据通用规范中对车辆横向间距的最小要求进行偏载的最不利横向布置。
|
| 图 16 最不利偏载工况1的纵向加载形式 Fig. 16 Longitudinal arrangement of the worst eccentric load condition 1 |
| |
表 2给出了偏载工况1下分别按ANSYS精细化三维空间模型与MIDAS杆系梁格模型得到的支座反力数值。对比可知,由于杆系梁格模型的扭转刚度模拟不够准确,使得左右侧支反力分配与精细化三维空间模型存在较大差别,B6墩处支反力差别甚至高达62.8%,其余位置差别也均超过10%。因此,采用精细化三维空间模型研究单塔单索面宽体斜拉桥的偏载受力特性,偏载工况1下的全桥变形见图 17。
| 模型 | 支座 | |||||||
| B3 左 |
B3 右 |
B4 左 |
B4 右 |
B6 左 |
B6 右 |
B7 左 |
B7 右 |
|
| Midas | 109 | 656 | -342 | 285 | -93 | 2 863 | -211 | -526 |
| Ansys | 97 | 712 | -450 | 336 | -250 | 3 015 | -314 | -404 |

|
| 图 17 偏载变形图 Fig. 17 Deformation under eccentric load |
| |
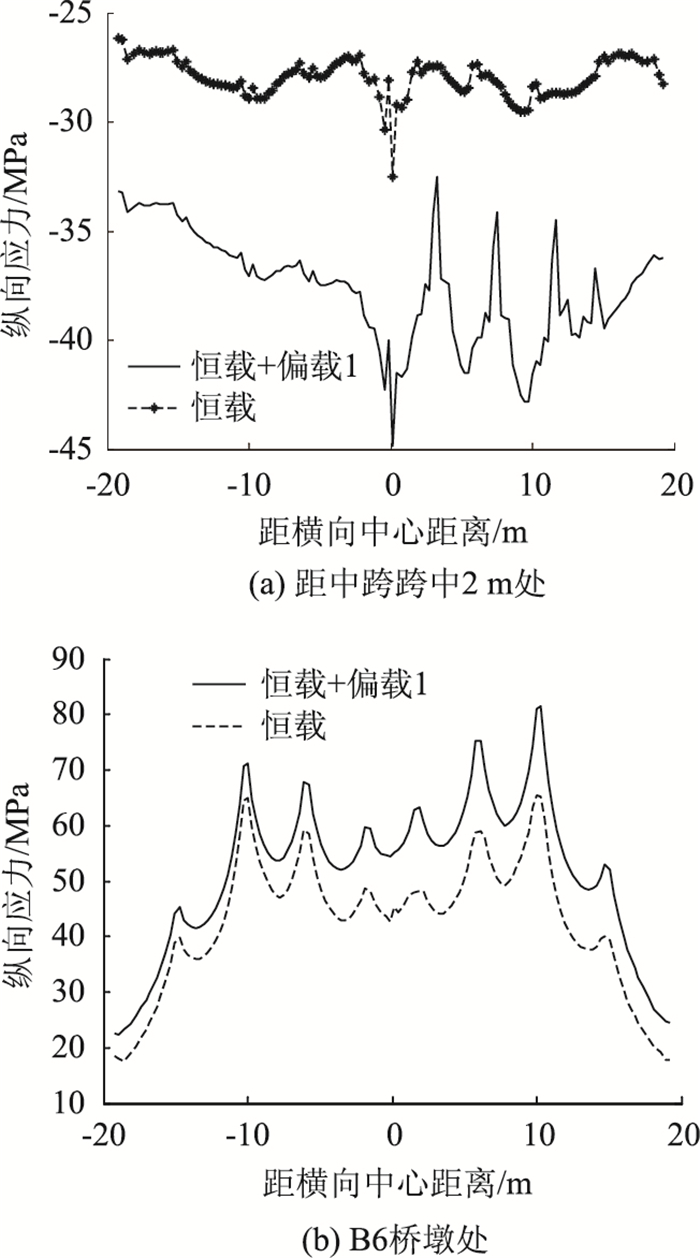
偏载工况1与恒载共同作用下全桥顶板最大纵向应力为100 MPa,出现在B6桥墩位置;最大压应力为116 MPa,出现在主跨跨中加载点位置附近。图 18(a)为离加载点位置2 m处的纵向应力分布,对比恒载工况下的受力可知,在偏载作用下,顶板的纵向应力大幅度增加,由于偏载效应,右侧受力更大,在腹板位置出现峰值,但最大压应力水平不高。图 18(b)为B6桥墩处顶板纵向应力分布,类似地,在偏载作用下,顶板应力水平有较大提高,尤其右侧腹板位置,应力水平较高。由应力分布图可知,偏载作用下剪力滞效应更为明显。
|
| 图 18 偏载工况1下顶板纵向应力横向分布 Fig. 18 Longitudinal stress distribution of top plate along transverse direction under eccentric load condition 1 |
| |
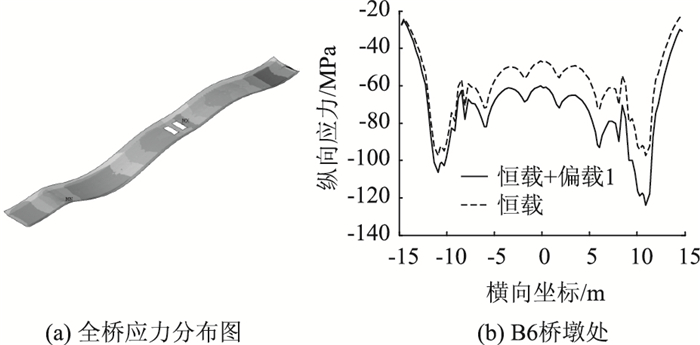
图 19(a)与19(b)分别给出了偏载工况1下全桥纵向应力分布及B6桥墩处底板正应力分布,在偏载作用下,右侧支座位置应力达到近130 MPa。可以看出,偏载效应(应力不均匀分布特性)在底板处并不如顶板明显,仅在桥墩处表现出较强的剪力滞效应。
|
| 图 19 偏载工况1下底板纵向应力横向分布 Fig. 19 Longitudinal stress distribution of bottom plate along transverse direction under eccentric load condition 1 |
| |
(2) 偏载工况2
以边跨跨中竖向挠度最大、横向最不利进行偏载布置,作为本研究的最不利偏载工况2,研究结构的偏载受力特性。
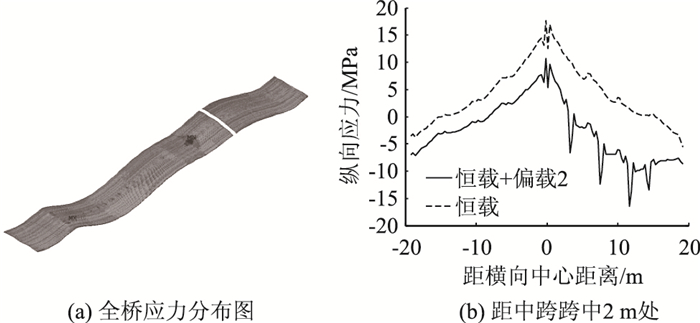
由于布载长度较工况1短,偏载工况2与恒载作用下全桥顶板纵向应力水平相对工况1有所减少。图 20 (a)给出了全桥顶板应力分布,最大拉应力和最大压应力出现在B6桥墩和塔梁固结处,分别为80 MPa和75 MPa。图 20(b)为距边跨跨中2 m处的应力分布,在偏载作用下,顶板拉应力减小,某些位置为压应力,在荷载加载位置出现峰值。
|
| 图 20 偏载工况2下顶板纵向应力横向分布 Fig. 20 Longitudinal stress distribution of top plate along transverse direction under eccentric load condition 2 |
| |
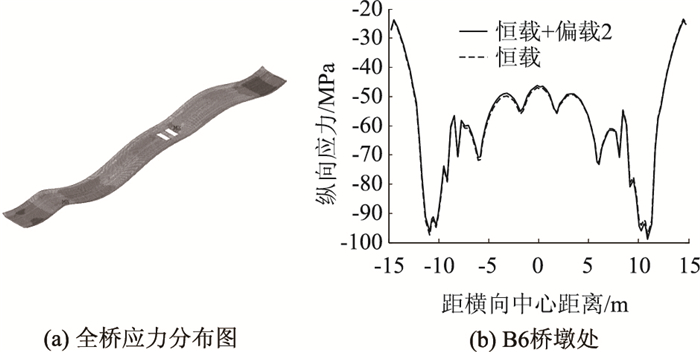
图 21(a)给出了偏载工况2下全桥底板纵向应力分布,最大拉应力与最大压应力出现在B6桥墩和塔梁固结处,分别为46 MPa和154 MPa。图 21(b)为B6处底板纵向应力分布,由于最不利布置位置不在主跨,主跨受到偏载扭转效应较小,底板应力与恒载工况相比变化不大。
|
| 图 21 偏载工况2下底板纵向应力横向分布 Fig. 21 Longitudinal stress distribution of bottom plate along transverse direction under eccentric load condition 2 |
| |
可以看出,在偏载工况2下,顶板在偏载作用下剪力滞效应同样明显,但对于远离加载区域的底板,荷载偏载效应(应力不均匀分布特性)较小,远不如对顶板明显。
(3) 偏载工况3
以B6号墩处最大负弯矩最大、横向最不利进行偏载布置,作为本研究的最不利偏载工况3研究结构的偏载受力特性。
偏载工况3下,由于车道荷载中的集中力施加点刚好位于横隔梁与顶板交界处,因此应力集中效应不明显。全桥顶板最大拉应力和压应力分别出现在B6桥墩位置和塔梁固结段,应力值分别为110 MPa和94 MPa。而底板纵向最大拉应力与最大压应力出现在塔梁固结处和B6桥墩支座处。
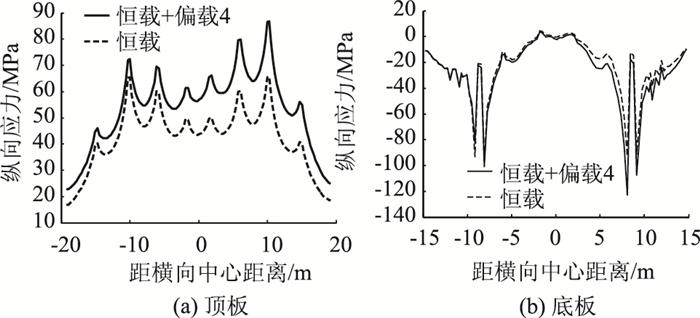
图 22(a)给出了B6桥墩处顶板纵向应力沿横向的分布,在活载作用下右侧桥梁应力增幅较大,腹板位置出现峰值。图 22(b)为B6桥墩处底板纵向应力沿横向的分布,在支座位置出现了明显的应力集中现象。
|
| 图 22 偏载工况3下B6桥墩处纵向应力横向分布 Fig. 22 Longitudinal stress distribution at pier B6 along transverse direction under eccentric load condition 3 |
| |
可以看出,在负弯矩最大的偏载工况3下,顶板仍具有较明显的剪力滞效应,并且由于支座的影响,底板的应力不均匀分布特性也同样突出,偏载效应也较之前两种工况明显。
另外,通过计算,偏载工况1~3中主梁均发生明显扭转和竖弯耦合变形,主梁整体最大扭转角为0.001 8 rad。
4 结论(1) 对于单塔单索面不对称钢箱梁斜拉宽桥,传统的杆系梁格分析模型无法确保结构空间受力特性描述的准确性,特别是对象变形及扭转行为,无论是动力还是静力分析,均会导致较大的计算误差,建议使用精细化三维空间模型进行该类桥型结构的空间效应分析。
(2) 对于单塔单索面超宽钢箱梁,无论是纵向正应力还是横向正应力,沿截面横向均具有非常明显的分布不均匀现象,特别是在一些复杂构造处不均匀性更加明显。另外,不仅是钢箱梁顶板,底板也会表现出突出的剪力滞效应,计算底板有效宽度时也建议考虑。
(3) 对于该类桥型的局部构件受力,虽然应力数值均不会太大,但同样具有强烈的空间性,最大值与最小值分布在不同位置,并且与主体结构(如主梁)的应力分布具有相似的规律。
(4) 在偏载作用下,顶板应力水平会有明显提高,尤其偏载侧腹板位置的应力水平较高,偏载作用会进一步加剧顶板剪力滞的效应。由于不直接作用,偏载效应(应力不均匀分布特性)在底板处并不如顶板明显,由于支座的影响,仅在桥墩处表现出较强的剪力滞效应或应力不均匀分布特性。
(5) 用于市政桥梁的单塔单索面斜拉桥主梁宽度与其长度相比通常较宽,空间效应非常明显,在设计时,建议采用精细化三维空间模型对其空间受力进行分析,并基于该空间受力分析的结果,对其横向构件及抗扭构件进行精细设计与优化,同时充分考虑顶、底板的应力不均匀分布特性,确保结构安全的同时提高设计的经济性。
| [1] |
李晓莉. 独塔斜拉桥的设计理论研究[D]. 上海: 同济大学, 2006. LI Xiao-li. Study on Design Theory of Single Pylon Cable-stayed Bridges[D]. Shanghai: Tongji University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10247-2007050357.htm |
| [2] |
张敬天. 单塔单索面混凝土斜拉桥施工控制研究[D]. 成都: 西南交通大学, 2010. ZHANG Jing-tian. Study on Construction Control of Cable-stayed Bridges with Single Pylon and Single Cable Plane[D]. Chengdu: Southwest Jiaotong University, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1687365 |
| [3] |
杨林. 空间梁格法对扁平型钢箱梁结构分析[D]. 西安: 长安大学, 2010. YANG Lin. Analysis of Flat Steel Box Girder Based on Spatial Grillage Method[D]. Xi'an: Chang'an University, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1729325 |
| [4] |
熊文, 涂雪, 肖汝诚. 考虑正应力空间效应斜拉桥后期荷载状态评估[J]. 同济大学学报:自然科学版, 2008, 36(10): 1344-1348. XIONG Wen, TU Xue, XIAO Ru-cheng. Real-time Service Load Condition Assessment of Cable-stayed Bridge Based on a Consideration of the Spatial Effect of Stress Distribution[J]. Journal of Tongji University:Natural Science Edition, 2008, 36(10): 1344-1348. |
| [5] |
董锐, 葛耀君, 杨詠昕, 等. 非对称独塔斜拉桥多振型抖振等效静力风荷载计算方法[J]. 中国公路学报, 2016, 29(11): 108-115. DONG Rui, GE Yao-jun, YANG Yong-xin, et al. Buffeting Equivalent Static Wind Loading Calculation Method of Asymmetric Single Tower Cable-stayed Bridges Based on Multi Modes[J]. China Journal of Highway and Transport, 2016, 29(11): 108-115. |
| [6] |
福州大学. 独塔单索面混合梁斜拉桥(八尺门大桥)建设关键技术研究[R]. 福州: 福州大学, 2014. Fuzhou University. Research on Critical Technologies of Single Tower and Single Cable Plane Cable-stayed Bridge with Composite Girder (Bachi Gate Bridge)[R]. Fuzhou: Fuzhou University, 2014. |
| [7] |
陈志军, 刘洋, 杨立飞, 等. 基于粒子群优化算法的独塔斜拉桥成桥索力优化[J]. 桥梁建设, 2016, 46(3): 40-44. CHEN Zhi-jun, LIU Yang, YANG Li-fei, et al. Optimization of Stay Cable Tension of Completed Bridge of Single-pylon Cable-stayed Bridge Based on Particle Swarm Optimization Algorithm[J]. Bridge Construction, 2016, 46(3): 40-44. |
| [8] |
谢官模, 刘志. 不对称独塔斜拉桥塔梁同步施工的可行性研究[J]. 公路工程, 2014, 39(1): 169-171, 176. XIE Guan-mo, LIU Zhi. The Feasibility Study of Tower-beam-imultaneous Construction Method in Asymmetric Single Tower Cable-stayed Bridge Construction[J]. Highway Engineering, 2014, 39(1): 169-171, 176. |
| [9] |
刘旭政, 黄平明, 许汉铮. 独塔斜拉桥参数敏感性分析[J]. 长安大学学报:自然科学版, 2007, 27(6): 63-66. LIU Xu-zheng, HUANG Ping-ming, XU Han-zheng. Analysis of Parameters' Sensitiveness of Cable-stayed Bridges with Single Tower[J]. Journal of Chang'an University:Natural Science Edition, 2007, 27(6): 63-66. |
| [10] |
JTG D6-2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D6-2004, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
| [11] |
XIONG W, XIAO R, DENG L, et al. Methodology of Long-term Real-time Condition Assessment for Existing Cable-stayed Bridges[J]. Advances in Structural Engineering, 2010, 13(1): 111-126. |
| [12] |
王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2007. WANG Xin-min. Numerical Simulation of Engineering Structure Using ANSYS[M]. Beijing: China Communications Press, 2007. |
| [13] |
王生武, 项纯夫, 李腾腾, 等. 异形独塔斜拉桥参数敏感性分析[J]. 公路工程, 2015, 40(1): 137-142, 147. WANG Sheng-wu, XIANG Chun-fu, LI Teng-teng, et al. Analysis of Parameters' Sensitivenes of Cable-stayed Bridge with Shaped Single Tower[J]. Highway Engineering, 2015, 40(1): 137-142, 147. |
| [14] |
马保林, 尚鑫, 徐岳, 等. 混凝土斜拉桥结构健康状态评估模型[J]. 长安大学学报:自然科学版, 2006, 26(2): 47-50. MA Bao-lin, SHANG Xin, XU Yue, et al. Health Condition Assessment Model of Concrete Cable-stayed Bridges[J]. Journal of Chang'an University:Natural Science Edition, 2006, 26(2): 47-50. |
| [15] |
金文成, 张晓飞, 简方梁, 等. 斜拉桥塔索锚固区空间应力分析[J]. 公路交通科技, 2007, 24(9): 69-73. JIN Wen-cheng, ZHANG Xiao-fei, JIAN Fang-liang, et al. Spatial Stress Analysis of the Cable Anchorage Zone of Cable-stayed Bridge[J]. Journal of Highway and Transportation Research and Development, 2007, 24(9): 69-73. |
| [16] |
陶海, 李海波, 林岩松. 斜拉桥PK断面主梁的空间应力分析与简化计算方法[J]. 强度与环境, 2008, 35(5): 9-16. TAO Hai, LI Hai-bo, LIN Yan-song. Study on 3D Stress Analysis and Simplified Calculating Methods for PK Section Girder of Cable Stayed Bridges[J]. Structure & Environment Engineering, 2008, 35(5): 9-16. |
| [17] |
郝超. 大跨度钢斜拉桥的施工监控及其目标精度值[J]. 中国公路学报, 2003, 16(1): 54-57. HAO Chao. Construction Control and Control Precision Goal of Long-span Steel Cable-stayed Bridge[J]. China Journal of Highway and Transport, 2003, 16(1): 54-57. |
| [18] |
孙全胜, 孟安鑫. 基于影响矩阵法的非对称独塔斜拉桥索力优化[J]. 中外公路, 2016, 36(3): 85-88. SUN Quan-sheng, MENG An-xin. Optimization of Stay Cable Forces of Asymmetric Single-pylon Cable-stayed Bridge Based on Influence Matrix Method[J]. Journal of China & Foreign Highway, 2016, 36(3): 85-88. |
 2018, Vol. 35
2018, Vol. 35
