扩展功能
文章信息
- 常柱刚, 王林凯, 夏飞龙
- CHANG Zhu-gang, WANG Lin-kai, XIA Fei-long
- 基于CV Newmark-β法的桥梁风致振动FSI数值模拟
- FSI Numerical Simulation of Bridge Wind-induced Vibration Based on CV Newmark-β Method
- 公路交通科技, 2018, 35(8): 55-63
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(8): 55-63
- 10.3969/j.issn.1002-0268.2018.08.009
-
文章历史
- 收稿日期: 2017-05-08
2. 安徽省交通规划设计研究总院股份有限公司, 安徽 合肥 230000
2. Anhui Transport Consulting & Design Institute Co., Ltd., Anhui Hefei 230000, China
随着新材料的应用、结构设计和施工水平的提高,现代桥梁结构趋向于向大跨、柔性、轻质的方向发展,使得桥梁结构对风的敏感性增强,风致振动问题对大跨度桥梁变得愈显突出,桥梁抗风设计成为了大跨度桥梁设计施工中一个重要组成部分[1]。桥梁风致振动属于流体与固体相互作用的范畴。根据振动性质的不同,桥梁风致振动可以划分为发散振动和限幅振动两类[2]。其中,颤振和驰振属于发散振动,是两种最主要的气动弹性不稳定现象,有可能引发桥梁的灾难性后果;而抖振和涡振属于限幅振动,虽然不会引起结构毁灭性破坏,但长时间的振动容易导致桥梁构件的疲劳及行车安全等问题。
随着计算力学的发展和计算机计算能力的提高,多物理场的耦合分析开始广泛应用于各个领域, 如航空、医学、电磁学等。在结构工程领域,结构的风振破坏日益严重, 有必要进行基于流固耦合理论的分析[3]。曹丰产等[4]采用动网格方法考虑圆柱体与流体的耦合,采用二阶投影法和多重网格法求解N-S方程,柱体振动方程采用Newmark-β方法进行求解,实现了圆柱涡激振动响应的数值模拟。J. B. Frandsen等[5]将桥梁断面看作弹性支撑于流场中的刚体,建立了基于任意拉格朗日-欧拉(Arbitrary Lagrangian-Euler, ALE)格式有限元法的流固耦合模型(流场和固域均采用有限元法求解),对Great Belt东桥主梁断面的颤振临界风速进行了流固耦合仿真。R. P. Selvam等[6-8]均构造了采用有限元方程求解流体N-S方程和结构振动方程、通过ALE方法实现结构网格运动的流固耦合模型,并且进行了相应的桥梁结构颤振稳定性计算。刘志文等[9]通过在Fluent中植入UDF的方式,构造了采用Newmark-β方法进行求解结构运动方程,采用SST k-w湍流模型求解不可压缩流N-S方程,利用动网格技术建立驱动结构运动的流固耦合计算模型,对宽高比为4的矩形断面涡激振动响应进行了计算,数值模拟结果与试验结果吻合较好。刘小兵[10]通过该模型获取了某双幅桥面的桥梁颤振临界风速,并且与风洞试验结果吻合较好。张瑞琴等[11]采用Ansys进行结构计算,采用CFX进行流场计算,并利用两者间的数据交互平台传递流场压力载荷和结构位移数据,实现了对NACA0012翼型进行流固耦合作用下的颤振研究。P. H. Hallak等[12]采用有限体积法离散N-S方程,采用Runge-Kutta法求解结构响应方程,构造了基于FVM的流固耦合模型,利用该模型研究了桥上车辆对Rio-Niteroi大桥气弹响应的影响。李永乐等[13]以Fluent为研究工具,利用微分方程的数值解法和动网格技术,将Newmark-β算法通过UDF植入Fluent中,实现了CFD与CSD耦合分析,进行了方柱涡激振动与平板颤振数值模拟。刘克同等[14]采用MRT-LBM-DSM大涡模拟技术作为流场求解器替代求解黏性不可压缩流N-S方程获得流场信息,利用四阶Runge-Kutta法求解桥梁主梁断面的瞬态动力学响应,构造了一种显式求解流固耦合问题的分区交替求解算法,采用该算法研究了大带东桥主梁断面的颤振稳定性问题。A. H. Lee[15]采用OpenFOAM耦合延迟分离涡湍流模型求解流体运动方程,采用FENAL有限元求解器求解刚体运动方程,研究了圆柱断面的涡激振动问题。J. R. Tawekal[16]采用OpenFOAM中的动网格不可压缩流求解器pipmpleDyMFoam模拟了二维与三维圆柱的涡激振动响应。
综上所述,不同的学者采用不同的求解流体力学N-S方程、结构响应方程及实现网格运动的方法构造了相应的流固耦合计算模型,针对桥梁断面的涡激振动与颤振这两种典型的流固耦合振动问题作出了相应的分析。
桥梁结构风致振动的卓越模态通常频率较低,流体与结构之间的耦合可以认为是弱耦合。鉴于有限体积法物理意义明确,采用基于有限体积法求解N-S方程的流固耦合模型得到了越来越多的研究和应用[15-21]。然而弱耦合模型中结构振动方程数值计算中的位移与网格更新的实际位移是否相等,网格运动能否按照数值计算中的运动状态进行运动等问题值得注意与研究。为此本研究以Fluent为计算工具,提出一种修正速度法的Newmark-β类算法, 并且将其与常规算法进行对比, 以期对合理构造桥梁风致振动流固耦合计算模型的方法有借鉴作用。
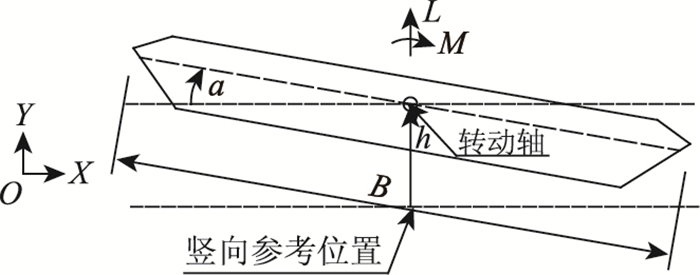
1 计算方法二维桥梁模型在均匀流场中的受力如图 1所示。
|
| 图 1 桥梁断面受力示意图 Fig. 1 Schematic diagram of forces on bridge section |
| |
对应二维振动方程可表示为:
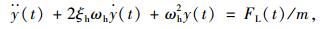
|
(1) |
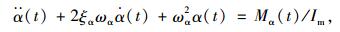
|
(2) |
式中,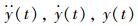
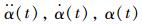
为求解上述微分方程(1)~(2),可以选择欧拉法、Runge-Kutta法、Newmark-β法等数值方法进行求解。
Runge-Kutta法是用于微分方程数值求解的方法, 也是在工程上应用广泛的高精度单步算法之一。
Runge-Kutta法从式(3)出发:
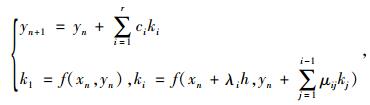
|
(3) |
式中, yn, yn+1为在xn与xn+1点上的函数值;r为xn与xn+1之间计算点数;ki,ci (i=1, 2, …, r)分别为xn与xn+1之间各计算点数对应的函数导数值和待求系数;f(xn, yn)为y的导函数,f(xn, yn)=y′(xn);h为x的增量,h=xn+1-xn;当xn表示时间t时,y表征位移时,f(xn, yn)表征速度;λi,μij均为系数。当f(xn, yn)可微时,有:
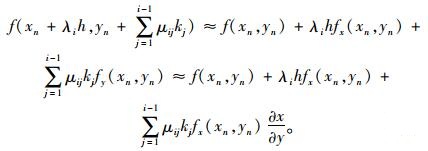
|
(4) |
将式(4)与y的r阶泰勒展开式进行对比:
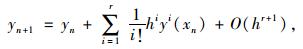
|
(5) |
式中,yi(xn)为函数第i阶导数值; O(hr+1)为佩亚诺余项。
利用系数相等的原则可以求得各个满足条件的系数λi,μij。以下介绍工程中常用的一种四阶Runge-Kutta法,简称R-K45法。
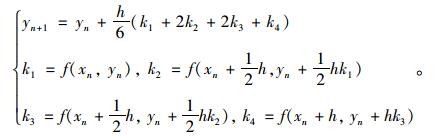
|
(6) |
将式(1)~(2)化成一阶表达形式。如研究竖向运动,令y1=y(t),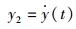
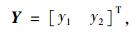
|
(7) |
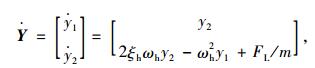
|
(8) |
然后结合式(4)与式(6)进行显示迭代。
值得注意的是,作为典型的求解微分方程的方法,经典4阶Runge-Kutta法已经被编入各种计算软件中去,如Matlab中的ode45,使用Matlab求解式(1)只需要定义一个方程:
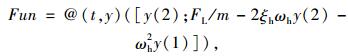
|
(9) |
然后用ode45函数进行求解:
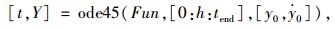
|
(10) |
式中,Fun即式(9)中定义的函数;[0:h:tend]为从0到tend公差为h的自变量数列;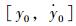
而Newmark-β法作为专门的求解动力响应微分方程的方法,该方法则假设:
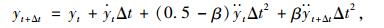
|
(11) |
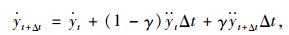
|
(12) |
式中,yt为当前时刻的位移值;yt+Δt为下一时刻的位移值;β和γ均为系数。将式(11)~(12)中的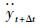
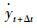
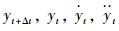
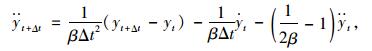
|
(13) |
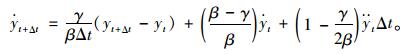
|
(14) |
将式(13)~(14)代入式(1)中,并且写成如下显式形式:
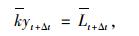
|
(15) |
式中,k为等效刚度;Lt+Δt为t+Δt时刻的等效外力。
通过整理可得:
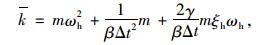
|
(16) |
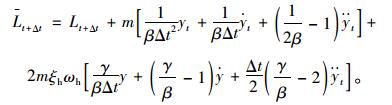
|
(17) |
进而计算下一时刻的位移值:
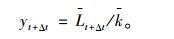
|
(18) |
获取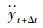
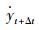
从计算精度上来看,R-K45能够达到针对位移计算的4阶精度,Newmark-β类法同样也能达到针对位移计算的4阶精度。为选择更为精确的求解振动方程的方法,将两类数值求解方法获取的位移时程曲线与含有符号解的振动方程的精确解进行对比。
对某一无外荷载扭转振动系统研究,其中初始扭转角α0=0.174 5,初始扭转角速度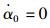
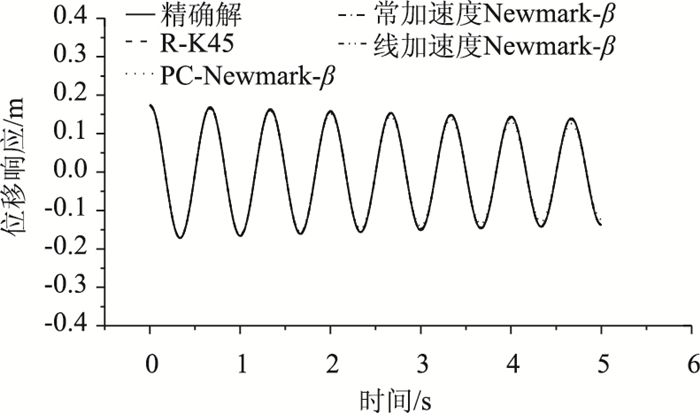
分别用PC Newmark-β法[19],常加速度Newmark-β法(β=1/4),线加速度Newmark-β法(β=1/6)和R-K45法进行对比,计算分别得到的位移曲线如图 2所示。计算时间步长均取0.001 s。
|
| 图 2 自由衰减振动下不同数值解法的位移响应 Fig. 2 Displacement responses under free attenuation vibration obtained by different numerical solutions |
| |
可以看出,除PC Newmark-β法外,其他方法识别的位移相应曲线基本上与符号解重合。为此,定义最大误差值:
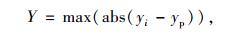
|
(19) |
式中, yi为不同方法识别的位移值; yp为通过符号解获取的位移值。得到不同方法识别值与精确解之间的最大绝对误差值(表 1)。
| 方法 | R-K45 | PC Newmark-β | Newmark-β(β=1/4) | Newmark-β(β=1/6) |
| 最大误差值 | 6.3E-4 | 1.4E-2 | 4.7E-5 | 2.3E-5 |
可以看出,线加速度Newmark-β法精度最高,常加速度Newmark-β其次,而PC Newmark-β精度最低,已经退化为只有一阶精度(相对加速度)的欧拉法。
为进一步进行对比,将上述算例增加一简谐外荷载,其运动微分方程表示为:
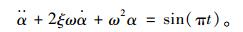
|
(20) |
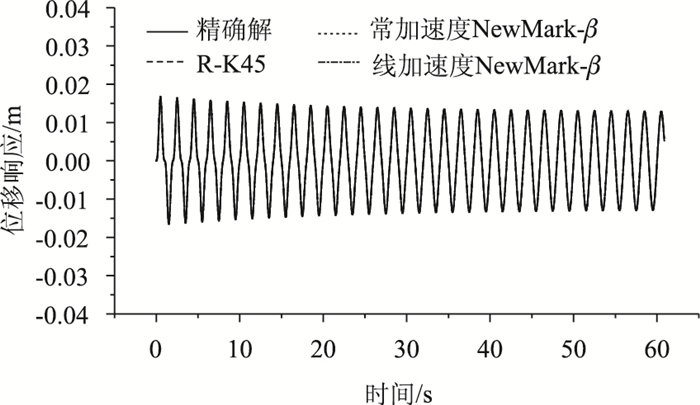
简谐外荷载作用下的不同方法的计算结果见图 3。
|
| 图 3 简谐外荷载作用下不同数值解法的位移响应 Fig. 3 Displacement responses under harmonic load obtained by different numerical solutions |
| |
最大误差计算结果如表 2所示。
| 方法 | R-K45 | Newmark-β(β=1/4) | Newmark-β(β=1/6) |
| 最大误差值 | 1.5E-4 | 1.0E-5 | 1.0E-5 |
从计算结果看,常加速度Newmark-β法和线加速度Newmark-β法计算结果精度相当,均比R-K45法精度高。因此进行桥梁风致振动FSI数值模拟,优先选择Newmark-β类算法。
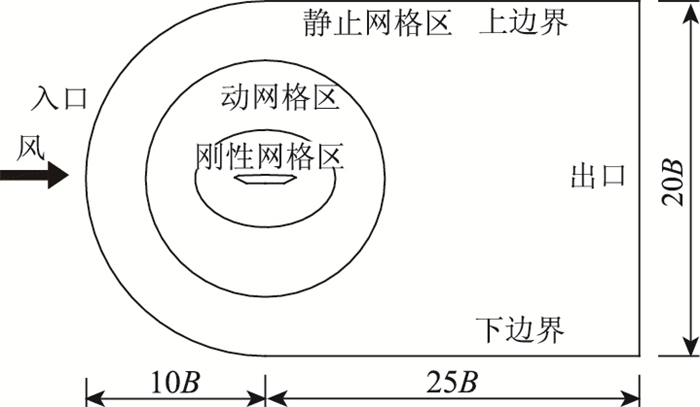
1.3 桥梁断面FSI数值模拟实现方法确定流体计算域,以桥梁宽带B为参考长度,计算域的设置需满足阻塞率的要求。为实现流固耦合计算,选择“刚性网格+动网格”的方案设置网格运动。在桥梁断面周边附近设置为刚性网格区域,这部分网格随桥梁断面一起做刚体运动。与刚体区域外连接区域设置为三角形动网格区域,这部分网格在计算过程中会发生变形,外周边其他区域网格则在计算工程中一直处于静止状态。网格计算域与分块设置如图 4所示。网格左侧外风速入口,上下边界为对称边界,出口设置外压强出口。动网格更新方式设置为弹性光顺方式以保证效率,同时结合网格局部重构以保证动网格质量。
|
| 图 4 网格计算区域划分示意图 Fig. 4 Schematic diagram of computing gridding |
| |
计算在Ansys Fluent中植入自定义函数的方式实现,使用动网格宏DEFINE_CG_MOTION来实现动网格更新。DEFINE_CG_MOTION宏接口用于控制刚体的运动,把刚体质心运动速度和角速度分别赋值给vel[]和omega[], Fluent根据他们的值来自动计算出刚体下一步的位置,从而实现网格的运动。
假设在t时刻的网格的运动速度和当前位移为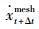
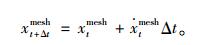
|
(21) |
植入UDF开始计算时,将初始运动状态赋予网格状态,利用Compute_Force_And_Moment宏从流场中获取桥梁刚体断面气动力Lt与Mt,并且采用显式处理,用Lt与Mt代替Lt+Δt与Mt+Δt,用计算得到的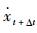
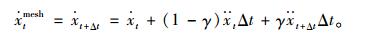
|
(22) |
这样将式(22)代入式(21)得到下一步的网格位移为:
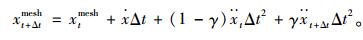
|
(23) |
而由式(11)可得:
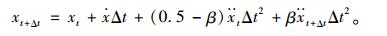
|
(24) |
如果将t时刻计算得到的位移赋予给网格位移,即:
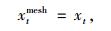
|
(25) |
那么根据式(23)与式(24),有:
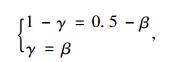
|
(26) |
无法求得一组β, γ值,使得:
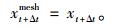
|
(27) |
因此,要实现完整意义上的FSI计算,就不能够将Newmark-β计算获取的速度直接赋值给网格运动的速度,否则Newmark-β法计算得到的位移与网格运动的位移就会不一致,并且这种误差会随着显示计算的迭代一步一步叠加,直至得出错误的计算结果。
单从式(11)与式(21)中可以看出,式(11)中的位移计算不仅包含速度项,还包含加速度项,而表达式(21)中的网格更新仅仅包含速度项,两者从计算精度上就不一致。因此必须对网格更新的速度进行更改,本研究提出一组修正速度法(CV Newmark-β)进行流固耦合数值模拟, 即令:
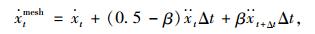
|
(28) |
或者表示为:
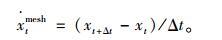
|
(29) |
Newmark-β法中的速度项仍然按式(12)进行计算,这样就能确保一旦从流场中获取气动力,通过数值算法求解的结果依然具有原算法的高精度的特点。
这样通过修正网格运动速度的方法,实现了具备高精度的完整意义上的流固耦合计算模型。
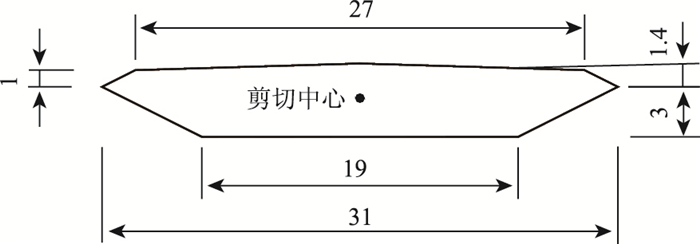
2 算例研究选取大带东桥为算例进行流固耦合计算。该桥主跨跨径为1 624 m,宽度为31 m,高度为4.4 m, 其截面形式如图 5所示。
|
| 图 5 大带东桥横断面图(单位:m) Fig. 5 Cross-section of Great Belt East Bridge (unit:m) |
| |
该断面的剪切中心位于距离桥面0.465倍截面高度处。
表 3对应的是该桥的结构动力参数,其中m为每延米的质量,I为每延米的质量惯矩,fh和fa分别为实桥的第1阶竖弯频率和第1阶扭转频率。
利用网格前处理软件按照图 4所示的计算域,绘制计算网格,如图 6、图 7所示。刚性运动区域网格数量为34 535个,动网格区域三角形网格数量为65 774个,静止区域网格数量为5 406个,网格总数为105 715个,壁面处首层网格高度为1×10-5B。将网格文件导入Fluent中,进行1:80的缩尺,湍流模型选择SST k-ω模型,给予初始均匀流场湍流特征,湍流强度为0.5%,湍流黏性比为2。编写UDF时,为满足相似比,结构动力参数在表 3的基础上进行缩尺,质量缩尺比为1:802, 扭转质量缩尺比为1:804,频率比设置为10:1。

|
| 图 6 网格整体图 Fig. 6 Gridding |
| |

|
| 图 7 网格细部图 Fig. 7 Detailed gridding |
| |
2.1 涡振状态
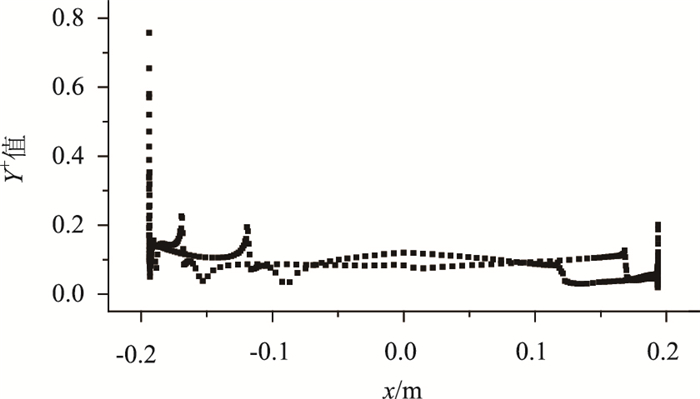
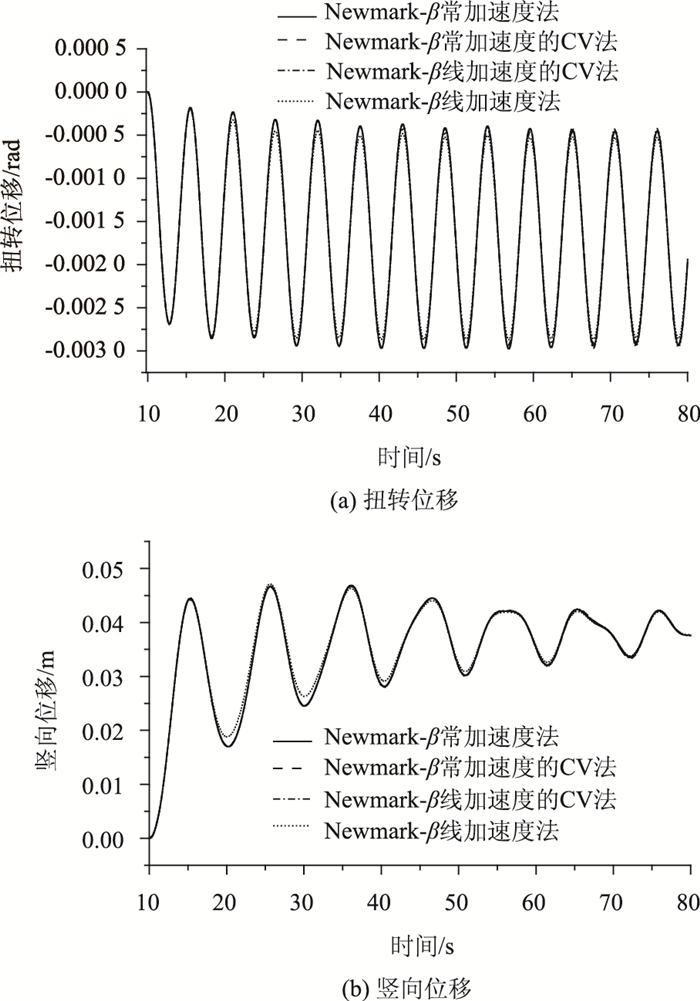
根据采样定理,计算时间取0.001 s足以捕捉到最大频率为20 Hz的信号。为获取稳定流场, 动网格计算前先进行10 s的静止绕流计算。图 8给出了壁面处的Y+分布,可以看出,网格Y+的最大值小于1,满足SST k-ω湍流模型对网格最小尺寸的要求。图 9给出了实桥风速为15.72 m/s时不同方法的计算结果。
|
| 图 8 壁面Y+分布 Fig. 8 Wall Y+ distribution |
| |
|
| 图 9 位移时程曲线 Fig. 9 Displacement time history curves |
| |
可以看出,该风速下扭转振动呈现出明显的限幅运动,即扭转涡激振动状态,这与试验结果[22]较为吻合。竖弯运动则呈现出衰减运动趋势。不同方法获得的位移曲线基本上重合。将各种方法获得的扭转位移曲线的平均值、振动幅值及振动频率汇于表 4。
| 不同方法 | Newmark-β(β=1/4) | CV Newmark-β(β=1/4) | CV Newmark-β(β=1/6) | Newmark-β(β=1/6) |
| 平均值/rad | -1.650E-3 | -1.649E-3 | -1.649E-3 | -1.654E-3 |
| 幅值/rad | 1.490E-3 | 1.480E-3 | 1.485E-3 | 1.435E-3 |
| 频率/Hz | 0.18571 | 0.185 71 | 0.185 71 | 0.185 71 |
从表 4中可以看出,在涡振小位移情况下,不同方法计算的结果差距不大,其中常加速度的Newmark-β修正速度法(CV Newmark-β, β=1/4)与线加速度的Newmark-β修正速度法(CV Newmark-β, β=1/6)之间差距最小。由于涡激振动位移较小,不同的方法计算的位移差距并不很明显,常规Newmark-β法得出的结果能够一定程度上逼近正确结果,这也是很多学者用常规Newmark-β法能够较为准确地获取结构涡激振动响应的原因。
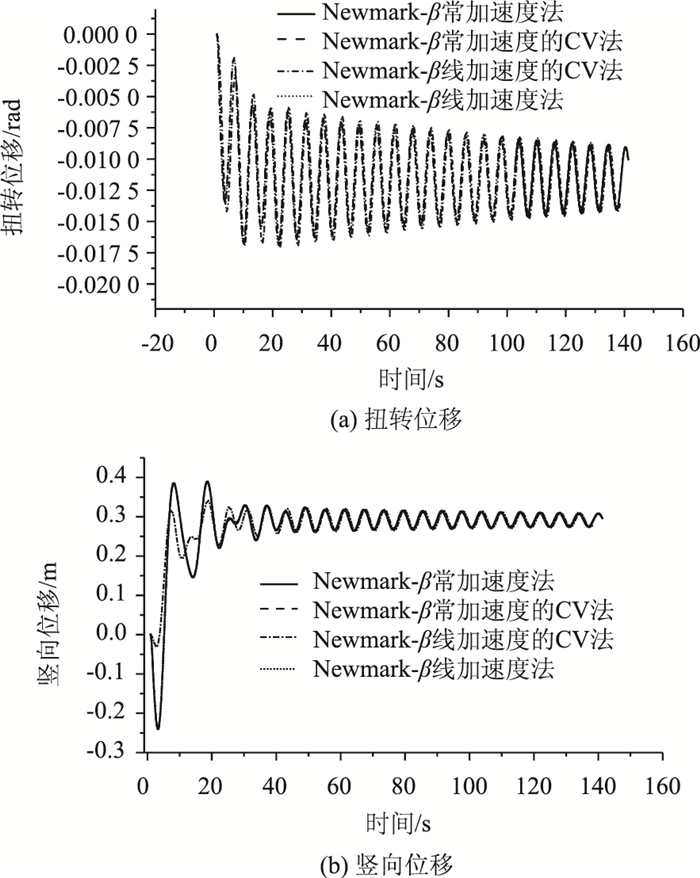
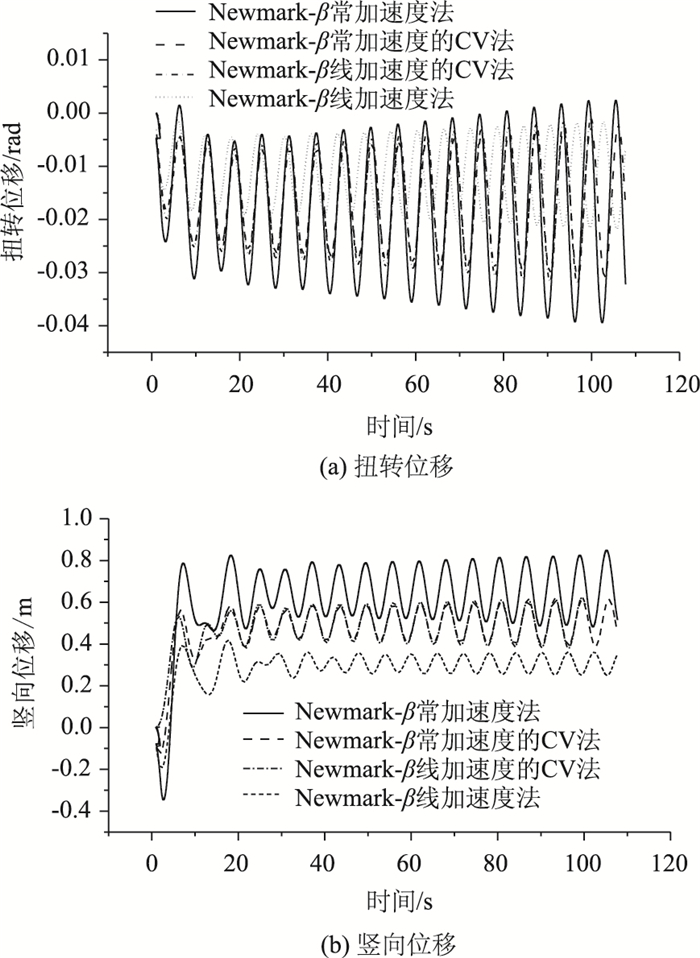
2.2 颤振状态文献[1]指出,该桥风洞试验获得的颤振临界风速为36 m/s,而通过数值计算得到的颤振临界风速为40 m/s。为此,研究36 m/s和40 m/s时桥梁断面的FSI数值模拟情况。图 10为桥梁断面在风速为36 m/s情况下的扭转位移和竖向位移时程曲线。可以看出,不同的数值计算方法得到的位移曲线基本上吻合。从曲线趋势看,该桥在36 m/s时未出现颤振发散情况。图 11为桥梁断面在风速为40 m/s情况下的扭转位移和竖向位移时程曲线。可以看出,该桥在40 m/s时呈现出明显的颤振发散状态。而不同的方法之间差距特别明显,从计算程序中读入网格的真实位移,发现其结果与CV Newmark-β流固耦合模型结果完全一致,而与使用常规Newmark-β法建立起的流固耦合模型结果则相差较大,因此常规Newmark-β法建立起的流固耦合模型在结构位移较大时计算结果明显不可信。
|
| 图 10 风速36 m/s的位移 Fig. 10 Displacements at wind speed of 36 m/s |
| |
|
| 图 11 风速40 m/s的位移 Fig. 11 Displacements at wind speed of 40 m/s |
| |
经过大量风洞试验研究,桥梁进入颤振临界状态时,并非呈现突发性的发散运动,而是呈现稳定的大振幅运动,并且在较长的风速范围持续这种现象,即软颤振现象。这种情况下,相比于涡激振动而言,桥梁运动位移较大,常规的Newmark-β法因计算过程中使用的位移值与网格更新的真实位移值差距较大而造成的误差不可忽略。因此在研究大振幅的FSI桥梁断面模拟时,建议检查这种位移偏差造成的影响。而本研究采用的修正速度法不存在这种误差,因而可以作为研究桥梁软颤振的直接数值模拟方法的储备。从图 11中可以看出,两种修正速度法在大振幅下依然吻合较好,因此可以认为本研究的计算方法获得的结果是较为精确的。
3 结论本研究分别采用求解微分方程的不同数值方法,先后对桥梁小振幅运动的涡激振动状态和大振幅运动的颤振状态进行了数值模拟对比,通过比较得出如下结论。
(1) 小振幅运动下,不同数值方法获得的位移时程曲线基本吻合,由于计算中使用的位移与网格真实位移之间的误差较小,对计算结果造成的影响可以忽略。
(2) 桥梁断面大振幅颤振下,不同数值方法获得的位移时程曲线差距较大。这种因为位移不一致效应造成的误差不可忽略,在计算大振幅流固耦合时应该尤为注意。使用常规Newmark-β法建立起的流固耦合算法在结构位移较大时计算结果明显不可信。
需要说明的是,本研究主要介绍基于CV Newmark-β法的桥梁风致振动流固耦合计算模型,并且进行了小位移和大位移振动下某大桥的算例研究,验证了大位移下依据常规Newmark-β法建立的流固耦合算法的缺陷,为合理建立准确的流固耦合模型提供了新的处理方式。
| [1] |
陈政清. 桥梁风工程[M]. 北京: 人民交通出版社, 2005. CHEN Zheng-qing. Bridge Wind Engineering[M]. Beijing: China Communications Press, 2005. |
| [2] |
项海帆. 风工程力学和大跨度桥梁的空气动力学问题[J]. 中国科学基金, 1994(3): 232-234. XIANG Hai-fan. Wind Engineering Mechanics and Aerodynamics of Long-span Bridges[J]. Bulletin of National Natural Science Foundation of China, 1994(3): 232-234. |
| [3] |
钱若军, 董石麟, 袁行飞. 流固耦合理论研究进展[J]. 空间结构, 2008, 4(1): 3-15. QIAN Ruo-jun, DONG Shi-lin, YUAN Xing-fei. Advances in Research on Fluid-structure Interaction Theory[J]. Spatial Structures, 2008, 4(1): 3-15. |
| [4] |
曹丰产, 项海帆. 圆柱非定常绕流及涡激振动的数值计算[J]. 水动力学研究与进展(A辑), 2001, 16(1): 111-118. CAO Feng-chan, XIANG Hai-fan. Calculation of Unsteady around Circular Cylinder and Vortex-induced Vibration[J]. Journal of Hydrodynamics, 2001, 16(1): 111-118. |
| [5] |
FRANDSEN J B. Numerical Bridge Deck Studies Using Finite Elements. Part Ⅰ:Flutter[J]. Journal of Fluids & Structures, 2004, 19(2): 171-191. |
| [6] |
SELVAM R P, GOVINDASWAMY S, BOSCH H. Aeroelastic Analysis of Bridges Using FEM and Moving Grids[J]. Wind & Structures, 2002, 5(2/3/4): 257-266. |
| [7] |
DETTMER W, PERIC' D. A Computational Framework for Fluid-rigid Body Interaction:Finite Element Formulation and Applications[J]. Computer Methods in Applied Mechanics & Engineering, 2006, 195(13/14/15/16): 1633-1666. |
| [8] |
BRAUN A L, AWRUCH A M. Finite Element Simulation of the Wind Action over Bridge Sectional Models:Application to the Guamá River Bridge (Pará State, Brazil)[J]. Finite Elements in Analysis & Design, 2008, 44(3): 105-122. |
| [9] |
刘志文, 周帅, 陈政清. 宽高比为4的矩形断面涡激振动响应数值模拟[J]. 振动与冲击, 2011, 30(11): 153-156. LIU Zhi-wen, ZHOU Shuai, CHEN Zheng-qing. Numerical Simulation of Vortex Induced Vibration of Rectangular Cylinder with Aspect Ratio 4[J]. Journal of Vibration and Shock, 2011, 30(11): 153-156. |
| [10] |
刘小兵. 大跨度双幅桥面桥梁气动干扰研究[D]. 长沙: 湖南大学, 2011: 118-120. LIU Xiao-bing. Study on Aerodynamic Interferences of Long-span Bridges with Twin Separate Parallel Decks[D]. Changsha: Hunan University, 2011: 118-120. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1908787 |
| [11] |
张瑞琴, 翁建生. 基于流固耦合的叶片颤振分析[J]. 计算机仿真, 2011, 28(3): 48-51. ZHANG Rui-qin, WENG Jian-sheng. Blade Flutter Analysis Based on Fluid Solid Coupling[J]. Computer Simulation, 2011, 28(3): 48-51. |
| [12] |
HALLAK P H, PFEIL M S, OLIVEIRA S R C D, et al. Aerodynamic Behavior Analysis of Rio-Niterói Bridge by Means of Computational Fluid Dynamics[J]. Engineering Structures, 2013, 56: 935-944. |
| [13] |
李永乐, 朱佳琪, 唐浩俊. 基于CFD和CSD耦合的涡激振和颤振气弹模拟[J]. 振动与冲击, 2015, 34(12): 85-89. LI Yong-le, ZHU Jia-qi, TANG Hao-jun. Aeroelastic Simulation of Vortex-induced Vibration and Flutter Based on CFD/CSD Coupling Solution[J]. Journal of Vibration and Shock, 2015, 34(12): 85-89. |
| [14] |
刘克同, 汤爱平, MIONKIP K. 基于LBM流固耦合算法的桥梁颤振稳定性分析[J]. 四川大学学报:工程科学版, 2014, 46(5): 73-80. LIU Ke-tong, TANG Ai-ping, MIONKI P K. Numerical Investigation for Flutter Instability of Bridge Using FSI Model Within the Lattice Boltzmann Framework[J]. Journal of Sichuan University:Engineering Science Edition, 2014, 46(5): 73-80. |
| [15] |
LEE A H, CAMPBELL R L, HAMBRIC S A. Coupled Delayed-detached-eddy Simulation and Structural Vibration of a Self-oscillating Cylinder due to Vortex-shedding[J]. Journal of Fluids & Structures, 2014, 48: 216-234. |
| [16] |
TAWEKAL J R. CFD Simulation of the Flow over a Two-dimensional Pipe and Vortex Induced Vibration of the Pipe with 1 Degree of Freedom[D]. Stavanger, Norway: University of Stavanger, 2015: 112-218.
|
| [17] |
唐友刚, 樊娟娟, 张杰, 等. 高雷诺数下圆柱顺流向和横向涡激振动分析[J]. 振动与冲击, 2013, 32(13): 88-92. TANG You-gang, FAN Juan-juan, ZHANG Jie, et al. In Line and Transverse Vortex-induced Vibration Analysis for a Circular Cylinder under High Reynolds Number[J]. Journal of Vibration and Shock, 2013, 32(13): 88-92. |
| [18] |
邓跃. 低雷诺数下均匀流和振荡流共同作用的圆柱体受迫振动和涡激振动研究[D]. 青岛: 中国海洋大学, 2014. DENG Yue. Study on Forced Oscillation and Vortex-induced-vibration(VIV) of Circular Cylinder under Combined Uniform Flow and Oscillatory Flow at Low Reynolds Numbers[D]. Qingdao: Ocean University of China, 2014. http://industry.wanfangdata.com.cn/dl/Detail/Thesis?id=Thesis_D548565 |
| [19] |
邓小龙. 基于PC Newmark-β法的流固耦合涡激振动数值模拟[D]. 杭州: 浙江大学, 2015. DENG Xiao-long. Numerical Simulation of Vortex-induced Vibrations Using PC-Newmark-β-based Fluid-structure Interaction Method[D]. Hangzhou: Zhejiang University, 2015. http://www.doc88.com/p-7728265339613.html |
| [20] |
NARIMAN N A. Influence of Fluid-structure Interaction on Vortex Induced Vibration and Lock-in Phenomena in Long Span Bridges[J]. Frontiers of Structural & Civil Engineering, 2016, 10(4): 1-22. |
| [21] |
龚慧星, 刘志文. 矩形断面柱体涡激振动数值模拟与机理分析[J]. 公路交通科技, 2016, 33(8): 76-85. GONG Hui-xing, LIU Zhi-wen. Numerical Simulation and Mechanism Analysis of Vortex-induced Vibration of Rectangular Cylinder[J]. Journal of Highway and Transportation Research and Development, 2016, 33(8): 76-85. |
| [22] |
LARSEN A. Aerodynamic Aspects of the Final Design of the 1624 m Suspension Bridge Across the Great Belt[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1993, 48(2): 261-285. |
 2018, Vol. 35
2018, Vol. 35
