扩展功能
文章信息
- 杨国峰, 王浩仰, 潘玉利
- YANG Guo-feng, WANG Hao-yang, PAN Yu-li
- 基于混合效应模型的沥青路面使用性能预测
- Prediction of Asphalt Pavement Performance Based on Mixed Effect Model
- 公路交通科技, 2018, 35(8): 19-27
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(8): 19-27
- 10.3969/j.issn.1002-0268.2018.08.004
-
文章历史
- 收稿日期: 2018-05-16
2. 交通运输部公路科学研究院, 北京 100088;
3. 中公高科养护科技股份有限公司, 北京 100095;
4. 公路养护技术国家工程研究中心, 北京 100095
2. Research Institute of Highway, Ministry of Transport, Beijing 100088, China;
3. Roadmaint Co., Ltd., Beijing 100095, China;
4. National Engineering Research Center of Road Maintenance Technologies, Beijing 100095, China
路面使用性能在各种因素的作用下,随着路龄的增长而逐渐衰减,及时有效的养护干预显得十分必要。截至2016年末,全国公路总里程达到469.63万km,公路养护比例达到97.7%[1]。对使用期内路况进行科学评价并依据评价结果预测路面性能衰减趋势,成为路面养护规划与对策研究的核心。因此,路面使用性能的预测成为管理部门十分重视的问题[2-3]。本研究以华北某地区普通公路干线网为研究对象,根据2008—2015年以来检测结果,结合路面结构、交通状况、养护历史和地形等不同因素,利用统计原理建立沥青路面使用性能PCI,RQI和RDI预测模型,具体采用混合效应模型方法对模型参数进行估计,最终通过实例验证模型的应用效果和预测精度。
1 预测方法研究依据建模方法对使用性能预测模型进行分类,总体上可归纳为确定型模型和概率型模型。确定型模型是根据经验分析、力学分析或机理分析预测路面使用性能参数的单一数值,具体表现为力学模型;力学-经验模型、经验模型;近年来一些基于现代数学理论模型则包含:灰色系统理论[4]、人工神经网络[5-8]、时间序列[9]、混合效应模型[10]等。
对于路网级养护管理而言,以实测数据为基础的经验统计模型仍然是路面性能预测的主流形式。同济大学孙立军教授在对路面使用性能长期研究的基础上提出了以使用性能指数PPI(表征PCI、RQI或其综合参数)为指标的路面使用性能衰变模型[11]。性能预测模型也可以用于路面结构设计中,如在AASHTO的力学-经验路面设计指南[12-13](MEPDG, Mechanistic-Empirical Pavement Design Guide)中,预测模型主要立足于使用性能角度对设计方法的合理性进行检验并融入于设计方法中。虽然实测数据能够较好地反映路面损坏、平整度和车辙等指标在荷载作用下随时间变化的实际情况,但是受检测误差影响,时间序列短且不连续,给传统经验模型的建模和参数估计带来诸多困难。以往预测模型中,如时间序列模型,通常仅能考虑其中一个维度。受大中修及预防性养护的影响,国内的路面性能数据往往难以获得多年连续的观测值,因此更加难以得到稳定的参数估计。其次,大部分模型仅关心研究对象的确定型模型及其平均行为,却忽略了个体之间或群体之间存在的序列相关性及差异性,这将会对模型的准确性造成影响。
事实上,沥青路面检测数据是一类典型的面板数据[14],这类数据同时包括时间和截面两个维度的数据:从横截面看是若干个体在某一时刻构成的截面观测值,它包括描述路面不同属性及影响因素的数据;从纵向上看为路面检测数据随时间发生演化的时间序列数据。基于面板数据的需求,20世纪80年代初针对资料的非独立性问题提出了混合效应模型(Linear mixed effect model)[10]。其又被称为多水平模型(Multilevel Model)、广义估计方程(GEE)等,是分析多水平数据、重复调查数据及面板数据的近代统计方法。模型既能反映数据的整体变化趋势,又能刻画个体差异,因此在医学、经济学、生物学等领域均得到广泛应用。在性能预测方面,混合效应模型采取路段内部差异和路段间的差异,这种差异的分解产生了模型参数的统计学有效估计。因此,针对面板数据的预测分析求助于混合模型是必要的。
为提高路面损坏、平整度和车辙等的预测精度,减少预测结果的偏差,本研究基于分析标定法(即理论分析与试验数据标定结合:利用理论知识,充分发挥研究人员的主观能动性,建立理想模型;同时通过试验或观测数据,利用分析工具,标定和修正理想模型待定参数)[15],采用混合效应模型研究沥青路面性能指标的演化规律,该模型的优势如下:(1)模型由固定效应和随机效应两部分组成,其中固定效应反映总体特性及平均变化趋势,而随机效应则反映个体之间的差异,反映无法观测得到或潜在的影响因素。(2)模型能够针对两层或多层数据进行综合分析,在面板数据中,每个路段性能观测值均有一个完整的随时间推移而变化的趋势(时间上的相关性),又有在特定时间点上组合形成的横断面观测值,具有传统多元统计模型无法比拟的优势。(3)其不仅能估计固定效应影响,得到总体的平均变化趋势,还能分析个体的随机效应,并且一次获得所有个体的参数估计。当样本量非常大时,将在很大程度上减少数据分析的工作量[14]。(4)混合效应模型能够充分整合有效信息,适用于解决含有随机缺失数据的分析。
2 预测指标及影响因素 2.1 预测指标的确定选取预测指标即明确预测对象。通常,对网络级管理系统,较多采用综合性的路况指标;而对于项目级管理系统,则主要采用单项性能指标或者构成该指标的某项基本元素。
具体到本研究,以沥青路面作为研究对象,有检测数据的单项指标主要有3项:路面损坏状况指数(PCI)、路面行驶质量指数(RQI)、路面车辙深度指数(RDI)[16]。
2.2 影响因素路面使用性能的影响因素可以分为内部因素(路面结构和材料性能)和外部因素(交通荷载、环境、施工等)两类。为建立可靠的路面使用性能预测模型,应充分考虑因素的影响特性或机理。然而,实践过程中,不可能也不必将所有因素纳入到模型之中,须针对具体研究对象进行选取。
2.2.1 路面结构及材料路面的结构组成主要是指面层、基层的类型和厚度,而材料性能则主要体现在各结构层所用原材料的种类及其性质上。不同路面结构组成和材料性能分别对应着不同的路面结构强度,反映了路面在交通荷载和环境因素作用下不同的承载能力。
以往的模型中通常采用两种方式:一是根据面层、基层类型以及厚度等特性对路面进行分类,针对不同类别分别建立预测模型[17];二是依据AASHTO 1993年路面设计规范中提出的结构指数表征路面结构特性建立预测模型[18]。基于该地区普通干线调研的数据可知,基层绝大部分属于半刚性基层类型,本研究针对半刚性基层路面,选用路面面层厚度作为影响变量。
2.2.2 环境因素环境因素包括温度和湿度(降雨)等,其作用途径主要有两种:(1)直接影响路面材料的性能;(2)通过叠加在行车荷载上间接影响。由于各地温度、湿度等环境因素的差异,路面使用性能的衰变规律也不尽相同。通过对该地区气温、地面温度以及降雨量等情况的调查分析,见表 1、表 2。本研究近似认为,各地区之间环境因素影响差异不大,温度和湿度的变化在各年度之间表现的周期性较强,其影响可以通过时间变量加以反映,引入地区所属养管单位来间接反映区域的不同。
| 项目 | 气温/℃ | 年平均气温/℃ | 地面极端气温/℃ | 地面 | 最大冻土厚度/cm | |||||||
| 1月 | 4月 | 7月 | 10月 | 全年 | 最高 | 最低 | 冻结日期 | 解冻日期 | ||||
| 区1 | -5.7 | 16.8 | 29.7 | 13.3 | 13.6 | 11.7 | 66.7 | -13.3 | 12月7日 | 2月27日 | 70 | |
| 区2 | -5.3 | 17.8 | 30.3 | 14.2 | 14.3 | 10.1 | 68 | -14.2 | 12月11日 | 2月24日 | 70 | |
| 区3 | -5.8 | 16.5 | 30.3 | 13.4 | 13.7 | 11.5 | 68.4 | -13.4 | 12月8日 | 2月24日 | 69 | |
| 区4 | -6.5 | 18.3 | 31 | 14.4 | 14.5 | 11.6 | 68 | -14.4 | 12月3日 | 2月24日 | 81 | |
| 区5 | -9.7 | 14 | 28.3 | 10.8 | 10.9 | 8.4 | 66.1 | -10.8 | 11月25日 | 3月3日 | 115 | |
| 区6 | -7 | 17.1 | 30.7 | 13.5 | 13.6 | 10.8 | 66 | -13.5 | 12月1日 | 2月24日 | 69 | |
| 区 | 地区降雨量/mm | ||||||||||||
| 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | 全年 | |
| 区1 | 2.7 | 6.7 | 7.8 | 20.1 | 29.4 | 77.4 | 204.5 | 204.4 | 55.4 | 25.2 | 6.2 | 2.3 | 642.1 |
| 区2 | 2.9 | 6.6 | 9.8 | 19.5 | 31.5 | 69.9 | 230.6 | 187.6 | 57.9 | 26.6 | 5.4 | 2.2 | 650.5 |
| 区3 | 2.9 | 6.8 | 7.2 | 20.4 | 24.5 | 73.4 | 184.0 | 186.1 | 44.3 | 23.4 | 6.1 | 2.7 | 581.8 |
| 区4 | 2.6 | 6.0 | 7.4 | 20.0 | 24.3 | 71.6 | 212.7 | 175.1 | 49.0 | 24.9 | 6.6 | 2.6 | 602.8 |
| 区5 | 2.0 | 5.4 | 8.6 | 19.1 | 23.9 | 60.4 | 147.4 | 138.9 | 46.0 | 24.2 | 5.8 | 1.7 | 483.4 |
| 区6 | 2.4 | 5.2 | 9.8 | 18.0 | 25.9 | 78.2 | 229.7 | 196.9 | 58.7 | 29.1 | 5.3 | 2.0 | 661.2 |
2.2.3 交通荷载
交通荷载是路面状况恶化的主要外部肇因,这种影响体现在两个方面:一是荷载大小,二是荷载作用次数。因此,在路面使用性能预测中经常将标准轴载累计作用次数或路面使用时间作为主要的影响变量。由于交通轴载数据较难获取,将年平均日交通量(AADT)及车型组成作为影响变量。
2.2.4 养护历史鉴于新建路段从通车开始的路况检测数据较难获取,本研究重点在于构建养护干预下的路面使用性能衰变模型。引入养护类型变量,分为以下几种情况,如表 3所示。
| 序号 | 分类 |
| 1 | BZM薄层罩面类 |
| 2 | MH磨耗层类 |
| 3 | WB微表处 |
| 4 | WF雾封层 |
| 5 | XJ稀浆封层 |
| 6 | 加铺上面层 |
| 7 | 加铺上中面层 |
| 8 | 铣刨重铺上面层 |
| 9 | 铣刨重铺上中面层 |
| 10 | 铣刨重铺上中下面层 |
| 11 | 铣刨重铺上面层+基层 |
| 12 | 铣刨重铺上中面层+基层 |
| 13 | 铣刨重铺上中下面层+基层 |
2.2.5 其他因素
路面使用性能的衰变同道路施工质量密切相关,施工质量同施工技术、施工工艺和施工设备等诸多因素有关,大多难以量化。对于难以量化的因素影响,本研究研究引入行政等级、技术等级、养管单位以及地形等分类变量,来间接反映研究对象的区域类聚性。
综上所述,本研究在进行路面使用性能预测时,对于影响变量,通过面层厚度考虑路面结构的影响,通过交通量(AADT)及车型组成考虑行车荷载的影响,通过将养护措施分类考虑养护历史的影响,同时将路面使用年限作为预测模型的影响变量,并引入行政等级、技术等级、养管单位以及地形等分类变量。
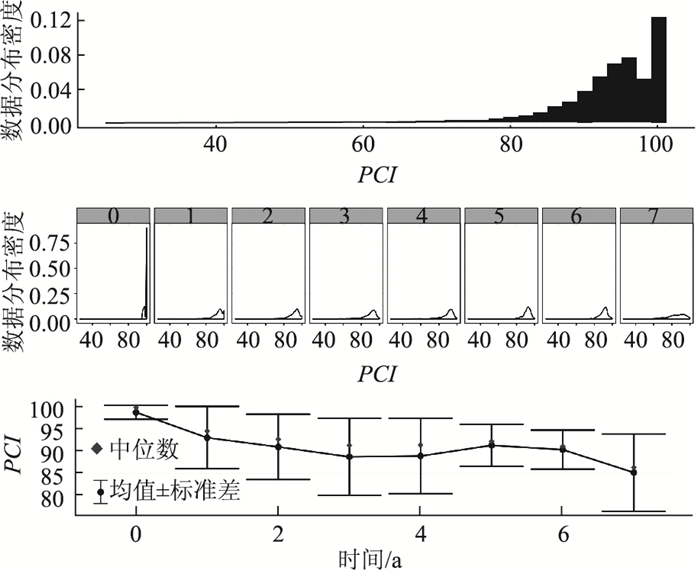
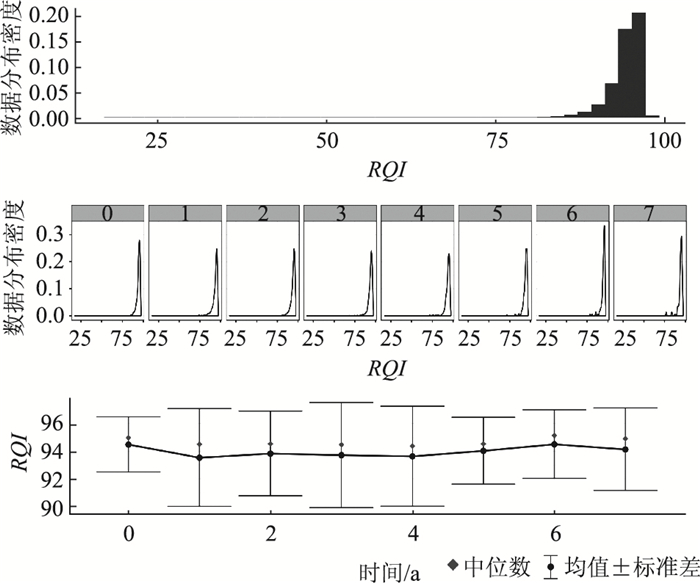
3 模型构建与参数估计 3.1 检测数据预处理建模中重要的影响变量包括:养管单位,包括技术等级(一级、二级、三级和四级),行政等级(国G、省S、县X),地形(平原、山岭、微丘和重丘),养护类型,路龄,交通量以及路面厚度。为方便处理和标记路段数据,设置路段ID作为路段唯一标识符,共涉及13 683个路段(ID)有结果变量数据。根据养护历史记录筛选,剔除无交通量等基础数据样本,最后可使用的路段分别为:PCI剩余可用信息,3 636条路段(ID);RQI剩余可用信息,3 664条路段(ID);RDI剩余可用信息,422条路段(ID)。各指标可用路段如表 4所示。PCI数据和RQI数据分布情况分别如图 1和图 2所示。
|
| 图 1 PCI数据分布情况 Fig. 1 PCI data distribution |
| |
|
| 图 2 RQI数据分布情况 Fig. 2 RQI data distribution |
| |
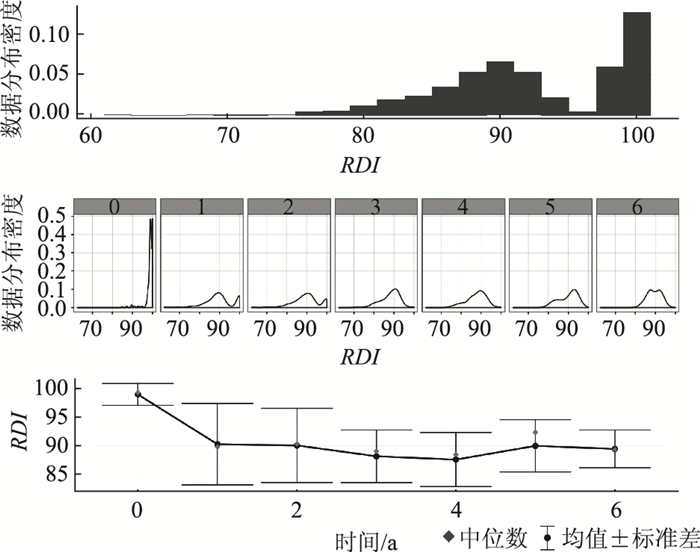
|
| 图 3 RDI数据分布情况 Fig. 3 RDI data distribution |
| |
如表 5及图 1所示,路段个体PCI变化差异很大。当时间T<4时,存在一些路况极低值,说明样本中混杂了一些养护措施质量不佳路段或者受影响变量影响衰变过快路段。同样地,对RDI,RQI进行统计分析可得:相对于PCI,RDI而言,RQI路段变化的离散程度明显小,T<4时,存在一些路况极低值,说明样本中仍混杂了一些养护措施质量不佳的路段或者受影响变量影响衰变过快的路段。而由RDI数据可知,在T=1时,数据整体趋势曲线上,明显存在一个拐点,后续数据变化较缓。因而在建模时,应充分考虑这一特点。
| T | 个数 | 最小值 | 最大值 | 均值 | 标准差 | 中位数 |
| 0 | 2 741 | 95.01 | 100 | 98.90 | 1.56 | 100 |
| 1 | 2 666 | 30.40 | 100 | 93.20 | 7.07 | 94.70 |
| 2 | 2 005 | 26.48 | 100 | 91.10 | 7.46 | 92.86 |
| 3 | 1 350 | 44.14 | 100 | 88.84 | 8.80 | 91.46 |
| 4 | 785 | 43.21 | 100 | 89.02 | 8.61 | 91.53 |
| 5 | 365 | 55.24 | 100 | 91.46 | 4.80 | 92.38 |
| 6 | 168 | 70.49 | 100 | 90.47 | 4.48 | 91.24 |
| 7 | 37 | 63.12 | 95.98 | 85.23 | 8.84 | 86.38 |
| 总体 | 10 117 | 26.48 | 100 | 93.31 | 7.53 | 94.98 |
3.2 方差分析
采用多因素方差分析,分析影响变量对结果变量的影响,为模型函数的建立提供依据。由表 6可知,统计学意义上,时间、养护类型、行政等级、养管单位、技术等级对PCI,RQI,RDI均有显著影响。因而在模型构建时,应着重考量这些显著影响变量。
| 影响因素 | P值 | ||
| PCI | RQI | RDI | |
| 时间 | <.000 1* | <.000 1* | <.000 1* |
| 养护类型 | <.000 1* | <.000 1* | 0.000 3* |
| 地形 | <.000 1* | <.000 1* | 0.590 1 |
| 行政等级 | 0.003 8* | <.000 1* | 0.034 9* |
| 养管单位 | <.000 1* | <.000 1* | <.000 1* |
| 技术等级 | 0.000 1* | <.000 1* | 0.004 8* |
| 注:标记为*的表示该因素对结果变量在统计上具有显著影响。 | |||
3.3 模型构建
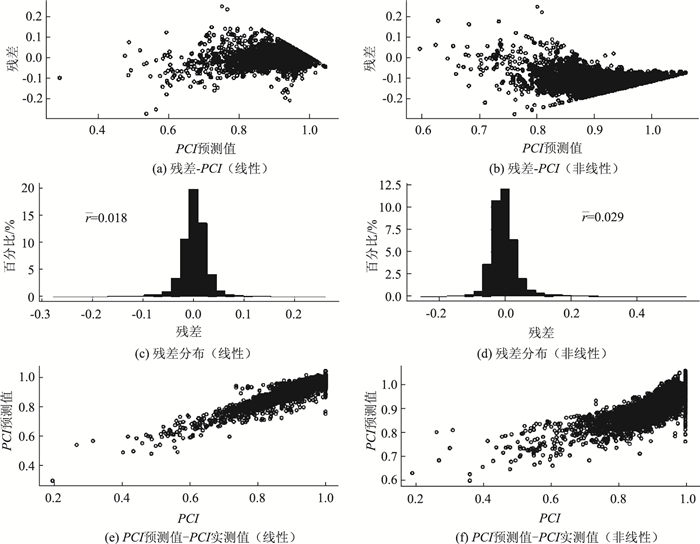
虽然多因素方差分析基本确定了主要的影响因素,但在模型实际建立过程中,尤其是考虑到因素与时间之间的交互作用时,方差分析的结果会不断变化,因此需要通过反复纳入、排除,确定模型中最终的影响因素。本研究所涉及因素远多于之前相关研究,且数据量更大,数据包含的可能未考察的混杂因素更多。在模型形式探索过程中发现,针对数据特点,直接采用线性混合效应模型公式(2)比非线性混合效应模型公式(4)拟合效果好。以PCI指标为例,对于归一化后的数据,线性混合效应模型平均误差为0.018(对应实际数据,平均误差为1.8),非线性混合效应模型为0.029(对应实际数据,平均误差为2.9)。通过残差分析可以确定,直接使用线性混合效应模型比非线性模型更合适。结果见图 4。
|
| 图 4 线性与非线性混合效应模型结果对比图 Fig. 4 Comparison of analysis results obtained from linear mixture effect model & nonlinear mixed effect model |
| |
线性混合效应模型:
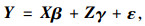
|
(1) |
式中,Y为因变量;X为固定效应项;Z为随机效应项;β为固定效应项系数;γ为随机效应项系数;ε为随机误差。

|
(2) |
式中,MaintainDetail为养护类型;LandForm为地形;AdminLevel为行政等级;MaintainDept为养管单位;RoadLevel为道路技术等级;SurThick为路面厚度;wt_Total为交通量AADT;βi为模型参数;tij为第i个路段,j时刻时间变量;γ1i为第i个路段对应常数项随机效应系数;γ2i为第i个路段对应时间变量随机效应系数;eij为第i个路段j时刻随机误差。
非线性混合效应模型:
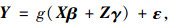
|
(3) |
式中,Y为因变量;X为固定效应项;Z为随机效应项;β为固定效应项系数;γ为随机效应项系数;ε为随机误差。
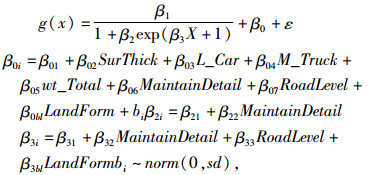
|
(4) |
式中,SurThick为路面厚度;L_Car为小汽车数量;M_Truck为货车数量;wt_Total为交通量AADT;MaintainDetail为养护类型;RoadLevel为道路技术等级;LandForm为地形;β0i为第i个路段对应的变量β0;β1i为第i个路段对应的变量β1;β2i为第i个路段对应的变量β2;βi为模型参数;bi为第i个路段随机误差;sd为标准差。
3.4 参数估计经验证,本研究3个指标均采用线性混合效应模型,考虑RDI数据在T=1时,整体趋势曲线上明显存在一个拐点,因而确定RDI为分阶段的线性混合效应模型。PCI,RQI,RDI混合效应模型分别为:

|
(5) |
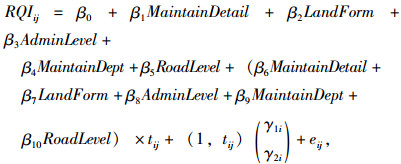
|
(6) |
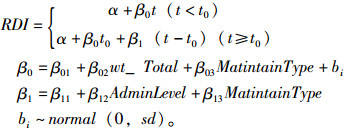
|
(7) |
以PCI指标为例,行政等级参数估计结果如表 7所示。假设G,X,S,以及与时间的交互项T· AdminLevel即T·G,T·X,T·S的参数估计值分别为1, 2, 0, 4, 5, 0这6个数。在模型中,如果该路段为G,则计算形式为:PCI=(其他因素)…1+4×t…;如果为X,则计算形式为:PCI=(其他因素)…2+5×t…;如果为S,PCI=(其他因素)…0+0×t…。这样计算,本质上是因为,对于所有分类变量,在建模时需建立哑变量。例如行政等级共有3个值,可以用两个哑变量来表示,不妨令其为(AL1, AL2)。G,X,S这3个值用哑变量表示为(1, 0),(0, 1)和(0, 0)。在模型训练时,此项在方程中的形式为:β1AL1+β2AL2,因而只需要训练两个参数就可以代表 3个水平的变化。
| 效应 | 分类变量值 | 估计 | 标准误差 | t值 | Pr > |t| |
| AdminLevel | G | 0.003 71 | 0.002 083 | 1.78 | 0.074 9 |
| AdminLevel | S | 0.009 252 | 0.001 483 | 6.24 | <.0001 |
| AdminLevel | X | 0 | . | . | . |
| T*AdminLevel | G | 0.018 01 | 0.003 967 | 4.54 | <.000 1 |
| T*AdminLevel | S | 0.009 352 | 0.002 961 | 3.16 | 0.001 6 |
| T*AdminLevel | X | 0 | . | . | . |
| Intercept | 0.985 9 | 0.008 445 | 116.75 | <.000 1 | |
| SurThick | 0.00187 | 0.000 778 | 2.4 | 0.016 2 | |
| T*wt_Total | -0.002 4 | 0.001 775 | -1.35 | <.000 1 | |
| 注:1.对应实际数据,估计值=表中数值*100; 2.参数估计结果中,有些参数估计值为0,表示该项是此分类变量不同值的基准项,在使用中参数带入0即可。 | |||||
从表 7得出以下结论:(1)wt_Total的斜率为负,表明当其他因素保持不变时,随着交通量AADT的增大,路面破损加快衰变,与专业认知相符合;(2)从行政等级的衰变速度来看,县道>市道>国道。
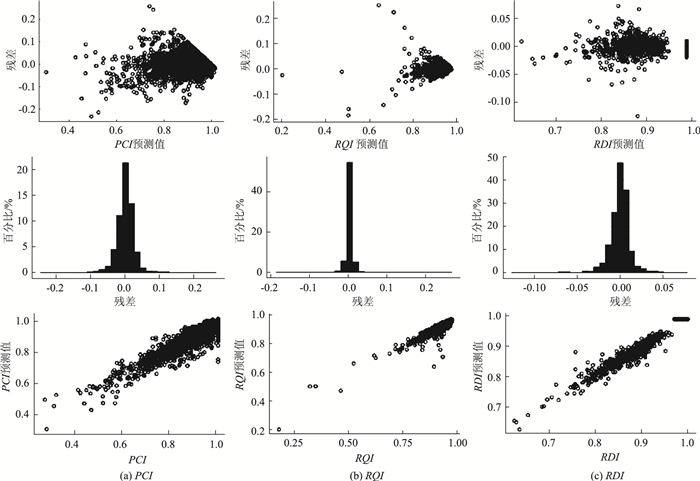
3.5 预测精度和残差分析如图 5所示,对于归一化的结果变量数据,PCI平均误差为0.018(对应实际数据,平均误差为1.8),RQI为0.005(对应实际数据,平均误差为0.5),RDI为0.008(对应实际数据,平均误差为0.8)。同时,研究PCI,RQI,RDI按照分类变量不同水平分别观察残差的分布情况,发现残差均近似接近正态分布,各水平无明显偏态。残差分布接近正态,说明模型很好地解释了数据的变异性。
|
| 图 5 PCI(左)、RQI(中)、RDI(右)残差分析图 Fig. 5 Residual analysis of PCI(left), RQI(middle)and RDI(right) |
| |
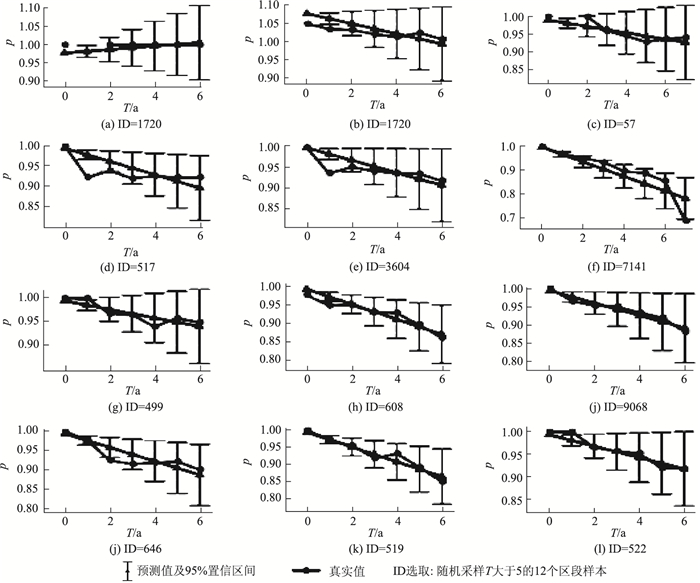
PCI在随机抽样下的预测值和实测值对比如图 6所示,可见模型预测精度较高。
|
| 图 6 PCI随机抽样样本预测值和实测值对比 Fig. 6 Comparison of predicted values and measured values(PCI random sampling) |
| |
4 模型应用
基于混合效应模型得到的训练参数,可以使用模型对新的数据进行预测。假设选取一个不在训练集中的全新路段,则可计算其结果的边际期望值,忽略随机效应项。计算公式如下:

|
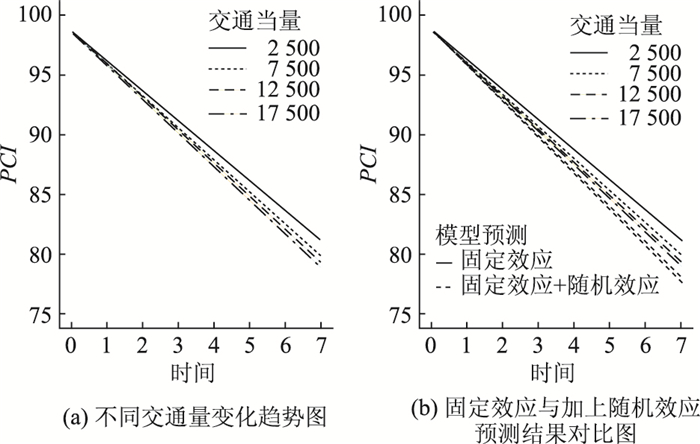
代入相应的道路信息,交通量,即可得到相应的趋势。例如养护类型为MH磨耗层类,养管单位为A区,地处平原,行政等级为G,道路等级为二级公路,路面面层厚度为10 cm,交通当量不同时,变化趋势如图 7(a)所示。若训练模型内包含该路段的信息,则可以利用该路段独有的随机效应项系数,对期望值进行校正:
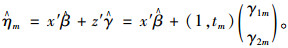
|
|
| 图 7 混合效应模型拟合效果 Fig. 7 Fitting effect by mixed effect model |
| |
不妨以道路信息为ID=319的路段为例,通过查找随机效应项的解,可知γ1m=-0.000 13,γ2m=-0.001 72,代入方程计算。预测结果如图 7(b)。
5 结论本研究开展华北某地区普通公路沥青路面长期使用性能研究,挖掘全市多年累积的公路基础数据价值,建立了市级养护干预下的PCI,RQI和RDI预测模型,主要结论如下:
(1) 构建了路面破损PCI、路面平整度RQI和路面车辙RDI的线性混合效应模型,PCI,RQI和RDI预测的平均误差为1.8,0.5和0.8。残差分布接近正态,说明模型很好地解释了数据的变异性。
(2) 模型简单,预测精度高,并且解释和量化了时间、养护类型、地形、行政等级、养管单位、技术等级、路面厚度以及交通量等因素对指标预测的影响。
(3) 路面车辙RDI变化曲线存在明显的拐点特征,基于此,建立了RDI分阶段线性混合效应模型。
(4) 实例表明:混合效应模型既可反映总体性能衰变趋势,亦可体现路段个体差异。
| [1] |
交通运输部. 2016年交通运输行业发展统计公报[J]. 交通财会, 2017(5): 92-97. Ministry of Transport. Development and Statistics Bulletin of Transportation Industry in 2016[J]. Finance & Accounting for Communications, 2017(5): 92-97. |
| [2] |
张金喜. 道路路面性能评价理论及其应用[M]. 北京: 科学出版社, 2014. ZHANG Jin-xi. Road Pavement Performance Evaluation Theory and Application[M]. Beijing: Science Press, 2014. |
| [3] |
曾峰. 高等级公路沥青路面大中修养护周期及适用性能预测技术研究[D]. 西安: 长安大学, 2011. ZENG Feng. Research on Maintenance Cycle and Applicable Performance Forecasting Technology of High-grade Highway Asphalt Pavement[D]. Xi'an: Chang'an University, 2011. |
| [4] |
邓聚龙. 灰色理论基础[M]. 武汉: 华中科技大学出版社, 2002. DENG Ju-long. Gray Theoretical Basis[M]. Wuhan: Huazhong University of Science and Technology Press, 2002. |
| [5] |
KARGAH-OSTADI N, STOFFELS S M, TABATABAEE N. Network-level Pavement Roughness Prediction Model for Rehabilitation Recommendation[J]. Transportation Research Record, 2010, 2155: 124-133. |
| [6] |
倪富健, 屠伟新. 基于神经网络技术的路面性能预估模型[J]. 东南大学学报:自然科学版, 2000, 30(5): 91-95. NI Fu-jian, TU Wei-xin. Pavement Performance Forecasting Model by Using Neural Network[J]. Journal of Southeast University:Natural Science Edition, 2000, 30(5): 91-95. |
| [7] |
李莉娟. 基于预防性养护的山区高等级公路路面使用性能预测和养护决策研究[D]. 重庆: 重庆交通大学, 2012. LI Li-juan. Study on Prediction of Pavement Performance and Maintenance Decision-making of High-grade Highway in Mountain Area Based on Preventive Maintenance[D]. Chongqing: Chongqing Jiaotong University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10618-1013136941.htm |
| [8] |
周鹏飞, 温胜强, 康海贵. 基于马尔可夫链与神经网络组合的路面使用性能预测[J]. 重庆交通大学学报:自然科学版, 2012, 31(5): 997-1001. ZHOU Peng-fei, WEN Sheng-qiang, KANG Hai-gui. Pavement Performance Combining Forecasting Based on BP Neural Network and Markov Model[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2012, 31(5): 997-1001. |
| [9] |
倪富健, 方昱, 薛智敏. 时间序列在路面平整度预测中的应用[J]. 东南大学学报:自然科学版, 2006, 36(4): 634-637. NI Fu-jian, FANG Yu, XUE Zhi-min. Prediction of Pavement Roughness with Time Series Autoregression Model[J]. Journal of Southeast University:Natural Science Edition, 2006, 36(4): 634-637. |
| [10] |
CHU C Y, DURANGO-COHEN P L. Estimation of Infrastructure Performance Models Using State-space Specifications of Time Series Models[J]. Transportation Research Part C:Emerging Technologies, 2007, 15(1): 17-32. |
| [11] |
孙立军. 沥青路面结构行为理论[M]. 北京: 人民交通出版社, 2005. SUN Li-jun. Structural Behavior Theory of Asphalt Pavement[M]. Beijing: China Communications Press, 2005. |
| [12] |
JABLONSKI B, REGEHR J, REMPEL G. Guide for Mechanistic-empirical Design of New and Rehabilitated Pavement Structures[R]. Champaign, Illinois: ARA, Inc., 2001.
|
| [13] |
PERERA R W, KOHN S D. NCHRP Web Document 40: LTPP Data Analysis: Factors Affecting Pavement Smoothness[R]. Washington, D. C. : Transportation Research Board, 2001.
|
| [14] |
袁捷, 苏尔好, 杜先照, 等. 基于线性混合效应模型的道面使用性能预测[J]. 同济大学学报:自然科学版, 2014, 42(5): 707-713. YUAN Jie, SU Er-hao, DU Xian-zhao, et al. Linear Mixed Effect Model for Airport Pavement Performance Prediction[J]. Journal of Tongji University:Natural Science Edition, 2014, 42(5): 707-713. |
| [15] |
BANDARA N, GUNARATNE M. Current and Future Pavement Maintenance Prioritization Based on Rapid Visual Condition Evaluation[J]. Journal of Transportation Engineering, 2001, 127(2): 116-123. |
| [16] |
JTG H20-2007, 公路技术状况评定标准[S]. JTG H20-2007, Highway Performance Assessment Standards[S]. |
| [17] |
薛志敏. 现代高速公路沥青路面路面管理系统框架及其预测模型研究[D]. 南京: 东南大学, 2006. XUE Zhi-min. Research on Asphalt Pavement Management System Framework and Prediction Model of Modern Expressway[D]. Nanjing: Southeast University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10286-2007031792.htm |
| [18] |
AASHTO GDPS-4-1993, Guide for Design of Pavement Structures[S].
|
 2018, Vol. 35
2018, Vol. 35
