扩展功能
文章信息
- 蔡建荣, 黄中祥, 吴立烜
- CAI Jian-rong, HUANG Zhong-xiang, WU Li-xuan
- 基于无人驾驶车辆的可变车道优化方法
- An Optimization Method of Reversible Lane Based on Autonomous Vehicles
- 公路交通科技, 2018, 35(7): 136-141, 150
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(7): 136-141, 150
- 10.3969/j.issn.1002-0268.2018.07.019
-
文章历史
- 收稿日期: 2017-12-21
实施可变车道,调整道路时空资源是解决潮汐交通现象、缓解城市交通拥堵的有效措施[1-5]。将轻交通流方向的道路资源调节给重交通流方向,能在一定程度上减缓重交通流方向的交通压力,提高整个道路网络系统的运行效率[6-7]。
Zhang[8]论证了可变车道调节能大幅提高道路网络储备容量。Li[9]为使可变交通系统的周期性流动方向变化得更加顺畅,提出了适用于城市干道从非高峰期到高峰期的可变车道调节方法。Hausknecht[10]指出可变车道系统能够增加拥挤路段的容量,有效减少高峰期的交通拥挤,并有利于出行用户的紧急疏散。Wolshon等[11]对可变车道设置能够解决的问题进行了分析,认为在规划可变车道时应着重对各种设计方案的费用、优缺点以及整个交通系统的长远效益进行综合考虑。岳雷[12]论证了上海世博会召开期间实施可变车道调节的必要性及可行性,并对具体的实施方案进行了初步探讨。史峰等[13]以降低城市交通网络高峰期出行总费用和减少可变车道设置管理成本为目标,建立了一主二从双层规划模型。张好智等[14-15]以道路网络总阻抗最小为目标构建了可变车道优化双层规划模型,其中上层为交通管理部门的可变车道设置方案,下层为根据所设置的方案对出行用户进行用户最优配流。虽然此模型在可变车道调节之后,能一定程度上使道路网络结构更好地匹配居民出行需求,均衡各路段的饱和度,降低系统总出行时间,但是所采用的用户最优是限制交通系统运行效率提高的重大障碍[16]。系统最优才是道路网络最高效运行的方式,而且当前已经可以运用边际收费等方式来实现[17-18]。未来可能所有车辆都是无人驾驶的,交通管理者完全可以运用ITS等先进的技术手段来调控道路网络达到系统最优状态[19]。此时再结合可变车道调节,实现人、车、路的协同,将更好地发挥道路资源的作用,极大提高道路网络系统的运行效率。显然,基于系统最优的可变车道调节方法具有重要应用前景,ITS和无人驾驶技术的快速发展和完善为其早日实现提供了基础。
本研究将通过ITS调控所有无人驾驶车辆实现系统最优状态的可行方法,以此为基础,进一步从系统层面对可变车道优化设置方法进行研究,提升系统最优性能指标。
1 道路网络系统最优实现方法记路段集为A,各路段a的流量为xa,其行驶时间函数为ta(xa),根据Wardrop第一原理,如果所有出行者准确知道各条道路所需的行驶时间ta(xa),并选择行驶时间最短的道路,最终道路网络将达到用户最优状态。
然而根据道路网络用户最优和系统最优之间的关系,令:
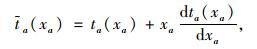
|
(1) |
式中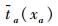
有:
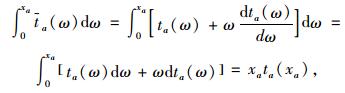
|
(2) |
式中ω为积分变量符号。
记OD对的集合为w,OD对(r, s)间的第k条路径上的交通量为fkrs,OD对(r, s)间的出行需求为qrs,路径与路段的关联关系为δa, krs,当路径k经过路段a时,δa, krs=1,否则δa, krs=0。不难得到以边际行驶时间函数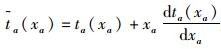
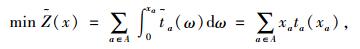
|
(3) |
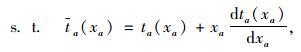
|
(4) |
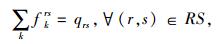
|
(5) |
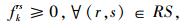
|
(6) |
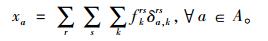
|
(7) |
因此,只要道路网络系统中所有出行者以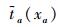
随着交通科技的发展,可以期待系统最优在这样的假设下出现:假设ITS能实时获取道路网络的完全信息,并为车辆提供边际最短路径;假设未来所有车辆均为无人驾驶车辆,并严格执行ITS发布的路径诱导指令。通过无人驾驶车辆的相互协作,系统最优状态即可实现。
2 可变车道优化模型记整个可变道路网络的节点集合为N,路段a和a所组成的双向路段为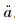
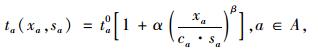
|
(8) |
式中α,β为待定参数。
根据前面的分析,各可变车道路段的边际行驶时间函数采用:
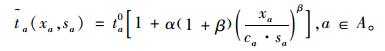
|
(9) |
假设ITS一方面引导所有无人驾驶车辆在道路网络上达到系统最优状态,一方面通过可变车道调节使道路网络结构更好地匹配居民出行需求,二者结合后将很好地协调人、车、路之间的关系,最大程度发挥道路资源的作用,提高道路网络系统的运行效率。
对于整个道路网络,根据交通需求的分布特性,存在多种可变车道设置方案。因此,在用户遵循系统最优原理的前提下,寻找能够最大限度优化当前系统性能指标的可变车道设置方案可由下述模型给出。
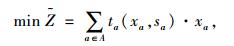
|
(10) |
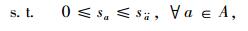
|
(11) |
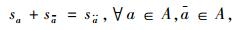
|
(12) |
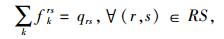
|
(13) |
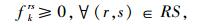
|
(14) |
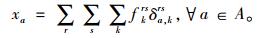
|
(15) |
式中,fkrs为OD对(r, s)间第k条路径上的流量;qrs为OD对(r, s)间的出行需求;δa, krs为路径与路段的关联系数,当路径k经过路段a时,δa, krs=1,否则δa, krs=0。式(11)表明路段a的车道数调节范围为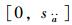
式(11)~(15)是一个非线性混合整数规划问题,求解非常困难。本研究采用混沌粒子群算法[20-21]来对模型进行求解,算法步骤如下。
Step 0:初始化。令迭代次数为γ,最大允许迭代次数为γmax,粒子群规模为m,最大速度为va, max,缩小系数分别为b1,b2,动态延误期为ξ,惯性权因子为κ,加速系数分别为q1,q2,第i(i=1, 2, …, m)个粒子第γ次迭代的位置(…, ϕa, γi, …)对应到第i种可变车道优化方案第γ次迭代的状态(…, sa, γi, …),路段a的最大粒子位置为ϕa, max,对应到路段a的最大车道设置数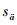
Step 1:计算适应度。针对每个可行粒子求解系统最优分配模型,再根据路段流量求解相应的目标函数值,即为该粒子的适应度。
Step 2:针对粒子群中的粒子进行混沌化处理并更新粒子群中粒子的适应度。利用Logistic映射对粒子进行ψmax次混沌迭代处理。假设与(…, ϕa, γi, …)相同维数的搜索空间元素为Y=(…, yi, …),yi为向量Y的第i个分量,且yi∈[0, 1],按yik+1=μyik(1-yik)进行迭代,当迭代次数达到ψmax时,得到向量Y的第i个分量yi(i=1, 2, …)的混沌序列{yij|j=1, 2, …, k}。当μ=4时,Logistic映射所获得的混沌序列处于完全混沌状态,ψmax足够大时,混沌序列能够遍历搜索空间的所有值。
Step 3:更新个体和群体的历史最优位置。对于第i(i=1, 2, …, m)个粒子,用当前最优适应度对应的位置来更新个体极值pbesta, γi;对于粒子群,用所有pbesta, γ中最优的位置来更新群体极值gbesta, γ。若连续经过ξ次迭代后gbesta, γ没有改善,则令κ=b1κ,va, max=b2va, max。
Step 4:根据va, γ+1i=κva, γi+q1R1(pbesta, γi-ϕa, γi)+q2R2(gbesta, γ-ϕa, γi)更新粒子速度,其中va, γi为第i(i=1, 2, …, m)个粒子第γ次迭代的速度,R1和R2为(0, 1)之间的随机数,各粒子的速度应四舍五入取为整数。若va, γ+1i>va, max,则令va, γ+1i=va, max。
Step 5:根据ϕa, γ+1i=ϕa, γi+va, γi更新粒子位置。若ϕa, γ+1i不满足约束条件0≤ϕa, γ+1i≤ϕa, max,则将其舍弃,不更新第i个粒子的位置;若满足约束条件,对第i个粒子进行判断,如果该粒子使得某OD对之间无路径连通,则舍弃该新位置,不更新第i个粒子的位置,否则将第i个粒子更新为该新位置。
Step 6:终止检验。若满足终止条件,则停止迭代,输出gbesta, γ作为最优调整方案;否则,令γ=γ+1,返回Step 1。
4 算例分析测试道路网络如图 1所示,该网络由4个节点和5条双向路段组成。假定有4个OD对,需求量分别为q14=5 600辆/h,q41=1 200辆/h,q23=1 600辆/h,q32=700辆/h。BPR函数的参数取值为α=0.15,β=4。
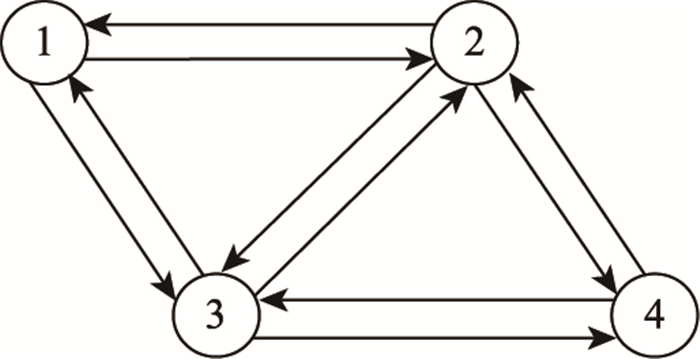
|
| 图 1 测试道路网络 Fig. 1 Test road network |
| |
各路段的特性参数见表 1。
| 路段 | 自由流行驶时间/h | 单车道通行能力/(辆·h-1) | 车道数 |
| 1-2 | 0.25 | 600 | 4 |
| 2-1 | 0.25 | 600 | 4 |
| 2-4 | 0.20 | 600 | 4 |
| 4-2 | 0.20 | 600 | 4 |
| 1-3 | 0.15 | 800 | 3 |
| 3-1 | 0.15 | 800 | 3 |
| 2-3 | 0.10 | 800 | 3 |
| 3-2 | 0.10 | 800 | 3 |
| 3-4 | 0.25 | 800 | 3 |
| 4-3 | 0.25 | 800 | 3 |
针对各路段的车道数,取ϕ1-2, max=8,ϕ2-4, max=8,ϕ1-3, max=6,ϕ2-3, max=6,ϕ3-4, max=6,v1-2, max=8,v2-4, max=8,v1-3, max=6,v2-3, max=6,v3-4, max=6。同时,为提高算法的收敛速度及保证其有效收敛,取m=15,b1=0.8,b2=0.8,ξ=5,q1=2,q2=2,κ=1.4,γmax=100,μ=4, ψmax=100。系统总出行时间随迭代次数变化如图 2所示。
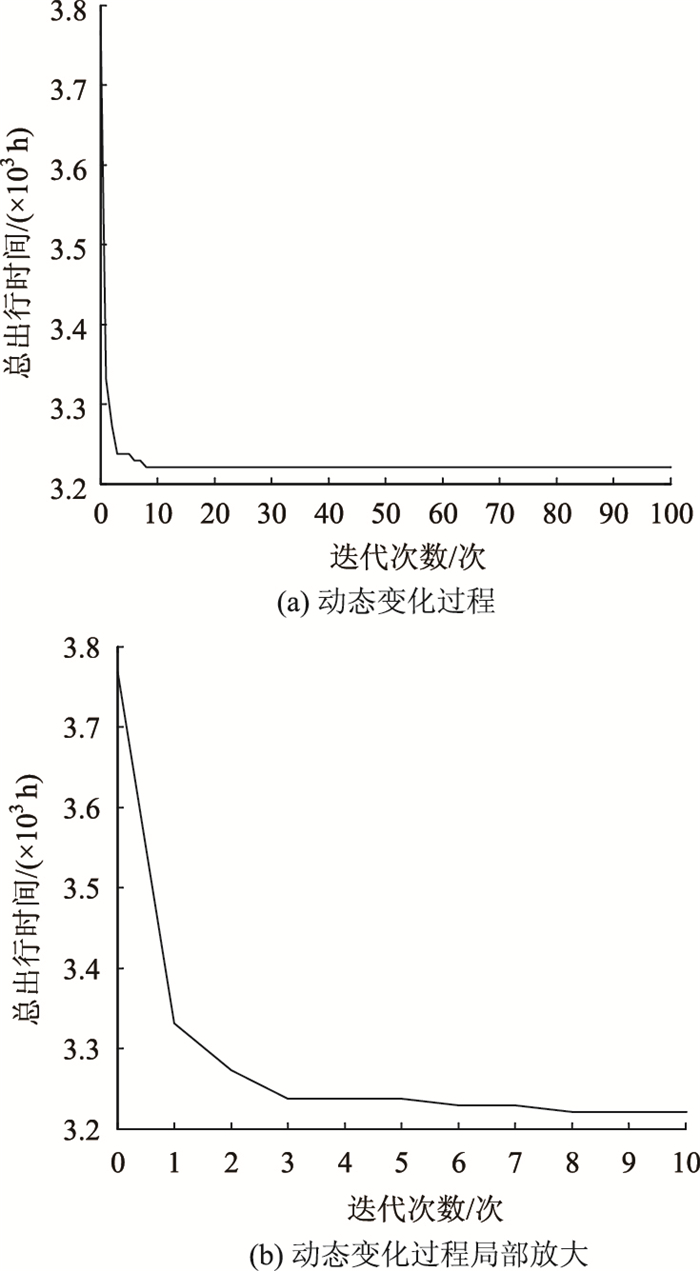
|
| 图 2 系统总出行时间随迭代次数的变化 Fig. 2 Total travel time of system varying with iteration times |
| |
针对有无可变车道设置的两种系统最优状态的对比如表 2所示。
| 路段 | 车道数 | 容量/(辆·h-1) | 流量/(辆·h-1) | 饱和度 | 行程时间/h | ||||||||||||||
| 用户最优 | 系统最优 | 可变车道 | 用户最优 | 系统最优 | 可变车道 | 用户最优 | 系统最优 | 可变车道 | 用户最优 | 系统最优 | 可变车道 | 用户最优 | 系统最优 | 可变车道 | |||||
| 1-2 | 4 | 4 | 8 | 2 400 | 2 400 | 4 800 | 2 610 | 2 623 | 3 112 | 1.09 | 1.10 | 0.65 | 0.302 4 | 0.303 5 | 0.256 6 | ||||
| 2-1 | 4 | 4 | 0 | 2 400 | 2 400 | — | 0 | 0 | — | 0.00 | 0.00 | — | 0.250 0 | 0.250 0 | — | ||||
| 2-4 | 4 | 4 | 8 | 2 400 | 2 400 | 4 800 | 2 610 | 2 820 | 3 112 | 1.09 | 1.18 | 0.65 | 0.242 0 | 0.257 2 | 0.205 3 | ||||
| 4-2 | 4 | 4 | 0 | 2 400 | 2 400 | — | 0 | 0 | — | 0.00 | 0.00 | — | 0.200 0 | 0.200 0 | — | ||||
| 1-3 | 3 | 3 | 4 | 2 400 | 2 400 | 3 200 | 2 990 | 2 977 | 2 488 | 1.25 | 1.24 | 0.78 | 0.204 2 | 0.203 2 | 0.158 2 | ||||
| 3-1 | 3 | 3 | 2 | 2 400 | 2 400 | 1 600 | 1 200 | 1 200 | 1 200 | 0.50 | 0.50 | 0.75 | 0.151 4 | 0.151 4 | 0.157 1 | ||||
| 2-3 | 3 | 3 | 4 | 2 400 | 2 400 | 3 200 | 1 600 | 1 600 | 1 600 | 0.67 | 0.67 | 0.50 | 0.103 0 | 0.103 0 | 0.100 9 | ||||
| 3-2 | 3 | 3 | 2 | 2 400 | 2 400 | 1 600 | 700 | 897 | 700 | 0.29 | 0.37 | 0.44 | 0.100 1 | 0.100 3 | 0.100 5 | ||||
| 3-4 | 3 | 3 | 4 | 2 400 | 2 400 | 3 200 | 2 990 | 2 780 | 2 488 | 1.25 | 1.16 | 0.78 | 0.340 3 | 0.317 5 | 0.263 7 | ||||
| 4-3 | 3 | 3 | 2 | 2 400 | 2 400 | 1 600 | 1 200 | 1 200 | 1 200 | 0.50 | 0.50 | 0.75 | 0.252 3 | 0.252 3 | 0.261 9 | ||||
通过对比可以发现:用户最优状态的系统总出行时间为3 768 h,基于无人驾驶车辆的系统最优总出行时间为3 748 h,小幅下降0.5%,考虑最优可变车道设置方案的系统最优总出行时间为3 222 h,降幅达14.5%,效果显著,道路网络的运行效率得到了很大的提高。
用户最优状态时,路段1-2,2-4,1-3,3-4的饱和度均超过1,特别是路段1-3,3-4的饱和度达到了1.25,十分拥堵。而路段2-1,4-2的饱和度为0,完全没有流量,道路资源没有得到有效利用。可见道路网络潮汐现象十分明显,交通拥堵和道路资源闲置并存的问题非常突出。
通过ITS调控所有无人驾驶车辆在道路网络达到系统最优状态后,原本十分拥堵的路段3-4的饱和度由1.25下降到1.16,行驶时间由0.340 3 h下降到0.317 5 h,与道路网络处于用户最优状态相比较,其拥堵程度得到了小幅的缓解,但仍然比较拥堵。而路段2-1和4-2完全没有流量,其饱和度仍然为0,道路资源没有得到有效利用。道路网络中各路段的饱和度介于0~1.24之间,潮汐现象仍然十分明显,交通拥堵和道路资源闲置并存的问题仍然非常突出。这说明单纯将道路网络从用户最优状态调控为基于无人驾驶车辆的系统最优状态,由于不能很好地利用轻交通流方向闲置的道路资源来提高重交通流方向路段的容量从而调节道路网络结构更好地匹配居民出行需求,因此对于缓解因潮汐现象所导致的交通拥堵和道路资源闲置并存的问题效果并不突出,对于提高道路网络的运行效率亦有限。
而通过ITS将无人驾驶下的道路网络系统最优进一步结合可变车道优化后,原本十分拥堵的路段1-3和3-4的饱和度均由1.25下降到0.78,其拥堵程度得到了很大的缓解,路段行驶时间也得到了有效缩减,分别由0.204 2 h,0.340 3 h下降到0.158 2 h,0.263 7 h。原本没有流量的路段2-1和4-2,其闲置的道路资源全部被用来提高重交通流方向的容量,从而将反向路段1-2和2-4的饱和度分别由1.10,1.18下降到0.65,路段行驶时间则分别由0.302 4,0.242 0 h下降到0.256 6,0.205 3 h。道路网络中各路段的饱和度比较均衡,介于0.44~0.78之间,各路段既不过度拥堵,也没有道路资源闲置造成资源浪费的现象。这说明即便在未来能够调控所有无人驾驶车辆实现道路网络系统最优的情境下,实行可变车道优化仍然是有效缓解因潮汐现象所导致的交通问题的重要措施。ITS将无人驾驶下的道路网络系统最优和可变车道优化相结合,可以很好地协调人、车、路之间的关系,实现人、车、路的有机结合, 从而利用轻交通流方向闲置的道路资源来提高重交通流方向路段的容量,调节道路网络结构更好地匹配居民出行需求,均衡各路段的饱和度,优化流量在道路网络上的分布,明显减少道路网络系统总出行时间,保障道路网络系统高效运行。因此对于更为一般的道路网络系统,只要存在因潮汐现象所导致的交通拥堵和道路资源闲置并存的问题,采用本研究所提的方法便能有效缓解。
5 结论(1) 根据道路网络用户最优和系统最优之间的关系,得到了边际行驶时间函数,给出了ITS调控所有无人驾驶车辆在道路网络达到系统最优状态的可行方法,结合可变车道调节构建了基于无人驾驶车辆的系统最优可变车道模型。
(2) 采用混沌粒子群算法对模型进行求解,验证了混沌粒子群算法在该问题上的有效性和优越性。通过与用户最优状态及基于无人驾驶车辆的系统最优状态进行对比,论证了本研究所提可变车道优化方法在降低系统总出行时间方面的效果十分显著。
(3) 单纯通过ITS调控所有无人驾驶车辆在道路网络达到系统最优状态,对于缓解因潮汐现象所导致的交通拥堵和道路资源闲置并存的问题效果并不突出,对于提高道路网络的运行效率亦有限。而结合可变车道优化后,可以很好地协调人、车、路之间的关系,调节道路网络结构更好地匹配居民出行需求,均衡各路段的饱和度,优化流量在道路网络上的分布,显著减少道路网络系统总出行时间,在最大程度上发挥道路资源的作用,保障道路网络系统高效运行,有效缓解因潮汐现象所导致的交通拥堵和道路资源闲置并存的问题。
| [1] |
马莹莹, 曾令宇, 陈纲梅, 等. 可变车道行驶方向的动态控制方法研究[J]. 控制理论与应用, 2016, 33(11): 1457-1462. MA Ying-ying, ZENG Ling-yu, CHEN Gang-mei, et al. Study on Dynamic Traffic Control for Reversible Lanes[J]. Control Theory and Applications, 2016, 33(11): 1457-1462. |
| [2] |
SHEU J B, RITCHIE S G. Stochastic Modeling and Real-time Prediction of Vehicular Lane-changing Behavior[J]. Transportation Research Part B:Methodological, 2001, 35(7): 695-716. |
| [3] |
WONG C K, WONG S C. Lane-based Optimization of Signal Timings for Isolated Junctions[J]. Transportation Research Part B:Methodological, 2003, 37(1): 63-84. |
| [4] |
张卫华, 韩高峰, 颜冉, 等. 城市道路路段可变车道设置效果评价方法[J]. 重庆交通大学学报:自然科学版, 2014, 33(4): 128-133. ZHANG Wei-hua, HAN Gao-feng, YAN Ran, et al. Evaluation on Effect of Setting Variable Lane in Urban Road Section[J]. Journal of Chongqing Jiaotong University, 2014, 33(4): 128-133. |
| [5] |
崔妍, 刘东. 北京市朝阳路可变车道交通组织研究[J]. 道路交通与安全, 2006, 6(9): 21-24. CUI Yan, LIU Dong. Study on Reversible Lane of Chaoyang Street in Beijing[J]. Road Traffic & Safety, 2006, 6(9): 21-24. |
| [6] |
JIANG Y H, BAO L X. Study on Setting of Variable Lanes near Intersection between One-way and Two-way Traffic[J]. Journal of Shanghai Jiaotong University, 2011, 45(10): 1562-1566. |
| [7] |
YU Q, TIAN R. Research on Reversal Lane Application Method of Urban Road Network Based on the Bi-level Programming[M]. Berlin: Springer Berlin Heidelberg, 2014: 983-992.
|
| [8] |
ZHANG P, LI W, CHANG Y. Reserve Capacity Model for Urban Road Network with Variable Lanes[J]. Journal of Southwest Jiaotong University, 2010, 45(2): 255-260. |
| [9] |
LI X, CHEN J, WANG H. Study on Flow Direction Changing Method of Reversible Lanes on Urban Arterial Roadways in China[J]. Procedia-Social and Behavioral Sciences, 2013, 96: 807-816. |
| [10] |
HAUSKNECHT M, AU T C, STONE P, et al. Dynamic Lane Reversal in Traffic Management[C]//14th International IEEE Conference on Intelligent Transportation Systems. Washington, D. C. : IEEE, 2011: 1929-1934.
|
| [11] |
WOLSHON B, LAMBERT L. Reversible Lane Systems:Synthesis of Practice[J]. Journal of Transportation Engineering, 2006, 132(12): 933-944. |
| [12] |
岳雷, 徐天东, 夏海平, 等. 上海世博会可变车道设置方案研究[J]. 城市交通, 2010, 8(2): 25-30. YUE Lei, XU Tian-dong, XIA Hai-ping, et al. Reversible Lane Design for Shanghai World Expo 2010[J]. Urban Transport of China, 2010, 8(2): 25-30. |
| [13] |
史峰, 苏焕银, 王雄. 适用于路网潮汐流的可变车道设置方法研究[J]. 交通运输系统工程与信息, 2015, 15(4): 57-62. SHI Feng, SU Huan-yin, WANG Xiong. Design of Reversible Lanes with Tidal Flow on Road Network[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(4): 57-62. |
| [14] |
高自友, 张好智, 孙会君. 城市交通网络设计问题中双层规划模型、方法及应用[J]. 交通运输系统工程与信息, 2004, 4(1): 35-44. GAO Zi-you, ZHANG Hao-zhi, SUN Hui-jun. Bi-level Programming Models, Approaches and Applications in Urban Transportation Network Design Problems[J]. Journal of Transportation Systems Engineering and Information Technology, 2004, 4(1): 35-44. |
| [15] |
张好智, 高自友. 可变车道的道路交通网络设计优化方法[J]. 中国管理科学, 2007, 15(2): 86-91. ZHANG Hao-zhi, GAO Zi-you. Optimization Approach for Traffic Road Network Design Problem[J]. Chinese Journal of Management Science, 2007, 15(2): 86-91. |
| [16] |
BRAESS D, NAGURNEY A, WAKOLBINGER T. On a Paradox of Traffic Planning[J]. Transportation Science, 2005, 39(4): 446-450. |
| [17] |
黄中祥. 交通分配模型的经济学含义及模型的扩展[J]. 经济数学, 1998(4): 25-31. HUANG Zhong-xiang. The Implications and Extentions of Traffic Assignment Models[J]. Mathematics in Economics, 1998(4): 25-31. |
| [18] |
余孝军, 黄海军. 多用户类多准则交通分配的势博弈与拥挤定价[J]. 系统科学与数学, 2010, 30(8): 1070-1080. YU Xiao-jun, HUANG Hai-jun. Potential Game of Multi-class, Multi-criteria Traffic Assignment and Congestion Pricing[J]. Journal of Systems Science and Mathematical Sciences, 2010, 30(8): 1070-1080. |
| [19] |
DUELL M, LEVIN M W, BOYLES S D, et al. System Optimal Dynamic Lane Reversal for Autonomous Vehicles[C]//18th IEEE International Conference on Intelligent Transportation Systems. Las Palmas: IEEE, 2015: 1825-1830.
|
| [20] |
MENDEL E, KROHLING R A, CAMPOS M. Swarm Algorithms with Chaotic Jumps Applied to Noisy Optimization Problems[J]. Information Sciences, 2011, 181(20): 4494-4514. |
| [21] |
柴宝仁, 谷文成, 韩金库. 基于混沌粒子群算法的Ad Hoc网络优化研究[J]. 北京理工大学学报, 2017, 37(4): 381-385. CHAI Bao-ren, GU Wen-cheng, HAN Jin-ku. Research on Ad Hoc Network Optimization Based on Chaotic Particle Swarm Optimization[J]. Transactions of Beijing Institute of Technology, 2017, 37(4): 381-385. |
 2018, Vol. 35
2018, Vol. 35
