扩展功能
文章信息
- 卢媛媛, 郭志坚, 王宝玲, 张倩茹, 芦奇
- LU Yuan-yuan, GUO Zhi-jian, WANG Bao-ling, ZHANG Qian-ru, LU Qi
- 趋近理想灰关联多约束的交通救援中心中值选址模型
- A Traffic Rescue Centre Median Location Model Approaching Ideal Grey Relational Constraints
- 公路交通科技, 2018, 35(7): 114-119
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(7): 114-119
- 10.3969/j.issn.1002-0268.2018.07.016
-
文章历史
- 收稿日期: 2017-03-27
2. 山西陆成建筑安装工程有限公司, 山西 太原 030024;
3. 太原 理工大学 经济管理学院, 山西 太原 030024;
4. 中国移动通信集团终端有限公司山西分公司, 山西 太原 030006
2. Shanxi Lucheng Construction and Installation Engineering Co., Ltd., Taiyuan Shanxi 030024, China;
3. School of Economics & Management, Taiyuan University of Technology, Taiyuan Shanxi 020024, China;
4. Shanxi Branch of China Mobile Communications Group Co., Ltd., Taiyuan Shanxi 030006, China
近年来,我国交通救援水平在一定程度上得到了提高,但交通突发事故仍是我国伤亡事故较严重的领域。高温、燃爆、烟尘等恶劣环境决定了交通事故中被困及受伤人员存活率很低,因此救援的时效性显得尤为重要[1]。交通救援要求时效性优先,而随着交通道路条件的改善和运输工具的进步,其他因素与时效性相比权重加大。因此,交通救援中心选址是以时效性为优先条件,加以综合其他因素的多目标决策问题。
在选址领域中常用的有最大化覆盖模型、P-中值选址模型、集合化覆盖模型,这些模型的核心理论是资源供给点与需求点之间的距离[2]。如杜乐乐等[3]利用重心算法将最大化覆盖模型应用于成品油配送中心的选址。为了将物资的损耗降到最低,时曼曼等[4]将P-中值模型应用于体育设施的选址。但以上几种模型均为单因素决策体系,而交通救援中心选址是多目标选址问题,决策方案中指标如交通负荷量、物资补给能力等是无法定量的灰色信息,它们之间不是完全独立的,这就决定了只有综合考虑各种因素才能更加科学。本研究提出的综合模型有机地将灰色系统理论、优劣解距离法和矢量投影方法结合起来,是一条解决相关决策问题的理想途径。在交通救援中心的选址过程中综合利用P-中值模型与趋近于理想灰关联的投影模型,取得了较好的决策结果[5]。
1 趋近于理想灰关联多约束的交通救援P-中值选址模型交通事故造成的人员伤亡率与财产损失程度与救援的时效有着极为紧密的关系,这就要求救援中心与事故的距离要尽可能地小。交通救援中心选址是以时间目标为优先的选址问题,而P-中值模型在解决该类问题过程中具有极强的应用性。救援中心的建立还要考虑建设用地成本、医疗资源协调力、物资补给能力等一系列复杂的因素,而且这些因素之间的权重并不相同。灰色关联分析法由于特有的优势成为其中比较理想的一种,针对残缺、模糊的小样本系统时有明显的分析优势,其核心思想是依据各项评价指标的理想数据,在计算出候选样本与理想方案样本之间的关联度大小的基础上,判断候选地址样本与理想样本的趋近程度。趋近理想灰关联模型充分考虑了交通救援中心选址方案中不同指标的权重,可以有效避免信息流失和减小误差。候选方案双向关联于理想方案。本研究同时考虑正负理想方案的关联来避免单方向偏差,在反映各方案间的差异上才更加全面与准确。
2 模型求解 2.1 中值模型的应用本研究中的救护网络是无向赋权的,定义如下:G=(V, F), G为网络的逻辑集合,其中V=(X, U)为救援中心候选地址的点集;X={x1, x2, …, xp}为交通点集;U为连接定点的弧线上排除定点的点集;F为网络图内所有的连接点之间曲线的有限集;fij为曲线的长度;W={wi}为弧长fij的权重;ui为集合H={hi}的权重[6]。a点与b点间的极短路径为d(a, b);两点之间单向联通的时间为t(a, b)。本研究认为定点之间的运输效率是一致的,因此用空间变量代替时间变量。
根据最长路径O(n)算法,最长路径的一半是局部中心距离,假设顶点xi的最远顶点是xj,顶点xj的最远顶点是xt,则最远路径就是xi到xt的距离[7]。
局部中心距离计算过程步骤如下:
设距离目标为s。
(1) 令j=1,最短距离矩阵的构建是根据顶点[8]的个数n构建n阶矩阵S,假设最大的元素是d(vj, vk), vk为距离p(vj, vk)点最远的顶点,则首先从第j行中将其找到,然后依据最短路径矩阵S,比较并且筛选出不在路径p(vj, vk)上的次最大元素d(vj, vl)。
(2) 计算局部半径:
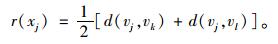
|
(1) |
(3) 令j=j+1,若j < n,则转到步骤(2)。
(4) 统计各个定点的局部中心距离,根据d*(xk)<s筛选出相对应的顶点[9]。
(5) 通过中值选址模型进行第1轮筛选,然后利用趋近于理想灰色关联投影的多约束决策模型进一步筛选交通应急救援站的最优选址地点。
2.2 趋近理想灰色关联投影模型的应用趋近于理想灰色关联投影的多约束决策模型算法如下:
(1) 候选方案集合是A,方案中每项数据归属于指标集V,建立初始决策矩阵Y;许多指标属于灰色信息指标,表征并不定量,对于这样的指标,在建立方案决策矩阵之前数量化处理[10]。
设有n个非定量分级灰色指标x(1), x(2), …, x(n)对应于“高水平、良好水平、中等水平、…”等n个相似的定性信息,并设存在映射f,f:x(k)→μk,如有:
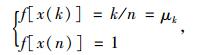
|
(2) |
式中μk为初值化处理的结果; f[x(n)]为灰量的线性白化权函数。
设有区间灰量x∈[a, b],同时存在映射f,有:
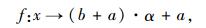
|
(3) |
式中,α为决策方案中不同类别的指标所占的权重系数[11],通常取α=0.5。
非定量的原始决策矩阵指标不能直接进行后续运算,必须经过数量化处理,假设Vj是方案Ai中的决策指标,xij代表Vj的白化特征值,则有如下决策矩阵:
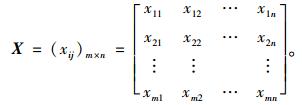
|
(3) |
(2) 当决策矩阵中的各项指标均达到所有决策方案中该项指标值最理想时,包含这些最优指标的矩阵称之为正理想初始决策矩阵[12],反之为负理想初始决策矩阵,因此建立相应的正、负理想初始决策矩阵X+和X-,初值化后列出正、负理想决策矩阵Y+和Y-。
(3) 求出候选方案与理想方案间的灰色关联度,然后建立正、负理想灰关联决策矩阵G+和G-。
定义γk(xi, x0)为数据列x0和xi在k点的灰关联度,其中x0的数值表示灰色关联度[13],根据算式求得:
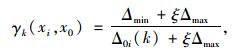
|
(4) |
式中,ξ为分辨系数,通常取0.5;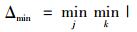
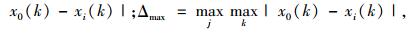
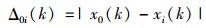
提取di理想决策矩阵Y+与Y-的全部行向量,求出的n(m+1)个灰色关联度组成正、负理想灰色关联决策矩阵G+和G-。
(4) 不同的评价指标在决策方案中所占的权重各不相同,所以加权处理灰色关联度矩阵[14]。设权重向量矩阵为:
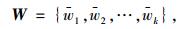
|
(5) |
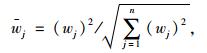
|
(6) |
式中wj为权重决策方案中评价指标的j灰色关联投影值。
(5) 计算灰关联投影值Di+和Di-
投影值的概念建立在向量的基础上,这里将决策方案抽象化。假设一个行向量的原始抽象对象是决策方案Ai,另一个行向量的原始抽象对象是理想方案A*,则称θi是两个行向量之间的夹角,同时也是两个向量之间的灰色关联投影角[15]。
则θi的余弦值为:
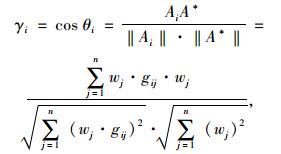
|
(7) |
式中Di+为理想决策矩阵中与(1-Ei)相对应的矩阵元素值。
度量候选方案在多大程度上趋近理想方案,需要一个量化的标量,这里用Ai在A*上的灰色关联投影值Di表示该标量[16]:
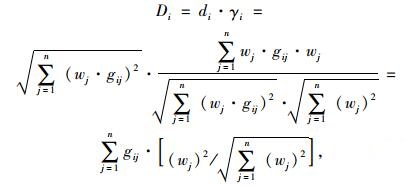
|
(8) |
式中, di为决策方案抽象为数学矢量的模,γi为决策方案矢量与理想方案矢量夹角的余弦。
得到:
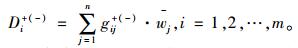
|
(9) |
(6) 由灰色关联投影系数Ei的大小最终判断候选方案的优劣。
定义Ei为灰色关联投影系数,接近正理想方案的程度量化为Ei,远离负理想方案的程度量化为(1-Ei),从而实现统一衡量接近度与远离度的目的。投影系数最大的方案为最优方案[17]。
根据方案Ai,以Ei与Di+的乘积的灰关联投影值趋近于正理想方案的灰关联投影值Di+,以(1-Ei)与Di-的乘积的灰关联投影值趋近于负理想方案的灰关联投影值Di-。在极小平方和的基础上构建以下约束函数:
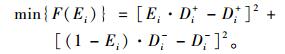
|
(10) |
令∂F(Ei)/∂Ei=0,推出:
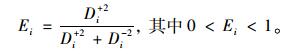
|
(11) |
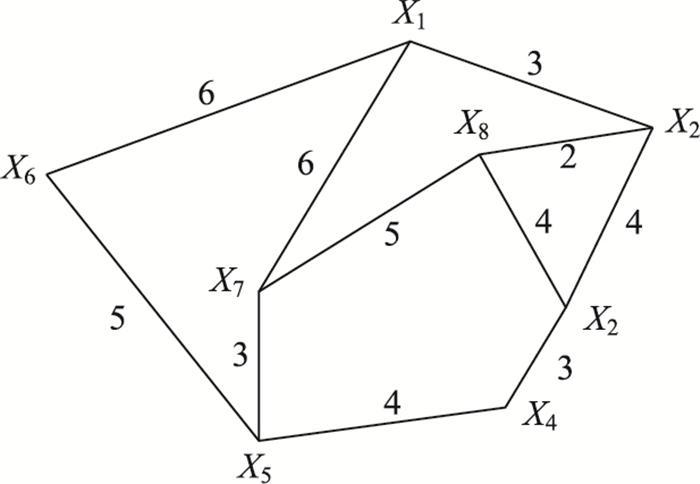
利用本研究提出的选址模型针对交通应急救援中心选址问题进行算例分析。如图 1所示,8个定点代表 8座候选地址,每个候选地址都代表其附近有1块事故高发区域。到其他候选地址的距离即到其他事故高发区的距离。Xn代表n号地址,如X1代表 1号地址。
|
| 图 1 矿区交通分布图 Fig. 1 Traffic distribution in mining area |
| |
| 评价指标 | X2 | X4 | X5 | X8 |
| 加权平均距离 | 6 | 6.714 | 6.571 | 6 |
| 交通负荷量 | 98 | 107 | 105 | 112 |
| 物资补给能力 | 1.2 | 1.3 | 1.6 | 1.45 |
| 站用土地价格 | 8 | 7.6 | 7 | 8.4 |
| 医疗资源协作能力 | 124 | 137 | 135 | 128 |
| 行政指挥统筹能力 | 10 | 14 | 16 | 13.8 |
网络中每个顶点的权重由其代表的区域发生事故的概率决定,因此取权重hi=1(i=1, 2, …, n); 由时间目标计算得距离目标s=8。在网络图中连接定点间线段的长度代表两点间最短的距离,最短距离矩阵F为:

|
最短路径矩阵L如下:

|
根据前文中的具体算法,求出每个定点的局部中心距离。
根据距离目标s=8,经过计算符合d*(xk)<s条件的有:X2, X4, X5, X8,所以X2,X4,X5,X8为入围下一轮筛选的应急救援站候选点,最优结果将根据多约束决策模型的结果来判定。
将候选地址各权重因素进行指标的量化,因计算过程以及数据较为繁琐,限于篇幅,因此不再赘述,具体结果见表 1。
正理想灰色关联决策阵G+:
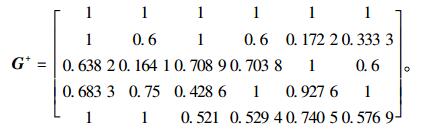
|
负理想灰色关联决策阵G-:

|
取权重向量W={0.2 0.16 0.14 0.11 0.24 0.15},得到灰色关联投影权值向量W={0.095 0.120 8 0.046 5 0.028 7 0.136 8 0.053 4}。
计算得到:
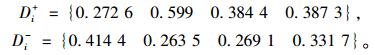
|
4个候选方案的灰色关联投影系数Ei={0.302 0.838 0.671 2 0.576 9}。
将灰色关联投影系数Ei的值作为4个候选地址各决策方案排序的依据,次序由高到低依次为:X4,X5,X8,X2,因此4号候选地址为最优。
4 结论交通救援中心的选址严格要求时效性,而中值模型在解决时间约束的选址问题上针对性很强,简便易行。影响选址的其他因素联合构成了多约束决策,但是相关数据之间的关系往往不确定,而且信息的完整程度并不一定很高,因此这样的系统本质上是灰色多约束决策系统。趋近灰色关联投影模型依托灰色系统理论,结合矢量投影方法,理论清晰,应用性强。实际算例表明,本研究提出的多约束决策模型跳出了旧有模型的窠臼,为相关领域提供了新的思路,评价结果真实可靠,在实际的决策过程中具有推广和应用价值。
| [1] |
姜燕宁, 郝书池. 基于部分跨级和集中存储模式的库存配置与选址决策模型[J]. 公路交通科技, 2016, 33(11): 152-158. JIANG Yan-ning, HAO Shu-chi. Inventory Allocation and Location Decision Model Based on Partial Cross-level and Centralized Storage[J]. Journal of Highway and Transportation Research and Development, 2016, 33(11): 152-158. |
| [2] |
杜乐乐, 燕子宗, 李静, 等. 油库选址的最大覆盖模型研究[J]. 长江大学学报:自然科学版, 2008, 5(3): 138-139. DU Le-le, YAN Zi-zong, LI Jing, et al. Research on Location of Fuel Depot Maximum Coverage Model[J]. Journal of Yangtze University:Natural Science Edition, 2008, 5(3): 138-139. |
| [3] |
时曼曼, 张守健, 吴婉弘. 基于P中值模型的村镇文化体育设施配置研究[J]. 工程管理学报, 2014, 28(1): 36-40. SHI Man-man, ZHANG Shou-jian, WU Wan-hong. Study on Configuration of Public Culture and Sports Facilities Based on P-median Model for Village and Town[J]. Journal of Engineering Management, 2014, 28(1): 36-40. |
| [4] |
汤旻安, 袁爽, 王晓明. 基于优化灰色神经网络模型预测公交换乘需求量的换乘枢纽选址[J]. 公路交通科技, 2013, 30(6): 115-119. TANG Wen-an, YUAN Shuang, WANG Xiao-ming. Location of Public Transport Transfer Hub Based on Transfer Demand Forecast by Using Optimized Gray Neural Network Model[J]. Journal of Highway and Transportation Research and Development, 2013, 30(6): 115-119. |
| [5] |
王亚阳, 王汉斌. 煤矿区应急救援站多目标选址决策[J]. 安全与环境工程, 2015, 22(1): 121-125. WANG Ya-yang, WANG Han-bin. Location Selection for Emergency Rescue Station of Coal Mining Area Based on Multi-objective Decision[J]. Safety and Environmental Engineering, 2015, 22(1): 121-125. |
| [6] |
柯宏发, 陈永光, 夏斌. 一种基于逼近于理想灰关联投影的多目标决策算法[J]. 电子学报, 2007, 35(9): 1757-1761. KE Hong-fa, CHEN Yong-guang, XIA Bin. An Algorithm of Multiple Criteria Decision-making Based on Similarity to Ideal Grey Relational Projection[J]. Acta Electronica Sinica, 2007, 35(9): 1757-1761. |
| [7] |
门宝辉, 赵燮京, 梁川. 多目标决策灰色关联投影法在水利工程开发中的应用[J]. 武汉大学学报:工学版, 2003, 36(4): 36-39. MEN Bao-hui, ZHAO Xie-jin, LIANG Chuan. Application of Multi-criteria Decision Grey Relation Projection Method to Hydro-engineering Development Plan Decision-making[J]. Engineering Journal of Wuhan University, 2003, 36(4): 36-39. |
| [8] |
孙立炜, 王杰贵. 逼近理想灰关联投影多目标决策的点迹-航迹关联算法[J]. 火力与指挥控制, 2012, 37(4): 138-140. SUN Li-wei, WANG Jie-gui. A Measurement-track Association Algorithm Based on Similarity to Ideal Gray Correlation Projection of Multiple Criteria Decision-making[J]. Fire Control & Command Control, 2012, 37(4): 138-140. |
| [9] |
张彩庆, 赵璐. 基于P-中值模型的电网检修公司分部选址模型[J]. 系统管理学报, 2014, 23(4): 501-506. ZHANG Cai-qing, ZHAO Lu. Division Location Model for Power Grid Maintenance Company Based on P-median[J]. Journal of Systems & Management, 2014, 23(4): 501-506. |
| [10] |
代颖, 马祖军. 应急物流系统中的随机定位-路径问题[J]. 系统管理学报, 2012, 21(2): 212-217. DAI Ying, MA Zu-jun. Stochastic Location-routing Problem in Emergency Logistics Systems[J]. Journal of Systems & Management, 2012, 21(2): 212-217. |
| [11] |
关菲, 张强. 模糊多目标物流配送中心选址模型及其求解算法[J]. 中国管理科学, 2013, 21(11): 57-62. GUAN-Fei, ZHANG Qiang. A Fuzzy Multi-objective Logistics Distribution Center Location Model and Its Solution Algorithm[J]. Chinese Journal of Management Science, 2013, 21(11): 57-62. |
| [12] |
方磊, 何建敏. 应急系统优化选址的模型及其算法[J]. 系统工程学报, 2003, 18(1): 49-54. FANG Lei, HE Jian-min. Optimal Location Model and Algorithm of Emergency Systems[J]. Journal of Systems Engineering, 2003, 18(1): 49-54. |
| [13] |
胡德慧, 钱瑛, 熊琦, 等. 回收物流系统中回收中心选址模型优化[J]. 物流科技, 2013, 36(5): 89-91. HU De-hui, QIAN Ying, XIONG Qi, et al. The Recycling Logistics Center Location of the Model Optimization in Recycling Logistics System[J]. Logistics Sci-tech, 2013, 36(5): 89-91. |
| [14] |
席煜宸. 煤矿应急管理体系建设探讨[J]. 中国安全科学学报, 2010, 20(1): 159-164. XI Yu-chen. Study on Construction Mode of Mine Emergency Management System[J]. China Safety Science Journal, 2010, 20(1): 159-164. |
| [15] |
甘蜜, 陈思, 陈钉均. 关于物流多目标选址规划仿真研究[J]. 计算机仿真, 2015, 32(4): 149-153. GAN Mi, CHEN Si, CHEN Ding-jun. Simulation of Multi-objective Facility Location Planning[J]. Computer Simulation, 2015, 32(4): 149-153. |
| [16] |
张曦, 杨超, 黄松. 双目标多元需求的截流设施选址问题研究[J]. 公路交通科技, 2011, 28(2): 117-120. ZHANG Xi, YANG Chao, HUANG Song. Flow Intercepting Facility Location Problem with Bi-objective and Multi-demand[J]. Journal of Highway and Transportation Research and Development, 2011, 28(2): 117-120. |
| [17] |
杨兆升, 张茂雷. 基于模糊综合评判的道路交通状态分析模型[J]. 公路交通科技, 2010, 27(9): 121-126. YANG Zhao-sheng, ZHANG Mao-lei. A Model for Road Traffic State Analysis Based on Fuzzy Comprehensive Evaluation[J]. Journal of Highway and Transportation Research and Development, 2010, 27(9): 121-126. |
 2018, Vol. 35
2018, Vol. 35
