扩展功能
文章信息
- 梁庆国, 边磊, 张钦鹏, 黄俊, 王猛
- LIANG Qing-guo, BIAN Lei, ZHANG Qin-peng, HUANG Jun, WANG Meng
- 大断面黄土隧道洞口段地震动力特性研究
- Study on Seismic Dynamic Characteristics of Large Section Loess Tunnel Portal
- 公路交通科技, 2018, 35(7): 65-76
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(7): 65-76
- 10.3969/j.issn.1002-0268.2018.07.010
-
文章历史
- 收稿日期: 2017-05-10
2. 甘肃省道路桥梁与地下工程重点实验室, 甘肃 兰州 730070
2. Gansu Provincial Key Laboratory of Road & Bridge & Underground Engineering, Lanzhou Gansu 730070, China
近年来,在山岭地区修建公路或铁路时,由于受地形地貌及复杂地质环境的约束,线路往往不可避免地以隧道形式穿越高边坡地区。由于隧道的开挖过程破坏了原有边坡内部的平衡状态,因此不可避免地增加了边坡产生滑坡的可能;反过来,滑坡体的下滑力又作用于隧道洞口段的衬砌结构上,如果发生地震,在地震动荷载作用下隧道洞口段衬砌结构就可能发生严重破坏。针对隧道洞口段的动力稳定性,国内外学者从地震波本身、隧道衬砌结构、埋深、隧道抗震设防长度、洞口段地质条件等多个方面进行了研究。关振长等[1]以海西福永高速ZK132+300段典型土岩二元结构边坡为原型,重点关注坡体高程、地震动幅值、地震动频率特征对加速度放大系数(Acceleration Amplification Coefficient, AAC)的影响并得出一定的结论,但对边坡隧道模型的AAC放大系数的变化规律并未进行详细的研究。刘明星等[2]采用连续介质快速拉格朗日分析方法FLAC3D,对于含单一顺坡向结构面的边坡,通过时程分析法从结构面角度在动力反应三量(位移、速度和加速度)等方面讨论了边坡的地震动力响应规律及失稳机理,但对隧道地震动力响应规律的研究还不够深入。本研究以宝兰客运专线上典型的黄土隧道(王家沟隧道)为工程背景,对边坡坡度为60°坡脚进洞工况进行了振动台试验。对边坡坡度为60°坡脚、0.3H高程、0.6H高程进洞进行数值模拟,在振动台试验中利用相似性原理确定配比并采用相似性材料建造模型。利用放置在模型中的监测传感器元件,既能监测边坡内部应力-应变状态,又能显示模型在地震波作用下边坡的失稳破坏过程,从而分析相应的破坏机理。数值模拟则通过提取坡面及隧道衬砌内的加速度、土压力、位移来对不同进洞高程进行分析对比,得出等坡度不同进洞高程在地震作用下的动力响应变化规律,最后将振动台试验与数值模拟结果进行对比,从而证明有限元分析的科学性与参考性。
1 振动台模型试验利用振动台模型试验来研究边坡坡度为60°坡脚进洞工况在地震作用下的动力响应特征。
1.1 试验设备与模型设计模型试验借助某研究所的大型电伺服式地震振动台。该振动台台面尺寸为4 m×6 m,由28台伺服电机共同驱动,其中,垂直向由16台22 kW的AC伺服电机驱动,水平向由12台37 kW水冷式伺服电机驱动。
试验采用刚性密封模型箱,尺寸为2.8 m×1.4 m×1.1 m,模型箱实物如图 1所示。长度方向两侧为3 cm厚的有机玻璃板,宽度方向两侧为2 cm厚的钢板。箱体四角固定M20吊环以便吊装,底部采用50个六角螺钉组M16×60固定在振动台台面上。为减小模型箱所造成的边界条件的影响,在土体与模型箱接触的前后两侧加入锯末掺合土缓解边界土体的变形。

|
| 图 1 试验模型箱 Fig. 1 Test model box |
| |
(1) 模型填土选取
模型试验所用的填土取自兰州刘家坪某边坡表层剥落松散的Q3原状黄土,取土过程中尽量剔除所含杂质和较大颗粒,共取土量约6.5 m3。然后取少量填土试样进行室内试验,得到试验填土的液限WL=33.8%, 塑限WP=17.6%。塑性指数IP=WL-WP=16.2,最佳含水量为16.5%,相应的最大干密度为1.78 g/cm3,因此模型填土时应尽量使含水量和密度达到对应值,但考虑到现场蒸发和测定误差,模型填土压实度按95%控制。
(2) 模型相似性
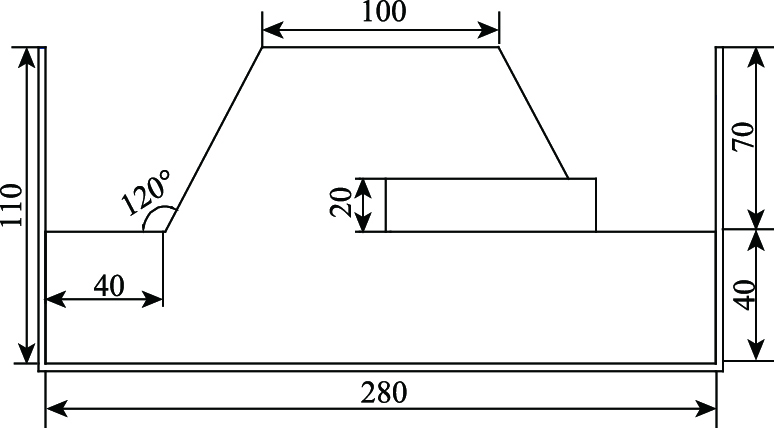
试验原型为宝兰客运专线典型大断面黄土隧道,振动台模型试验按照1:70的比例将原型进行缩小。模型边坡高0.7 m,两侧仰坡坡度均为60°,坡底长2.8 m,坡顶长1 m,横向坡宽1.4 m,底部土层厚0.4 m,一侧边坡存在隧道,另一侧为纯边坡。隧道模型外径18 cm,内径16 cm,衬砌厚2 cm。原型与试验模型结构尺寸见表 1,试验模型示意图见图 2。
| 相似比 | 坡高/m | 隧道最大跨径/m | 衬砌结构厚度/cm | |
| 原型 | 70 | 50 | 13 | 70 |
| 模型 | 1 | 0.7 | 0.2 | 2 |
|
| 图 2 试验模型示意图(单位: cm) Fig. 2 Schematic diagram of experimental model (unit: cm) |
| |
原型土、模型土压实后的物理力学参数对比见表 2。黄土隧道衬砌施工时通常采用C25混凝土,因此试验中以石膏这类脆性材料来模拟隧道衬砌比较合适,为使石膏衬砌模型与现场混凝土衬砌满足相似比,衬砌都采用水:石膏=2:1的混合材料来制作;为了保证衬砌抗弯刚度的相似,采用直径1 mm的铁丝网来模拟衬砌内的钢筋网,为保证衬砌强度相似,衬砌制作完成后静置1周。
| 干密度/ (g·cm-3) |
含水 率/% |
黏聚力/ kPa |
内摩擦 角/(°) |
|
| 原型土 | 1.65 | 21.6 | 34.7 | 21.9 |
| 模型填土压实 | 1.70 | 15.5 | 21.5 | 28.2 |
(3) 地震动加载
振动台试验采用输入加速度时程曲线来模拟地震波,为了研究在动力作用时不同进洞高程下边坡失稳特性及隧道洞口段的动力响应特征,分别采用正弦波(3~50 Hz)、汶川卧龙波、EL-Centro波3种加载波形,采用水平方向(x)和竖直方向(z)为加载方向,试验设置14个加载工况,见表 3。
| 工况 | 台面加载波形 | 加载方向 | 震级 | 台面输入峰值 加速度/(×g) |
| 1 | 汶川卧龙波 | 水平 | 7度 | 0.11 |
| 2 | EL-Centro波 | 水平 | 0.10 | |
| 3 | 汶川卧龙波 | 竖直 | 0.11 | |
| 4 | EL-Centro波 | 竖直 | 0.10 | |
| 5 | 汶川卧龙波 | 水平 | 8度 | 0.22 |
| 6 | EL-Centro波 | 水平 | 0.21 | |
| 7 | 汶川卧龙波 | 竖直 | 0.22 | |
| 8 | EL-Centro波 | 竖直 | 0.21 | |
| 9 | EL-Centro波 | 水平 | 9度 | 0.42 |
| 10 | EL-Centro波 | 水平 | >9度 | 0.84 |
| 11 | EL-Centro波 | 水平 | 1.26 | |
| 12 | EL-Centro波 | 水平 | 1.43 | |
| 13 | 汶川卧龙波 | 水平 | 1.43 | |
| 14 | 正弦波 | 水平 | 1.63 |
1.2 传感器布置与模型填筑
(1) 传感器布置
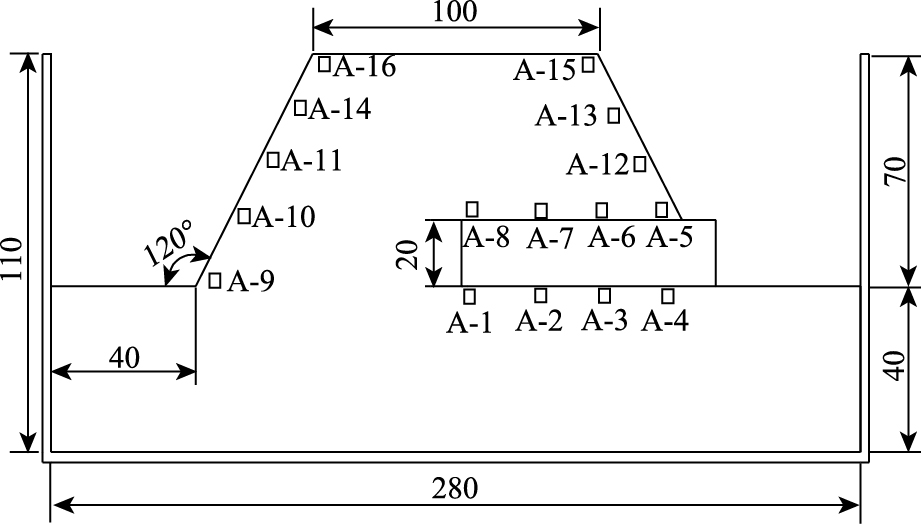
试验的加速度传感器采用东华DH301型电容式加速度传感器,如图 3(a)所示。图 4为加速度传感器布置,试验布置16个加速度传感器:A1~A4和A5~A8分别每隔25 cm埋设1个传感器,A4距右边缘20 cm,传感器紧贴衬砌上下面布置,周围用土压实;两侧边坡传感器对称布置,其中A9,A10,A11,A14,A19沿无隧道边坡均匀布置,A12,A13,A15沿有隧道边坡衬砌结构上方均匀布置,传感器离边坡表面的水平距离为3 cm。

|
| 图 3 传感器 Fig. 3 Sensors |
| |
|
| 图 4 土加速度传感器布置图(单位: cm) Fig. 4 Arrangement of soil acceleration sensors (unit: cm) |
| |
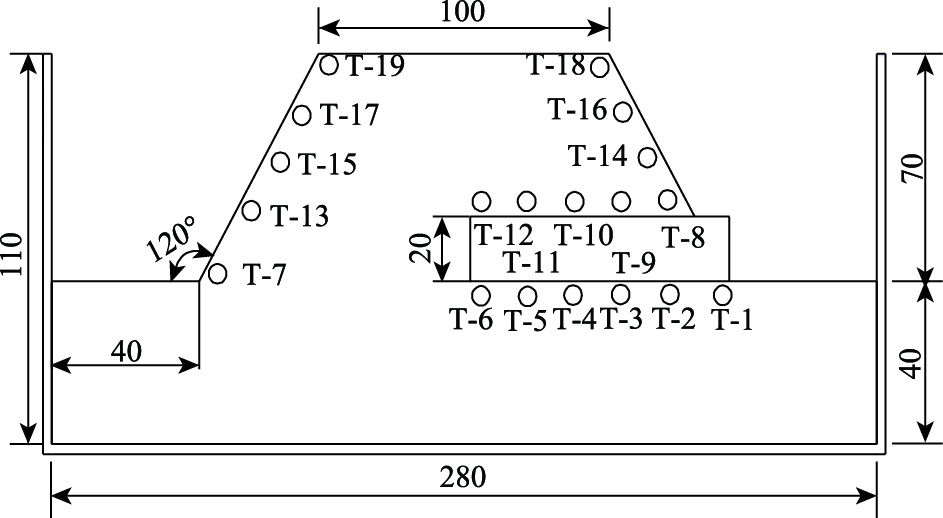
土压力传感器为CYY9型土壤岩石压力传感器,如图 3(b)所示。量程为-500~+500 kPa,准确度等级为0.25%,信号输出范围为0~5 VDC,温度适用范围为-10~70 ℃。土压力传感器的具体布置见图 5,试验布置19个土压力传感器:T1~T6和T8~T12分别每隔20 cm埋设1个传感器,离衬砌的垂直距离为2 cm;两侧边坡传感器对称布置,其中T7,T13,T15,T17,T19沿无隧道边坡均匀布置;T14,T16,T18沿有隧道边坡衬砌结构上方均匀布置,传感器离边坡表面的水平距离为3 cm。加速度和土压力数据采集系统采用东华DH5929型处理分析仪。
|
| 图 5 土压力传感器布置图(单位: cm) Fig. 5 Arrangement of soil pressure sensors (unit: cm) |
| |
(2) 模型填筑
将土配成含水率为16.5%的试验填土均匀翻拌,两组试验分别在模型填土完成并静置24 h后进行,模型静置时用塑料覆盖好。按照传感器竖向分布距离分层进行填筑,每层填筑15~25 cm,填筑时采用人工分层夯实,控制每层土体的夯实密度为1.70 g/cm3,即控制压实度为95%,填筑完成后的最终含水率为15.5%,制作完成的模型吊装到振动台上,如图 6所示。

|
| 图 6 模型的原件布置与成型 Fig. 6 Model prototype layout and molding |
| |
1.3 试验模型结构变形破坏特征
试验选择隧道在一侧坡脚处进入边坡,另一侧边坡无隧道。由于含水量保持在最优含水率附近,最终模型压实度较高,因此当地震动峰值加速度达到0.11g(7度基本烈度)和0.22g(8度基本烈度)时均未发现明显裂缝和坡体破坏痕迹。随着台面输入峰值加速度的增大,模型仰坡整体保持稳定。当地震动峰值加速度达到0.40g(9度基本烈度)时,有隧道一侧坡顶上部边缘出现少量纵向裂缝,最长的约为16 cm;坡顶前部出现一条较浅的横向裂缝,隧道洞口拱顶上方出现若干条较浅的竖向裂缝,最长的约为8 cm,裂缝示意图如图 7所示,图 7(c)是典型的洞门结构裂损,坡顶裂纹是振动过程中的坡顶拉剪破坏。拱顶竖向裂缝是振动过程中隧道衬砌与上部土体自振频率不同导致的错动,纯边坡一侧暂未发现明显破坏痕迹。

|
| 图 7 模型裂缝 Fig. 7 Cracks in model |
| |
当地震动峰值加速度达到0.82g时,如图 8所示,纵向裂缝发展明显,坡顶中间一条纵向裂缝基本贯通。横向裂缝宽度变化不大,在靠近坡顶前部边缘处出现第2条很浅的横向裂缝,坡顶前部边缘有少量土体滑落。拱顶处竖向裂缝发展不明显。两侧坡脚处出现横向裂缝且发展速度较快,由于剪应力集中程度增加产生剪切挤出破坏,两侧边坡均出现了坡面鼓出现象。当地震动峰值加速度达到1.20g时,坡顶中间的纵向裂缝宽度明显加大,最宽处达到0.5 cm,整体来看有隧道一侧裂缝长度和宽度大于纯边坡一侧。洞口拱顶处出现零星小的掉块,仰拱和拱脚处出现若干细小裂缝。坡脚处横向裂缝变宽,边坡鼓出现象越来越明显。

|
| 图 8 模型裂缝发展 Fig. 8 Crack propagation in model |
| |
当地震动峰值加速度达到1.60g时,坡顶沿着贯通的纵向裂缝出现了明显的震陷现象,出现约1 cm高的错台。坡顶沿前部边缘的横向裂缝发生滑塌,横向裂缝最宽处达到3 cm,裂缝到坡顶边缘的距离约为20 cm。模型坡面整体发生破坏,震陷滑塌现象很明显且大块土体整体滑落,少量块体水平抛射滑落堆积在洞门处,隧道洞口被整体掩埋。坡脚处出现一系列破坏裂缝,土体已基本被震酥。整体来看,有隧道一侧滑塌破坏程度大于纯边坡一侧。模型整体破坏和永久性破坏裂缝示意图如图 9、图 10所示。上述现象与王帅帅[3]、吴冬[4]等的试验结果所反映的破坏特征基本一致。

|
| 图 9 模型整体破坏 Fig. 9 Overall failure of model |
| |

|
| 图 10 永久性破坏裂缝 Fig. 10 Permanent damage cracks |
| |
1.4 试验模型加速度响应特征
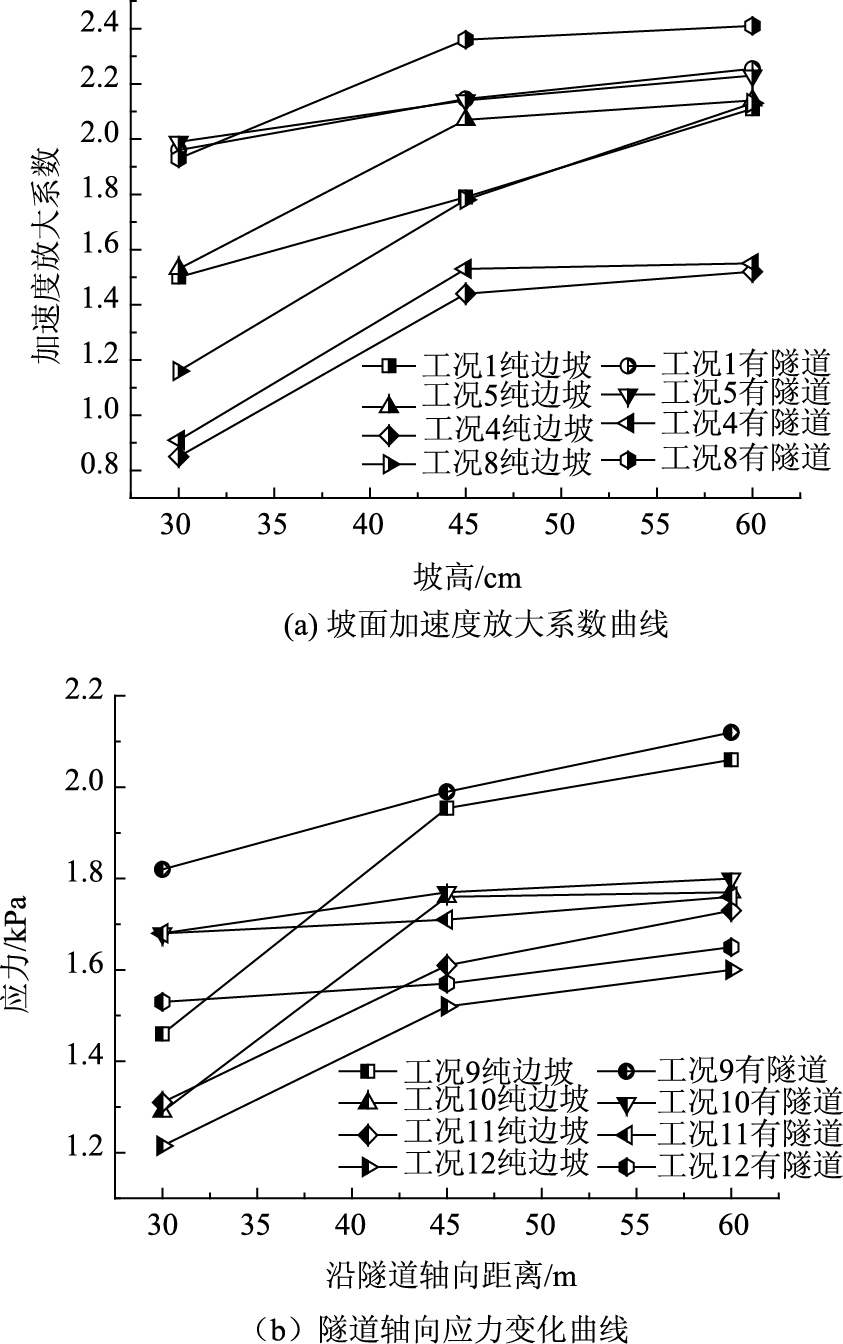
隧道存在对黄土边坡动力响应的影响。利用加速度放大系数AAC来表征这一影响,表示在同一工况下,两侧边坡上各监测点的加速度最大值与台面所测加速度最大值的比值。参照图 4的传感器布置得到图 11的隧道AAC,由图 11(a)可知,60°仰坡的纯边坡一侧与有隧道从坡脚穿过的另一侧,其加速度均随坡高的增加而快速增大,45 cm(约0.6倍坡高)之后缓慢增大,但存在隧道的模型坡面加速度大于纯边坡模型的坡面加速度,可见隧道的存在对于黄土边坡坡面的动力稳定性有重要影响。整体来看,两侧边坡加速度放大效应在坡高为45 m附近时最接近,距坡脚30~45 m(约0.6倍坡高)之间放大系数增大较快。放大效应并不是一味随着坡高的增大而增大,而是在0.65倍坡高附近趋于稳定甚至出现略微的减小。
|
| 图 11 隧道存在对坡面加速度放大系数的影响 Fig. 11 Effect of tunnel on acceleration amplification coefficient of slope |
| |
由图 11(b)可知,在同种波形和输入方向,输入峰值加速度增大,加速度放大效应略微减小,出现放大效应趋于饱和的现象。坡体的加速度反应不再随台面输入加速度峰值的增加而显著增长。范刚等[5]认为这种饱和现象与边坡材料的非线性、阻尼特性有关。
(2) 隧道洞口段的加速度响应特征
蒋树屏等[6-8]研究表明,从衬砌关键位置(拱顶、拱肩、拱脚、仰拱)的动力响应峰值分布来看,拱顶和仰拱位置处的动力响应比其他位置更为强烈。因此,提取4种不同工况下沿隧道轴向各监测点仰拱和拱顶加速度峰值的最大值及所在位置,如表 4所示。由表 4可知,仰拱最大加速度多出现在A2附近,拱顶最大加速度多出现在A7周围。参照图 4可知,A2-A7断面到洞口的距离为70 cm,是隧道最大跨径18 cm的3.89倍。仰拱处最大加速度普遍大于拱顶处。
| 工况 | 监测点 | 最大加速度/(m·s-2) | 位置 | |
| 汶川卧龙波 (x向) |
1 | 仰拱 | 1.93 | A2 |
| 拱顶 | 3.24 | A6 | ||
| 5 | 仰拱 | 3.10 | A3 | |
| 拱顶 | 2.71 | A7 | ||
| EL-Centro波 (z向) |
4 | 仰拱 | 0.63 | A2 |
| 拱顶 | 0.33 | A7 | ||
| 8 | 仰拱 | 2.45 | A2 | |
| 拱顶 | 2.18 | A5 |
监测点最大加速度多出现在距洞口大约3.89~4.06倍隧道跨径处,加速度沿隧道轴向先快速增大再减小。考虑到洞口结构的特殊性,建议洞口抗震设防长度为5倍隧道跨径处较为合适,这与数值计算所得结论一致。
(3) 试验模型应力响应特征
黄土隧道洞口段的动应力响应特征数据如表 5所示。根据图 5,提取4种工况下沿隧道轴向各监测点仰拱和拱顶应力峰值的最大值及所在位置。由表 5可知,仰拱应力值普遍大于拱顶处的值,T3-T9断面到洞口的距离为42 cm,是隧道最大跨径18 cm的2.33倍。由图 5可知,隧道洞口段应力也存在一个先快速增大再减小的过程,随着台面峰值加速度的增大,仰拱应力数值较为稳定,拱顶应力数值呈现增大的趋势。
| 工况 | 监测点 | 最大应力值/Pa | 位置 | |
| 汶川卧龙波 (x向) |
1 | 仰拱 | 1 732.55 | T2 |
| 拱顶 | 951.61 | T9 | ||
| 5 | 仰拱 | 1 850.91 | T3 | |
| 拱顶 | 639.33 | T9 | ||
| EL-Centro波 (z向) |
4 | 仰拱 | 1 567.64 | T3 |
| 拱顶 | 1 039.98 | T9 | ||
| 8 | 仰拱 | 1 541.03 | T3 | |
| 拱顶 | 1 407.87 | T10 |
2 数值模拟分析
数值模拟可以借助计算机直观反映原型的受力特点,利用有限元计算软件Midas-GTS(4.0版本)进行大断面黄土隧道洞口段动力响应分析。对边坡坡度为60°的坡脚、0.3H、0.6H(H为边坡高度)进洞3种工况进行建模分析,分别提取坡面位移、坡面加速度及洞口段衬砌的位移、加速度、应力进行对比分析。
2.1 确定模型参数围岩和衬砌结构物理力学参数的合理选取将保证数值模拟计算结果的准确性。在应用Midas-GTS有限元软件建模时,需要用到内摩擦角、黏聚力、弹性模量、密度、容重、抗拉强度等参数。本研究参考梁庆国[9-12]、吴旭阳[13]、李春清[14]、孙纬宇[15]等针对兰州周边及宝兰客专隧道黄土参数的研究,并结合黄土隧道的工程实际确定了相关物理力学参数,如表 6所示。利用弹性模量、剪切弹性模量和体积弹性模量3者的相互关系转化而得到剪切弹性模量G=43 MPa,体积弹性模量K=200 MPa。
| 弹性模 量/MPa |
泊松比 | 重度/ (kN·m-3) |
抗拉强 度/kPa |
黏聚 力/kPa |
内摩擦 角/(°) |
|
| 围岩 | 120 | 0.4 | 21 | 13 | 34.7 | 21.9 |
| 初衬 | 28 000 | 0.22 | 24 | — | — | — |
| 二衬 | 30 000 | 0.2 | 24 | — | — | — |
2.2 地震波选取
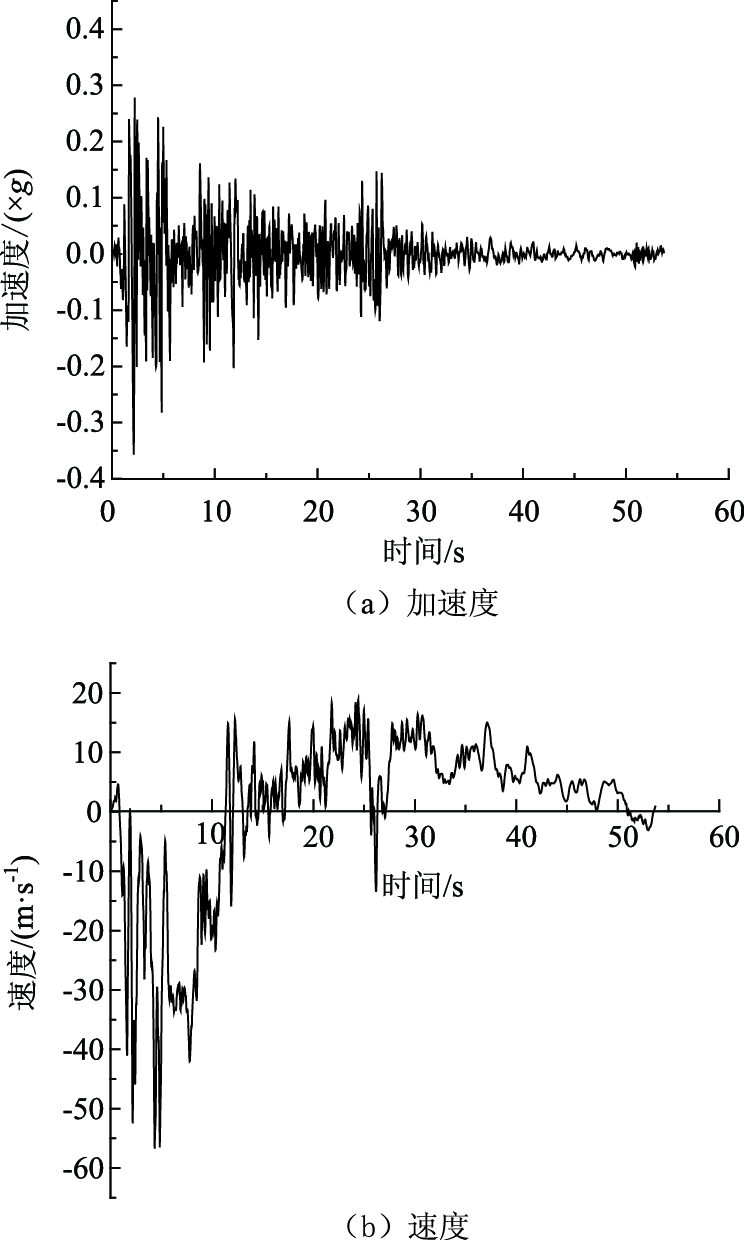
目前对于隧道的地震动力响应分析,应最先考虑地震波的正确选取。本研究工程背景为宝兰客运专线典型大断面黄土隧道,根据《建筑抗震设计规范》(GB50011—2001)[16]、《中国地震动参数区划图》(GB18306—2015)[17]和《铁路工程抗震设计规范》(GB50111—2006)[18]的相关要求,结合隧道洞口段的设计资料建立模型。选用Midas-GTS软件中典型的EL-Centro Site地震波进行计算分析并结合选取地震波时需要遵循的基本原则,对所选地震波进行滤波和基线校正。利用seismosignal软件校正后的加速度、速度时程曲线见图 12。
|
| 图 12 校正基线后的地震加速度和速度无量纲时程曲线 Fig. 12 Dimensionless time history curve of seismic acceleration and velocity after baseline correction |
| |
2.3 建立模型
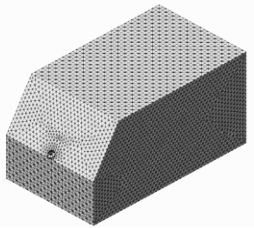
相关研究结果表明,模型计算范围的设置对隧道动力响应的计算结果有较大影响。本研究隧道最大跨径为13 m,由于边坡应力场主要影响1倍坡高范围以内坡体的应力分布,因此建立模型时y向(沿隧道轴向方向)范围不宜过短[19]。故采取的计算范围为:x向为130 m、y向为220 m、z向为110 m(坡高H为60 m)。围岩和初期支护结构采用Midas-GTS中的实体单元,二次衬砌采用板单元,围岩材料采用摩尔-库伦强度破坏准则,支护结构均为弹性模型。具体模型及网格划分如图 13所示。
|
| 图 13 坡脚进洞模型 Fig. 13 Model of slope foot at portal |
| |
在计算前,首先对计算模型进行振型分析,即得到有限元体系的特征周期。在Midas-GTS软件中,采用弹性边界条件进行特征值分析,采用曲面弹簧定义边界条件,弹簧系数可利用地基反力系数来计算。
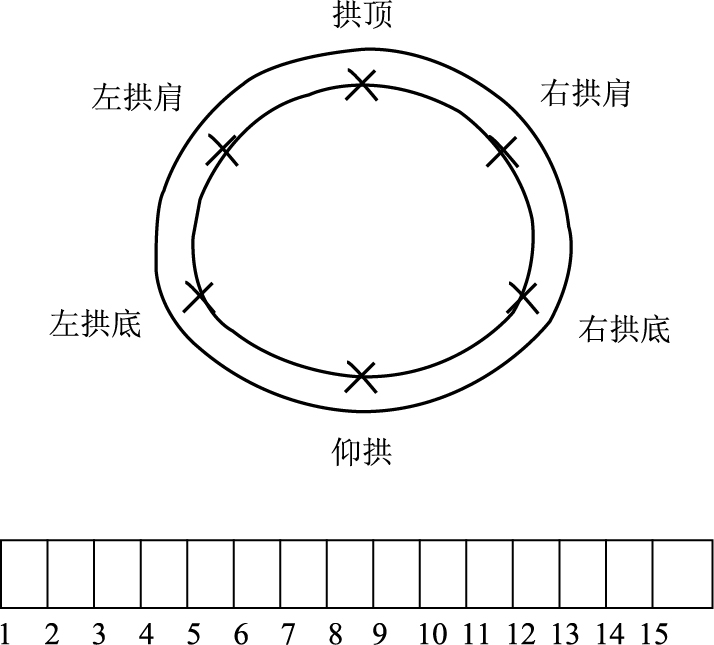
结合隧道受力特点,数值模拟分析沿隧道断面的结果提取点示意图如图 14所示,共在拱顶、仰拱、左右拱肩、左右拱脚处布置6个监测点。在各监测点提取最大加速度和计算过程的最终位移。由于本研究重点为洞口段,因此沿隧道轴向共布置15个监测断面,分别为Y=0,10,20,30,40, …,130,140,150 m,监测数据均提取自二次衬砌。
|
| 图 14 数据提取点示意图 Fig. 14 Schematic diagram of data extraction |
| |
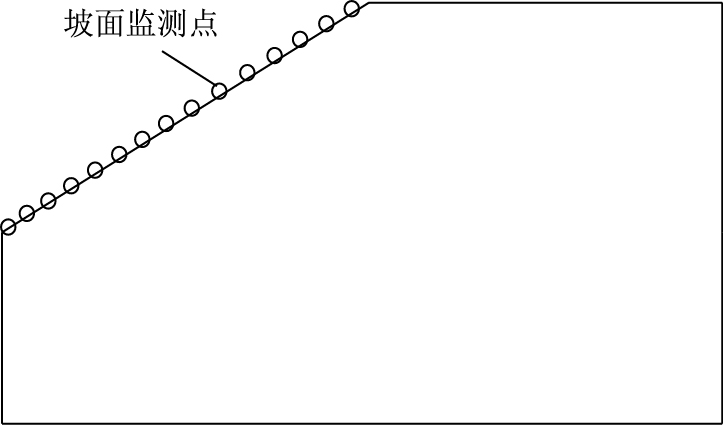
边坡坡面的数据提取点如图 15所示,共布置15个监测点(竖向间隔为4 m),各监测点等距分布。
|
| 图 15 仰坡坡面的数据提取点 Fig. 15 Data extraction point of front slope |
| |
2.4 结果分析研究 2.4.1 进洞高程对仰坡坡面位移的影响
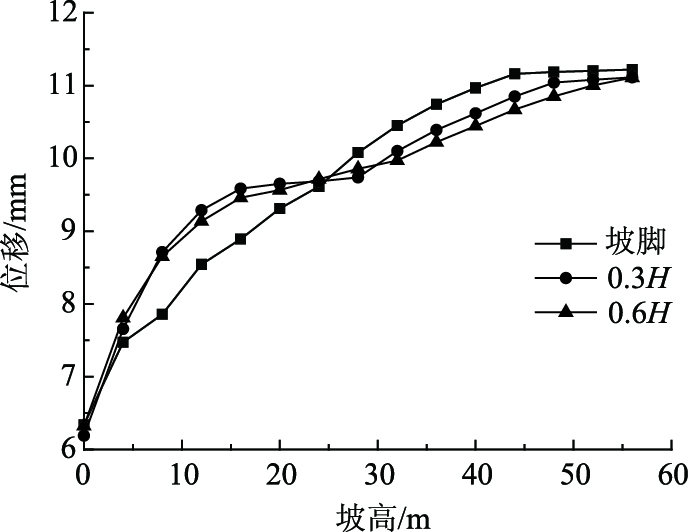
从图 16可知,在坡高为30 m处出现拐点,拐点之后坡面变形速率加快。整体来看,1/2坡高附近是坡面位移变化的拐点,从坡底到1/2坡高附近,不同进洞高程下的坡面位移变化趋势基本相同,最大位移一般出现在坡顶处。坡脚进洞的最大位移为11.219 cm,0.3H进洞的最大位移为11.112 cm,0.6H进洞高程的最大位移为11.109 cm,因此进洞高程越大坡面最大位移越小,同时坡面位移随坡高的增大而增大。这与赖天文[20]、王丽丽[21]等所得“边坡顶部对地震动力的反应较边坡底部存在明显的放大效应”的结论基本一致。图 17为模型整体位移云图。
|
| 图 16 坡面位移变化曲线 Fig. 16 Curves of slope displacement |
| |

|
| 图 17 坡脚进洞模型整体位移云图(单位: cm) Fig. 17 Overall displacement nephogram of model of slope foot at portal(unit: cm) |
| |
2.4.2 进洞高程对仰坡坡面加速度的影响
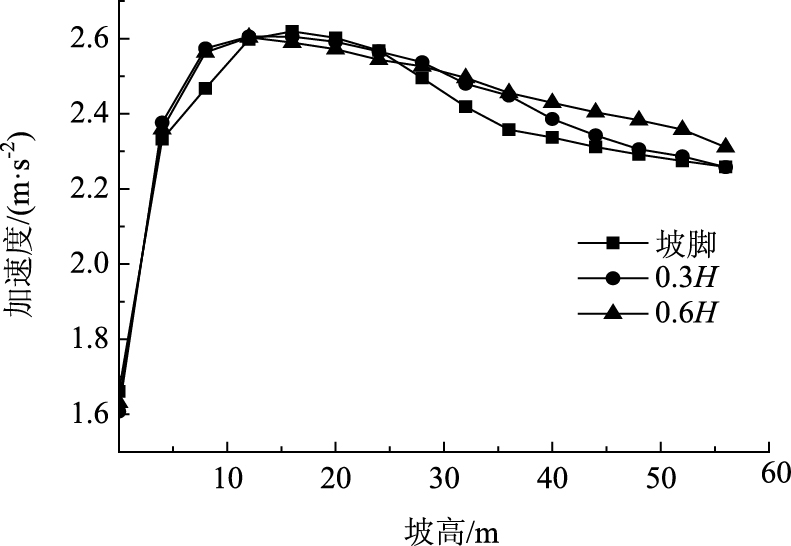
由图 18可知,坡面加速度随坡高的增大先增大而后减小,坡高30 m之后趋于平稳。坡面加速度变化的拐点位置大致位于距坡底15 m和30 m处,坡顶加速度随着进洞高程的增大而增大,坡面最大加速度在15 m坡高附近。
|
| 图 18 坡面加速度变化曲线 Fig. 18 Curves of acceleration of slope |
| |
2.4.3 进洞高程对洞口段衬砌结构位移的影响
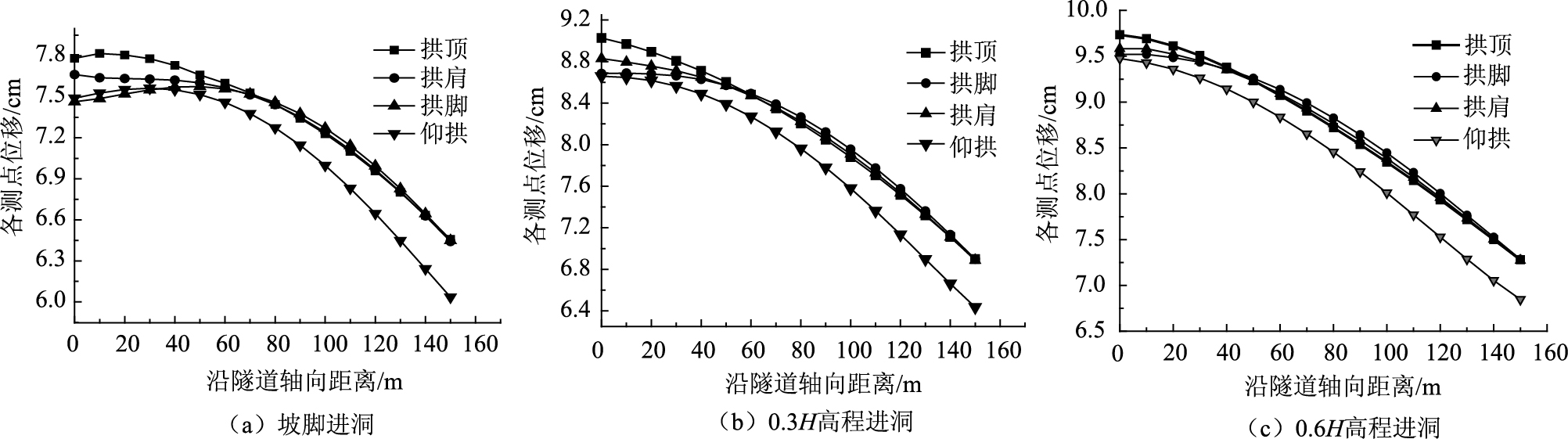
由图 19可知,隧道进洞60 m之后监测点位移快速减小,拱顶和仰拱位移在坡脚进洞时,都有一个略微增大再减小的过程,因此洞口对拱顶和仰拱的加速度具有放大效应,建议在洞口内15~20 m范围内加强抗震支护。位移最大点多出现在进洞60 m处。本研究的黄土隧道最大跨径为13 m,因此在距洞口4.6倍洞径时出现了位移变化拐点。隧道洞口段地震破坏特征呈现出由洞外到洞内逐步减轻的趋势,即存在合理的抗震设防长度。耿萍[22]等借助数值模拟和振动台试验等方法,认为隧道洞口段的抗震设防合理长度为3~4倍隧道跨度,其研究的隧道最大跨径为6.4 m。高峰[23]等认为抗震设防长度和洞口段土体性质密切相关,洞口段软弱围岩越长,隧道的抗震设防长度就相对越长。苏惠等[24-25]根据洞口段的应力变化趋势认为,当洞口围岩性质较好时,抗震设防长度取30 m比较合适;当洞口围岩性质较差时,抗震设防长度取50 m比较安全。因此综合考虑到进洞高程、仰坡坡度、洞口围岩性质、隧道最大跨径等因素,大断面黄土隧道取5倍隧道跨度为抗震设防长度较为合适,也趋于安全。
|
| 图 19 不同高程下各监测点位移沿隧道轴向的变化曲线 Fig. 19 displacement curves of different monitoring points with different elevations along tunnel axis |
| |
整体看来,拱顶处的位移峰值最大,拱肩的位移值略大于拱脚,拱脚的位移值略大于仰拱。随着进洞高程的增大,各个位置的位移也增大,说明随着进洞高程的增加,隧道受地震作用的影响更大,应相应地加强抗震加固措施。
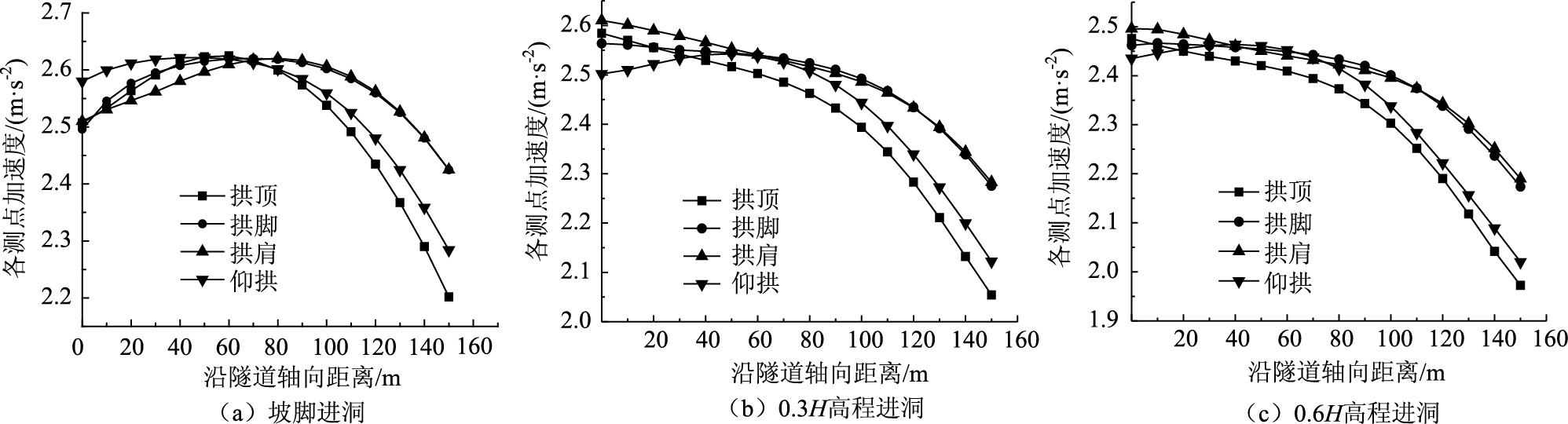
2.4.4 进洞高程对洞口段衬砌结构加速度的影响通过对图 20分析可知,随着进洞高程的增加,衬砌测点加速度拐点位置逐渐靠近洞口,在Y=60 m附近仰拱加速度出现拐点,开始逐渐减小,坡脚进洞时减小速率最大,这与衬砌位移所得到的结论一致。随着进洞高程的增加,隧道各位置的加速度先增大后减小,0.3H高程进洞时加速度最大。在Y=60 m时,仰拱加速度略大于拱顶加速度,其各点的加速度变化规律基本一致。
|
| 图 20 不同高程下各监测点位移沿隧道轴向的变化曲线 Fig. 20 Displacement curves of different monitoring points with different elevations along tunnel axis |
| |
2.4.5 进洞高程对衬砌结构应力响应的影响
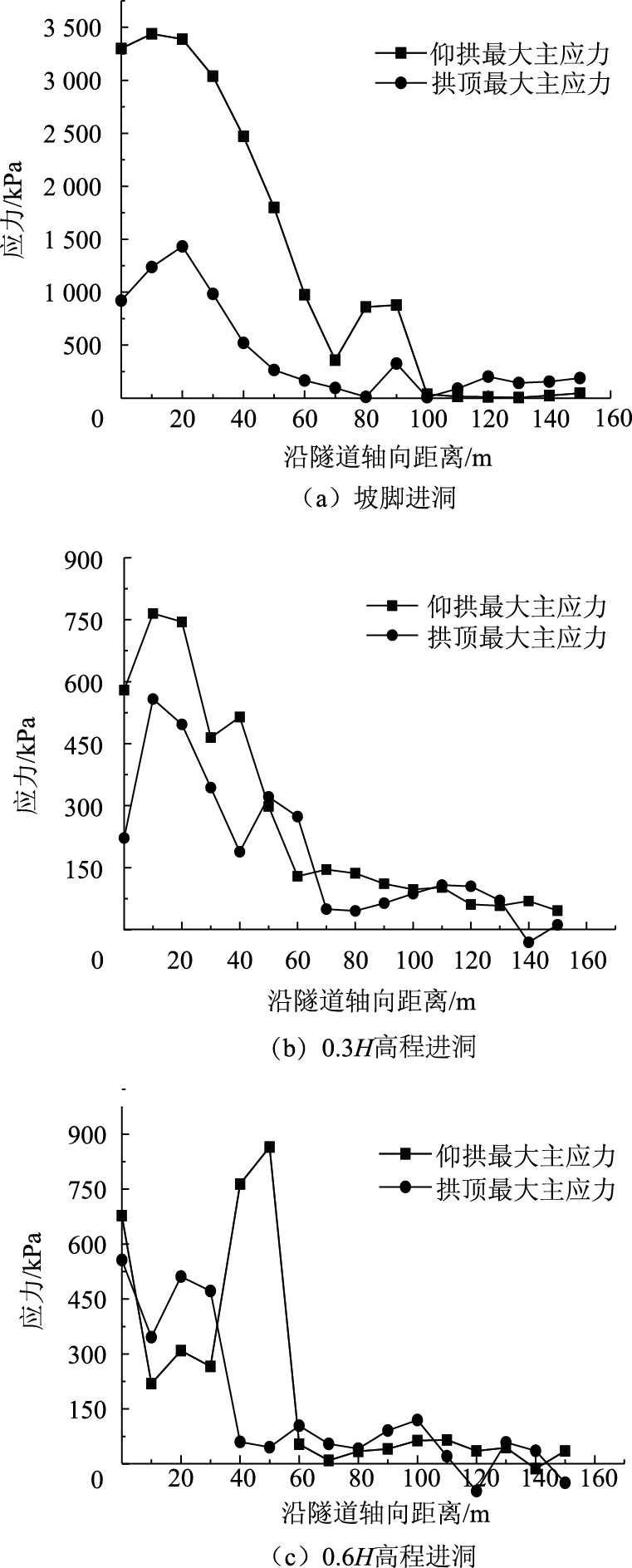
沿隧道轴向提取不同仰坡坡度下各监测断面拱顶和仰拱处的最大主应力,如图 21所示。可以看出,洞口段仰拱处最大主应力整体大于拱顶处最大主应力,但二者变化趋势基本一致;距洞口0~50 m之间应力波动较大,数值整体偏大,50 m后监测点应力迅速减小并逐渐趋于平稳。随进洞高程的增大,洞口段应力整体减小。进洞高程对应力峰值的影响较大,随进洞高程的增大,最大应力峰值逐渐减小,坡脚处应力峰值最大,这与陶连金等[26]试验所得的结论一致。
|
| 图 21 最大主应力沿隧道轴向的变化曲线 Fig. 21 Curves of maximum principal stress along tunnel axis |
| |
3 振动台试验与数值模拟结果对比
隧道洞口段是线路由地下转为地表的过渡段,洞口隧道结构和边仰坡本身的内力、变形和位移都与地震动引起的加速度响应有密切联系。因此,以加速度响应特征为重点,将数值计算结果与模型试验结果进行对比分析。提取隧道衬砌特征部位的加速度响应,绘制加速度变化曲线。模型试验中监测元件埋设部位按1:70的几何相似比换算为相应距离。
在振动台试验中,坡面加速度随着坡高的增大而增大,0.6倍坡高后增大速率变缓,0.65倍坡高后加速度趋于稳定,监测得到的最大坡面加速度为2.21 m/s2,在29.3 m(2.25倍洞径)坡高附近。在数值模拟中,坡面加速度先增大后减小,30 m(0.5倍坡高)后趋于稳定,最大坡面加速度为2.49 m/s2,在28 m(2.15倍洞径)坡高附近。因此两者结论相似,说明数值模拟也可较好地反映坡面加速度的变化规律。
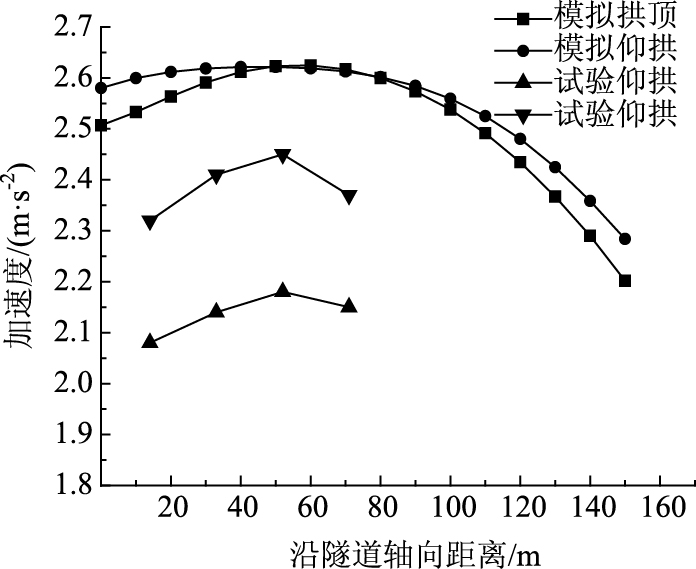
对于洞口隧道段加速度,从图 22可看出,振动台试验和数值模拟中仰拱加速度均大于拱顶加速度且变化趋势相似,加速度随着进洞距离的增大而增大,振动台试验中仰拱和拱顶最大加速度出现在距离洞口51 m处,为3.87倍洞径,而数值模拟中仰拱和拱顶最大加速度出现在距洞口60 m处,为4.62倍洞径。分析认为,输入地震波幅值的不同会使数值计算中衬砌加速度不同于振动台模型试验监测结果,加速度达到稳定值时的位置距洞口的距离(抗震设防长度)主要受制于模型试验和数值计算的边界条件。由于振动台试验是在模型箱内进行,地震波在边界上很容易发生反射引起的模型箱效应,对试验结果可能有一定影响。所以从单纯模型试验得到的抗震设防长度具有局限性,但监测数据得到的动力响应变化趋势与数值模拟基本相符,因此具有一定的参考价值。从振动台试验和数值模拟的结果对比可知,数值模型在衬砌大多数部位的计算结果明显大于试验值,说明数值模拟结果整体要偏保守,但需要注意的是,在实际情况下衬砌个别断面的相关位置处,由于各种复杂因素(软硬围岩交接、衬砌刚度变化等)会导致衬砌的动力响应急剧增大,因此从安全方面考虑,隧道洞口段的抗震设防长度设为5倍洞径是比较合理的。
|
| 图 22 隧道衬砌加速度对比曲线 Fig. 22 Comparative curves of tunnel liner acceleration |
| |
4 结论
(1) 在振动台试验加载过程中,坡顶出现拉剪破坏。隧道衬砌与上部土体自振频率不同导致错动形成竖向裂缝,两侧坡脚处出现横向裂缝且发展速度较快,模型坡面整体发生破坏,震陷滑塌现象很明显且大块土体整体滑落。整体来看,有隧道一侧滑塌破坏程度大于纯边坡一侧。
(2) 应力值和最大加速度仰拱普遍大于拱顶处,隧道洞口段应力存在一个先快速增大再减小的过程,应力最大值断面到洞口的距离为隧道最大跨径的2.33倍。最大加速度多出现在距洞口大约3.89~4.06倍隧道跨径处。随着台面峰值加速度的增大,拱顶应力数值呈现增大的趋势。
(3) 坡面位移随坡高的增大而增大,坡面加速度随坡高的增大先增大而后减小,变化的拐点位置大致位于距坡底15 m和30 m处,坡面最大加速度在15 m坡高附近。在同种波形和输入方向,输入峰值加速度增大,加速度放大效应略微减小,出现放大效应趋于饱和现象。
(4) 隧道洞口段最大主应力仰拱大于拱顶,洞口段最大主应力先增大后减小,一般在距洞口15 m达到峰值,距洞口50 m后趋于平稳,坡脚进洞时主应力最大。
(5) 洞口段监测点位移随轴向距离先缓慢增大再减小,其中前60 m位移减小速率较小,60 m后位移减小速率明显增大,由于临空面的存在,洞口段具有明显的动力放大效应。
(6) 从试验和数值模拟的结果对比可知,数值模型在衬砌大多数部位的计算结果明显大于试验值,说明数值模拟结果整体要偏保守,但是可以较好地反映出加速度和土压力的基本变化规律,因此具有一定的参考价值。从安全方面考虑,隧道洞口段的抗震设防长度设为5倍洞径是比较合理的。
| [1] |
关振长, 龚振峰, 罗志彬, 等. 特大断面隧道地震动力特性的振动台试验研究[J]. 岩土力学, 2016, 37(9): 2553-2560. GUAN Zhen-chang, GONG Zhen-feng, LUO Zhi-bin, et al. Seismic Property of a Large Section Tunnel Based on Shaking Table Model Tests[J]. Rock and Soil Mechanics, 2016, 37(9): 2553-2560. |
| [2] |
刘明星, 刘恩龙, 张世殊, 等. 地震荷载作用下危岩体边坡动力响应及失稳机理探讨[J]. 工程地质学报, 2016, 24(2): 187-196. LIU Ming-xing, LIU En-long, ZHANG Shi-shu, et al. Numerical Investigation of Dynamic Response and Instability Mechanism for Dangerous Rock Mass Slope under Earthquake Loads[J]. Journal of Engineering Geology, 2016, 24(2): 187-196. |
| [3] |
王帅帅, 高波, 隋传毅, 等. 不同地质条件下隧道洞口仰坡地震破坏特性研究[J]. 岩土力学, 2014, 35(增1): 278-284. WANG Shuai-shuai, GAO Bo, SUI Chuan-yi, et al. Shaking Table Test for Seismic Behavior of Upward Slope at Tunnel Entrance in Different Geological Conditions[J]. Rock and Soil Mechanics, 2014, 35(S1): 278-284. |
| [4] |
吴冬, 高波, 申玉生, 等. 隧道仰坡地震动力响应特性振动台模型试验研究[J]. 岩土力学, 2014, 35(7): 1921-1928. WU Dong, GAO Bo, SHEN Yu-sheng, et al. Shaking Table Test Study of Seismic Dynamic Response of Tunnel Entrance Slope[J]. Rock and Soil Mechanics, 2014, 35(7): 1921-1928. |
| [5] |
范刚, 张建经, 付晓, 等. 含泥化夹层顺层岩质边坡动力响应大型振动台试验研究[J]. 岩石力学与工程学报, 2015, 34(9): 1751-1757. FAN Gang, ZHANG Jian-jing, FU Xiao, et al. Large-scale Shaking Table Test on Dynamic Response of Bedding Rock Slopes with Silt Intercalation[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(9): 1751-1757. |
| [6] |
蒋树屏, 方林, 林志. 不同埋置深度的山岭隧道地震响应分析[J]. 岩土力学, 2014, 35(1): 211-216. JIANG Shu-ping, FANG Lin, LIN Zhi. Seismic Response Analysis of Mountain Tunnels in Different Depths[J]. Rock and Soil Mechanics, 2014, 35(1): 211-216. |
| [7] |
马小莉, 闫坤伐, 刘晓燕, 等. 边坡地震动力响应的振动台模型试验[J]. 公路交通科技, 2016, 33(11): 34-41, 56. MA Xiao-li, YAN Kun-fa, LIU Xiao-yan, et al. Shaking Table Model Test of Slope Seismic Dynamic Response[J]. Journal of Highway and Transportation Research and Development, 2016, 33(11): 34-41, 56. |
| [8] |
周志军, 赵涛, 钟世福, 等. 基于地震力作用下的黄土边坡稳定性分析[J]. 公路交通科技, 2013, 30(9): 38-42, 60. ZHOU Zhi-jun, ZHAO Tao, ZHONG Shi-fu, et al. Analysis on Stability of Loess Slope Based on Effect of Earthquake Force[J]. Journal of Highway and Transportation Research and Development, 2013, 30(9): 38-42, 60. |
| [9] |
梁庆国, 李洁, 李德武, 等. 黄土隧道围岩分级研究的若干问题[J]. 岩土工程学报, 2011, 33(增1): 170-176. LIANG Qing-guo, LI Jie, LI De-wu, et al. Some Problems on Surrounding Rock Classification of Loess Tunnels[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(S1): 170-176. |
| [10] |
梁庆国, 赵磊, 安亚芳. 兰州Q4黄土各向异性的初步研究[J]. 岩土力学, 2012, 33(1): 17-24. LIANG Qing-guo, ZHAO Lei, AN Ya-fang. Preliminary Study of Anisotropy of Q4 Loess in Lanzhou[J]. Rock and Soil Mechanics, 2012, 33(1): 17-24. |
| [11] |
LIANG Q, WU X, LI C. Mechanical Analysis Using the Unconfined Penetration Test on the Tensile Strength of Q3 Loess around Lanzhou City, China[J]. Engineering Geology, 2014, 183: 324-329. |
| [12] |
LIANG Q, LI J, WU X. Anisotropy of Q2 Loess in the Baijiapo Tunnel on the Lanyu Railway, China[J]. Bulletin of Engineering Geology and the Environment, 2016, 75(1): 109-124. |
| [13] |
吴旭阳. 黄土各向异性及抗拉本构关系在隧道工程中的应用[D]. 兰州: 兰州交通大学, 2015. WU Xu-yang. Application of Anisotropy and Tensile Constitutive Relation of Loess in Tunnel Engineering[D]. Lanzhou: Lanzhou Jiaotong University, 2015. |
| [14] |
李春清, 梁庆国, 吴旭阳, 等. 重塑黄土抗拉强度试验研究[J]. 地震工程学报, 2014, 36(2): 233-238. LI Chun-qing, LIANG Qing-guo, WU Xu-yang, et al. Study on the Test of Tensile Strength of Remolded Loess[J]. Chinese Journal of Earthquake Engineering, 2014, 36(2): 233-238. |
| [15] |
孙纬宇, 梁庆国, 欧尔峰, 等. 陕西延安Q2原状与重塑黄土抗拉强度对比试验研究[J]. 土木工程学报, 2015, 48(增2): 53-58. SUN Wei-yu, LIANG Qing-guo, OU Er-feng, et al. Comparative Experimental Study on Tensile Strength of Undisturbed and Remolded Q2 Loess from Yan'an Shaanxi, China[J]. China Civil Engineering Journal, 2015, 48(S2): 53-58. |
| [16] |
GB50011-2010, 建筑抗震设计规范[S]. GB50011-2010, Code for Seismic Design of Buildings[S].
|
| [17] |
GB18306-2015, 中国地震动参数区划图[S]. GB18306-2015, Seismic Ground Motion Parameters Zonation Map of China[S].
|
| [18] |
GB50111-2006, 铁路工程抗震设计规范[S]. GB50111-2006, Code for Seismic Design of Railway Engineering[S].
|
| [19] |
黄润秋, 王金安, 姚磊华, 等. 工程地质数值法[M]. 北京: 科学出版社, 2006. HUANG Run-qiu, WANG Jin-an, YAO Lei-hua, et al. Numerical Method of Engineering Geology[M]. Beijing: Science Press, 2006. |
| [20] |
赖天文, 陈国瑛. 隧道洞口岩质高仰坡动力反应分析[J]. 兰州交通大学学报, 2012, 31(3): 8-11. LAI Tian-wen, CHEN Guo-ying. Analysis of Earthquake Response for High Rock Slope of Tunnel Portal[J]. Journal of Lanzhou Jiaotong University, 2012, 31(3): 8-11. |
| [21] |
王丽丽, 吴志坚, 梁庆国, 等. 仰坡坡度对隧道洞口段动力响应的影响分析[J]. 地震工程学报, 2016, 38(4): 519-524. WANG Li-li, WU Zhi-jian, LIANG Qing-guo, et al. Influence of Slope Gradient on Dynamic Response in Portal Section of Tunnel[J]. Journal of Earthquake Engineering, 2016, 38(4): 519-524. |
| [22] |
耿萍, 曹东杰, 唐金良, 等. 铁路隧道洞口合理抗震设防长度[J]. 西南交通大学学报, 2012, 47(6): 942-948. GENG Ping, CAO Dong-jie, TANG Jin-liang, et al. Rational Seismic Protective Length for Portal of Railway Tunnel[J]. Journal of Southwest Jiaotong University, 2012, 47(6): 942-948. |
| [23] |
高峰, 石玉成, 严松宏, 等. 隧道洞口段的抗震设防长度[J]. 中国公路学报, 2006, 19(3): 65-69. GAO Feng, SHI Yu-cheng, YAN Song-hong, et al. Anti-seismic Fortified Length in Tunnel Outlet[J]. China Journal of Highway and Transport, 2006, 19(3): 65-69. |
| [24] |
苏惠, 贾良, 严松宏, 等. 隧道洞口段结构地震响应分析[J]. 水利与建筑工程学报, 2010, 8(2): 156-158. SU Hui, JIA Liang, YAN Song-hong, et al. Analysis of Anti-seismic Fortified Length in Tunnel Portal and Outlet[J]. Journal of Water Resources and Architectural Engineering, 2010, 8(2): 156-158. |
| [25] |
苏惠, 焦胜军, 杨江朋. 右江南岸隧道洞口段结构抗震设防长度研究[J]. 路基工程, 2010(6): 167-169. SU Hui, JIAO Sheng-jun, YANG Jiang-peng. Study on Earthquake-proof Defense Length of Nan'an Tunnel Portal Section in Youjiang[J]. Subgrade Engineering, 2010(6): 167-169. |
| [26] |
陶连金, 侯森, 赵旭, 等. 不同仰坡度数的山岭隧道洞口段动力响应振动台试验研究[J]. 岩土力学, 2014, 35(增1): 91-98. TAO Lian-jin, HOU Sen, ZHAO Xu, et al. Large-scale Shaking Table Test for Dynamic Response in Portal Section of Mountain Tunnel with Different Gradients of Upward Slope[J]. Rock and Soil Mechanics, 2014, 35(S1): 91-98. |
 2018, Vol. 35
2018, Vol. 35
