扩展功能
文章信息
- 郭蓉, 彭志会, 郭娇, 杜力峰, 赵少伟
- GUO Rong, PENG Zhi-hui, GUO Jiao, DU Li-feng, ZHAO Shao-wei
- 有黏结预应力CFRP板加固RC梁抗弯疲劳试验与理论分析
- Experimental and Theoretical Analysis on Bending Fatigue Performance of RC Beam Reinforced with Bonded Prestressed CFRP Plate
- 公路交通科技, 2018, 35(7): 50-57, 85
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(7): 50-57, 85
- 10.3969/j.issn.1002-0268.2018.07.008
-
文章历史
- 收稿日期: 2017-09-15
2. 天津市公路养护工程处, 天津 300250
2. Tianjin Highway Maintenance Engineering Department, Tianjin 300250, China
碳纤维增强复合材料(CFRP)具有轻质高强、易于施工、耐久性好等特点,广泛应用于加固补强工程中。大量相关静载试验研究[1-8]表明,预应力CFRP板加固方法可以有效提高CFRP的材料利用率和加固结构的承载能力,改善CFRP板剥离和加固结构的开裂情况。在加固结构的疲劳性能方面,Ghafoori[9]通过对比有黏结预应力加固和无黏结预应力加固两种加固方式对预应力CFRP加固混凝土梁进行了疲劳试验;Xie[10]、彭晖[11]、Lu[12]分别进行了预应力CFRP板加固混凝土梁的疲劳性能研究;何初生[13]进行了预应力CFRP布对预应力CFRP加固混凝土梁疲劳性能进行研究。上述试验结果均表明有粘结预应力碳纤维板加固方法能够显著提高钢筋混凝土梁的疲劳寿命,改善裂缝开裂情况,并且在疲劳荷载作用后,加固梁仍能保持绝大部分刚度和承载力,但上述研究大多侧重于对加固结构疲劳损伤后承载能力的研究,而对加固结构而言,疲劳荷载作用下的结构损伤累积规律对于评估结构的损伤状态和预测结构的剩余寿命具有重要意义,但目前研究基本侧重于钢筋混凝土梁的疲劳损伤累积规律研究,如汤红卫[14]、李可[15]得到了钢筋混凝土梁的疲劳损伤累积规律、朱红兵[16]提出了钢筋混凝土梁的刚度退化计算公式。而针对预应力CFRP加固梁的疲劳损伤累积规律的研究很少,只有Xie[11]进行了有黏结预应力CFRP板加固混凝土梁的疲劳损伤累积规律的研究,但其试验中CFRP板预应力水平低,仅为材料强度的6%~11%,实际加固效果不理想;本研究前期研制的锚具能够对CFRP板施加高预应力,预应力度能够达到材料强度的60%,并通过预应力CFRP板加固混凝土梁的抗弯静载试验证明,在整个加载过程中锚具的工作性能良好[6],拟进一步对高预应力水平的CFRP板加固混凝土梁的疲劳损伤累积规律进行研究,研究成果能够有效地对该类型加固结构疲劳累积损伤和结构剩余疲劳寿命进行评估,对其加固工程的鉴定和加固维修具有重要意义。
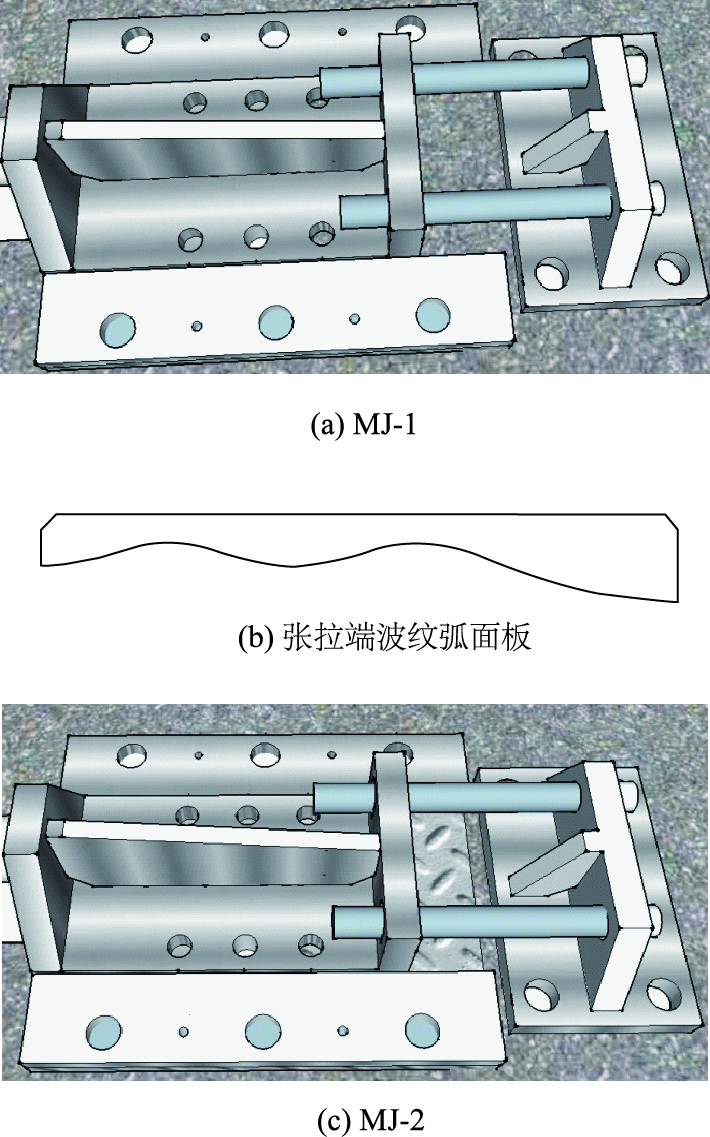
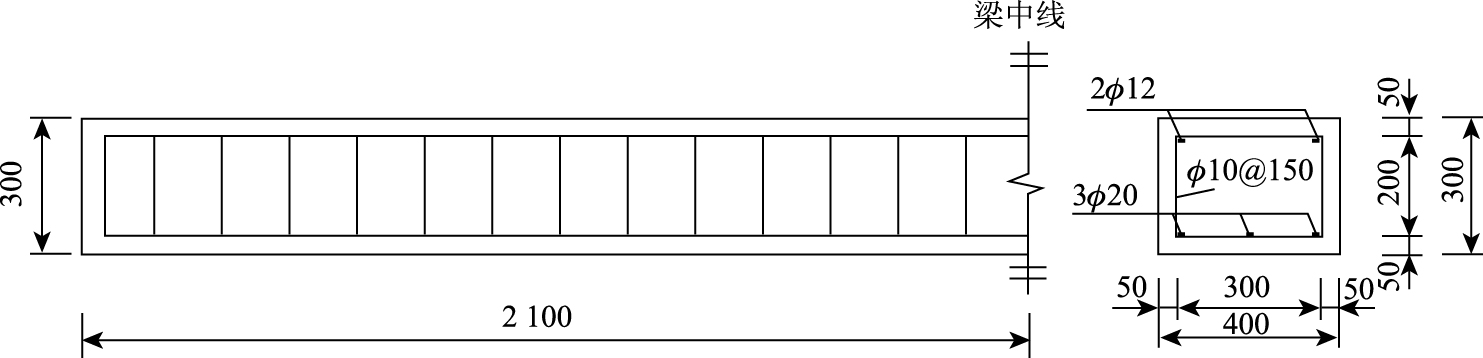
1 试验概况 1.1 试件设计试验共设计了6根有黏结预应力CFRP板加固混凝土梁试件,其中疲劳试验试件3根,静载试验试件3根,利用本研究自行研制的锚具张拉CFRP板,实物图如图 1所示。由CFRP板的应变控制张拉预应力,两种锚具的施工工艺不同,MJ-1通过波纹板的弧面(图 1(b))来实现CFRP板紧贴试验梁,锚固板直接在混凝土表面滑动,能够实现不开槽加固;MJ-2两端不存在弧面,需要在梁底开槽,滑槽底面是光滑的钢板。试件预应力施加情况如表 1所示。试件跨度为4 200 mm,计算跨度为3 900 mm,截面尺寸为400 mm×300 mm,试件尺寸及配筋如图 2所示,受拉纵筋选用HRB400钢筋,实测屈服强度为461 MPa,屈服应变为2 195.2 με,试件采用的混凝土强度等级为C50,实测立方体抗压强度为54.6 MPa,实测弹性模量值为3.63×104 MPa,选用的专用碳纤维板双组分胶黏剂,CFRP板的力学性能如表 2所示。
| 试件 编号 |
预应 力水 平/% |
初始 应变/ με |
有效 应变/ με |
有效预 应力水 平/% |
锚具 种类 |
加载 方式 |
疲劳下 限/疲劳 上限/kN |
| PB1-40 | 40 | 6 000 | 5 541 | 37 | MJ-1 | 静载 | — |
| PB1-60 | 60 | 9 000 | 7 632 | 51 | MJ-1 | 静载 | — |
| PB2-40 | 40 | 6 000 | 5 403 | 36 | MJ-2 | 静载 | — |
| FPB1-40 | 40 | 6 000 | 5 271 | 35 | MJ-1 | 疲劳荷载 | 20/55 |
| FPB1-60 | 60 | 9 000 | 7 615 | 51 | MJ-1 | 疲劳荷载 | 20/65 |
| FPB2-40 | 40 | 6 000 | 5 296 | 35 | MJ-2 | 疲劳荷载 | 20/55 |
| 注: PB和FPB分别表示静载试件和疲劳试件;1,2分别表示使用锚具1和锚具2;40,60分别表示试件预应力水平;有效预应力为加载前CFRP板的实测值。 | |||||||
|
| 图 2 试件尺寸配筋(单位:mm) Fig. 2 Dimensions and reinforcement of specimen(unit: mm) |
| |
| 类别 | 规格/ (mm×mm) |
抗拉强度/ MPa |
弹性模量/ GPa |
伸长率/% |
| 碳纤维板 | 1.4×50 | 2 424 | 164 | 1.65 |
1.2 试验加载
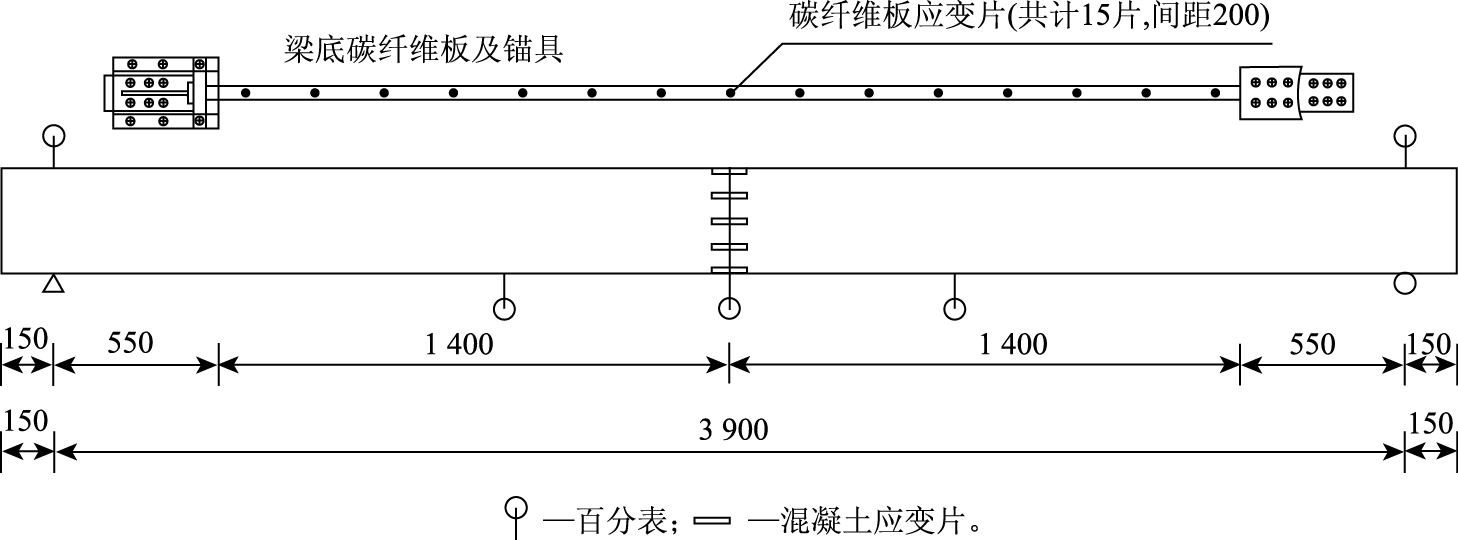
根据《混凝土结构试验方法标准》(GB/T 50152—2012)[17]进行静力试验加载和疲劳试验加载,加载装置如图 3所示。试验采用三分点对称加载,在跨中、三分点处及支座处架设激光位移计记录梁体变形情况,应变测点布置如图 4所示。

|
| 图 3 加载装置 Fig. 3 Loading device |
| |
|
| 图 4 测点布置(单位:mm) Fig. 4 Arrangement of measuring points(unit: mm) |
| |
3根静力加载试件用来确定试件的开裂荷载、屈服荷载和极限荷载,3根疲劳加载试件用以研究预应力水平及试件损伤对试件疲劳性能的影响。疲劳荷载上限采用0.2 mm (B类桥梁最大允许裂缝)对应的荷载组合值,疲劳荷载下限以试验梁和加载分配梁不产生脱离为原则确定,各个试件的疲劳上限、下限如表 1所示。疲劳荷载采用荷载控制,加载频率为5 Hz。若试件在200万次循环荷载作用后未发生疲劳破坏,则对试件进行全过程静载破坏试验,以确定试件的剩余刚度与剩余承载力。
2 试验结果及分析 2.1 静载试验结果对试件PB1-40,PB1-60,PB2-40进行静载试验。
(1) 试验现象:至加载结束,试件锚具完好、CFRP板未发生滑移现象,表明两种锚具锚固效果良好。其中试件PB1-40与PB2-40的破坏现象为受拉钢筋屈服后梁顶混凝土被压碎,这是由于钢筋屈服后CFRP板应变远低于其极限应变,试件能够继续承载直到混凝土应变先于CFRP板达到极限应变,所以混凝土压碎时CFRP板没有断裂。试件PB1-60在接近破坏时,黏结胶层在混凝土主裂缝处出现剥离裂缝并在高应力状态下迅速扩展,当弯剪区CFRP板剥离长度过大且发展至锚具处时,受力体系发生改变,由胶层提供的剪力转移到锚具上,锚具附近的CFRP板受拉剪复合作用被拉断并发出巨大声响(见图 5),梁顶混凝土被压碎、梁体挠度迅速增大,承载能力迅速降低,并在梁端带混凝土剥落,试件宣告破坏。

|
| 图 5 CFRP板拉断 Fig. 5 Tension fracture of CFRP plate |
| |
试验结果分析:主要试验结果如表 3所示。从表 3可计算出:在承载力方面,试件PB1-60较试件PB1-40,PB2-40的开裂荷载、屈服荷载和极限荷载均有提高;在破坏特征方面,试件PB1-40与PB2-40破坏时受拉钢筋屈服,梁顶混凝土压碎,碳板未断裂,破坏过程缓慢,破坏前有明显预兆,试件PB1-60破坏时的CFRP板在高拉应力状态下同时受剪力作用,发生突然断裂,破坏过程迅速且无明显预兆。
| 试件 编号 |
开裂荷 载/kN |
屈服荷 载/kN |
极限荷 载/kN |
破坏特征 |
| PB1-40 | 32 | 154 | 208 | 受拉钢筋屈服, 梁顶混凝土压碎 |
| PB1-60 | 38 | 160 | 216 | 受拉钢筋屈服, CFRP板拉断 |
| PB2-40 | 32 | 152 | 211 | 受拉钢筋屈服, 梁顶混凝土压碎 |
2.2 疲劳试验结果
疲劳试件FPB1-40,FPB1-60,FPB2-40经过2万次疲劳荷载作用后,均未发生破坏,试件因疲劳损伤累积导致刚度退化,钢筋应变和CFRP板应变均有一定增长,跨中挠度增大。
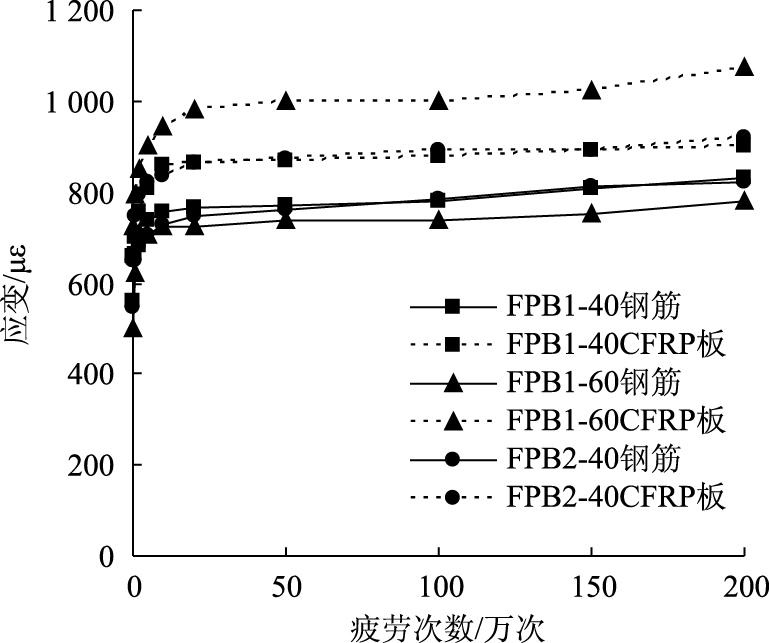
2.2.1 受拉钢筋与CFRP板的应变分析如图 6所示,定义试件加载前CFRP板和钢筋的应变均为0,绘制各试件钢筋和CFRP板在疲劳上限作用下的应变-疲劳次数曲线图。从图 6中可以看出,钢筋应变小于CFRP板应变,在200万次疲劳荷载作用过程中,其受拉钢筋与CFRP板的应变发展分为快速发展与稳定发展两个阶段:2万次循环之前,受拉钢筋和CFRP板应变增长速度由快变慢,这是因为梁的裂缝发展趋于稳定;2万次之后,两者应变增长变缓,梁体裂缝开展均匀、梁内应力重分布基本完成,钢筋和CFRP板应变发展平稳,试件整体工作性能良好,说明试件设计合理, 能够达到预期要求。
|
| 图 6 钢筋和CFRP板的应变-疲劳次数曲线 Fig. 6 Curves of strain vs. cycle number of steel bar and CFRP plate |
| |
对比分析图 6各加固试件钢筋与CFRP板在疲劳上限作用下的应变-疲劳次数关系曲线,可以得到以下结果。
(1) 疲劳荷载的影响:分别对比钢筋与CFRP板的应变值,可以看出200万次疲劳荷载后应变增长明显,试件FPB1-40,FPB1-60和FPB2-40钢筋应变分别增加了48.7%,56.0%和50.9%;CFRP板的应变分别增加了36.7%,49.0%和41.8%。一方面,构件因为疲劳作用产生损伤导致裂缝扩张,裂缝在疲劳作用下宽度增加,数量增多造成钢筋和CFRP板应变明显增加;另一方面,钢筋较CFRP板损伤累积更加明显、应变增加比例更大,宏观表现为裂缝沿梁高呈现“中间宽、两端窄”的现象,表明CFRP板对于裂缝宽度的约束作用明显。
(2) 预应力水平的影响:试件FPB1-40和FPB2-40的钢筋应变小于CFRP板应变,差值约为100~150 με;试件FPB1-60的钢筋应变较CFRP板应变降低了200~260 με。钢筋和CFRP板之间应力差变大,同时钢筋的应力水平更低,表明提高预应力水平后,截面上拉应力更多转移至CFRP板上。
(3) 锚固方式的影响:在锚固系统满足使用要求的前提下,锚固方式对CFRP板、钢筋的应变发展有较小影响,经过200万次疲劳作用后试件没有破坏,表明本试验采取的两种锚具均有良好的工作性能,能够满足预期要求。
2.2.2 截面应变分析跨中截面应变分布研究显示所有试件的跨中截面应变分布符合相同规律,以试件FPB1-40为例,说明试件经过200万次疲劳作用后跨中截面应变分布规律,如图 7所示。可以看出截面应变呈线性分布,符合平截面假定。随着荷载增加,中和轴高度基本不变,混凝土应变分布基本为三角形,试件呈现出较好的弹性。
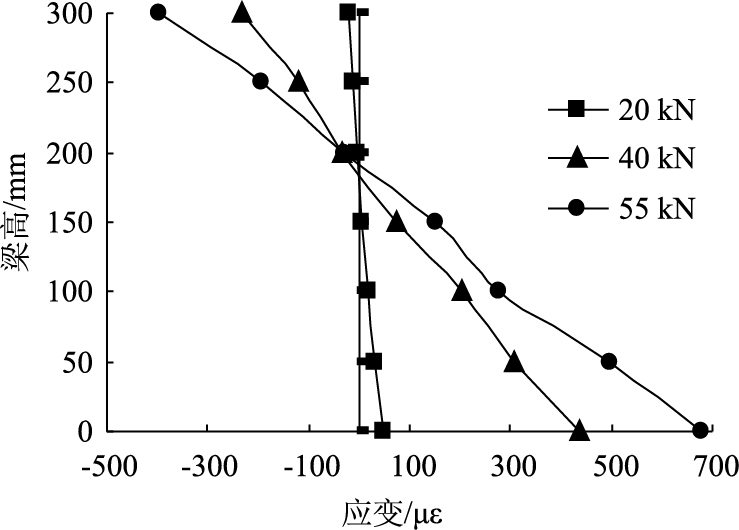
|
| 图 7 FPB1-40跨中截面应变分布 Fig. 7 Distribution of strains of FPB1-40 |
| |
图 8对比了0次和200万次之后,各试件在55 kN荷载下的跨中截面混凝土应变,从图中可以看出,试件FPB1-40,FPB1-60和FPB2-40经过疲劳荷载作用后,梁顶混凝土压应变增加,增幅分别为38.4%,15.8%和34.3%。其中,试件FPB1-60因疲劳作用增加的应变值明显低于其他试件,这是因为预应力水平增加后,梁顶混凝土应力降低、应变减小。
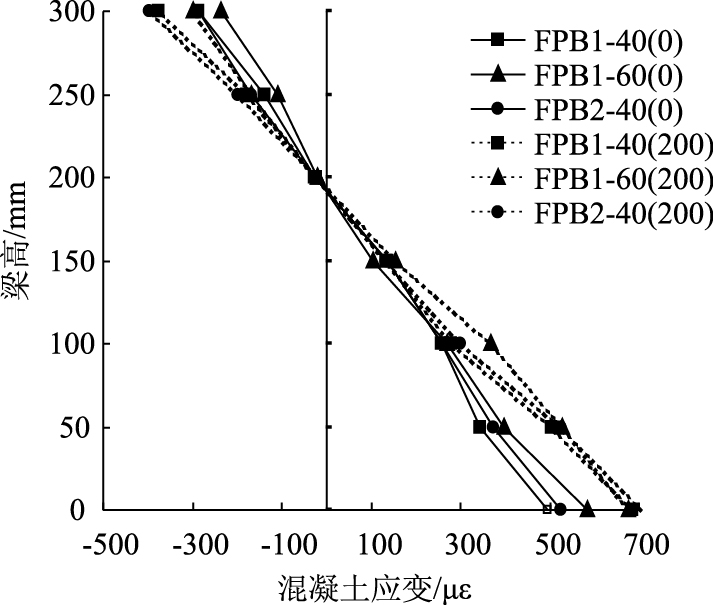
|
| 图 8 疲劳前后试件跨中截面混凝土应变分布对比 Fig. 8 Comparison of strain distributions of concrete in mid-span section before and after fatigue |
| |
2.3 疲劳后静载试验结果
所有试件经200万次循环荷载作用均未发生疲劳破坏,通过静载破坏试验了解试件疲劳损伤后的静力性能。经过疲劳荷载作用,所有试件的静载受弯破坏形式均为CFRP板与梁体剥离后拉断。这是因为在疲劳荷载作用下,胶层产生损伤累积,虽然在应力较低时能够正常工作,但钢筋屈服后,随着裂缝开展、试件变形增加,弯剪区胶层提前发生破坏导致CFRP板剥离后拉剪破坏,因此,对于试件的弯剪区内CFRP板剥离现象应当足够重视,可以采取适当锚固措施。
表 4统计了静载和疲劳后静力加载的各试件屈服荷载和极限荷载值。可以看出,经过疲劳荷载之后,所有试件的屈服荷载和极限荷载均有下降,例如试件FPB1-40相较于试件PB1-40,屈服荷载、极限荷载分别下降了7.8%和11.1%,这是由于疲劳荷载作用导致材料出现损伤累积,试件的胶层在接近破坏时出现剥离裂缝并最终导致CFRP板剥离并在锚具附近拉剪破坏。试件FPB1-60较试件FPB1-40的屈服荷载和极限荷载提升不明显。
| 试件编号 | 屈服荷载/kN | 极限荷载/kN |
| PB1-40 | 154 | 208 |
| PB1-60 | 160 | 216 |
| PB2-40 | 152 | 211 |
| FPB1-40 | 142 | 185 |
| FPB1-60 | 145 | 190 |
| FPB2-40 | 135 | 170 |
分析发现试件PB1-40、试件PB1-60和试件PB2-40的荷载挠度曲线相近;试件FPB1-40、试件FPB1-60和试件FPB2-40的荷载挠度曲线相近。为图示方便以试件PB1-40和试件FPB1-40的荷载-挠度进行说明,如图 9所示。可以看出试件的荷载-挠度曲线变化规律相近,荷载-挠度曲线上均存在拐点,约为极限荷载的90%,拐点之前,试件刚度基本不变,承载力有足够储备,工作性能良好;拐点之后,曲线斜率降低,构件刚度明显下降,试验中出现明显破坏现象,在设计中该拐点可以考虑作为承载能力极限状态的取值依据。

|
| 图 9 荷载-挠度曲线 Fig. 9 Load-deflection curves |
| |
3 疲劳累积损伤分析 3.1 疲劳刚度退化分析
目前研究表明[14-16]钢筋混凝土试件的刚度退化分为3阶段:第1阶段刚度退化速率由大变小,第2阶段刚度退化速率趋于定值,占据疲劳寿命的大部分,第3阶段为疲劳破坏阶段,刚度退化速率瞬时加快,试件发生疲劳破坏。但试件刚度退化的各阶段历时尚存在分歧,文献[14]和文献[16]得到的试件刚度退化曲线近似呈倒“S”形,第1阶段历时约为疲劳寿命的5%~10%;文献[15]得到的刚度退化第一阶段历时为疲劳寿命的1%。为研究有黏结预应力CFRP加固混凝土梁的刚度退化规律,本研究将各试件的Bn/B0绘制成曲线图,其中B0,Bn分别为试件的初始刚度、经受n次疲劳加载后刚度,如图 10所示。从图中可以看出,所有试件在前2万次刚度退化速度明显,2万次之后趋于平稳,可以认为2万次左右时,疲劳刚度退化的第1阶段完成。依据两个预应力水平的加固梁刚度退化的试验数据进行回归分析,得到加固梁刚度退化的回归公式,如式(1)所示:

|
(1) |
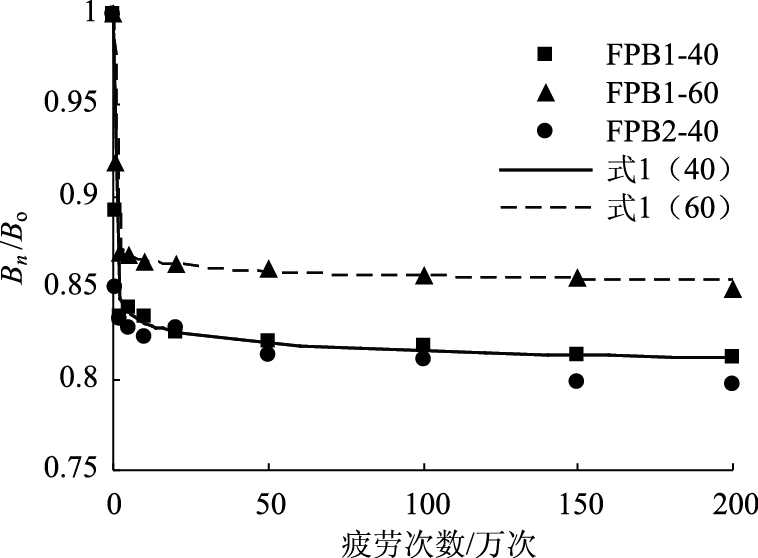
|
| 图 10 刚度退化曲线 Fig. 10 Stiffness degradation curves |
| |
3.2 疲劳损伤分析
文献[14]基于损伤力学定义了累积损伤值D,见式(2);文献[15]通过有限元模拟给出矩形钢筋混凝土梁在前两个阶段的疲劳累积损伤公式,经过换算为式(3):
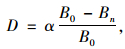
|
(2) |
式中α为修正系数,α=3.317。
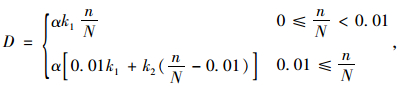
|
(3) |
式中k1,k2与钢筋最大初始应力σmax有关,即第一次疲劳加载时疲劳上限作用下钢筋的应力值,并且分别为疲劳损伤累积曲线第1、第2阶段的损伤累积速率,由式(4)确定:
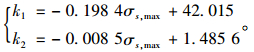
|
(4) |
本研究对200万次疲劳荷载作用下加固梁的累积损伤值D进行回归分析,式(5)为40%预应力水平下的回归公式,式(6)为60%预应力水平下的回归公式,其中N′为200万次。
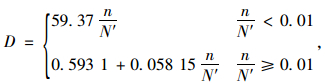
|
(5) |

|
(6) |
因试件CFRP板的预应力程度不同,试件FPB1-40和FPB2-40的钢筋应力高于试件FPB1-60的钢筋应力,因此根据式(3)计算的到的损伤累积函数不同,分别由式3(40)和式3(60)表示。图 11绘制了试件累积损伤值D的试验数据和各拟合公式,从图中可以看出疲劳损伤累积的第1阶段和第2阶段线性特征明显。
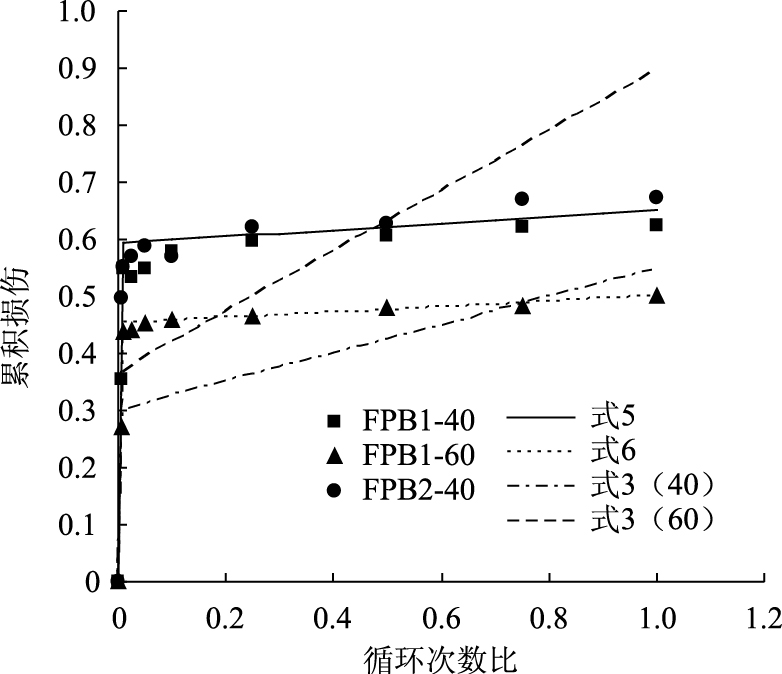
|
| 图 11 试件损伤累积数据及拟合公式 Fig. 11 Damage accumulation data and fitting formula of specimen |
| |
式(5)和式(6)的拟合情况良好而式3(40)和式3(60)与试验数据存在明显差别:第1阶段完成时,计算值较试验值的累积损伤偏小,即k1值偏小;第2阶段计算值较试验值的累积速率偏大,即k2偏大,说明有黏结预应力CFRP板加固法可以减小钢筋混凝土梁的疲劳损伤累积速率。对比图 11中式(5)和式(6)可以看出,预应力水平提高后,试件的疲劳损伤累积明显降低,疲劳损伤累积曲线的第2阶段斜率更小,即疲劳损伤累积速率更低,说明预应力水平对疲劳损伤累积值和第2阶段的疲劳损伤累积速率有着密切关系。
文献[15]采取钢筋最大初始应力σmax作为变量计算累积损伤前两阶段的斜率,本研究考虑到试件的CFRP板预应力水平和疲劳上限值的不同均会造成钢筋最大初始应力σmax不同,采用上述的计算方式是合理的,并对累积损伤前两个阶段的斜率进行计算,得到有黏结预应力CFRP板加固混凝土梁疲劳损伤累积计算公式,如式(7)所示。其第1阶段和第2阶段的曲线斜率均为常数并与钢筋最大初始应力有关,其中k1, k2的值由式(8)确定。
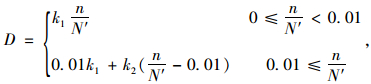
|
(7) |
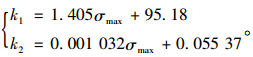
|
(8) |
文献[14]根据试验得出梁的剩余疲劳刚度为初始刚度的69.857%时,钢筋混凝土梁将发生疲劳破坏,并基于Miner理论通过第2阶段的损伤累积速率计算试件的疲劳寿命,在D=1时试件发生疲劳破坏。文献[18]提出对于FRP加固混凝土梁,修正Miner理论估算得到的疲劳寿命偏保守且较其他理论更为精确,采用D=a=1.278计算试件疲劳寿命,即D=1.278时试件疲劳破坏。本研究采取上述两种方法估算试件的疲劳寿命,得到的试件疲劳寿命如表 5所示。
| 试件类型 | Miner理论/万次 | 修正Miner理论/万次 |
| 40%预应力水平 | 1 399 | 2 355 |
| 60%预应力水平 | 2 288 | 3 450 |
由表 5中的数据可以看出,不论是Miner理论还是修正Miner理论,所有试件的疲劳寿命均远大于试验次数200万次,这说明有黏结预应力CFRP板加固混凝土梁的疲劳损伤累积第1阶段小于疲劳寿命的1%,这与钢筋混凝土梁的疲劳累积模型存在明显差别。
对比不同预应力水平试件的疲劳寿命可以看出,预应力水平提高后,试件的疲劳寿命有着明显提高,说明提高CFRP板预应力水平降低了疲劳损伤累积,从而延长试件疲劳寿命。因试件未因疲劳破坏,且有黏结预应力CFRP板加固混凝土梁的疲劳损伤累积相关研究资料不足,本研究得出的公式仍需更多试验数据验证。例如开展对有黏结预应力CFRP板加固混凝土梁在200万次疲劳荷载之后的损伤累积规律进行研究,能够获得第3阶段的有黏结预应力CFRP板加固梁疲劳损伤累积发展规律,对于完善疲劳累积损伤公式及构件疲劳寿命计算均具有重要意义。
4 结论(1) 在疲劳试验过程中,两套锚具均安全可靠,未出现滑移,CFRP的预应力水平提高至60%。分别采用MJ-1,MJ-2锚固的试件FPB1-40,FPB2-40在截面应变、跨中挠度和疲劳寿命方面均无明显差别。
(2) 有黏结预应力CFRP加固梁的疲劳性能优于钢筋混凝土梁的疲劳性能,试件钢筋和梁顶混凝土的应变降低,试件疲劳性能得到改善、疲劳寿命明显延长,但应当注意试件弯剪区胶层-混凝土黏结的损伤累积,在加载过极限荷载90%后,此处产生的剥离裂缝致使加固梁提前破坏。
(3) 提出的有黏结预应力CFRP板加固混凝土构件疲劳损伤累积计算公式能够通过疲劳损伤累积规律反算预应力构件的剩余疲劳寿命。有黏结预应力CFRP加固混凝土梁疲劳损伤累积的第1阶段和第2阶段的曲线斜率均为常数并与钢筋最大初始应力有关;疲劳寿命计算表明提高CFRP板预应力水平能够降低疲劳损伤累积,延长加固构件疲劳寿命。
(4) 有黏结预应力CFRP板加固混凝土梁的疲劳与钢筋混凝土梁的疲劳损伤累积模型存在明显不同,疲劳损伤第1阶段历时更短、第2阶段的损伤累积速率更低且试件的疲劳寿命更长。为获得第3阶段的有黏结预应力CFRP板加固梁疲劳损伤累积发展规律、计算疲劳寿命,应当开展对有黏结预应力CFRP板加固混凝土梁在200万次疲劳荷载之后的损伤累积研究。
| [1] |
FRANCA P, COSTA A, APPLETON J. Prestressed CFRP Laminates for Flexural Strengthening of Reinforced Concrete Beams[J]. Structural Concrete, 2007, 8(4): 175-185. |
| [2] |
YU P Y, SILVA P, NANNI A. Flexural Performance of RC Beams Strengthened with Prestressed CFRP Sheets[C]//International SAMPE Symposium and Exhibition. Long Beach, United States: SAMPE, 2004.
|
| [3] |
WANG B, PENG H, ZHANG J R. Behavior of Pre-cracked Reinforced Concrete Beam Strengthened with Prestressed CFRP Plate[J]. Applied Mechanics and Materials, 2013, 1397-1403. |
| [4] |
ZHOU R, ZHANG M Z, ZONG Z H. Experimental Study on Flexural Behavior of Damaged RC Beams Strengthened with Prestressed CFRP Plate[J]. Advanced Materials Research, 2011, 2263-2270. |
| [5] |
郭蓉, 吴二朋, 张宝虎, 等. 预应力碳纤维板加固钢筋混凝土梁试验研究[J]. 河北工业大学学报, 2016, 45(5): 106-111. GUO Rong, WU Er-peng, ZHANG Bao-hu, et al. Experimental Study on Fiexura Behavior of Reinforced Concrete Strengthened with Carbon Fiber Plates[J]. Journal of Hebei University of Technology, 2016, 45(5): 106-111. |
| [6] |
赵少伟, 欧高龙, 李春明, 等. 预应力碳纤维板加固钢筋混凝土梁的张拉锚具研究[J]. 山东科技大学学报:自然科学版, 2015, 34(5): 27-31. ZHAO Shao-wei, OU Gao-long, LI Chun-ming, et al. Tension Anchorage of Reinforced Concrete Beams Strengthened with Prestressed CFRP Plates[J]. Journal of Shandong University of Science and Technology:Natural Science Edition, 2015, 34(5): 27-31. |
| [7] |
林于东, 宗周红, 张美珍, 等. 预应力CFRP板加固RC和PPC梁抗弯性能试验[J]. 中国公路学报, 2013, 26(4): 109-118. LIN Yu-dong, ZONG Zhou-hong, ZHANG Mei-zhen, et al. Test on Flexural Performance of RC & PPC Girders Strengthened with Prestressed CFRP Plates[J]. China Journal of Highway and Transport, 2013, 26(4): 109-118. |
| [8] |
尚守平, 张宝静, 吕新飞. 预应力碳纤维板加固梁桥长期徐变性能的试验研究[J]. 公路交通科技, 2015, 32(5): 68-74. SHANG Shou-ping, ZHANG Bao-jing, LÜ Xin-fei. Experimental Study on Long-term Creep Behavior of Beam Bridge Strengthened with Prestressed CFRP Plate[J]. Journal of Highway and Transportation Research and Development, 2015, 32(5): 68-74. |
| [9] |
GHAFOORI E, MOTAVALLI M, BOTSIS J, et al. Fatigue Strengthening of Damaged Metallic Beams Using Prestressed Unbonded and Bonded CFRP Plates[J]. International Journal of Fatigue, 2012, 44(2): 303-315. |
| [10] |
XIE J H, HUANG P Y, GUO Y C. Fatigue Behavior of Reinforced Concrete Beams Strengthened with Prestressed Fiber Reinforced Polymer[J]. Construction and Building Materials, 2012, 27: 149-157. |
| [11] |
彭晖, 尚守平, 张建仁, 等. 预应力碳纤维板加固受弯构件的疲劳性能研究[J]. 土木工程学报, 2009, 42(8): 42-49. PENG Hui, SHANG Shou-ping, ZHANG Jian-ren, et al. Fatigue Behavior of Reinforced Concrete Beams Strengthened Wit Hprestressed Carbon Fiber Reinforced Polymer Plates[J]. China Civil Engineering Journal, 2009, 42(8): 42-49. |
| [12] |
LU Y Y, HU L, LI S, et al. Experimental Study and Analysis on Fatigue Stiffness of RC Beams Strengthened with CFRP and Steel Plate[J]. Journal of Central South University, 2016, 23(3): 701-707. |
| [13] |
何初生, 王文炜, 杨威, 等. 预应力CFRP布加固钢筋混凝土梁疲劳性能试验研究[J]. 东南大学学报:自然科学版, 2011, 41(4): 841-847. HE Chu-sheng, WANG Wen-wei, YANG Wei, et al. Experimental Study on Fatigue Behavior of Reinforced Concrete Beams Strengthened by Prestressed CFRP Sheets[J]. Journal of Southeast University:Natural Science Edition, 2011, 41(4): 841-847. |
| [14] |
汤红卫, 李士彬, 朱慈勉. 基于刚度下降的混凝土梁疲劳累积损伤模型的研究[J]. 铁道学报, 2007, 29(3): 84-88. TANG Hong-wei, LI Shi-bin, ZHU Ci-mian. A Fatigue Cumulative Damage Model of RC Beam Based on Stiffness Degradation[J]. Journal of the China Railway Society, 2007, 29(3): 84-88. |
| [15] |
李可. 碳纤维加固钢筋混凝土梁疲劳性能研究[D]. 南京: 东南大学, 2015. LI Ke. Study on Fatigue Performance of RC Beams Strengthened with CFRP[D]. Nanjing: Southeast University, 2015. |
| [16] |
朱红兵, 赵耀, 李秀, 等. 疲劳荷载作用下钢筋混凝土梁的刚度退化规律及计算公式[J]. 土木建筑与环境工程, 2014, 36(2): 1-5, 13. ZHU Hong-bing, ZHAO Yao, LI Xiu, et al. Reinforced Concrete Beam's Stiffness Degeneration Regulation and Its Calculation Formula under the Action of Fatigue Load[J]. Journal of Civil, Architectural & Environmental Engineering, 2014, 36(2): 1-5, 13. |
| [17] |
GB/T 50152-2012, 混凝土结构试验方法标准[S]. GB/T 50152-2012, Standard for Test Method of Concrete Structures[S].
|
| [18] |
陈绪军, 戴木香, 朱晓娥. BFRP布加固钢筋混凝土梁的变幅疲劳寿命试验研究[J]. 公路交通科技, 2017, 34(2): 75-80. CHEN Xu-jun, DAI Mu-xiang, ZHU Xiao-e. Experimental Study on Variable Amplitude Fatigue Life of RC Beams Strengthened with BFRP[J]. Journal of Highway and Transportation Research and Development, 2017, 34(2): 75-80. |
 2018, Vol. 35
2018, Vol. 35