扩展功能
文章信息
- 张宝龙, 范文
- ZHANG Bao-long, FAN Wen
- 临空条件对边坡稳定性的影响
- Influence of Free Face Condition on Slope Stability
- 公路交通科技, 2018, 35(7): 35-41
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(7): 35-41
- 10.3969/j.issn.1002-0268.2018.07.006
-
文章历史
- 收稿日期: 2018-02-07
2. 内蒙古交通设计研究院有限责任公司, 内蒙古 呼和浩特 010010
2. Inner Mongolia Transport Design and Research Institute, Huhehot Inner Mongolia 010010, China
随着我国交通建设事业的迅速发展,与之相伴的各种形态的边坡大量涌现,在这些工程中,不同临空条件下边坡的合理设计形式及其稳定性一直是普遍关注的热点问题[1-8]。边坡的临空条件包括边坡的高度、坡度、断面几何形状等,主要取决于现场工程地质条件和边坡的设计形式。临空条件属于边坡的固有性质,其对边坡的稳定性有着至关重要的影响。
一般来说,随着坡度的增加,边坡坡面附近应力卸荷带范围扩大,坡脚应力逐渐集中,因此发生滑坡的概率也相应提高。张茂省等人研究发现小于30°时黄土边坡失稳的概率较低,坡度在30°~60°之间时,滑坡发生概率随坡度的增加而增加,在坡度大于60°以后,失稳概率会剧增[9];雷祥义对陕西228处典型黄土滑坡进行了统计,发现并得出坡度大于35°后斜坡失稳的概率剧增,与张茂省等人的结论基本类似[10]。相对于坡度,坡高对边坡的稳定性影响权重要稍小一些[11-12],坡高虽然没有改变斜坡内应力的分布状态,但其影响着斜坡内各处应力值的大小,随着坡高的增加,应力值呈线性增加。研究发现在延安宝塔区境内滑坡主要发生在20~120 m坡高范围,随坡高的增加斜坡稳定性逐渐减弱,大于100 m后失稳概率剧增[9]。就几种常见坡面形态而言,阶梯状边坡比一坡到顶的边坡稳定性会更好一些,开挖台阶能够较明显地减小边坡内部的塑性应变[13],且能够有效减小水流的侵蚀,只要在边坡下部支护措施得当,其稳定性会比其他坡型边坡好一些[14]。另外,凹、凸形边坡也是常见的边坡类型,相对于凹形边坡,直线形和凸形边坡在维持稳定性上具有一定局限性[15-16]:高广岩等人曾对高堆石坝的合理边坡形状进行了分析,指出高堆石坝的合理边坡形状为类似于上陡下缓的凹形函数曲面形状[17];徐晓惠等人分析了凹坡参数对稳定性的影响,发现在强度参数相同的情况下,凹形斜坡稳定性更好[18]。这些理论分析成果在野外也得到了很好的印证,薛强等人对延安宝塔区滑坡调查后就发现,研究区地质灾害主要发生在直线形与凸形斜坡上[19];就直线形边坡的凸形边坡而言,虽然其在破坏时的后缘拉张裂隙位置相当,但由于凸形边坡受约束的程度低于直线形边坡,所以其更容易发生失稳破坏[20]。
总的来看,已有研究成果对各种临空条件的边坡形式都有涉及,虽然多倾向于坡高、坡度对边坡稳定性的影响研究,但均可为本研究提供参考。然而,公路作为一种纵向延伸的线性工程,需穿越不同的地形、地貌单元,边坡设计选形所受的限制重重,这就赋予了公路边坡种类广、数量多的特征,数量之多以至于对于公路边坡我们并不能像矿山、水利工程一样对每个危险边坡进行专门性研究。但如果处理不当,边坡失稳破坏则可能带来中断交通,人员伤亡等一系列社会问题。所以这就需要对不同形式的公路边坡进行稳定性评价,来为公路边坡的设计奠定理论基础。
鉴于此,本研究结合自身研究经历,在充分调研的基础上,选取各种常见形式的公路边坡为研究对象,对其稳定性和可能的破坏模式进行研究,进而为公路边坡工程实践提供理论依据。
1 研究方案本研究主要就坡高、坡度,断面形状(即:直线形、阶梯形、凹形、凸形)对公路边坡稳定性的影响进行分析。计算参数来源于各边坡的实测参数,破坏形式借助有限元计算进行分析,稳定性系数主要基于极限平衡法进行计算。具体研究方案如表 1所示。
| 临空条件 | 变化范围 | 边坡结构 | 研究方法 |
| 坡高/m | 5~50 | 均质、土- 岩二元结构 | 有限元法、 极限平衡法 |
| 坡度/(°) | 5~90 | 均质、土-岩 二元结构 | 有限元法、 极限平衡法 |
| 断面形状 | 阶梯形 | 均质 | 有限元法、 极限平衡法 |
| 直线形 | |||
| 凹形 | |||
| 凸形 |
2 不同临空条件边坡的稳定性分析 2.1 坡高对边坡稳定性影响
(1) 均质土坡
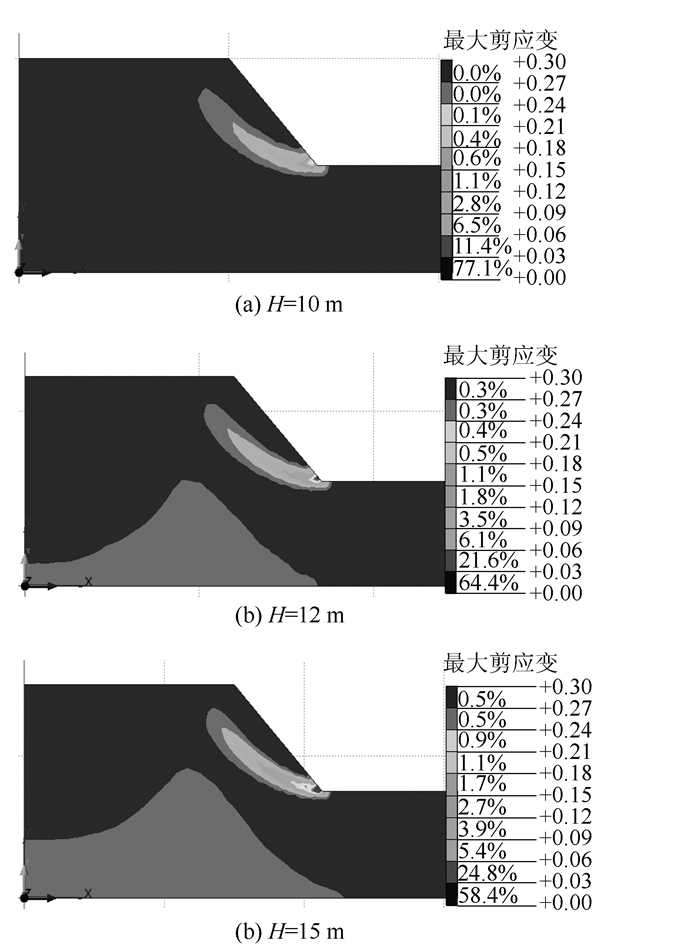
图 1所示为3个坡度50°的均质土坡在不同坡高条件下边坡内部最大剪应变分布情况。可以看出,随着坡高的增加,坡脚处剪应力越来越集中,最大剪应变数值不断增大,最大剪应变分布范围也在逐渐扩大。从剪应变发展趋势来看,边坡在破坏时,坡体内将形成圆弧形滑动面,并沿坡脚剪出发生破坏。
|
| 图 1 不同坡高条件下坡体内最大剪应变分布图 Fig. 1 Max shear strain distribution in slopes with different slope heights |
| |
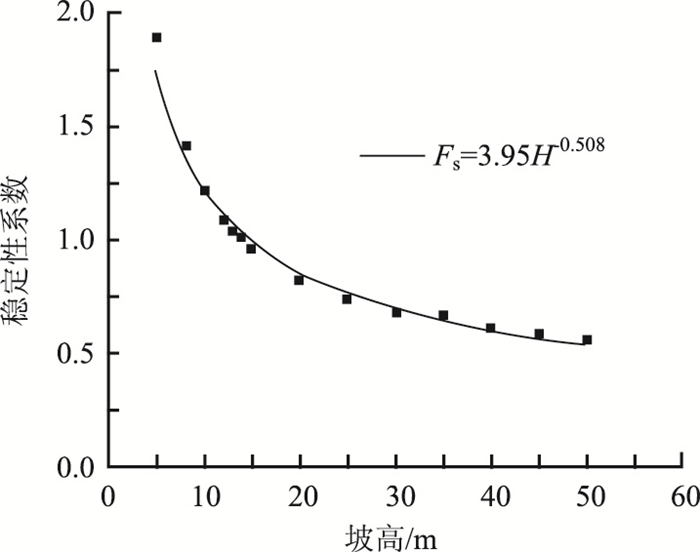
根据岩土体强度测试结果,确定边坡土体黏聚力C为20 kPa,内摩擦角φ为20°。固定其他因素,只考虑坡高对边坡稳定系数的影响,发现随着坡高增大,稳定系数在不断减小(图 2),且边坡坡高与稳定系数之间呈现出较好的幂函数关系,可表示为Fs=3.95H-5.08。另外还可看出,坡高小于20 m时,坡高对于稳定性系数来说属于敏感因素,而当坡高大于20 m后稳定性系数变化趋缓。
|
| 图 2 边坡稳定性系数随坡高变化曲线 Fig. 2 Curve of Fs vs. H |
| |
(2) 土-岩二元结构边坡
针对实际工程中某土-岩二元结构边坡,同样就坡高对其稳定性影响展开研究。边坡坡度β1=30°,覆盖层黏聚力C1=40 kPa,内摩擦角φ1=20°;接触面强度参数为黏聚力C2=10 kPa,内摩擦角φ2=10°,接触面倾角β2=4°。图 3为坡高10 m时边坡内部剪应变分布情况。可以看出,此时接触面上剪应力相对集中,最大剪应变区沿着接触面分布。边坡在破坏时将在覆盖层内拉张产生圆弧形滑面,并沿接触面发生复合式滑动。

|
| 图 3 二元结构下坡体内最大剪应变分布图 Fig. 3 Max shear strain distribution in a dual structure slope |
| |
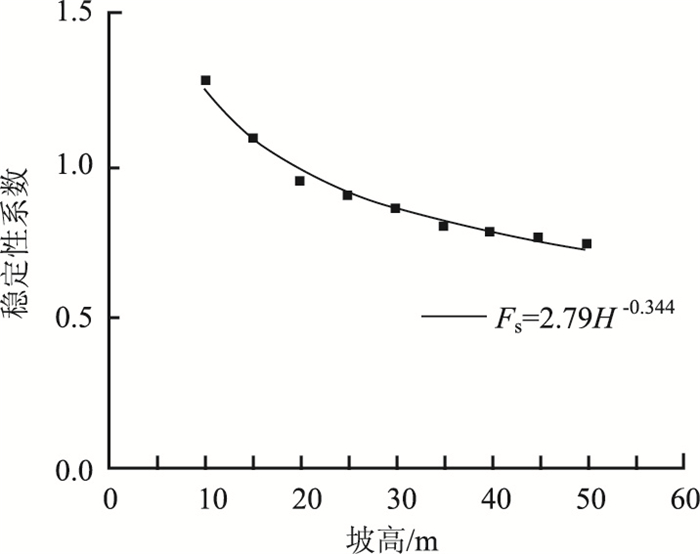
分别计算坡高为10~50 m时此边坡的稳定性。图 4给出了不同边坡覆盖层厚度时边坡的稳定系数曲线。可以看出,土-岩二元结构边坡的稳定系数与覆盖层厚度同样呈幂函数关系,其大小随边坡坡高的增大而减小,但结合图 3可以断定此时边坡的稳定性将主要受接触面的性质所控制,此时结构面的倾角、强度参数对边坡稳定性起着至关重要的作用。
|
| 图 4 二元结构下边坡稳定性系数随坡高变化曲线 Fig. 4 Curve of Fs vs. H in a dual structure slope |
| |
2.2 坡度对边坡稳定性影响
一般而言,坡度越大边坡的稳定性越差。一方面,随着边坡变陡,坡面附近张力带范围和深度随之扩大和增加,成坡过程中,上部土体向临空面运动的趋势将变得更加明显;另一方面边坡坡度越陡,边坡中的最大应力越靠近坡面,坡脚剪应力水平也随之增高。
(1) 均质土坡
图 5为坡高20 m时,坡度从30°增加到40°过程中,边坡内最大剪应变分布情况。总的来看,最大剪应变随坡度的增加而增加。另外,坡度在30°~35°区间时,最大剪应变区变化并不算大;而当坡度在35°~40°坡度区间变化时,最大剪应变数值快速增加,且最大剪应变区贯通,表明此阶段坡体内剪应力存在一个快速增加过程。如果坡度继续增加,将在坡体内沿最大剪应变带形成圆弧形滑面,从而发生失稳破坏。

|
| 图 5 不同坡度条件下坡体内最大剪应变分布图 Fig. 5 Max shear strain distribution of slopes with different slope angles |
| |
固定其他影响因素,只考虑坡度β对边坡稳定系数的影响,边坡土体计算参数同样为黏聚力C=20 kPa,内摩擦角φ=20°。计算结果如图 6所示,可以看出,边坡坡度与稳定系数同样呈幂函数关系,随着坡度增大,稳定系数在不断减小,尤其是当坡度小于40°时,稳定系数对坡度的变化十分敏感;当坡度大于40°之后曲线逐渐变缓,两者之间的关系式可表示为Fs=15.28H-0.724 7。

|
| 图 6 边坡稳定性系数随坡度变化曲线 Fig. 6 Curve of Fs vs.β |
| |
(2) 土-岩二元结构边坡
针对实际工程中另一土-岩二元结构边坡,就坡度对其稳定性的影响进行研究。覆盖层黏聚力C1=22 kPa,内摩擦角φ1=24°;接触面强度参数为C2=11 kPa,φ2=12°,接触面倾角β2=10°。这种情况下坡体内剪应变分布与图 3中类似,最大剪应变区沿着接触面分布,边坡的稳定性也主要被软弱接触面所控制。图 7为不同坡度时边坡稳定性系数变化曲线,边坡的稳定系数同样与坡度呈幂函数关系,随坡度的增加而减小。

|
| 图 7 二元结构下边坡稳定性系数随坡度变化曲线 Fig. 7 Curve of Fs vs. β in a dual structure slope |
| |
2.3 断面几何形状对边坡稳定性的影响
经过人工开挖的公路边坡,其断面形状多呈直线形、阶梯形,同时也常见一些凹、凸形边坡,下面就不同断面形式边坡的稳定性进行分析。
(1) 阶梯形边坡稳定性对比分析
为了研究阶梯形边坡的稳定性,在常见坡形的基础上,建立3种计算模型,各模型边坡形态参数及稳定性计算参数如表 2所示。
| 模型 | 坡高/m | 综合坡度/ (°) | 台阶数 | 台阶垂直 间距/m | 台阶宽度/ m | 各级坡度/ (°) | 计算参数 | ||||
| 弹性模量 E/MPa | 泊松比ν | 重度/ (kN·m-3) | 黏聚力 C/kPa | 内摩擦角 φ/(°) | |||||||
| 模型1 模型2 模型3 | 30 30 30 | 53.4 53.4 53.4 | 1 2 3 | 30 15 10 | — 2.5 5 | — 60 60 | 10 | 0.3 | 19 | 30 | 28 |
通过计算,各坡形坡体内最大剪应变分布如图 8所示。可以发现,在保证综合坡率一定的情况下,由于阶梯形边坡局部具备更高的坡率,所以其并不能有效减小边坡内剪应变的数值及分布区大小,而且随台阶级数的增加,最大剪应变分布区范围反而更大。

|
| 图 8 阶梯形边坡剪应变分布图 Fig. 8 Max shear strain distribution in step-shaped slope |
| |
上述3种边坡稳定系数如表 3所示。对比可知,在其他条件相同的情况下,采用阶梯形坡面,可以提高边坡的稳定系数,这是因为阶梯形边坡从坡形上相当于开挖上部坡体减少了边坡的下滑推力,同时反压坡脚提高了抗滑力;另外还发现,在综合坡率一定的情况下,平台的尺寸大小对边坡整体稳定系数影响甚小,可以忽略。
(2) 凹、凸形边坡稳定性对比分析
在实际工程中,同样存在不同类型的原始坡形,以凹、凸坡形典型均质土边坡为对象,进行数值模拟分析。分别建立边坡坡高为20 m,综合坡度60°的微凸、微凹形边坡计算模型。边坡的稳定性计算参数与表 1中相同。
对模型进行静力分析发现,强度参数相同情况下,凹、凸坡形边坡的最大剪应变分布区形状显著差异(如图 9所示),微凸形边坡由于上部土体自重较大,滑动面上剪应力数值高于微凹形边坡,最大剪应变数值及分布区自然大于微凹形边坡。

|
| 图 9 凹、凸边坡剪应变分布图 Fig. 9 Max shear strain distribution in concave and convex shaped slopes |
| |
应变区的分布状态与边坡的稳定性密切相关,运用有限元强度折减法对直线形、凹、凸形边坡稳定性进行计算,得到其稳定性系数如表 4所示。可以看出,微凹形边坡由于下部土体起到一定支撑作用,应力集中程度明显减弱,其稳定性明显优于微凸形边坡。
3 讨论
(1) 边坡稳定性对坡高、坡度的敏感性分析
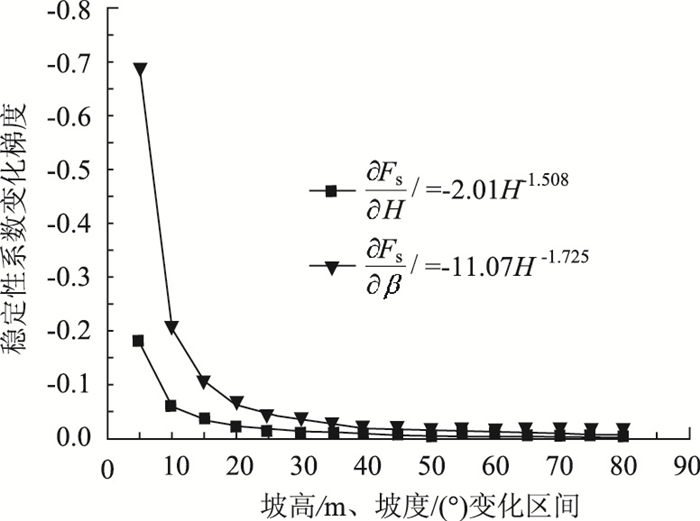
边坡的坡高、坡度是工程中最直观的设计因素。通过本研究发现,在计算参数相同的情况下,边坡的稳定性系数随坡高、坡度均呈幂函数形式减小,那么稳定性系数对坡高、坡度两个因素哪一个更敏感?图 10为稳定性系数随坡高(5~80 m)、坡度(5°~80°)两个因素的变化梯度。可以明显看出,稳定性系数对坡度的敏感性明显要更高一些。
|
| 图 10 稳定性系数随坡高、坡度的变化梯度 Fig. 10 Gradient of Fs varying with H and β |
| |
(2) 坡形的选择
针对不同断面形式的边坡,通过本研究可知,阶梯形坡面更有利于坡体稳定。同时其还具备对坡面水流缓冲消能,截留坡面剥落及少量崩塌体等优点。但是在工程中,综合坡度一定的情况下,阶梯形边坡局部具有更高的坡率,尤其是对于大平台阶梯形边坡,各级边坡自身的稳定性不容忽视。另外,在实际工程中建议合理利用凹形边坡,而对于凸形边坡应该慎重利用。
4 结论结合常见的公路边坡类型,论文从坡高、坡度、坡面几何形状几个方面,对临空条件对边坡稳定性的影响进行了研究,得到结论如下:
(1) 随着坡高、坡度的增加,坡脚处剪应变不断增加,稳定性系数以幂函数形式减小。坡度对坡体应力、应变分布以及稳定性的影响更大一些。对于土-岩二元结构,接触面外倾时,其稳定性主要受接触面性质控制,稳定性系数同样随坡高、坡度呈以幂函数形式减小。
(2) 综合坡度一定的情况下,阶梯形边坡更有利于边坡稳定,但台阶级数对边坡稳定性的影响并不明显。实际工程中对于大平台阶梯形边坡,各级边坡自身的稳定性不容忽视。
(3) 凹形边坡下部土体起到支撑作用,受力状态要好于凸形边坡,剪应变集中程度明显减缓,其稳定性明显优于微凸形边坡。在实际工程中,可对此类有利于稳定的原始地貌进行合理利用。
(4) 本次研究是在二维条件下展开的,在进一步研究中拟建立边坡的三维数值模型,对不同临空条件下边坡内部应力应变分布、滑坡推力以及稳定性系数进行研究,更深入剖析临空条件对边坡稳定性的影响机制。
| [1] |
张常亮, 李萍, 陶福平, 等. 黄土强度指标对边坡稳定性的影响研究[J]. 公路交通科技, 2011, 28(3): 20-24. ZHANG Chang-liang, LI Ping, TAO Fu-ping, et al. Research of Effect of Strength Index on Loess Slope Stability[J]. Journal of Highway and Transportation Research and Development, 2011, 28(3): 20-24. |
| [2] |
CALA M. Convex and Concave Slope Stability Analyses with Numerical Methods[J]. Archives of Mining Sciences, 2007, 52(1): 75-89. |
| [3] |
FARZANEH O, ASKARI F, GANJIAN N. Three-dimensional Stability Analysis of Convex Slopes in Plan View[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2008, 134(8): 1192-1200. |
| [4] |
BAKER R, LESHCHINSKY D. Stability Analysis of Conical Heaps[J]. Soils & Foundations, 2008, 27(4): 99-110. |
| [5] |
李萍, 王秉纲, 李同录. 自然类比法在黄土路堑边坡设计中的应用研究[J]. 公路交通科技, 2009, 26(2): 1-5. LI Ping, WANG Bing-gang, LI Tong-lu. Study on Analogism Used in Highway Cutting Loess Slope Design[J]. Journal of Highway and Transportation Research and Development, 2009, 26(2): 1-5. |
| [6] |
赵衡, 宋二祥. 圆形凸坡的稳定性分析[J]. 岩土工程学报, 2011, 33(5): 730-737. ZHAO Heng, SONG Er-xiang. Stability Analysis of Circular Convex Slopes[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(5): 730-737. |
| [7] |
卢坤林, 朱大勇. 坡面形态对边坡稳定性影响的理论与试验研究[J]. 岩石力学与工程学报, 2014, 33(1): 35-42. LU Kun-lin, ZHU Da-yong. Theoretical and Experimental Study of Effect of Slope Topography on Its Stability[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(1): 35-42. |
| [8] |
张宝龙, 范文. 土-岩混合边坡的破坏模式研究[J]. 公路交通科技, 2018, 35(4): 33-39. ZHANG Bao-long, FAN Wen. Study on Failure Mode of Soil-rock Composite Slope[J]. Journal of Highway and Transportation Research and Development, 2018, 35(4): 33-39. |
| [9] |
张茂省, 孙传尧, 校培喜, 等. 延安市宝塔区地质灾害详细调查示范[J]. 西北地质, 2007, 40(2): 29-55. ZHANG Mao-sheng, SUN Chuan-yao, XIAO Pei-xi, et al. A Demonstration Project for Detailed Geo-hazard Survey in the Baota District, Yan'an[J]. Northwestern Geology, 2007, 40(2): 29-55. |
| [10] |
雷祥义. 黄土地质灾害的形成机理与防治对策[M]. 北京: 北京大学出版社, 2014. LEI Xiang-yi. Cause of Formation, Prevention and Cure of Geological Disasters of Loess[M]. Beijing: Peking University Press, 2014. |
| [11] |
赵建军, 贺宇航, 黄润秋, 等. 基于因子分析法的边坡稳定性评价指标权重[J]. 西南交通大学学报, 2015, 50(2): 325-330. ZHAO Jian-jun, HE Yu-hang, HUANG Run-qiu, et al. Weights of Slope Stability Evaluation Indexes Based on Factor Analysis Method[J]. Journal of Southwest Jiaotong University, 2015, 50(2): 325-330. |
| [12] |
张俊义, 杨强, 杨秀元, 等. 陇东地区黄土滑坡稳定性分析[J]. 中国水土保持, 2012(7): 48-51. ZHANG Jun-yi, YANG Qiang, YANG Xiu-yuan, et al. Stability of Loess Landslides in Eastern Gansu Province[J]. Soil and Water Conservation in China, 2012(7): 48-51. |
| [13] |
张永双, 王红才. 砂黄土高边坡稳定性的数值模拟研究[J]. 地质力学学报, 2004, 10(4): 357-365. ZHANG Yong-shuang, WANG Hong-cai. Numerical Simulation of the Stability of High Sand Loess Slopes[J]. Journal of Geomechanics, 2004, 10(4): 357-365. |
| [14] |
胡晋川, 谢永利, 王文生. 黄土公路阶梯状高路堑边坡稳定性研究[J]. 岩石力学与工程学报, 2010, 29(增1): 3093-3100. HU Jin-chuan, XIE Yong-li, WANG Wen-sheng. Study of Stability Characteristics of Multi-stair High Cut Slope in Loess Highway[J]. Chinese Journal of Rock Mechanics & Engineering, 2010, 29(S1): 3093-3100. |
| [15] |
ASKARI F, TOTONCHI A, FARZANEH O. 3D Stability Analysis of Convex Slopes in Plan View Using Lower Bound Linear Finite Element[J]. International Journal of Civil Engineering, 2012, 36(C2): 181-194. |
| [16] |
FARZANEH O, ASKARI F, GANJIAN N. Three-dimensional Stability Analysis of Convex Slopes in Plan View[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2008, 134(8): 1192-1200. |
| [17] |
高广岩, 张天宝. 高堆石坝合理边坡形状的静力有限元分析[J]. 四川大学学报:工程科学版, 2002, 34(1): 28-31. GAO Guang-yan, ZHANG Tian-bao. Static Finite Element Analysis of Reasonable Slope Shape of High Rockfill Dams[J]. Journal of Sichuan University:Engineering Science Edition, 2002, 34(1): 28-31. |
| [18] |
徐晓惠, 姚再兴. 凹边坡参数对边坡稳定性的影响[J]. 力学季刊, 2015, 36(1): 105-114. XU Xiao-hui, YAO Zai-xing. Effects of Concave Slope Parameters on Slope Stability[J]. Chinese Quarterly of Mechanics, 2015, 36(1): 105-114. |
| [19] |
薛强, 张茂省, 李林. 基于斜坡单元与信息量法结合的宝塔区黄土滑坡易发性评价[J]. 地质通报, 2015, 34(11): 2108-2115. XUE Qiang, ZHANG Mao-sheng, LI Lin. Loess Landslide Susceptibility Evaluation Based on Slope Unit and Information Value Method in Baota District, Yan'an[J]. Geological Bulletin of China, 2015, 34(11): 2108-2115. |
| [20] |
卢坤林, 朱大勇, 杨扬. 边坡失稳过程模型试验研究[J]. 岩土力学, 2012, 33(3): 778-782. LU Kun-lin, ZHU Da-yong, YANG Yang. Model Test Study of Slope Failure Progress[J]. Rock & Soil Mechanics, 2012, 33(3): 778-782. |
 2018, Vol. 35
2018, Vol. 35
