扩展功能
文章信息
- 郑燕, 黄承锋, 张政
- ZHENG Yan, HUANG Cheng-feng, ZHANG Zheng
- 长江流域汽车整车运输路径选择研究
- Study on Path Selection of Finished Automobile Transport in Yangtze River Valley
- 公路交通科技, 2018, 35(6): 145-158
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(6): 145-158
- 10.3969/j.issn.1002-0268.2018.06.020
-
文章历史
- 收稿日期: 2017-02-22
近十年来我国汽车产销量不断增加,汽车行业发展迅速。随着小汽车销量的逐年增加及国家对公路运输超长、超限的治理等,汽车运输市场正面临着严峻的挑战,最近几年兴起的长江内河滚装运输为长江沿线的小汽车运输提供了保障。整车运输的及时、经济与其运输方式、运输路径的选择息息相关,通过公水联合运输的方式可以极大地降低整车运输的时间、费用及碳排放。目前,很多运输企业在运输方式及路径的选择方面大多凭借以往经验,而没有科学、有效的决策方法。
国内外学者对多式联运运输方式及路径选择方面已做了一系列研究,取得一定的成果。张雄[1]基于最小化运输费用和时间,建立多目标线性规划模型,求解出相应的最优路径。杨文东等[2]在路径优化选择时以时间为约束,建立了时间目标下的多式联运模型,运用蚁群算法进行求解。Ziliaskopoulos[3]以时间最短为目标进行了多式联运路径选择研究,提出了时间目标下多式联运路径选择模型。Chang Tsung-sheng[4]研究集装箱综合运输方式的运输,以时间、费用最小为目标,求解处于特定约束下的路径选择模式。
多式联运路径选择方面的研究很多是基于单目标比如时间、费用等其中的一个,亦或将多目标最终转换成单目标进行求解;目前将多式联运和低碳结合的文献较少,一些学者在运输过程中考虑二氧化碳的排放,但多存在于理论研究,在运输决策中考虑碳排放量的路径优化模型更是少之又少。在温室效应、雾霾越来越严重的今天,公水联运作为一种环境友好型的运输方式,可以极大地降低碳排放。
应对气候变化已成为全球共同面临的环境挑战,减少CO2排放,推行低碳经济已成为世界各国的共识[5]。建模时考虑碳排放量,可以帮助企业寻找到碳排放量低的运输方式组合及线路,发展低碳交通,保护空气及长江水资源,响应国家低碳、可持续发展政策,这也是每个企业家应该有的责任意识。应用运筹学理论建立多目标函数模型显得非常重要。
因此本研究从长江中下游汽车整车运输路径选择的实际出发,以最小化运输费用、运输时间、碳排放为目标,引入道路拥挤度、模糊时间及碳排放因子,建立了多目标路径选择模型,并提出改进的遗传算法,求解实际问题时引入随机算例验证了算法的求解效果的优势性。
1 问题描述及参数 1.1 问题描述有一批汽车整车将要从生产地运送到消费地,生产地和消费地是已知且确定的,运输途中要经过若干个运输转换的中转节点,这些节点是由不同的城市组成,且相邻两任意节点间均有几种运输方式可供选择。不同的运输方式对应着不同的运输路径,同时运输时间、运输费用、碳排放量等都会有所不同。汽车整车可以根据运输费用的预算、交货期、国家规定的碳排放政策等选择在某个中转节点处转换运输方式。需要解决的问题是在考虑换装费用及换装时间的情况下,针对制造商对费用、时间、碳排放量的不同敏感程度找到从生产地到消费地的最优运输路径及运输方式的组合模式。
1.2 参数说明公水联运网络G=(V, E, P)。V=(v1, v2, …, vn)为节点城市的集合; 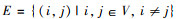
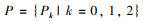
Q为运输过程中的货运量;dijkq为节点i, j之间采用第k中运输方式第q条路径的距离;cijkq为节点i, j之间采用第k中运输方式第q条路径单位距离单位货运量的费用;Z为不同运输方式之间进行转换时的换装费用;β为公路运输时的拥挤度;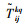
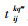
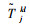
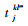
在汽车整车公水联运问题中,运输过程中运输时间和换装时间往往具有不确定性,很难用一具体的时间点来表示,但可以用某一时间范围来表示,因此文章引入模糊数的概念来表示两类时间的不确定性。
一般来讲,公水联运过程中有一个最可能的时间点即预期时间,但在实际运输中却不能保证每次都按期运输,因此可在预期时间点的基础上延伸出一个最短时间和一个最长时间,如此便能很好地用三角模糊数来表示运输时间和换装时间[6]。
假设节点i, j之间的运输时间为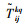
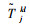
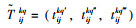
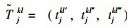
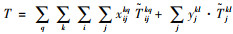
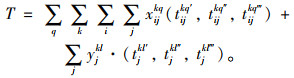
|
(1) |
为了便于后续的计算,文章将模糊数表示的时间进行转换,即将模糊规划问题转化为确定的数学规划问题。CooPer[7]提出当涉及到不确定性约束时,有时无法得到精确的结果,可保证模糊约束在一定条件下得到满足,即保证模糊约束成立的概率不小于某一个给定的置信水平α[8]。
假设x是决策变量,ξ是模糊向量,某一事件在置信水平αi(i=1, 2, …, n)上发生的可能性可表示为Pos{f(x, ξ)=fi*}≥αi, i=1, 2, …, n,其中f(x, ξ)为目标函数,fi*为目标函数的最可能取值,Pos{A}为事件A发生的可能性。相应地,公水联运过程中总运输时间可表示为
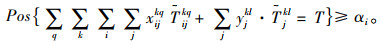
|
(2) |
鉴于一般追求运输时间的最小化,式(2)可转换为
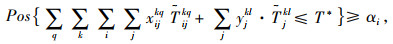
|
(3) |
即公水联运过程中总运输时间在置信水平αi上取到的最小值为T*[9],由于在置信水平αi下会有若干时间值满足式(3),因此:
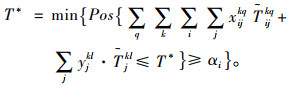
|
(4) |
在此即可以在式(4)的基础上进行确定性数学规划的转换,假设有三角模糊数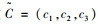
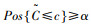
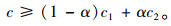
|
(5) |
由三角模糊数的四则运算规则[12-13]有,式(1)可表示为:
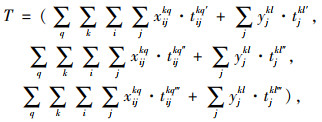
|
(6) |
相应地,式(6)可转换为:
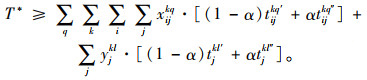
|
(7) |
不同运输方式采用运载工具的不同会导致碳排放量的差异,碳排放量包括运输过程中的碳排放以及换装过程中的碳排放,其中运输过程碳排放主要包括载有汽车整车的滚装车公路运输环节的碳排放以及滚装船运输的碳排放。文章将从燃料消耗、利用率等方面来计算。
(1) 假设陆运过程中的碳排放因子为γijkq,则定义运输过程中碳排放因子计算公式为:
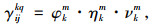
|
(8) |
式中,φkm为陆运过程中采用第k种运输方式,使用第m种燃料的每吨货物每公里的燃料消耗量;ηkm为对应燃料单位热值的含碳量;νkm为不同运输设备的碳氧化率。
(2) 滚装运输碳排放因子γijkq数据来源于文献[14]。
1.4 公水联运基本假设在我国基于滚装运输的汽车整车公水联运尚处于初步发展阶段,不同的运输方式依赖的运输工具不同,从起始地到目的地将会出现多条可行路径。为了避免出现理解上的差异,将对本研究设定以下条件:
(1) 汽车整车的公水联运是由汽车整车装载于滚装车的公路运输、滚装车依靠自有动力滚上滚下滚装船的装载卸载。
(2) 运载工具有滚装车、滚装船,运输方式有公路、水路,运输路径是由公路与水路无缝衔接组成的多条路径。
(3) 相邻两个城市节点之间只能选择一种运输方式,如水路的滚装运输,公路的高速、非高速运输。
(4) 各种运输方式的速度和单位费用在任意两个城市之间是相同的。
(5) 每辆滚装车装载同一型号的汽车整车,并且运往同一目的地,不可在运输途中进行分割重组。
(6) 载有汽车整车的滚装车在各个城市最多进行一次中转。
(7) 运载滚装车的滚装船可以装载其他类型的载货车辆。
(8) 基于每种运输方式有一条以上路径可供选择,分别以运输费用、运输时间、碳排放量为目标进行多目标路径选择研究。
1.5 模型建立综合考虑汽车整车公水联运路径选择过程中的主要影响因素,建立以运输总费用、运输总时间及运输总碳排放量为目标函数的汽车整车公水联运路径选择数学模型如下:
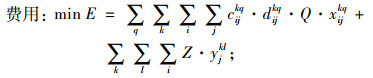
|
(9) |
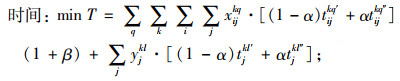
|
(10) |
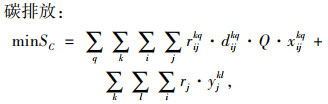
|
(11) |
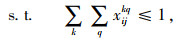
|
(12) |
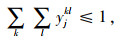
|
(13) |
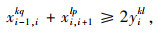
|
(14) |
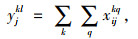
|
(15) |
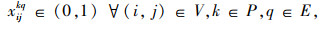
|
(16) |
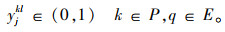
|
(17) |
式(9)表示汽车整车公水联运总费用,包括运输费用和中转时的换装费用,下同;式(10)表示汽车整车公水联运总时间;式(11)表示汽车整车公水联运总碳排放;式(12)表示若节点i, j之间存在路径,则只能采用其中一种运输方式的一条运输路径;式(13)表示在i节点处,若要进行运输方式的装换,则存在且只存在一种转换;式(14)表示运输方式的连续性,即节点i与之前一节点采用第k种运输方式第q条路径,与之后一节点采用第l种运输方式第p条路径,则其在节点i处必须要从第k种运输方式第q条路径转换成第l种运输方式第p条路径;式(15)表示在进行路径选择时每个节点至多被访问一次;式(16)、(17)表示决策变量是0-1变量。
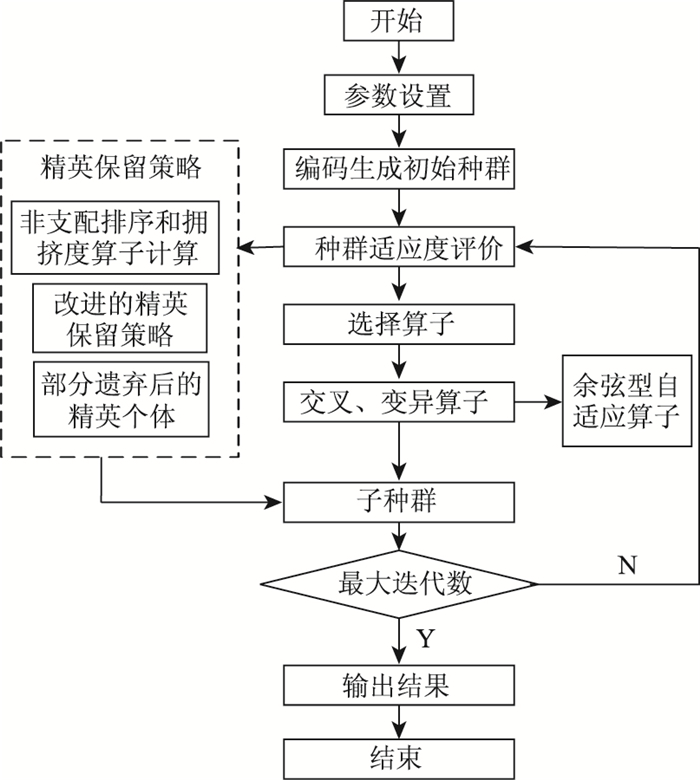
2 模型求解算法考虑到传统GA对初始种群选择的依赖性,及容易陷入早熟,设计了改进的遗传算法。采用随机方式生成初始种群,进化过程中对种群实行精英保留策略,并采取部分遗弃的方式避免局部最优,交叉变异过程采用改进型自适应算子,最后若干次迭代引入爬山操作,以提高算法的收敛速度和精度。
|
| 图 1 改进遗传算法流程图 Fig. 1 Flowchart of improved genetic algorithm |
| |
2.1 多目标的处理
通过对上述模型的分析,0-1规划模型的多目标间存在矛盾,很难科学地选择目标间的权重系数,加之量纲的不统一,直接转化为单目标模型进行求解并不科学[15],因此,鉴于公水联运多目标优化问题一般得不到唯一最优解,文章多目标模型求解结果将以一组具有同等优化级别的非劣解集[16]展示,以供不同需求环境下运用。
2.2 编码方式采用实数编码的方式。在遗传算法编码方式上,Holland[17]建议采用二进制编码,并得到了很大的推广,在一些问题上,Yang[18]在采用遗传算法进行优化计算时发现,用二进制编码时部分有精度不高的缺点,使用实数编码在一些问题上会有更好的性能[19]。
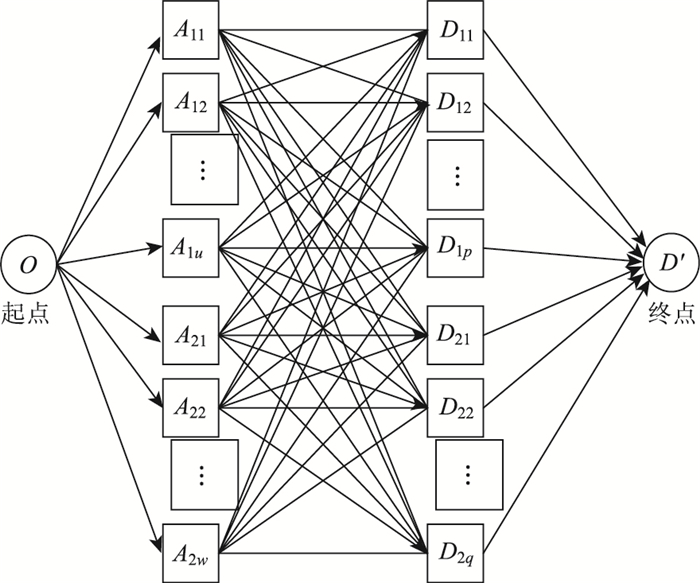
文章将运输网络中城市节点及运输线路进行一定的变换,采用改进的遗传算法进行求解[20-21]。除始发点O之外,将运输过程中涉及到的城市节点依据运输方式及运输线路划分为若干个小节点,假设从始发点O到终点D之间通过中间城市节点A,节点间均有两种运输方式,即公路运输和滚装船运输,始发点O与A之间针对两种运输方式分别有u条和w条运输路径可选,A与终点D之间针对两种运输方式分别有p条和q条运输路径可选,则进行如下划分:
节点A→(A11, A12, …, A1u; A21, A22, …, A2w),节点D→(D11, D12, …, D1p; D21, D22, …, D2q),同时创建虚拟终结点D′。示意图如图 2所示。
|
| 图 2 虚拟节点网络图 Fig. 2 Diagram of virtual nodes network |
| |
采用实数编码方式,如图所示的简例可令染色体X为二维向量,即X=(x1, x2),且x1∈[1, u+w],x2∈[u+w+1, u+w+p+q],x1, x2均为实数,任一向量X均代表采用不同运输方式的可行路线,根据实例中对城市的标号,可以对应出实际的运输路线。类似地,针对实例中存在s个中间节点城市,染色体X可相应地扩展为(s+1)维向量。
2.3 初始种群生成采用随机方法生成若干初始染色体构成初始种群P0,在Matlab软件环境下运用randint函数随机生成设定范围内的自然数,依据运输费用、时间及碳排放因子对可行路径进行选择计算,生成满足约束的路径集,最优解集将通过P0遗传进化得到。
2.4 适应度函数此处适应度函数采用目标函数,鉴于目标函数是求费用、时间或碳排放的最小值,在Matlab软件环境下将适应度函数设定为:fitness(i)=-f(x),如此,目标函数越小,染色体越优良。
2.5 选择算子算法求解的选择操作是在NSGA—Ⅱ的算法基础上进行的,选择共分为以下几部分。
(1) 采用随机遍历抽样法,提供了零偏差和最小个体扩展[22],设定n为需要选择的个体数目,以1/n为距离进行等距离选择个体,第一指针的位置在区间[0, 1/n]间均匀随机决定。
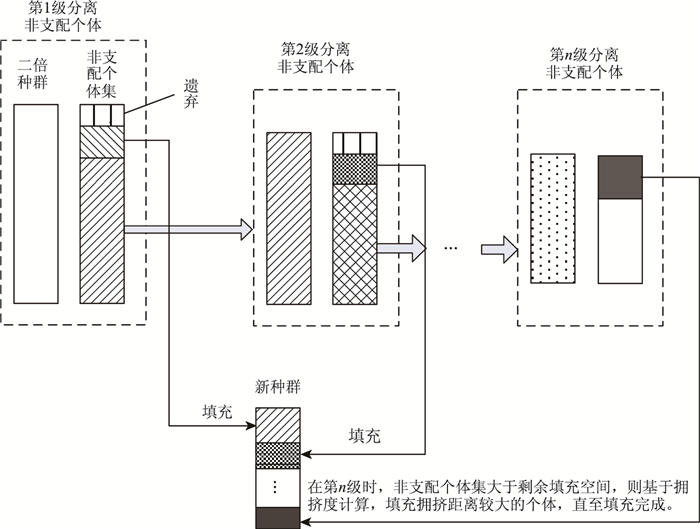
(2) 精英保留策略。①快速非支配排序和拥挤度算子计算[23]。每个个体保存两个量,支配个数ni和被支配个体集合Gi,分别代表解空间中可支配个体P的所有数量及被P支配的个体数量集,将群体中不被其他个体支配的个体定义为非支配个体,其Pareto排序定为1,将所有排序为1的个体组成第一级非支配个体,之后将第一级去除,类似地从中选择产生第二级非支配个体集,直到将所有个体进行排序[24]。在进行拥挤度算子计算时,鉴于涉及到3个目标函数的计算,个体的拥挤度取3个拥挤度算子的均值[25]。②改进的NSGA—Ⅱ精英保留策略。假设种群中绝大部分都在级别为1的层面,采用NSGA—Ⅱ中的选择策略很大程度上会导致非支配解精英数量很多,造成局部最优或是提前收敛[26]。为此,在快速非支配排序之后得到的第1级个体后,不将所有的Pareto解填充到下一代中,作适当的保留,在多级排序之后会有少部分精英缺失,但可以防止提前收敛,同时保证大部分精英得以保留[27-28],如图 3所示。
|
| 图 3 改进的精英保留策略示意图 Fig. 3 Schematic diagram of improved elite retention policy |
| |
2.6 交叉算子
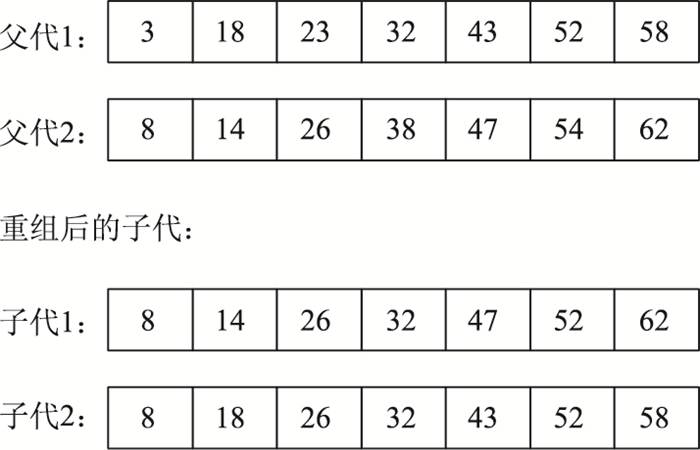
由于文章采用实数编码方式,交叉方式采用实数重组的离散重组方式,子代的变量按照等概率随机从父代中选取,示意图如图 4所示。
|
| 图 4 交叉操作 Fig. 4 Crossover |
| |
同时进行交叉自适应调整,若在种群中出现较多适应度接近平均适应度的个体,同时平均适应度与当代种群中的最大适应度接近,自适应交叉调整曲线会变得更陡峭,这些个体的交叉率也产生较大差异,导致大部分个体只能拥有较低的交叉率,使演化停滞不前。因此,在文献[29]的基础上采用余弦改进型自适应遗传算子,定义自适应交叉算子为: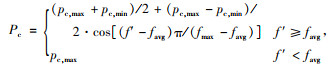
改进之后压低了适应度处于区间[(favg+fmax)/2, fmax]个体的交叉率,利于保留优良的种群模式[30]。
2.7 变异算子个体的适当变异可以保持种群多样性,防止陷入局部最优,但变异率不宜过大,本研究采用实值变异方式,同时加入自适应处理,定义自适应变异算子为: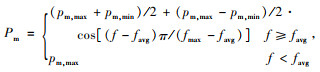
在迭代过程中引入爬山操作进行局部寻优,采用基因算子实现,在遗传迭代过程中设置参数λ,在最后λ次迭代时进行爬山操作,随机选择个体的基因并交换位置,通过判断交换后适应值的变化情况选择是否替代原个体,重复爬山操作直到迭代完成,利用爬山法进行局部寻优,可避免早熟,提高遗传算法的收敛速度和精度[31]。
3 算例分析 3.1 算例描述长江作为四大滚装运输市场中唯一的内河滚装运输通道,其沿线分布着众多的小汽车生产基地,鉴于本研究的多式联运是基于滚装车的公路运输与滚装船的水路运输,因此在其他开展滚装运输的区域具有借鉴意义,未开展滚装运输区域的汽车整车多采用陆路运输来实现。本研究以重庆到上海汽车整车公水联运路径选择为算例,选择有代表性的13个中转城市进行路径选择,城市节点序号编码表如表 1所示。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 重庆 | 宜昌 | 宜昌 | 宜昌 | 荆州 | 荆州 | 荆州 | 武汉 | 武汉 | 武汉 | 黄石 | 黄石 | 黄石 | 九江 | 九江 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 九江 | 安庆 | 安庆 | 安庆 | 铜陵 | 铜陵 | 铜陵 | 芜湖 | 芜湖 | 芜湖 | 马鞍山 | 马鞍山 | 马鞍山 | 南京 | 南京 |
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | |
| 南京 | 镇江 | 镇江 | 镇江 | 江阴 | 江阴 | 江阴 | 南通 | 南通 | 南通 | 上海 | 上海 | 上海 | 虚拟终点城市 | |
据实地调研,运输费用因子cijkq水运取为0.352元/(t·n mile),陆运高速取为0.35元/(t·km),非高速取为0.22元/(t·km),汽车整车公水联运货运量Q取为37.6 t。
陆运拥挤度β依据不同的城市取值见表 2。
| 序号 | 城市节点对 | 拥挤度 | 序号 | 城市节点对 | 拥挤度 | |||||
| 非高速 | 高速 | 滚装 | 非高速 | 高速 | 滚装 | |||||
| 1 | 重庆—宜昌 | 0.55 | 0.40 | 0 | 18 | 安庆—南京 | 0.53 | 0.53 | 0 | |
| 2 | 重庆—荆州 | 0.55 | 0.40 | 0 | 19 | 铜陵—芜湖 | 0.54 | 0.42 | 0 | |
| 3 | 宜昌—武汉 | 0.55 | 0.40 | 0 | 20 | 铜陵—马鞍山 | 0.54 | 0.42 | 0 | |
| 4 | 宜昌—黄石 | 0.55 | 0.40 | 0 | 21 | 铜陵—南京 | 0.53 | 0.53 | 0 | |
| 5 | 荆州—武汉 | 0.55 | 0.40 | 0 | 22 | 芜湖—镇江 | 0.53 | 0.53 | 0 | |
| 6 | 荆州—黄石 | 0.55 | 0.40 | 0 | 23 | 芜湖—江阴 | 0.53 | 0.53 | 0 | |
| 7 | 武汉—九江 | 0.45 | 0.30 | 0 | 24 | 芜湖—南通 | 0.53 | 0.53 | 0 | |
| 8 | 武汉—安庆 | 0.54 | 0.42 | 0 | 25 | 马鞍山—镇江 | 0.53 | 0.53 | 0 | |
| 9 | 武汉—铜陵 | 0.54 | 0.42 | 0 | 26 | 马鞍山—江阴 | 0.53 | 0.53 | 0 | |
| 10 | 黄石—九江 | 0.45 | 0.30 | 0 | 27 | 马鞍山—南通 | 0.53 | 0.53 | 0 | |
| 11 | 黄石—安庆 | 0.54 | 0.42 | 0 | 28 | 南京—镇江 | 0.53 | 0.53 | 0 | |
| 12 | 黄石—铜陵 | 0.54 | 0.42 | 0 | 29 | 南京—江阴 | 0.53 | 0.53 | 0 | |
| 13 | 九江—芜湖 | 0.54 | 0.42 | 0 | 30 | 南京—南通 | 0.53 | 0.53 | 0 | |
| 14 | 九江—马鞍山 | 0.54 | 0.42 | 0 | 31 | 镇江—上海 | 0.92 | 0.88 | 0 | |
| 15 | 九江—南京 | 0.53 | 0.53 | 0 | 32 | 江阴—上海 | 0.92 | 0.88 | 0 | |
| 16 | 安庆—芜湖 | 0.54 | 0.42 | 0 | 33 | 南通—上海 | 0.92 | 0.88 | 0 | |
| 17 | 安庆—马鞍山 | 0.54 | 0.42 | 0 | ||||||
| 注:数据来源于2015年中国交通年鉴。 | ||||||||||
城市节点之间不同运输方式的运输距离dijkq和模糊时间表示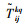
| 序号 | 城市节点对 | 运输距离 (km, n mile)/运输时间 (h) |
序号 | 城市节点对 | 运输距离 (km, n mile)/运输时间 (h) |
|||
| 公路运输 | 滚装运输 | 公路运输 | 滚装运输 | |||||
| 1 | 重庆—宜昌 | — | 356/ (28.66, 32.96, 36.63) |
3 | 重庆—宜昌 | 714.0/ (19.30, 20.40, 22.31) |
— | |
| 2 | 重庆—宜昌 | 618.2/ (12.36, 13.74, 15.08) |
— | 4 | 重庆—荆州 | — | 436/ (35.10, 40.37, 44.86) |
|
| 5 | 重庆—荆州 | 692.7/ 13.85, 15.39, 16.90) |
— | 28 | 黄石—九江 | — | 62/ (4.99, 5.74, 6.38) |
|
| 6 | 重庆—荆州 | 833/ (22.51, 23.80, 26.03) |
— | 29 | 黄石—九江 | 159.4/ (3.19, 3.54, 3.89) |
— | |
| 7 | 宜昌—武汉 | — | 338/ (27.21, 31.30, 34.77) |
30 | 黄石—九江 | 219.0/ (5.92, 6.26, 6.84) |
— | |
| 8 | 宜昌—武汉 | 319.5/ (6.39, 7.10, 7.79) |
— | 31 | 黄石—安庆 | — | 146/ (11.76, 13.52, 15.02) |
|
| 9 | 宜昌—武汉 | 352.0/ (9.51, 10.06, 11.00) |
— | 32 | 黄石—安庆 | 274.8/ (5.50, 6.11, 6.70) |
— | |
| 10 | 宜昌—黄石 | — | 415/ (33.41, 38.43, 42.70) |
33 | 黄石—安庆 | 270.1/ (7.30, 7.72, 8.44) |
— | |
| 11 | 宜昌—黄石 | 411.5/ (8.23, 9.14, 10.04) |
— | 34 | 黄石—铜陵 | — | 196/ (15.78, 18.15, 20.16) |
|
| 12 | 宜昌—黄石 | 444.5/ (12.01, 12.70, 13.89) |
— | 35 | 黄石—铜陵 | 386.5/ (7.73, 8.59, 9.43) |
— | |
| 13 | 荆州—武汉 | — | 258/ (20.77, 23.89, 26.54) |
36 | 黄石—铜陵 | 388.2/ (10.49, 11.09, 12.13) |
— | |
| 14 | 荆州—武汉 | 219.6/ (4.39, 4.88, 5.36) |
— | 37 | 九江—芜湖 | — | 187/ (15.06, 17.31, 19.24) |
|
| 15 | 荆州—武汉 | 235.9/ (6.38, 6.74, 7.37) |
— | 38 | 九江—芜湖 | 357.5/ (7.15, 7.94, 8.72) |
— | |
| 16 | 荆州—黄石 | — | 330/ (26.57, 30.56, 33.95) |
39 | 九江—芜湖 | 362.6/ (9.80, 10.36, 11.33) |
— | |
| 17 | 荆州—黄石 | 308.5/ (6.17, 6.86, 7.52) |
— | 40 | 九江—马鞍山 | — | 213/ (17.15, 19.72, 21.91) |
|
| 18 | 荆州—黄石 | 328.4/ (8.88, 9.38, 10.26) |
— | 41 | 九江—马鞍山 | 397.7/ (7.95, 8.84, 9.70) |
— | |
| 19 | 武汉—九江 | — | 134/ (10.79, 12.41, 13.79) |
42 | 九江—马鞍山 | 403.0/ (10.89, 11.51, 12.59) |
— | |
| 20 | 武汉—九江 | 243.0/ (4.86, 5.40, 5.93) |
— | 43 | 九江—南京 | — | 230/ (18.52, 21.30, 23.66) |
|
| 21 | 武汉—九江 | 267.8/ (7.24, 7.65, 8.37) |
— | 44 | 九江—南京 | 450.6/ (9.01, 10.01, 10.99) |
— | |
| 22 | 武汉—安庆 | — | 215/ (17.31, 19.91, 22.12) |
45 | 九江—南京 | 460.7/ (12.45, 13.16, 14.40) |
— | |
| 23 | 武汉—安庆 | 344.6/ (6.89, 7.66, 8.40) |
— | 46 | 安庆—芜湖 | — | 106/ (8.53, 9.81, 10.91) |
|
| 24 | 武汉—安庆 | 363.9/ (9.84, 10.40, 11.37) |
— | 47 | 安庆—芜湖 | 191.4/ (3.83, 4.25, 4.67) |
— | |
| 25 | 武汉—铜陵 | — | 278/ (22.38, 5.74, 28.60) |
48 | 安庆—芜湖 | 221.9/ (6.00, 6.34, 6.93) |
— | |
| 26 | 武汉—铜陵 | 469.3/ (9.39, 10.43, 11.45) |
— | 49 | 安庆—马鞍山 | — | 120/ (9.66, 11.11, 12.35) |
|
| 27 | 武汉—铜陵 | 481.8/ (13.02, 13.77, 15.06) |
— | 50 | 安庆—马鞍山 | 231.5/ (4.63, 5.14, 5.65) |
— | |
| 51 | 安庆—马鞍山 | 262.4/ (7.09, 7.50, 8.20) |
— | 74 | 马鞍山—镇江 | 137.8/ (2.76, 3.06, 3.36) |
— | |
| 52 | 安庆—南京 | — | 159/ (12.80, 14.72, 16.36) |
75 | 马鞍山—镇江 | 129.9/ (3.51, 3.71, 4.06) |
— | |
| 53 | 安庆—南京 | 284.4/ (5.69, 6.32, 6.94) |
— | 76 | 马鞍山—江阴 | — | 136/ (10.95, 12.59, 13.99) |
|
| 54 | 安庆—南京 | 302.3/ (8.17, 8.64, 9.45) |
— | 77 | 马鞍山—江阴 | 207.1/ (4.14, 4.60, 5.05) |
— | |
| 55 | 铜陵—芜湖 | — | 56/ (4.51, 5.19, 5.76) |
78 | 马鞍山—江阴 | 220.9/ (5.97, 6.31, 6.90) |
— | |
| 56 | 铜陵—芜湖 | 93.9/ (1.88, 2.09, 2.29) |
— | 79 | 马鞍山—南通 | — | 163/ (13.12, 15.09, 16.77) |
|
| 57 | 铜陵—芜湖 | 90.4/ (2.44, 2.58, 2.83) |
— | 80 | 马鞍山—南通 | 300.0/ (6.00, 6.67, 7.32) |
— | |
| 58 | 铜陵—马鞍山 | — | 82/ (6.60, 7.59, 8.44) |
81 | 马鞍山—南通 | 324.0/ (8.76, 9.26, 10.13) |
— | |
| 59 | 铜陵—马鞍山 | 134.0/ (2.68, 2.98, 3.27) |
— | 82 | 南京—镇江 | — | 46/ (3.70, 4.26, 4.73) |
|
| 60 | 铜陵—马鞍山 | 134.3/ (3.63, 3.84, 4.20) |
— | 83 | 南京—镇江 | 72.8/ (1.46, 1.62, 1.78) |
— | |
| 61 | 铜陵—南京 | — | 108/ (8.70, 10.00, 11.11) |
84 | 南京—镇江 | 73.2/ (1.98, 2.09, 2.29) |
— | |
| 62 | 铜陵—南京 | 186.9/ (3.74, 4.15, 4.56) |
— | 85 | 南京—江阴 | — | 119/ (9.58, 11.02, 12.24) |
|
| 63 | 铜陵—南京 | 192.0/ (5.19, 5.49, 6.00) |
— | 86 | 南京—江阴 | 161.6/ (3.23, 3.59, 3.94) |
— | |
| 64 | 芜湖—镇江 | — | 105/ (8.45, 9.72, 10.80) |
87 | 南京—江阴 | 159.6/ (4.3, 4.56, 4.99) |
— | |
| 65 | 芜湖—镇江 | 175.6/ (3.51, 3.90, 4.28) |
— | 88 | 南京—南通 | — | 135/ (10.87, 12.50, 13.89) |
|
| 66 | 芜湖—镇江 | 169.2/ (4.57, 4.83, 5.29) |
— | 89 | 南京—南通 | 245.1/ (4.90, 5.45, 5.98) |
— | |
| 67 | 芜湖—江阴 | — | 162/ (13.04, 15.00, 16.67) |
90 | 南京—南通 | 230.3/ (6.22, 6.58, 7.20) |
— | |
| 68 | 芜湖—江阴 | 230.0/ (4.60, 5.11, 5.61) |
— | 91 | 镇江—上海 | — | 145/ (11.67, 13.43, 14.92) |
|
| 69 | 芜湖—江阴 | 241.0/ (6.51, 6.89, 7.53) |
— | 92 | 镇江—上海 | 254.7/ (5.09, 5.66, 6.21) |
— | |
| 70 | 芜湖—南通 | — | 188/ (15.14, 17.41, 19.34) |
93 | 镇江—上海 | 258.5/ (6.99, 7.39, 8.08) |
— | |
| 71 | 芜湖—南通 | 323.2/ (6.46, 7.18, 7.88) |
— | 94 | 江阴—上海 | — | 100/ (8.05, 9.26, 10.29) |
|
| 72 | 芜湖—南通 | 365.6/ (9.88, 10.45, 11.43) |
— | 95 | 江阴—上海 | 159.0/ (3.18, 3.53, 3.88) |
— | |
| 73 | 马鞍山—镇江 | — | 74/ (5.96, 6.85, 7.61) |
96 | 江阴—上海 | 155.2/ (4.19, 4.43, 4.85) |
— | |
| 97 | 南通—上海 | — | 57/ (4.59, 5.28, 5.86) |
99 | 南通—上海 | 121.3/ (3.28, 3.47, 3.79) |
— | |
| 98 | 南通—上海 | 126.7/ (2.53, 2.82, 3.09) |
— | |||||
| 注:公路运输距离单位为km,滚装运输距离单位为n mile。滚装车高速路速度v1=41~50 km/h,非高速公路速度v2=32~37 km/h,滚装船速度v3=9.72~12.42 nmi/h。 | ||||||||
| 运输方式 | 中转费用/元 | 中转时间/h | 中转碳排放量/g | |||||
| 公路 | 滚装 | 公路 | 滚装 | 公路 | 滚装 | |||
| 公路 | — | 10 | — | 0.1 | — | 69.7 | ||
| 滚装 | 10 | — | 0.1 | — | 69.7 | — | ||
| 注:换装距离按0.1 km计。 | ||||||||
3.2 求解与分析
文章采用Matlab求解多目标公水联运路径选择模型,置信水平α=0.95,遗传算法基本参数:种群大小Pop=20,遗传迭代次数G=100,初始交叉概率Pc=0.7,初始变异概率Pm=0.01,设置在最后15代进行爬山操作。通过Matlab程序设计改进遗传算法求解得到公水联运路径组合。
表 6给出了在综合考虑3个目标函数的情况下,通过计算所得到的几组Pareto最优解,包含Matlab的输出结果及对应的解码运输方式及路径。
| 序号 | 方案 | 费用/元 | 时间/h | 碳排放/kg |
| 1 | 1-12-20-27-37-40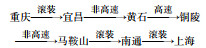 |
16 201.65 | 89.813 | 770.04 |
| 2 | 1-12-13-28-33-40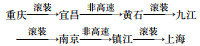 |
14 817.93 | 94.424 | 590.38 |
| 3 | 4-9-13-28-31-40 |
15 087.45 | 100.839 | 450.86 |
长江沿线汽车整车公水联运运输路径及运输方式选择时,从考虑最小碳排放的路径选择来说,与费用最小的路径选择方式对比,即使费用有所增长,但碳排放量会出现显著的减少;从考虑最短运输时间的路径选择来说,相比于另外两种的路径选择方式,运输时间明显缩短。
目前我国已经不再处于牺牲环境来换取经济发展的时期,每个社会人都应该为低碳作出贡献。因此较好的决策是根据整车运输企业对以上3个目标倾向程度的不同,并尽可能地考虑碳排放对周边环境的影响,从以上几个非劣解中选择最合适的运输方式组合及运输路径。
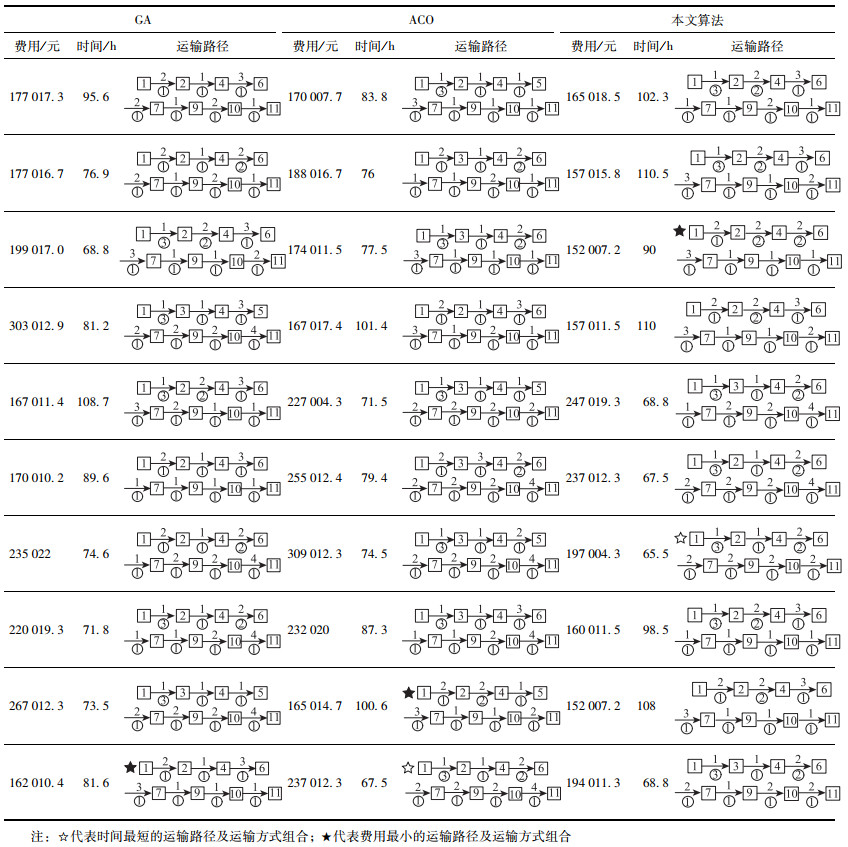
3.3 算例对比为验证算法的求解效果,文章对目前不同算法的求解结果进行对比分析,Lingo在求解优化问题时,对于线性的、简单的非线性规划模型能够求得最优解,且求解速度也较快,但对于相对大型或是较为复杂的非线性规划模型的求解会耗时较多,且不一定能求出最终解[32],在此不进行具体的数值对比分析。文章采用随机算例文献[33],将蚁群算法及常规的遗传算法与文中改进的遗传算法求解结果进行对比,3种算法分别运行10次,运行结果、对应的运输方式组合及运输路径如表 7所示。
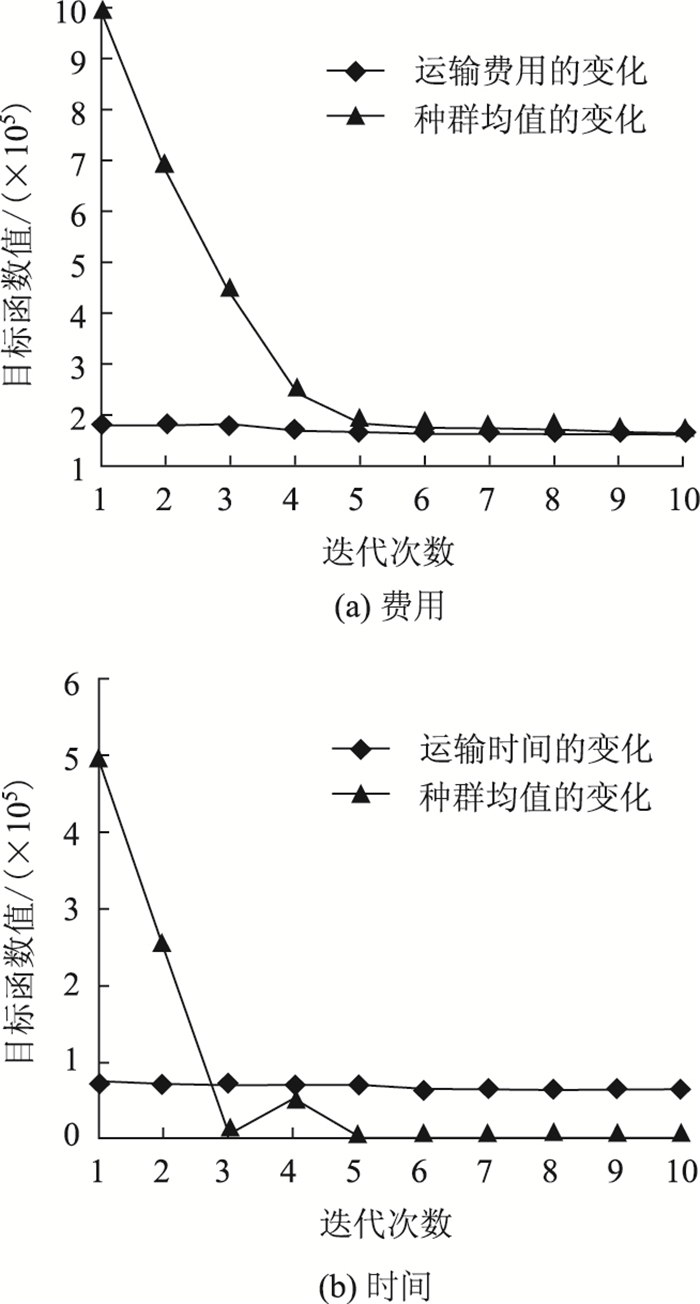
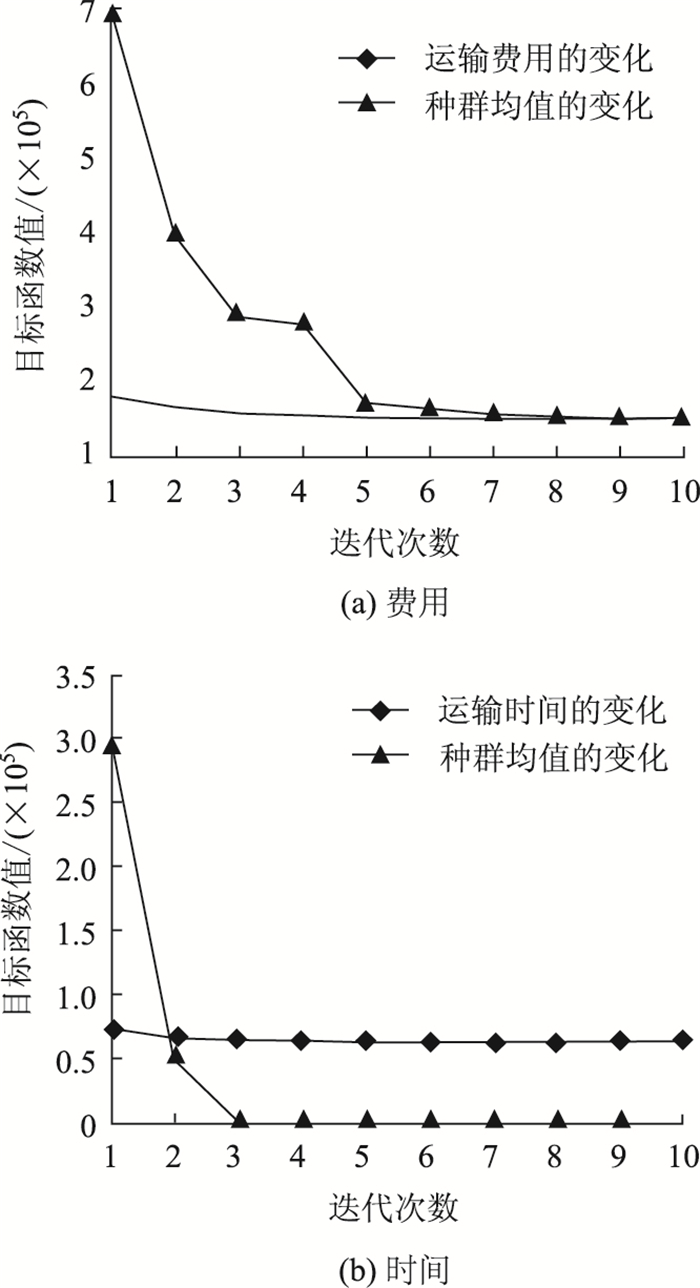
GA最优目标值随迭代次数的变化情况如图 5所示;ACO最优目标值随迭代次数的变化情况如图 6所示。本研究算法最优目标值随迭代次数的变化情况如图 7所示。
|
| 图 5 费用及时间变化图(1) Fig. 5 Variation tendency of cost and time (1) |
| |
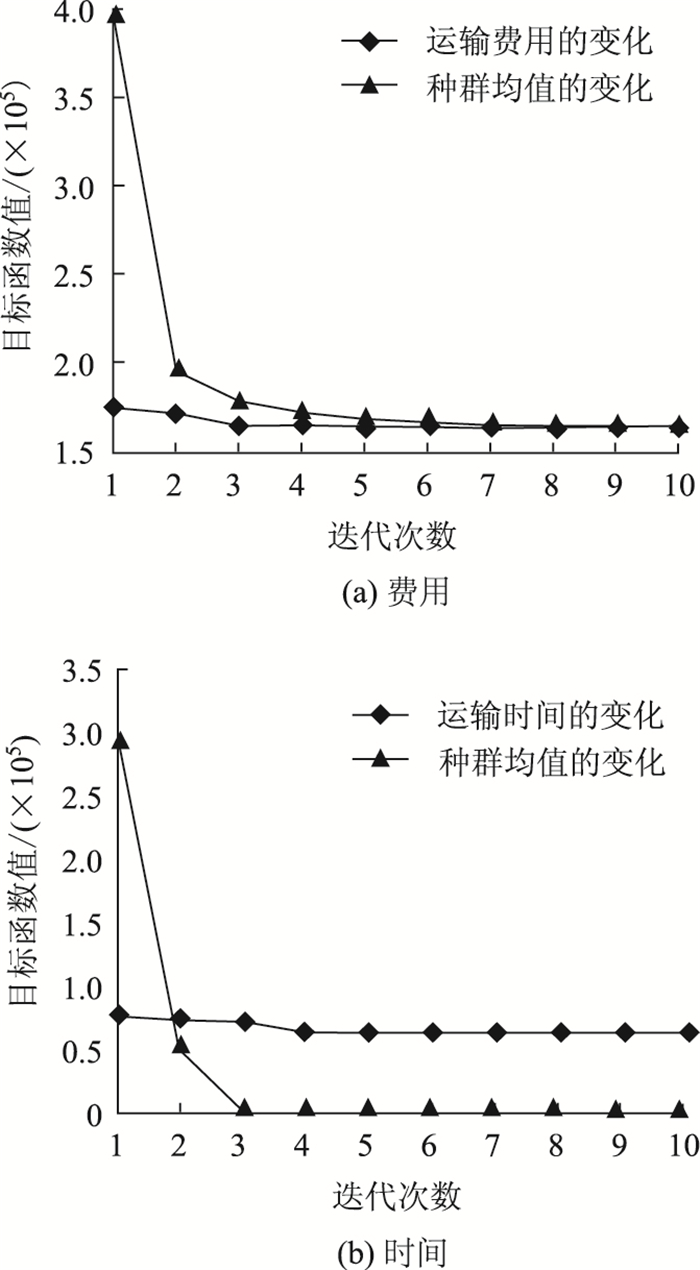
|
| 图 6 费用及时间变化图(2) Fig. 6 Variation tendency of cost and time (2) |
| |
|
| 图 7 费用及时间变化图(3) Fig. 7 Variation tendency of cost and time (3) |
| |
可以看出,与另两种算法相比本研究算法求得的费用和时间目标值均较优。综上,本研究算法的设计在求解效果上有一定的优势性。
4 结论为了缓解汽车整车运输的严峻局面,汽车整车公水联运依托长江流域滚装运输势在必行。本研究创新性地将目前的川江载货汽车滚装运输航线延伸至长江中下游,以单个载有汽车整车的滚装车为研究对象,基于3方面目标来研究长江流域汽车整车公水联运运输方式的最优组合,设计了0-1多目标规划问题,通过改进的遗传算法求解得到了相应的运输方式及运输路径,通过综合考虑多方面目标,为长江流域汽车整车运输企业提供基于科学决策的可选择路径。
| [1] |
张雄. 多式联运运输网络模型研究[J]. 物流工程与管理, 2010, 32(6): 69-70. ZHANG Xiong. Multimodal Transport Network Model Research[J]. Logistics Engineering And MAnagement, 2010, 32(6): 69-70. |
| [2] |
杨文东, 王文芳. 有时间窗的多式联运问题分析与建模[J]. 南京航空航天大学学报, 2009, 41(1): 111-115. YANG Wen-dong, WANG Wen-fang. Analyzing and Modeling of Multimodal Transportation with Time Window[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2009, 41(1): 111-115. |
| [3] |
ZILIASKOPOULOS A, WARDELL W. An Intermodal Optimum Path Algorithm for Multimodal Networks with Dynamic Arc Travel Times and Switching Delays[J]. European Journal of Operational Research, 2000, 125(3): 486-502. |
| [4] |
CHANG T S. Best Routes Selection in International Intermodal Networks[J]. Computers & Operations Research, 2013, 35(9): 2877-2891. |
| [5] |
刘燕华, 葛全胜, 何凡能, 等. 应对国际CO2减排压力的途径及我国减排潜力分析[J]. 地理学报, 2008, 63(7): 675-682. LIU Yan-hua, GE Quan-sheng, HE Fan-neng, et al. Countermeasures against International Pressure of Reducing CO2 Emissions and Analysis on China's Potential of CO2 Emission Reduction[J]. Acta Geographica Sinica, 2008, 63(7): 675-682. |
| [6] |
王慧, 汪传旭. 模糊需求环境下集装箱多式联运箱型和运输方式的选择[J]. 公路交通科技, 2012, 29(4): 153-158. WANG Hui, WANG Chuan-xu. Selection of Container Types and Transport Modes for Container Multi-modal Transport with Fuzzy Demand[J]. Journal of Highway and Transportation Research and Development, 2012, 29(4): 153-158. |
| [7] |
WILLIAMS K B. Management Models and Industrial Applications of Linear Programming[J]. Journal of the Operational Research Society, 1962, 13(3): 274-275. |
| [8] |
LIU B, IWAMURA K. Chance Constrained Programming with Fuzzy Parameters[J]. Fuzzy Sets & Systems, 1998, 94(2): 227-237. |
| [9] |
刘宝碇. 随机规划与模糊规划[M]. 北京: 清华大学出版社, 1998.
|
| [10] |
赵晓煜. 供应链中二级分销网络优化设计方法的研究[D]. 沈阳: 东北大学, 2001. ZHAO Xiao-yu. Research on Bi-level Distribution Network Optimization Design in Supply Chain Management[D]. Shenyang: Northeastern University, 2001. |
| [11] |
李丹丹. 供应链中二级分销网络模糊优化设计研究[D]. 武汉: 武汉理工大学, 2006. LI Dan-dan. Study on the Fuzzy Optimization Design of Bi-level Distribution Network in the Supply Chain[D]. Wuhan: Wuhan University of Technology, 2006. |
| [12] |
黄智力, 罗键. 三角模糊数型不确定多指标决策的可能度关系法[J]. 控制与决策, 2015, 30(8): 1365-1371. HUANG Zhi-li, LUO Jian. Possibility Degree Relation Method for Triangular Fuzzy Number-based Uncertain Multi-attribute Decision Making[J]. Control and Decision, 2015, 30(8): 1365-1371. |
| [13] |
江文奇. 基于FVIKOR的三角模糊数型多准则决策方法[J]. 控制与决策, 2016, 31(7): 1330-1334. JIANG Wen-qi. Multi-criteria Decision Method with Triangular Fuzzy Numbers Based on FVIKOR[J]. Control and Decision, 2016, 31(7): 1330-1334. |
| [14] |
FALZARANO A. An Evaluation of Energy Consumption and Emissions from Intermodal Freight Operations on the Eastern Seaboard: AGIS Network Analysis Approach[D]. Rochester, US: Rochester Institute, 2008.
|
| [15] |
黄丽霞, 帅斌. 危险货物多式联运路径优化问题的多目标优化算法[J]. 中国安全生产科学技术, 2014, 10(9): 10-16. HUANG Li-xia, SHUAI Bin. Multi-objective Optimized Algorithm for Routing Optimization Problem in Intermodal Transportation of Hazardous Materials[J]. Journal of Safety Science and Technology, 2014, 10(9): 10-16. |
| [16] |
马亚轩. 不确定环境下的多式联运时间-费用模型优化研究[D]. 重庆: 重庆大学, 2013. MA Ya-xuan. Optimization Research on Time and Cost Model of Multimodal Transport under Uncertain Environment[D]. Chongqing: Chongqing University, 2013. |
| [17] |
HOLLAND J H, ANDREW A M. Systems:An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence[J]. Robotica, 1993, 11(5): 489-489. |
| [18] |
YANG X, YANG Z, YIN X, et al. Chao Gray Coded Genetic Algorithm and Its Application for Pollution Source Identifications in Convection-diffusion Equation[J]. Communications in Nonlinear Science & Numerical Simulation, 2008, 13(8): 1676-1688. |
| [19] |
玄光男. 遗传算法与工程优化[M]. 北京: 清华大学出版社, 2004.
|
| [20] |
陈相东, 刘彦良, 王鹏涛, 等. 多种运输方式模型优化及求解[J]. 天津师范大学学报:自然科学版, 2005, 25(3): 66-69. CHEN Xiang-dong, LIU Yan-chang, WANG Peng-tao, et al. Optimal and Solution of Multiple Transportation Modes[J]. Journal of Tianjin Normal University:Natural Science Edition, 2005, 25(3): 66-69. |
| [21] |
贺竹磬, 孙林岩, 李晓宏. 时效性物流联运方式选择模型及其算法[J]. 管理科学, 2007, 20(1): 8-12. HE Zhu-qin, SUN Lin-yan, LI Xiao-hong. Mode Choice Model and Algorithm in Intermodal for Time Definite Logistics[J]. Journal of Management Sciences, 2007, 20(1): 8-12. |
| [22] |
胡妙娟, 胡春, 钱锋. 遗传算法中选择策略的分析[J]. 计算机与数字工程, 2006, 34(3): 1-3. HU Miao-juan, HU Chun, QIAN Feng. General Analysis of Selection Strategy in Genetic Algorithm[J]. Computer and Digital Engineering, 2006, 34(3): 1-3. |
| [23] |
CAMPISI D, GASTALDI M. Environmental Protection, Economic Efficiency And Intermodal competition in Freight Transport[J]. Transportation Research Part C:Emerging Technologies, 1996, 4(6): 391-406. |
| [24] |
唐云岚, 赵青松, 高妍方, 等. Pareto最优概念的多目标进化算法综述[J]. 计算机科学, 2008, 35(10): 25-27. TANG Yun-lan, ZHAO Qing-song, GAO Yan-fang, et al. Overview on the Pareto Optimal-based Multiobjective Evolutionary Algorithms[J]. Computer Science, 2008, 35(10): 25-27. |
| [25] |
VAN VELDHUIZEN D A, LAMONT G B. Multi Objective Evolutionary Algorithms:Analyzing the State-of-the-art[J]. Evolutionary Computation, 2000, 8(2): 125. |
| [26] |
毕娜. 基于多目标遗传算法的配送路径问题研究[D]. 杭州: 浙江工业大学, 2007. BI Na. Study of Distribution Routing Problem Based on Multiple Objective Genetic Algorithm[D]. Hangzhou: Zhejiang University of Technology, 2007. |
| [27] |
MURUGAN P, KANNAN S, BASKAR S. NSGA-Ⅱ Algorithm for Multi-Objective Generation Expansion Planning Problem[J]. Electric Power Systems Research, 2009, 79(4): 622-628. |
| [28] |
张晓菲, 张火明. 精英策略的改进非支配遗传算法[J]. 中国计量学院学报, 2010, 21(1): 56-62. ZHANG Xiao-fei, ZHANG Huo-ming. Improved Non-dominated Sorting Genetic Algorithm Ⅱ Based on the Elitist Strategy[J]. Journal of China University of Metrology, 2010, 21(1): 56-62. |
| [29] |
石山, 励庆孚, 王兴华. 基于自适应遗传算法的无刷直流电机的优化设计[J]. 西安交通大学学报, 2002, 36(12): 1215-1218. SHI Shan, LI Qing-fu, WANG Xing-hua. Design Optimization of Brushless Direct Current Motor Based on Adaptive Genetic Algorithm[J]. Journal of Xi'an Jiaotong University, 2002, 36(12): 1215-1218. |
| [30] |
王小平, 曹立明. 遗传算法:理论、应用及软件实现[M]. 西安: 西安交通大学出版社, 2002.
|
| [31] |
柴岩, 周艳钊. 遗传算法的爬山法改进[J]. 辽宁工程技术大学学报, 2014(7): 996-999. CAI Yan, ZHOU Yan-zhao. Improved Genetic Algorithm Based on Climbing[J]. Journal of Liaoning Technical University:Natural Science Edition, 2014(7): 996-999. |
| [32] |
王旭, 迟增彬, 葛显龙. 带时间窗的整车多式联运模型研究与解析[J]. 计算机应用研究, 2011, 28(2): 563-565. WANG Xu, CHI Zeng-bin, GE Xian-long. Research and Analysis for Time-limited Multimodal Transport Model of Vehicle[J]. |
| [33] |
康凯, 牛海姣, 朱越杰, 等. 多式联运中运输方式与运输路径集成优化模型研究[J]. 计算机应用研究, 2010, 27(5): 1672-1675. KANG Kai, NIU Hai-jiao, ZHU Yue-jie, et al. Research of Improved Integrated Optimization Model for Mode and Route in Multimodal Transportation[J]. Application Research of Computers, 2010, 27(5): 1672-1675. |
 2018, Vol. 35
2018, Vol. 35