扩展功能
文章信息
- 珠兰, 胡大伟
- ZHU Lan, HU Da-wei
- 不确定情形下的绿色物流网络和库存问题研究
- Study on Green Logistic Network and Inventory Problem under Uncertain Condition
- 公路交通科技, 2018, 35(6): 121-130
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(6): 121-130
- 10.3969/j.issn.1002-0268.2018.06.017
-
文章历史
- 收稿日期: 2017-08-29
近年来,人口的增长和市场竞争的加剧导致了环境问题的日益突出,如何缓解和防止污染已成为亟待解决的问题。2014年,国务院提出通过实施《国家应对气候变化规划(2014-2020年)》,我国力争实现到2020年,单位GDP二氧化碳排放将比2005年下降40%~50%[1]。因此近年来,将可持续发展的理念融入供应链管理,成为众多学者的研究热点。美国密歇根州立大学的制造研究协会于1996年首次提出绿色供应链(GSC)的概念:绿色供应链是在整个供应链中综合考虑环境影响和资源效率的一种现代管理模式,以绿色制造理论和供应链管理技术为基础,涉及供应商、生产厂、销售商和用户,其目的是使得产品从物料获取、加工、包装、仓储、运输、使用到报废处理的整个过程中,对环境的影响最小,资源效率最高[2]。该理念的诞生,为众多企业带来了机遇和挑战,在一定程度上实现了环保与经济的双赢。如,宜家(IKEA)已建立自己的铁路交通网络,实现低碳运营;华为通过先进的绿色包装技术,仅2014年便实现CO2减排约5.4万吨。
一个流畅的绿色供应链运作流程必然需要依附于一个良好的绿色物流网络。绿色物流网络设计中除涉及选址、库存、运输等主要决策外,还涉及到环境决策。环境要素的度量方法是绿色物流网络设计中的研究重点,碳排放是最普遍使用的度量指标。生命周期评价法(Life Cycle Assessment,LCA)是用于量化与评估产品生命周期内环境影响因素的有效方法体系,包括CML2001、Eco-indicator 99、IMPACT 2002+、ReCiPe2008等方法。M.S. Pishvaee等[3]提出了一个制药行业可持续供应链网络可能性规划模型,使用ReCiPe方法将18种环境影响归纳分为3类,再利用基于权重的方法将这3种环境影响进行集成。李进[4]研究了多级低碳物流网络战略层的选址定位问题和战术层的多商品流、多生产技术和多运输方式的选择问题,以最小化物流网络的总成本和总碳排放为目标,环境影响基于Eco-indicator99数据库中的CO2当量作为指标,通过eco-it 1.4软件进行计算。上述方法以瑞士Ecoinvent数据库或欧盟生命周期基础数据库(ELCD)为基础,在理论与实践中都发挥了重大作用。然而,在绿色物流网络环境影响因素的建模中,以中国国民经济与社会发展规划和环境保护政策为背景、以国内数据库为基础的研究还十分有限。联合国政府间气候变化委员会(IPCC)提出的碳排放计量方法是目前最具代表性的计算方法。IPCC提供了3类排放因子:IPCC缺省排放因子、国别排放因子、利用模型工具的复杂方法[5]。本研究以运输过程的CO2排放作为环境要素,选取IPCC国别排放因子,基于《IPCC国家温室气体清单指南》[6],选取适用于我国国民经济与社会发展和环境保护规划的清单数据。
物流网络的动态性和复杂性引发的不确定性会对网络运作的效率产生显著影响,对网络设计中不确定性的研究逐渐受到学者们的重视。Z. Sazvar[7]将描述不确定性的方法归纳为基于概率分布的方法和基于情形的方法,分别用于描述连续量和离散量的不确定状态。解决不确定性的主要方法有:模糊规划、鲁棒优化、随机动态规划和随机规划,Sahinidis[8]分别对这些方法进行了详细讨论,随后大量学者运用这些方法解决物流网络设计中的不确定性问题。叶立鹏[9]研究了危险废弃物物流中的不确定因素和危险废弃物的回收模式,构建了多周期的优化模型,以模糊变量描述回收数量和质量的不确定性。胡青蜜等[10]研究了轴辐式网络节点之间货流的不确定性,运用随机规划方法确定辐节点的吞吐能力,建立轴辐式网络混合整数随机规划模型。物流网络中需求的不确定性导致供应链与需求量之间产生差异,即导致库存。决策周期是进行库存决策的重要参数,实际上,供应链的运作周期与决策周期并不一定重合,而现阶段大部分研究均以供应链的运作周期作为决策周期对不确定性进行研究。本研究以情形数法描述客户需求的不确定性,建立了一个多阶段随机规划模型。以不确定性发生为界将模型分为两部分,即不确定定性未发生的阶段和不确定性发生后的阶段,每一阶段代表决策者获得的信息更新一次所需的时间,而并非严格对应各时间周期。
多目标物流网络优化模型通常基于多目标优化方法进行求解,近代发展起来的一些多目标启发式方法可以有效求解这类问题,如:Srinivas[11]和Deb[12]提出的非支配排序遗传算法NSGA和NSGA-Ⅱ;Fonseca C M等[13]提出的多目标遗传算法(MOGA);Zitzler E[14]和:Laumanns M[15]提出强度进化算法SPEA和SPEA2等。此后有大量学者在应用过程中结合具体问题对上述算法进行改进。朱加园[16]提出一种改进的多目标混合差分进化算法对多目标配送车辆路径问题进行求解,求解过程以差分进化算法为主体,通过引入双种群机制和变邻域下降搜索策略,有效平衡多种群在解空间的全局搜索能力。赵海茹等[17]通过改进的多目标粒子群算法(MOPSO)求解物流节点选址问题,改进的算法采用Pareto支配关系和拥挤距离来更新外部存档,提高非劣解分布的均匀性;并通过动态变异概率的引入,提高算法全局寻优能力。本研究针对NSGA Ⅱ算法中同支配等级个体拥挤距离较大则邻域解较少的问题,提出一种自适应交叉与变异概率的改进方式,从而提高求解效率。
综上所述,文中研究了多周期不确定情形下的绿色物流网络建模问题,考虑了战术层的运输与库存决策,提出一个双目标多阶段随机规划模型。环境要素的度量基于《IPCC国家温室气体清单指南》数据库对运输过程中的CO2排放进行测算;本研究采用情形树法描述不确定性,并以不确定性的发生为界将模型分为两阶段进行分析。此外,本研究改进带精英策略的非支配排序遗传算法(NSGA-Ⅱ)求解上述模型。
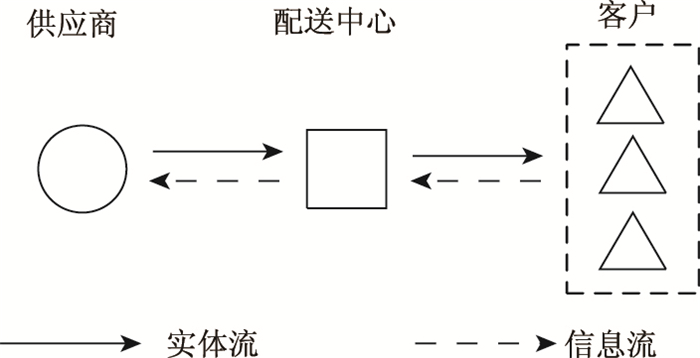
1 问题描述 1.1 供应链结构本研究以一个存储型配送中心为核心,同时包括其上游供应商和下游客户的两级供应链网络,如图 1所示。实体流在供应链中自上而下,信息流自下而上。供应商将产品按照客户需求运输至配送中心,再由配送中心完成客户的配送。
|
| 图 1 供应链网络结构示意图 Fig. 1 Schematic diagram of supply chain network structure |
| |
对所建模型作如下科学假设:(1)假设客户每周期的需求不确定,以不同情形描述,需求量在每周期初反馈至配送中心处;(2)只有到每周期末还的剩余产品产生库存持有成本,库存持有成本与库存量相关,以分段函数形式给出;(3)当配送中心发生缺货时,假设允许缺货量中的一部分α延迟至下一周期配送,其余部分(1-α)则无法到达客户处。(4)配送中心的初始库存I0可为零或正数;(5)假设各级运输由多种具有不同运输成本、容量以及排放能力的车辆完成;(6)假设以运输过程中的CO2排放作为环境要素的度量;(7)假设该网络总成本包括配送中心的补货成本、产品购买成本、车辆运输成本、配送中心库存持有成本、配送中心延期交货成本和缺货损失成本。
本研究的目标旨在寻求客户需求不确定情况下,使得网络总成本最低且环境污染最小的最佳订货、库存及车辆调度方案。
1.2 环境目标的度量本研究以运输过程中产生的温室气体作为环境要素的度量。将基于《IPCC国家温室气体清单指南》数据库及其测算方法,选取IPCC国别排放因子,计算CO2当量,如式(1)~式(2)所示。其中,各种燃料的原始排放系数、我国热值和碳氧化因子可由《IPCC国家温室气体清单指南》数据库得到。
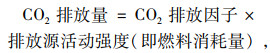
|
(1) |

|
(2) |
此外,运输过程中的CO2排放量还与车辆类型、行驶速度、负载状况有关,Irina Harris[18]给出了40 t和5 t货车在不同负载率f、平均车速v下的油耗,如表 1所示。
| f | v | ||||||
| 40 t | 5 t | ||||||
| 54 | 36 | 30 | 54 | 36 | 30 | ||
| 100 | 0.380 | 0.359 | 0.369 | 0.275 | 0.259 | 0.267 | |
| 90 | 0.369 | 0.349 | 0.358 | 0.263 | 0.248 | 0.255 | |
| 75 | 0.353 | 0.334 | 0.343 | 0.245 | 0.231 | 0.238 | |
| 60 | 0.336 | 0.318 | 0.326 | 0.228 | 0.215 | 0.221 | |
| 0 | 0.270 | 0.256 | 0.262 | 0.175 | 0.165 | 0.170 | |
1.3 不确定性的描述
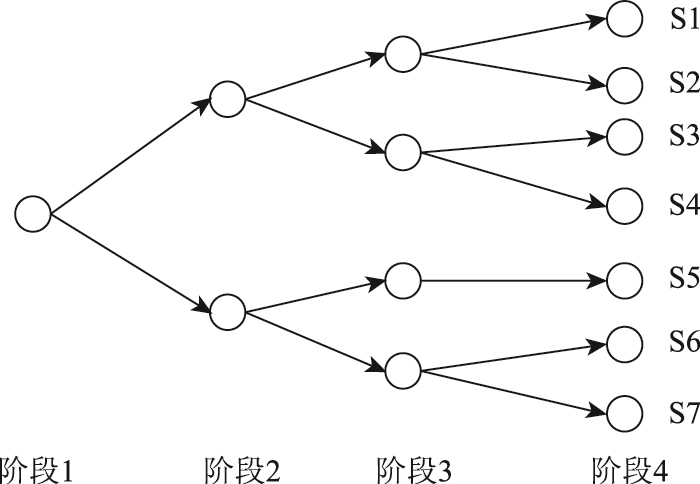
对于各周期客户需求的不确定性,本研究采用情形树法来进行描述,如图 2所示。在一个情形树中,每一阶段代表决策者获得的信息更新一次所需的时间。因此,在多周期随机规划问题中,情形树中的各阶段并不一定完全对应于各周期。每个阶段由一系列节点和分枝构成:每个节点代表该阶段可能出现的一种随机状态,根节点表示当前状态;每个分枝代表下一阶段以一定概率可能出现的情形。每个节点的概率等于连接根节点和该节点所有分枝出现概率的乘积,且每阶段所有节点的概率之和为1。因此,从根节点到一个叶子节点的一条路径就表示从当前状态到某一周期为止可能出现的一种情形。
|
| 图 2 情形树法示意图 Fig. 2 Diagram of scenario tree method |
| |
2 数学模型 2.1 多周期非线性随机规划模型
文中研究的需求不确定下绿色物流网络库存优化问题可由如下随机规划模型描述:
集合:T为周期集合;S为情形集合;V为车辆种类集合;L为库存水平集合。
参数:Ats为周期t内,情形s下的配送中心的补货成本;ac为固定补货成本;pc为产品的单位价格;hc为配送中心库存持有成本;bc为配送中心延期交货成本;lc为配送中心缺货损失成本;tcv为车辆种类v的单位运输成本;α为延期配送的货物占缺货量的比例;Dts为周期t内,情形s下的客户总需求;Ps为情形s出现的概率;capv为车辆种类v某负载率对应的容量;ds为情形s下从供应商到配送中心,再从配送中心到客户的全部运输距离的平均值;fcv为车辆种类v单位油耗;λv为车辆种类v的CO2转换因子;il为等级为l的库存水平;
变量:Qts为周期t内,情形s下的订货量;Its为周期t末,情形s下的库存量;Bts为周期t末,情形s下的缺货量;Ntsv为周期t末,情形s下使用车辆种类v的数量。
目标函数:
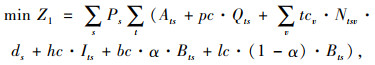
|
(3) |
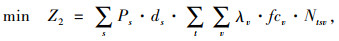
|
(4) |
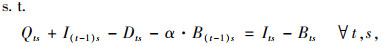
|
(5) |
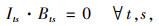
|
(6) |
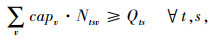
|
(7) |
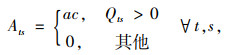
|
(8) |
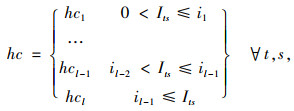
|
(9) |
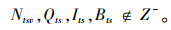
|
(10) |
目标函数Z1,即最小化包括配送中心的补货成本、产品购买成本、车辆总运输成本(包括供应商到配送中心、配送中心到客户两级)、配送中心库存持有成本、配送中心延期交货成本和缺货损失成本在内的网络总成本;目标函数Z2最小化运输过程产生的CO2排放当量;式(5)为库存平衡约束;式(6)表示库存和缺货不可能同时发生;式(7)为车辆容量约束;式(8)定义了订货量的取值;式(9)表示本研究库存持有成本。Zeinab Sazvar[7]提出,非线性表达式更适用于描述生鲜、易变质产品的存储;对于普通产品,该值可由一定值表示。本研究模型以较为复杂的前者表示库存持有成本, 式(10)定义了变量的属性。
由于模型中存在非线性表达式(6), 式(8)和式(9),因此该模型属性为非线性随机规划模型。
2.2 两阶段线性随机规划模型如1.3节所述,多周期随机规划问题中的各阶段并不一定完全对应于每个周期,而对应于决策者获得的反馈信息被更新的时间。因此,本研究将上述模型分为两个阶段进行分析,即不确定性未发生的阶段和不确定性发生后的阶段。假设当一次信息更新后,当前客户需求已知,且客户需求在每周期期末进行反馈。因此,第一阶段需要做出的决策与可能出现的各情形无关,包括第一周期的订货量Q1与使用车辆v的数量N1v;第二阶段的决策过程依赖于各情形,包括第一周期可能出现的库存量I1s、缺货量B1s以及后续周期的所有决策。因此,目标函数式(3), 式(4)以及约束式(5), 式(7)均可由两部分表示,如式(11)~式(17)所示。
此外,为了便于求解,本研究通过一些线性化技术将模型中涉及的非线性表达式线性化。首先,线性化式(7),引入二元变量Wts,令Wts= 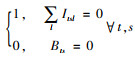
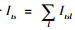
综上,经线性化的两阶段随机规划模型如下所示:
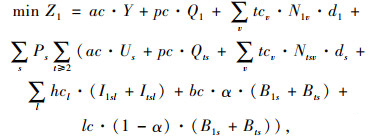
|
(11) |
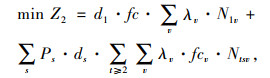
|
(12) |
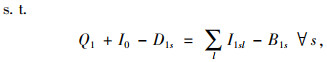
|
(13) |
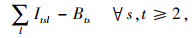
|
(14) |
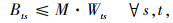
|
(15) |
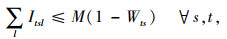
|
(16) |
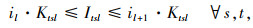
|
(17) |
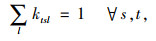
|
(18) |
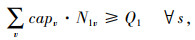
|
(19) |
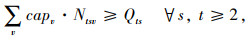
|
(20) |
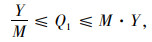
|
(21) |
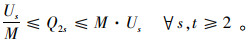
|
(22) |
该模型描述的问题属于典型的多目标组合优化问题,具有很高的求解复杂性,多目标进化算法可以有效地对其进行求解。
3.1 算法概述NSGA Ⅱ算法是目前最流行的多目标进化算法之一,由Srinivas和Deb于2000年在第一代非支配排序遗传算法NSGA的基础上提出,其优势在于:(1)利用快速非支配排序方法,将种群中的个体划分到不同非劣等级中,显著降低计算复杂度;(2)采用精英策略,将父代种群跟子代种群进行合并,使下一代的种群从双倍的空间中进行选取,从而保留了优秀个体;(3)引入拥挤度比较机制,克服了NSGA中需要人为指定共享参数的缺陷,使个体能均匀地扩展到整个Pareto域。NSGA Ⅱ算法的主要流程如下:
步骤1:随机产生规模为N的初始种群Pt,t=0。
步骤2:对种群Pt进行选择、交叉和变异,产生一个规模为N的子代种群Qt。将Pt与Qt合并为规模为2N的混合种群Rt。
步骤3:对种群Rt进行快速非支配排序得到非支配解集{F1, F2, …Fi},设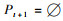
步骤4:t=t+1,若t>T(T为最大进化代数),则算法终止;否则转入步骤2。
3.2 算法改进NSGA Ⅱ的拥挤度比较机制,即比较种群中的给定点周围个体的密度,但对于同一支配等级中的个体,存在拥挤距离较大则邻域解较少的问题。对此,本研究改进NSGA Ⅱ中交叉与变异概率的确定方式,提出一种自适应多目标遗传算法(Self-Adaptive NSGA Ⅱ, 下文简称SA-NSGA Ⅱ),根据种群个体拥挤距离自适应调整交叉变异概率,即拥挤距离大的个体对应较大的交叉变异概率,从而增强算法的邻域搜素能力,增加种群多样性。
式(23), 式(24)分别表示改进的交叉概率和变异概率的确定方法,其中,Pc1和Pc2分别为预设的交叉概率的最大值和最小值;Pm1和Pm2为预设的变异概率最大值和最小值;D(i)为个体i的拥挤距离值;Dmax为种群最大拥挤距离;Davg为种群平均拥挤距离。
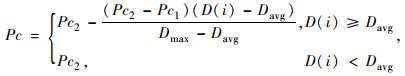
|
(23) |
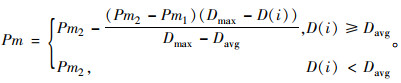
|
(24) |
本研究分别从算法的收敛性和分布性对SA-NSGA-Ⅱ算法进行评估。
本研究采用基于距离的收敛性度量方法,如式(25)所示。其中,P为求得的Pareto最优解集;P*为真实的Pareto前沿。λ(P, P*)越小,表明算法收敛性越好。
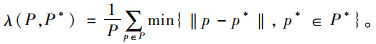
|
(25) |
本研究采用Shott提出的间距评估法[19](Metric of Spacing)来度量Pareto最优解的均匀性,如式(26), 式(27)所示。其中,di和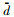
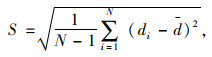
|
(26) |
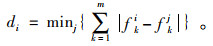
|
(27) |
ZDT测试函数集由K.Deb[20]1999年提出,是多目标算法性能的常用测试函数。本研究利用测试函数ZDT1~ZDT5对SA-NSGA Ⅱ与NSGA Ⅱ的收敛性和分布性进行比较。在这5个测试问题中,两种算法采用相同的设置:实数编码,种群大小为500,规模为2的联赛选择,进化代数为500。
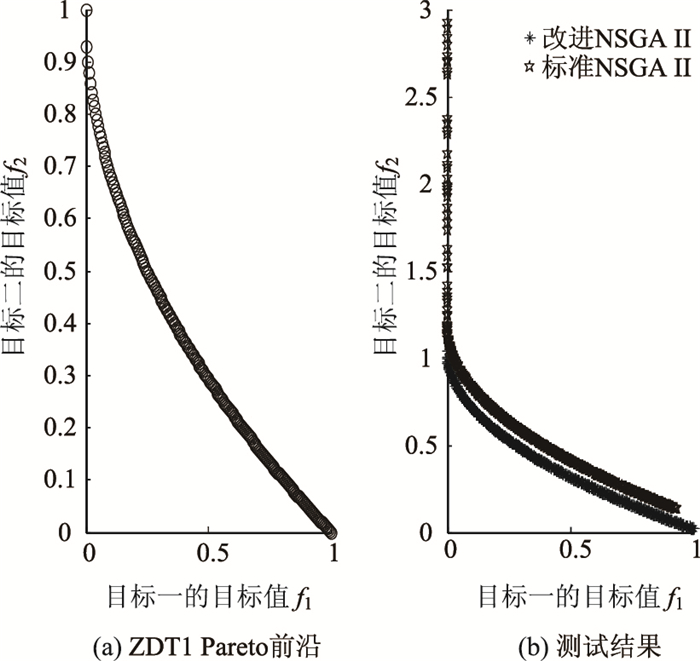
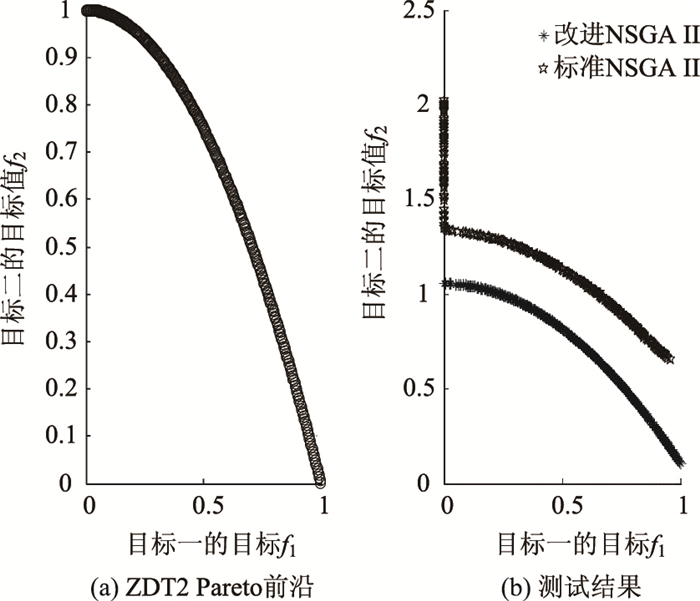
3.4 测试结果将SA-NSGA Ⅱ算法在ZDT系列测试函数上运行10次,取最优结果作为测试结果。图 3~图 4以ZDT1和ZDT2结果为例展示测试结果,其中图 3(a)和图 4(a)为ZDT函数的理想Pareto前沿,图 3(b)和图 4(b)为SA-NSGA Ⅱ与NSGA Ⅱ的Pareto前沿比较。由图可以看出,SA-NSGA Ⅱ对理想Pareto前沿的逼近能力更强,说明改进后的算法能在很大程度上提高种群多样性,增强算法的全局搜索能力。
|
| 图 3 ZDT1结果 Fig. 3 Results of ZDT1 |
| |
|
| 图 4 ZDT2测试结果比较 Fig. 4 Results of ZDT2 |
| |
表 2所示为算法改进前后的收敛性和分布性均值(方差)。由表可知,SA-NSGA Ⅱ在收敛性方面远优于NSGA Ⅱ,分布性能稍差于NSGA Ⅱ,但是差别不大。由于两个算法得到的结果不在同一个Pareto前沿面上,越是接近理想Pareto前沿面,分布性能越难保证,因此该结果是合理的。综上所述,SA-NSGA Ⅱ在增强了全局收敛的同时还保持着较好的分布性能,因此可以说明算法改进的效果是比较理想的。
| 性能 | 算法 | 均值(方差) | ||||
| ZDT1 | ZDT2 | ZDT3 | ZDT4 | ZDT6 | ||
| 收敛性 | SA-NSGA-Ⅱ | 0.017 4 (1.689 5e-05) |
0.049 0 (4.519 5e-06) |
0.005 6 (2.369 0e-05) |
0.000 33 (8.239 0e-08) |
5.899 4e-05 (8.558 5e-09) |
| NSGA-Ⅱ | 0.158 5 (0.081 2) |
0.380 6 (0.037 4) |
0.167 4 (0.008 0) |
7.026 0e-04 (1.679 1e-08) |
0.708 6 (0.004 9) |
|
| 分布性 | SA-NSGA-Ⅱ | 0.006 0 (0.002 6) |
0.005 3 (0.001 8) |
0.007 9 (0.004 6) |
0.009 4 (0.003 8) |
0.003 3 (0.003 5) |
| NSGA-Ⅱ | 0.004 6 (0.007 1) |
0.004 0 (0.003 2) |
0.003 0 (0.001 8) |
0.004 6 (0.004 2) |
0.003 0 (0.003 2) |
|
4 应用与分析 4.1 算例设计
本节设计了一个两级供应链物流网络算例,各级运输由40 t柴油货车(v1)、40 t汽油货车(v2)和5 t柴油货车(v3)3种不同类型的车辆完成。假设车辆以36 mph(≈57.6 km/h)的平均速度、90%负载行驶,则每千米油耗可由表 1得到。各种车辆的碳排放因子由式(2)求得。由此,得到车辆相关参数如表 3所示。
| 车辆 | capv/件 | λv/(kg·L-1) | fcv/(L·km-1) |
| v1 | 700 | 2.73 | 0.349 |
| v2 | 500 | 2.26 | 0.349 |
| v3 | 300 | 2.73 | 0.248 |
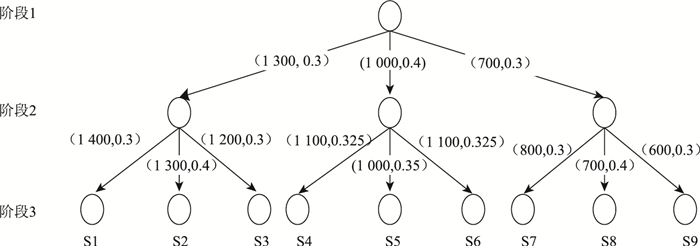
假设,由于客户需求的周期性变动,仅可预测当前状态后两周期的需求量,每周期初,决策者根据经验预测可能出现的情形,图 5所示为本研究中算例情形树模型,定义了两周期内的9种可能出现的情形,括号中数据分别代表该情形下的需求量和该情形出现的概率。
|
| 图 5 算例情形树模型 Fig. 5 Scenario tree model in calculation case |
| |
此外,根据不确定的需求和供应量之间的关系,配送中心在周期末会出现以下3种情形:(1)既无库存也无缺货;(2)发生缺货,假设全部需求量的80%将延期至下一周期交货,由此导致50元/件的延迟交货成本,而其余未能到达客户的货物将导致100元/件的缺货损失成本。(3)产生库存,且库存量对应一个分段库存成本。
4.2 数值试验本节分别进行了成本最小化的单目标试验和成本最小化兼顾环境污染最小化的双目标试验,以比较本研究中考虑了环境要素的模型与传统只考虑成本的模型对库存决策、运输方式决策以及各目标值的变化规律的影响。其中,单目标试验通过IBM ILOG CPLEX 12.5优化求解器实现,双目标试验通过基于MATLAB2014的SA-NSGA Ⅱ算法实现。
表 4和表 5给出了单目标试验结果。表 4显示了单目标试验的目标函数值及第一阶段结果,结果显示配送中心第一周期的订货量为1 100件,并通过两辆v1车辆进行配送。表 5为单目标试验中第二阶段结果,该阶段结果与情形相关,结果给出了不同情形下的库存、订货和车辆使用决策及其期望值。
| 目标函数值 | 第一阶段决策变量 | |||||
| Z1 | Z2 | Q1 | N1v | |||
| 231217 | 361 | 1 100 | 2 | 0 | 0 | |
| 情形 | 第二阶段决策变量 | ||||||||
| 第一周期 | 第二周期 | ||||||||
| I1s | B1s | I2s | B2s | Q2s | N2sv | ||||
| 1 | 0 | 0 | 0 | 200 | 1 200 | 2 | 0 | 0 | |
| 2 | 0 | 0 | 0 | 100 | 1 200 | 2 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 0 | 1 200 | 1 | 0 | 1 | |
| 4 | 300 | 0 | 0 | 0 | 800 | 0 | 1 | 1 | |
| 5 | 300 | 0 | 0 | 700 | 0 | 1 | 0 | 0 | |
| 6 | 300 | 0 | 0 | 600 | 0 | 0 | 1 | 1 | |
| 7 | 600 | 0 | 0 | 200 | 0 | 0 | 1 | 0 | |
| 8 | 600 | 0 | 0 | 100 | 0 | 1 | 1 | 0 | |
| 9 | 600 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 期望 | 300 | 0 | 0 | 236 | 645 | — | — | — | |
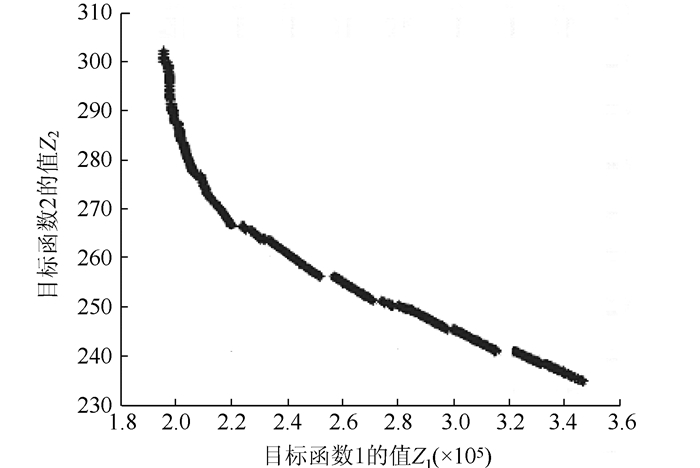
双目标试验结果由图 6和表 6给出。图 6显示了双目标下Pareto前沿的趋势。为了将双目标优化的结果与成本最小化的单目标结果进行比较,我们首先通过对成本目标的限定来对帕累托解集进行筛选,假设该配送中心两周期成本预算上限为260 000元,按照该原则筛选出总成本在260 000附近的10组帕累托解,表 6给出了10组最优解及其均值,第二阶段决策变量由所有情形的期望值给出。
| 解集 | 目标函数 | 第一周期 | 第二周期 | ||||||||
| Z1 | Z2 | Q1 | N1v | E(I1s) | E(B1s) | E(I2s) | E(B2s) | E(Q2s) | |||
| 1 | 243 720 | 258 | 1 100 | 1, 0, 1 | 300 | 0 | 0 | 0 | 597 | ||
| 2 | 240 090 | 260 | 1 100 | 1, 0, 1 | 600 | 0 | 0 | 0 | 597 | ||
| 3 | 257 910 | 257 | 1 191 | 1, 0, 1 | 0 | 0 | 0 | 600 | 612 | ||
| 4 | 258 490 | 254 | 1 196 | 1, 0, 1 | 0 | 300 | 0 | 500 | 613 | ||
| 5 | 245 460 | 255 | 1 117 | 1, 0, 1 | 0 | 500 | 0 | 800 | 600 | ||
| 6 | 230 670 | 270 | 976 | 0, 0, 1 | 0 | 0 | 0 | 600 | 571 | ||
| 7 | 251 520 | 256 | 1 048 | 1, 0, 1 | 0 | 200 | 0 | 500 | 605 | ||
| 8 | 249 540 | 264 | 952 | 1, 0, 1 | 300 | 0 | 0 | 0 | 688 | ||
| 9 | 239 650 | 260 | 800 | 0, 0, 1 | 500 | 0 | 0 | 0 | 580 | ||
| 10 | 230 260 | 264 | 1 095 | 1, 0, 1 | 500 | 0 | 0 | 0 | 596 | ||
| 均值 | 244 731 | 260 | 1 057 | — | 220 | 100 | 0 | 300 | 606 | ||
|
| 图 6 多目标试验帕累托前沿图 Fig. 6 Pareto front curve of multi-objective |
| |
库存决策方面,比较第二阶段结果(表 5与表 6)可知,双目标情形下,第一阶段和第二阶段的订货量Q1和Q2s均减少,库存量I1s和I2s明显降低,第二阶段产生的缺货量B1s和B2s有所上升。这说明,在当前缺货成本和延迟配送比例下,模型通过尽可能地降低多余的运输量来调节来自运输的CO2排放。因此,配送中心可适当通过减少订货量来降低库存,以得到更高的环境效益。
运输决策方面,比较第一阶段结果(表 4和表 6),取两种情形订货量相同或接近情形(Q1≈1 100)进行比较,表 6中解1,2,10的N1v结果与表 4不同,说明考虑环境要素也将导致不同的车辆分配方案。
目标值方面,由图 6中帕累托最优前沿的趋势可知,CO2排放量的降低以成本的增加为代价。比较表 4和表 6中的目标函数值可知,考虑排放目标后的决策导致了5.84%的成本增加(从231 217增加到244 731),相应地排放量降低了28%(从361到260),说明模型中环境目标的引入能够在有效减排的同时避免明显的成本增加。
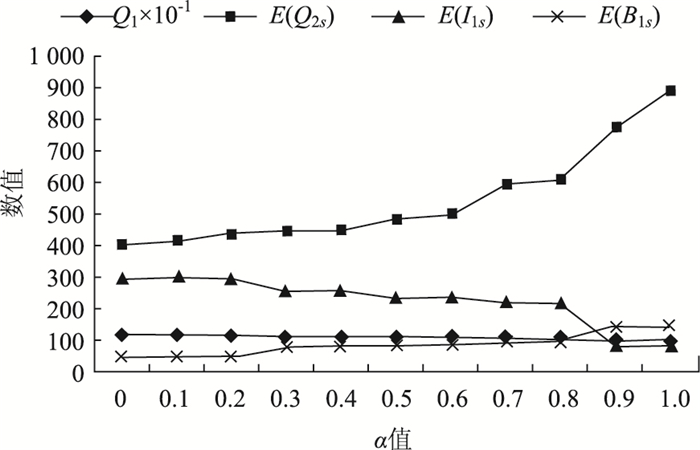
此外,为了说明货物延期配送对库存及订货决策的影响,本研究中对延期配送的货物占缺货量的比例α关于第一周期库存及订货决策的敏感性进行分析,如图 7所示。其中α从0到1以0.1等步长增加。由图可知,当α增加时候,即客户可以接受第一周期内的缺货可延迟至第二周期配送的比例不断增加时,第一周期的订货量Q1的均值呈现下降趋势,由此导致第一周期较多的库存量不再必要,即E(I1s)减少;也导致该周期更多的缺货量被接受,即E(B1s)增加。此外,由于第一周期延迟配送比例的增加,第二周期的订货量E(Q2s)增加。
|
| 图 7 各决策要素关于α的敏感度分析 Fig. 7 Sensitive analysis of each decision-making element to α |
| |
5 结论
本研究对多周期不确定情形下的绿色物流网络和库存问题进行了研究,提出一个两阶段双目标随机规划模型,并基于改进的NSGA-Ⅱ算法对其进行求解,得出如下研究结论:
(1) ZDT系列测试函数测试结果表明改进的NSGA Ⅱ算法比原算法具有更强的收敛性。
(2) 算例求解结果表明,环境目标的引入通过对订货、库存及运输方式决策产生影响来降低运作对环境的影响,决策者可以在小范围成本增加(5.84%)的代价下大幅度降低环境影响(28%)。
(3) 对α的敏感度分析结果表明,当客户可接受的延迟配送比例增加时,配送中心可相应地减少订货及库存以寻求较低的成本。
本研究未来的研究扩展方向包括:
(1) 在绿色物流的基础上添加社会要素,完善可持续性的描述。
(2) 考虑具体类别产品的存储,研究存储过程中的CO2排放。
(3) 需求量的不确定性通过统计方法精确预测。
(4) 对企业真实案例进行有针对性的建模分析。
| [1] |
国家发展和改革委员会. 国务院关于国家应对气候变化规划(2014-2020年)的批复[EB/OL]. (2014-09-19)[2017-04-18]. http://www.ndrc.gov.cn/zcfb/zcfbtz/201411/t20141104_642612.html. National Development and Reform Commission. The State Council's Approval of the National Climate Change Programme (2014-2020)[EB/OL]. (2014-09-19)[2017-04-18]. http://www.ndrc.gov.cn/zcfb/zcfbtz/201411/t20141104_642612.html. |
| [2] |
王能民. 打造绿色供应链之绿色标准建设[J]. 物流技术与应用, 2015, 20(8): 92-94. WANG Neng-min. Green Standard Construction in Building Green Supply Chain[J]. Logistics & Material Handling, 2015, 20(8): 92-94. |
| [3] |
PISHVAEE M S, RAZMI J, TORABI S A. An Accelerated Benders Decomposition Algorithm for Sustainable Supply Chain Network Design under Uncertainty:A Case Study of Medical Needle and Syringe Supply Chain[J]. Transportation Research Part E:Logistics & Transportation Review, 2014, 67: 14-38. |
| [4] |
李进. 基于可信性的低碳物流网络设计多目标模糊规划问题[J]. 系统工程理论与实践, 2015(6): 1482-1492. LI Jin. Credibility-based Multi-objective Fuzzy Programming Problem for Low-carbon Logistics Network Design[J]. System Engineering-Theory and Practice, 2015(6): 1482-1492. |
| [5] |
程豪. 碳排放怎么算——《2006年IPCC国家温室气体清单指南》[J]. 中国统计, 2014(11): 28-30. CHENG Hao. How Carbon Emissions are Calculated:2006 IPCC National Greenhouse Gas List Guide[J]. China Statistics, 2014(11): 28-30. |
| [6] |
Intergovernmental Panel on Climate Change. IPCC Nional Geenhouse Gas List Gide[M]. Paris: Global Environmental Institute, 2006.
|
| [7] |
SAZVAR Z, AL-E-HASHEM S M J M, BABOLI A, et al. A Bi-objective Stochastic Programming Model for a Centralized Green Supply Chain with Deteriorating Products[J]. International Journal of Production Economics, 2014, 150(6): 140-154. |
| [8] |
SAHINIDIS N V. Optimization under Uncertainty:State-of-the-art and Opportunities[J]. Computers & Chemical Engineering, 2004, 28(6): 971-983. |
| [9] |
叶立鹏. 不确定条件下危险废弃物物流网络设计[D]. 成都: 西南交通大学, 2015. YE Li-peng. Design of Hazardous Waste Logistics Network under Uncertain Conditions[D]. Chengdu: Southwest Jiaotong University, 2015. |
| [10] |
胡青蜜, 胡志华. 考虑不确定货流及其影响的轴辐式网络随机规划模型[J]. 华中师范大学学报:自然科学版, 2014, 48(2): 197-205. HU Qing-mi, HU Zhi-hua. Stochastic Programming Model for Flow Uncertainty and Its Effects on Hub-and-spoke Network[J]. Journal of Huazhong Normal University:Natural Science Edition, 2014, 48(2): 197-205. |
| [11] |
SRINIVAS N, DEB K. Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms[J]. Evolutionary Computation, 1994, 2(3): 221-248. |
| [12] |
DEB K, PRATAP A, AGARWAL S, et al. A Fast and Elitist Multiobjective Genetic Algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. |
| [13] |
FONSEC C M, FLEMING P J. Genetic Algorithms for Multiobjective Optimization: Formulation, Discussion and Generalization[C]//Proceedings of 5th International Coference on Genetic Algorithms, UrbanaChampaign: Morgan Kaufmann Publishers, 1999: 416-423.
|
| [14] |
ZITZLER E. Evolutionary Algorithms for Multiobjective Optimization: Methods and Applications[D]. Zurich: Swiss Federal Institute of Technology, 1999.
|
| [15] |
ZITZLER E, LAUMANNS M, THIELE L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm for Multiobjective Optimization[C]//Evolutionary Methods for Design, Optimization and Control with Applications To Industrial Problems. Proceedings of the EUROGEN 2001 Conference. Athens: National Technical University of Athens, 2001.
|
| [16] |
朱加园. 物流配送车辆路径问题建模及多目标优化算法研究[D]. 沈阳: 沈阳建筑大学, 2014. ZHU Jia-yuan. Research on Modeling VRP of Logistics Distribution and Multi-objective Optimization Algorithm[D]. Shenyang: Shenyang Construction University, 2014. |
| [17] |
赵海茹, 陈玲. 改进MOPSO在物流节点选址模型中的应用[J]. 计算机工程与应用, 2016, 52(12): 239-245. ZHAO Hai-ru, CHEN Ling. Application of Improved MOPSO in Logistics Node Location Model[J]. Computer Engineering and Applications, 2016, 52(12): 239-245. |
| [18] |
HARRIS I, NAIM M, PALMER A, et al. Assessing the Impact of Cost Optimization Based on Infrastructure Modelling on CO2 Emissions[J]. International Journal of Production Economics, 2010, 131(1): 313-321. |
| [19] |
SCHOTT J R. Falt Tolerant Design Using Single and Multicriteria Genetic Algorithm Optimization[D]. Cambridge: Massachusetts Institute of Technology, 1995.
|
| [20] |
DEB K. Solving Goal Programming Problems using Multi-objective Genetic Algorithms[C]//Proceedings of the 1999 Congress on Evolutionary Computation. Washington, D. C. : IEEE, 1999.
|
 2018, Vol. 35
2018, Vol. 35
