扩展功能
文章信息
- 李成兵, 魏磊, 高巍, 李奉孝
- LI Cheng-bing, WEI Lei, GAO Wei, LI Feng-xiao
- 城市群复合交通网络级联抗毁性
- Invulnerability of Urban Agglomeration Compound Traffic Network against Cascading Failure
- 公路交通科技, 2018, 35(6): 95-104
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(6): 95-104
- 10.3969/j.issn.1002-0268.2018.06.014
-
文章历史
- 收稿日期: 2017-04-17
2. 北京航空航天大学 交通科学与工程学院, 北京 100191
2. School of Transportation Science and Engineering, Beihang University, Beijing 100191, China
随着经济技术的不断发展,交通运输系统规模不断庞大,客流突增、自然灾害等异常事件频繁发生,某一站点或线路发生故障时,级联效应的存在令故障大范围传播,甚至导致整个交通网络瘫痪,令人民生命财产遭受巨大损失。网络的级联抗毁性已引起国内外学者越来越多的关注。文献[1]通过构建负载容量线性模型,首次研究了网络级联失效问题,发现异构网络的级联失效对蓄意攻击较为敏感;文献[2]分别研究了多种类型的复杂网络在最大负载攻击和随机攻击下的级联失效问题;文献[3]将小世界网络模块化,研究了网络的级联鲁棒性,发现模块化水平会显著影响网络级联鲁棒性;文献[4-6]对无标度网络的级联抗毁性进行仿真,给出了抗毁性优化的措施。文献[7]对相依网络进行研究,基于渗流模型分析了双层耦合网络的级联故障,之后大量学者对双层网络进行研究[8-13];文献[14]研究发现异常事件会通过节点之间的连接关系引起其它节点发生故障,这样就会产生连锁效应,最终导致大部分甚至整个网络崩,因此,级联故障同样存在于交通运输系统,之后学者以城市道路交通网络为研究对象[15-18],研究交通网络的级联失效问题。
综上所述,对于级联抗毁性的研究,目前已有的研究成果大都是针对基于图论的复杂网络模型,并不适用于城市群交通运输系统。虽然也有学者以城市道路交通网络为研究对象进行分析,但没有考虑不同运输方式之间的相互影响。随着城市群规模的不断扩大,交通基础设施日益完善,道路、轨道、水运、航空多种运输方式共同承担着城市群内的交通压力,仅对单种交通运输方式网络进行研究早已不能满足城市群的发展需要。除此之外,目前关于抗毁性的研究,运用的攻击策略大多为需获取网络全部准确信息的蓄意攻击和无法获取网络任何信息的随机攻击。而在现实当中,攻击者可以获取的网络信息往往是一种不完全信息,这2种攻击策略均为极端现象,与实际情况差异较大。
基于此,本研究考虑不同交通运输方式之间的关联性和差异性,提出城市群复合交通网络及其级联失效模型的构建方法,采用基于观测信息模糊度的不完全信息攻击策略,对城市群复合交通网络级联抗毁性进行深入研究。旨在为城市群交通网络的维护提供理论依据,优化网络级联抗毁性,提高网络抵抗突发灾害的能力,保障城市群交通运输系统安全运营。
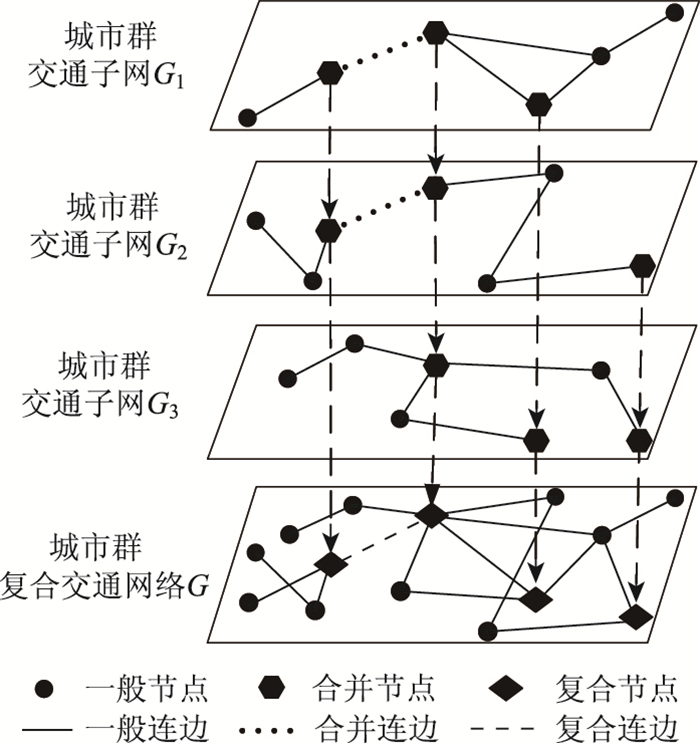
1 城市群复合交通网络级联失效分析 1.1 城市群复合交通网络模型构建在构建城市群复合通网络模型之前,先做出如下假设和定义:
假设1:不考虑交通网络的方向性。若某一节点可以到达另一节点,则假设另一节点也可返回该节点,即城市群交通网络是无向图。
定义1:交通子网。将城市群内道路、轨道、水运、航空4种运输方式交通网络定义为交通子网。以城市群内站点为网络节点,连接站点的各条线路为网络连边,构建交通子网模型,记作Gs(Vs, Es, Ws, Hs)。
其中,Vs表示城市群第s个交通子网内节点的集合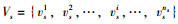
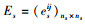
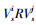
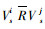
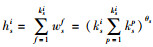
定义2:复合节点。对2个或2个以上交通子网进行叠加,将地理位置较近的汽车站、火车站、港口、机场忽略地理距离进行合并得到的节点称为复合节点。若旅客在站点之间换乘的步行时间在可接受的合理范围内则认为站点地理位置较近。用V′表示所有合并节点的集合,V″表示复合节点的集合。
定义3:复合边。交通子网叠加后,若2个节点之间有多条边相连,将其视为一条边相连,称该边为复合边。用E′表示所有合并连边的集合,E″表示复合边的集合。
基于上述假设和定义,本研究根据城市群内交通基础设施现状,通过复合节点、复合边将多个不同类型的交通子网进行连接构建城市群复合交通网络模型,记作G(V, E, W, H),构建过程如图 1所示。其中,V表示城市群复合交通网络节点的集合,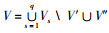
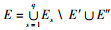
|
| 图 1 城市群复合交通网络模型构建示意图 Fig. 1 Schematic diagram of constructing urban agglomeration's compound traffic network model |
| |
权重修正过程如下:用xs表示G的第s个交通子网对应的客货运分担率,xs≤1,对于G中第z条边eij而言,若eij∉E″,则该边为普通边,边权修正为wz=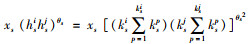
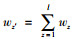
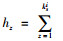
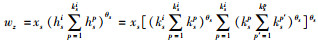
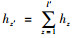
当某一节点或边发生故障,网络原有的负载量会根据节点状态,按照某种规律向与其具有某种耦合关系的节点或边重新分配,进而引发新的节点或边发生故障,产生连锁效应。由于复合节点、复合边将城市群内多个交通子网相连接,某一节点或边发生故障,除了能引起自身交通子网负载重新分配,还会引起与其复合的多个交通子网负载发生变化,这2种情形相互关联,引发城市群复合交通网络整体发生级联失效。
现有的研究大多假定网络中的节点只存在2种状态即“正常”和“失效”[16-18],但在城市群复合交通网络中,当某一节点所承受的负载量超过其最大容量,仅会导致该节点运行速率减慢,当超过容量的负载逐渐疏散后,该节点又会恢复正常。例如,城市群内某航空公司因为恶劣天气导致航班无法正常飞行,此时乘客大量滞留,机场工作人员并不会对所有乘客进行紧急疏散,而是待天气转好后再安排航班飞行。基于此,本研究以“暂停”的概念描述这种处于短暂失效的节点状态,将城市群复合交通网络中的节点状态分为正常、暂停、失效3种状态。对于正常节点,下一时刻接受新的负载分配;对于暂停节点,下一时刻不接受新的负载分配,仅疏散其过载,待过载疏散完后,该节点恢复正常;对于失效节点,下一时刻疏散其所有负载,并删除该节点和与其直接相连的所有边。
2 城市群复合交通网络级联抗毁性建模 2.1 初始负载文献[14]等的研究指出,节点介数与其度值和其邻居节点度值总和的乘积形式是呈正相关的。同时,在交通网络中,某一节点介数越大表示该站点承担的最短路越多,交通压力便越大。因此,可以设定节点vi在遭受破坏之前,如果没有接受额外的负载,该节点的负载就等于其权重hi。用L表示节点负载:
(1) 普通节点初始负载:

|
(1) |
(2) 复合节点初始负载:
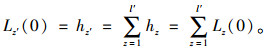
|
(2) |
在城市群复合交通网络中,往往负载较小的节点会拥有较大的闲余容量,负载较大的节点反而闲余容量较小。例如:城市群内旗县地区站点规模虽然较小,但发车经常出现空载现象,浪费运力,说明节点闲余容量较大。而核心城市地区站点规模虽然较大,但常常因客流量过大导致一票难求,说明节点闲余容量较小。因此,节点的负载与容量不一定呈线性关系。本研究构建负载容量非线性模型,用C表示节点的容量:
(1) 普通节点容量:
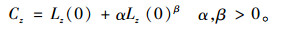
|
(3) |
(2) 复合节点容量:
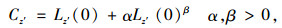
|
(4) |
式中,α,β为容量可调参数,用以调整容量与初始负载的关系。节点容量为节点初始负载和额外负载之和。
2.3 负载重分配 2.3.1 节点状态识别本研究用ΔLi(t+1)表示节点vi下一时刻向其邻居节点分配的负载量:
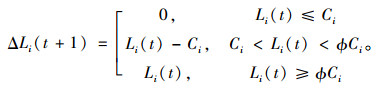
|
(5) |
式(5)分别对应于节点vi的3种状态:当ΔLi(t+1)=0时,节点t时刻的负载小于其容量,此时节点处于正常状态,t+1时刻不需向其他节点分配负载;当ΔLi(t+1)=Li(t)-Ci时,节点t时刻的负载介于其容量和最大可调容量之间,此时节点处于暂停状态,t+1时刻将其过载Li(t)-Ci向其邻居节点进行分配;当ΔLi(t+1)=Li(t)时,节点t时刻负载大于其最大可调容量,此时节点处于失效状态,t+1时刻将其全部负载Li(t)向其邻居节点分配。其中,φ为过载能力调节参数,φ≥1,φ越大,节点由正常变为暂停或失效的概率越小。φCi又可称为节点过载承受能力。
2.3.2 负载重分配模型当网络中某一节点发生故障时,其负载会分配给与其相连的邻居节点,引发网络负载重分配。由于城市群复合交通网络节点的负载与容量不一定呈线性关系,同时,在现实交通网络中,空闲容量大的站点可以分担更多的交通流。因此,本研究采用基于节点空闲容量比例的择优分配模型,对节点负载进行重分配。用Pij(t)表示t时刻节点vi向其邻居节点vj的分配概率:
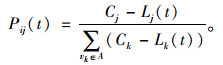
|
(6) |
(1) 若vi为暂停节点:
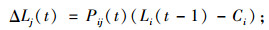
|
(7) |
(2) 若vi为失效节点:
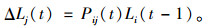
|
(8) |
式中,ΔLj(t)为t时刻vj接受的新负载量;Cj,Ck,Ci分别为节点vj,vk,vi的容量;Lj(t),Lk(t),Li(t-1)分别为节点vj,vk,vi在相应时刻的负载;A表示节点vi的邻居节点集合。
2.4 不完全信息攻击策略目前,研究网络抗毁性大多假定网络面临2种攻击策略即随机性攻击和蓄意性攻击。随机攻击假设攻击前无法获得网络的任何信息,随机选择对象进行攻击,而蓄意攻击则是假设已获取网络的全部准确信息,按照一定的策略选择对象进行攻击。然而,在现实生活中,攻击者在攻击前获得网络的信息是一种不完全信息,即使可以获得网络的全部信息,但这些信息也可能存在偏差。
为了更接近于真实情况,根据灰色系统理论:设X为观测信息的模糊度,X∈[0, 1];设随机变量δ落在区间[0, 1]长度相等的各自子区间概率相等,即δ在[0, 1]满足均匀分布;网络中节点的最大负载和最小负载分别用Lmax,Lmin表示;节点vi的真实负载用Li表示,观测负载Li′为:
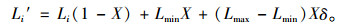
|
(9) |
当X=0时,Li′=Li,节点负载观测值与真实值相等,对应的攻击策略便是蓄意攻击;当X=1时,Li′=Lmin+(Lmax-Lmin)δ,Li′是在[Lmin, Lmax]上均匀分布的随机变量,对应的攻击策略便是随机攻击;当X介于(0, 1)之间,观测到的信息便是受模糊度影响的不完全信息,对应的攻击策略即不完全信息攻击策略。
2.5 级联抗毁性评估为了衡量级联失效对网络抗毁性造成的影响,采用节点遭受攻击后,网络最终达到稳定状态时的最大连通子图相对规模来对其进行评估。但考虑到城市群复合交通网络中不同节点之间的差异较大,仅用失效节点的数目来评估级联失效造成的影响明显是不合理的。需要对传统的最大连通子图相对规模进行修正:
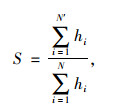
|
(10) |
式中,hi为节点vi的点权;N′为复合交通网络发生级联失效后达到稳定状态时最大连通子图内的节点数;N为未发生级联失效前复合交通网络内的节点数。当S=1时,网络处于全连通状态,抗毁性最强。修正后的最大连通子图相对规模既考虑了节点的重要程度,又表征了网络级联失效的规模。
n次攻击使网络瘫痪后,将每次得到的最大连通子图相对规模之和的平均值定义为修正最大连通子图平均相对规模,用Sn表示:
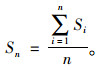
|
(11) |
基于上述分析,构建城市群复合交通网络级联抗毁性模型,具体步骤如下:
Step 1:网络初始化。在城市群复合交通网络G(V, E, W, H)中,按照式(1)~(4)对普通节点和复合节点加载初始负载Li(0)、容量Ci及过载能力φCi。
Step 2:输入观测信息模糊度X。当X=0时,对应的攻击策略是蓄意攻击;当X=1时,对应的攻击策略是随机攻击;当X介于(0, 1)之间,对应的攻击策略是不完全信息攻击策略。
Step 3:攻击节点。按照式(9)计算网络中所有节点的观测负载Li′,攻击观测负载最大的节点失效,从网络中删除该节点。
Step 4:负载分配。删除失效节点后,按照式(6)确定的节点剩余容量分配概率Pij(t),将删除失效节点的负载按照式(8)分配给邻居节点。
Step 5:更新网络节点负载Li(t)。按照式(5)计算t时刻失效节点集合Vut、暂停节点集合Vpt、正常节点集合Vnt。
Step 6:判断t时刻是否发生级联失效现象。若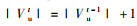
Step 7:负载重分配。将级联失效引发的失效节点负载按照式(8)进行重分配、暂停节点负载按照式(7)进行重分配,更新t+1时刻失效节点集合Vut+1、暂停节点集合Vpt+1、正常节点集合Vnt+1。
Step 8:判断级联失效现象是否结束。若Vut+1=Vut,则网络没有新节点变为失效状态,转至Step 9,否则转至Step 7。
Step 9:输出城市群复合交通网络修正最大连通子图相对规模S。
Step 10:判断攻击是否结束。若|Vnt+1|=0,则转至Step 11,否则转至Step 3。
Step 11:攻击结束。输出修正最大连通子图平均相对规模Sn和累计攻击次数。
3 呼包鄂城市群实例仿真分析 3.1 复合交通网络构建本研究以呼包鄂城市群为例进行实例分析,以城市群内所有汽车站、火车站为节点,若站点之间通车,则节点以边相连,分别构建道路交通子网G1、轨道交通子网G2。其中,|V1|=203,|E1|=316, |V2|=24, |E2|=23。由于呼包鄂城市群位于我国西北部内陆地区,无水路运输且航空运输网络单一,承担城市群内客货运输比例较小,故将道路交通子网和轨道交通子网进行叠加,构建城市群复合交通网络G。其中,|V′|=10,|V″|=5,V=V1∪V2∪V″\V′,|V|=217,|E′|=6,|E″|=3, E=E1∪E2∪E″\E′, |E|=347。所有合并节点、复合节点、合并连边、复合边如表 1、表 2所示。
| 合并节点 | 交通网络类型 | 复合节点 | 距离/m | 旅客换乘步行时间/min |
| 呼和浩特汽车西站 | 道路交通子网 | 呼和浩特汽车西站-火车站 | 200 | 3 |
| 呼和浩特火车站 | 轨道交通子网 | |||
| 察素齐火车站 | 轨道交通子网 | 察素齐汽车站-火车站 | 10 | 1 |
| 察素齐汽车站 | 道路交通子网 | |||
| 包头东河汽车站 | 道路交通子网 | 包头东河汽车站-火车东站 | 730 | 8 |
| 包头火车东站 | 轨道交通子网 | |||
| 东胜汽车站 | 道路交通子网 | 东胜汽车站-火车西站 | 800 | 9 |
| 东胜火车西站 | 轨道交通子网 | |||
| 达拉特旗汽车站 | 道路交通子网 | 达拉特旗汽车站-火车西站 | 320 | 5 |
| 达拉特旗火车西站 | 轨道交通子网 |
| 合并连边 | 交通网络类型 | 复合边 |
| 呼和浩特汽车西站至察素齐汽车站 | 道路交通子网 | 呼和浩特汽车西站-火车站至察素齐汽车站-火车站 |
| 呼和浩特火车站至察素齐火车站 | 轨道交通子网 | |
| 达拉特火车站至包头东河火车站 | 轨道交通子网 | 达拉特旗汽车站-火车西站至包头东河汽车站-火车东站 |
| 达拉特汽车站至包头东河汽车站 | 道路交通子网 | |
| 东胜汽车站至达拉特汽车站 | 道路交通子网 | 东胜汽车站-火车西站至达拉特旗汽车站-火车西站 |
| 东胜火车站至达拉特火车站 | 轨道交通子网 |
为了分析轨道子网的叠加对节点、边性能的影响,现对城市群复合交通网络中的节点、边逐个攻击,并与其叠加之后的复合节点、边进行特性对比。固定X=0, φ=1.15,θ1=θ2=0.1,α=0.5,β=1,利用式(1)、式(2)分别计算节点初始负载,利用式(3)、式(4)分别计算节点容量。计算边初始负载将与该条边直接相连的所有节点的初始负载求和,计算边容量将与该条边直接相连的所有节点的容量求和。网络发生级联失效后的相关特征值如表 3、表 4所示,其中S变化量表示该节点失效前后网络的修正最大连通子图相对规模大小之差。
| S变化量 | 节点初始负载 | 节点容量 | ||||||
| 合并节点(复合节点) | 道路网络 | 复合网络 | 道路网络 | 复合网络 | 道路网络 | 复合网络 | ||
| 呼和浩特汽车西站(呼和浩特汽车西站-火车站) | 0.175 8 | 0.156 6 | 270.365 1 | 490.611 2 | 405.548 1 | 735.916 2 | ||
| 包头东河汽车站(包头东河汽车站-火车东站) | 0.193 2 | 0.111 5 | 195.212 2 | 381.008 3 | 292.819 5 | 571.512 3 | ||
| S变化量 | 边初始负载 | 边容量 | ||||||
| 合并连边(复合边) | 道路网络 | 复合网络 | 道路网络 | 复合网络 | 道路网络 | 复合网络 | ||
| 呼和浩特汽车西站至察素齐汽车站(呼和浩特汽车西站-火车站至察素齐汽车站-火车站) | 0.002 6 | 0.002 1 | 7.724 7 | 16.8265 | 11.587 1 | 25.239 8 | ||
| 东胜汽车站至达拉特汽车站(东胜汽车站-火车西站至达拉特旗汽车站-火车西站) | 0.001 2 | 0.000 8 | 2.368 2 | 4.865 8 | 3.552 3 | 7.298 7 | ||
以攻击呼和浩特汽车西站为例,由表 3的仿真结果可以看出,由于轨道子网的叠加使S变化量由0.175 8减少到0.156 6,其他复合节点也呈现出相似的变化规律。表明网络的叠加减小了这些节点对网络级联抗毁性的影响程度。同时,复合后节点的容量和过载承受能力成倍提高,且容量的变化量大于初始负载的变化量,利于负载疏导。对城市群复合交通网络中的部分边进行相似的对比分析,发现对于同样的边而言,失效后对复合交通网络级联抗毁性造成的破坏程度更小,同样说明网络的叠加减小了这些边对网络级联抗毁性的影响程度,而且攻击节点的攻击性要明显强于攻击边。因此,加强对复合节点交通流的疏导显得尤为重要。
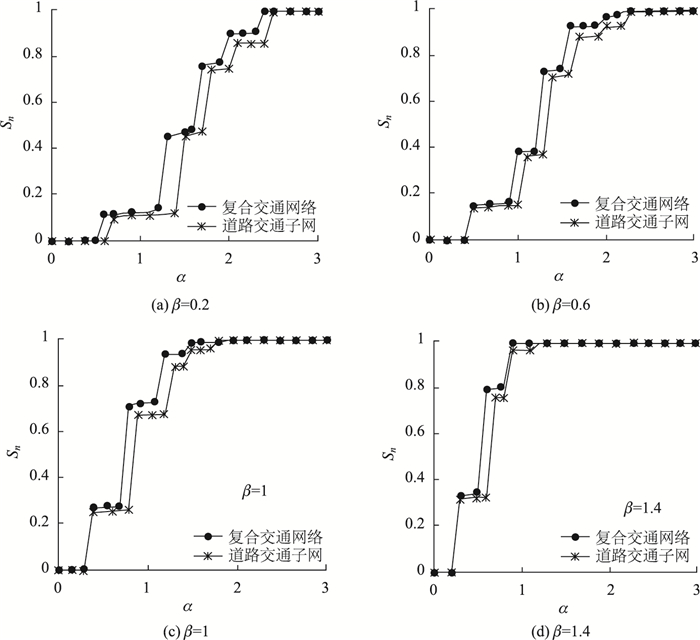
3.2 容量参数对网络级联抗毁性的影响为了研究不同容量参数对城市群复合交通网络及其子网级联抗毁性的影响,现固定X=0, θ1=θ2=0.1, φ=1.15,仿真α, β与Sn的关系曲线,仿真流程如2.6节所述。考虑到呼包鄂城市群轨道交通子网节点数较少,网络结构单一,因此,只对比复合交通网络和道路交通子网的变化,仿真结果如图 2所示。其中,Sn表示n次攻击之后,S的平均值。
|
| 图 2 网络级联抗毁性随容量参数α、β变化曲线 Fig. 2 Curves of network invulnerability against cascading failure varying with capacity parameters α and β |
| |
从图 2的仿真结果可以看出,对于固定的β值,随着α的增大,Sn逐渐增大,网络的级联抗毁性不断增强。对于固定的α值,随着β的增大,Sn同样逐渐增大。因此,α,β的增大都可提高网络的级联抗毁性。但当α=1.2时,若网络任意一节点失效都不会引发网络级联失效即Sn=1,β需增大到1.4,当β=1.2时,若Sn=1,α只需增大到1。因此,容量参数α对网络级联抗毁性的影响要弱于β。同时,无论容量参数如何取值,复合交通网络的级联抗毁性均优于道路子网。究其原因是由于轨道子网的叠加增大了网络的聚集程度,提高了网络稳定性。
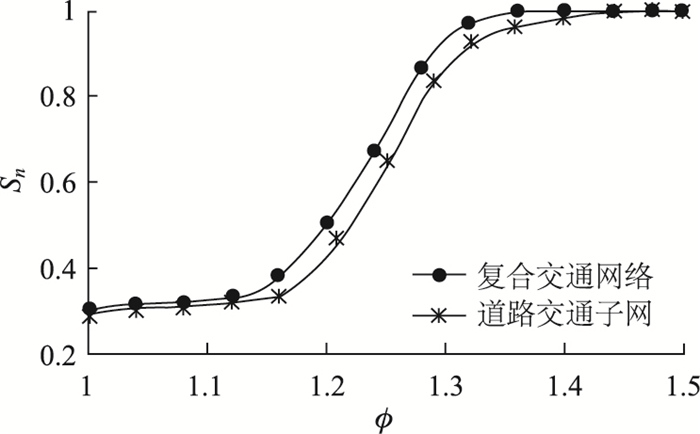
3.3 过载能力调节参数对网络级联抗毁性的影响为了研究过载能力调节参数对网络级联抗毁性的影响,现固定X=0, θ1=θ2=0.1, α=β=0.3,仿真φ与Sn的关系曲线,仿真流程如2.6节所述,仿真结果如图 3所示。
|
| 图 3 网络级联抗毁性随过载能力调节参数φ变化曲线 Fig. 3 Curves of network invulnerability against cascading failure varying with overload capacity adjustment parameter φ |
| |
从图 3仿真结果可以看出,复合交通网络和道路交通子网起初对于φ的增大变化十分平缓,究其原因是由于网络中失效和正常节点所占比例较大。当φ继续增大,即φ≥1.15时,两条曲线变化较为剧烈。此时,由于过载承受能力成倍增长,使得原先的失效节点大量转换为暂停节点,因此,负载按节点剩余容量择优分配网络达到稳定状态后,修正最大连通子图相对规模中增加了这部分暂停节点承担的负载,导致Sn迅速增大。当φ进一步增大,即φ≥1.35时,Sn几乎保持稳定,网络极强的过载承x受能力使得任意一节点失效均不在引发级联失效,网络级联抗毁性达到最强。
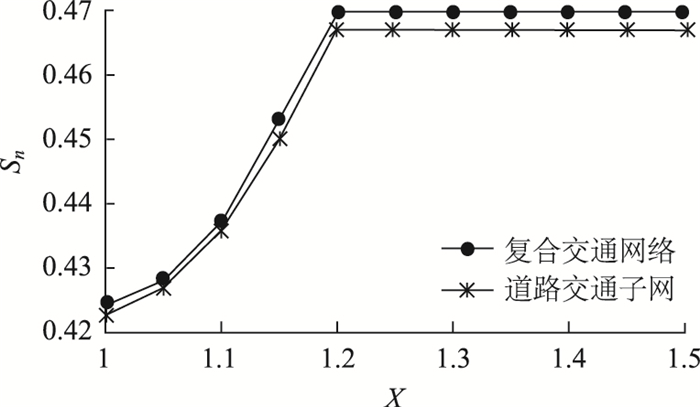
3.4 观测信息模糊度对网络级联抗毁性的影响为了分析观测信息模糊度对复合交通网络及其子网级联抗毁性造成的影响,现固定φ=1.15, θ1=θ2=0.1, α=β=0.3,对比分析不同观测信息模糊度X下,修正最大连通子图平均相对规模Sn的变化。仿真结果取10次独立试验的平均值,仿真流程如2.6节所述,仿真结果如图 4所示。
|
| 图 4 网络级联抗毁性随观测信息模糊度X变化曲线 Fig. 4 Curves of network invulnerability against cascading failure varying with observation information fuzzy degree X |
| |
由图 4仿真结果可看出,不论复合交通网络还是道路子网,对于Sn而言,当X≤0.4时,增长都较为平缓;当X≥0.4时,增长速度保持不变。说明观测信息的模糊度存在明显的阈值。对于呼包鄂城市群复合交通网络而言;当X减小到0.4时,攻击者便可迅速找到关键节点,造成网络大规模级联失效。
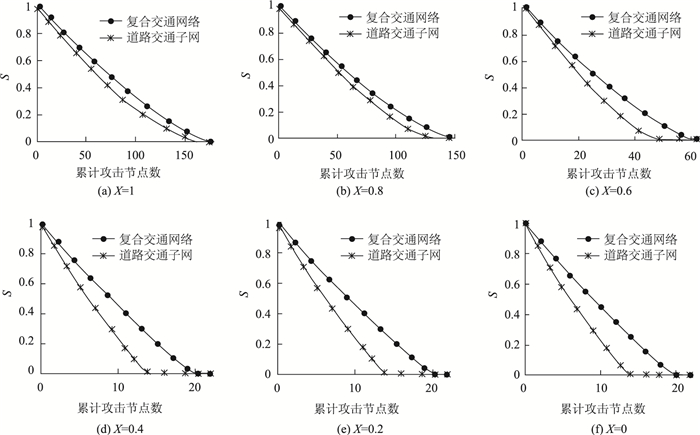
为了进一步分析在不同模糊度X下,复合交通网络及其子网在攻击过程中表现出的级联抗毁性与累计攻击节点数目的关系。现固定X,对比累计攻击节点数与S的关系,仿真结果如图 5所示。
|
| 图 5 不同模糊度下修正最大连通相对规模与累计攻击节点数的关系 Fig. 5 Relationship between modified maximal connected relative scale and cumulative number of attack nodes under different fuzzy degrees |
| |
由图 5可明显看出,不论复合交通网络还是道路子网,随着X的减小,网络达到级联崩溃所需累计攻击的节点数都在减少。当X≤0.4时,不完全信息下的攻击策略,其攻击效果与蓄意攻击相同,累计攻击网络10%的节点便可令复合交通网络迅速瓦解,使得S降为0。究其原因是由于当X减小到0.4时,X达到阈值,网络中的关键节点被迅速识别,此后X再减小对每次攻击对象选择产生的影响变得微乎其微。因此,呼包鄂城市群复合交通网络的关键节点数量应该维持在10%。表 5列出了这部分关键节点,由于观测信息模糊度存在的阈值现象,对关键节点加强防护显得尤为重要。
| 节点名称 | S | 初始负载 | 过载承受 |
| 呼和浩特长途汽车站 | 0.939 1 | 682.36 | 784.78 |
| 呼和浩特汽车西站-火车站 | 0.879 7 | 490.61 | 564.26 |
| 包头东河汽车站-火车东站 | 0.821 8 | 381. 01 | 438.22 |
| 呼和浩特通达汽车站 | 0.765 4 | 356.26 | 409.71 |
| 达拉特旗汽车站-火车西站 | 0.710 5 | 256.98 | 295.53 |
| 东胜汽车站-火车西站 | 0.657 1 | 289.36 | 332.76 |
| 包头昆区汽车站 | 0.605 3 | 248.62 | 285.94 |
| 察素齐汽车站-火车站 | 0.553 4 | 210.3 | 241.85 |
| 鄂托克前旗汽车站 | 0.503 1 | 285.63 | 328.48 |
| 固阳县汽车站 | 0.452 7 | 200.35 | 230.42 |
| 土默特右旗汽车 | 0.399 8 | 263.25 | 302.75 |
| 鄂托克旗汽车站 | 0.348 5 | 198.25 | 227.99 |
| 伊金霍洛旗汽车站 | 0.298 6 | 162.3 | 186.65 |
| 杭锦旗汽车站 | 0.250 3 | 120.3 | 138.35 |
| 三道河汽车站站 | 0.203 5 | 80.65 | 92.75 |
| 百灵庙汽车站 | 0.158 2 | 75.65 | 87.02 |
| 托县汽车站 | 0.112 9 | 89.36 | 102.77 |
| 乌审旗汽车 | 0.069 1 | 100.25 | 115.29 |
| 满都拉汽车站 | 0.026 3 | 69.25 | 79.65 |
| 和林县汽车站 | 0.009 5 | 78.76 | 90.58 |
3.5 仿真总结
(1) 通过对比复合前后节点、连边特征值的变化,发现合并节点、合并连边初始负载、容量成倍增大,但容量的变化量大于初始负载的变化量,利于负载疏导。同时,轨道子网的叠加增大了节点的过载承受能力,将大量失效节点转变为暂停节点,有效控制了级联失效的传播范围。因此,复合交通网络的构建提高了单一运输方式交通子网的级联抗毁性。
(2) 容量参数α,β过载能力调节参数φ越大,复合交通网络的容错性越高,最大连通子图平均相对规模越大,网络的级联抗毁性越强。因此,可以通过增大节点容量并提高其过载承受能力,防止级联失效对复合交通网络产生的不利影响。
(3) 通过观测信息模糊度X这一可调参数来控制获取信息的精度,仿真不完全信息下网络表现出的级联抗毁性,发现X越大,网络级联抗毁性不一定越强,X产生作用的阈值为0.4。当X≤0.4时,网络级联抗毁性对X的变化并不敏感,不完全信息攻击策略产生的攻击效果都与蓄意攻击相同。
(4) 通过对比分析不同观测信息模糊度下修正最大连通子图相对规模与累计攻击节点数的关系,识别出了呼包鄂城市群复合交通网络的关键节点。通过对识别出的关键节点加强防护,避免其发生内部故障,可以进一步优化复合交通网络的级联抗毁性,减小部分站点失效导致网络瘫痪的风险。
4 结论本研究提出了城市群复合交通网络及其级联失效模型的构建方法,在考虑节点暂停状态对网络性能影响的基础上,对复合交通网络级联抗毁性进行了深入研究。同时,针对复合交通网络中节点与连边的差异性修正了抗毁性测度指标,并引入基于观测信息模糊度的不完全信息攻击方式,进一步完善了攻击策略。最后以呼包鄂城市群为例进行了实例仿真,给出优化复合交通网络级联抗毁性的方法。
通过实证研究发现城市群交通子网的叠加可以增大节点的过载承受能力,将大量失效节点转变为暂停节点。同时,容量参数、过载能力调节参数越大网络的级联抗毁性越强,而观测信息模糊度越大,网络级联抗毁性不一定越强,其产生作用存在阈值。
以上得出的这些结论,不仅具有很强的实用价值,可以为呼包鄂城市群交通网络的维护提供直接依据,促进交通运输系统安全运营,而且对于未来我国城市群内不同运输方式间的协调发展研究具有重要的理论意义。后续研究工作将进一步考虑城市群内各交通子网的方向性对复合交通网络级联失效产生的影响。
| [1] |
MOTTER A E, LAI Y C. Cascade-based Attacks on Complex Networks[J]. Physical Review E:Statistical, Nonlinear, and Soft Matter Physics, 2002, 66(2): 114-129. |
| [2] |
LI S, LI L, YANG Y, et al. Revealing the Process of Edge-based-attack Cascading Failures[J]. Nonlinear Dynamics, 2012, 69(3): 837-845. |
| [3] |
BABAEI M, GHASSEMIEH H, JALILI M. Cascading Failure Tolerance of Modular Small-world Networks[J]. IEEE Transactions on Circuits & Systems Ⅱ:Express Briefs, 2011, 58(8): 527-531. |
| [4] |
BAO Z J, CAO Y J, DING L J, et al. Comparison of Cascading Failures in Small-world and Scale-free Networks Subject to Vertex and Edge Attacks[J]. Physica A:Statistical Mechanics & Its Applications, 2009, 388(20): 4491-4498. |
| [5] |
王甲生, 吴晓平, 陈永强. 加权无标度网络级联抗毁性研究[J]. 复杂系统与复杂性科学, 2013, 10(2): 13-19. WANG Jia-sheng, WU Xiao-ping, CHEN Yong-qiang. Invulnerability of Weighted Scale-free Networks against Cascading Failure[J]. Complex Systems and Complexity Science, 2013, 10(2): 13-19. |
| [6] |
彭兴钊, 姚宏, 张志浩, 等. 基于节点蓄意攻击的无标度网络级联抗毁性研究[J]. 系统工程与电子技术, 2013, 35(9): 1974-1978. PENG Xing-zhao, YAO Hong, ZHANG Zhi-hao, et al. Research on Cascading Invulnerability of Scale-free Networks under Node-based-attack[J]. Systems Engineering and Electronics, 2013, 35(9): 1974-1978. |
| [7] |
BULDYREV S V, HAVLIN S, PARSHANI R, et al. Catastrophic Cascade of Failures in Interdependent Networks[J]. Nature, 2010, 464(7291): 1025-1028. |
| [8] |
陈世明, 邹小群, 吕辉. 面向级联失效的相依网络鲁棒性研究[J]. 物理学报, 2014, 63(2): 428-437. CHEN Shi-ming, ZOU Xiao-qun, LÜ Hui. Research on Robustness of Interdependent Network for Suppressing Cascading Failure[J]. Acta Physica Sinica, 2014, 63(2): 428-437. |
| [9] |
CHEN Z, DU W B, CAO X B, et al. Cascading Failure of Interdependent Networks with Different Coupling Preference under Targeted Attack[J]. Chaos Solitons & Fractals, 2015, 80: 7-12. |
| [10] |
WANG J, Li Y, ZHENG Q. Cascading Load Model in Interdependent Networks with Coupled Strength[J]. Physica A:Statistical Mechanics & Its Applications, 2015, 430: 242-253. |
| [11] |
种鹏云, 帅斌. 危险品运输关联网络级联失效建模及耦合特性[J]. 交通运输系统工程与信息, 2015, 15(5): 150-156. CHONG Peng-yun, SHUAI Bin. Cascading Failure Model and Coupling Properties for Interdependent Networks of Hazardous Materials Transportation[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(5): 150-156. |
| [12] |
彭兴钊, 姚宏, 杜军, 等. 负荷作用下相依网络中的级联故障[J]. 物理学报, 2015, 64(4): 351-358. PENG Xing-zhao, YAO Hong, DU Jun, et al. Load-induced Cascading Failure in Interdependent Network[J]. Acta Physica Sinica, 2015, 64(4): 351-358. |
| [13] |
韩海艳, 杨任农, 李浩亮, 等. 双层相依指挥控制网络级联失效研究[J]. 中南大学学报:自然科学版, 2015(12): 4542-4547. HAN Hai-yan, YANG Ren-nong, LI Hao-liang. Cascading Failure of Two-layered Interdependent Command and Control Network[J]. Journal of Central South University:Science and Technology Edition, 2015(12): 4542-4547. |
| [14] |
吴建军. 城市交通网络拓扑结构复杂性研究[D]. 北京: 北京交通大学, 2008. WU Jian-jun. Study on Complexity of Topology Structure in Urban Traffic Network[D]. Beijing: Beijing Jiaotong University, 2008. |
| [15] |
王正武, 况爱武, 王贺杰. 考虑级联失效的交通网络节点重要度测算[J]. 公路交通科技, 2012, 29(5): 96-101. WANG Zheng-wu, KUANG Ai-wu, WANG He-jie. Calculation of Node Important Degree for Traffic Network Considering Cascading Failure[J]. Journal of Highway and Transportation Research and Development, 2012, 29(5): 96-101. |
| [16] |
CHEN B Y, LAM W H K, SUMALEE A, et al. Vulnerability Analysis for Large-scale and Congested Road Networks with Demand Uncertainty[J]. Transportation Research Part A:Policy & Practice, 2012, 46(3): 501-516. |
| [17] |
JENELIUS E, MATTSSON L G. Road Network Vulnerability Analysis of Area-covering Disruptions:A Grid-based Approach with Case Study[J]. Transportation Research Part A:Policy & Practice, 2012, 46(5): 746-760. |
| [18] |
王正武, 王杰, 黄中祥. 控制城市道路交通网络级联失效的关闭策略[J]. 系统工程, 2016, 34(2): 103-108. WANG Zheng-wu, WANG Jie, HUANG Zhong-xiang. Closing Strategies to Control Cascading Failure in Urban Road Traffic Networks[J]. Systems Engineering, 2016, 34(2): 103-108. |
 2018, Vol. 35
2018, Vol. 35
