扩展功能
文章信息
- 李浩, 赵池航
- LI Hao, ZHAO Chi-hang
- 基于线性分割的车辆对地平均压强实时监测系统
- Real-time Monitoring System of Average Pressure of Vehicle to Pavement Based on Linear Segmentation
- 公路交通科技, 2018, 35(6): 80-86
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(6): 80-86
- 10.3969/j.issn.1002-0268.2018.06.012
-
文章历史
- 收稿日期: 2017-03-28
2. 东南大学 交通学院, 江苏 南京 210000
2. School of Transportation, Southeast University, Nanjing Jiangsu 210000, China
车辆超载,是一个全球性的道路交通安全问题,会导致人员、车辆、公路基础设施的损毁。目前对车辆超载的界定依据是车辆总重和单轴/轴组是否超重,即车辆对地直接压力的大小。然而受轮胎直径、宽度、气压等参量的影响,在同等压力状态下,不同大小的受力面积受到的影响差异巨大。例如大型多轴复轮车辆,即使整车负载100 t,也不会造成路面损坏;相反,一辆两轴车,在高胎压状态下,即使只装载20 t,其对路面造成的破坏远大于多轴复轮车辆。因此,仅依据车辆荷载来判断是否超载是很不精确的。近年来,随着传感器技术以及信息感知技术的发展,对于动态车辆实时对地压强的测量方法被众多学者以及科研机构提上日程。例如长安大学王选仓教授于2016年提出了一种以窄条压电式传感器辅以小弯板作为动态称重单元,以激光扫描仪为测面单元的对地压强检测系统,该系统在车速小于5 km/h的速度下识别率能达到85%;学者Carlos A. Duchanoy于2016年提出了一种新型的递归神经网络软质传感器系统,用于估计和预测汽车轮胎与地面接触面积。该系统通过安装在车轮上的11个传感点来反馈车轮实时对地接触面积,识别率达到85%。中国汽车工程学会越野车技术分会于2016年学术年会上提出一种使用图像处理手段对轮胎花纹印迹面积进行计算的方法[1]。然而无论哪种方法都无法完全做到车辆高速运动(15 km/h以上)状态下的轮胎对地压强实时监测。这是由于车辆在运动状态下,受道路环境的影响,会产生不规则震动,这种震动导致车辆对地压力以及轮胎触地面积每一时刻都产生变化,而测量车重和轮胎触地面无法使用同一设备进行,导致重量与轮胎触地面积无法实时进行匹配,会产生较大误差,特别是在非正常行驶状态下。例如突然加减速时,误差会显著增加[2]。因此要采用轮胎对地压强作为超限依据,存在着很多困难。基于以上问题,本研究将动态称重模型进行了改进,利用线性分割原理,将传感器响应按照时间点进行切割,得到瞬时对地压力,同时根据响应电频的积分与车辆瞬时速度相结合,得到轮胎触地长度,使用一种混合模型将2种不同的量值相匹配,再配合测宽阵列得到实时轮胎触地宽度,最终得到精确的车辆轮胎实时对地压强,使轮胎实施对地压强的监测得以实现。
1 整体框架设计系统整体由动态称重模块以及对地接触面积测量模块构成,动态称重模块将得到的对地压力响应进行线性分割,得到多个对地压力峰值。对地接触面积测量模块将分割后的压电信号进行线性积分、求和,得到与每个分割点所对应的触地长度。将每个分割峰值响应时刻作为测宽阵列的取样点,得到相应的轮胎触地宽度,将3个量值进行计算,即得到动态车辆实时对地压强值。
各个量值计算依据以及推导过程如下:充气轮胎属于流体,轮胎内部以及轮胎对地的压强分布符合帕斯卡原理,因此轮胎整体对地压强,可认为是平均压强[3],即ATP(Average Tyre Presure),可记为:
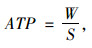
|
(1) |
式中,W为车体重量;S为轮胎触地面积。
在车辆运动状态下,车辆的轮重可由动态称重模型表示[4],即:
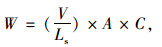
|
(2) |
式中,Ls为传感器宽度;V为车辆速度;A为车轮负载的波形面积;C为标定系数。
轮胎与地面接触的区域如图 1所示,近似于矩形,用长和宽即可表述其面积。长度为车轮滚动、前进方向与地面接触的长度,记为h,利用压电石英测力传感器进行测量,这种传感器宽度为50 mm,小于轮胎最大轮迹(经有限元计算模型确定,车辆轮胎印迹长度不超过400 mm,如若传感器最小量程大于400 mm无法进行长度测量,类似于无法用最小刻度为厘米的尺子测量毫米级别的物体),经过线性分割,可将传感器以类似于“扫描”的方式获取车轮沿触地长度方向的负荷分布,经过积分变换得到触地长度。宽度为平行车轴方向,车轮与地面接触部分的宽度,记为k,其可由测宽线阵测得。长、宽之乘积为车轮触地面积,记为S,即S=h×k在已知车轮荷载条件下,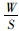

|
| 图 1 轮胎触地横向扫描图 Fig. 1 Horizontal scan diagram of tire contact to earth |
| |
2 模型建立与优化 2.1 动态称重模型的优化
利用WIM稀疏阵列对动态车辆进行称重,其基本模型的数学抽象如式(3)所示:
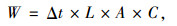
|
(3) |
式中,L为传感器间隔距离;Δt为前后两根传感器响应的时间差;A为车轮负载的波形面积;C为标定系数。
由式(3)可知,由基本模型得到的动态称重数据与车辆速度以及车轮负载整体响应有关,而对于实时监测所需要的瞬时响应以及与之对应的实时轮迹长度无法通过式(3)得到。本研究采用线性分割法将模型进行改进。首先将传感器响应波形进行线性分割,按照划分的时点取极值,使之与分割时点相对应即得到轮胎对地瞬时压力;其次将时点进行线性积分、求和即得到相应的瞬时轮迹长度,最后根据分割时点,将瞬时压力与瞬时轮迹长度相对应则得到准确的瞬时压力与触地长度,推导过程如下:
设轮胎碾压传感器稀疏阵列得到的响应经过低通滤波(高斯牛顿法)后,其响应波形可变换为与整车响应相关的高斯拉普拉斯函数即:
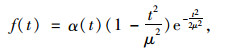
|
(4) |
式中,α(t)为整车响应波形的面积积分和;μ为在单位时间内行驶速度的高斯响应标准差;t为车轮通过传感器的响应时间。
轮胎在通过传感器时与地面有相对滑动,车轮荷载由所碾压的路面及传感器共同分担,传感器可视为相对静止的分割线,并以矢量分割的方式获取了车轮沿触地长度方向的荷载分布。这时整车重量可由分割后的每个时间点的瞬时重量的积分和表示,记为:
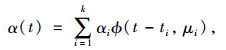
|
(5) |
式中,α(t)为整车响应波形面积积分和;αi为第i个轴时刻的响应峰值;t为车轮整体通过时间;φ(t-ti, μi)为第i个轴的响应变化函数。
则整车重量可表示为:

|
(6) |
式中,T为通过传感器间距的时间;L为两条传感器的间距;α(t)为整车响应波形面积;C为标定系数。
这时整车重量或单个轮/轴组的重量就被转化为单个时刻(精确度与ti分割大小相关)得到的重量的积分和,便于与对应时刻的轮胎触地长度进行匹配。
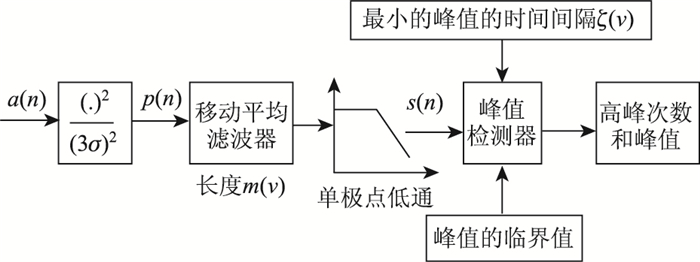
2.2 轮胎触地长度测量模型学者S Hernandez在文献[5]中提出了一种利用单只传感器测量轮胎对地响应的方法来估算车轮触地响应位置,该方法原理图如图 2所示。
|
| 图 2 触地点检测算法框图 Fig. 2 Block diagram of contact to earth point detection algorithm |
| |
该算法从测得的加速度找到平稳的功率信号,并且能定位充分分离的信号峰值所处的时间。原始信号a(n)被归一化, 使得不在轴上的信号幅度低于1,把归一化后的信号加权平方,得出功率信号P(n)。这一步增加了峰值信号与基底噪声之间的差异, 因为噪声加权平方后被减弱,然而峰值信号比1大,平方后变大。下一步,将P(n)低通滤波从而实现对P(n)进行的平滑处理。这个阶段输出的信号的功率与m个响应点的平均功率s(n)相等,因此它与m个样本的总功率成正比。由于触地点引发的对地加速度与车速成正比,因此触地长度可由车速和响应时间来表示[5]。根据此模型,结合式(4)可知,将传感器响应波形按照时间点分割求极值,有效波形(仅轮胎碾压传感器时才能产生的信号波形)所包含的切片总数即代表以mm为单位的轮胎触地长度。第1个响应点可记为t1,车辆从第1个响应点至第i个响应点所用的时间记为ti,这时ti可以用车速v和传感器宽度di的比所表示,即
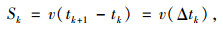
|
(7) |
式中,tk为第k个触点的响应时间;v为车轮通过传感器的瞬时速度。
当响应时间t与式(6)中的响应时刻相对应时,得到的距离Sk为轮胎触地长度。
2.3 轮胎触地宽度测量因石英称重传感器内部多个换能单元(即石英晶片)采用并联输出方式,因此轮胎触地宽度无法直接通过压电石英称重传感器获得,只能依靠另外的、沿石英传感器轴线方向(即与行驶方向垂直)分布的一维传感器阵列获得[7],该阵列的功能是在一个维度中判断轮胎所占的位置即轮胎触地宽度[8]。因压电石英传感器经过线性分割后,其可认为是地面的一部分,与地面共同承担车轮荷载,同时车辆轮迹长度为80~400 mm,只要将测宽线阵与压电石英传感器并排放置,且其宽度之和小于80 mm时,就能够保证两者测量时序的同步性。
测宽线阵从原理上来讲基本分为压力开关,压力传感器,表面波或光电扫描器件。每种器件特性如表 1所示。
| 元器件类型 | 测量方式 | 置信度 | 耐久性 | 受环境影响 |
| 压力开关 | 接触式 | 高 | 高 | 一般 |
| 压力传感器 | 接触式 | 一般 | 一般 | 小 |
| 表面波扫描器 | 非接触式 | 高 | 一般 | 大 |
| 光电扫描器 | 非接触式 | 高 | 低 | 大 |
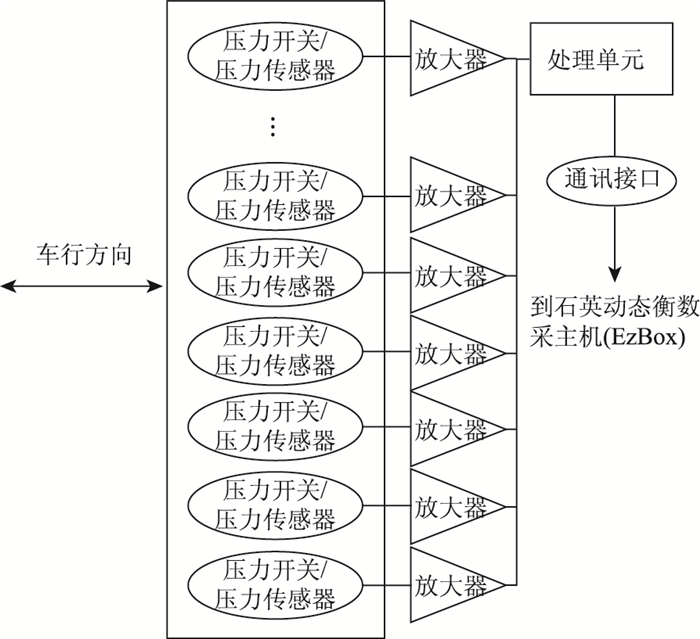
由表 1所列可知,压力开关耐久性好,然而设备在安装后易出现机械位移的现象,当公路环境恶劣时,会产生填充位移空间,并固化使之不能产生位移,因此使用寿命严重降低,一般3~5个月就会出现故障[9],压力传感器可靠性较好,但其内部电路受上面层形变影响较大,疲劳后易发生漂移[10]。表面波和光电扫描方式易受环境影响不适合此类应用。因此选择接触式器件较为合理[11]。同时为了提升器件的可靠性,可采用压力传感器与压力开关互补排列的方式进行放置,同时将测量值转化为开关量。其示意图见图 3。
|
| 图 3 测宽线阵原理图 Fig. 3 Width gauge linear array principle |
| |
如图 3所示,测宽线阵分为数据采集与数据处理2个部分。数据采集部分由压力传感器、压力开关、电荷放大器构成。压力传感器与压力开关采用交错放置的布局,这种设计能够弥补2种传感器件间的劣势,实现互补同时只需记录哪些传感点有响应,即将轮胎触地宽度转换为开关量进行统计。电荷放大器将采集到的信号经处理单元处理后,交由压电石英传感器数采主机进行数据融合,使之与所得到的实时车重与轮胎触地长度数据进行匹配。
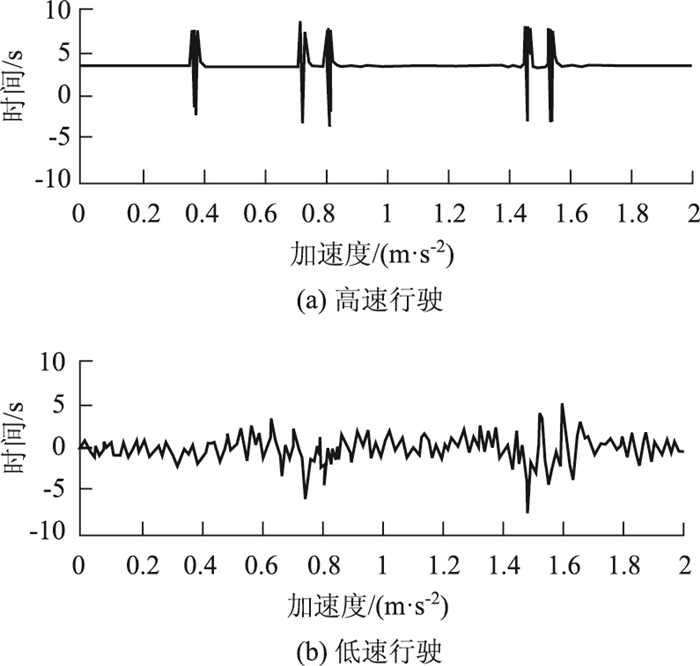
2.4 数据的优化处理由于动态称重的结果是一个代换后的估计值,同时轮胎触地长度与轮胎震动响应之间存在较大关系(同对地压力影响相同),因此会产生一定的误差,例如当车辆以不同速度通过传感器时,所产生的震动波形存在较大差异[12]。其波形响应如图 4所示。
|
| 图 4 不同车速下传感器响应波形图 Fig. 4 Sensor response waveforms at different vehicle speeds |
| |
由图 4可知在车辆通过传感器时,当车速在一定范围内时(经试验验证8~60 km/h),其不规则振动带来的噪声较小,当车速较低时,不规则振动带来的噪声会随着车速的降低而增加,同时,噪声的大小还与路面状况有一定的关系[13]。因此所得到的数据需经过优化处理。目前常用的方法有卡尔曼滤波法、约束最小二乘法、二重积分法等[14]。由于文中的数据以及计算方法是由多个混合模型得到的,因此需根据每部分的模型对数据进行优化。受学者V D Kollipara在文献[15]中的方法所启发,整车重量以及触地长度的计算均采用同一基本模型进行改进时,采用单一的优化方法往往达不到效果,如若将测量的响应以一系列的函数f(k, t)来表示,再代入模型进行优化,就能够将复杂问题简单化[15]。文中采用的基础模型均为动态称重模型,噪声为车辆不规则震动产生的噪声,因此函数可以根据所用到的路面响应的基础模型来进行转换,可在测得的响应极值am(t)中直接去除了噪声[16]。
设通过两根传感器之间的震动响应为a(t),车轮位移即触地长度可用d(t)表示,则得到:
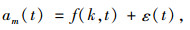
|
(8) |
式中,ε(t)为t时刻的测量误差或噪声;k是混合模型参数,震动响应a(t)可以用如下方程组进行代换:
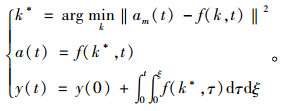
|
(9) |
假设当Δt→0时即线性分割无穷小时,即y(0)=0时得到:
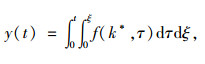
|
(10) |
式中,y(t)为线性分割后的积分和,即拟合值,对于连续车轮响应来说可以理解为耦合响应。
3 试验验证 3.1 试验过程试验硬件系统由压电石英传感器、测宽线阵、电荷放大器、称重数采控制器、数据融合主机构成。其中传感器为瑞士Kistler公司生产的9195 E/F511型压电石英传感器,其最大承载面宽度为50 mm,称量速度范围5~200 km/h,响应频率0.1 μs,有效量程为30 t/轴,电荷放大器采用奇石乐生产的5163E/F5114CH,称重数据采集器DAQ采用奇石乐生产的RDA7802—O型,数据融合主机采用研华ARK—6322型嵌入式工控机。软件系统采用EZbox配套动态称重软件以及自制数据融合分析软件。测试车辆为华菱之星HN1160C16C8M4型2轴单轮载重货车,试验地点为哈尔滨东收费站。
3.2 试验结果分析(1) 定性分析:
由于本次试验所测量的物理量是一个动态物理量,加之目前我国对车辆超载是以重量为标准进行衡量,因此并未有标准计量仪器,同时车轮对地压强分布,并非分布均匀,因此在计算时采用平均对地压强进行表述[17]。将测得的数据利用有限元分析软件进行分析,结果如图 5所示。

|
| 图 5 静止状态下轮胎对地压强分布 Fig. 5 Distribution of tire pressure on ground in stationary state |
| |
由图 5的压强分布表述可以看出,传感器反馈的数据符合轮胎对地压强的规律,即轮胎触地面中心部分压强较大,随着车轮与触地面的相对滑动,压强逐渐减小,因此本研究所述方法能够得到运动车辆实时对地压强。在处理数据时可以设置阈值压强和平均压强2个参量作为参考,这样能够使参考数据更准确。同时也可以看出轮胎触地中心点压强较大,最大可为边缘点的10倍,即验证了整车、轮/轴荷载并不能作为治超限重的准确依据。
(2) 定量分析
对于车辆称重以及轮胎触地面积的测量,静态测量数据远高于动态,因此测试标尺采用车辆静止状态下的测量值。同时根据车辆振动模型可知,车辆在匀速运动状态下,受空气阻力以及相对摩擦力的影响,对地面的压力略小于静止状态,即车轮平均对地压强只要小于静态标定状态下,即可认为是安全的[18]。
测量结果与比对结果采用平均误差与标准方差来描述。车辆匀速行驶状态下与车辆静止状态下测量的误差为:
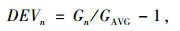
|
(11) |
式中,DEVn为n次测量值的偏差;Gn为第n次测量值;GAVG为测量平均值。
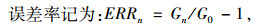
|
(12) |
式中,ERRn为n次测量的偏差;Gn为第n次测量值;G0为标准参考值。
则标准方差可表示为:
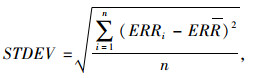
|
(13) |
式中,STDEV为标准方差;ERRi为第i个偏差;ERR为平均误差。
标准方差越小则表示与标准值差别越小。
测试数据如表 2所示,车辆在静止状态下测得重量为14.00 t,轮胎触地面积为0.129 6 m2,胎压8.5×10-1 MPa,静态轮胎对地压强1.083 5×10-1 MPa,每一项统计的数据为10次的平均值。
| 重量/t | 平均速度/ (km·h-1) |
平均误 差/% |
修正误 差/% |
触地面积/ cm2 |
平均对地压强/ (×10-1 MPa) |
| 13.716 | 0 | 2.47 | 1.88 | 0.129 2 | 1.069 7 |
| 14.042 | 4.88 | 1.76 | 1.14 | 0.129 3 | 1.086 0 |
| 14.169 | 11.24 | 2.75 | 1.34 | 0.129 1 | 1.097 5 |
| 14.344 | 15.53 | 3.36 | 2.82 | 0.128 9 | 1.112 8 |
| 14.745 | 21.35 | 6.87 | 4.85 | 0.128 9 | 1.143 9 |
| 14.036 | 25.87 | 1.02 | 0.78 | 0.128 3 | 1.093 9 |
从表 2中的数据可知,在95%的置信区间内,系统测得的实时轮胎平均对地压强与静态时的误差均在5%以内(修正后),且离散性较大,不存在线性相关。这是由于车辆在运动时会产生多自由度不规则震动,因此所测得的数据具有偶发性,耦合度低,同时经线性分割后的测量值与车速关联度低,无内聚性,因此避免了由车速带来的误差。测量的数值只与动态称重精度线性相关。当动态称重精度误差越小,平均对地压强与标准值越接近,即整个系统的优化与校调与标定只需将动态称重传感器校调标定至最佳状态,便可得到较为精准的值。
4 结论(1) 轮胎对地压强的实时监测是一种能够用具体量值精确衡量车辆对公路、桥梁影响的手段,对于单纯利用整车、轮/轴荷载来判定是否超重,其更适合衡量运动车辆对交通基础设施的破坏程度,能够促进制订更加科学合理的交通法规。同时其具有的动态性、实时性、可靠度高的特点能够有效地推动货车ETC、非现场执法治超等应用的实施。
(2) 使用线性分割法对动态称重模型进行了重构,使测量值与行车速度线性不相关,从而提高了收费场站的通行能力,同时使用这种方法得到的响应数据是累加的结果,避免了单一瞬时响应值的特异化,从而纠正了车辆因异常状态行驶(冲称、跳称、走S形等)造成的误差,同时使用的模型优化法避免了单一优化方法对不同模型优化时的局限性。
(3) 由于轮胎对地压强的检测标准与衡量指标尚属空白,因此动态状态下实时监测也无标准依据,目前只能够用平均对地压强进行表述,这种表述是否准确合理尚待论证,同时更需要交管部门出台相应的法规与标准。目前所采用的动态称重模型,其本身也存在一定的缺陷,例如在车辆突然刹车,车轮滑动通过传感器时(拖称状态)传感器无响应,会产生非常大的误差,这种误差目前尚无好的方法解决,在未来的研究中可考虑利用宽度更小,接触面与路面无缝连接的“隐形”传感器面层来解决。
(4) 通过本次研究发现,轴组秤、弯板等承载面大于最小轮迹的动态汽车衡并不能很好地适用于动态称重,更无法做到对运动车辆对地压强的实时监测。压电石英传感器虽然能够满足要求,但就其工作原理以及数学模型而言依然有着很大的缺陷,在未来的试验中,将考虑使用光纤传感器等新型传感器来解决这些问题。
| [1] |
王磊, 周伟, 董敏毅, 等. 高速公路EWTC系统场站布设方案研究[J]. 公路交通科技, 2016, 33(9): 120-126. WANG Lei, ZHOU Wei, DONG Yi-min, et al. Study on Station Arrangement for Expressway EWTC System[J]. Journal of Highway and Transportation Research and Development, 2016, 33(9): 120-126. |
| [2] |
NASSIRI S, BAYAT A, KILBURN P. Traffic Inputs for Mechanistic-empirical Pavement Design Guide Using Weigh-in-motion Systems in Alberta[J]. International Journal of Pavement Engineering, 2014, 15(6): 483-494. |
| [3] |
李建波, 牛昱光. 基于μC/OS-Ⅲ的整车式动态称重仪表[J]. 仪表技术与传感器, 2015(7): 28-31. LI Jian-bo, NIU Yu-guang. Full-vehicle Dynamic Weighing Instrument Based on μC/OS-Ⅲ[J]. Instrument Technique and Sensor, 2015(7): 28-31. |
| [4] |
王磊, 尹燕, 周伟, 等. 高精度阵列式压电石英动态称重系统研究[J]. 中国公路学报, 2016, 29(5): 137-143. WANG Lei, YIN Yan, ZHOU Wei, et al. Study on Dynamic Weighing System of High Precision Array Piezoelectric Quartz[J]. China Journal of Highway and Transport, 2016, 29(5): 137-143. |
| [5] |
HERNANDEZ S V, TOK A, RITCHIE S G. Integration of Weigh-in-motion and Inductive Signature Technology for Advanced Truck Monitoring[C]//Transportation Research Board 93rd Annual Meeting. Washington, D. C. : Transportation Research Board, 2013: 1-14.
|
| [6] |
HERNANDEZ S V, TOK A, RITCHIE S G. Integration of Weigh-in-motion (WIM) and Inductive Signature Data for Truck Body Classification[J]. Transportation Research Part C:Emerging Technologies, 2016, 68: 1-21. |
| [7] |
JENG S T, CHU L, CETIN M. Weigh-in-motion Station Monitoring and Calibration Using Inductive Loop Signature Technology[C]//Transportation Research Board 94th Annual Meeting. Washington, D. C. : Transportation Research Board, 2015: 45-55.
|
| [8] |
刘浪, 尤吉. 公路桥梁车辆荷载效应的外推计算[J]. 土木工程学报, 2015, 48(4): 59-64. LIU Lang, YOU Ji. Extrapolation Method for Truck Load Effects on Highway Bridges[J]. China Civil Engineering Journal, 2015, 48(4): 59-64. |
| [9] |
蔡钊, 马林华, 黄绍城, 等. 基于序数势博弈的WSN拓扑控制算法[J]. 计算机科学与探索, 2016, 10(8): 1112-1121. CAI Zhao, MA Lin-hua, HUANG Shao-cheng, et al. Ordinal Potential Game Based Topology Control Algorithm for WSN[J]. Journal of Frontiers of Computer Science and Technology, 2016, 10(8): 1112-1121. |
| [10] |
王强, 刘仰韶, 张文忠, 等. 光纤高速汽车动态称重系统[J]. 长安大学学报:自然科学版, 2014, 34(3): 145-150. WANG Qiang, LIU Yang-shao, ZHANG Wen-zhong, et al. High Speed WIM Based on FBG for Vehicles[J]. Journal of Chang'an University:Natural Science Edition, 2014, 34(3): 145-150. |
| [11] |
CHAO S H, LOH C H. Application of Singular Spectrum Analysis to Structural Monitoring and Damage Diagnosis of Bridges[J]. Structural and Infrastructure Engineering, 2014, 10(6): 708-727. |
| [12] |
杨晓明, 李宗津. 基于水泥基压电传感器的车辆监测研究[J]. 传感技术学报, 2013, 26(2): 266-270. YANG Xiao-ming, LI Zong-jin. Monitoring of Vehicle Using Cement-based Piezoelectric Sensors[J]. Chinese Journal of Sensors and Actuators, 2013, 26(2): 266-270. |
| [13] |
黄必飞, 冯志敏, 张刚, 等. 压电薄膜车辆动态称重系统算法研究[J]. 传感技术学报, 2016, 29(6): 941-946. HUANG Bi-fei, FENG Zhi-min, ZHANG Gang, et al. Research on Algorithm of Piezo-film Vehicle Weigh-in-motion System[J]. Chinese Journal of Sensors and Actuators, 2016, 29(6): 941-946. |
| [14] |
柳江, 林晨, 叶明, 等. 馈能悬架变论域模糊控制[J]. 上海交通大学学报, 2016, 50(8): 1139-1143. LIU Jiang, LIN Chen, YE Ming, et al. Variable Universe Fuzzy Control of Energy-regenerative Suspension[J]. Journal of Shanghai Jiaotong University, 2016, 50(8): 1139-1143. |
| [15] |
KOLLIPARA V D. A Rheology Model of Soft Elastomeric Capacitor for Weigh-in-motion Application[D]. Ames, USA: Iowa State University, 2013.
|
| [16] |
NASSIRI S, BAYAT A, KILBURN P. Traffic Inputs for Mechanistic-empirical Pavement Design Guide Using Weigh-in-motion Systems in Alberta[J]. International Journal of Pavement Engineering, 2014(6): 483-494. |
| [17] |
ZHANG Y, ZHAO C, HE J, et al. Vehicles Detection in Complex Urban Traffic Scenes Using Gaussian Mixture Model with Confidence Measurement[J]. LET Intelligent Transport Systems, 2016, 10(6): 445-452. |
| [18] |
邵仙鹤, 鲁志成, 王翥. 基于最小二乘曲面拟合的流量计量温度补偿算法[J]. 传感技术学报, 2016, 29(6): 897-902. SHAO Xian-he, LU Zhi-cheng, WANG Zhu. Temperature Compensation Algorithm Based on Least Squares Curve Fitting in Flow Measurement[J]. Chinese Journal of Sensors and Actuators, 2016, 29(6): 897-902. |
 2018, Vol. 35
2018, Vol. 35
