扩展功能
文章信息
- 吴安杰, 杨万理, 赵雷
- WU An-jie, YANG Wan-li, ZHAO Lei
- 洪水对桥墩的瞬间冲击效应
- Moment Impact Effect of Flood on Bridge Pier
- 公路交通科技, 2018, 35(6): 67-73
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(6): 67-73
- 10.3969/j.issn.1002-0268.2018.06.010
-
文章历史
- 收稿日期: 2017-01-12
2. 西南交通大学 土木工程学院, 四川 成都 610031
2. School of Civil Engineering, Southwest Jiaotong University, Chengdu Sichuan 610031, China
近年来,极端气候条件频发,洪水导致桥梁损毁的事故常有发生。2007年位于四川省平昌县白衣镇的白衣大桥,因该区域发生的百年一遇的“7.6”大洪灾,桥墩在建造过程中受到此次洪水的袭击而垮塌,该事件导致工程停工9个月,使国民经济蒙受巨大损失。这只是众多事故中的一个缩影,国内外其他地区发生的类似水毁事件不在少数。例如,1989年,位于美国田纳西州的Hatchie桥在洪水作用下毁于一旦[1];2001年,葡萄牙的Hintze Ribeiro桥被洪水冲毁[2];2010年,位于四川安县的先林大桥被特大洪水冲垮;2011年,中国北部的巴彦塔拉河铁路桥被洪水冲毁。2016年,受强降雨影响,据调查,国内许多桥梁基础设施在水流冲击中受损严重。
发生水毁桥墩的原因是多方面的:其一,由于水流对桥址长期冲刷致使桥墩基础底部被淘空。另外,由于洪水对桥墩的瞬间冲击而产生过大的作用力,包括洪水中夹杂物(如泥沙、杂物)的作用。在桥墩冲刷方面[3-7]目前已开展了较为深入细致的研究,而在洪水的冲击作用方面涉入不深。肖诗云等[8]提出了一维洪水演进模型,并推导出一维洪水冲击荷载的计算公式;韩林峰等[9]基于三参数Weibull分布,建立了洪水作用下丁坝可靠度分析模型,利用水毁等效原理,推导出丁坝受洪水循环作用下失效概率计算式;于文等[10]通过水槽试验,研究了山洪对乡村房屋的作用机理和作用特性;文献[11]和文献[12]采用有限元软件,分析了水流对桥墩结构振动特性(自振频率)的影响规律;文献[13]利用FLUENT流体软件对并联双桥墩在溃坝洪水冲击下进行了简单数值模拟(单向计算,即未考虑流固耦合效应),KIM和SIM[14]研究建立了考虑泥石流影响的桥梁洪水易损性曲线;部分学者[15-16]在泥石流对桥墩的冲击作用方面开展了一定研究。
相对而言,洪水冲击作用在房屋和坝体领域研究居多,人们对现代桥梁结构的水毁机理认识还不够清晰,现仍没有一种特别有效的防治方法。在这方面还需要开展大量的研究工作。本研究借助流固耦合瞬态分析软件ANSYS-CFX,研究了不同截面形式的桥墩在洪水冲击下的全过程响应特征,并从本质上揭示了瞬间冲击响应较大的原因。将分析的结果与规范值作比较,对规范在该方面内容的完善和修订有一定的参考意义。
1 模型与方法 1.1 原理洪水冲击桥墩属于典型的双向流固耦合作用问题,即桥墩在洪水力的作用下发生振动和变形,同时流场特征由于墩的运动而发生变化,进而作用在桥墩上的水压幅值和分布相应地发生改变。对桥墩进行有限元离散,其瞬态动力学控制方程为:

|
(1) |
式中,[M],[C],[K]分别为结构的质量矩阵、阻尼矩阵和刚度矩阵;{u}、
对于流体介质,其控制方程可以写成通用的形式:

|
(2) |
方程各项从左到右按顺序分别为瞬态项、对流项、扩散项和源项。其中,t为时间;ρ为流体密度;xj为流场欧拉坐标(j=1, 2, 3对应3个不同方向坐标);uj为流体速度(j=1, 2, 3对应3个不同坐标方向的流体速度);Γφ为相应于φ的广义扩散系数;Sφ为能量源项;φ为广义变量,例如,表示连续方程时φ取1,代表动量方程时φ取速度量。
类似的,对于流场部分,采用有限体积方法对计算区域和控制方程进行离散。对于流场计算本质上是求解黏性可压缩流体的Navier-Stokes方程。
根据界面速度连续条件和界面力连续条件,由流固耦合面将结构域和流体域的计算结果进行互相交换传递。待此时刻的收敛条件满足,从而进行下一时刻的计算,依次而行求得最终结果。
1.2 数值模型讨论3种截面形式的桥墩,圆形墩截面直径D=5 m,方形墩截面边长D=5 m,矩形墩截面短边D=5 m、长边L=7.5 m(水流方向垂直于短边),墩高H均为40 m。材料参数为:弹性模量E=30×109 Pa,泊松比μs=0.18,密度ρs= 2 300 kg/m3(采用CFX软件默认的混凝土材料);考虑水为黏性可压缩流体,密度ρ= 997 kg/m3,动力黏度μ=0.894×10-3 Pa·s,水介质中声速c=1 460 m/s,外部流域平面尺寸为50 m×25 m。数值试验表明[12, 17]:当流体区域大于结构半径的5倍时,其结果与无限流体域的计算结果误差小于1%。
在ANSYS Workbench平台上,建立墩-水耦合振动数值分析模型,采用Transient Structural(ANSYS)和CFX耦合场模块对洪水冲击桥墩过程进行流固耦合瞬态模拟。
在仿真模型中,如图 1所示,桥墩采用六面体结构单元Solid 186(20节点)模拟,而水域被离散为结构化网格。墩的边界为底部固结上端自由,因在墩顶为水平活动支座,可将上部结构简化为具有竖向分量的集中质量块。流场边界由7个面组成:在入口边界设置水流速度,出口边界设置为水流压力出口,顶面设置相对静压为零,两侧面为对称边界,底面为无滑移墙面,中间的流固耦合面用来记录网格特征和数据交换。

|
| 图 1 数值模型 Fig. 1 Numerical model |
| |
在紊流数值计算中,湍流模型采用标准k-epsilon两方程模式(近壁面采用Scalable函数处理),求解器离散格式设置为高精度(High Resolution),时间积分方法采用二阶迎风后插欧拉(Second Order Backward Euler)技术。
洪水的速度(用v表示)范围一般为4~15 m/s,属于低速流动范畴,经典的流体动力学理论适用。从研究角度出发,分析中考虑流速范围为1~15 m/s,以增量v=1 m/s变化。水量高度(用h表示)范围为1/4H~1H(H为墩高),以增量h=1/4H变化。
2 计算结果分析 2.1 冲击效应通过分析,洪水冲击桥墩的过程大致分为3个阶段:瞬间冲击、逐渐衰减、稳定绕流。以洪水速度为4 m/s、水量高度为30 m时的冲击力及墩顶位移响应时程曲线为例进行说明,如图 2、图 3所示。

|
| 图 2 洪水作用于桥墩的冲击力时程曲线(v=4 m/s, h=0.75H) Fig. 2 Time-history curves of flood force on bridge piers subjected to flood impact (v=4 m/s, h=0.75H) |
| |

|
| 图 3 洪水冲击桥墩的位移响应时程曲线(v=4 m/s, h=0.75H) Fig. 3 Time-history curves of displacement response of bridge piers subjected to flood impact (v=4 m/s, h=0.75H) |
| |
第1阶段:从初始时刻开始,经过一个短暂的时间,在A点处出现峰值,称为瞬间冲击状态。在相同的迎水面积下,方形墩受到的冲击力最大、矩形墩次之,圆形墩最小。顺流向响应峰值大于横向(垂直水流方向)响应峰值。
第2阶段:从A点到B点,曲线以谐波振荡型式逐渐衰减变化,然后趋于平稳,称为衰减阶段。矩形墩衰减最快,方形墩次之,圆形墩最慢,圆形墩冲击响应在顺流向比横向衰减得快。
第3阶段:在B点以后,曲线波动幅值趋于某一定常值(非零值),叫作稳定绕流阶段。在此阶段,不同截面形式的墩表现出的特征差异较大。洪水作用桥墩时,流态为紊流,漩涡充分发展,由于水流的脉动性,圆形截面墩在顺流向波动较明显;绕流时,墩尾部存在不规则涡脱现象,因截面形式的差异,漩涡释放规律不同,故在横向产生的周期性振动存在显著差异。从图中可知,圆形墩后的漩涡释放周期小于方形和矩形墩。横向振动幅度相比来流方向较小,但不可忽略。
当洪水的冲击锋面接触到桥墩迎水面的瞬间,水质点速度为零,那么速度变化率即加速度较大。由能量守恒原理可知,此时,这一部分动能将以冲击荷载的形式作用于桥墩。类似于有压管道或泵结构的水击作用(“水锤效应”),因水介质的压缩性和墩结构的弹性,故会产生弹性波向上游和墩两侧传播。当流速减小Δv时,则压强增大Δp,由动量定理可以推导出:水击压强与速度减少量的近似关系,即Δp=-ρcΔv,此关系有别于绕流阶段的绕流压力p=CDρv2,CD为绕流压力系数。由于水介质声速c值相比水流速度是一个较大的值,所以瞬间冲击作用往往较大。
不同于有压管道,由于桥墩迎水面两侧不受约束,水流冲击桥墩之后,可以沿墩两侧自由流动,随着弹性波的传播,响应会逐渐衰减,如图 3所示。衰减形式一般呈简谐波振荡形式,然后进入稳定绕流阶段。绕流阻力包括2个部分:一是由于水流边界层分离而产生的墩迎水面和背面的压差,二是黏性水流沿着墩壁面的摩擦力。黏性作用一般较小,对于圆形、方形和矩形截面墩黏性力分别约为水流总阻力的0.51%,0.37%和0.18%(以h=0.5H,v=4 m/s为例)。实际上,对于洪水冲击桥墩问题,水流速度往往较大,属于大雷诺数范畴,当迎水宽度即墩径为5 m时,雷诺系数Re=0.22~0.83×105(v=4~15 m/s)。由流体力学基本理论可知:桥墩为钝形体,在绕流阶段,由于边界层分离,此雷诺数区间,分离点较靠前,形成很宽的分离区,阻力以形状阻力为主。已有研究表明:只计摩擦阻力得到的阻力系数CD值,比计入摩擦阻力与压差阻力得到的CD值要小得多,特别是在雷诺数Re>500的范围内,后者比前者大一个数量级以上,说明在实际的钝形体绕流情况下,与压差阻力相比可以将摩擦阻力忽略不计。
在瞬态冲击阶段,因无量纲的雷诺数Re表征惯性力与黏性力的比值大小关系,当雷诺数较大时,流体的惯性作用远大于黏性作用,实际流体的流动接近于无黏性力作用的理想流体的流动,因此可以忽略黏性作用。由于惯性力起主导作用,而惯性力与水质点加速度直接相关,因冲击的瞬间,加速度极大,从而进一步解释洪水冲击桥墩瞬间响应较大的现象。
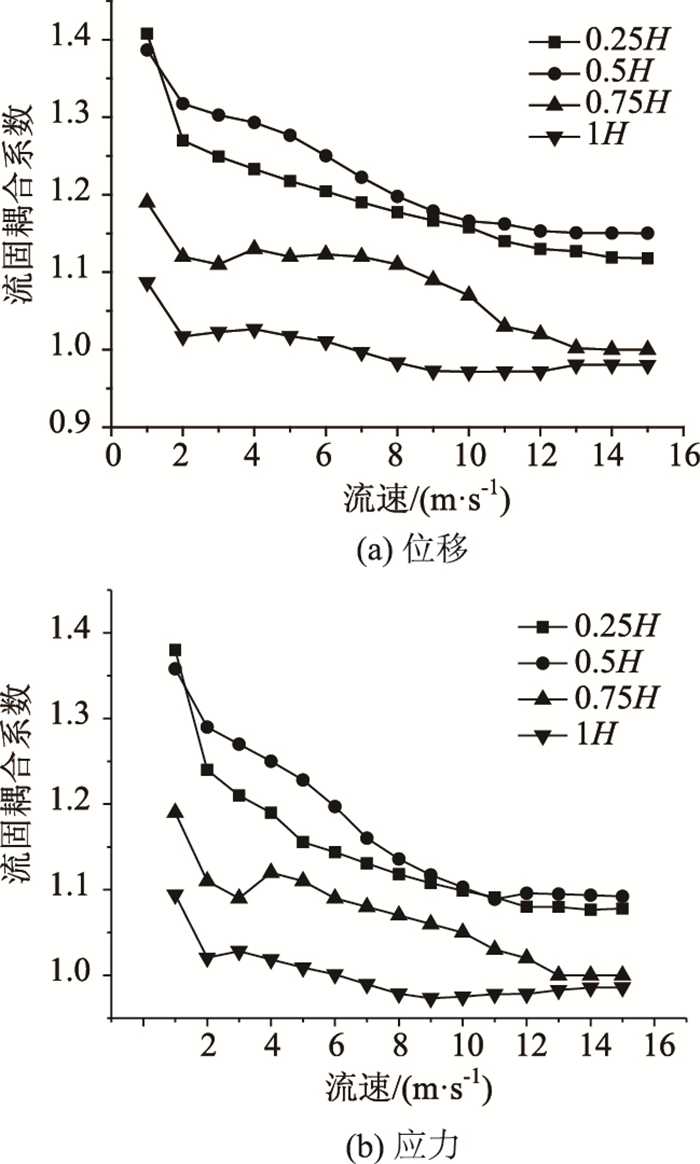
为了定量地描述瞬间冲击效应大小,首先定义冲击放大系数fmag为瞬间冲击洪水力峰值与冲击后稳定绕流阶段的水流力幅值的比值。我们知道,水流力与迎水面积成比例关系,而与速度呈二次关系,不妨定义冲击效应系数fimp为:
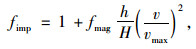
|
(3) |
式中,h/H为水量高度比;v/vmax为相对流速比;均为无量纲量。h为水量高度;H为墩高;v为洪水行近速度;vmax为最大洪水行近速度。
图 4展示了不同截面形式的桥墩受洪水作用时的冲击放大系数与行近流速和水量高度的变化曲线。由图 4可知:冲击放大系数范围为1.67~2.62,说明洪水冲击力峰值相比稳定绕流阶段的水流力较大。冲击放大系数随着行近流速v的增大而减小,当v<4 m/s时,曲线下降速率较快,后逐渐趋于平缓。在水量高度较大时,冲击放大系数随流速的变化不明显。通过比较,圆形墩的冲击放大系数最大,方形墩次之,矩形墩最小。冲击放大系数随着水量高度h的增加而增大,增加的速率随着水量高度的增大而减小。

|
| 图 4 洪水对桥墩的瞬间冲击放大系数与行近流速和水量高度的关系 Fig. 4 Relations of moment impact amplification coefficient with flood velocity and water height when bridge piers subjected to flood impact |
| |
根据式(3),将洪水冲击效应系数绘制成数据图,如图 5所示。在相等的水量高度下,冲击效应随流速增大呈非线性增加的趋势,相比之下,圆形墩冲击效应最显著。当h=0或v=0时,fimp=1,显然此时不存在冲击效果;当h=0.25H,v=1m/s时,fimp =1.002 1~ 1.002 7(矩形~圆形),此时冲击作用效果不明显,可忽略;当h=0.5H,v=4 m/s时,fimp =1.066~1.088,虽然水量高度增加了1倍,但流速较小,冲击作用效果仍不明显;当h=0.5H,v=8 m/s时,fimp=1.26~1.33,速度增加1倍后,冲击效应增强较明显;当h=0.75~1H,v=8~10 m/s时,此时洪水流量高度较大,流速处于中等范围,而冲击效应系数值大多接近于2且部分大于2,此时瞬间冲击效应不容忽视。当流速不小于14 m/s且水量高度接近墩顶甚至漫过桥墩时,冲击效应系数将大于3,这是一种较极端的情况,此时的作用力几乎已超过了桥梁结构的安全储备。总体来说,行近流速和水量高度同时较大时,对桥墩结构的安全威胁是较大的,在骤然大暴雨后,洪水量大且急,很多桥梁毁于一旦,其原因之一也在此。
|
| 图 5 洪水对桥墩的冲击效应系数与行近流速和水量高度的关系 Fig. 5 Relations of impact effect coefficient with flood velocity and water height when bridge piers subjected to flood impact |
| |
2.2 流固耦合效应
以墩顶位移和墩底应力为研究量,定义流固耦合系数为流固耦合瞬态计算值(取稳定绕流阶段的值)与不考虑流固耦合效应计算值的比值。
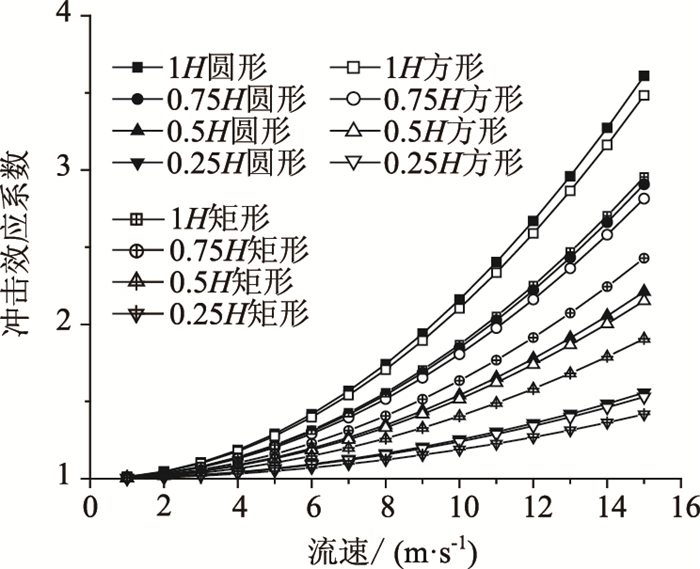
由图 6可知:圆形墩的流固耦合系数范围为0.98~1.41,随着行近流速的增大而减小,当流速较大时,变化趋于稳定。随着水量高度的增大,流固耦合系数先增大后减小。在h=0.75~1H且v>13 m/s时,流固耦合系数值接近于1,此时,水对桥墩的绕流作用计算可以不用考虑流固耦合效应。对方形和矩形墩有类似的规律(限于篇幅不再展开赘述)。注意到,流固耦合系数与汽车荷载对桥面的冲击系数颇为相似。需要指出的是:文献[18]规定的汽车冲击系数范围为1.05~1.45,均大于1,而流固耦合影响系数存在小于1的情况,如洪水速度为7~12 m/s,且水深与墩高齐平时。这说明流固耦合效应既会放大也会削弱结构响应程度,但大多数产生的是不利影响。这实质上与水对桥墩结构的振型和频率影响有关。
|
| 图 6 流固耦合效应与行近流速和水量高度的关系(圆形墩) Fig. 6 Relations of fluid-solid coupling effect with flood velocity and water height (circular pier) |
| |
2.3 水流力模拟值与规范值对比
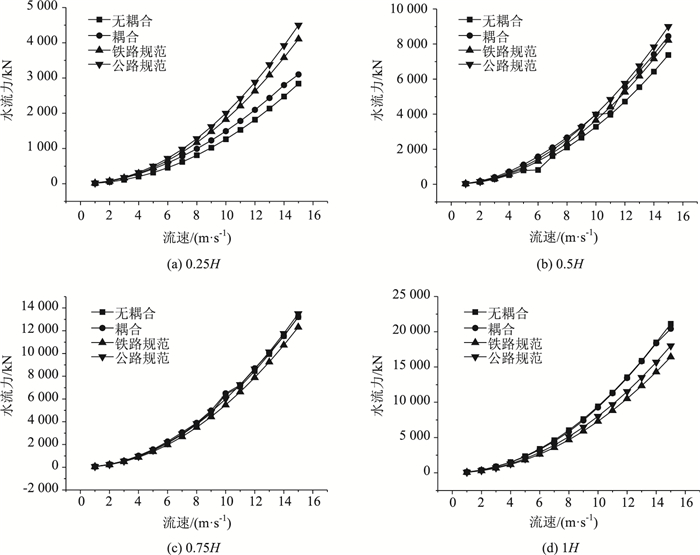
数值仿真考虑真实的黏性流体,以及墩-水间的流固耦合作用,附加假设条件少,可以得出较为准确的结果。下面将考虑和不考虑流固耦合效应的水流力仿真模拟值与桥梁规范[18-19]公式计算值进行比较,图 7展示了圆形墩的数据对比曲线。需要注意:这里的数值模拟值取的是稳定绕流阶段的水流力,并非瞬间冲击力计算值,行文中,将文献[18]和文献[19]分别简称公规和铁规。在水量高度为0.25H时,各流速点,公规和铁规水流力计算值都大于流固耦合数值解,规范值偏于保守;在水量高度为0.5H时,公规计算值最大,铁规计算值在流速较大时略小于流固耦合计算值;在水量高度为0.75H时,公规计算值与流固耦合数值解接近,铁规计算值偏小;在水量高度为1H时,公规和铁规计算值都小于仿真模拟值,规范取值偏于不安全。在这里的对比分析仅单纯地从流固耦合的角度进行的,实际中若计入洪水的瞬间冲击作用,规范值会偏于更不安全。对于矩形和方形墩,模拟值与规范计算值基本吻合,在水量高度0.75H以下时,规范值略大于模拟值(1.08~1.12倍)。
|
| 图 7 水流力仿真模拟值与桥梁规范公式计算值比较(圆形墩) Fig. 7 Comparison between current force simulation value and calculation value using formulas in bridge design codes (circular pier) |
| |
3 结论
(1) 洪水作用桥墩时,由于桥墩为钝形体且雷诺数较大,故而黏性作用较小,可以忽略不计。
(2) 洪水对桥墩的冲击效应与行近流速和流量高度有关。冲击过程可以分为3个阶段,瞬间冲击状态的洪水力峰值比绕流阶段的水流力要大1.67~2.62倍(即冲击放大系数),冲击效应系数为1~3.6,在水量高度较大时,瞬间冲击效应不容忽视。冲击作用在顺流向大于横向,但冲击响应在横向衰减得慢,也不可小觑。
(3) 桥涵规范对水流力取值在流量高度大于0.75倍墩高时,偏于不安全,尤其是《铁路桥涵设计基本规范》。为了保证桥墩稳定安全,减小洪水灾害,综合考虑瞬间冲击效应和流固耦合效应,建议规范对水流力取值适当乘以一个放大系数。
| [1] |
曹明旭, 刘钊, 孟杰. 美国桥梁病害及倒塌事故统计分析与思考[J]. 公路, 2009(7): 162-167. CAO Ming-xu, LIU Zhao, MENG Jie. Statistical Analysis and Reflections on Bridge Deficiencies and Disasters in the United States[J]. Highway, 2009(7): 162-167. |
| [2] |
SOUSA J J, BASTOS L. Multi-temporal SAR Interferometry Reveals Acceleration of Bridge Sinking before Collapse[J]. Natural Hazards and Earth System Sciences, 2013, 13(3): 659-667. |
| [3] |
张佰战, 王群. 桥渡冲刷可靠度计算[J]. 铁道工程学报, 2001, 18(1): 54-57. ZHANG Bai-zhan, WANG Qun. Reliability Calculation of Bridge Crossing Scour with Checking Point Method[J]. Journal of Railway Engineering Society, 2001, 18(1): 54-57. |
| [4] |
赵嘉恒, 张耀哲, 李敏. 复杂边界条件下桥墩冲刷的试验研究[J]. 泥沙研究, 2013(1): 14-19. ZHAO Jia-heng, ZHANG Yao-zhe, LI Min. Experimental Study of Piers Scour in Complex Boundary Condition[J]. Journal of Sediment Research, 2013(1): 14-19. |
| [5] |
黄进坤, 卢之伟. 筐网基桩群对桥墩冲刷保护之探讨[J]. 岩土工程学报, 2013, 35(2): 982-985. HUANG Jin-kun, LU Zhi-wei. Protection of Bridge Scour Using Pile Groups with Porous Basket[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 982-985. |
| [6] |
SHAMBHARKAR B M, NIMBALKAR P T, PAWAR P. Experimental Work to Estimate Bridge Pier Scouring around round Nosed Rectangular Pier and Protection Against Scouring Using Ripraps[J]. International Journal of Civil Engineering & Technology, 2017, 8(5): 1255-1262. |
| [7] |
KUMAR V, RAJU K G R, VITTAL N, et al. Reduction of Local Scour around Bridge Piers Using Slots and Collars[J]. Journal of Hydraulic Engineering, 1999, 125(12): 1302-1305. |
| [8] |
肖诗云, 王晓庆. 洪水演进模型及冲击荷载数值分析[J]. 工程力学, 2010, 27(9): 35-42. XIAO Shi-yun, WANG Xiao-qing. Study on Routing Model and Impact Loading of Flood[J]. Engineering Mechanics, 2010, 27(9): 35-42. |
| [9] |
韩林峰, 王平义, 刘怀汉, 等. 洪水作用下丁坝可靠度分析及剩余寿命预测[J]. 水利水运工程学报, 2013(6): 54-61. HAN Lin-feng, WANG Ping-yi, LIU Huai-han, et al. Analysis of Spur Dike Reliability by the Action of Flood and Evaluation of Residual Life[J]. Hydro-Science and Engineering, 2013(6): 54-61. |
| [10] |
于文, 葛学礼, 朱立新, 等. 山区乡村房屋模型水流作用试验[J]. 北京交通大学学报, 2011, 35(1): 24-29. YU Wen, GE Xue-li, ZHU Li-xin, et al. Simulated Experimental Study on Model of Buildings in Mountain Area under Flow Action[J]. Journal of Beijing Jiaotong University, 2011, 35(1): 24-29. |
| [11] |
谭上俞. 桥墩一流水耦合效应下水位变化对桥梁动力影响分析[D]. 重庆: 重庆交通大学, 2013. TAN Shang-yu. Analysis on Dynamic Effects of Water Level Change to Bridge under the Fluid-pier Interaction[D]. Chongqing: Chongqing Jiaotong University, 2013. |
| [12] |
杨吉新, 雷凡, 李昆. 水下桥墩结构的振动分析[J]. 世界桥梁, 2009(3): 40-42. YANG Ji-xin, LEI Fan, LI Kun. Vibration of Underwater Bridge Pier Structure[J]. World Bridges, 2009(3): 40-42. |
| [13] |
刘杰. 溃坝洪水对并联双桥墩冲击过程数值模拟[J]. 人民珠江, 2016, 37(8): 6-9. LIU Jie. The Numerical Simulate of Parallel Double Bridge Piers Impact by Dam-break Flood[J]. Pearl River, 2016, 37(8): 6-9. |
| [14] |
KIM H, SIM S H. Flood Fragility Analysis of Bridge Piers in Consideration of Debris Impacts[J]. Journal of the Korea Academia-industrial Cooperation Society, 2016, 17(5): 325-331. |
| [15] |
覃月璋. 泥石流对桥墩的冲击作用研究[D]. 成都: 西南交通大学, 2014. QIN Yue-zhang. Study of Bridge Pier Impacted by Debris Flow[D]. Chengdu: Southwest Jiaotong University, 2014. |
| [16] |
孙鸿斌. 简支梁桥桥墩受泥石流冲击作用的数值模拟[D]. 秦皇岛: 燕山大学, 2016. SUN Hong-bin. Numerical Simulation of Impact of Debris Flow on Simply Supported Girder Bridge Piers[D]. Qinhuangdao: Yanshan University, 2016. |
| [17] |
雷凡. 水下柔性结构流固耦合动力效应研究[D]. 武汉: 武汉理工大学, 2011. LEI Fan. Dynamic Response Research of Submarine Flexible Structures with Fluid-solid Interaction[D]. Wuhan: Wuhan University of Technology, 2011. |
| [18] |
JTG D60-2015, 公路桥涵设计通用规范[S]. JTG D60-2015, General Specifications for Design of Highway Bridges and Culverts[S]. |
| [19] |
TB 10002. 1-2005, 铁路桥涵设计基本规范[S]. TB 10002. 1-2005, Fundamental Code for Design on Railway Bridge and Culvert[S]. |
 2018, Vol. 35
2018, Vol. 35
