扩展功能
文章信息
- 邬晓光, 钱若霖, 苏佩
- WU Xiao-guang, QIAN Ruo-lin, SU Pei
- 考虑刚度损伤的装配式T梁桥横向分布计算
- Calculation of Transverse Distribution of Assembled T-beam Bridge Considering Stiffness Damage
- 公路交通科技, 2018, 35(6): 61-66
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(6): 61-66
- 10.3969/j.issn.1002-0268.2018.06.009
-
文章历史
- 收稿日期: 2017-04-18
多梁式T梁以其预制便捷,吊装方便,施工便利等优点得到大量应用。关于其荷载横向分布的计算研究多针对于新桥,或针对新型结构桥梁在传统理论的基础上加以修正,而对于在役桥梁的计算方法则研究甚少[1-6]。对于在役桥梁,考虑其梁底裂缝的影响,确定一种更加合理的横向分布理论方法,对其研究其横向荷载分布和承载力具有重要借鉴意义。传统的横向分布方法有:杠杆法,刚性横梁法,铰接梁(板)法,刚接梁(板)法,G-M法等[7-10],部分学者根据荷载试验结果对理论加以验证分析[11-18]。本研究拟采用刚性横梁法为基础,考虑裂缝带来的刚度损伤对刚性横梁法及修正的刚性横梁法加以修正,以一5梁式T梁桥为依托工程,结合荷载试验给出一种更适宜在役桥梁的荷载横向分布合理的计算方法。
1 刚度分配 1.1 开裂梁体刚度损伤基于文献[1]中对装配式T梁裂缝外观统计的方法,首先对简支梁裂缝区段进行划分,对各段梁均进行量化评估,即按照统计学方法建立一套评估裂缝特征的参数表达:包括裂缝平均高度hcr,裂缝平均间距lcr和裂缝总宽度Δcr,如式(1)所示:
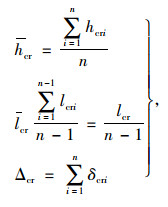
|
(1) |
式中,hcri为每条裂缝的高度;δcri为每条裂缝开展的程度;lcri为每条裂缝的间距;lcr为开裂范围;n为裂缝条数。
赵煜等在文献[1]中指出,裂缝的统计参数值可分别代入式(2)、(3)计算得名义拉应变,截面曲率。
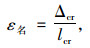
|
(2) |
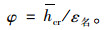
|
(3) |
再将式(2)、(3)代入式(4)最终求得开裂截面的损伤刚度:
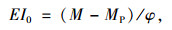
|
(4) |
式中,M为在役桥梁某种工况下外力对开裂截面换算截面形心轴产生的弯矩;MP为预应力对开裂截面换算截面形心的弯矩。
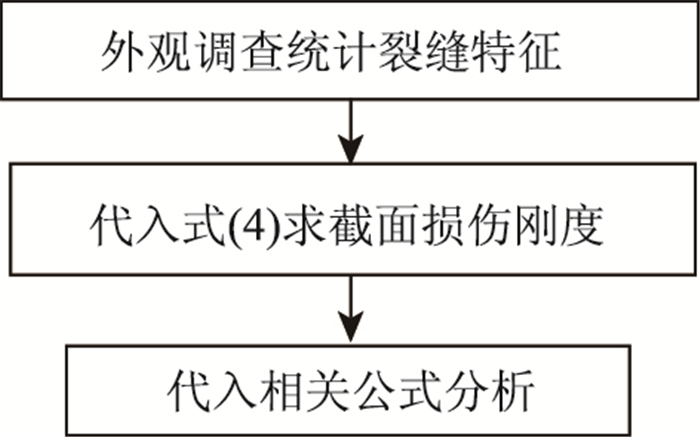
具体截面损伤刚度评估流程如图 1所示。
|
| 图 1 截面刚度评估流程 Fig. 1 Assessment process of section stiffness |
| |
刚度分布如图 2所示,实桥的刚度应呈多阶分布,下文横向分布的计算选取分析截面所在某段梁区间进行计算即可。

|
| 图 2 刚度阶梯变化示意 Fig. 2 Schematic diagram of stiffness staged change |
| |
1.2 T梁刚度重分配
由于开裂带来的刚度折减效应,在荷载作用下跨中挠度会呈增大趋势,挠度由两部分组成:梁体完好情况下产生的挠度w和梁体由于开裂刚度损伤产生的附加挠度Δf,在这提出一个刚度分配系数ξ的概念,荷载按该刚度修正系数分布,即(1-ξ)P和ξP。以跨中开裂梁段为例,刚度分配系数即荷载分布系数的计算如下所示:
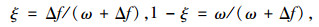
|
(5) |
挠度的增加等效视为抗弯刚度的折减:
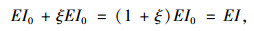
|
(6) |
代入式(4)得:
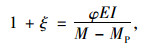
|
(7) |
式中,EI为不考虑裂缝梁体完好情况下结构抗弯刚度,EI0为考虑裂缝引起刚度损伤情况下结构抗弯刚度。为更好地与实桥荷载试验数据进行对比分析,有必要考虑主梁钢筋、桥面铺装和横隔板对主梁刚度的贡献作用,利用等效刚度原则及横隔板等效桥面板原则,对式(7)中的EI进行修正。
假设每片梁宽为b,混凝土T梁截面面积为Ah,混凝土弹性模量为Eh,钢筋面积为As,钢筋弹性模量为Es,桥面铺装层厚度为h1,横隔板等效桥面板厚为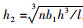
其中n为横隔板数量;b1为横隔板宽;h为横隔板高度;l为桥梁跨径。
修正系数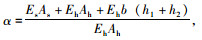
即:
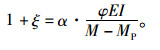
|
(8) |
刚性横梁法假设横隔梁的刚性无限大,在荷载作用下,桥梁仅发生刚性位移,即横隔梁变形后还保持为一条直线。其适用条件为:B/L≤0.5的窄桥。
对于由n片T梁组成的多梁式梁桥,第一部分挠度所产生的反力根据桥梁工程[8]中公式乘以相应的刚度分配系数1-ξ,即:
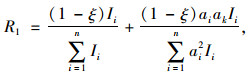
|
(9) |
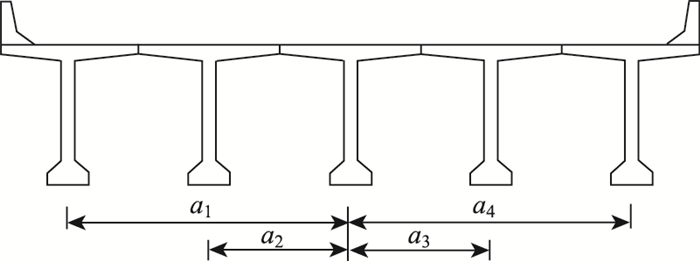
式中字母含义结合图 3说明如下(下同):Ii为第i片梁截面惯性矩;ai为第i片梁中心线距离桥梁宽中心线距离。对于第2部分附加挠度引起的反力推导如下:
|
| 图 3 参数示意 Fig. 3 Schematic diagram of parameters |
| |
(1) 中心荷载P=1作用下反力的计算
附加挠度为总挠度减去第一部分挠度,联立式(8):
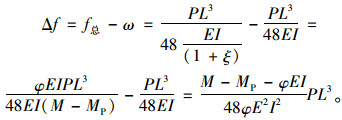
|
(10) |
式中分数部分基于外观统计的参数值和特定工况下的弯矩计算值均为已知,可知附加挠度Δf与荷载成线性关系,即:
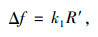
|
(11) |
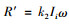
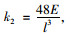
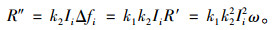
|
(12) |
根据荷载分配原则,附加挠度引起反力之和为ξ·1,即:
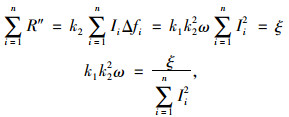
|
(13) |
代入式(12),故
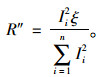
|
(14) |
(2) 偏心力偶矩M=1·e作用下反力的计算
推导过程同上,具体过程不再赘述,可反力计算公式为:
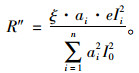
|
(15) |
综上,可得考虑裂缝损伤情况下主梁梁段荷载横向影响线数标值计算公式如下:
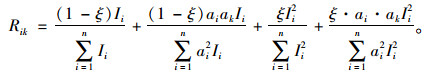
|
(16) |
由2.1节式可知,等号右边第1项,第2项由中心荷载P=1所引起,主梁仅产生挠度无转动,与主梁抗扭无关;第3项、第4项由力偶矩M=1·e引起,不仅会产生竖向挠度,而且会引起扭转,但式并没有计入主梁的抗扭作用,应对第3项、第4项给予修正。
抗扭修正系数,文献[9]中给出:
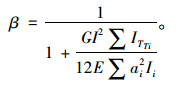
|
(17) |
修正后的计算公式为:
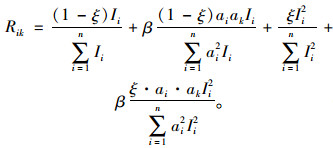
|
(18) |
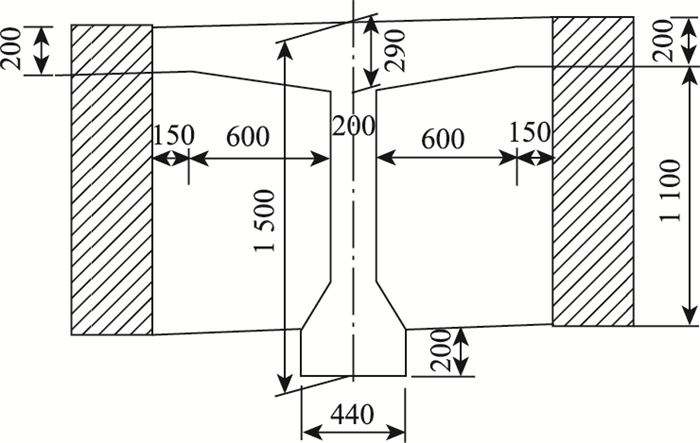
贵州某5梁式30 m预应力简支T梁桥,桥梁宽度12.5 m,跨径30 m,桥梁宽跨比为B/L=0.42,截面形式如图 4所示,主梁采用C50混凝土。算例分析选取跨中附近某裂缝梁段进行统计及计算分析。
|
| 图 4 T梁截面尺寸(单位:mm) Fig. 4 Sectional dimensions of T-beam(unit: mm) |
| |
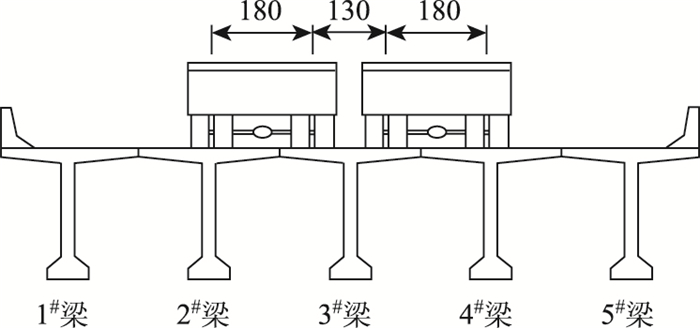
各计算方法均考虑中载两列车后轮作用于跨中的情况,具体布置如图 5、图 6所示:
|
| 图 5 横桥向加载示意(单位:cm) Fig. 5 Schematic diagram of transverse loading(unit: cm) |
| |
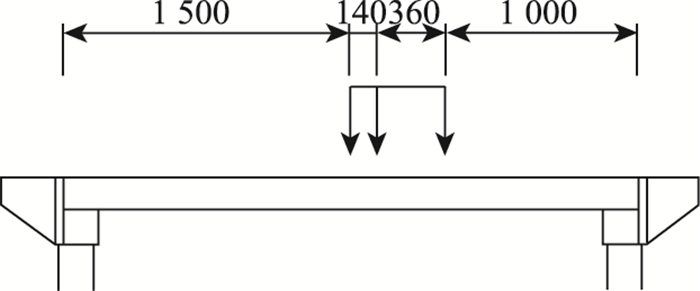
|
| 图 6 纵桥向加载示意(单位:cm) Fig. 6 Schematic diagram of longitudinal loading(unit: cm) |
| |
实桥荷载试验在各梁梁底布置挠度测点和应力测点,两种工况下实测挠度值及应力值如表 1所示,利用公式: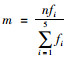
| 工况 | 梁号 | 挠度/mm | 应力/MPa |
| 两列车中载工况下 | 1 | 6.8 | 10.51 |
| 2 | 9.2 | 14.08 | |
| 3 | 12.6 | 20.21 |
如表 1所示,分别给出了中载工况下,针对该T梁宽桥5片主梁(结构对称,表中仅给出3片)的横向分布系数,包括传统的刚性横梁法,修正的刚性横梁法,考虑裂缝引起的刚度损伤条件下的刚性横梁法,修正的刚性横梁法,有限元数值方法与实桥荷载试验计算结果进行比较分析。
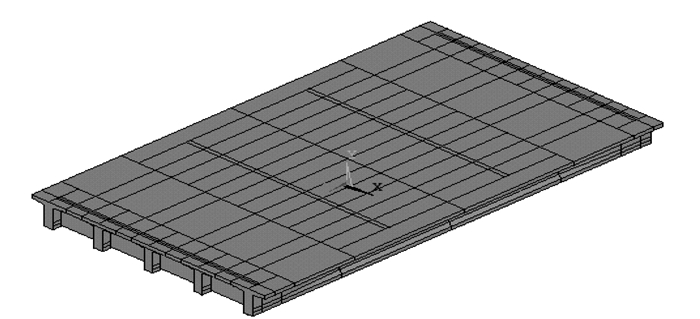
有限元建模采用ANSYS实体单元solid65进行梁单元模拟,solid65可以模拟钢筋混凝土的开裂和压碎,通过材料参数的定义考虑非线形对实桥进行精确模拟。模型见图 7。
|
| 图 7 ANSYS全桥实体模型 Fig. 7 ANSYS solid model of the whole bridge |
| |
本研究方法中的实桥裂缝参数根据实桥外观调查结果确定,根据第2小节中的计算方法及该桥定期检查外观报告可得刚度分配系数ξ,计算的各梁影响线竖标值,再根据最不利荷载计算横向分布系数,具体计算过程不在赘述,横向分布系数计算结果列于表 2。
| 工况 | 梁号 | 刚性横梁法 | 修正刚性横梁法 | 刚性横梁法 (考虑刚度损伤) |
修正刚性横梁法 (考虑刚度损伤) |
有限元解 | 荷载试验结果 |
| 两列车中载工况下 | 1 | 0.400 | 0.400 | 0.396 | 0.396 | 0.381 | 0.391 |
| 2 | 0.572 | 0.568 | 0.545 | 0.541 | 0.497 | 0.524 | |
| 3 | 0.808 | 0.802 | 0.783 | 0.780 | 0.711 | 0.752 |
从表 3可以看出:(1)刚性横梁法计算的横向分布系数最大,误差最高达到7.4%,修正后的刚性横梁法次之,与荷载试验结果误差有较大偏差,这是由于桥梁服役期间的裂缝段引起刚度损伤,理论计算并未考虑,但其对于桥梁的设计是偏安全的;(2)考虑裂缝造成的刚度损伤的刚性横梁法和修正的刚性横梁法较前两者结果偏小,与实桥荷载试验结果和有限元解更为接近,误差在1.3%~4.0%之间,这是因为实际桥梁的刚度损伤是不可忽略的,这一部分刚度的损伤必然会影响实桥的横向受力分布,影响大小与损伤程度有关,该实桥服役年限短,损伤程度较低,故按本研究的方法计算结果与传统方法差别不大,但对于服役年限久,损伤程度大的桥梁差别会更加明显;(3)ANSYS实体单元有限元模拟与荷载试验误差较小,均在6%以内,验证了实体单元建模的正确性;(4)考虑刚度损伤的修正刚性横梁法计算结果精度较高,与实桥荷载试验误差最小,这是因为在计算截面刚度分配系数时,考虑刚度损伤的同时还综合考虑了钢筋及预应力筋,桥面铺装和横隔板对截面刚度的贡献。
| 工况 | 梁号 | 刚性横梁法/% | 修正刚性横梁法/% | 刚性横梁法 (考虑刚度损伤)/% |
修正刚性横梁法 (考虑刚度损伤)/% |
有限元解/% |
| 两列车中载工况下 | 1 | 2.3 | 2.3 | 1.3 | 1.3 | 2.5 |
| 2 | 9.2 | 8.4 | 4.0 | 3.2 | 5.2 | |
| 3 | 7.4 | 6.6 | 4.1 | 3.7 | 5.5 |
4 结论
(1) 传统的刚性横梁法或修正的刚性横梁法对在役桥梁的荷载横向分布的计算具有偏差,偏差大小与损伤程度有关,设计时按传统的计算方法计算能够满足其安全性,但对在役桥梁的进一步评估则误差较大。
(2) 在役桥梁的荷载评估工作采用考虑裂缝带来的刚度损伤的刚性横梁法计算横向分布,研究其横向受力特性,具有理论意义,更接近实际,保证理论计算的精确度,对在役桥梁评估工作具有指导意义。
(3) 本研究的方法适用于窄桥,对于适用于大宽跨比的刚接板梁法,G-M法的修正有待进一步研究。
| [1] |
赵煜, 周博, 贺拴海, 等. 基于裂缝特征的PC简支梁损伤刚度评估方法[J]. 长安大学学报:自然科学版, 2011(4): 39-44. ZHAO Yu, ZHOU Bo, HE Shuan-hai, et al. Damage Stiffness Assessment Method Based on Fracture Characteristics of PC Simply-supported Beam[J]. Journal of Chang'an University:Natural Science Edition, 2011(4): 39-44. |
| [2] |
项贻强, 何余良, 刘丽思, 等. 考虑滑移的多梁式组合小箱梁桥荷载横向分布[J]. 哈尔滨工业大学学报, 2012, 44(8): 113-118. XIANG Yi-qiang, HE Yu-liang, LIU Li-si, et al. Lateral Load Distribution of Multi-box Steel-concrete Composite Girder Bridges for Considering Slipping Effect[J]. Journal of Harbin Institute of Technology, 2012, 44(8): 113-118. |
| [3] |
韦立林, 王文宁, 王建军, 等. 简支梁桥荷载试验横向分布系数分析方法[J]. 广西大学学报:自然科学版, 2007, 32(2): 183-185. WEI Li-lin, WANG Wen-ning, WANG Jian-jun, et al. The Method for Analyzing Transverse Distribution Factors in Load Test of Simple Supported Bridge[J]. Journal of Guangxi University:Natural Science Edition, 2007, 32(2): 183-185. |
| [4] |
周新平, 宗雪梅. 刚架拱桥荷载横向分布系数研究[J]. 郑州大学学报:工学版, 2007, 28(2): 101-104. ZHOU Xin-ping, ZONG Xue-mei. Analysis of Load Transverse Distribution Coefficient for Rigid Frame Arch Bridge[J]. Journal of Zhengzhou University:Engineering Science Edition, 2007, 28(2): 101-104. |
| [5] |
聂瑞锋, 石雪飞, 阮欣, 等. 在役多车道空心板梁桥弯矩横向分布系数计算方法研究[J]. 桥梁建设, 2014, 44(2): 56-60. NIE Rui-feng, SHI Xue-fei, RUAN Xin, et al. Research of Calculation Method for Moment Lateral Distribution Factors of Multi-Lane Hollow Slab Beam Bridges in Service[J]. Bridge Construction, 2014, 44(2): 56-60. |
| [6] |
韩清海. 中小跨径桥梁荷载横向分布系数计算方法的研究及其应用[D]. 长春: 吉林大学, 2009. HAN Qing-hai. Research on Calculation Method of Load Transverse Distribution Coefficient of Medium and Small Span Bridges and Its Application[D]. Changchun: Jilin University, 2009. |
| [7] |
刘华, 叶见曙, 俞博, 等. 桥梁荷载横向分布系数计算方法[J]. 交通运输工程学报, 2009(1): 62-66. LIU Hua, YE Jian-shu, YU Bo, et al. Calculation Method of Transversal Distribution Factor for Bridge Load[J]. Journal of Traffic and Transportation Engineering, 2009(1): 62-66. |
| [8] |
范立础. 桥梁工程[M]. 北京: 人民交通出版社, 2000. FAN Li-chu. Bridge Engineering (Volume 1)[M]. Beijing: China Communications Press, 2000. |
| [9] |
贺拴海, 谢仁物. 公路桥梁荷载横向分布计算方法[M]. 北京: 人民交通出版社, 1999. HE Shuai-hai, XIE Ren-wu. Calculation Method of Lateral Load Distribution of Highway Bridge[M]. Beijing: China Communications Press, 1999. |
| [10] |
李国豪, 石洞. 公路桥梁荷载横向分布计算[M]. 2版. 北京: 人民交通出版社, 1987. LI Guo-hao, SHI Dong. Calculation of Transverse Load Distribution of Highway Bridge[M]. 2nd ed. Beijing: China Communications Press, 1987. |
| [11] |
钱寅泉, 周正茂, 王素娟, 等. 装配式小箱梁桥荷载横向分布数值分析与试验[J]. 公路交通科技, 2012, 29(1): 86-90. QIAN Yin-quan, ZHOU Zheng-mao, WANG Su-juan, et al. Numerical and Experiment of Lateral Load Distribution of Fabricated Small Box Girder Bridge[J]. Journal of Highway and Transportation Research and Development, 2012, 29(1): 86-90. |
| [12] |
聂鑫, 樊健生, 付裕. 箱形截面连续组合梁桥的荷载横向分布[J]. 清华大学学报:自然科学版, 2009(12): 1930-1933. NIE Xin, FAN Jian-sheng, FU Yu. Transverse Load Distribution on Box Section Continuous Composite Steel-concrete Bridges[J]. Journal of Tsinghua University; Science and Technology Edition, 2009(12): 1930-1933. |
| [13] |
欧阳永金, 何旭辉, 叶斌. 三跨PC连续箱梁城市特宽桥空间受力分析研究[J]. 桥梁建设, 2004(6): 10-12. OUYANG Yong-jin, HE Xu-hui, YE Bin. Spatial Analysis of Wide Deck City Bridges of Three-Span PC Continuous Box Girder[J]. Bridge Construction, 2004(6): 10-12. |
| [14] |
郝海霞, 张建仁, 彭晖. 既有钢筋混凝土简支斜梁桥实桥试验荷载横向分布研究[J]. 中外公路, 2009, 29(4): 110-114. HAO Hai-xia, ZHANG Jian-ren, PENG Hui. Study on Transverse Load Distribution of Existing Reinforced Concrete Simply Supported Skew Beam Bridge[J]. Journal of China & Foreign Highway, 2009, 29(4): 110-114. |
| [15] |
潘桂梅, 李平杰, 马牛静. 旧铰接板梁桥横向分布系数现场试验研究[J]. 中外公路, 2012, 32(2): 163-168. PAN Gui-mei, LI Ping-jie, MA Niu-jing. Field Test Study on Transverse Distribution Coefficient of Old Articulated Beam Girder Bridge[J]. Journal of China & Foreign Highway, 2012, 32(2): 163-168. |
| [16] |
马磊, 周林云, 万水. 波形钢腹板连续组合箱梁桥的荷载横向分布[J]. 公路交通科技, 2013, 30(5): 58-62. MA Lei, ZHOU Lin-yun, WAN Shui. Lateral Load Distribution of Continuous Composite Box Girder Bridge with Corrugated Steel Webs[J]. Journal of Highway and Transportation Research and Development, 2013, 30(5): 58-62. |
| [17] |
李秀芳, 吴锐福. 无伸缩缝桥梁荷载横向分布系数的有限元分析[J]. 公路交通科技, 2013, 30(12): 86-92. LI Xiu-fang, WU Rui-fu. FEA of Transverse Load Distribution Factors for Jointless Bridge[J]. Journal of Highway and Transportation Research and Development, 2013, 30(12): 86-92. |
| [18] |
林阳子, 黄侨, 任远, 等. 再议梁板桥横向分布及其在加固中的问题[J]. 公路交通科技, 2008, 25(8): 82-86. LIN Yang-zi, HUANG Qiao, REN Yuan, et al. Reconsidering of Transverse Distribution of Beam-slab Bridge and Problems in Reinforcement[J]. Journal of Highway and Transportation Research and Development, 2008, 25(8): 82-86. |
 2018, Vol. 35
2018, Vol. 35
