扩展功能
文章信息
- 李夏元, 郭靖宇, 万水, Yi LungMo
- LI Xia-yuan, GUO Jing-yu, WAN Shui, Yi Lung Mo
- 基于Timoshenko梁理论的薄壁箱梁剪力滞效应研究
- Analysis on Shear Lag Effect of Thin-walled Box Girder Based on Timoshenko Beam Theory
- 公路交通科技, 2018, 35(6): 52-60, 94
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(6): 52-60, 94
- 10.3969/j.issn.1002-0268.2018.06.008
-
文章历史
- 收稿日期: 2017-12-04
2. 阜阳市公路管理局, 安徽 阜阳 236000;
3. 休斯敦大学 土木与环境工程系, 休斯敦 77204, 美国
2. Highway Administration Bureau of Fuyang, Fuyang Anhui 236000, China;
3. Department of Civil and Environmental Engineering, University of Houston, Texas 77204, USA
薄壁箱梁截面由于抗弯、抗扭性能好,目前,广泛应用于桥梁结构。近年来,随着预应力混凝土箱梁桥在我国迅速发展,截面大量采用腹板间距较大的宽箱以及大悬挑等结构形式。在对称弯曲荷载作用下,结构的变形已明显不服从Bernoulli梁的相关假定,存在剪力滞效应[1-2]——翼板将产生剪切变形, 导致翼板上的正应力沿宽度方向呈不均匀分布[3-4]。剪力滞效应的存在不仅会增加纵向应力幅值,而且会造成不考虑剪力滞效应主梁挠度计算偏小的现象[5]。
目前,剪力滞效应的近似方法较多,如:弹性板理论、比拟杆法、能量变分法等,其中能量变分法应用较为广泛。E.Reissner[6]假设翼板纵向位移沿横向二次抛物线分布解决了轴对称矩形箱梁剪力滞问题;O.Kuzmanovic[7]基于E.Reissner方法,分析了带对称悬臂板的单室箱梁。郭金琼[4]、李立峰[8]在E.Reissner研究基础上,将纵向横向分布函数改为三次抛物线,并用模型试验和数值分析进行了相关验证工作。由于横向分布三次抛物线假设不具有对称性,张士铎[9]引入了四次抛物线的假设分析薄壁箱梁剪力滞效应。倪元增[10]采用余弦函数作为翼板剪滞翘曲位移模式,并考虑剪滞翘曲应力的轴向自平衡条件,分析了槽形宽梁和箱梁的剪滞效应。钱寅泉[1]、倪元增[10]考虑了翼板宽度、到形心轴的距离以及轴力平衡对翘曲位移模式的影响,构造了一般对称的有任意宽度外伸板的单室箱梁纵向翘曲位移模式。罗旗帜[3]考虑了腹板剪切变形对纵向变形的影响,用能量变分法导出了控制微分方程和边界条件,获得了闭合解。蔺鹏臻、周世军[11]从薄壁箱梁的剪力滞效应是由于翼板剪切变形所致这一本质出发, 通过分析箱梁在竖向弯曲时翼板的剪力流分布规律, 提出利用翼板剪切变形规律来定义其剪滞翘曲函数的方法。张元海[12]从分析翼缘板的面内剪切变形和弯曲剪力流的分布规律入手,从理论上证明二次抛物线是箱型梁剪力滞效应分析的合理翘曲位移函数。文献[13-15]选取剪力滞效应引起的附加挠度作为描述剪力滞变形状态的广义位移,对翘曲位移函数进行了多参数修正,提出了薄壁箱梁剪力滞效应的分离解理论,该理论有效避免了剪力滞变形形状与初等梁挠度变形联合在一起分析的复杂性。目前大部分文献的研究重点主要在于翘曲函数选取。钱寅泉[1]、雒敏[16]在选取翘曲函数时,考虑了各翼板之间剪切位移幅值之间的差异,通过构造势能变分函数,解决了各翼板翘曲函数幅值之间的关系;考虑到翘曲位移函数模式下,箱梁轴力尚未平衡问题,钱寅泉[1]引入了横截面轴向均匀函数,解决了轴力自平衡;剪力滞效应研究大部分是基于Euler-Bernoulli梁所提出的平截面假定展开的,文献[3]考虑了剪切变形对纵向翘曲位移的影响,但是忽略了轴向自平衡和各翼板剪切变形幅值之间的关系。如何综合考虑轴向自平衡、剪切变形差幅值之间的关系以及腹板剪切变形对剪力滞翘曲位移模式函数的影响,建立相关的分析方法是非常必要的。
本研究以单箱单室薄壁箱梁为研究对象,基于Timoshenko梁理论,综合考虑各翼板翘曲位移函数幅值之间的关系,引入横截面轴向均匀函数,并对各翼板纵向翘曲位移函数模式进行了剪切变形影响修正,利用Euler-Largrange方程对总势能进行变分,建立起单箱单室薄壁箱梁剪力滞效应控制微分方程。选取某单箱单室混凝土薄壁箱梁,建立有限元数值模型,比较理论与有限元分析结果,对本研究所提的解析解进行验证性分析。
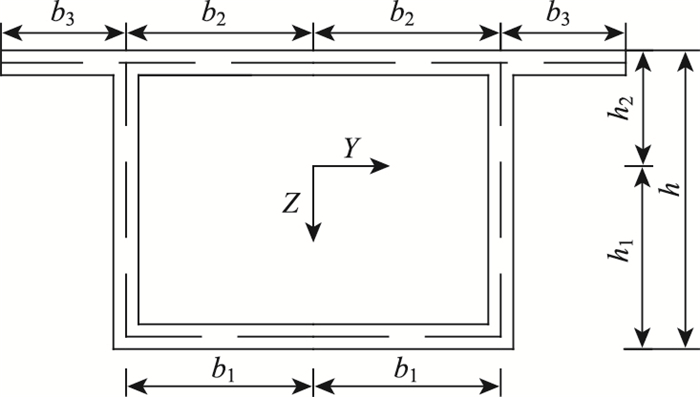
1 单箱单室混凝土薄壁箱梁剪力滞翘曲位移模式应用最小势能原理分析单箱单室混凝土薄壁箱梁(如图 1所示)的弯曲时,引入相关假定(上下翼板竖向应力σz=0,同时板平面外γxz=γyz=0及横向应变εy均很小,可以略去不计[4, 7])和两个广义位移,其中b1,b2, b3分别为各翼缘板宽度值。
|
| 图 1 横截面布置图 Fig. 1 Layout of cross-section |
| |
梁的竖向挠度w(x)与纵向位移u(x, y, z)。梁横截面上任意点纵向位移u(x, y, z)表达式可表示为:
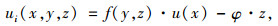
|
(1) |
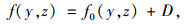
|
(2) |
式中,z为轴坐标值;f0(y, z)为各翼板的纵向翘曲位移函数,根据箱梁截面构造;u(x)为翼板剪切变形最大差值;φ为考虑剪切变形影响的转角(如图 2所示),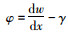
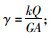
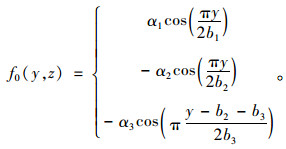
|
(3) |
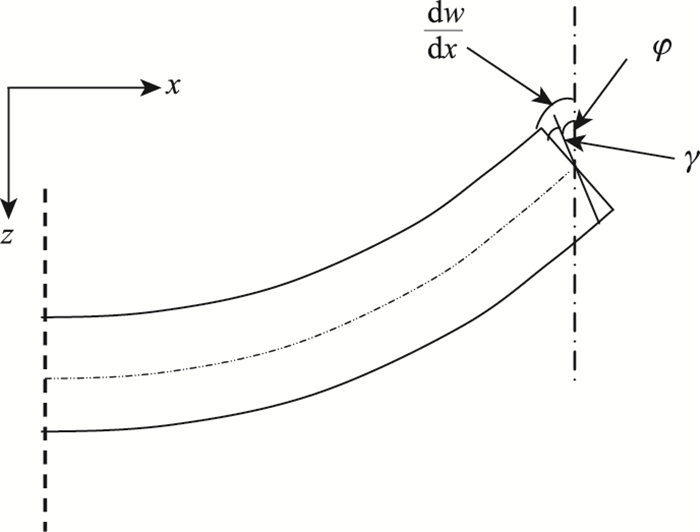
|
| 图 2 Timoshenko梁理论变形后截面示意图 Fig. 2 Schematic diagram of deformed Timoshenko beam |
| |
纵向位移u(x, y, z)可表示成:
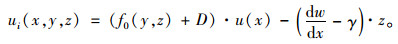
|
(4) |
α1,α2,α3相对幅值是由箱梁截面特性所决定的,与外荷载作用无关。为突出三者之间的关系,略去非重要项,简化式(4)中纵向位移函数表达式u1(x, y, z)=f0(y, z)·u1(x)-φ·z,其中f0(y, z)如式(3)所示。选取一根简支梁(如图 3所示),假设该梁在外荷载作用下的挠度变形近似取为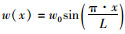
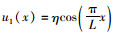
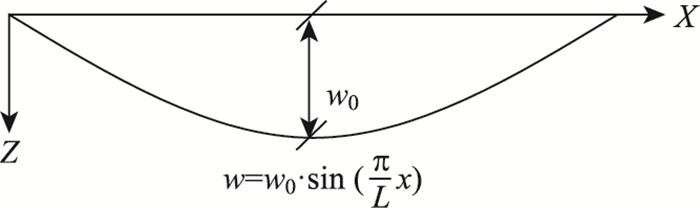
|
| 图 3 梁纵向变形图 Fig. 3 Longitudinal deformation of girder |
| |
荷载q作用下结构总势能:
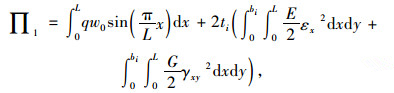
|
(5) |
式中,E为材料的弹性模量;G为剪切模量G=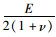
结构处于稳定平衡状态时,结构体系势能最小[17]。利用E-L方程对结构总势能变分,得到结构势能最小时,α1,α2,α3的取值。
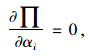
|
(6) |
得:
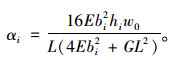
|
(7) |
令荷载q作用下结构的跨中挠度变形w0=1。则
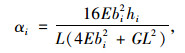
|
(8) |
式中, L为梁长; αi为相对幅值。
1.2 轴向均匀位移D弯曲荷载作用下,梁轴向内力应满足自平衡条件,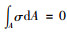
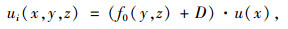
|
(9) |
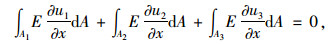
|
(10) |
得:
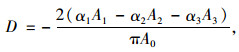
|
(11) |
式中,A0为箱梁顶底板截面面积A=A1+A2+A3,A1,A2,A3分别为箱梁底板、顶板内侧、顶板外侧的面积; u1, u2, u3分别为各翼缘板的纵向变形。
2 基本微分方程的建立结构处于稳定平衡状态时,体系总势能的变分为零,即:
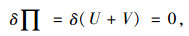
|
(12) |
式中,∏为总势能;V为外力势能;U为形变势能。
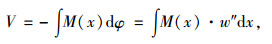
|
(13) |
式中M(x)为弯矩。
梁的形变势能各项分别为:
腹板形变势能:
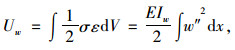
|
(14) |
式中Iw为腹板惯性矩。
上下各翼板形变势能:
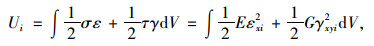
|
(15) |
式中,E,G分别为混凝土弹性模量和剪切模量;各翼板纵向应变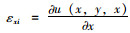
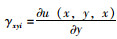
则总势能∏为:

|
(16) |
式中,
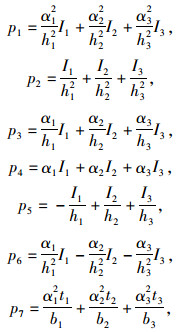
|
式中,I1,I2,I3,I分别为下底板、顶板内侧、顶板外侧、箱型截面惯性矩。
总势能取极值的充要条件E-L方程:
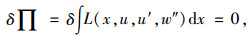
|
(17) |
由式(17)可得
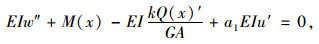
|
(18) |
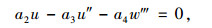
|
(19) |

|
(20) |
式中,
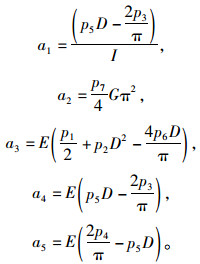
|
上式是由变分得到的剪力滞基本微分方程,式(20)为变分要求的纵向剪力滞位移函数的自然边界条件。
令:
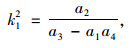
|
(21) |
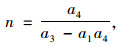
|
(22) |
式(18),式(19)可写成:
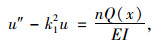
|
(23) |
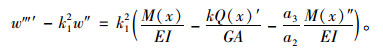
|
(24) |
边界条件:
当板固支时,
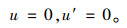
|
(25) |
当板非固支时,
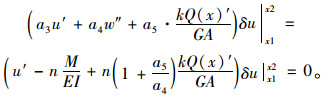
|
(26) |
下面介绍简支梁作用集中荷载P和沿纵向布置均布荷载q两种典型荷载工况,给出翼板剪切变形最大差值u(x)的推导过程,并给出纵向应力解析解计算公式。
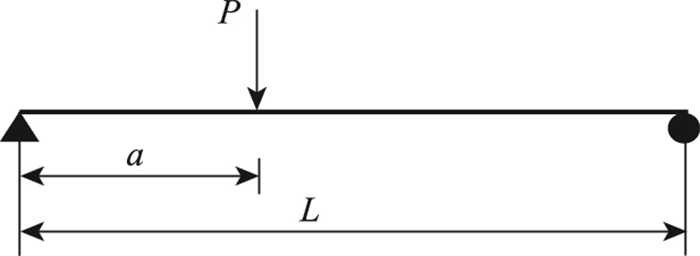
对于图 4所示作用集中荷载作用下(对称作用于箱梁的腹板上)的简支梁,梁内弯矩和剪力可以写成:
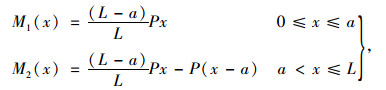
|
(27) |
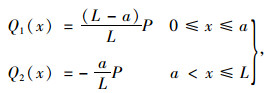
|
(28) |
|
| 图 4 简支梁受集中力 Fig. 4 Simply supported beam under concentrated load |
| |
式中,a为荷载距左端部距离;Q1(x), Q2(x)为剪力。
将式(27),式(28)分别代入式(23),考虑简支梁的边界条件:
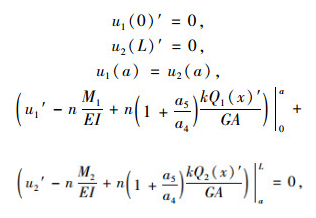
|
(29) |
可求得:
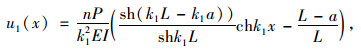
|
(30) |
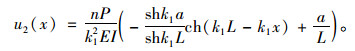
|
(31) |
弯曲应力表达式可写成:
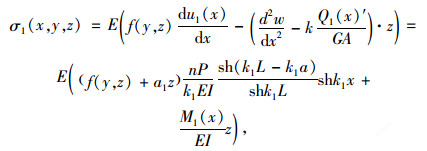
|
(32) |
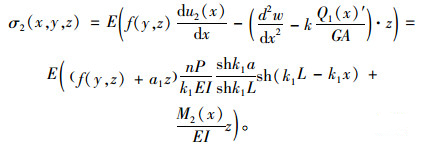
|
(33) |
同理,可得图 5所示均布荷载作用下(对称作用于箱梁的腹板上)的简支梁u(x)和σ(x, y, z):
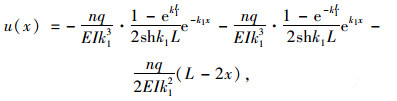
|
(34) |
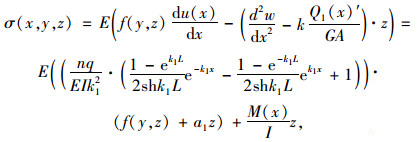
|
(35) |
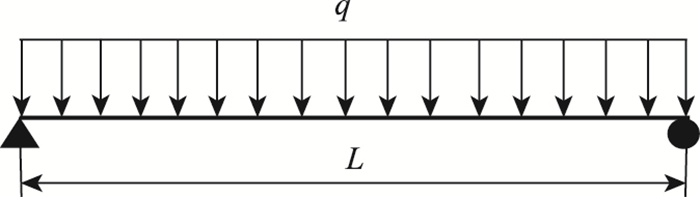
|
| 图 5 简支梁受均布力 Fig. 5 Simply supported beam under uniformly distributed load |
| |
式中ek1L和ek1x为数学幂函数表达式。
4 算例为验证本研究所提算法的正确性,分别对某单箱单室混凝土薄壁简支箱梁承受竖向集中力和均布力两种荷载工况下的剪力滞效应进行分析。
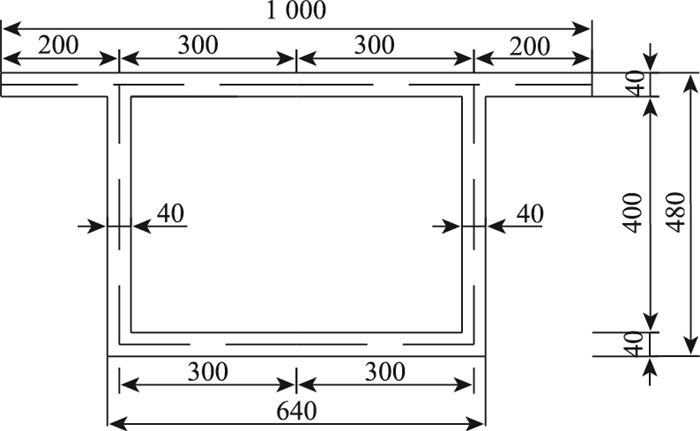
4.1 截面参数选取跨度为2.5 m的单箱单室薄壁箱梁为例,模型截面尺寸见图 6,材料的弹性模量E=3.45×104 MPa,泊松比μ=0.2。模型分别在P=2×12.5 kN的集中力和满跨布置q=2×5 kN/m(对称作用于箱梁的腹板上)的均布力。为了比较本研究所提理论的可靠性,使用ABAQUS有限元软件对两种加载工况分别进行三维数值建模分析(见图 7),其中混凝土采用C3D8I单元,该单元类型使用了增强变形梯度非协调模式,不仅可以有效克服剪切自锁问题,而且厚度方向不需要划分很密的网格就可以取得与二次单元相当的计算结果[18]。
|
| 图 6 薄壁箱梁横截面图(单位:mm) Fig. 6 Cross-section of thin-walled box girder (unit:mm) |
| |
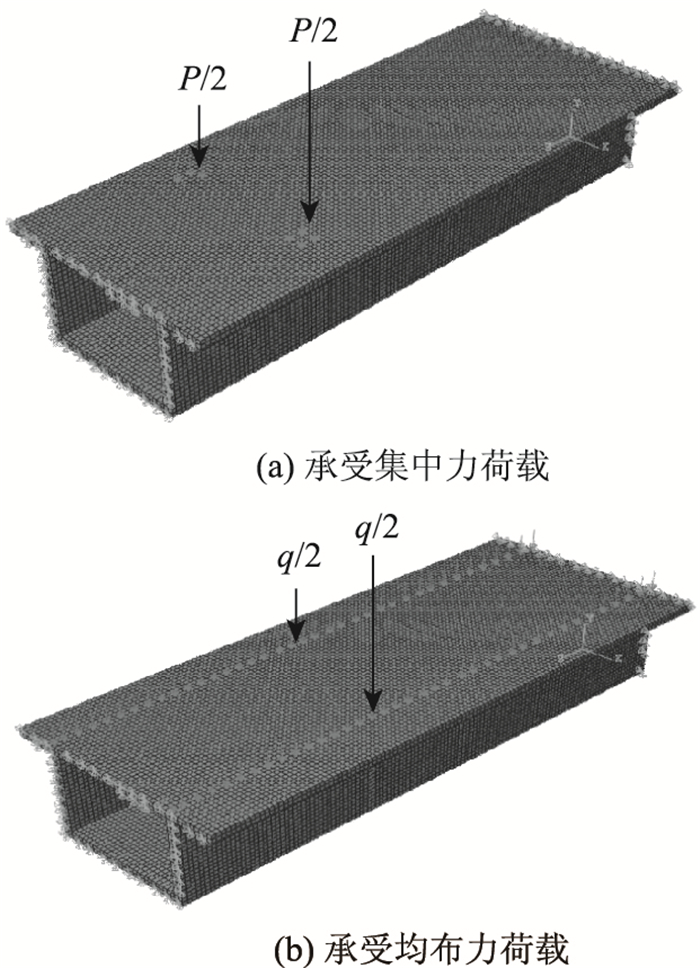
|
| 图 7 ABAQUS箱梁模型 Fig. 7 ABAQUS box girder model under uniformly distributed load |
| |
4.2 简支梁承受集中力作用
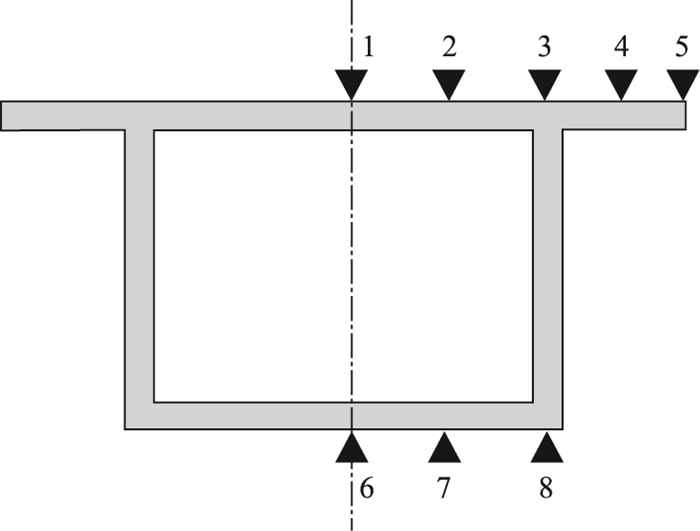
考虑集中力作用位置附近出现应力扰动现象,现将集中力分别施加在a=L/4和a=L/2断面两腹板处(如图 7所示),选取相邻两个间距L/8的断面作为研究对象,同时取图 8所示的测点进行数据分析。
|
| 图 8 横截面测点布置图 Fig. 8 Layout of measuring points on cross-section |
| |
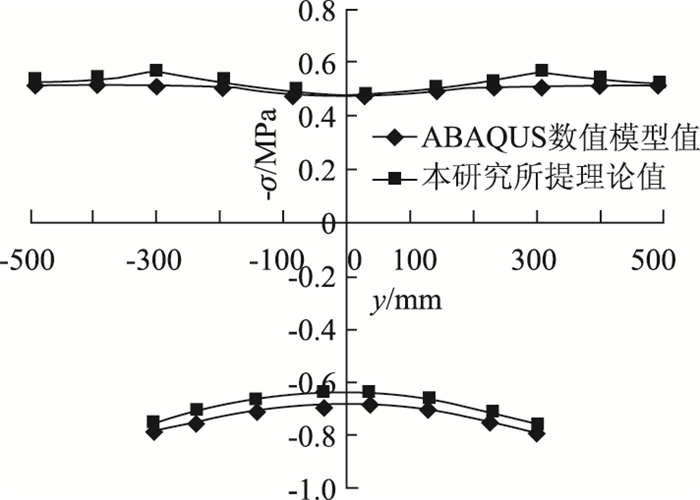
图 9~图 10分别列出了集中力作用于a=L/4时,3L/8,L/2断面顶底板纵向应力分布图,各断面测点的纵向应力值列于表 1~表 2中。
|
| 图 9 集中力作用下3L/8处顶底板纵向应力分布图 Fig. 9 Curves of longitudinal stress distribution of top and bottom plates at three-eighth span cross-section under concentrated load |
| |
|
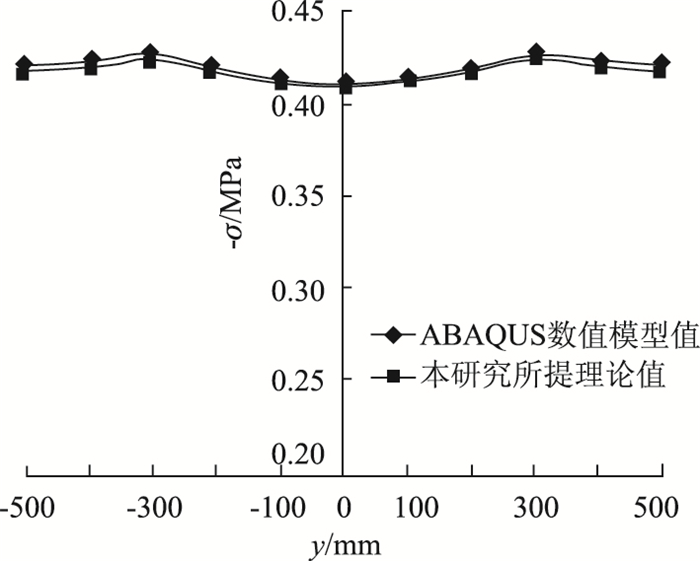
| 图 10 集中力作用下L/2处顶板纵向应力分布图 Fig. 10 Curves of longitudinal stress distribution of top and bottom plates at one-half span of under concentrated load |
| |
| 测点位置 | ABAQUS值 ②/MPa |
理论值 ①/MPa |
误差/% (①-②)/②×100 |
| 1 | -0.484 | -0.478 | 1.2 |
| 2 | -0.495 | -0.500 | 0.9 |
| 3 | -0.508 | -0.562 | 10.6 |
| 4 | -0.507 | -0.533 | 5.2 |
| 5 | -0.516 | -0.522 | 1.1 |
| 6 | 0.683 | 0.645 | 5.6 |
| 7 | 0.710 | 0.674 | 5.1 |
| 8 | 0.775 | 0.758 | 2.3 |
| 测点位置 | ABAQUS值 ②/MPa |
理论值 ①/MPa |
误差/% (①-②)/②×100 |
| 1 | -0.411 | -0.410 | 0.4 |
| 2 | -0.415 | -0.414 | 0.3 |
| 3 | -0.427 | -0.425 | 0.4 |
| 4 | -0.423 | -0.420 | 0.8 |
| 5 | -0.421 | -0.418 | 0.8 |
| 6 | — | — | — |
| 7 | — | — | — |
| 8 | — | — | — |
简支梁承受L/4断面作用的集中力荷载时,底板在L/2处出现了负剪力滞,因此,图 10、表 2仅分析顶板正剪力滞效应。由表 1、表 2可知,本研究中提出的考虑剪力滞效应的纵向应力理论解与ABAQUS数值解吻合度较高,表 1中测点3腹板处纵向应力误差略大,这是由于腹板受加载端应力扰动影响较大,远离腹板该影响则明显减弱,基本控制在5%左右,表 2中两者的误差小于1%。
图 11~图 12分别列出了集中力作用于a=L/2时,以5L/8,6L/8两个断面顶底板纵向应力分布图。取各断面的测点的纵向应力值于表 3~表 4中。
|
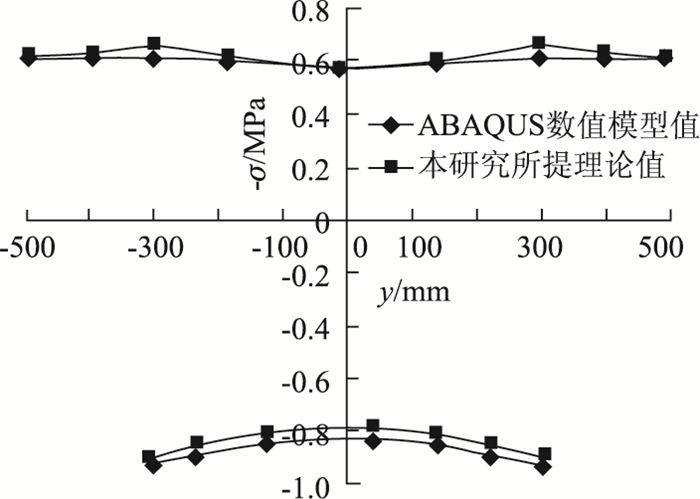
| 图 11 集中力作用下5L/8处顶底板纵向应力分布图 Fig. 11 Curves of longitudinal stress distribution of top and bottom plates at five-eighth span under concentrated load |
| |

|
| 图 12 集中力作用下6L/8处顶板纵向应力分布图 Fig. 12 Curves of longitudinal stress distribution of top and bottom plates at six-eighth span under concentrated load |
| |
| 测点位置 | ABAQUS值 ②/MPa |
理论值 ①/MPa |
误差/% (①-②)/②×100 |
| 1 | -0.587 | -0.583 | 0.7 |
| 2 | -0.598 | -0.604 | 1.0 |
| 3 | -0.611 | -0.666 | 9.1 |
| 4 | -0.610 | -0.638 | 4.6 |
| 5 | -0.619 | -0.626 | 1.2 |
| 6 | 0.822 | 0.785 | 4.4 |
| 7 | 0.849 | 0.814 | 4.0 |
| 8 | 0.914 | 0.898 | 1.7 |
| 测点位置 | ABAQUS值 ②/MPa |
理论值 ①/MPa |
误差/% (①-②)/②×100 |
| 1 | -0.402 | -0.410 | 1.9 |
| 2 | -0.406 | -0.414 | 1.9 |
| 3 | -0.417 | -0.425 | 2.0 |
| 4 | -0.413 | -0.420 | 1.5 |
| 5 | -0.411 | -0.418 | 1.5 |
| 6 | — | — | — |
| 7 | — | — | — |
| 8 | — | — | — |
与L/4作用集中力结论类似,简支梁承受L/2断面作用的集中力荷载时,底板在6L/8处出现了负剪力滞现象,受加载端扰动影响,相邻截面5L/8测点3误差较大,远离该区域的误差明显降低,表 4误差控制在2%以内,表明通过使用本研究中推导的考虑剪力滞效应的计算公式,可以较好地反映实际应力情况。
4.3 简支梁承受均布荷载为进一步验证本研究中剪力滞效应计算公式的适用性,分析了均布荷载作用下混凝土薄壁箱梁剪力滞效应。图 13~图 15为均布荷载作用下L/2,3L/8,2L/8处顶板纵向应力分布图,表 5~表 7列出了均布荷载作用下L/2,3L/8,2L/8处顶板测点应力值。

|
| 图 13 均布荷载作用下L/2处顶底板纵向应力分布图 Fig. 13 Curves of longitudinal stress distribution of top and bottom plates at one-half span under uniformly distributed load |
| |
|
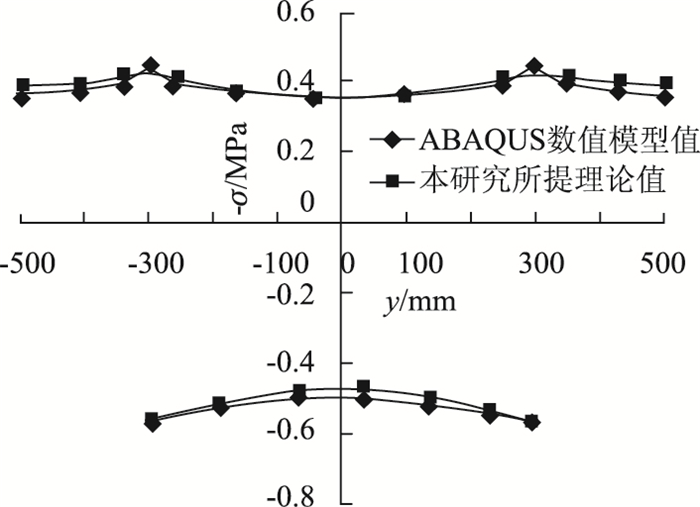
| 图 14 均布荷载作用下3L/8处顶底板纵向应力分布图 Fig. 14 Curves of longitudinal stress distribution of top and bottom plates at three-eighth span under uniformly distributed load |
| |

|
| 图 15 均布荷载作用下2L/8处顶底板纵向应力分布图 Fig. 15 Curves of longitudinal stress distribution of top and bottom plates at two-eighth span under uniformly distributed load |
| |
| 测点位置 | ABAQUS值 ②/MPa |
理论值 ①/MPa |
误差/% (①-②)/②×100 |
| 1 | -0.385 | -0.382 | 0.8 |
| 2 | -0.396 | -0.400 | 1.0 |
| 3 | -0.471 | -0.450 | 4.5 |
| 4 | -0.407 | -0.427 | 4.9 |
| 5 | -0.392 | -0.417 | 6.6 |
| 6 | 0.540 | 0.515 | 4.5 |
| 7 | 0.554 | 0.539 | 2.8 |
| 8 | 0.599 | 0.606 | 1.2 |
| 测点位置 | ABAQUS值 ②/MPa |
理论值 ①/MPa |
误差/% (①-②)/②×100 |
| 1 | -0.360 | -0.356 | 1.0 |
| 2 | -0.370 | -0.373 | 0.9 |
| 3 | -0.445 | -0.424 | 4.9 |
| 4 | -0.381 | -0.401 | 5.1 |
| 5 | -0.366 | -0.391 | 6.9 |
| 6 | 0.505 | 0.480 | 4.9 |
| 7 | 0.519 | 0.504 | 3.0 |
| 8 | 0.565 | 0.571 | 1.2 |
| 测点位置 | ABAQUS值 ②/MPa |
理论值 ①/MPa |
误差/% (①-②)/②×100 |
| 1 | -0.281 | -0.279 | 0.8 |
| 2 | -0.291 | -0.296 | 1.7 |
| 3 | -0.364 | -0.344 | 5.5 |
| 4 | -0.301 | -0.322 | 7.1 |
| 5 | -0.286 | -0.313 | 9.4 |
| 6 | 0.395 | 0.376 | 4.8 |
| 7 | 0.410 | 0.399 | 2.7 |
| 8 | 0.457 | 0.465 | 1.6 |
由图 13~图 15可见,均布荷载作用下各断面顶板纵向应力分布图几乎重合,顶板翼缘理论应力值较数值模型值大,基本可以实现包络。表 5~表 7中测点1~8数据表明箱梁内顶板和内底板的误差控制在5%左右,具有较高的精度,而箱梁顶悬臂板由于外侧端部是自由的,边界条件不能完全按照箱梁内侧的约束情况对其假设,存在一定的近似性,故其误差相对于内侧而言较大,测点3,4,5数据表明,误差随外伸长度增加而增加,但最大误差在10%以内。结论表明,本研究所提剪力滞效应理论计算公式具有较高的精度来描述实际应力情况。
5 结论(1) 箱形梁各翼板翘曲位移函数幅值αi、横截面轴力平衡轴向均匀函数D与外荷载形式无关,仅与截面参数和材料参数有关。
(2) 通过对比不同荷载工况下单箱单室混凝土薄壁箱梁的剪力滞效应的理论解析解与ABAQUS数值解,本研究中计算结果与有限元结果吻合良好,验证了本研究中所构造翘曲位移函数的合理性及剪力滞效应计算的适用性。
(3) 相关结论表明箱形梁剪切变形差u(x)的微分方程仅与剪力分布有关,而与剪切变形系数k无关,表明剪切变形对剪力滞效应没有影响,对挠曲变形影响较大,需要进一步分析其影响程度。
(4) 集中荷载作用下,加载点附近的正剪力滞效应明显,而远离加载点截面正剪力滞效应逐渐减弱;均布荷载作用下正剪力滞效应沿梁轴方向分布均匀。
| [1] |
钱寅泉, 倪元增. 箱梁剪力滞计算的翘曲函数法[J]. 铁道学报, 1990, 12(2): 57-70. QIAN Yin-quan, NI Yuan-zeng. Warping Displacement Fnction Method for Calculation of Shear Lag Effect in Box Girder[J]. Journal of the China Railway Society, 1990, 12(2): 57-70. |
| [2] |
吴文清, 叶见曙, 杨效中, 等. 薄壁箱梁剪力滞效应研究理论的若干问题讨论[J]. 桥梁建设, 2001(6): 53-57. WU Wen-qing, YE Jian-shu, YANG Xiao-zhong, et al. Discussions about the Existing Problems of the Theoretical Studies on Shear Lag Effect of Thin-walled Box Girder[J]. Bridge Construction, 2001(6): 53-57. |
| [3] |
罗旗帜, 吴幼明, 刘光栋. 变高度薄壁箱梁的剪力滞[J]. 铁道学报, 2003, 25(5): 81-87. LUO Qi-zhi, WU You-ming, LIU Guang-dong. Shear Lag of the Thin-wall Box Girder with Varying Depths[J]. Journal of the China Railway Society, 2003, 25(5): 81-87. |
| [4] |
郭金琼, 房贞政, 郑振. 箱形梁设计理论[M]. 第2版. 北京: 人民交通出版社, 2008. GUO Jin-qiong, FANG Zhen-zheng, ZHENG Zhen. Design Theory of Box Girder[M]. 2nd ed. Beijing: China Communications Press, 2008. |
| [5] |
张元海, 林丽霞, 刘勇. 剪力滞效应对箱形梁挠度影响的研究[J]. 计算力学学报, 2012, 29(4): 625-630. ZHANG Yuan-hai, LIN Li-xia, LIU Yong. Influence of Shear Lag Effect on Deflection of Box Girder[J]. Chinese Journal of Computational Mechanics, 2012, 29(4): 625-630. |
| [6] |
REISSNER E. Analysis of Shear Lag in Box Beams by the Principle of Minimum Potential Energy[J]. Quarterly of Applied Mathematics, 1946, 4(3): 268-278. |
| [7] |
KUZMANOVIC B O, GRAHAM H J. Shear Lag in Box Girders[J]. Journal of the Structural Division, 1981, 107(9): 1701-1712. |
| [8] |
李立峰, 彭鲲, 王文. 波形钢腹板组合箱梁剪力滞效应的理论与试验研究[J]. 公路交通科技, 2009, 26(4): 78-83. LI Li-feng, PENG Kun, WANG Wen. Theoretical and Experimental Study on Shear Lag Effect of Composite Box Girder with Corrugated Steel Webs[J]. Journal of Highway & Transportation Research & Development, 2009, 26(4): 78-83. |
| [9] |
CHANG S T, YUN D. Shear Lag Effect in Box Girder with Varying Depth[J]. Journal of Structural Engineering, 1988, 114(10): 2280-2292. |
| [10] |
倪元增. 槽型宽梁的剪力滞问题[J]. 土木工程学报, 1986, 19(4): 32-41. NI Yuan-zeng. Shear Lag Problems in Wide Channel Beams[J]. China Civil Engineering Journal, 1986, 19(4): 32-41. |
| [11] |
蔺鹏臻, 周世军. 基于剪切变形规律的箱梁剪力滞效应研究[J]. 铁道学报, 2011, 33(4): 100-104. LIN Peng-zhen, ZHOU Shi-jun. Analysis on Shear-lag Effect of Box Girders Based on Flange-slab Shear Deformation Law[J]. Journal of the China Railway Society, 2011, 33(4): 100-104. |
| [12] |
张元海, 白昕, 林丽霞. 箱形梁剪力滞效应的改进分析方法研究[J]. 土木工程学报, 2012, 45(11): 153-158. ZHANG Yuan-hai, BAI Xin, LIN Li-xia. An Improved Approach for Analyzing Shear Lag Effect of Box Girders[J]. China Civil Engineering Journal, 2012, 45(11): 153-158. |
| [13] |
张元海, 胡玉茹, 林丽霞, 等. 基于修正翘曲位移模式的薄壁箱梁剪力滞效应分析[J]. 土木工程学报, 2015, 48(6): 44-50. ZHANG Yuan-hai, HU Yu-ru, LIN Li-xia, et al. Analysis on Shear Lag Effect of Thin-walled Box Girders Based on a Modified Warping Displacement Mode[J]. China Civil Engineering Journal, 2015, 48(6): 44-50. |
| [14] |
杨绿峰, 周月娥, 曾有凤. 箱型梁附加挠度与剪力滞效应的一维有限元分析[J]. 土木工程学报, 2013, 46(4): 71-77. YANG Lü-feng, ZHOU Yue-e, ZENG You-feng. One-dimensional Finite Element Analysis on Additional Deflection and Shear-lag Effect of Box-girders[J]. China Civil Engineering Journal, 2013, 46(4): 71-77. |
| [15] |
张元海, 李琳, 林丽霞, 等. 以附加挠度作为广义位移时薄壁箱梁剪力滞效应的梁段有限元分析[J]. 土木工程学报, 2013, 46(10): 100-107. ZHANG Yuan-hai, LI Lin, LIN Li-xia, et al. Beam-segment Finite Element Analysis on Shear Lag Effect of Thin-walled Box Girder Adopting Additional Deflection as Generalized Displacement[J]. China Civil Engineering Journal, 2013, 46(10): 100-107. |
| [16] |
雒敏, 蔺鹏臻, 孙理想. 单箱双室箱梁的剪力滞效应分析[J]. 力学与实践, 2013, 35(6): 70-74. LUO Min, LIN Peng-zhen, SUN Li-xiang. Analysis of Shear Lag Effect of Twin-cell Box Girders[J]. Mechanics in Engineering, 2013, 35(6): 70-74. |
| [17] |
徐芝纶. 弹性力学简明教程[M]. 4版. 北京: 高等教育出版社, 2013. XU Zhi-lun. Elastic Mechanics Brief Tutorial[M]. 4th ed. Beijing: Higher Education Press, 2013. |
| [18] |
石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M]. 北京: 机械工业出版社, 2006. SHI Yi-ping, ZHOU Yu-rong. Finite Element Analysis Cases by ABAQUS[M]. Beijing: China Machine Press, 2006. |
 2018, Vol. 35
2018, Vol. 35
