扩展功能
文章信息
- 郭彤, 杨毅, 夏诚东, 杨倪坤
- GUO Tong, YANG Yi, XIA Cheng-dong, YANG Ni-kun
- 基于拉压模量同步测试的岩沥青改性沥青混合料疲劳损伤特性
- Fatigue Damage Characteristics of Rock Asphalt Modified Asphalt Mixtures Based on Tension and Compression Moduli Synchronous Test
- 公路交通科技, 2018, 35(6): 14-21
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(6): 14-21
- 10.3969/j.issn.1002-0268.2018.06.003
-
文章历史
- 收稿日期: 2018-01-19
2. 长沙理工大学, 湖南 长沙 410114
2. Changsha University of Science & Technology, Changsha Hunan 410114, China
随着国民经济的不断发展和道路网的形成,道路交通量日益增大,一些新建的高等级沥青路面通车1-2年,就出现了不同程度的车辙、裂缝、坑槽、松散等病害,严重影响了路网的服务水平,大大缩短了预期的使用寿命,并造成了极大的经济损失。在正常施工条件下,出现这些问题的根本原因一方面是因为沥青混合料的路用性能满足不了日益增长的交通量的需求,另一方面是因为道路结构设计的不合理所致。为解决路面沥青材料的问题,越来越多的改性沥青出现在人们的视野中,如SBS,PE,SBR,EVA等,然而这些聚合物改性剂的化学性质表现为非极性,这使得它们和沥青很难相容,在拌和运输过程中容易产生分层和离析,同时在聚合物的制备工艺上,需要特殊的剪切及碾磨设备,生产工艺复杂、造价较高,这些缺点在一定程度上限制了聚合物改性剂的广泛使用。
天然岩沥青是石油类物质在长期地质环境变化条件下、经历复杂物理化学变化后形成的产物,因此其与基质沥青之间具有很好的配伍性,两者之间相混时不存在离析现象。天然岩沥青作为一种新兴的改性剂,因其优良的使用性能、简单的施工工艺及合理的价格备受人们的青睐。研究表明[1-3]:岩沥青改性沥青混合料具有较好的抗高温稳定性、抗老化性能和抗水损害性能,其强度和模量与基质沥青混合料相比也得到了显著提升。因此,本研究以岩沥青改性沥青混合料、SBS改性沥青混合料为研究对象,开展2种沥青混合料的疲劳耐久性研究。
大量路面结构力学性能测试分析结果表明,交通荷载作用下的沥青路面结构中同时存在拉应力区与压应力区,而在沥青路面设计时大都认为材料在受拉和受压时表现出相同的力学响应特性[4]。我国通常采用抗压模量来表征路面材料的抗变形能力,实际上,沥青路面无论面层还是基层,材料的抗拉模量与抗压模量存在差异性,各层层底的抗拉强度与抗拉模量均小于其层顶的抗压强度与抗压模量[5]。因此采用单一抗压模量来计算处于复杂应力状态下的路面力学响应是不合适的,这将高估路面材料的力学性能,并使得设计计算结果存在较大的误差。因此,建立基于双模量理论的路面结构力学分析方法将是提高沥青路面设计的科学性与精准性的重要途径[6-7]。
本研究基于上述问题,基于吕松涛[8]提出的四点弯曲拉、压弯模量同步测试法, 对岩沥青与SBS改性沥青混合料进行了四点弯曲疲劳试验,同时得到沥青混合料拉、压和弯曲回弹模量,建立了沥青混合料不同模量衰变方程,揭示了2种沥青混合料疲劳过程中拉压模量的初始值、破坏值、临界破坏点以及模量衰减速率等指标的差异性。本研究对岩沥青材料的推广应用及合理选取沥青路面材料结构设计参数、提高沥青路面设计的精准性具有一定的意义。
1 沥青混合料疲劳试验方法简介 1.1 原材料试验及配合比设计疲劳试验选用的混合料为岩沥青改性沥青混合料和SBS改性沥青混合料,其中岩沥青为印尼产的布敦岩沥青,集料为石灰岩,矿粉为石灰岩质矿粉,级配采用AC-16C型3种沥青性能指标测试结果及沥青混合料级配分别如表 1~表 4所示。
| 技术指标 | 外观 | 灰分含量/% | 溶解度/% | 含水量/% |
| 检测结果 | 棕色粉末 | 74.17 | 25.83 | 0.9 |
| 技术指标 | 技术要求 | 检验结果 |
| 针入度(25 ℃,100 g,5 s)/(0.1 mm) | 60~80 | 74.8 |
| 延度(5 cm/min,15 ℃)/cm | ≥100 | > 100 |
| 软化点(环球法)/℃ | ≥46 | 54 |
| 密度(15 ℃)/(g·cm-3) | ― | 1.027 |
| 技术指标 | 技术要求 | 检验结果 |
| 针入度(25 ℃,100 g,5 s)/(0.1 mm) | 40~60 | 55 |
| 延度(5 cm/min,15 ℃)/cm | ≥20 | 33 |
| 软化点(环球法)/℃ | ≥60 | 75.5 |
| 密度(15 ℃)/(g·cm-3) | ― | 1.02 |
| 筛孔尺寸/mm | 合成级配各筛孔的通过率/% |
| 19 | 100 |
| 16 | 90.4 |
| 13.2 | 79.5 |
| 9.5 | 63.5 |
| 4.75 | 37 |
| 2.36 | 24.2 |
| 1.18 | 16 |
| 0.6 | 11.4 |
| 0.3 | 7.7 |
| 0.15 | 6.1 |
| 0.075 | 4.3 |
通过沥青混合料马歇尔配合比试验,考虑到试验结果的可比性,确定2种沥青混合料的最佳油石比均为4.6%, 根据所确定的级配及最佳油石比,通过气动型压实机振动成型车辙板,然后切割成380 mm×63.5 mm×50 mm的标准四点弯曲小梁试件。
沥青混合料是一种典型的黏弹性材料,在不同的温度、不同的加载速度和不同的应力状态下会表现出不同的力学响应特性。本研究采用应力控制的四点弯曲试验方法,加载波型为偏正弦波,加载频率为10 Hz,试验温度为15 ℃,疲劳试验仪器采用MTS-810材料试验系统。
首先分别对2种沥青混合料进行标准强度试验,根据强度试验结果确定疲劳试验时的应力比分别为0.2,0.3,0.4和0.6。
为了准确分析沥青混合料弯拉疲劳试验中拉压模量衰变规律的差异性,开展了沥青混合料弯拉疲劳试验,其中拉、压、弯模量测量方法如下:跨中挠度采用上表面放置的LVDT位移计来进行测量,用来计算试件的弯拉模量;跨中上表面的压应变与下表面的拉应变分别通过在其表面所贴的应变片进行测量,分别用来计算试件的压缩模量与拉伸模量应变片粘贴方式及测试装置如图 1所示。

|
| 图 1 四点弯曲法应变片的贴法与模量测试 Fig. 1 Strain gauge sticking way and modulus test using 4-point bending method |
| |
1.2 四点弯曲法拉、压模量计算模型
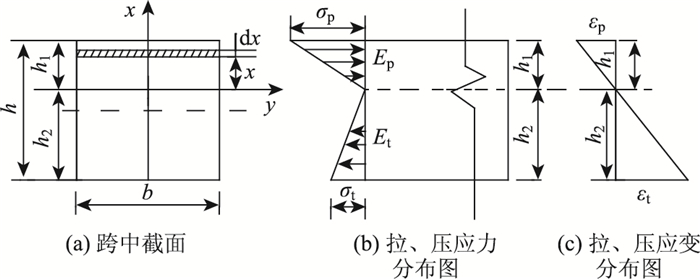
考虑拉、压模量的差异性,试件的中性面将发生上移,跨中截面拉、压应力应变分布如图 2所示。
|
| 图 2 试件跨中截面、应力、应变分布图 Fig. 2 Distributions of stresses and strains of specimen at mid-span |
| |
取平行于中性面的微面积单元如图 2(a)所示,即dA=bdx,对于跨中截面,内力引起的弯矩可以表示为:
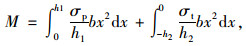
|
(1) |
积分可得:
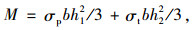
|
(2) |
即:
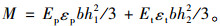
|
(3) |
根据平面假设,截面应变分布如图 2(c)所示:
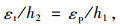
|
(4) |
根据平衡条件得:
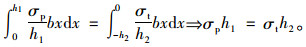
|
(5) |
根据Ep=σp/εp, Et=σt/εt,并联合式(3)、式(4)、式(5)可得:
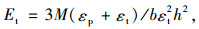
|
(6) |
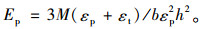
|
(7) |
因此,拉、压模量之比为:
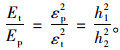
|
(8) |
试件跨中的弯矩:
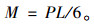
|
(9) |
将式(9)代入式(6)、式(7),可得拉、压模量计算公式分别为:
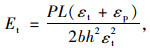
|
(10) |
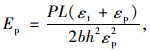
|
(11) |
式中,b为跨中截面宽度;h1为试件上表面至上移后的中性面的垂直距离;h2为下表面至中性面的垂直距离;σp为跨中上表面压应力;σt为跨中下表面拉应力;εp为跨中上表面压应变;εt为跨中下表面拉应变;P为荷载;L为跨距。。
2 两种沥青混合料疲劳耐久性分析 2.1 疲劳寿命对比分析采用应力控制的疲劳试验,以试件发生明显断裂作为破坏标准,在对试验结果分析时,首先应剔除严重偏离疲劳曲线的试验点。
疲劳试验结果采用传统S-N疲劳方程进行拟合分析:
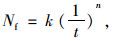
|
(12) |
式中,Nf为试件破坏时的加载次数;t为应力比;k为疲劳方程曲线截距;n表征疲劳方程曲线斜率。
2种沥青混合料的疲劳试验结果如表 5所示。
| 应力比t | 岩沥青Nf/次 | SBS Nf/次 |
| 0.2 | 619 422 | 441 029 |
| 0.2 | 604 783 | 626 475 |
| 0.2 | 525 081 | 538 081 |
| 0.3 | 55 907 | 45 859 |
| 0.3 | 51 774 | 53 842 |
| 0.3 | 55 840 | 62 840 |
| 0.4 | 7 176 | 4 223 |
| 0.4 | 12 669 | 4 707 |
| 0.4 | 5 510 | 4 676 |
| 0.6 | 1 445 | 1 439 |
| 0.6 | 1 501 | 1 269 |
| 0.6 | 1 458 | 934 |
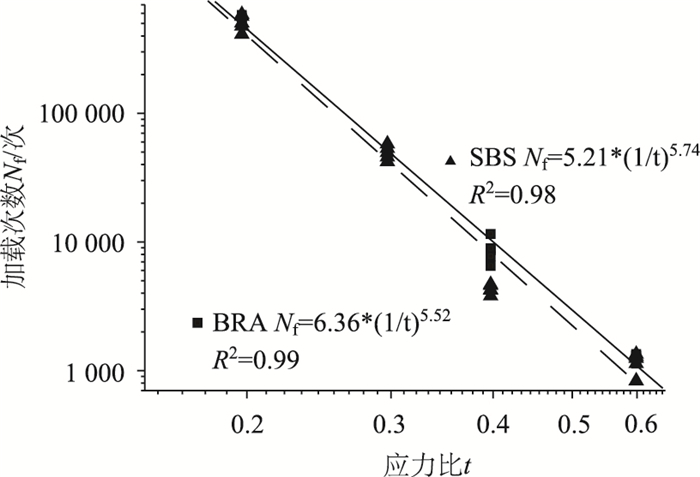
将表 5的试验结果在双对数坐标中进行拟合,拟合所得的疲劳曲线如图 3所示:
|
| 图 3 两种沥青混合料疲劳寿命随应力比变化规律 Fig. 3 Fatigue lives of 2 asphalt mixtures varying with stress ratio |
| |
在S-N疲劳方程曲线中,k为疲劳曲线的截距,k值越大疲劳耐久性越好;n反映了材料的敏感程度,n值越大,疲劳寿命随应力比越敏感,受应力比影响越显著。
从图 3可看出,2种沥青混合料的疲劳方程曲线在双对数坐标中均呈现直线关系;随着应力比的增大,疲劳寿命均减小;从疲劳寿命与疲劳方程参数来看,2种沥青混合料的参数值差别不大,说明岩沥青与SBS改性沥青混合料的疲劳性能相当。
2.2 疲劳损伤对比分析临界损伤是反映疲劳破坏与否的判据,试件在不同条件下发生疲劳破坏时所测得的临界损伤也是不同的,研究损伤临界值的影响因素及其变化规律,对于准确预测试件疲劳寿命是很有意义的。以动模量衰减定义为疲劳损伤变量,得到临界疲劳损伤计算公式为:
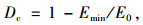
|
(13) |
式中,Dc为疲劳损伤临界值;E0为模量初始值;Emin为临界破坏时模量值。
不同应力比下岩沥青与SBS改性沥青混合料拉、压模量初始值、临界值、及临界损伤值分别如表 6~表 9所示。
| 应力比 | 拉伸模量初始均值E0/MPa | 拉伸模量临界均值Emin/MPa | 临界疲劳损伤Dct |
| 0.2 | 17 291 | 9 510 | 0.45 |
| 0.3 | 18 860 | 11 316 | 0.40 |
| 0.4 | 20 559 | 13 569 | 0.34 |
| 0.6 | 20 654 | 14 251 | 0.31 |
| 应力比 | 压缩模量初始均值E0/MPa | 压缩模量临界均值Emin/MPa | 临界疲劳损伤Dcp |
| 0.2 | 29 384 | 18 806 | 0.36 |
| 0.3 | 30 364 | 21 862 | 0.28 |
| 0.4 | 31 195 | 24 956 | 0.20 |
| 0.6 | 33 030 | 27 415 | 0.17 |
| 应力比 | 拉伸模量初始均值E0/MPa | 拉伸模量临界均值Emin/MPa | 临界疲劳损伤Dct |
| 0.2 | 18 042 | 9 743 | 0.46 |
| 0.3 | 18 436 | 10 693 | 0.42 |
| 0.4 | 19 402 | 12 611 | 0.35 |
| 0.6 | 20 170 | 14 321 | 0.29 |
| 应力比 | 压缩模量初始均值E0/MPa | 压缩模量临界均值Emin/MPa | 临界疲劳损伤Dcp |
| 0.2 | 30 281 | 19 985 | 0.34 |
| 0.3 | 31 138 | 22 108 | 0.29 |
| 0.4 | 31 639 | 24 678 | 0.22 |
| 0.6 | 33 048 | 26 769 | 0.19 |
从表 6~表 9中可看出在相同的试验条件下,岩沥青与SBS改性沥青混合料在相同应力比下拉压模量对应的初始值、临界值比较接近,说明了2种材料抗疲劳性能较为接近。
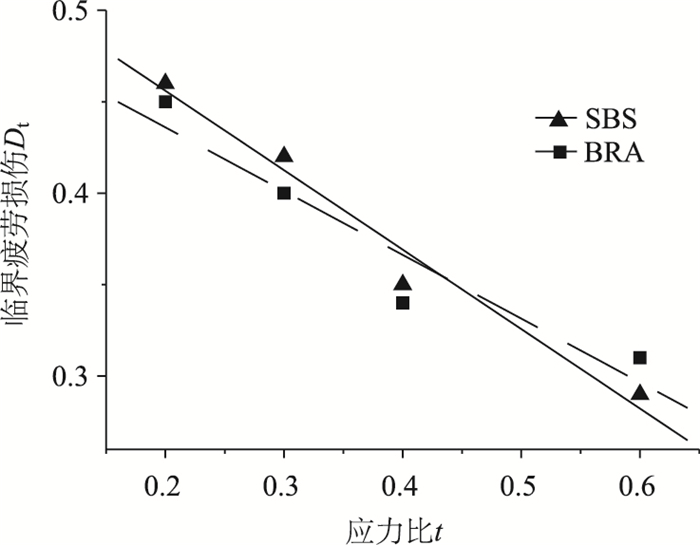
将岩沥青与SBS改性沥青混合料临界疲劳损伤Dc与应力比进行拟合,拟合结果如图 4、图 5及式(14)~式(17)所示。
|
| 图 4 以拉伸模量表征的临界疲劳损伤与应力比关系曲线 Fig. 4 Relationship curves of critical fatigue damage and stress ratio characterized by tension modulus |
| |
|
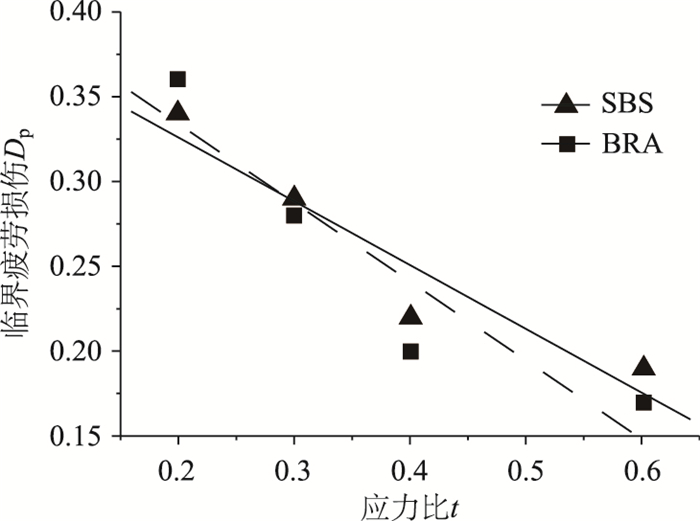
| 图 5 以压缩模量表征的临界疲劳损伤与应力比关系曲线 Fig. 5 Relationship curves of critical fatigue damage and stress ratio characterized by compression modulus |
| |
以拉伸模量表征的临界疲劳损伤值Dt与应力比拟合结果为:
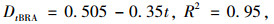
|
(14) |
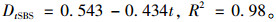
|
(15) |
以压缩模量表征的临界疲劳损伤值Dp与应力比拟合结果为:
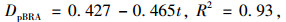
|
(16) |
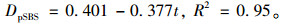
|
(17) |
由图 4、图 5及式(14)~式(17)得到岩沥青与SBS改性沥青混合料临界疲劳损伤差别不大,说明两者在疲劳试验过程中试件所受到的疲劳损伤较为接近,从损伤的角度得到了岩沥青与SBS改性沥青混合料抗疲劳性能较为接近的结论。
综合以上几点可以看出:岩沥青与SBS改性沥青混合料的疲劳性能相当,使用岩沥青改性沥青混合料铺筑路面能够延长其使用寿命,达到与SBS相当的效果。
3 以拉、压、弯模量表征的沥青混合料疲劳损伤特性分析沥青混合料疲劳损伤特性的研究从早期的Miner线性模型发展到当今广大研究者公认的非线性疲劳损伤模型,经历了跨越式的发展[9-14]
以模量衰减定义的损伤变量为:
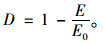
|
(18) |
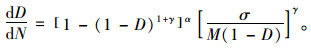
|
(19) |
当N=Nf时,D(N)=1,经化简得到疲劳损伤方程为:
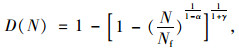
|
(20) |
进而得到模量衰变方程为:
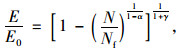
|
(21) |
式中,N为荷载循环作用次数;Nf为疲劳寿命;σ为应力幅值;M,α和γ为与温度相关的材料参数;M还依赖于平均应力幅值σ 。
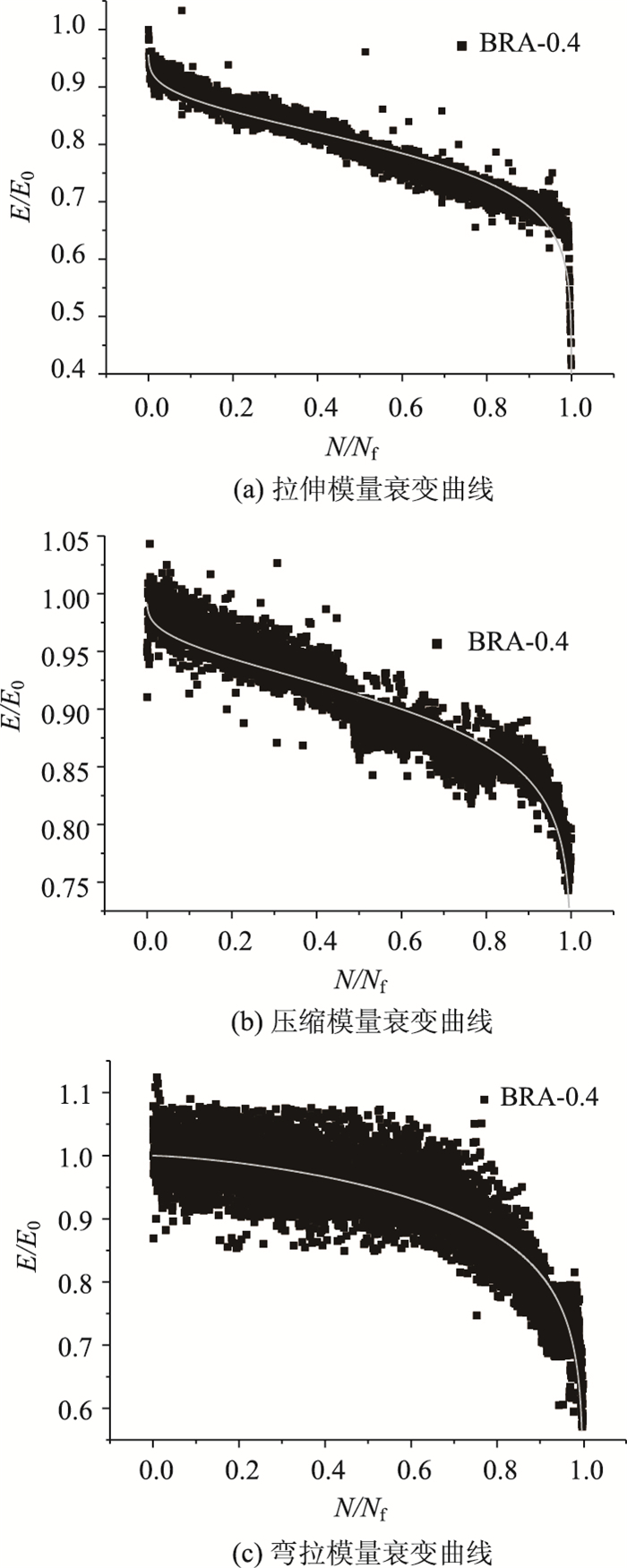
利用推导出的模量衰变方程式(21)对试验数据进行拟合,以岩沥青改性沥青混合料应力比0.4为例进行拉、压、弯模量衰变规律的分析,分别如图 6所示:
|
| 图 6 岩沥青混合料拉、压、弯模量衰减曲线 Fig. 6 Attenuation curves of tension, compression and bending moduli of rock asphalt mixture |
| |
将拉、压、弯模量衰变曲线拟合参数衰变模型列入表 10。
| 受力模式 | 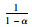
|

|
R2 |
| 拉伸 | 0.101 24 | 0.081 33 | 0.801 38 |
| 压缩 | 0.206 69 | 0.045 84 | 0.916 18 |
| 弯拉 | 1.386 19 | 0.103 68 | 0.779 3 |
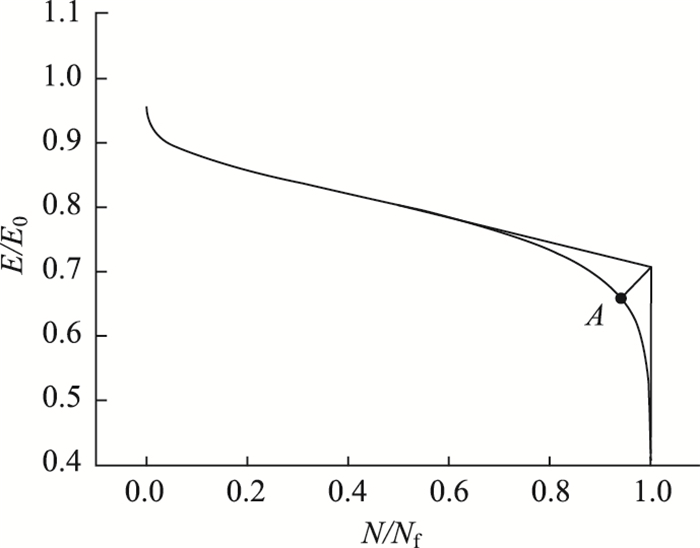
图 6中的曲线为模量衰变方程拟合曲线,为比较拉、压、弯模量的差异性,本研究选取以下3个指标进行分析:(1)稳定阶段疲劳循环比X=0.5时的切线斜率;(2)临界破坏点的横坐标值;(3)临界破坏点的纵坐标值。临界破坏点确定方法为:选取疲劳循环比X=0.5时所对应的切线及X=1时所对应的直线,取2条直线所构成夹角的角平分线与模量衰减曲线的交点为临界破坏点位置确定示意图如图 7所示,A点即为本研究定义的临界破坏点。
|
| 图 7 临界破坏点确定示意图 Fig. 7 Schematic diagram of determining critical failure point |
| |
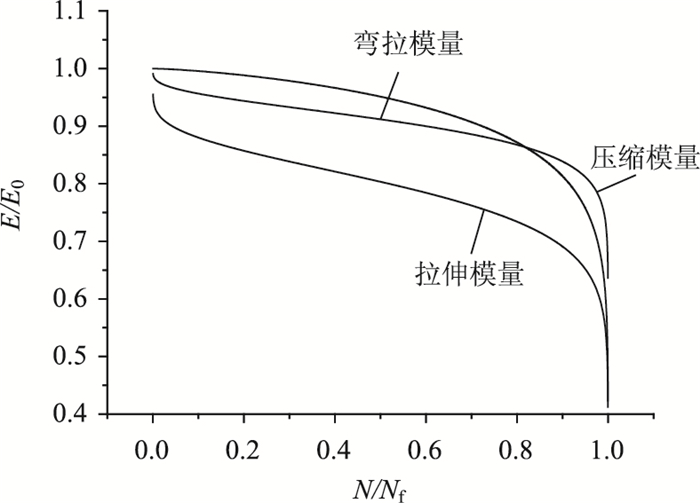
|
| 图 8 拉、压、弯3种模量衰变曲线图 Fig. 8 Attenuation curves of tension, compression and bending moduli |
| |
对前述3种疲劳损伤方程进行分析计算,得到切线方程与临界破坏点等,汇总如表 11所示。
| 受力模式 | 切线方程 | 临界破坏点 |
| 拉伸 | y=-0.179 6x+0.9 | (0.949,0.657) |
| 压缩 | y=-0.112 5x+0.99 | (0.954,0.808) |
| 弯拉 | y= -0.164x+1.03 | (0.932,0.789) |
(1) 在疲劳循环比0.2-0.8之间,3种模量的衰变基本处于稳定阶段,从得到的切线斜率绝对值大小来看,拉伸模量斜率最大,其次是弯拉模量,压缩模量斜率最小,拉伸模量斜率值比压缩模量斜率高出59.6%,说明此时在拉伸区域产生的损伤大于压缩区域产生的损伤,由于试件内部各点的应力状态不同,因此试件内部各点的模量衰减速率呈现不同的特征,用弯拉模量表征的衰变规律则无法体现弯拉试件内部各点由于拉、压应力状态的差异性而导致的模量衰变的差异性,由于拉伸模量过快的衰减速率导致中性面以下受拉区域损伤累积较快,最先发生开裂,故为试件的破坏源。
(2) 在疲劳循环比0.8-1之间,曲线斜率的绝对值急剧增大直至试件发生破坏,同时该阶段在整个疲劳寿命过程中所占比例非常小,此时比较斜率的大小已经没有实质意义,故本研究首先确定模量衰变曲线上横坐标X=0.5时的切线及X=1时的切线,定义2条切线夹角的角平分线与模量衰减曲线的交点为临界破坏点。
(3) 从临界破坏点横坐标值来看:压缩模量曲线所对应临界破坏点的横坐标值大于拉伸模量,说明压缩模量衰变曲线发生极限破坏的位置相对更为靠后,则发生极限破坏的时间位于拉伸模量之后,即试件发生开裂破坏并非是压缩模量的衰减所导致,而是由拉伸模量衰减过快所引起。
(4) 从临界破坏点纵坐标值来看:拉伸模量衰变曲线所对的纵坐标值小于压缩模量所对的纵坐标,临界破坏时拉伸模量的衰减比为34.3%,压缩模量的衰减比为19.8%。以拉伸表征的模量衰减幅度大于以压缩代表的模量衰减幅度,拉伸模量曲线的衰减比与压缩模量的衰减比相比高出了79.0%,即拉伸产生的损伤大于压缩产生的损伤,试件首先在受拉区开裂。
上述结论充分说明了模量衰变曲线稳定阶段拉伸模量衰减速率的过快及衰减末期压缩模量破坏点的滞后性,同时也间接反映出了拉伸模量衰变速率的快慢是决定沥青混合料疲劳性能是否优越的关键因素。
4 结论(1) 通过对疲劳寿命、疲劳方程参数与损伤值大小的分析表明了岩沥青与SBS改性沥青混合料疲劳性能相当,使用岩沥青改性沥青混合料铺筑路面能够延长其使用寿命。
(2) 从拉、压、弯模量衰减斜率绝对值大小来看,拉伸模量斜率最大,其次是弯拉模量,压缩模量斜率最小。拉伸模量过快的衰减速率导致中性面以下受拉区域损伤累积加剧,最先发生开裂,为试件的破坏源。
(3) 压缩模量曲线所对应破坏点的模量衰变率大于拉伸模量,说明压缩模量衰变曲线发生极限破坏的位置相对更为靠后,发生极限破坏的时间同样位于拉伸模量之后。
(4) 拉伸模量曲线所对应破坏点的疲劳荷载加载循环次数比小于压缩模量所对的,说明临界破坏时拉伸模量的衰减比大于压缩模量的衰减比,即试件发生开裂破坏并非是压缩模量的衰减所导致,而是由拉伸模量衰减过快所引起。
| [1] |
李瑞霞, 郝培文, 王春, 等. 布敦岩沥青改性机理[J]. 公路交通科技, 2011, 28(12): 16-20. LI Rui-xia, HAO Pei-wen, WANG Chun, et al. Modified Mechanism of Buton Rock Asphalt[J]. Journal of Highway and Transportation Research and Development, 2011, 28(12): 16-20. |
| [2] |
LIANG P, LIANG M, FAN W, et al. Improving Thermo-rheological Behavior and Compatibility of SBR Modified Asphalt by Addition of Polyphosphoric Acid (PPA)[J]. Construction & Building Materials, 2017, 139: 183-192. |
| [3] |
LIU G, NIELSEN E, KOMACKA J, et al. Rheological and Chemical Evaluation on the Ageing Properties of SBS Polymer Modified Bitumen:From the Laboratory to the Field[J]. Construction & Building Materials, 2014, 51(51): 244-248. |
| [4] |
OU Z M, LI F J. Studies the Key-technologies of Karamay Matrix Asphalt Used in SBS Modified Bitumen[J]. Applied Mechanics & Materials, 2015, 744-746: 1308-1311. |
| [5] |
LÜ Song-tao, LIU Chao-chao, YAO Hui, et al. Comparisons of Synchronous Measurement Methods on Various Moduli of Asphalt Mixtures[J]. Construction and Building Materials, 2018, 158: 1035-1045. |
| [6] |
SHEN L, WANG L, SONG Y, et al. Comparison between Dynamic Mechanical Properties of Dam and Sieved Concrete under Biaxial Tension-compression[J]. Construction and Building Materials, 2017, 132: 43-50. |
| [7] |
郑健龙. 基于结构层寿命递增的耐久性沥青路面设计新思想[J]. 中国公路学报, 2014, 27(1): 1-7. ZHENG Jian-long. New Structure Design of Durable Asphalt Pavement Based on Life Increment[J]. China Journal of Highway and Transport, 2014, 27(1): 1-7. |
| [8] |
郑健龙. 基于状态设计法的沥青路面弯沉设计标准[J]. 中国公路学报, 2012, 25(4): 1-9. ZHENG Jian-long. Deflection Design Standards of Asphalt Pavement Based on State Design Method[J]. China Journal of Highway and Transport, 2012, 25(4): 1-9. |
| [9] |
LEVENBERG E, UZAN J. Exposing the Nonlinear Viscoelastic Behavior of Asphalt-aggregate Mixes[J]. Mechanics of Time-dependent Materials, 2012, 16(2): 129-143. |
| [10] |
LIU F, MENG L Y, NING G F, et al. Fatigue Performance of Rubber-modified Recycled Aggregate Concrete (RRAC) for Pavement[J]. Construction and Building Materials, 2015, 95: 207-217. |
| [11] |
吕松涛. 基于非线性疲劳损伤的沥青路面轴载换算[J]. 工程力学, 2012, 29(10): 268-274. LÜ Song-tao. Axle Load Conversion of Asphalt Pavement Based on Nonlinear Fatigue Damage[J]. Engineering Mechanics, 2012, 29(10): 268-274. |
| [12] |
KRCMARIK M, VARMA S, KUTAY M E, et al. Development of Predictive Models for Low-temperature Indirect Tensile Strength of Asphalt Mixtures[J]. Journal of Materials in Civil Engineering, 2016, 28(11): 1-10. |
| [13] |
ESFANDIARPOUR S, SHALABY A. Local Calibration of Creep Compliance Models of Asphalt Concrete[J]. Construction and Building Materials, 2017, 132: 313-322. |
| [14] |
WU H, HUANG B, SHU X. Characterizing Fatigue Behavior of Asphalt Mixtures Utilizing Loaded Wheel Tester[J]. Journal of Materials in Civil Engineering, 2014, 26(1): 152-159. |
| [15] |
YIN W, YE F, LU H. Establishment and Experimental Verification of Stability Evaluation Model for SBS Modified Asphalt:Based on Quantitative Analysis of Microstructure[J]. Construction and Building Materials, 2017, 131: 291-302. |
| [16] |
RAHMANI E, DARABI M K, LITTLE D N, et al. Constitutive Modeling of Coupled Aging-viscoelastic Response of Asphalt Concrete[J]. Construction and Building Materials, 2017, 131: 1-15. |
| [17] |
YIN W, YE F, LU H. Establishment and Experimental Verification of Stability Evaluation Model for SBS Modified Asphalt:Based on Quantitative Analysis of Microstructure[J]. Construction and Building Materials, 2017, 131: 291-302. |
| [18] |
LI H, YU B. Fatigue Performance and Prediction Model of Multilayer Deck Pavement with Different Tack Coat Materials[J]. Journal of Materials in Civil Engineering, 2014, 26(5): 872-877. |
 2018, Vol. 35
2018, Vol. 35
