扩展功能
文章信息
- 赵纪飞, 叶建龙, 王骁帆, 刘朝晖, 李盛
- ZHAO Ji-fei, YE Jian-long, WANG Xiao-fan, LIU Zhao-hui, LI Sheng
- 连续配筋混凝土路面横向裂缝传荷作用的数值模拟和敏感性分析
- Numerical Simulation and Sensitivity Analysis on Load Transfer of Transverse Crack in Continuously Reinforced Concrete Pavement
- 公路交通科技, 2018, 35(6): 1-7
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(6): 1-7
- 10.3969/j.issn.1002-0268.2018.06.001
-
文章历史
- 收稿日期: 2017-06-22
2. 中国电建集团西北勘测设计研究院有限公司, 陕西 西安 710054;
3. 浙江省交通规划设计研究院, 浙江 杭州 310006;
4. 长沙理工大学 公路养护技术国家工程实验室, 湖南 长沙 410004
2. POWERCHINA Northwest Engineering Corporation Ltd., Xi'an Shaanxi 710054, China;
3. Zhejiang Provincial Institute of Communications Planning, Design and Research, Hangzhou Zhejiang 310006, China;
4. State Engineering Laboratory of Highway Maintenance Technology, Changsha University of Science and Technology, Changsha Hunan 410004, China
连续配筋混凝土路面(CRCP)作为一种长寿命耐久性路面结构,适用于重载交通国省级道路、机场道面、山岭隧道路面和海岸港口连接线工程[1-2]。美国、比利时和英国等国家有着近半个世纪的CRCP修筑和应用经验[2],中国则在湖南、湖北、江苏和浙江等诸多省份大力推广连续配筋混凝土下面层+沥青混凝土上面层(CRC+AC)复合式路面结构[3]。
CRCP和CRC+AC的主要路面病害有:由水泥混凝土材料温缩与干缩引起的CRC层横向开裂,由车辆循环荷载引起的横向裂缝处AC层的反射疲劳开裂[4-5]。当CRC层的裂缝宽度较大时,它的传荷能力逐渐减弱。若路面基层底部支撑不均匀,此时横向裂缝还会引起更严重的边缘冲断[6]。因此,CRCP配置纵向钢筋的作用主要是控制横向裂缝宽度和增强横向裂缝的传荷能力。AASHTO-2002[6]将横向裂缝宽度(bj)和裂缝传荷系数(LTE)作为结构设计的最重要参数。国内规范[7]和学者[2-5]较多关注bj控制值的研究,但是对LTE及其参数敏感性的分析还不够系统全面。罗圆月[8]等将水泥混凝土的塑性损伤模型和黏结单元法应用到了裂缝界面接触本构行为的模拟。用该方法建模简便快捷,但是无法准确体现裂缝的传荷机理,黏结单元刚度与钢筋抗剪刚度换算关系不够明确,用它模拟混凝土集料的嵌锁刚度时,其合理性也尚待验证。刘朝晖[9]和谭悦[10]等提出变刚度虚拟填缝材料的方法来模拟CRC板横向开裂后传荷能力的衰减过程,但是此方法同样存在不明确性[11]。Nishizwa[12]和左志武[4]等在横向裂缝两侧对应的节点位置设置了无尺寸的离散弹簧,通过定义弹簧单元的横向、竖向和纵向3个刚度来模拟裂缝的传荷刚度,此方法虽然繁琐,却能准确算出各独立节点的弹簧刚度。
本研究首先分析了CRCP横向裂缝的传荷机理;用剪切刚度弹簧模拟了CRCP横向裂缝的传荷作用,并提出了验证计算结果的方法;最后对横向裂缝传荷作用的影响因素进行了敏感性分析。研究成果可以为CRCP的结构设计和施工提供指导。
1 横向裂缝传荷机理 1.1 传荷机理分析裂缝的传荷能力是指裂缝将轴载的一侧轮载从直接受荷板传递至间接受荷板的能力[7]。CRCP主要通过纵向钢筋系统和集料嵌锁系统传荷。研究表明:纵向钢筋的传荷作用与配筋率、钢筋截面性质、钢筋剪切模量、裂缝宽度和结构层刚度等密切相关;集料的嵌锁作用则受缝隙宽度(一般≤3 mm)、开裂面的粗糙程度、开裂面尺寸、CRC板厚度、荷载作用次数、荷载作用位置和基层种类等因素的影响。
CRCP建成初期,横向裂缝较细,其开裂面的粗集料有较强的嵌锁、咬合作用,主要传递裂缝两侧面板间的切应力。早期传荷作用主要由集料嵌锁系统提供。CRCP建成后期,路面受到车辆荷载和温度梯度的双重作用,横向裂缝不断拓宽,集料剥落。此时,横向裂缝由集料嵌锁传荷逐步向钢筋传荷过渡。钢筋主要传递切应力和部分弯矩和扭矩。当横向裂缝两侧面板发生竖向相对位移时,钢筋通过自身的截面抗剪作用和CRC板的刚性支承作用传递切应力。
1.2 裂缝的传荷系数国内现行规范[7]建议在裂缝两侧设置测试点,用落锤式弯沉仪(FWD)在裂缝一侧施加设计轴载的一侧轮载,并通过量测两个测试点的挠度值wu和wl来表征裂缝的传荷系数LTE(%):
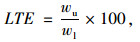
|
(1) |
式中,wu为未受荷板裂缝边缘的最大挠度;wl为受荷板裂缝边缘的最大挠度。
1.3 横向裂缝刚度裂缝刚度Q指单位长度裂缝由单位竖向相对位移引起的剪应力大小。国外学者Grovetti[式(2)]和Zollinger[式(3)]提出了无因次的裂缝刚度系数J和LTE(%)的相关方程[13-14]为:
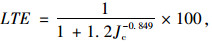
|
(2) |
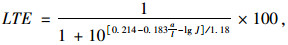
|
(3) |
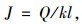
|
(4) |
式中,l为相对刚度半径[6];a为单轮荷载作用区域半径。
根据传荷机理不同,Q可以分为集料嵌锁刚度AGG(0.5×104~4.0×104 MPa)和钢筋剪切刚度q。AASHTO—2002[6]基于调查统计,建立了AGG对应的刚度系数J1与CRC板厚度hc、基层类型和车辆荷载等因素的回归公式为:
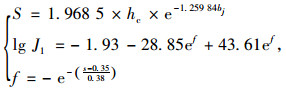
|
(5) |
式中s为裂缝抗剪能力。
Friberg[4]提出钢筋剪切刚度由钢筋本身的截面抗剪刚度和CRC板混凝土的支承刚度组成。钢筋本身的截面抗剪刚度Ss为:
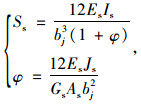
|
(6) |
式中,Es为钢筋的弹性模量;Gs为钢筋的剪切模量;Is为钢筋截面惯性矩;As为钢筋的有效截面积。CRC板混凝土的支承刚度Sc为:
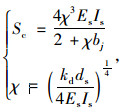
|
(7) |
式中,kd为CRC板对钢筋的支承模量,取4.07×105 MN·m-3;ds为钢筋的直径。由式(6)和式(7),得每根钢筋的组合抗剪刚度Ssc[式(8)]和钢筋剪切刚度q[式(9)]为:
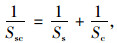
|
(8) |

|
(9) |
式中b为纵向钢筋间距。
2 横向裂缝传荷模拟和验证 2.1 结构尺寸和材料参数本研究以文献[2]实体工程的一个车道(宽3.75 m)作为基本算例, 具体参数见表 1。纵向钢筋ds=16 mm,间距124 mm,纵向配筋率ρ≈0.9%;横向钢筋直径14 mm,间距600 mm;钢筋网布置在板中位置;bj取设计最大值0.5 mm[6-7]。
| 结构层 | 计算参数 | 符号 | 单位 | 数值 |
| 面层 | 弹性模量 | E1 | MPa | 31 000 |
| 泊松比 | v1 | — | 0.15 | |
| 密度 | ρ1 | kg·m-3 | 2 400 | |
| 弯拉强度 | fv | MPa | 5.0 | |
| 厚度 | h1 | m | 0.18 | |
| 线膨胀系数 | α1 | ℃ | 1.1×10-5 | |
| 基层 | 弹性模量 | E2 | MPa | 1 000 |
| 泊松比 | v2 | — | 0.25 | |
| 密度 | ρ2 | kg·m-3 | 2 100 | |
| 厚度 | h2 | m | 0.20 | |
| 地基 | 地基反应模量 | k | MPa·m-1 | 50 |
| 相对刚度半径 | l | m | 0.754 | |
| 钢筋 | 弹性模量 | Es | MPa | 200 000 |
| 剪切模量 | Gs | MPa | 76 923 | |
| 泊松比 | vs | — | 0.28 | |
| 密度 | ρs | kg·m-3 | 7 800 | |
| 线膨胀系数 | αs | ℃ | 9.0×10-6 |
将表 1数据代入式(4)~(9),得AGG为709.02 MPa,q为649.98 MPa,Q为1 359.0 MPa。
2.2 单元选取和网格划分CRC板和基层采用C3D8R,计算代价小,对硬件的要求也低。为了获得较高的精确度,控制可能出现的沙漏,在种子密度定义和网格尺寸划分时,CRC板取0.06 m,基层取0.1 m。
钢筋在赋予截面面积和材料属性后,利用Embedded工具,直接嵌入到已建好的整体模型中。三维钢筋常用梁单元B31和桁架单元T3D2:B31可以传递弯矩和剪应力;T3D2用于模拟拉压杆,不能承受剪切和弯曲变形。B31可以模拟钢筋自身截面的抗剪能力,但是对于混凝土的支承抗剪能力无法定义。故采用T3D2模拟CRC板的纵向加强和裂缝处钢筋的正应力传递,裂缝的综合抗剪能力则用弹簧单元定义。钢筋的网格尺寸取0.20 m。
CRCP类似于一个离散化的桁架结构,根据面层网格划分,横向裂缝处共有4个板角节点、126个板边节点和122个板中节点,它们的刚度比等于节点的面积贡献比(1:2:4),因此,弹簧刚度分别为6.795,13.59 MPa和27.18 MPa。
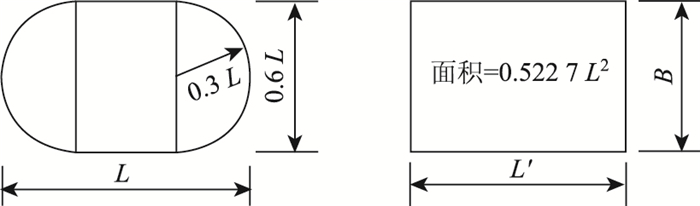
2.3 荷载和边界条件本研究采用BZZ-100标准双轮轴载:轴载P=4×25 kN,轮载F=25 kN,胎压为p=700 kPa。如图 1所示:为了方便建模,利用等效面积原理,将单轮着地面积Ac进一步简化为等宽矩形(L′×B)。联立式(10)~(12),代入F和p,得矩形尺寸为0.23 m×0.16 m。
|
| 图 1 轮胎着地面积等效计算图 Fig. 1 Calculation diagram of equivalent touching area of wheel tire |
| |
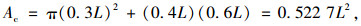
|
(10) |
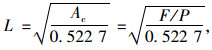
|
(11) |
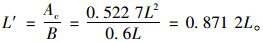
|
(12) |
参考现行规范[7]和相关文献[15],将单轮轴载置于板中,贴近横向裂缝一侧,模拟最不利荷载情况。横向靠近路面中线一侧和纵向两端施加法向位移约束;不考虑路肩对CRC板的剪力传递,横向靠近路肩一侧为自由端;基层四周边界施加法向位移约束;路基采用文克勒地基模型;CRC板与基层间的本构关系采用古德曼力学模型。
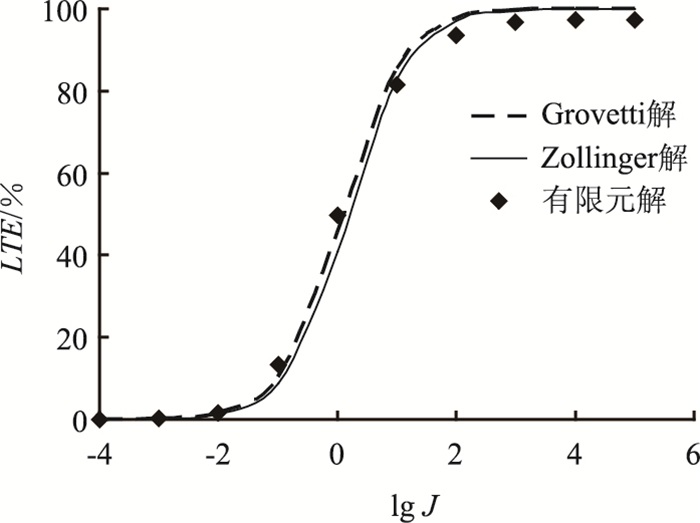
2.4 传荷模拟的验证裂缝两侧板长取1.5 m,将裂缝两侧挠度的有限元解代入式(1),和式(2)、式(3)作对比来验证有限元计算。调整J范围10-4~105,模拟传荷能力从几乎丧失到LTE接近100%的情况,计算结果见图 2。
|
| 图 2 传荷模拟的验证 Fig. 2 Verification of load transfer simulation |
| |
由图 2可知:用弹簧单元模拟传荷作用具有较好的可靠性。用Zollinger相关方程计算LTE时,需将CRCP的基层和面层按照抗弯刚度相同原则,等效为一定有效厚度的单层板。由于它忽略了基层与面板间的摩阻,因此计算结果偏小。
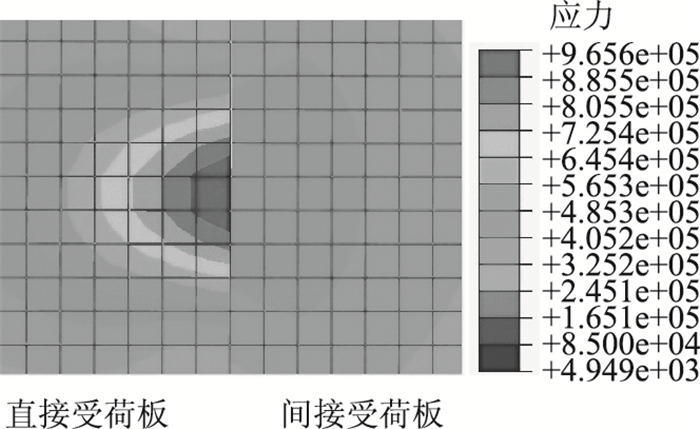
3 传荷模型的力学响应对表 1基本模型施加前述荷载和边界条件,绘制层底应力云图(见图 3)和路表弯沉变形云图(见图 4),对横向裂缝的传荷作用进行分析。
|
| 图 3 CRCP底部应力云图(单位:Pa) Fig. 3 Stress contour of bottom of CRCP slab(unit:Pa) |
| |
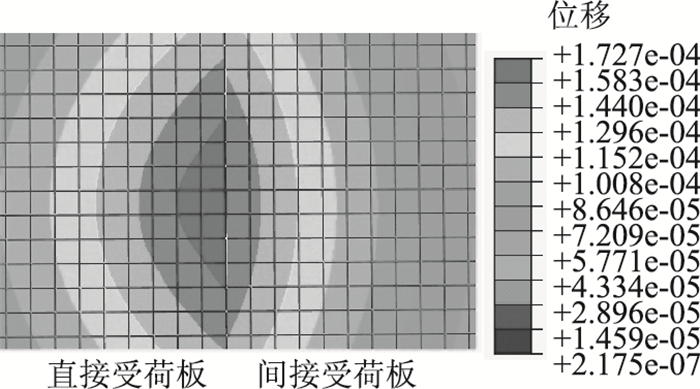
|
| 图 4 CRCP表面应变云图(单位:m) Fig. 4 Strain contour of surface of CRCP slab(unit:m) |
| |
由图 3可知:直接受荷板的板底拉应力在荷载分布区域较大;间接受荷板的应力分布较为均匀,横向裂缝处的纵向钢筋系统和集料嵌锁系统具有良好的荷载传递能力;直接受荷板的拉应力从板面到板底逐渐递增,对CRCP进行配筋设计时,建议纵向钢筋尽量靠近面层底部布置。
由图 4可知:横向裂缝的LTE(挠度系数)为89.73%,该CRCP实体工程的传荷能力评级为优[7];横向裂缝两侧的位移变形协调性较好,CRCP具有良好的整体性和行车舒适性。
4 传荷作用的敏感性分析本研究研究了配筋种类、纵向配筋率、横向裂缝宽度、基层类型和地基反应模量等因素对层底拉应力和裂缝传荷能力的影响。计算的基本参数与表 1一致,并赋予某一参数不同的取值水平研究其敏感性。
4.1 配筋种类的影响CRCP的纵向配筋一般采用HRB钢筋(Es=200 GPa,Gs=77 GPa),BFRP玄武岩纤维筋(Es=50 GPa,Gs=190 MPa)和GFRP玻璃纤维筋(Es=40 GPa,Gs=110 MPa)。
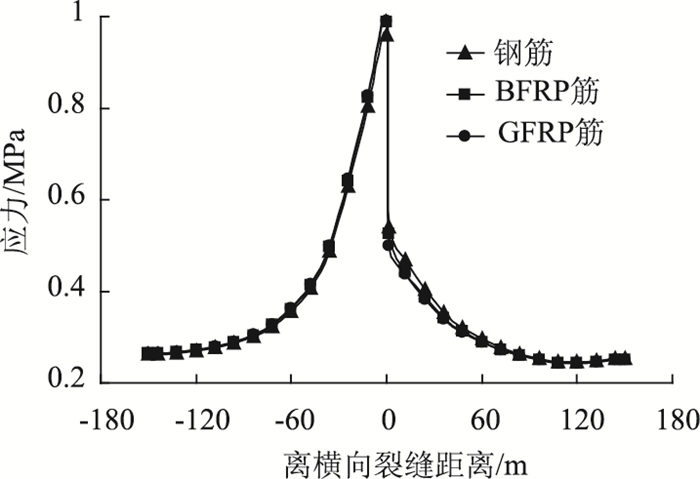
CRCP板底最大拉应力纵向分布见图 5。由图 5可知:配筋种类对横向裂缝两侧的层底拉应力影响不明显,3种筋材均具有较好的传荷性能;距离横向裂缝越远,配筋种类对板底拉应力的影响越小。钢筋对应的LTE(挠度系数)为89.73%,BFRP筋的LTE为88.11%,GFRP筋的LTE为87.73%。因此,3种筋材的传荷能力评级均为优,钢筋的传荷性能要略优于BFRP筋和GFRP筋。实际工程应用中,可以考虑BFRP筋和GFRP筋作为CRCP的配筋替代材料。
|
| 图 5 配筋种类对CRCP层底拉应力的影响 Fig. 5 Influence on reinforcement type on tensile stress of CRCP slab bottom |
| |
4.2 基层刚度的影响
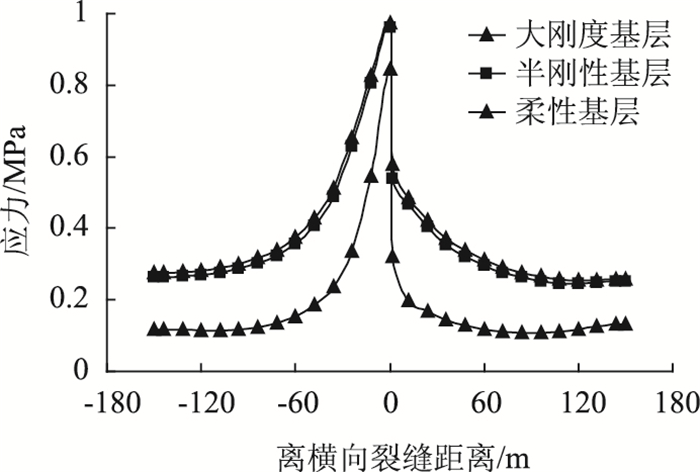
本研究分别取柔性基层、半刚性基层和大刚度基层的刚度代表值(500, 1 000 MPa和30 000 MPa),分析基层刚度对层底拉应力和裂缝传荷的影响,计算结果见图 6。
|
| 图 6 基层刚度对CRCP层底拉应力的影响 Fig. 6 Influence of base modulus on tensile stress of CRCP slab bottom |
| |
由图 6可知, CRC板层底拉应力随着基层刚度增大而显著减小,传荷能力随着基层刚度增加而递增。大刚度基层对应的LTE(挠度系数)为92.32%,半刚性基层的LTE为89.73%,柔性基层的LTE为89.47%。因此,将大刚度基层用于CRCP的修筑,不仅能减小层底拉应力,还可以增大横向裂缝的传荷能力。
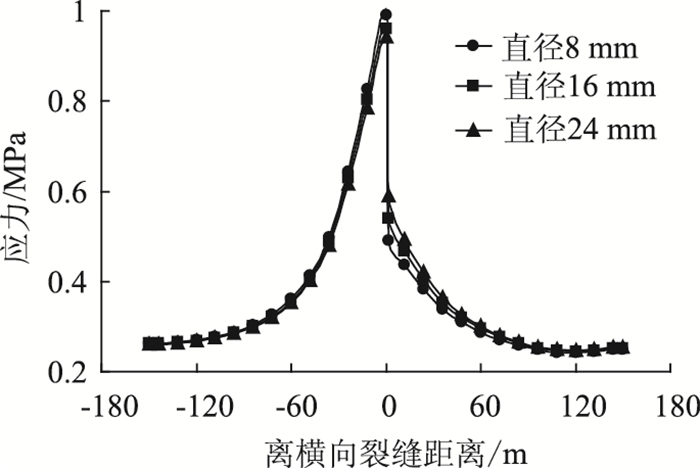
4.3 纵向配筋率的影响本研究分别取钢筋直径为8, 16 mm和24 mm,对应的纵向配筋率为0.23%,0.90%和2.03%,计算结果见图 7。
|
| 图 7 纵向配筋率对CRCP层底拉应力的影响 Fig. 7 Influence of longitudinal reinforcement ratio on tensile stress of CRCP slab bottom |
| |
由图 7可知,CRC板层底拉应力随着纵向配筋率增大而减小,传荷能力随着纵向配筋率增加而增强。8 mm直径对应的LTE(挠度系数)为87.77%,16 mm直径对应的LTE为89.73%,24 mm直径对应的LTE为92.55%。
我国现行规范建议CRCP的合理纵向配筋率应根据交通荷载等级和所在地区冰冻状况来确定[7]。该方法是基于CRCP三大设计指标,并未直接对横向裂缝的传荷进行控制,也未专门给出横向裂缝传荷能力的评级标准。根据图 7的计算结果,参照旧混凝土面层接缝的传荷评级标准,当配筋率由0.23%变化到2.03%时,传荷能力均为优良(LTE≥80%),说明CRCP的配筋设计无须直接控制LTE,现行配筋设计方法可行。因此,建议该实体结构依据现行规范要求[2, 16-18],最小配筋率取0.6%。
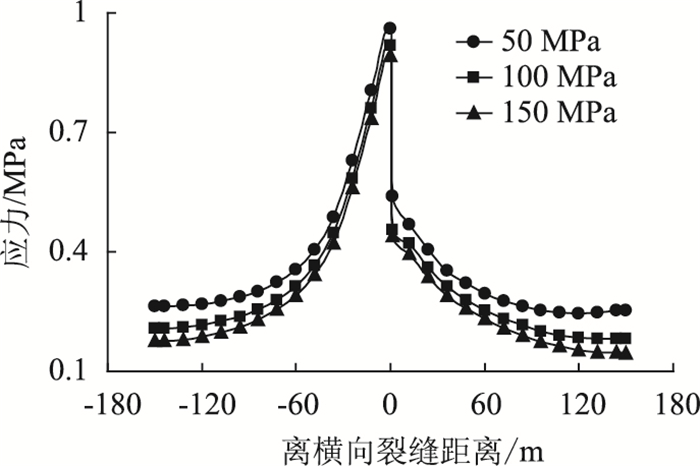
4.4 地基反应模量的影响分析地基反应模量对板底应力分布和裂缝传荷能力的影响,取地基反应模量50,100 MPa·m-1和150 MPa·m-1为例,计算结果如图 8所示。
|
| 图 8 地基反应模量对CRCP层底拉应力的影响 Fig. 8 Influence of foundation reaction modulus on tensile stress of CRCP slab bottom |
| |
由图 8可知:地基反应模量越大,层底最大拉应力越小,裂缝传荷能力越大。50 MPa对应的LTE(挠度系数)为89.73%,100 MPa对应的LTE为91.82%,150 MPa对应的LTE为99.04%。因此,增强地基反应模量可以显著提升CRCP横向裂缝的传荷系数。
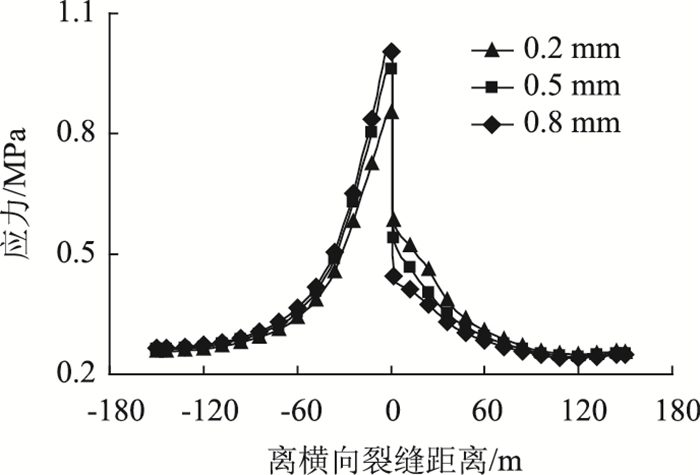
4.5 裂缝宽度的影响取横向裂缝宽度为0.2,0.5 mm和0.8 mm,对应的裂缝刚度Q为11 067.57,1 359.0 MPa和776.06 MPa,将参数代入有限元模型得到计算结果见图 9。
|
| 图 9 裂缝宽度对CRCP层底拉应力的影响 Fig. 9 Influence of crack width on tensile stress of CRCP slab bottom |
| |
由图 8可知,裂缝宽度越大,直接受荷板的层底最大拉应力越大,间接受荷板的层底拉应力越小,裂缝传荷能力越弱。0.2 mm裂缝宽度对应的LTE(挠度系数)为94.40%,0.5 mm裂缝宽度对应的LTE为89.73%,0.8 mm裂缝宽度对应的LTE为86.49%。
5 结论本研究分析了CRCP横向裂缝的传荷机理,建立横向裂缝的数值模型,并利用单轮荷载上午有限元弯沉试验,对横向裂缝的传荷敏感性和板底拉应力进行了分析,主要结论有:
(1) 剪切刚度弹簧可以模拟横向裂缝处钢筋和面板粗骨料的荷载传递作用,有限元计算结果和Grovetti解、Zollinger解相吻合,利用有限元方法计算裂缝的传荷系数结论可信。
(2) 对某实体工程结构的米塞斯应力分布进行了研究,它的LTE(挠度系数)为89.73%,传荷性能评级为优。
(3) 钢筋的传荷性能要略优于BFRP筋和GFRP筋;层底拉应力随着基层刚度增大而显著减小,传荷能力随着基层刚度增加而递增;层底拉应力随着纵向配筋率增大而减小,传荷能力随着纵向配筋率增加而增强;地基反应模量越大,层底最大拉应力越小,裂缝传荷能力越大;裂缝宽度越大,直接受荷板的层底最大拉应力越大,间接受荷板的层底拉应力越小,裂缝传荷能力越弱。
本研究的理论成果是对AASHTO-2002的理论补充,它的数值分析方法为研究各种因素对横向裂缝传荷作用的敏感性提供了手段。CRCP的带缝力学模型可用于研究路面结构在各种动静荷载作用下的力学响应,为完善CRCP的设计理论提供指导。
| [1] |
HUANG Y. Pavement Design and Analysis[M]. New York: Printice Hall, 2003.
|
| [2] |
刘朝晖, 王骁帆, 李盛, 等. 温缩和干缩对连续配筋混凝土路面纵向配筋的影响[J]. 中国公路学报, 2016, 29(11): 1-9. LIU Zhao-hui, WANG Xiao-fan, LI Sheng, et al. Influences of Thermal and Drying Shrinkages on Longitudinal Reinforcement in Continuously Reinforced Concrete Pavement[J]. China Journal of Highway and Transport, 2016, 29(11): 1-9. |
| [3] |
LI Sheng, LIU Xing-wu, LIU Zhao-hui. Interlaminar Shear Fatigue and Damage Characteristics of Asphalt Layer for Asphalt Overlay on Rigid Pavement[J]. Construction and Building Materials, 2014, 68: 341-347. |
| [4] |
左志武. 连续配筋混凝土路面横向裂缝分布和冲断预估研究[D]. 西安: 长安大学, 2010. ZUO Zhi-wu. Study on Distribution of Transverse Cracks and Pounchout Prediction of Continuously Reinforced Concrete Pavement[D]. Xi'an: Chang'an University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-11941-2010220756.htm |
| [5] |
葛倩如, 黄志义, 王金昌, 等. BFRP连续配筋复合式路面配筋设计[J]. 浙江大学学报:工学版, 2015, 49(1): 186-192. GE Qian-ru, HUANG Zhi-yi, WANG Jin-chang, et al. Reinforcement Design of Composite Pavement Continuously Reinforced with Basalt Fiber Reinforced Plastics Bars[J]. Journal of Zhejiang University:Engineering Science Edition, 2015, 49(1): 186-192. |
| [6] |
AASHTO-2002, Guide for Design of Pavement Structure[S].
|
| [7] |
JTG D40-2011, 公路水泥混凝土路面设计规范[S]. JTG D40-2011, Specifications for Design of Highway Cement Concrete Pavement[S]. |
| [8] |
罗圆月. BFRP筋连续配筋复合式路面结构分析及使用寿命探索[D]. 杭州: 浙江大学, 2014. LUO Yuan-yue. Structure Analysis and Useful Life Exploring of BFRP Continuously Reinforced Concrete Pavements[D]. Hangzhou: Zhejiang University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10335-1014171116.htm |
| [9] |
刘朝晖. 连续配筋混凝土刚柔复合式沥青路面研究[D]. 长沙: 长沙理工大学, 2007. LIU Zhao-hui. Research on Rigid-flexible Continuously Reinforced Concrete Composite Asphalt Pavement[D]. Changsha: Changsha University of Science and Technology, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10536-2008085292.htm |
| [10] |
谭悦. 机场水泥混凝土道面脱空响应及判断方法[D]. 上海: 同济大学, 2011. TAN Yue. Response and Identification Method of Void beneath Airport Cement Concrete Pavement[D]. Shanghai: Tongji University, 2011. |
| [11] |
明恩农. 考虑冲断破坏的玄武岩纤维筋连续配筋混凝土路面结构力学分析[D]. 广州: 华南理工大学, 2015. MING En-nong. Mechanical Analysis of Continuously Reinforced Concrete Pavements Using Basalt Fiber Reinforced Polymer Bars Considering Punchout[D]. Guangzhou: South China University of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10561-1015989296.htm |
| [12] |
NISHIZAWA T, SHIMENO S, KOMATSUBARA A, et al. Study on Thermal Stresses in Continuously Reinforced Concrete Pavement[J]. Transportation Research Record, 1998, 1629: 99-107. |
| [13] |
GROVETTIJ A. Evaluation of Jointed Concrete Pavement Systems Incorporating Open-graded Permeable Bases[D]. Urbana-Champaign: University of Illinois at Urbana-Champaign, 1984.
|
| [14] |
ZOLLINGER D G, BUCH D, XIN D, et al. Performance of Continuously Reinforced Concrete Pavement[R]. Washington, D. C. : Federal Highway Administrations, 1999.
|
| [15] |
李盛, 陈尚武, 刘朝晖, 等. 旧水泥混凝土路面弯沉测试的若干问题研究[J]. 中南大学学报:自然科学版, 2015(12): 4713-4718. LI Sheng, CHEN Shang-wu, LIU Zhao-hui, et al. Some Problems on Deflection Test of Old Cement Concrete Pavement[J]. Journal of Central South University:Science and Technology Edition, 2015(12): 4713-4718. |
| [16] |
王骁帆, 应正兵, 刘朝晖, 等. 温度场对连续配筋混凝土路面纵向配筋的影响[J]. 公路交通科技, 2017, 34(4): 16-24. WANG Xiao-fan, YING Zheng-bing, LIU Zhao-hui, et al. Effect of Temperature Field on Longitudinal Reinforcement of Continuously Reinforced Concrete Pavement[J]. Journal of Highway and Transportation Research and Development, 2017, 34(4): 16-24. |
| [17] |
王骁帆, 苏颖奇, 刘朝晖, 等. 连续配筋混凝土路面配筋设计及敏感性分析[J]. 公路, 2017(2): 1-5. WANG Xiao-fan, SU Ying-qi, LIU Zhao-hui, et al. Sensitivity Analysis of Steel Design for Continuously Reinforced Concrete Pavement[J]. Highway, 2017(2): 1-5. |
| [18] |
张翛, 胡圣能, 赵鸿铎, 等. 连续配筋混凝土路面裂缝间距特性[J]. 交通运输工程学报, 2013, 13(4): 1-7. ZHANG Xiao, HU Sheng-neng, ZHAO Hong-duo, et al. Characteristic of Crack Spacing for Continuously Reinforced Concrete Pavement[J]. Journal of Traffic and Transportation Engineering, 2013, 13(4): 1-7. |
 2018, Vol. 35
2018, Vol. 35
