近年来，电力电子设备及各种非线性负载的广泛使用，给电力系统注入了大量的谐波及无功^[1-2]. 无源滤波器、有源滤波器和混合有源滤波器(Hybrid Active Power Filter，HAPF)是目前应用最广泛的谐波治理装置. 无源滤波器结构简单、成本低，但滤波效果受电网参数影响较大^[3]；有源滤波和HAPF的滤波效果较好，HAPF在补偿谐波的同时可以补偿基波的无功分量，逐渐成为该领域研究的热点^[4]. 受功率半导体器件的容量及成本的限制，有源滤波和HAPF难以在中高压和大容量场合下应用^[5].

为了提高有源滤波器的适用电压等级，目前常见的方法是在滤波器前串联耦合变压器. 文献[6]提出了一种适用于中高压场合的注入式混合有源滤波器，在有源部分的接入端并联谐振频率为基波的串联谐振支路，达到降低有源部分的工作电压和容量的目的，但有源部分与基波串联谐振支路易产生较大的基波环流. 针对文献[6]存在的问题，文献[7-8]从控制策略和拓扑结构两方面开展研究. 这些注入式混合有源滤波器可以用于中高压场合，但结构复杂，需要耦合变压器，体积庞大^[9]. 文献[10-11]提出了利用单调谐LC滤波器与有源滤波器串联的混合有源滤波器，无源部分在承受基波电压的同时可以进行无功补偿. 文献[12]提出一种新型无变压器型并联混合有源电力滤波器(Transformerless Shunt Hybrid Active Power Filter，TLS-SHAPF)，文献[13]给出了TLS-SHAPF的设计方法，文献[14-15]通过不同的控制策略实现对TLS-SHAPF的控制，均取得较好效果. 文献[12-15]通过串联LC的方式，在减低有源部分电压的同时去除了耦合变压器，但系统的无源部分与有源部分串联，使得无功补偿电流全部流经有源部分，有源部分的工作电流大幅增加.

针对以上问题，本文提出了一种新型TLS-SHAPF，利用串联谐振的低阻抗的特点对特定次谐波进行补偿，通过增加一个与有源部分并联的电容支路进行无功补偿，避免无功电流流经有源部分，同时利用无源器件的分压特点降低有源部分的工作电压和容量，从而提高TLS-SHAPF的补偿能力.

图1给出了本文提出的一种新型TLS-SHAPF拓扑结构图，无源部分由L₀、C₀与C₁组成，其中，L₀、C₀对所补偿的特定的n次谐波产生串联谐振，使被补偿的n次谐波电流可以无衰减、无相移地注入电网. 利用L₀、C₀和C₁的分压特点，降低有源部分所承受的电压，提高TLS-SHAPF的适用电压等级. C₁提供了无功电流支路，避免TLS-SHAPF无功电流流经有源部分，使得系统中的有源部分只需提供谐波补偿电流.

图 1(Figure 1)

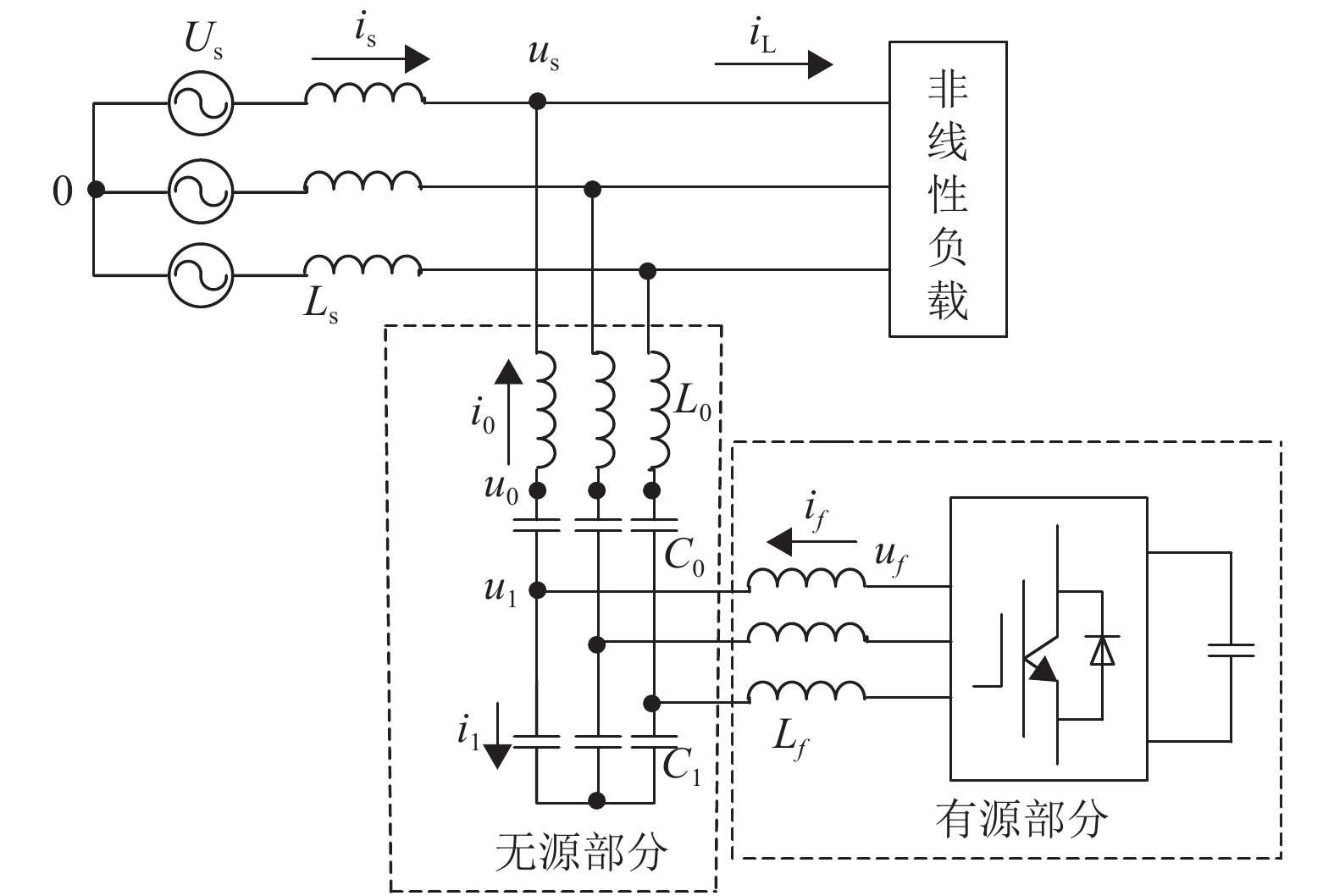
图 1 新型TLS-SHAPF拓扑结构图 Figure 1 Schematic diagram of the novel TLS-SHAPF

根据基尔霍夫定律，假定系统运行在三相对称的状态下，可以得到系统基于abc坐标系下的数学模型，为了实现解耦控制，利用坐标变换，可以得到如下与abc静止坐标系相对应的dq旋转坐标系的数学模型：

其中， ${R}_{L_f} $ ， ${R}_{L_0} $ ， ${R}_{C_0} $ ， ${R}_{C_1} $ 分别为L_f，L₀，C₀，C₁的等效内阻，u_fd，u_fq，u_0d，u_0q，u_1d，u_1q，u_sd，u_sq，i_fd，i_fq，i_0d，i_0q分别为u_f，u₀，u₁，u_s，i_f，i₀在dq旋转坐标系下的d轴与q轴分量.

系统包含特定次谐波补偿控制和有源部分直流侧电压控制两部分，图2为系统的控制框图.

图 2(Figure 2)

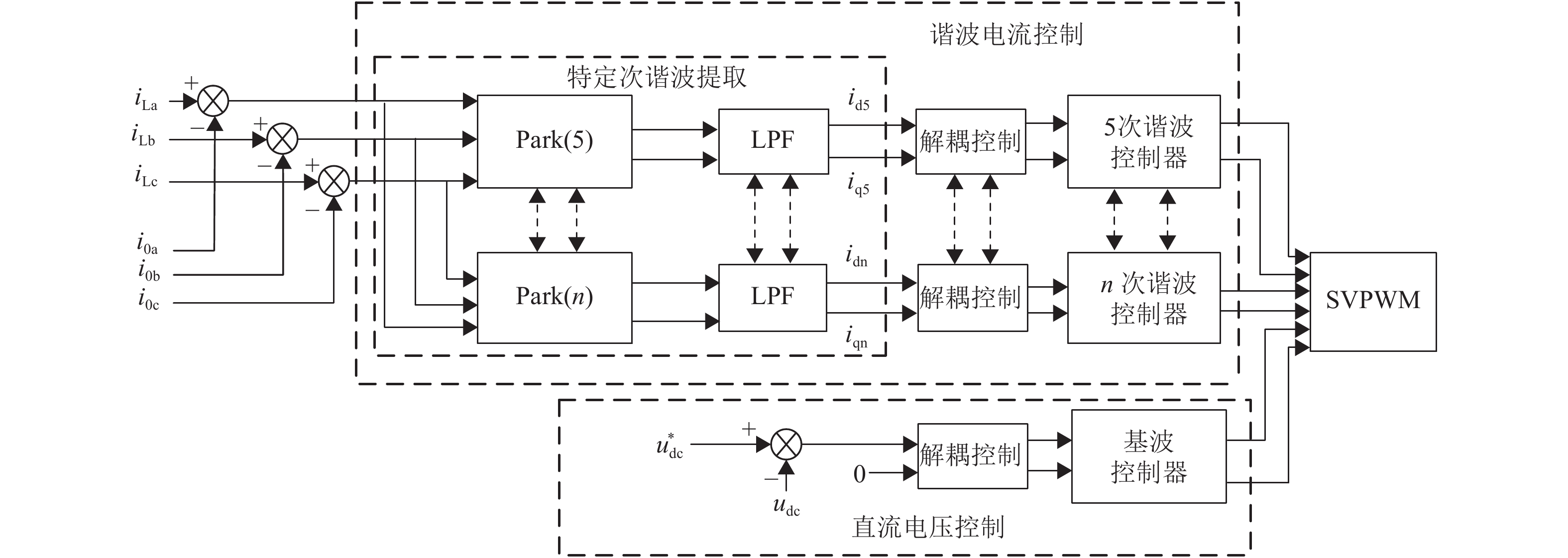
图 2 控制方案 Figure 2 Control scheme

由式(1)的数学模型，可得到TLS-SHAPF在dq旋转坐标系下的谐波电流控制框图，如图3所示,其中G_i1(s)为谐波电流控制器的传递函数， ${G}_{L_f}$ (s)， ${G}_{L_0}$ (s)， ${G}_{C_0}$ (s)， ${G}_{C_1}$ (s)分别为L_f，L₀，C₀，C₁的等效传递函数.

图 3(Figure 3)

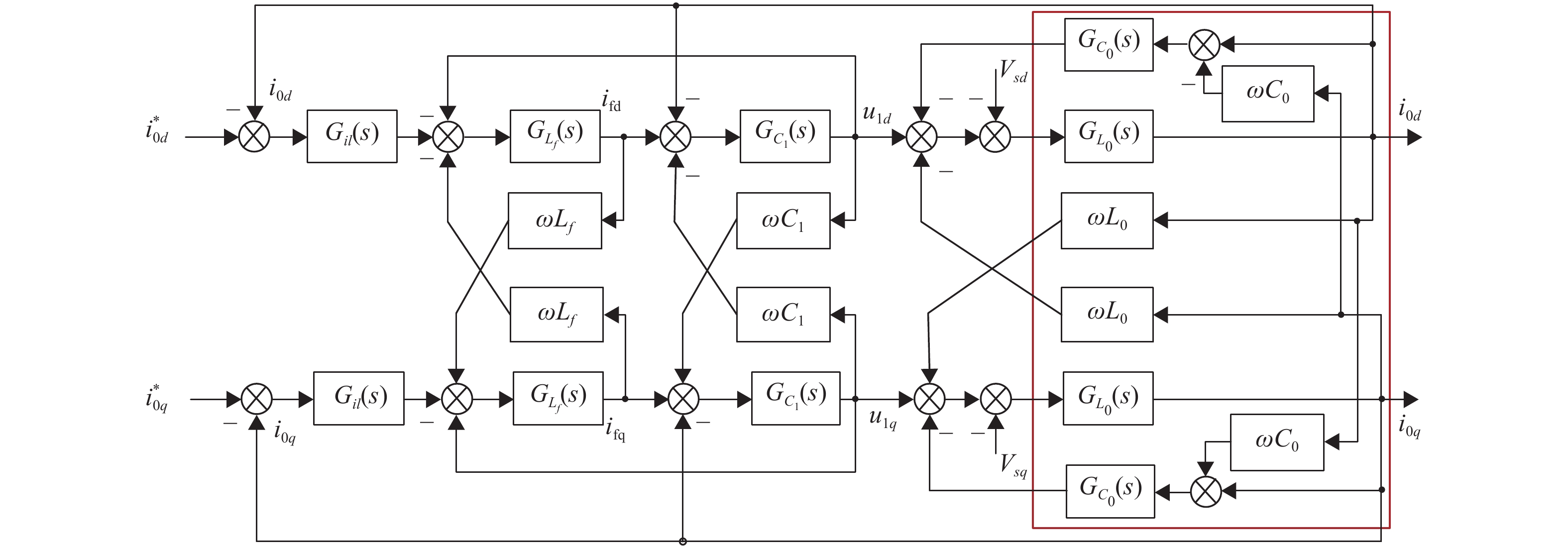
图 3 谐波电流控制框图 Figure 3 Harmonic current control block diagram

由图1可知，对特定补偿的n次谐波而言，L₀C₀支路串联谐振，可用等效内阻替代. 图3中方框内的部分可以等效为等效内阻，即d轴与q轴分量不存在耦合关系，因此n次谐波的解耦控制不需要考虑图3的方框内的耦合关系. 为了实现对系统特定次谐波的解耦，在控制对象的输入端叠加一个解耦输入量(图4中的x_d和x_q)，使得所加输入量在耦合分量处产生一个与耦合分量大小相等、方向相反的作用，实现d轴与q轴的解耦^[16]，解耦后控制框图如图4所示.

图 4(Figure 4)

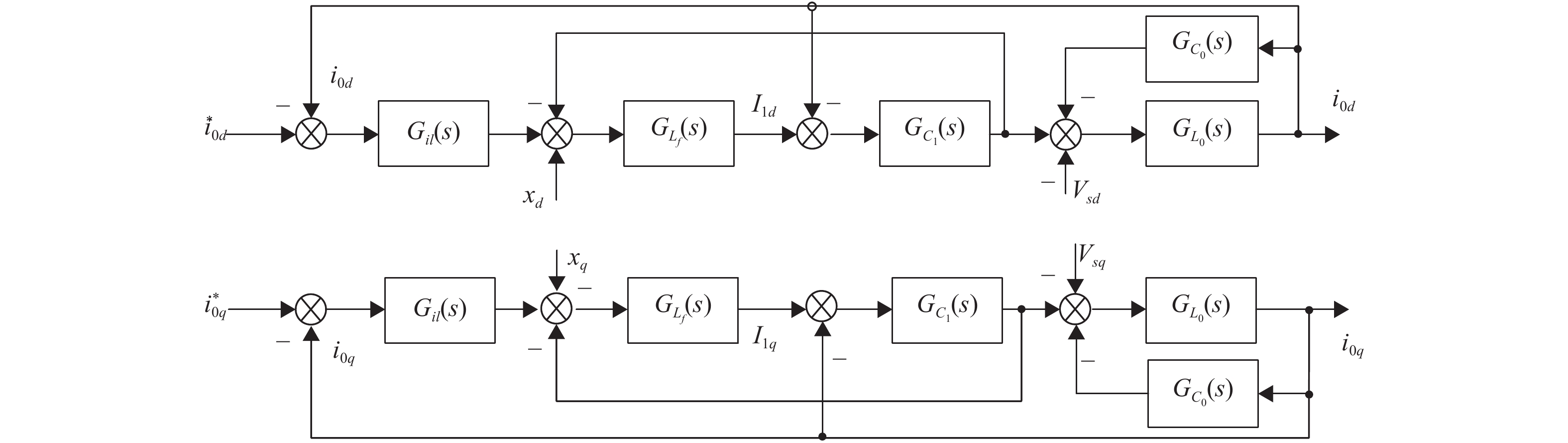
图 4 谐波电流解耦控制框图 Figure 4 Harmonic current decoupling control block diagram

为了验证本文所提出的实验方案的可行性，搭建了TLS-SHAPF实验系统, 对5次和7次特定次谐波进行补偿，LC谐振支路为分别对5次和7次谐波谐振的并联支路. 控制器采用TI公司TMS320F28035芯片，逆变桥采用英飞凌公司FP40R12KT3 IGBT模板，电路的其余参数如表1所示，测量仪器采用泰克公司MDO3024示波器、泰克公司A622电流探头和知用电子公司P1300电压探头.

表 1(Table 1)

表 1 实验关键参数 Table 1 Key experimental parameters 参数 取值 电网线电压/V 150 谐振电感L05/mH 4 谐振电感L07/mH 4 谐振电容C05/μF 100 谐振电容C07/μF 50 并联电容C1/μF 500 非线性负载电阻RL/Ω 24 无功负载电感L/mH 125 直流母线电压udc/V 90 直流母线电容Cdc/μF 3 350 开关频率f/kHz 10

表 1 实验关键参数 Table 1 Key experimental parameters

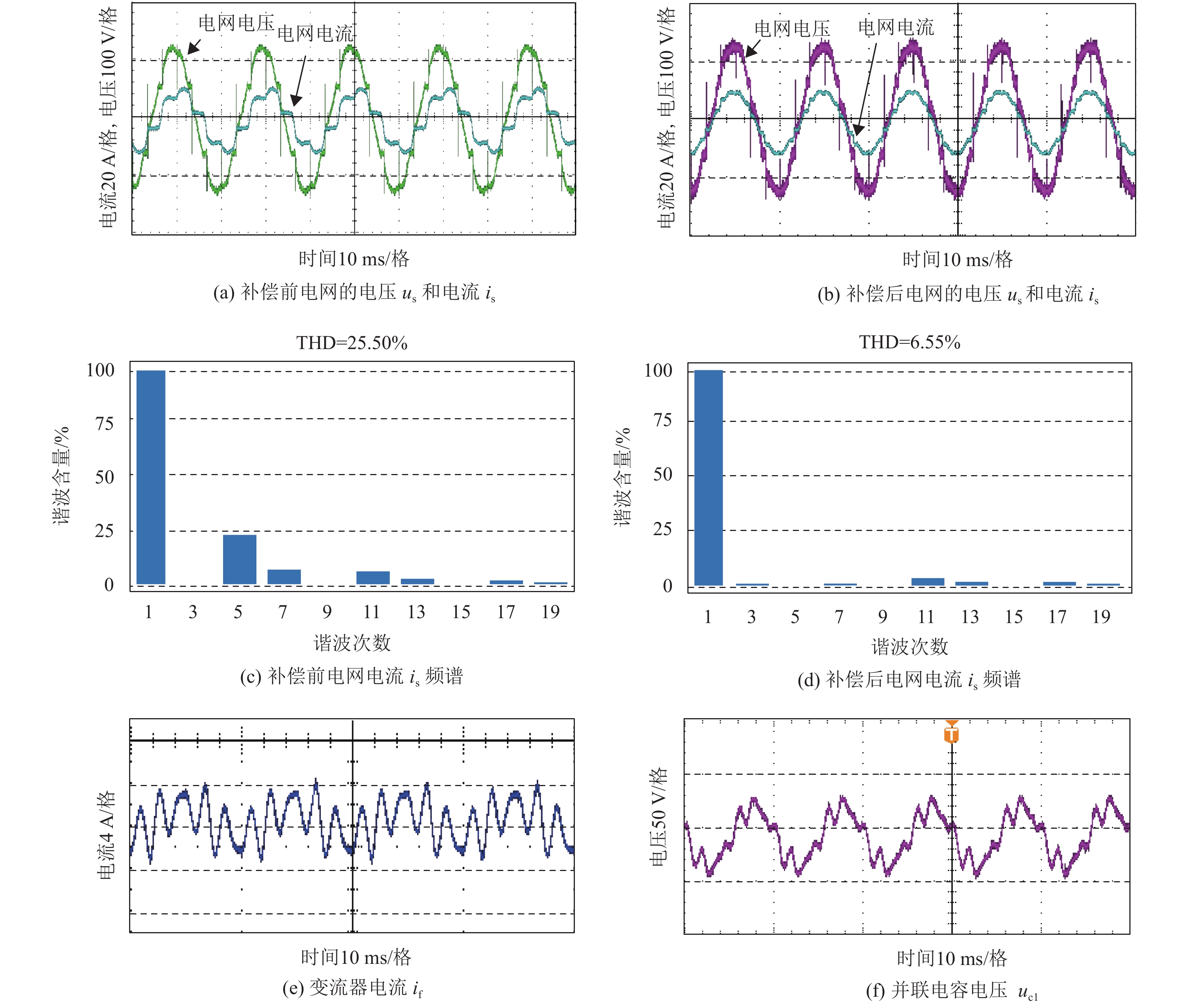
实验波形与频谱图如图5所示. 图5(a)是补偿前电网的电压u_s和电流i_s波形，补偿前电网的电压与电流存在明显相位差，系统无功含量大，图5(c)为补偿前电网电流频谱图，电流THD为25.5%，其中5次谐波电流含量为23.8%，7次谐波电流含量为7.99%. 系统投入后对5次和7次谐波进行补偿，电网电压、电流波形及电网电流频谱图如图5(b)和图5(d)所示，补偿后电网的电压与电流相位差小，电流THD为6.55%，5次谐波电流含量为0.2%，7次谐波电流含量为1.13%，谐波抑制效果明显. 图5(e)为变流器电流i_f波形，i_f频谱分析显示基波电流为1.05 A，图5(f)为并联电容电压波形图，可见其电压较电网电压显著减小，有利于其应用在高压大功率场合.

图 5(Figure 5)

图 5 实验波形与频谱图 Figure 5 Experimental waveform and spectrogram

实验数据显示，在混合有源滤波器投入补偿后，电网的电压和电流相位一致，5次和7次谐波得到有效抑制.

针对传统的TLS-SHAPF基波无功补偿电流需要流经变流器，限制装置容量的问题，结合某些场合特定次谐波含量严重超标、无功不足的实际情况，本文提出的一种新型无变压器型并联混合有源电力滤波器，利用串联谐振的低阻抗、无相移的特性对特定次谐波进行补偿，同时增加一个与有源部分并联的电容支路进行无功补偿，避免无功电流流经有源部分，无源器件的串联分压降低了有源部分承受的基波电压，降低直流母线电压，从而提高了有源部分的补偿能力，有利于其应用于高压大容量场合. 实验结果验证了系统实现的可行性，系统对所需补偿的特定次谐波及无功的补偿效果明显.