在许多现实应用场景中, 数据样本的维度总是很高. 比如人脸识别^[1]、手写字符识别^[2]、生物信息学分析^[3]、视觉跟踪^[4]等^[5-7]. 然而高维数据数据量大, 且通常含有大量冗余、噪声, 因此会降低学习算法的性能^[8]. 为了解决这些问题, 人们通常采用降维方法对数据进行预处理.

近些年提出了许多降维方法, 可分为特征选择^[9]和特征提取^[10]两大类. 特征提取通过将数据投影到低维子空间来减少数据维度. 由于低维子空间与原数据样本空间没有直接联系, 提取特征难以对应数据原有特征. 特征选择通过直接选择原数据特征的子集作为降维后的特征. 这能保持数据原有特征, 降维后的数据具有很好的解析性. 这在许多应用中是很重要的, 例如基因分类^[11]、文本分类^[12]等.

从利用标签信息的角度来看, 特征选择算法可以分为监督学习^[13]、半监督学习^[14]和无监督学习^[15]. 监督学习和半监督学习在某种程度上依赖于标签信息, 通过标签信息评估结果来选择特征. 然而, 许多实际应用是在没有标签的情况下收集大规模数据. 标记这些无标签数据非常昂贵且耗时^[16]. 因此, 无监督特征选择对于许多实际应用更具普遍性和挑战性.

Cai等^[17]提出了多簇特征选择(MCFS), 通过谱分析捕获局部流形结构, 然后选择能够最好地保留聚类结构的特征. Nie等^[18]提出了灵活流形嵌入(FME), FME作为降维的一般框架, 被许多特征选择方法所采用. Hou等^[19]基于FME和 ${l_{2,1}}$ 范数, 提出了联合嵌入学习和稀疏回归(JELSR), 给出了特征选择的一般框架. Li等^[20]联合使用FME、非负约束和 ${l_{2,1}}$ 范数来实现非负判别特征选择(NDFS). Qian等^[21]提出了鲁棒的无监督特征选择(RUFS), RUFS使用FME、非负矩阵分解(NMF)和 ${l_{2,1}}$ 范数同时实现鲁棒的聚类和特征选择. Shi等^[22]提出联合FME和 ${l_1}$ 范数实现的鲁棒谱特征选择(RSFS). Nie等^[23]提出了联合结构最优图和局部结构的结构最优图特征选择(SOGFS). 上述方法取得了显著的效果, 但在选择特征中并没有考虑到选择特征后数据的低秩子空间结构, 可能会使算法过分依赖局部结构, 导致对噪声数据敏感. 本文通过引入低秩表示不仅保留了转换空间后样本的全局结构, 而且学习其低秩子空间, 极大地降低了噪声的影响. 并且自适应学习样本间的局部结构, 将全局结构学习、局部结构学习和特征选择融合到一个框架中同时进行.

因此本文通过结合低秩子空间学习和自适应图嵌入方法, 提出了一个联合低秩表示与图嵌入的无监督特征选择方法. 本文主要贡献在于: (1)提出了一种保留选择特征局部结构方法, 同时考虑到选择特征的低秩子空间, 使其选择特征后数据具有低秩性质, 从而提高方法的鲁棒性; (2)选择特征的局部结构自适应学习, 无需预先计算, 从而选择最合适模型的局部结构.

1 相关工作 1.1 低秩子空间学习

低秩表示假设原始数据可分解成多个独立子空间来近似表示, 从而发现数据本质结构中, 其子空间最低秩的表示^[24]. 给定数据集 ${{X}} = [{{{x}}_1},{{{x}}_2},\cdots,{{{x}}_n}] $ $\in {R^{d \times n}} $ , 其中 ${{{x}}_i} \in {R^d}$ 为数据集中的某个样本. 本文构建一个字典 ${{D}} = [{{{d}}_1},{{{d}}_2},\cdots,{{{d}}_m}] \in {R^{d \times m}}$ 来重构数据集X, 使得 ${{X}} = {{DZ}}$ , 其中 ${{Z}}$ 为重构系数矩阵, $ {{Z}} =$ $ [{{{z}}_1},{{{z}}_2},\cdots,{{{z}}_n}] \in {R^{m \times n}}$ . 通过对 ${{Z}}$ 添加低秩约束, 其目的是为了寻找其最低秩解, 因此上述模型如下:

$\mathop {\min }\limits_{{Z}} \begin{array}{*{20}{c}} {} \end{array}{\rm{rank}} ({{{\rm Z}}})\begin{array}{*{20}{c}} {}&{} \end{array}{\rm{s} .\rm{t}.}\begin{array}{*{20}{c}} {}&{{{X}} = {{DZ}}}. \end{array}$

(1)

上述问题是NP难问题, 难以直接求解. Candès等^[25]通过使用核范数来代替低秩约束, 可转换为如下凸优化问题:

$\mathop {\min }\limits_{{Z}} \begin{array}{*{20}{c}} {} \end{array}||{{Z}}|{|_*}\begin{array}{*{20}{c}} {}&{} \end{array}{\rm{s} .\rm{t}.}\begin{array}{*{20}{c}} {}&{{{{X}} = {{DZ}}}} . \end{array}$

(2)

其中 $||.|{|_*}$ 表示矩阵的核范数, 即矩阵奇异值之和. 使用原数据 ${{X}}$ 作为字典, 式(2)可转化为

$\mathop {\min }\limits_{{Z}} \sum\limits_i^n {||{{{x}}_i} - {{X}}{{{z}}_i}|{|^2} + \alpha ||{{Z}}|{|_*}}, $

(3)

其中 $\alpha $ 为正则项参数.

1.2 图嵌入方法

随着谱分析和流形学习的发展, 许多无监督特征选择方法通过保留样本间的局部流形结构均取得较好的结果. 这表明局部结构在特征选择过程中具有重要作用. 本文利用自适应过程来确定保持局部关系的相似矩阵. 给定数据集 ${{X}} = [{{{x}}_1},{{{x}}_2},\cdots,{{{x}}_n}] \in$ $ {R^{d \times n}} $ . 其中 ${{{x}}_i} \in {R^d}$ 可被其他样本 ${{{x}}_j}$ 通过概率 ${p_{ij}}$ 表示, 其中 ${p_{ij}}$ 为相似矩阵 ${{P}} \in {R^{n \times n}}$ 的元素. 任意两个样本作为邻居的概率可以看作它们之间的相似性. 因此较近的样本应具有较大的概率, 即 ${p_{ij}}$ 与 ${{{x}}_i}$ 和 ${{{x}}_j}$ 之间的距离成反比. 因此相似矩阵 ${{P}}$ 可由式(4)求解:

$\mathop {\min }\limits_{{{p}}_i^{\rm{T}}{{{\textit{1}}}_n} = 1,0 \leqslant {p_{ij}} \leqslant 1} \sum\limits_{ij} {(||{{{x}}_i} - {{{x}}_j}|{|^2}{p_{ij}} + \mu p_{ij}^2{\rm{)}}}, $

(4)

其中 $\mu $ 为正则化参数, 正则项 $\mu p_{ij}^2$ 可避免退化解. ${{{\textit{1}}}_n}$ 为长度为 $n$ , 元素全为 $1$ 的向量.

2 联合低秩表示与图嵌入的无监督特征选择

此处, 给出本文使用的符号. 矩阵 ${{M}} \in {R^{m \times n}}$ , ${m_{ij}}$ 为矩阵 ${{M}}$ 的第 $i$ 行 $j$ 列的元素. ${{{m}}_i}$ 为矩阵 ${{M}}$ 的第 $i$ 行向量. ${\rm{Tr}}({{M}})$ 表示矩阵 ${{M}}$ 的迹, ${\rm{ < }}{{M}}{\rm{,}}{{M}}{\rm{ > }} = {\rm{Tr}}({{{M}}^{\rm{T}} }{{M}})$ . 矩阵 ${{M}}$ 的 ${\rm{F}}$ 范数表示为 $||{{M}}|{|_{\rm{F}}}$ . 矩阵 ${{M}}$ 的 ${l_{2,1}}$ 范数表示为 $||{{M}}|{|_{2,1}}$ , 其中 $||{{M}}|{|_{2,1}} = \displaystyle\sum\limits_{i = 1}^m {\sqrt {\sum\limits_{j = 1}^n {m_{ij}^2} } } $ .

2.1 JLRRGE模型

根据上述子空间学习方法和自适应局部结构学习方法, 由式(3)和式(4)可得:

$\left\{\begin{aligned} &\mathop {\min }\limits_{{{Z}},{{P}}} \sum\limits_i^n {||{{{x}}_i} - {{X}}{{{z}}_i}|{|^2} + \alpha ||{{Z}}|{|_*}} +\\ &\quad\beta \sum\limits_{ij}^n {||{{{x}}_i} - {{{x}}_j}|{|^2}{P_{ij}} + \mu {P_{ij}^2}}. \\ &{\rm{s} .\rm{t}.}\qquad{{P}}{{{\textit{1}}}_n} = {{{\textit{1}}}_n},{{P}} > 0. \end{aligned} \right.$

(5)

式(5)中, 第一部分为低秩子空间学习, ${{X}}{{{z}}_i}$ 为样本 ${{{x}}_i}$ 在低秩子空间下重构样本. 对于整个重构后的数据 ${{XZ}}$ , 其低秩结构能更好地还原数据的本质结构, 降低噪声对数据影响. 第二部分为自适应局部结构学习, 自适应学习数据的局部相似性矩阵 ${{P}}$ , 使其保留原有的局部流形结构.

根据式(5), 本文提出一种联合低秩表示与图嵌入的无监督特征选择学习, 如式(6)所示:

$\left\{\begin{split} &\mathop {\min }\limits_{{{W}},{{Z}},{{P}}} \sum\limits_i^n {||{{{W}}^{\rm{T}}}{{{x}}_i} - {{{W}}^{\rm{T}}}{{X}}{{{z}}_i}|{|^2} + \alpha ||{{Z}}|{|_*}} + \\ &\beta \sum\limits_{ij}^n {||{{{W}}^{\rm{T}}}{{{x}}_i} - {{{W}}^{\rm{T}}}{{{x}}_j}|{|^2}{P_{ij}} + \mu {P_{ij}}^2} + \gamma ||{{W}}|{|_{2,1}}. \\ &{\rm{s} .\rm{t}.}\qquad{{P}}{{{\textit{1}}}_n} = {{{\textit{1}}}_n},{{P}} > 0,{{{W}}^{\rm{T}}}{{X}}{{{X}}^{\rm{T}}}{{W}} = {{I}}. \end{split} \right.$

(6)

其中 ${{W}} \in {R^{d \times c}}$ 为特征选择矩阵, c为选择特征的维持, $\beta ,\gamma $ 为正则化参数. 上述模型的第一和第二项通过低秩表示学习样本在转换空间后的低秩子空间, 并保留了样本的全局结构. 其中在重构系数矩阵Z的低秩约束下, 重构后的样本能极大降低噪声样本的影响. 并且W具有行稀疏, 能极大降低噪声或冗余特征的影响. 通过引入低秩表示重构数据, 同时降低了噪声样本、噪声特征以及冗余特征对特征选择的影响. 第三和第四项自适应学习样本间的局部流形结构, 保留了样本间的局部结构.

2.2 模型优化

式(6)中 ${{W,Z,P}}$ 均未知, 很难直接求出目标函数的最优解. 因此本文使用增广拉格朗日乘子法(ALM)来尝试求解目标函数的最小值, 如式(7)所示:

$\left\{\begin{split} &\Gamma ({{W}}{\rm{,}}{{S}}{\rm{,}}{{P}}{\rm{,}}{{Q}}{\rm{,}}{{T}}{\rm{,}}{{{Y}}_1}{\rm{,}}{{{Y}}_2}{\rm{,}}{{{Y}}_3}{\rm{,}}{\mu _1}) = ||{{{W}}^{\rm{T}}}{{X}} - {{{W}}^{\rm{T}}}{{XZ}}||_{\rm{F}}^2 + \\ &\alpha ||{{T}}|{|_*} + \beta \sum\limits_{ij}^n {||{{{W}}^{\rm{T}}}{{{x}}_i} - {{{W}}^{\rm{T}}}{{{x}}_j}|{|^2}{P_{ij}} + \mu {P_{ij}}^2} + \\ & \gamma ||{{W}}|{|_{2,1}} + < {{{Y}}_1},{{P}}{{{\textit{1}}}_n} - {{{\textit{1}}}_n} > + < {{{Y}}_2},{{P}} - {{Q}} > + \\ &< {{{Y}}_3},{{Z}} - {{T}} > + \frac{{{\mu _1}}}{2}(||{{P}}{{{\textit{1}}}_n} - {{{\textit{1}}}_n}||_{\rm{F}}^2 + ||{{P}} - {{Q}}||_{\rm{F}}^2 + ||{{Z}} - {{T}}||_{\rm{F}}^2).\\ & {\rm{s} .\rm{t}.}\qquad{{{W}}^{\rm{T}}}{{X}}{{{X}}^{\rm{T}}}{{W}} = {{I}},{{Q}} > 0. \end{split} \right.$

(7)

其中 ${{{Y}}_1}$ , ${{{Y}}_2}$ 和 ${{{Y}}_3}$ 为拉格朗日乘子, ${\mu _1}$ 为惩罚参数. 式(7)可通过不精确拉格朗日乘子法(IALM)求解.

IALM在求解最小值过程中, 在每一步中更新一个变量, 同时固定其他变量不变. 并依次迭代更新所有变量直到收敛. 主要的求解步骤如下:

1) 更新 ${{W}}$ . 在式(6)中对 ${{W}}$ 求偏导数可得

$\frac{{{{({{X}}{{{X}}^{\rm{T}}})}^{ - 1}}({{{G}}^{\rm{T}}} + {{G}})}}{2}{{W}} = {{\varLambda W}},$

(8)

其中 ${{G}} = {{XL}}{{{X}}^{\rm{T}}} + \gamma {{{D}}_{{W}}}$ , ${{{D}}_{{W}}}$ 为对角矩阵且第 $i$ 个对角元素为

${D_{{W_{ii}}}} = \frac{1}{{2||{{{W}}_i}|{|_2}}},$

(9)

${{L = I + Z}}{{{Z}}^{\rm{T}}} - {{{Z}}^{\rm{T}}} - {{Z}} + \beta ({{{D}}_{{P}}} + {{{D}}_{{{{P}}^{\rm{T}}}}} - {{2P}})$ , 其中 ${{{D}}_{{P}}}$ 和 ${{{D}}_{{{{P}}^{\rm{T}}}}}$ 为对角矩阵, 其中对角元素分别为 ${D_{{P_{ii}}}} = $ $ \displaystyle\sum\nolimits_j {{p_{ij}}} $ 和 ${D_{P_{ii}^{\rm{T}}}} = \displaystyle\sum\nolimits_i {{p_{ij}}} $ . 显而易见, ${{W}}$ 的最优解对应于特征值分解问题的c个最小特征值的特征向量.

2) 更新 ${{Z}}$ . 对 ${{Z}}$ 求偏导数可得

${{{Z}}^*} = {({{F}} + {\mu _1}{{I}})^{ - 1}}{{F}} - {{T}}{\mu _1} - {{{Y}}_3},$

(10)

其中 ${{F}} = 2{{{X}}^{\rm{T}}}{{W}}{{{W}}^{\rm{T}}}{{X}}$ .

3) 更新 ${{P}}$ . 对 ${{P}}$ 求偏导数可得

${{{P}}^*} = \frac{{{E}}}{{2\mu + {\mu _1}}}{\left({{I}} + \frac{{{\mu _1}}}{{2\mu + {\mu _1}}}{{{\textit{1}}}_n}{{\textit{1}}}_n^{\rm{T}}\right)^{ - 1}},$

(11)

其中

$\begin{split}&{{E}} = ({\mu _1}{{{\textit{1}}}_n}{{\textit{1}}}_n^{\rm{T}} + {\mu _1}{{Q}} - \beta {{B}} - {{{Y}}_1}{{\textit{1}}}_n^{\rm{T}} - {{{Y}}_2}),\\ &{B_{ij}} = ||{{{W}}^{\rm{T}}}{{{x}}_i} - {{{W}}^T}{{{x}}_j}|{|^2}.\end{split} $

4) 更新 ${{T}}$ . 对 ${{T}}$ 求偏导数可得

${{{T}}^*} = {\upsilon _{1/{\mu _1}}}\left({{Z}} + \frac{{{{{Y}}_3}}}{{{\mu _1}}}\right),$

(12)

其中 ${\upsilon _{1/{\mu _1}}}({{X}}) = {{U}}{S_\tau }({{\Sigma }}){{V}}$ 是关于奇异值 $\tau $ 的阈值算子, ${S_\tau }({\Sigma _{ij}}) = {\rm{sign}}({\Sigma _{ij}})\max (0,|{\Sigma _{ij}} - \tau |)$ 为软阈值算子, ${{X}} = $ ${{U}}{{\Sigma }}{{V}} $ 为 ${{X}}$ 的奇异值分解.

5) 更新 ${{Q}}$ . 对 ${{Q}}$ 求偏导数可得

${{Q}}{\rm{*}} = \max \left({{P}} + \frac{{{{{Y}}_2}}}{{{\mu _1}}},0\right).$

(13)

6) 最后更新拉格朗日乘子和惩罚参数:

${{{Y}}_1} = {{{Y}}_1} + {\mu _1}({{P}}{{{\textit{1}}}_n} - {{{\textit{1}}}_n}).$

(14)

${{{Y}}_2} = {{{Y}}_2} + {\mu _1}({{P}} - {{Q}}).$

(15)

${{{Y}}_3} = {{{Y}}_3} + {\mu _1}({{Z}} - {{T}}).$

(16)

${\mu _1} = \min ({\mu _{\max }},\rho {\mu _1}).$

(17)

其中 $\rho > 0$ 为迭代步长, ${\mu _{\max }}$ 为常数.

2.3 时间复杂度

上述优化过程中时间复杂度分析如下: 第1步为特征值分解问题, 其运算矩阵的大小 $d \times d$ , 所以时间复杂度为 $o({d^3})$ ; 第2步中矩阵求逆需要 $o({n^3})$ ; 第4步中的时间复杂度为 $o({n^3})$ . 因此整个优化算法的时间复杂度为 $o(\tau ({d^3} + 2{n^3}))$ ,其中 $\tau $ 为算法优化过程中的迭代次数.

2.4 收敛性分析

在本节中, 将JLRRGE运行1-最近邻分类器(NN). 在2个数据集上运行本文所提方法, 以显示其收敛性质, 包括JAFFE 和MFEA数据集. 当所有变量和分类准确率都稳定, 则该算法趋于收敛. 在上述优化过程中, 使用变量 ${{Q}}$ 和 ${{T}}$ 来分别逼近变量 ${{P}}$ 和 ${{Z}}$ . 本文认为当 ${{Q}}$ 接近于 ${{P}}$ 且 ${{T}}$ 接近于 ${{Z}}$ 时, 所有变量趋于稳定. 因此定义了如下目标函数:

${\rm{obj}} = {\rm{||}}{{P}} - {{Q}}{\rm{|}}{{\rm{|}}_{\rm{F}}} + ||{{Z}} - {{T}}|{|_{\rm{F}}}.$

(18)

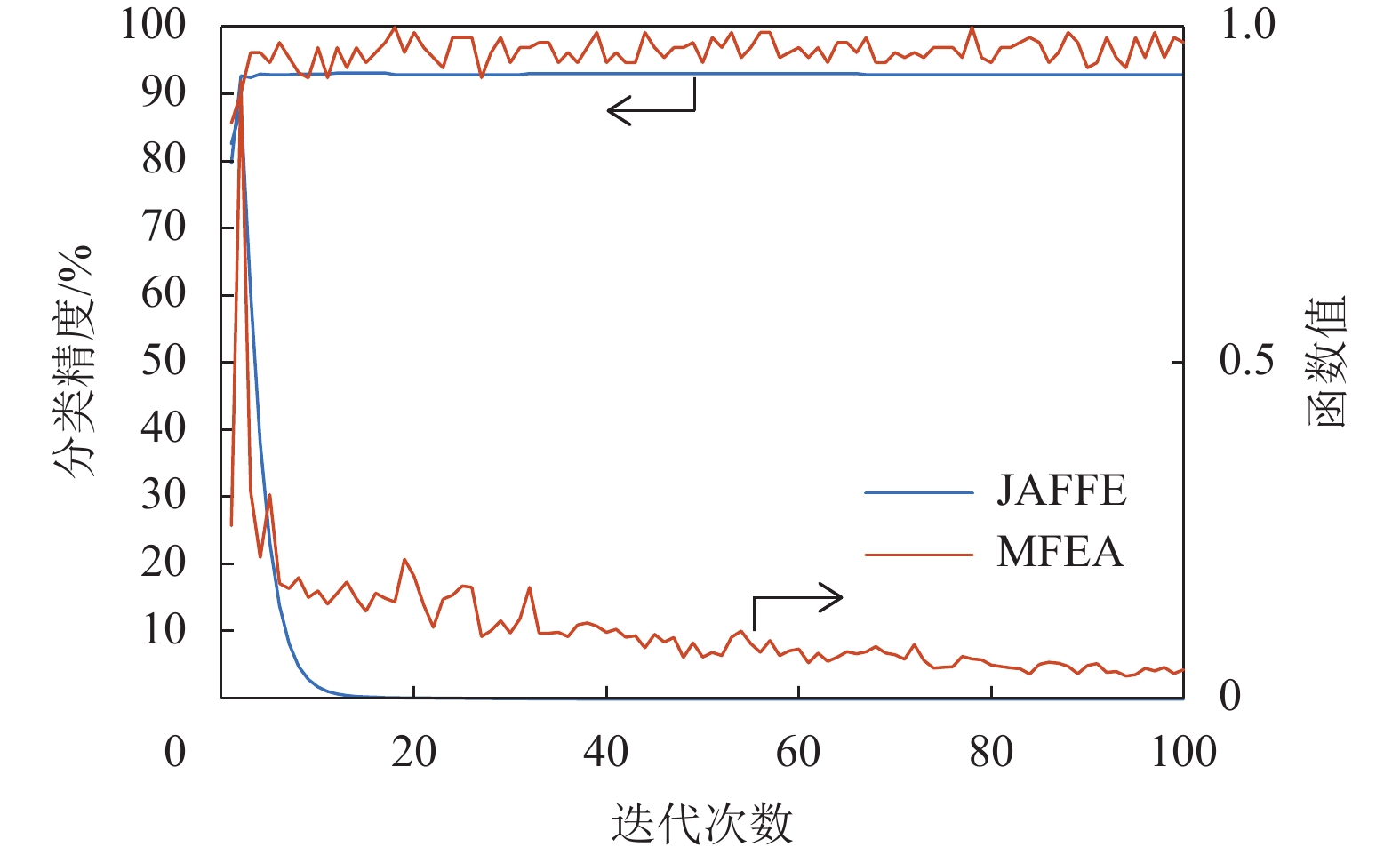
在上述两个数据集上运行本文所提方法并进行100次迭代, 并在图1中显示了目标函数值、分类精度和迭代之间的关系.

由图1可知, 随着迭代次数的增加, 目标函数整体上不断减少且分类准确率整体上不断升高, 并在一定迭代次数后趋于稳定. 在JAFFE数据集中目标函数值先上升后下降, 可能是由于在优化过程中, 随机初值所造成的影响. 总体而言, 由目标函数值和分类准确率曲线可知本文提出的方法具有较强的鲁棒性, 能够快速逼近局部最优解, 并具有良好的收敛性.

3 实验

本文所提出的JLRRGE将与4种具有代表性的特征选择算法如拉普拉斯评分的特征选择(Laplacian Score, LS)、多类簇特征选择(MCFS)、无监督判别特征选择(UDFS)和最优结构图的特征选择(SOGFS)进行详细对比.

3.1 实验数据集

本文使用以下5个常用数据集, 如表1所示.

COIL数据集包含20个对象, 每个对象有72个样本, 共1 440个样本. 样本以5度为间隔从同方向进行捕获, 所有图像被调整为1 024个像素.

ORL数据集包含40个对象, 每个对象拍摄10幅图片, 共400张图. 每个对象在不同的时间、光照、面部表情(睁/闭眼、微笑/不微笑)和面部细节(是否戴眼镜)下拍摄, 所有图像被调整为 $32 \times 32$ 个像素.

JAFFE数据集包含213张7种面部表情的图像, 包括6种基本面部表情和1种中性表情.

UMIST数据集包含575张20人的图像. 每个人从侧面到正面都摆出一系列姿势, 而且他们来自不同的种族. 这些文件都是PGM格式, 灰度为256个阴影.

MFEA数据集包含一系列的手写数字(0~9), 这些数字是从一组荷兰实用地图中提取的. 一幅图像的大小为15×16像素.

3.2 参数设置与评价指标

本文实验对每个数据集做4组对比实验. 每组实验在每一类中分别随机抽取10%、20%、30%和40%作为训练样本, 其余作为测试样本. 在训练过程中, 每组实验选取特征数目分别为c = {10, 20, 30, 40, 50, 60, 70, 80, 90, 100}. 最终结果运行在1-最近邻分类器(NN)中验证本文算法的性能.

对于LS和MCFS算法生成的近邻矩阵时, 参数k统一设置为5. LS热核计算权重矩阵 ${{W}}$ 时, $\sigma $ 取值1. UDFS和SOGFS中参数 $\gamma $ 设置为{10⁻³, 10⁻², 10⁻¹, 1, 10, 10², 10³}. 本文提出的算法JLLRGE中参数 $\alpha $ , $\beta $ , $\gamma $ 均设置为{10⁻³, 10⁻², 10⁻¹, 1, 10, 10², 10³}.

此外, 算法的鲁棒性也是需要考虑的范畴. 由算法目标函数可知, 参数 $\alpha $ 和 $\beta $ 对优化过程起重要作用. 本文在各数据集抽取10%作为训练样本的情景下, 随机固定参数 $\lambda $ 和选择特征个数, 在不同的参数 $\alpha $ 和 $\beta $ 下, 进行实验并记录其对应的准确率, 结果如图2所示.

3.3 实验结果与分析 3.3.1 COIL20数据集

由表2可知, JLRRGE在随机抽取20%的训练样本的实验中, 比MCFS的分类效果略差. 其余情况均取得较好的分类结果, 且整体分类效果比其他对比算法好.

由图2(a)可知, 当 $\alpha \in [0.001,10]$ 时, JLRRGE取得较好的结果. 当 $\alpha \in [10,1000]$ 时, JLRRGE分类性能略微下降. 整体上, JLRRGE在数据集COIL中对参数 $\alpha $ 和 $\beta $ 的变化并不敏感, 即JLRRGE对于数据集COIL具有较好的鲁棒性.

3.3.2 ORL32数据集

由表3可知, 除了在抽取20%作为训练样本的情况, JLRRGE均取得最好的分类结果.

由图2(b)可知, 当 $\alpha \in [0.001,1]$ 时, 取得较好的结果. 当 $\alpha \in [10,1\;000]$ 时, 分类准确率骤降. 即过于注重ORL数据的全局结构, 而导致其分类准确率下降. 由此表明参数 $\alpha $ 的变化对JLRRGE在数据集ORL上的分类效果具有较大的影响.

3.3.3 JAFFE数据集

由表4可得, JLLRGE在JAFFE数据集上, 对于不同百分比的训练样本, 均取得较好的效果.

由图2(c)可得, 当 $\alpha \in [0.001,100]$ 时, JLRRGE取得较好的结果. 当 $\alpha \in [100,1\;000]$ 时, JLRRGE分类性能略微下降. 整体上, JLRRGE在数据集JAFFE上具有较强的鲁棒性, 对参数 $\alpha $ 和 $\beta $ 并不敏感.

3.3.4 UMIST数据集

由表5可知, JLRRGE的整体分类性能略差于MCFS, 仅在随机抽取10%训练样本的情况下取得较好的分类结果.

由图2(d)可得, 当 $\alpha \in [0.001,1]$ 时, JLRRGE取得较好的结果. 当 $\alpha \in [1,1\;000]$ 时, JLRRGE分类性能略微下降. 整体上, JLRRGE在数据集UMIST对参数 $\alpha $ 和 $\beta $ 并不敏感.

3.3.5 MFEA数据集

由表6可得, JLRRGE在各情况下均取得较好的分类结果.

由图2(e)可得, 当 $\alpha \in [10,1\;000]$ 时, JLRRGE分类性能略微下降. 整体上, JLRRGE在数据集MFEA对参数 $\alpha $ 和 $\beta $ 并不敏感, 具有较强的鲁棒性.

4 结束语

本文提出了一种新颖的无监督特征选择方法. 通过低秩表示选择具有低秩结构的特征, 使选择的特征更具鲁棒性. 同时结合图嵌入方法, 自适应学习数据的局部相似性矩阵, 使数据降维后仍保留其局部流形结构. 实验表明, 本文所提的方法比其他对比方法在绝大部分情况下均取得更好的分类结果, 并且该方法具有良好的鲁棒性. 在未来将尝试优化模型的复杂度, 减少模型的训练时间.