桌子是人们日常工作和生活当中不可或缺的必需品,目前市场上的桌子一般分为固定型与折叠型. 固定型的桌子面积固定,难以适应人数变化的场合;而大多数折叠型桌子通过合页或者铰链及其他机构连接在一起,通过折叠板来达到面积增大的效果. 这类型的桌子虽然适应性比固定型的桌子有所提高,但也存在桌面的面积改变有限等缺点,因而需要对桌子进一步创新设计,以满足用户对桌面倍增的需求.
产品创新设计需要创新方法支撑,常用的创新设计方法有公理化设计、TRIZ理论、可拓创新方法等. 程贤福等[1]利用公理化设计了起重机的起升机构,周杨等[2]基于TRIZ理论的纸盒成型机主轴结构的优化设计,吴培旭[3]应用可拓创新方法设计了多功能烘干器,唐文艳等[4]基于折叠纸打印夹的创新设计. 近年来,产品的创新设计方法向融合的方向发展,尤其是TRIZ理论与其他方法的集成,成为了许多学者研究的重点[5],如江帆[6]进行了TRIZ与可拓学比较及融合机制的研究;黄斌达[7]集成了公理化与TRIZ来设计机床夹具;李苏洋等[8]利用TRIZ理论与可拓学对飞机整流罩进行了优化;江帆等[9]融合TRIZ与可拓学进行了血管机器人驱动机构的设计.
根据集成的思路,本文将TRIZ与可拓学相结合,提出了基于TRIZ与可拓学的产品创新优化设计方法,并参考了已公开的专利,陈尚理[10]申请的转盘式变形餐桌,杨颖等[11]申请的一种负压自动变形桌,建立一种可变面积方桌的创新设计方案.
1 融合TRIZ与可拓学的产品优化创新设计 1.1 TRIZ理论与可拓学TRIZ理论是苏联科学家根里奇·阿奇舒勒在20世纪中叶创建的,直译为“发明问题解决理论”,是一种创新型解决问题的理论. 其主要目的是研究人类在进行发明创造和解决技术难题的过程中所遵循的科学原理和法则. 该理论现在已广泛应用于各个工程领域.
可拓学是由中国学者蔡文于1983年提出的一门原创性横断学科,它以形式化的模型,探讨事物拓展的可能性以及开拓出新的规律与方法,并用于解决矛盾问题. 可拓学的基本理论是可拓论,它包括基元理论、可拓集合理论和可拓逻辑3个组成部分. 在创新应用中主要通过可拓建模、拓展、变换、优度评价等4个步骤获得创意[12]. 目前,可拓学已进入一些研究领域并取得一系列成果.
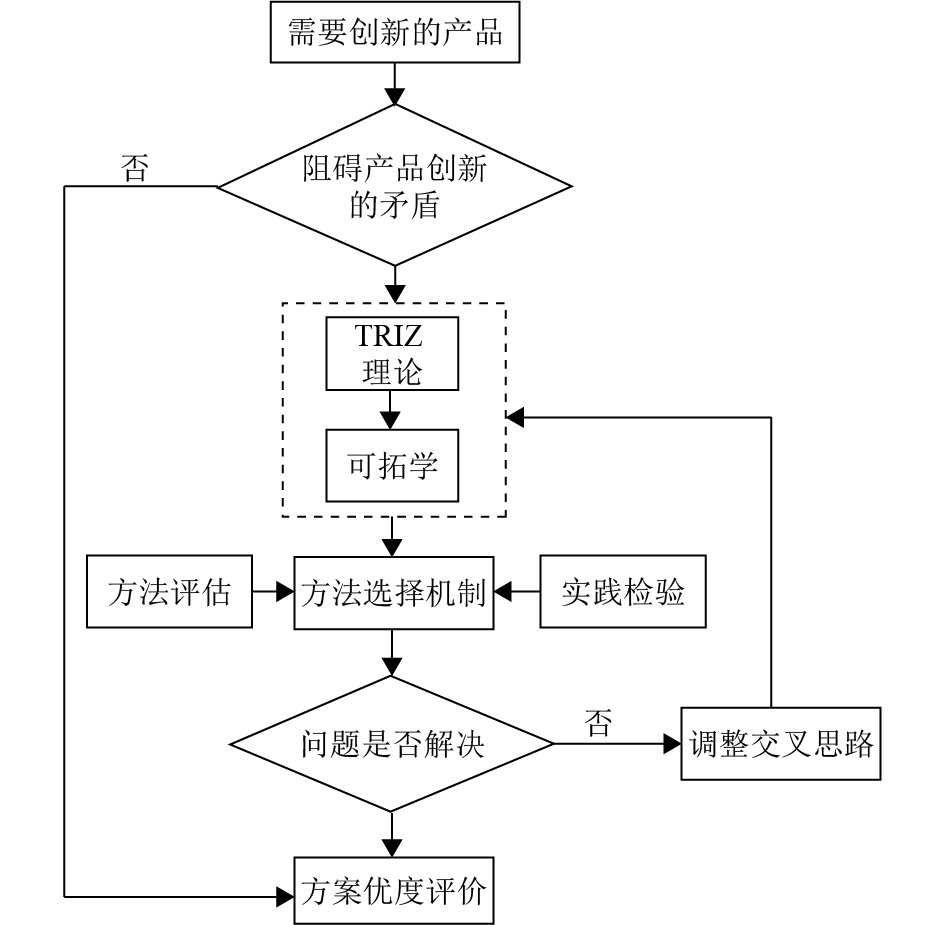
1.2 基于TRIZ与可拓学的产品创新优化设计方法创新设计中会碰到很多问题,融合TRIZ理论与可拓创新方法会降低求解难度,其关键点是矛盾识别与矛盾求解,这里集成TRIZ工具与可拓创新方法,建立的创新方法如图1所示. 其具体流程为:(1) 针对创新设计问题,利用基元模型将涉及的问题简化,找出阻碍产品创新的矛盾;(2) 利用TRIZ的矛盾矩阵找到阻碍创新的可行解;(3) 利用可拓变换对解进行可拓变换,消除阻碍创新的矛盾;(4) 通过方法评估和实践检验来验证方法选择机制是否合理,如果不合理,则需要返回再次进行方案选择,直到选择方案合理,解决阻碍创新的问题;(5) 众多解决问题的方案中选择最佳方案.
|
图 1 TRIZ与可拓学交叉融合模式 Figure 1 The cross fusion model of TRIZ and Extenics |
根据桌子设计中面临的问题,希望桌子能增加桌面面积,而桌面轮廓形状不发生任何改变,故存在的问题是桌子表面面积在增加的同时表面外轮廓形状发生改变.
2.1 基于基元模型的问题分析根据可拓学的形式描述,建立可变面积方桌最终实现的目标G,目标事元即为
| $G{\rm{ = }}\left[ {\begin{array}{*{20}{l}} \text{增加}&\text{支配对象}&\text{桌面}\\ {}&\text{要求}&\text{形状不变} \end{array}} \right].$ |
普通桌子目前的面积为a,根据可拓学的形式描述,其条件物元L即为
| $L{\rm{ = }}\left[ {\begin{array}{*{20}{l}} \text{桌面}&\text{面积}&{\rm{a}}\\ {}&\text{形状}&\text{正四边形} \end{array}} \right].$ |
很明显,这构成了一个不相容问题:面积变大,形状就会发生改变,即
根据不相容问题模型,进行拓展分析,提取出一个矛盾:如果增加桌面的面积,则会导致桌面形状发生改变. 应用标准的工程技术参数描述,改善的参数:运动物体的面积(No.05),导致恶化的参数:形状(No.12).
2.2 基于TRIZ创新原理的可行性解预测使用TRIZ矛盾矩阵[13]查询得到,推荐的发明原理为:No.05,No.34,No.29,No.04,以下简单说明.
No.05组合原理:(1) 把空间相邻的物体或相邻的操作联合起来;(2) 把时间上相同的物品或相邻的操作联合起来.
No.34抛弃原理与修复原理的结合:(1) 采用溶解、蒸发等手段抛弃已完成功能的零部件,或者在系统运行过程中直接修改它们;(2) 在工作过程中迅速补充系统或物体中消耗的部分.
No.29气压和液压结构原理:用气体结构和液体结构代替物体的固体部分,如充气和充液的结构,以及静液的和液体反冲的结构.
No.04不对称原理:(1) 把原来对称的物体改为不对称的结构;(2) 增加不对称物体的不对称程度.
根据上述原理,可知抛弃原理与修复原理,气压和液压结构原理不适用于桌子,暂不考虑. 同时桌子应尽量保持稳定,所以应该选择对称结构. 根据组合原理的提示,把相邻的物体的操作联合起来,可以增加机构,使桌子表面进行整体的联动操作,这样桌子面积可以变大,同时桌子形状不会发生改变.
2.3 可行解的基元变换根据TRIZ原理解的提示,需要增加组合机构,以增加桌面面积,且不改变桌子表面形状,扩展面积较大,理论上单一的组合机构无法满足大面积的拓展需求,因此考虑添加两组机构以满足拓展需要,考虑两组机构基元变换的可行性,避免机构拓展时相互干涉,选用上下错开的两组机构. 考虑到方桌的特殊形状和操作的便利性,采用常用的曲柄滑块机构、曲柄连杆机构、凸轮机构和齿轮机构等进行组合驱动面积倍增和桌形保持不变[14]. 设定3种方案
方案一,曲柄滑块机构和曲柄连杆机构的组合. 机构本身比较简单、容易实现功能、杆可以长度变化、实现远距离的控制、寿命长、成本低. 缺点是精度比较低,不容易实现精确复杂的运动规律.
方案二,凸轮机构和曲柄连杆机构的组合. 凸轮机构优势比较明显,结构简单、加工方便、结构紧凑、可靠性高. 但是凸轮机构的缺点也较为显著,线接触的地方容易磨损、行程不大.
方案三,齿轮机构和曲柄连杆机构的组合. 齿轮机构的优点主要为承载力大和传动精度高. 缺点主要为安装精度差和传动噪音大.
对于方案的选择,一般可以应用优度评价进行优选,这里考虑篇幅,仅进行简单的定性比较. 3种组合方案优缺点如表1所示,考虑到问题的本质,方桌本身不需要较大的承载力,同时需要转动过程产生的音量越低越好,因此方案三不符合要求. 方案二结构简单,但是行程太小,这样会导致拓展的面积较小,无法达到拓展的需求. 方案一结构简单,虽然精度较低,不易进行复杂运动,但是对于当前的问题并不产生影响,故综上所述,应该选择方案一.
| 表 1 3种组合方案对比 Table 1 Comparison of three combination schemes |
方案一中初步选择上层(第一驱动机构)为曲柄滑块机构,首先做变换
| ${T_1}{\rm{ = }}\left[ {\begin{array}{*{20}{l}} \text{增加}&\text{施动对象}&{{L_1}}\\ {}&\text{支配对象}&{{L_{11}}}\\ {}&\text{变换结果}&{{L_1} \oplus {L_{11}}} \end{array}} \right],\;\;\;\;\;\;\;\;\;\;\;\;\;$ |
| ${L_{11}}{\rm{ = }}\left[ {\begin{array}{*{20}{l}} \text{曲柄滑块机构}&\text{个数}&4\\ {}&\text{运动方式}&\text{滑动}\\ {}&\text{位置}&\text{上层} \end{array}} \right];$ |
下层(第二驱动机构)为曲柄连杆机构,因此还需要做变换
| ${T_2}{\rm{ = }}\left[ {\begin{array}{*{20}{l}} \text{增加}&\text{施动对象}&{{L_1}}\\ {}&\text{支配对象}&{{L_{12}}}\\ {}&\text{变换结果}&{{L_1} \oplus {L_{12}}} \end{array}} \right],\;\;\;\;\;\;\;\;\;\;\;\;\;$ |
| ${L_{12}}{\rm{ = }}\left[ {\begin{array}{*{20}{l}} \text{曲柄连杆机构}&\text{个数}&4\\ {}&\text{运动方式}&\text{滚动}\\ {}&\text{位置}&\text{下层} \end{array}} \right].$ |
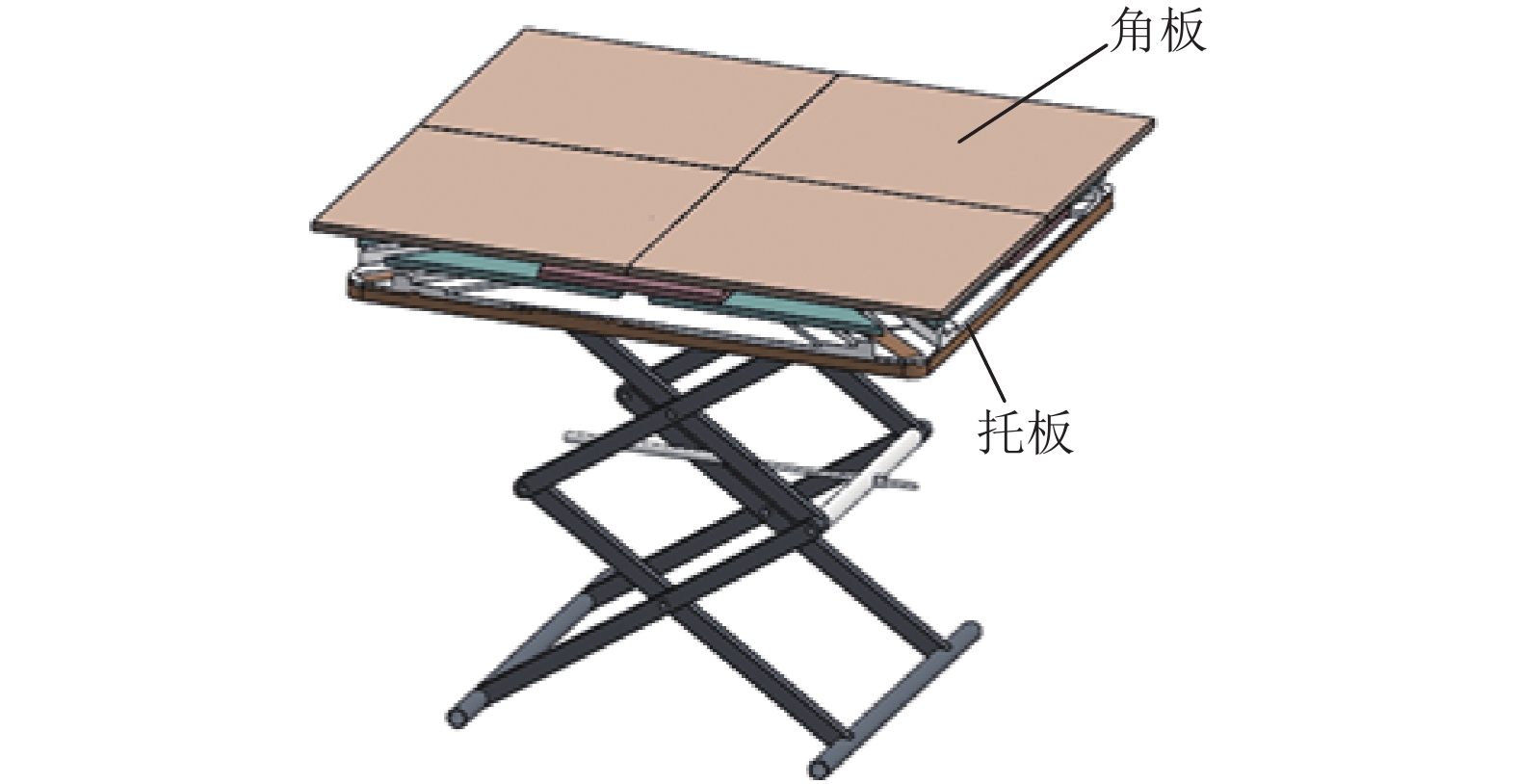
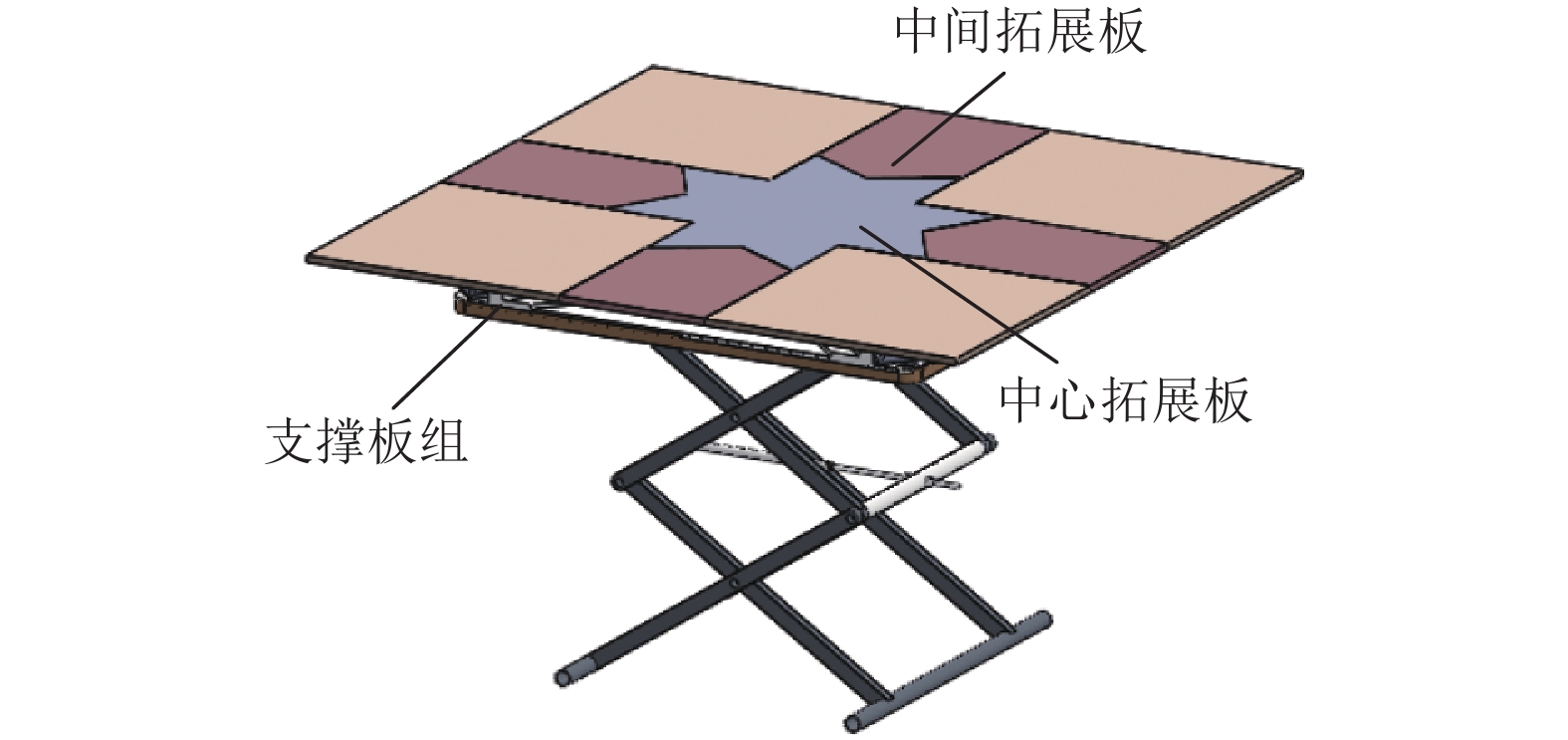
将增加曲柄滑块机构和曲柄连杆机构,曲柄滑块机构由上向下运动,曲柄连杆机构由下向上运动. 方桌面积扩展前如图2所示,扩展后效果如图3所示.
|
图 2 桌子拓展前 Figure 2 Before the table expands |
|
图 3 桌子拓展后 Figure 3 After the table expands |
根据“一特征多量值”的发散分析原理[15],按照面积拓展类型进行发散分析得到以下2种方案. (1) 桌面拓展部分直接在原有桌面的四周添加. (2) 桌面拓展部分可以通过原有桌面的变形,从中间和四周同时添加. 考虑到桌子机构运动的可行性,机构上下运动不干扰,选择从中间和四周同时拓展.
整体机构操作如下,桌面在曲柄滑块的作用下,外层四块板由内层向外层运动,是下降运动. 扩展之后,外层四块板中间出现了孔隙,需要物体补充中间的孔隙. 内层的拼接板在曲柄连杆的作用下由内向外运动,同时是上升运动,上升之后的高度正好与中心拓展板等高. 根据组合原理,在两组机构的组合下,桌面面积增大同时桌面形状不发生任何的改变,仍为变换前的正方形.
下面根据拓展分析的思路,对2个驱动机构进行具体的结构设计.
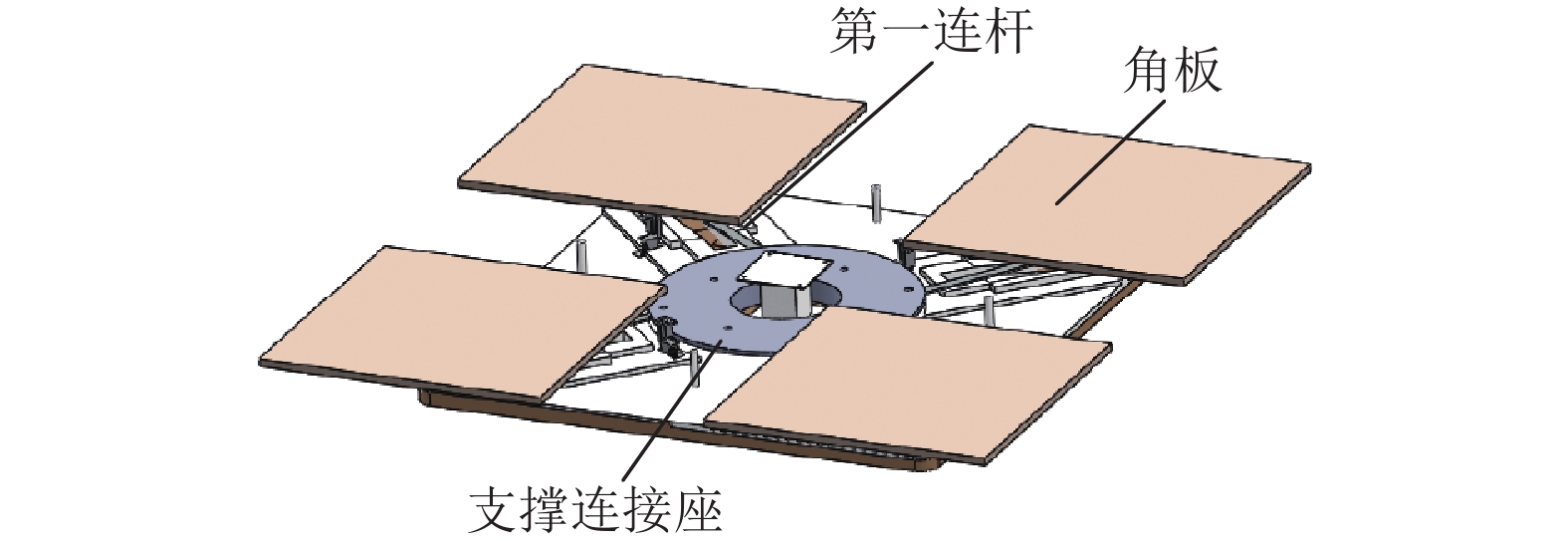
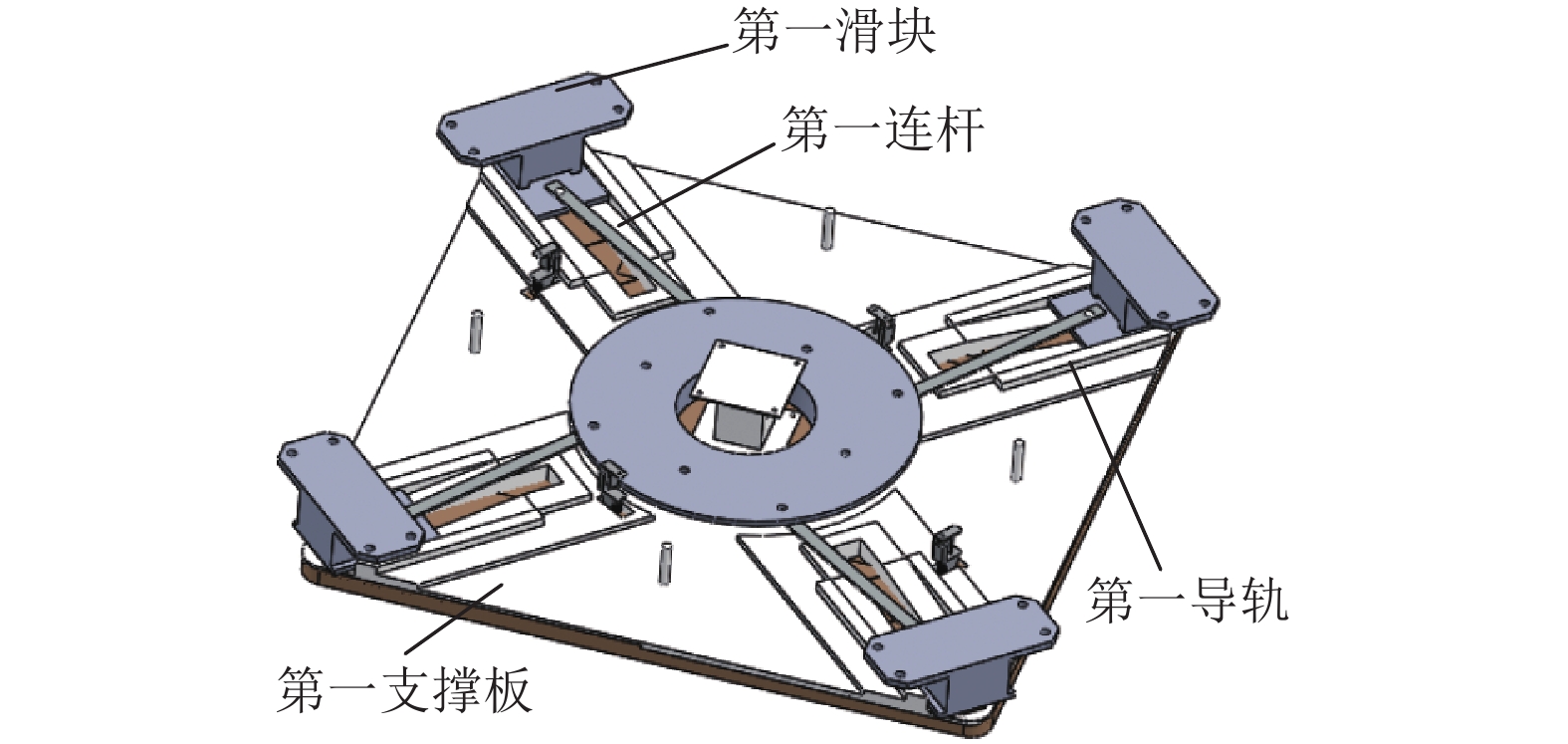
3.2 曲柄滑块机构设计如图4、图5和图6所示,第一驱动机构为曲柄滑块机构,包括一端与支撑连接座铰接的第一连杆、与第一连杆的另一端铰接的第一滑块以及与第一滑块配合的第一导轨;其中,第一滑块与角板固定连接,第一导轨设置在支撑板组上,该第一导轨上具有由内层向外层向下倾斜的倾斜面,支撑板组与托板之间转动连接. 工作时,沿着圆周方向推动位于支撑板组(第一支撑板和第二支撑板组成)上的角板使得支撑板组与连接座之间发生相对转动,该转动会通过第一连杆带动第一滑块在第一导轨上运动,由于第一导轨上具有由内层向外层向下倾斜的倾斜面,因此第一滑块由内层向外层的运动是下降运动,第一滑块由外层向内层的运动是抬升运动,从而满足角板的运动需求. 此设计的优势为:只需要沿着圆周方向对角板或连接座施加推力时,就能够实现大桌面到小桌面之间的自由变换,操作简单、方便.
|
图 4 角板和第一驱动机构的结构示意图 Figure 4 Schematic diagram of angle plate and first drive mechanism |
|
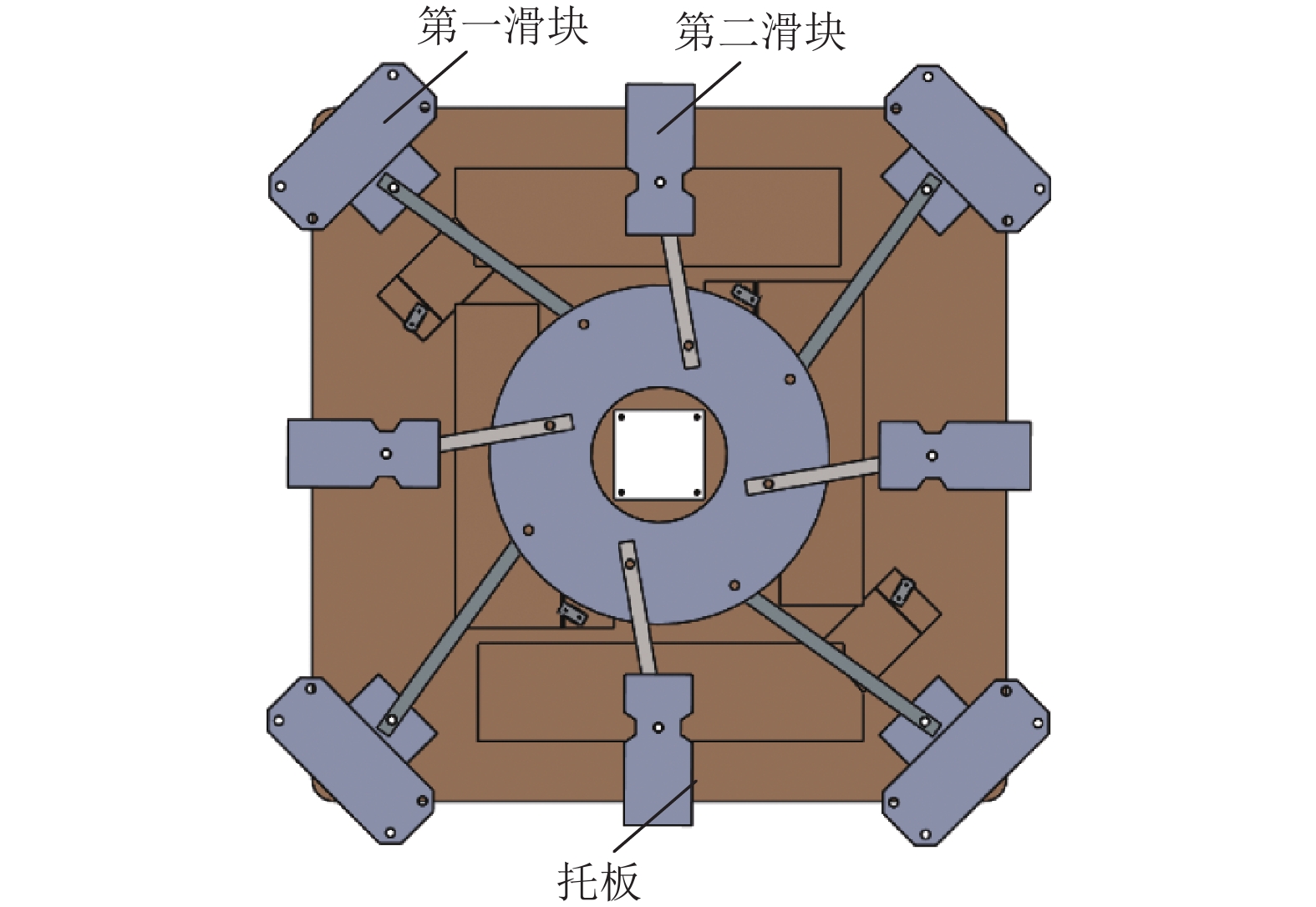
图 5 去除角板后的结构示意图 Figure 5 Schematic diagram of structure after removal of angle plate |
|
图 6 支撑板组与托板之间转动连接时的结构示意图 Figure 6 Schematic diagram of the connection between supporting plate group and supporting plate |
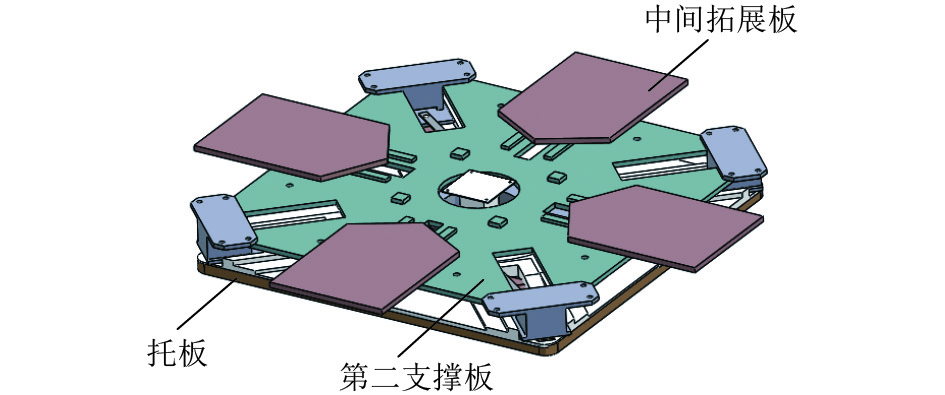
如图7和图8所示,第二驱动机构为曲柄连杆机构,包括一端与支撑连接座铰接的第二连杆、与第二连杆的另一端铰接的第二滑块以及与第二滑块配合的第二导轨;其中,第二滑块与中间拓展板固定连接,第二导轨设置在支撑板组上,该第二导轨上具有由内层向外层向上倾斜的倾斜面,支撑板组与托板之间转动连接. 工作时,当沿着圆周方向推动位于支撑板组上的角板时,在第二曲柄滑动机构的驱动下,第二滑块在第二导轨上运动,由于第二导轨上具有由内层向外层方向倾斜的上升段,因此第二滑块由内层向外层的运动是抬升运动,第二滑块由外层向内层的运动是下降运动,从而满足中间拓展板的运动需求.
|
图 7 中间拓展板和第二驱动机构的结构示意图 Figure 7 Schematic diagram of the structure of the intermediate expansion plate and the second driving mechanism |
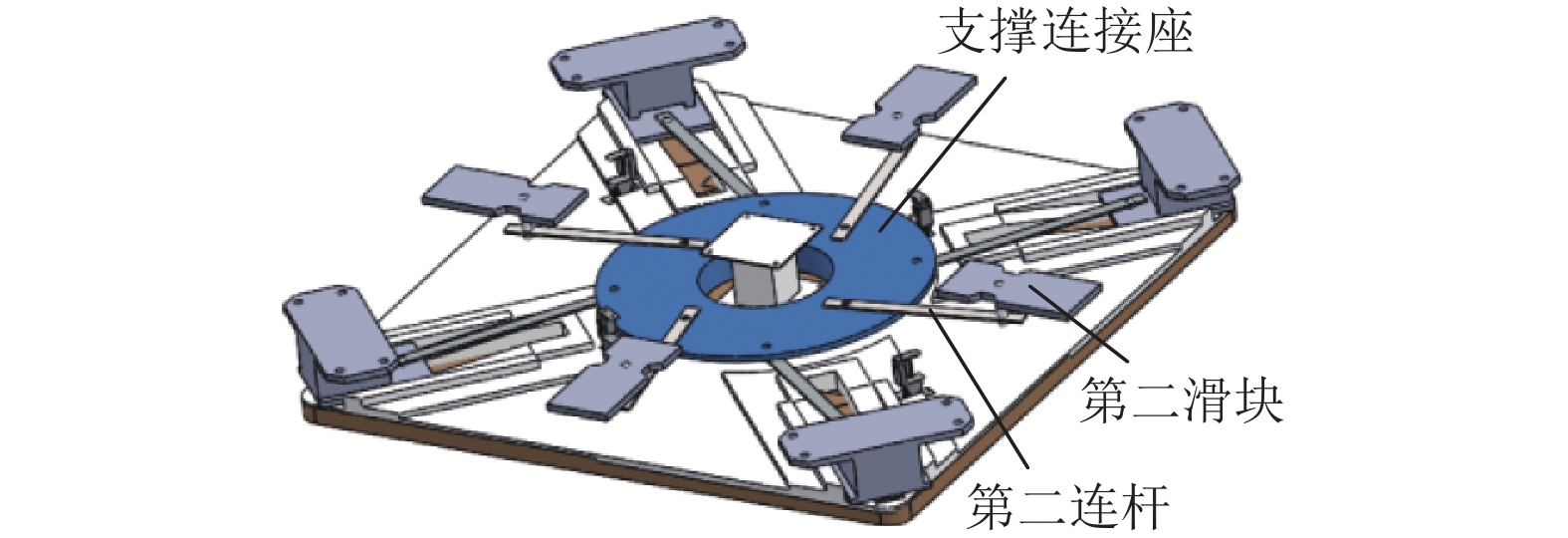
|
图 8 去除中间拓展板后的结构示意图 Figure 8 Schematic diagram of structure after removal of intermediate expansion panels |
(1) 建立了TRIZ和可拓创新方法相融合的产品设计方法,利用可拓工具简化问题、提取矛盾、变换可行解、优度评价,利用TRIZ工具寻求矛盾求解的发明原理. 采用融合的创新设计,可以降低产品创新设计中求解创新问题的难度.
(2) 针对现有方桌的不足,采用融合创新设计方法进行改进设计,经过矛盾分析与求解,及可行解的变换分析、方案评价,建立可变面积的方桌设计方案:联用曲柄滑块机构和曲柄连杆机构,实现面积倍增,而保持桌面形状不变.
| [1] |
程贤福, 肖人彬. 基于公理化设计理论的起重机起升机构分析[J].
机械设计, 2005, 22(1): 45-47.
DOI: 10.3321/j.issn:1003-8728.2005.01.012. |
| [2] |
周杨, 邓援超, 王爱群, 等. 基于TRIZ理论的纸盒成型机主轴结构的优化设计[J].
包装工程, 2018, 39(9): 125-130.
|
| [3] |
吴培旭, 刘建群. 基于可拓设计方法的多功能产品创造法[J].
广东工业大学学报, 2015, 32(3): 10-17.
WU P X, LIU J Q. Solution to creating multi-function product based on extension design methods[J]. Journal of Guangdong University of Technology, 2015, 32(3): 10-17. DOI: 10.3969/j.issn.1007-7162.2015.03.003. |
| [4] |
唐文艳, 吕文阁, 张晓伟, 等. 折叠纸打印夹的创新设计[J].
广东工业大学学报, 2017, 34(1): 15-18.
TANG W Y, LYU W G, ZHANG X W, et al. An innovation design of print clip for folded paper[J]. Journal of Guangdong University of Technology, 2017, 34(1): 15-18. DOI: 10.12052/gdutxb.160133. |
| [5] |
刘志峰, 高洋, 胡迪, 等. 基于TRIZ与实例推理原理的产品绿色创新设计方法[J].
中国机械工程学报, 2012, 23(9): 1105-1107.
|
| [6] |
江帆. TRIZ与可拓学比较及融合机制研究[M]. 北京: 北京理工大学出版社, 2015.
|
| [7] |
黄斌达, 周来水, 安鲁陵, 等. 集成TRIZ的机加夹具方案公理化设计[J].
仪器仪表学报, 2017, 38(4): 1031-1040.
DOI: 10.3969/j.issn.0254-3087.2017.04.030. |
| [8] |
李苏洋, 杨春燕, 张晓伟, 等. 运用可拓学与TRIZ方法解决矛盾问题[J].
广东工业大学学报, 2013, 30(1): 7-12.
LI S Y, YANG C Y, ZHANG X W, et al. The application of extenics and the TRIZ[J]. Journal of Guangdong University of Technology, 2013, 30(1): 7-12. DOI: 10.3969/j.issn.1007-7162.2013.01.002. |
| [9] |
江帆, 杨鹏海. TRIZ理论与可拓学的融合方法研究[J].
广州大学学报(自然科学版), 2014, 13(6): 59-64.
|
| [10] |
陈尚理. 转盘式变形餐桌: 93236122.6[P]. 1994-02-02.
|
| [11] |
杨颖, 郭秋帆, 罗秀雯, 等. 一种负压自动变形桌: 201420037964.9[P]. 2014-01-21.
|
| [12] |
杨春燕, 蔡文. 基于可拓学的创意生成与生产研究[J].
广东工业大学学报, 2016, 33(1): 12-16.
YANG C Y, CAI W. Generating creative Ideas for production based on extenics[J]. Journal of Guangdong University of Technology, 2016, 33(1): 12-16. DOI: 10.3969/j.issn.1007-7162.2016.01.002. |
| [13] |
江帆, 黎斯杰. 今天你创新了吗——TRIZ创新小故事[M]. 北京: 知识产权出版社, 2017.
|
| [14] |
江帆, 韩立发, 董克权. 机械原理[M]. 北京: 机械工业出版社, 2013.
|
| [15] |
杜宇上, 刘银萍. 基于可拓学的特征变式方法[J].
广东工业大学学报, 2017, 34(6): 9-14.
DU Y S, LIU Y P. The variation of features based on extenics[J]. Journal of Guangdong University of Technology, 2017, 34(6): 9-14. DOI: 10.12052/gdutxb.170116. |
 2019, Vol. 36
2019, Vol. 36
