采用后张预应力连接的节段拼装式桥墩具有施工快,质量易保证,对环境影响小等优点[1],但桥墩安全性能对预应力筋可靠度依赖太大,当侧向荷载需求增大时,预应力筋引起的轴压比将成倍增加,可能造成底节段混凝土压碎. 预应力大小作为节段拼装桥墩设计的关键参数,如今却尚未有一个系统的确定方法,这成为了推广该种桥墩应用的障碍之一.
虽然至今已有许多采用节段拼装桥墩的桥梁,如国内有港珠澳大桥[2]以及杭州湾跨海大桥[3],国外有约翰肯尼迪大桥[4]以及新泽西胜利大桥,但目前的国内外研究主要还是集中于预应力节段拼装桥墩的抗震性能上.
国内研究方面,1999年我国学者田琪等[5]进行了节段拼装双柱墩的拟静力试验,研究了插入式接头及后张预应力接头的抗震性能;在2005年,台湾交通大学的周中哲等[6]改进了Hewes的试验和分析方法,对两组钢管混凝土节段拼装桥墩进行了拟静力试验,分析了阻尼器对节段拼装桥墩抗震性能影响. 2007年叶列平等[7]研究了预应力轴压比、预应力度、配筋率等因素对桥墩抗震性能影响. 在2008年罗海燕等[8]研究了预应力度对无粘结预应力混凝土柱抗震性能影响. 在2011年布占宇等[9]利用拟静力试验,研究了轴压比,预应力配筋率以及接缝构造等参数对结构抗震性能影响.
国外方面,1997年,美国纽约大学的Mander和Cheng[10]研究了无粘结预应力筋的干接缝节段拼装桥墩的震后修复加固性能. 1999年,Kurama[11]推导出了在侧向荷载作用下,无粘结节段拼装墙板的基底剪力与顶部位移的显式解. 2008年,韩国学者Kim[12]发现具有抗剪连接结构的节段拼装桥墩残余位移比现浇桥墩的残余位移小,延性和滞回能力也较强. 2010年,布法罗大学的Ou和Tsai[13]发现高性能耗能钢筋能极大增强节段拼装桥墩耗能能力,且无粘结预应力钢筋能减少节段拼装桥墩的残余位移.
总的来说,国内外已有的研究主要集中在预应力对节段拼装桥墩的耗能能力、自复位能力等抗震性能上,但预应力大小对其力学性能的影响却少有研究. 为了得到一个具有良好力学性能的预应力值,从而推广节段拼装桥墩的应用,需要进一步研究预应力对节段拼装桥墩力学性能的影响.
本文以一节段拼装桥墩为原型,以预应力轴压比为变化参数,利用ABAQUS建立了5种节段拼装桥墩有限元模型,其中第1种模型是文献[14]中的静力试验桥墩模型(无预应力节段拼装桥墩),其余模型则是在第1个模型的基础上通过配置预应力筋,施加预应力所得. 通过比较第1种模型的数值模拟结果与试验结果来验证模型模拟方法的正确性,然后分析其他4种模型的数值模拟结果来研究预应力轴压比对节段拼装桥墩力学性能影响.
1 数值模拟方案设计为了研究预应力轴压比对节段拼装桥墩的力学性能影响,首先进行数值模拟方案设计.
文献[14]进行了节段式混凝土桥墩模型的加载试验,研究其在一定竖向荷载作用下,施加水平力时构件的力学性能. 为了方便验证有限元模拟方法的正确性,本文选择文献[14]中的无预应力节段拼装桥墩静力试验模型作为第1个方案,方案编号为RC. 混凝土采用C50混凝土,普通钢筋采用HRB335钢筋. 节段间采用胶接缝进行连接,胶接缝的材料弹性模量为4 500 MPa,泊松比0.35,拉伸强度为32 MPa. 桥墩计算长度为1 200 mm,分3个节段,节段高度为350 mm,截面为空心矩形截面,截面外尺寸为400 mm×400 mm,内尺寸为200 mm×200 mm,RC方案节段拼装桥墩具体构造尺寸如图1所示,钢筋工程数量表如表1所示.
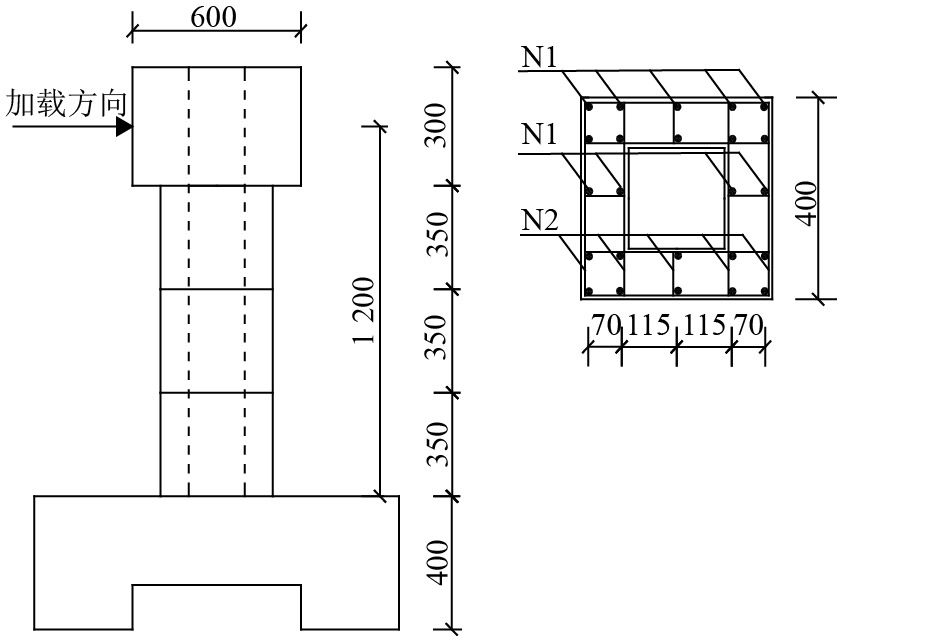
|
图 1 RC方案节段式混凝土墩构造图(mm) Figure 1 RC segmental concrete pier structure diagram(mm) |
| 表 1 钢筋工程数量表 Table 1 Quantity of reinforcing steel works |
其余4个方案则是在方案1的基础上,通过配置预应力钢筋,并施加预应力轴压比分别为10%、20%、30%、40%的预应力而得到,对应方案编号分别为PSC1-PSC4. 预应力钢筋采用直径为15.2 mm,抗拉极限强度为1 860 MPa的钢绞线. PSC1-PSC4方案的具体构造尺寸如图2所示,钢筋工程数量表如表2所示.
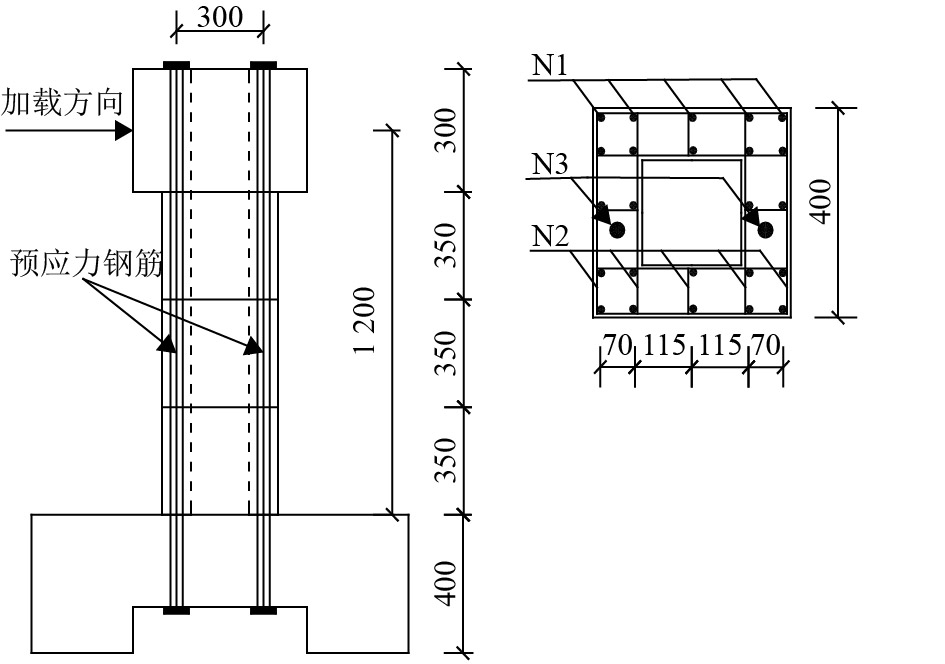
|
图 2 PSC1-PSC4方案节段式混凝土墩构造图(mm) Figure 2 PSC1-PSC4 segmental concrete pier structure diagram(mm) |
| 表 2 钢筋工程数量表 Table 2 Quantity of reinforcing steel works |
加载方面,在水平加载前,在墩顶竖向预加荷载300 kN. 在完成竖向荷载加载后,开始进行水平荷载逐级加载. 水平荷载加载方式采用位移控制加载,以1 mm的加载级数加至6 mm;再以2 mm的加载级数加至12 mm;随后分别以4 mm、6 mm、10 mm的加载级数加至28 mm、40 mm、50 mm;最后以20 mm的加载级数加至70 mm. 加载模式如图3所示.
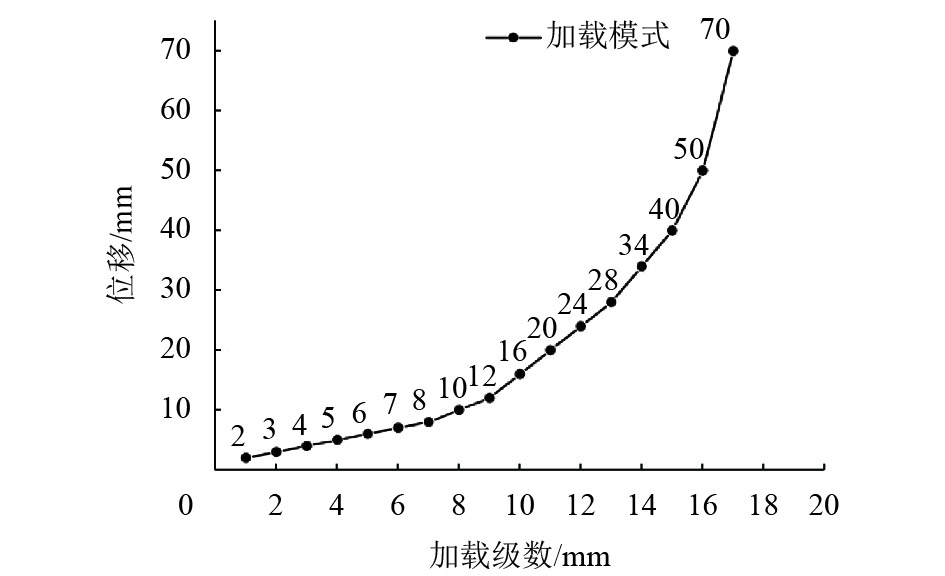
|
图 3 加载模式 Figure 3 Loading mode |
综上所述,为了研究预应力轴压比对节段拼装桥墩力学性能影响,本文设计了5种方案. 为了方便验证有限元模拟正确性,本文选择文献[14]中的节段拼装桥墩静力试验模型作为方案RC. 然后在方案RC的基础上,通过配置预应力钢筋,并施加预应力而得到方案PSC1-PSC4. 具体方案设计参数如表3所示.
| 表 3 方案设计参数 Table 3 Pier model design parameters |
本文的RC模型是以文献[14]中的静力试验桥墩作为原型建立,其余模型(编号PSC1-PSC4)则是在RC模型的基础上通过配置预应力筋,施加预应力而得到的模型. 构件尺寸如图1以及图2所示.
RC模型的混凝土本构采用文献[15-17]中所建议的损伤塑性模型,钢筋本构采用理想弹塑性模型. 普通钢筋单元嵌入混凝土单元,结构底部与地面固结. 同时为了增加收敛性,建立了两个参考点,并将其分别与竖向荷载加载面和横向荷载加载面进行耦合,将竖向和横向荷载加载于参考点上. 节段混凝土采用C3D8R实体单元进行模拟,节段内钢筋则采用T3D2桁架单元进行模拟. RC方案实体有限元模型如图4所示.

|
图 4 RC方案有限元实体模型 Figure 4 RC scheme finite element entity model |
PSC1-PSC4方案的模型是在RC方案的基础上配置预应力筋,并施加预应力所得的模型,因此其选择的混凝土以及普通钢筋的本构模型与RC方案一样,预应力筋采用理想弹塑性模型.
PSC1-PSC4方案的预应力用降温法[18-19]来进行施加. 降温法表达式为P=T/αE,其中T为温降大小,P为预加力,α为钢筋的温度膨胀系数,A为钢筋截面积. 本文温度膨胀系数定为10−5.
后张预应力钢束与锚具选择MPC绑定进行约束,锚具与锚固端采用绑定(Tie)约束,并将钢束嵌入到混凝土单元中以模拟其粘结作用. PSC1-PSC4方案的有限元模型如图5所示.
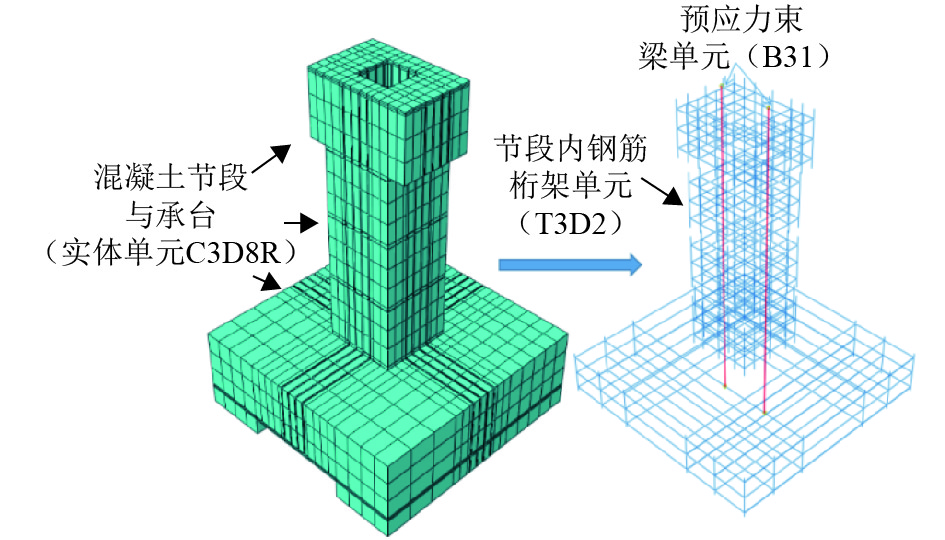
|
图 5 PSC1-PSC4方案有限元实体模型 Figure 5 PSC1-PSC4 scheme Finite element entity model |
为了得到正确的有限元模拟方法,首先需要对上面所建立的模型进行验证.
为了方便验证模型建模方法的正确性,本文选择将方案RC(即不含预应力的节段拼装桥墩)的模型模拟结果与文献[14]中的试验结果进行对比. 以下将从荷载位移曲线以及关键位移点的塑性应变两个角度来验证模型的可行性.
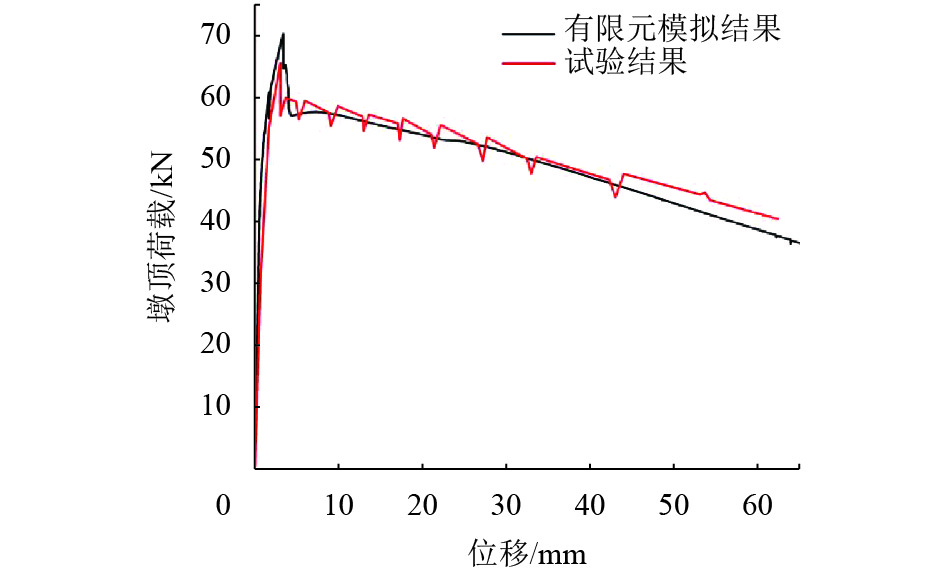
有限元模拟得出RC方案的墩顶荷载−位移曲线与试验结果[14]对比如图6所示.
|
图 6 RC方案侧向荷载−位移曲线对比图 Figure 6 Comparison of RC scheme Load-displacement curve |
在弹性阶段,有限元模拟得出的荷载位移曲线斜率稍大,这是由于有限元模拟没有考虑钢筋与混凝土滑移,软件高估了结构的侧向刚度所致. 结构承载力在达到极限承载力后突然下降,荷载−位移曲线在此处形成“尖点”,这恰好说明了试验现象[7]中结构具有脆性破坏的特征. 而结构破坏后,丧失承载力时,有限元模拟得出的下降段与试验所得的下降段斜率基本一致.
| 表 4 参数提取表 Table 4 Parameter extraction table |
由表4可知,理论计算得出的极限承载力与试验值相差7%,极限承载力对应的位移与试验值相差13%,弹性极限位移与试验值相差10%,差距均在15%以内.
有限元模拟得出的关键位移加载点对应的塑性应变云图如图7所示.

|
图 7 塑性应变图 Figure 7 Plastic strain diagram |
由文献[14]中的桥墩试验结果概况可知,当位移达到3 mm时,可以在桥墩底节段观察到角部附近出现裂缝,位移达到24 mm时结构底节段出现斜裂纹. 从位移达到3 mm时的塑性应变图(图7(a))可知,此时的塑性拉应变主要集中于底节段的角部,这说明了试验过程中底节段角部首先出现裂缝的现象. 观察位移达到24 mm时的塑性应变(图7(b))可以发现,此时塑性应变从底节段角部出发,斜向上扩散,这恰好能说明试验中在加载到24 mm时斜裂缝的出现. 同时受压区也出现了较大的塑性应变.
综上所述,无论是从总体的受力性能(墩顶荷载−位移曲线),还是从试验与模拟过程中,关键位移加载点的塑性应变对比来看,利用该模型模拟节段拼装桥墩是可行的,精度可以满足工程要求.
3 预应力轴压比对结构力学性能影响为了获得具有良好力学性能的预应力轴压比,本文以预应力轴压比为参数,分析预应力轴压比分别为10%、20%、30%、40%时节段拼装桥墩的力学性能. 以下将从力学行为、关键参数、塑性发展3个角度进行分析,研究预应力轴压比对节段拼装桥墩的力学性能影响.
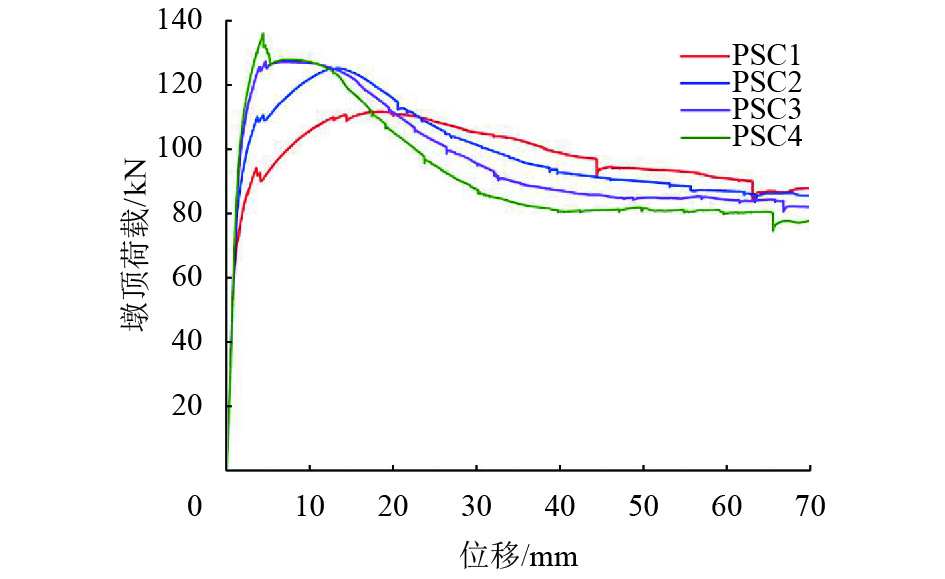
3.1 力学行为分析4种节段装配式桥墩的墩顶荷载位移曲线如图8所示.
|
图 8 荷载-位移曲线结果对比图 Figure 8 Comparison of load-displacement curve results |
由图8可知,在弹性阶段,4种节段拼装桥墩的荷载位移曲线基本重合,说明在结构弹性阶段,预应力轴压比对结构侧向刚度贡献很少.
结构进入塑性阶段后,当施加的预应力轴压比在10%~20%之间时,由于节段间有预应力钢束穿过的原因,结构的荷载位移曲线出现了明显的屈服段和强化段,相比于没有施加预应力时结构的脆性破坏,施加预应力轴压比在10%~20%之间的桥墩在破坏前有较明显征兆,是结构设计中更理想的荷载位移曲线. 当预应力轴压比达到30%时,结构极限承载力与屈服极限很接近,在强化段结构承载能力几乎不上升;当轴压比达到40%时,屈服段消失,其破坏模式与未施加预应力的桥墩相似,结构承载力在达到极限承载力后瞬间下降,呈现出脆性破坏的特征.
当结构达到极限承载力后,可以发现预应力轴压比越大,结构下降段斜率越大,结构丧失承载力的速度越快.
3.2 关键参数分析结构从屈服开始到达最大承载能力或达到以后而承载力没有显著下降期间的变形能力,称之为延性,延性是表征节段拼装桥墩力学性能的重要指标之一. 结构的延性用延性系数来表示,公式为
从图8荷载−位移曲线结果对比图中进一步提取结果,得到一系列关键参数,具体如表5所示.
| 表 5 关键参数提取结果表 Table 5 Key parameter extraction result table |
由表5可知,极限承载力和屈服极限随着预应力轴压比的增大而增大,极限位移则是随着预应力轴压比增大而减小. 而随着轴压比增大,极限点与屈服点将会越来越接近,也就是说结构屈服后储存的承载力也越来越小,脆性破坏的特征越来越明显. 结构的延性系数随着预应力轴压比增大而变小,即随着轴压比增大,结构表现出的延性越差. 中国建筑抗震规范[20]中建议的位移延性系数不小于2.86,由表3可知,控制预应力轴压比在20%以下时可以获得设计中比较理想的延性系数.
3.3 塑性发展分析结构达到极限承载力时的普通钢筋的塑性应变最大值如表6所示.
| 表 6 普通钢筋塑性应变最大值 Table 6 Reinforced plastic strain maximum |
在结构达到极限承载力时,普通钢筋的塑性应变均集中于受拉区. 普通钢筋的塑性应变随着预应力轴压比增大而减小. 当预应力轴压比在10%~20%时,受拉区普通钢筋能在结构达到极限承载力时屈服(大于0.002),可以充分发挥作用,而当预应力轴压比增大到40%时,普通钢筋塑性应变为0,此时普通钢筋未能充分发挥作用.
不同预应力轴压比下,结构达到极限承载力时的混凝土塑性应变最大值以及最小值如表7所示.
| 表 7 混凝土塑性应变最大值 Table 7 Concrete plastic strain maximum |
当混凝土的塑性应变大于材料的极限应变时,可以认为结构拉裂或者压碎. 由表7可知,10%~20%预应力轴压比下的节段拼装桥墩在达到极限承载力时,其最大压应变大于或接近于混凝土的极限压应变(0.003),证明预应力轴压比在10%~20%的结构在达到极限承载力时,其受压区将会出现压碎现象. 同时可以从表7观察到,除了预应力轴压比为10%和20%的结构的塑性压应变最大值相差较大以外,其他塑性应变最大值均比较接近,且变化率有正有负,相差较大,规律不明显.
4种预应力轴压比下的混凝土的塑性应变分布云图如图9所示.

|
图 9 混凝土塑性应变值 Figure 9 Concrete plastic strain magnitude |
由图9可知,随着预应力轴压比增大,产生塑性拉应变的范围逐渐缩小到接缝附近. 其中底节段角部附近塑性拉应变最大.
预应力轴压比在10%~30%的结构在达到极限承载力时,其塑性拉应变分布于底节段中以及第2节段中. 而轴压比达到40%的结构,塑性应变仅仅分布于节段的键齿附近,节段大部分地方未出现塑性应变.
4 结论本文以预应力轴压比大小作为变化参数,利用ABAQUS分别建立5个模型,其中第一个模型以文献[14]中的静力试验桥墩作为原型建立,通过比较两者墩顶荷载−位移曲线以及关键位移点的塑性应变来验证模型的可行性,然后研究4种预应力轴压比大小对结构力学性能影响. 具体结论如下:
(1) 预应力轴压比在10%~20%时,结构在加载过程中有明显的屈服段以及强化段,且达到极限承载力时钢筋屈服,混凝土压碎,破坏前将有明显征兆.
(2) 控制预应力轴压比在20%以下时可以获得理想的延性系数.
(3) 预应力轴压比对结构达到极限承载力时的塑性应变最大值影响不明显,但对塑性应变分布范围影响较大. 随着预应力轴压比增大,塑性应变范围将逐渐缩小到接缝附近.
| [1] |
葛继平, 闫兴非, 王志强. 机械套筒连接的轨道交通预制拼装桥墩抗震性能试验研究[J].
地震工程与工程振动, 2017, 37(6): 143-152.
GE J P, YAN X F, WANG Z Q. Seismic performance analysis of rail transit segmental bridge columns with mechanical splices[J]. Earthquake Engineering and Engineering Dynamics, 2017, 37(6): 143-152. |
| [2] |
郭熙冬. 港珠澳大桥承台墩身工厂化预制施工技术[J].
桥梁建设, 2014, 44(2): 107-111.
GUO X D. Construction techniques for factory precasting of pile caps and pier shafts of Hong Kong-Zhuhai-Macao bridge[J]. Bridge Construction, 2014, 44(2): 107-111. |
| [3] |
曾平喜, 唐衡, 冯永明. 杭州湾跨海大桥预制墩身施工技术[C]//中国公路学会桥梁和结构工程分会2005年全国桥梁学术会议论文集. 杭州: 中国公路学会, 2005.
|
| [4] |
BILLINGTON S. A precast segmental substructure system for standard bridges[J].
Jour Pci, 1999, 44(4): 56-73.
DOI: 10.15554/pcij. |
| [5] |
田琪, 陈兴冲, 朱东生, 等. 拼装式桥墩接头的承载能力与滞回特性的试验研究[J].
工程力学, 1999, 16(2): 107-113.
TIAN Q, CHEN X C, ZHU D S, et al. Experimental Study on loading capacity and hysteretic properties of assembled bridge pier joints[J]. Engineering Mechanics, 1999, 16(2): 107-113. |
| [6] |
CHOU C C, CHEN Y C. Cyclic tests of post‐tensioned precast CFT segmental bridge columns with unbonded strands[J].
Earthquake Engineering & Structural Dynamics, 2010, 35(2): 159-175.
|
| [7] |
叶列平, 林旭川, 汪训流. 预应力混凝土结构的自复位性能与抗震性能[C]//全国混凝土及预应力混凝土学术会议. 长沙: 中国土木工程学会, 2007.
|
| [8] |
罗海艳. 预应力度对无粘结部分预应力混凝土柱复位性能的影响研究[D]. 扬州: 扬州大学, 2008.
|
| [9] |
布占宇, 唐光武. 无黏结预应力带耗能钢筋预制节段拼装桥墩抗震性能研究[J].
中国铁道科学, 2011, 32(3): 33-40.
BU Z Y, TANG G W. Seismic performance investigation of unbonded prestressing precast segmental bridge piers with energy dissipation bars[J]. China Railway Science, 2011, 32(3): 33-40. |
| [10] |
HAMID N H, MANDER J B. Damage avoidance design for buildings[J].
Ksce Journal of Civil Engineering, 2014, 18(2): 541-548.
DOI: 10.1007/s12205-014-0016-2. |
| [11] |
KURAMA Y C, SHEN Q. Seismic design and response evaluation of unbonded post-tensioned hybrid coupled wall structures[J].
Earthquake Engineering & Structural Dynamics, 2010, 37(14): 1677-1702.
|
| [12] |
KIM T H, LEE K M, YOON C, et al. Inelastic behavior and ductility capacity of reinforced concrete bridge piers under earthquake numerical validation[J].
Journal of Structural Engineering, 2003, 129(9): 1208-1219.
DOI: 10.1061/(ASCE)0733-9445(2003)129:9(1208). |
| [13] |
Ou Y C, TSAI M S, CHANG K C, et al. Cyclic behavior of precast segmental concrete bridge columns with high performance or conventional steel reinforcing bars as energy dissipation bars[J].
Earthquake Engineering & Structural Dynamics, 2010, 39(11): 1181-1198.
|
| [14] |
高聪. 节段预制拼装混凝土桥墩静力行为研究[D]北京: 北京交通大学, 2015.
|
| [15] |
庄茁. ABAQUS有限元软件6.4版入门指南[M]. 北京: 清华大学出版社, 2004.
|
| [16] |
周小军. ABAQUS中弥散裂缝模型与损伤塑性模型的比较[J].
福建建筑, 2010(5): 49-50.
ZHOU X J. The comparison of smeared crack model and concrete damage plasticity model in ABAQUS[J]. Fujian Architecture, 2010(5): 49-50. |
| [17] |
王中强, 余志武. 基于能量损失的混凝土损伤[J].
建筑材料学报, 2004, 7(4): 365-369.
WANG Z Q, YU Z W. Concrete damage model based on energy loss[J]. Journal of Building Material, 2004, 7(4): 365-369. DOI: 10.3969/j.issn.1007-9629.2004.04.001. |
| [18] |
潘月辉. 预应力钢筋混凝土梁的有限元分析[J].
山西建筑, 2005, 31(2): 13-15.
PAN Y H. Finite element analysis of prestressed reinforced concrete girder[J]. Shanxi Architecture, 2005, 31(2): 13-15. DOI: 10.3969/j.issn.1009-6825.2005.02.009. |
| [19] |
何琳, 王家林. 模拟有效预应力的等效荷载-实体力筋降温法[J].
公路交通科技, 2015, 32(11): 75-80.
HE L, WANG J L. Method of equivalent load and temperature reduction on prestressing tendon for effective prestress simulation[J]. Journal of Highway and Transportation Research and Development, 2015, 32(11): 75-80. DOI: 10.3969/j.issn.1002-0268.2015.11.012. |
| [20] |
沈蒲生. 高层建筑结构疑难释义[M]. 北京: 中国建筑工业出版社, 2003.
|
 2019, Vol. 36
2019, Vol. 36

 ,
,