2. 广州擎天实业有限公司,广东 广州 510300
2. Guangzhou Kinte Industrial Co., Ltd., Guangzhou 510300, China
由于单相电压型PWM整流器具有能量双向流动和高功率因数的优点,使其广泛应用于包括微电网系统、电能补偿装置在内的各种单相并网系统中[1-3]. 为了获得更优异的性能,国内外研究人员已经提出了多种控制策略,例如间接电流控制策略[4]、瞬态直接电流控制策略[5]、直接功率控制策略[6]、预测控制策略[7]、矢量控制策略[8]和传统比例谐振(PR,Proportional Resonance)控制策略[9]等. 如果在单相电压型PWM整流器中使用间接电流控制策略和瞬态直接电流控制进行策略控制,PWM整流器将存在动态响应慢和抗干扰能力弱等缺陷,现阶段已很少使用. 为了在单相电压型PWM整流器中使用直接功率控制策略、预测控制策略和矢量控制策略等高性能控制策略,需要虚构出与PWM整流器输入电流和电压相正交的电流和电压量. 并且PWM整流器的性能非常依赖虚构量的准确性. 在这些控制策略中,PR控制策略虽然具有控制结构简单和抗干扰能力强的优点,但在这种控制策略下,PWM整流器易受电网频率波动的影响,且PWM整流器的稳态性能难以达到采用直接功率控制策略、预测控制策略和矢量控制策略控制下的稳态性能.
针对以上问题,本文以单相电压型PWM整流器中得到广泛应用的经典矢量控制策略为研究对象. 利用等效变换的方法,将旋转坐标下的单相电压型PWM整流器数学模型变换到静止坐标系下,构建了静止坐标系下单相电压型PWM整流器虚拟电流控制策略的归一化模型,分析该模型与传统PR控制模型的异同;同时对归一化模型下的虚拟电流控制策略进行优化设计,提出控制器参数配置准则,改善系统鲁棒性. 并利用仿真和实验来验证所提出的控制策略的可靠性.
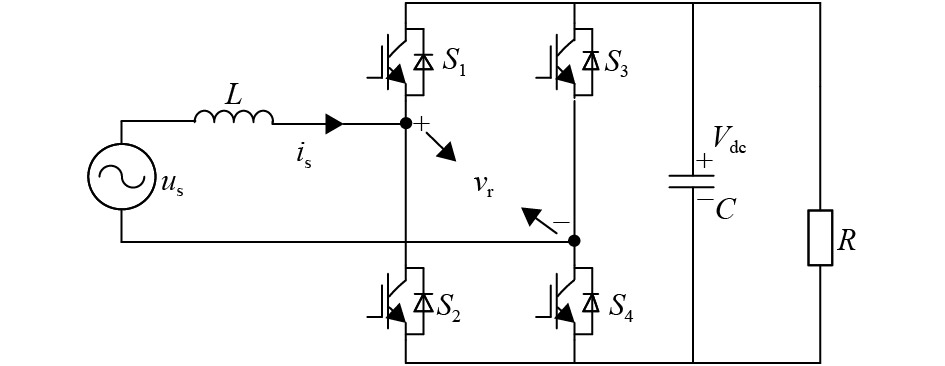
1 静止坐标系下的单相电压型PWM整流器归一化模型单相电压型PWM整流器主电路拓扑如图1所示,其中us是交流侧电压,is是交流侧电流,Vdc为直流侧电压,vr为全桥逆变电路的输出. L为单相PWM整流器的滤波电感,C是直流侧电压支撑电容,R为电阻负载,S1~S4为全桥逆变电路的4个功率开关管.
|
图 1 单相电压型PWM整流器主电路 Figure 1 The circuit of single-phase voltage source PWM rectifier |
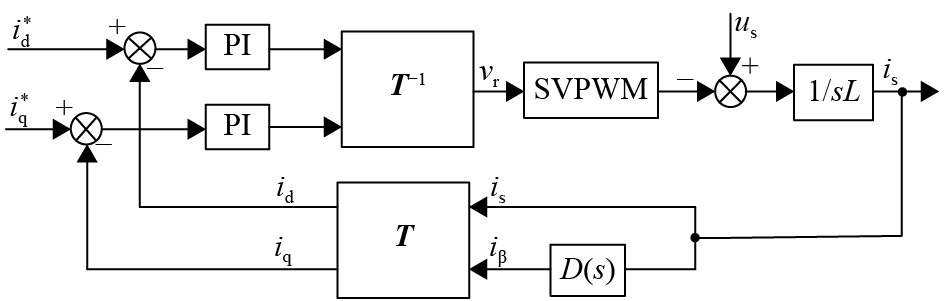
由图1主拓扑,可以获得经典的单相PWM整流器电流内环控制框图,如图2所示. 在图2中,PI(Proportion Integration)为电流内环比例积分控制器,其参数为Kp和Ki;SVPWM为功率开关管驱动脉冲生成环节;D(s)是虚拟电流生成环节,用于生成与电流is正交的虚拟电流量iβ,且D(s)应满足D(jω0)=–j,其中ω0为电网基波角频率;矩阵
| ${T}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\sin \theta }&{ - \cos \theta } \\ {\cos \theta }&{\sin \theta } \end{array}} \right],$ | (1) |
| ${{T}^{ - 1}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\sin \theta }&{\cos \theta } \\ { - \cos \theta }&{\sin \theta } \end{array}} \right].$ | (2) |
id、iq分别为电流量is和iβ在矩阵
利用旋转坐标和静止坐标的转换关系[11],可将图2所示的旋转坐标系下的单相电压型PWM整流器电流控制图转换为如图3所示的静止坐标系下的单相电压型PWM整流器电流控制环归一化模型.
|
图 2 旋转坐标系下的单相电压型PWM整流器电流内环控制框图 Figure 2 The current loop control diagram of single-phase voltage PWM rectifier in rotating coordinate system |

|
图 3 静止坐标系下单相电压型PWM整流器矢量控制的电流环控制归一化模型 Figure 3 Current control loop normalization model for vector control of single-phase voltage PWM rectifier in static coordinate system |
从图3可以看出,单相电压型PWM整流器的电流环控制归一化模型与比例谐振控制策略下的单相电压型PWM整流器电流环模型非常相似,不同之处仅在于归一化模型增加了
| $G\left( s \right) = {K_{\rm p}} + \frac{{2{K_{\rm i}}{B_{\rm c}}s}}{{{s^2} + 2{B_{\rm c}}s + \omega _0^2}} - \frac{{2{K_{\rm i}}{B_{\rm c}}{\omega _0}}}{{{s^2} + 2{B_{\rm c}}s + \omega _0^2}}D(s),$ | (3) |
其中,Bc为截止频率. 影响谐振带宽,Bc越小,比例谐振控制器对输入信号的调节效果越明显,但对系统频率波动越敏感,为保证系统的稳态性能同时增强抗干扰能力,选取Bc=2π.
改进后的静止坐标系下单相电压型PWM整流器矢量控制的电流控制环归一化模型如图4所示. 从图4中,可以看出D(s)作为系统前向通路的一部分,其参数的设计对系统的性能至关重要,下面的章节着重分析D(s)的选择及其参数的设计.
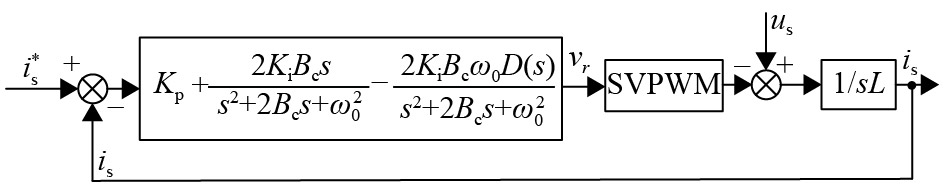
|
图 4 改进后的静止坐标系下单相电压型PWM整流器矢量控制的电流控制环归一化模型 Figure 4 Improved current control loop normalization model for vector control of single-phase voltage PWM rectifiers in static coordinate system |
现阶段,虚拟电流生成环节的表述形式有多种,其主要的产生方法如表1所示,其中T0为基波周期,d1、d2为控制器参数.
| 表 1 虚拟电流控制器 Table 1 Virtual current controller |
由于方法1和方法4无法抑制高频谐波,对噪声的抑制能力低,方法2在电网频率发生波动时,无法准确的虚构出正交于输入信号的控制量,因此本文采用方法3状态观测作为虚拟电流生成环节,保证归一化模型具有更优异的抗干扰能力和提高系统稳定性,令
| $D\left( s \right) = \frac{{ - s{d_2} + {\omega _0}{d_1}}}{{{s^2} + s{d_1} + {\omega _0}{d_2} + \omega _0^2}}.$ | (4) |
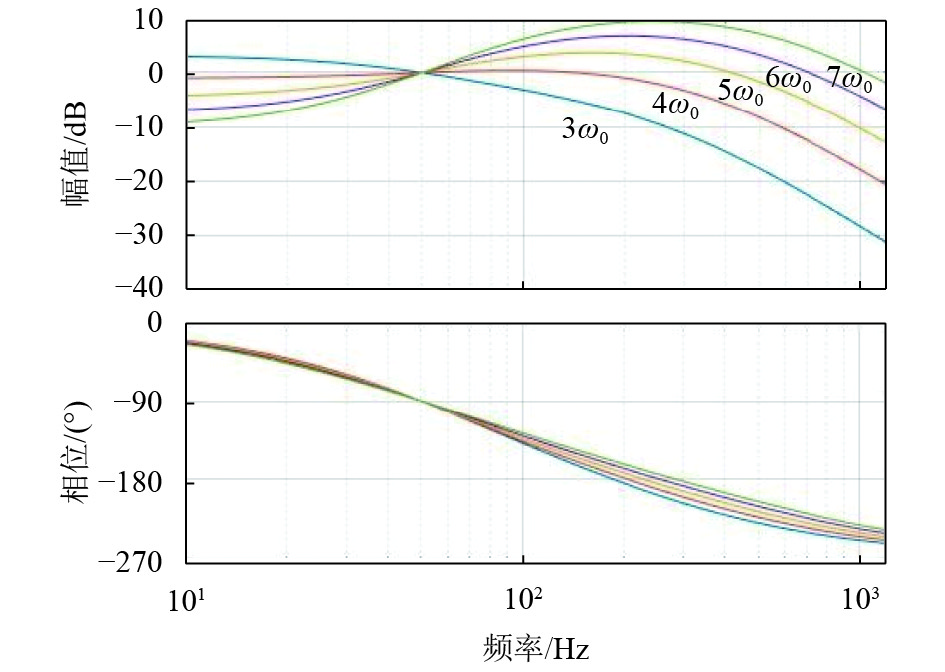
为了使状态观测器获得较好的稳态性能且具有一定的动态性能,需要合理配置d1和d2的数值. 图5分别绘制出状态观测器极点分布在3ω0、4ω0、5ω0、6ω0和7ω0处的伯德图. 从图5可以看出当状态观测器的极点配置在5ω0处,状态观测器可在稳态和动态性能中达到平衡. 故式(4)中,可取d1=10
此外,为了保证直流误差能通过反馈被抑制,开环系统的直流增益必须为正. 在此约束条件下有
| $G(s)\left| {_{s = 0}} \right. = {K_{\rm p}} - \frac{{2{K_{\rm i}}{B_{\rm c}}}}{{{\omega _0}}}D(0),$ | (5) |
| $D\left( 0 \right) = \frac{{{d_1}}}{{{d_2} + {\omega _0}}}.$ | (6) |
将参数d1、d2和Bc代入式(5)、(6),发现存在Ki>62.5Kp,则式(5)将出现负值,意味着闭环系统呈现直流正反馈,导致系统不稳定. 为了避免开环系统直流增益出现负值以及使得Kp和Ki的配置互不影响,配合一阶高通滤波器对D(s)进行优化设置,改进的虚拟电流控制器为
| ${D_m}(s) = \frac{{ - s{d_2} + {\omega _0}{d_1}\sqrt {d_2^2{K_2} + 1} }}{{{s^2} + s{d_1} + {\omega _0}{d_2}\sqrt {d_1^2{K_2} + 1} + \omega _0^2}}\frac{{s\sqrt {1 + K_1^2} }}{{{K_1}{\omega _0} + s}},$ | (7) |
其中,为了确保D(jω0) = −j,故引入参数K1、K2.
假设高通滤波器在基波频率处的相角为
| $\begin{split}& {D_m}(s) = \\ &\dfrac{{ - s{d_2}\cos \phi + {\omega _0}\left( {{d_1} - {d_2}\sin \phi } \right)}}{{{s^2}\cos \phi + s{d_1}\cos \phi + {\omega _0}\left( {{d_2} - {d_1}\sin \phi } \right) + \omega _0^2\cos \phi }}\times\\ &\dfrac{s}{{{\omega _0}\sin \phi + s\cos \phi }},\;\;\quad\phi \in \left( {0,{\rm{\pi }}/2} \right).\end{split}$ | (8) |
在式(8)中,对
| $\mathop {\lim }\limits_{\phi \to 0} {D_m}(s){\rm{ = }}\frac{{ - s{d_2} + {\omega _0}{d_1}}}{{{s^2} + s{d_1} + {\omega _0}{d_2} + \omega _0^2}},$ | (9) |
| $\mathop {\lim }\limits_{\phi \to {\text{π} /2}} {D_m}(s){\rm{ = }}\frac{{ - s}}{{{\omega _0}}}.$ | (10) |
Dm(s)的极限表明,当
|
图 5 D(s)不同极点处的幅频特性 Figure 5 The frequency response at different poles of D(s) |
通过图5选择D(s)的极点在5ω0处,使Dm(s)的部分极点也在5ω0的同时改变
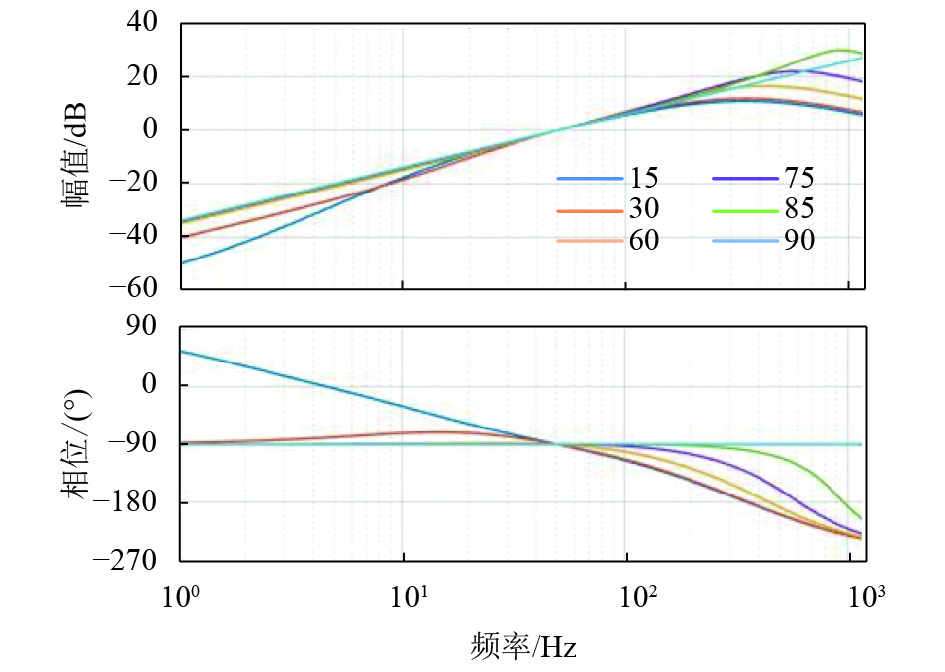
|
图 6 不同
|
根据图4改进后的静止坐标系下单相电压型PWM整流器矢量控制的电流控制环归一化模型,除D(s)外决定系统性能的还有比例系数Kp和积分系数Ki. 确定Kp、Ki的方法有多种,如试凑法、遗传算法、工程法等,本文通过配置控制系统的截止频率fc和相位裕度
| $ G\left( s \right)\frac{1}{{sL}}\left| {_{s = {\rm j}2{\text{π}} {f_{\rm c}}}} \right. = 1\angle \left( {{\varphi _{\rm m}} - {\text{π }}} \right), $ | (11) |
| $\begin{split} &{K_{\rm p}} = {\omega _{\rm c}}L\sin {\varphi _{\rm m}} + \\ &\dfrac{{{\omega _{\rm c}}L\cos {\varphi _{\rm m}}\left[ {2{\omega _{\rm c}}{\omega _0}{B_{\rm c}}R - 2{\omega _{\rm c}}{B_{\rm c}} - {\omega _0}I\left( {\omega _0^2 - \omega _{\rm c}^2} \right)} \right]}}{{\left( {\omega _0^2 - \omega _{\rm c}^2} \right)\left( {R{\omega _0} - 1} \right) + 2{\omega _{\rm c}}{\omega _0}{B_{\rm c}}I}},\end{split}$ | (12) |
| ${K_{\rm i}} = \frac{{L\left[ {{{\left( {\omega _0^2 - \omega _{\rm c}^2} \right)}^2} + 4\omega _{\rm c}^2B_{\rm c}^2} \right]\cos {\varphi _{\rm m}}}}{{2{B_{\rm c}}\left[ {\left( {\omega _0^2 - \omega _{\rm c}^2} \right)\left( {R{\omega _0} - 1} \right) + 2{\omega _{\rm c}}{\omega _0}{B_{\rm c}}I} \right]}},$ | (13) |
其中,
图7给出了整个系统截止频率在1 kHz、相位裕度为60°条件系的开环幅频特性,其中实线为本文改进后系统的幅频特性,模型如图4所示;虚线表示为相同系统参数条件下,传统PR控制策略的开环幅频特性. 图7表明,给出截止频率和相位裕度能够按照要求计算出系统参数;且在相同参数下,归一化模型增加的部分使得控制系统具有更高的开环增益,保证系统获得更小的稳态误差.
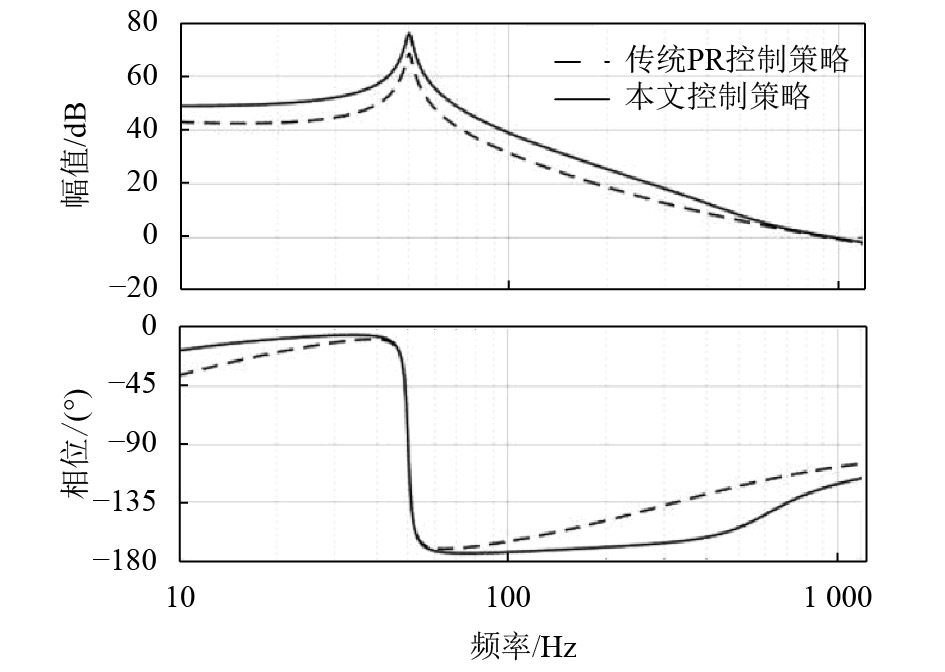
|
图 7 系统的开环幅频特性 Figure 7 Open-loop frequency response of the system |
为了验证本文提出的改进后的静止坐标系下单相电压型PWM整流器矢量控制的电流环归一化模型的有效性,在Matlab/Simulink中建立该仿真模型,并搭建以TMS320F28035作为核心的实验平台. 该实验平台采用IRG4PH50UD作为整流器的开关器件. 仿真与实验平台基本参数如表2所示.
| 表 2 实验基本参数 Table 2 Experimental parameters |
图8分别给出了旋转坐标系下电流PI控制和静止坐标系下的电流PR控制的单相电压型PWM整流器实验波形. 图9、图10给出相同控制器参数条件下归一化模型下的仿真和实验结果,其中图10为交流输入电压不变的条件下,输出功率从500 W突变到1 kW的动态仿真及实验结果. 图8~图10中,us为交流侧输入电压信号;is为与us同相位的交流侧电流,Vdc为直流侧电压信号.
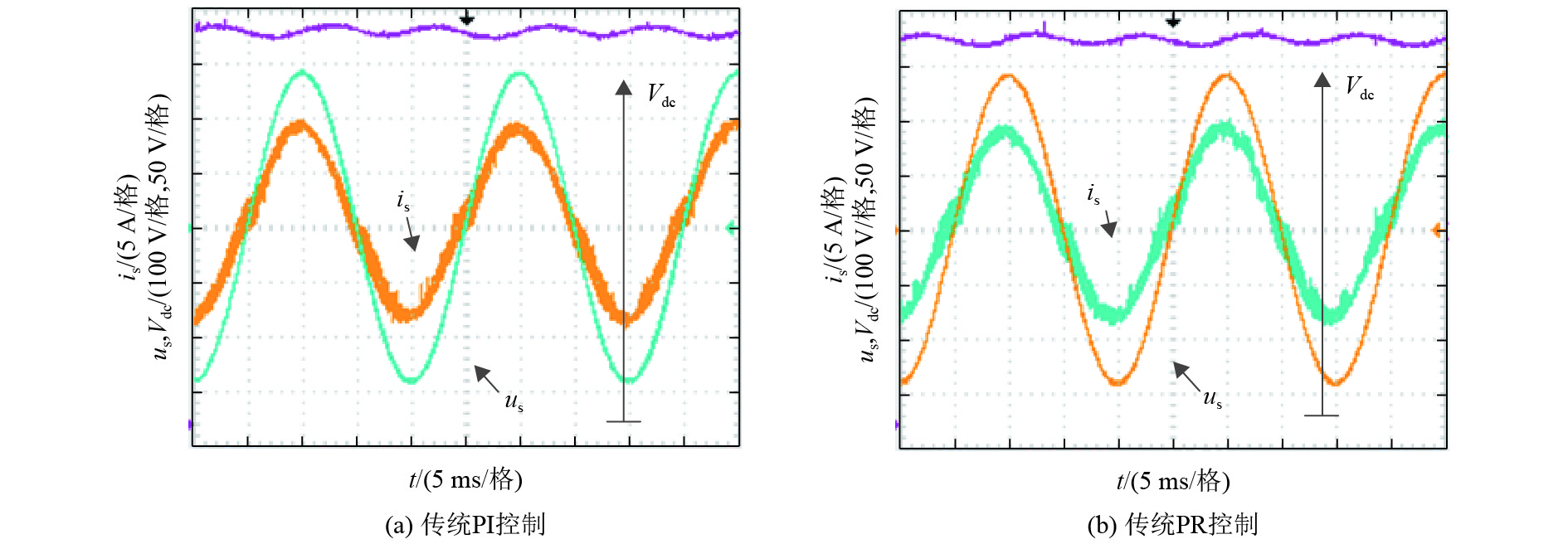
|
图 8 传统电流控制系统稳态实验 Figure 8 The steady-state experiment of traditional current control |

|
图 9 归一化模型系统稳态实验 Figure 9 The steady-state experiment of the normalized model system |
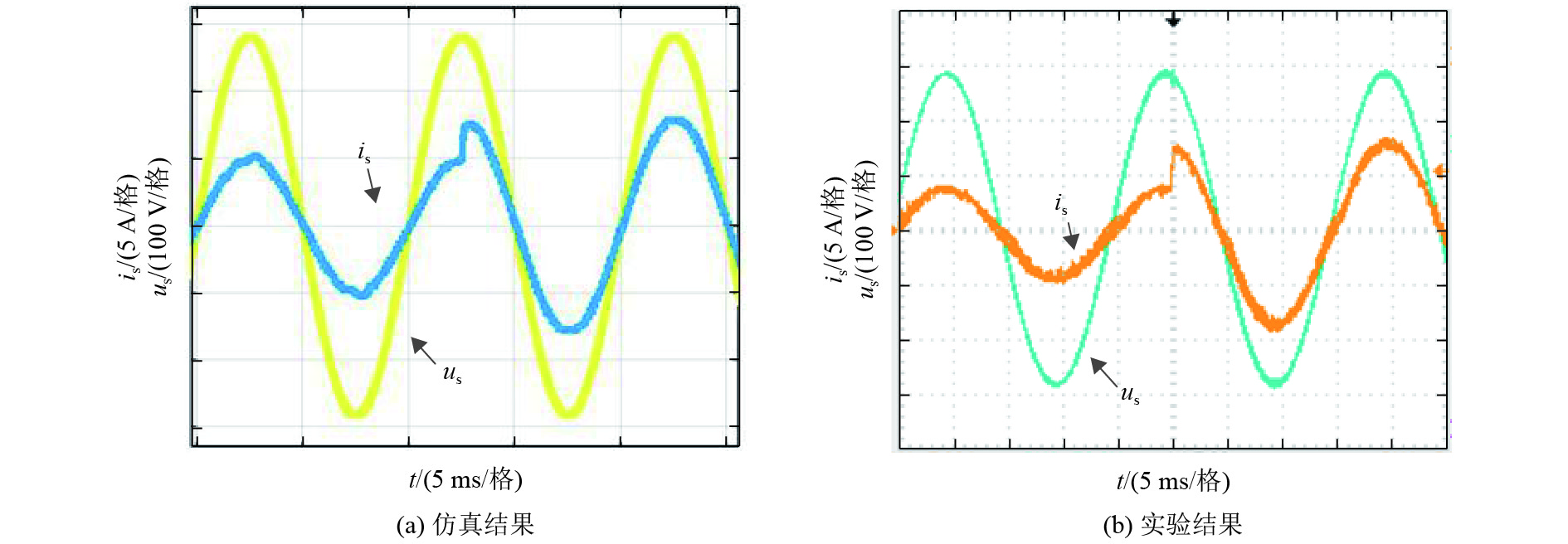
|
图 10 归一化模型系统动态实验 Figure 10 The dynamic experiment of the normalized model system |
由图8和图9对比分析,归一化模型的仿真和实验波形基本相似;由于归一化模型是由传统矢量控制系统(如图2所示)转化所得,故图8(a)与图9(b)实验结果基本相似;图8与图9(b)实验结果相比,改进的归一化模型实验结果相比于图8(a)、(b)都更平滑,验证了归一化模型相比于传统PR控制模型增加的部分,有利于提高系统对直流误差和噪声的抑制能力,使系统电流输出矢量更趋于正弦.
图9、图10可以看出,实验结果严格对应于仿真结果,证明所提出的虚拟电流控制策略的有效性及模型的准确性. 其中,由图9所示的稳态结果可以看出,改进的虚拟电流控制策略能够使系统工作在单位功率数条件下,且具有良好的稳态性能. 图10给出该控制策略的动态实验结果,由图10可得知,该控制策略能够快速响应功率给定信号的阶跃变化,具有系统动态过程短的特性.
4 结论本文对经典的旋转坐标系下的单相电压型PWM整流器电流内环控制进行了简化设计,建立了静止坐标系下的归一化模型;基于归一化模型改进和设计虚拟电流控制环节,并分析了归一化模型比传统PR控制模型增加部分对系统性能的影响;利用明确的准则配置归一化模型的控制器参数,给出参数设计表达式;实验结果验证了本文所提出模型及控制策略的可行性.
| [1] |
王兆安, 刘进军. 电力电子技术[M]. 5版. 北京: 机械工业出版社, 2009.
|
| [2] |
张兴, 张崇巍. PWM整流器及其控制[M]. 北京: 机械工业出版社, 2012.
|
| [3] |
张淼, 郭兴屹, 张兴旺. 基于状态反馈的单相LCL逆变器研究[J].
广东工业大学学报, 2018, 35(5): 60-64, 69.
ZHANG M, GUO X Y, ZHANG X W. Research on single phase LCL inverter based on state feedback abstract[J]. Journal of Guangdong University of Technology, 2018, 35(5): 60-64, 69. DOI: 10.12052/gdutxb.170165. |
| [4] |
刘和平, 邱斌斌, 彭东林, 等. 电流型脉宽调制整流器间接电流控制改进策略[J].
电网技术, 2012, 36(6): 182-187.
LIU H P, QIU B B, PENG D L, et al. An improved indirect current control strategy for current source PWM filter[J]. Power System Technology, 2012, 36(6): 182-187. |
| [5] |
郑俊, 冯晓云, 谢望玉, 等. 单相PWM整流器瞬态电流控制策略的研究[J].
电力电子技术, 2009, 43(12): 2-3.
ZHENG J, FENG X Y, XIE W Y, et al. The transient current control for single phase PWM rectifiers[J]. Power Electronics, 2009, 43(12): 2-3. DOI: 10.3969/j.issn.1000-100X.2009.12.002. |
| [6] |
唐雄民, 朱燕飞, 章云. 基于功率预测模型的单相PWM整流器直接功率控制[J].
控制与决策, 2012, 27(6): 845-849.
TANG X M, ZHU Y F, ZHANG Y. Model-based predictive direct power control of single-phase pulse width modulation rectifier[J]. Control and Decision, 2012, 27(6): 845-849. |
| [7] |
曹晓冬, 谭国俊, 王从刚, 等. 一种低开关频率PWM整流器的满意预测控制策略[J].
中国电机工程学报, 2013(27): 69-77.
CAO X D, TAN G J, WANG C G, et al. A research on low switching frequency PWM rectifiers with satisfactory and model predictive control[J]. Proceedings of the CSEE, 2013(27): 69-77. |
| [8] |
杜荣茂, 陈小强, 景利学. PWM整流器两种空间矢量控制策略的比较研究[J].
电气传动自动化, 2012, 34(3): 6-13.
DU R M, CHEN X Q, JING L X. Comparison research on two types of space vector control strategy of PWM rectifiers[J]. Electrical Drive Automation, 2012, 34(3): 6-13. DOI: 10.3969/j.issn.1005-7277.2012.03.002. |
| [9] |
张淼, 苏协飞. 基于比例谐振和谐波补偿控制技术的单相逆变并网研究[J].
广东工业大学学报, 2016, 33(5): 59-64.
ZHANG M, SUN X F. Research on proportional-resonant controller and harmonic compensation for grid-connected inverter[J]. Journal of Guangdong University of Technology, 2016, 33(5): 59-64. DOI: 10.3969/j.issn.1007-7162.2016.05.011. |
| [10] |
陶兴华, 李永东, 孙敏, 等. 一种基于同步旋转坐标变换的单相锁相环新算法[J].
电工技术学报, 2012, 27(6): 147-152.
TAO X H, LI Y D, SUN M, et al. A novel single-phase locked loop algorithm based on synchronous reference frame[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 147-152. |
| [11] |
ZMOOD D N, HOLMES D G, BODE G H. Frequency-domain analysis of three-phase linear current regulators[J].
IEEE Transactions on Industry Applications, 2001, 37(2): 601-610.
DOI: 10.1109/28.913727. |
| [12] |
宋修奎, 唐雄民, 章云, 等. 一种适合于单相电压型逆变电源的并联控制方案研究[J].
广东工业大学学报, 2015, 32(2): 79-85.
SONG X K, TANG X M, ZHANG Y, et al. A method of parallel control for single-phase voltage source inverters[J]. Journal of Guangdong University of Technology, 2015, 32(2): 79-85. DOI: 10.3969/j.issn.1007-7162.2015.02.015. |
| [13] |
KIM R Y, CHOI S Y, SUH I Y. Instantaneous control of average power for grid tie inverter using single phase D-Q rotating frame with all pass filter[C]//30th Annual Conference of IEEE Industrial Electronics Society. Busan, South Korea: IEEE, 2004: 274-279.
|
| [14] |
FRANCESCHINI G, LORENZANI E, TASSONI C, et al. Synchronous reference frame grid current control for single-phase photovoltaic converters[C] //2008 IEEE Industry Applications Society Annual Meeting. Edmonton, AB: IEEE. 2008: 1-7.
|
| [15] |
SARITHA B, JANKIRAMAN P A. Observer based current control of single-phase inverter in DQ rotating frame[C]// 2006 International Conference on Power Electronic. New Delhi: IEEE, 2007: 1-5.
|
| [16] |
ROSHAN A, BURGOS R, BAISDEN A C, et al. A d-q frame controller for a full-bridge single phase inverter used in small distributed power generation systems[C] //APEC 07-Twenty-Second Annual IEEE Applied Power Electronics Conference and Exposition. Anaheim, CA, USA: IEEE, 2007: 641-647.
|
 2019, Vol. 36
2019, Vol. 36
