随着多旋翼无人机的广泛应用,机载小型惯性导航系统逐渐成为人们的研究热点. 惯性导航系统主要由三轴陀螺仪、加速度计和磁力计构成,是无人机飞控获取自身姿态信息的主要来源和稳定飞行的保障[1],广泛应用于消费级、行业等领域无人机. 磁力计是测量磁场强度和方向,用于定位设备方位的模块,也称磁力仪或高斯计[2]. 磁力计在多旋翼无人机的惯性导航系统中提供绝对偏航信息,其精度决定了飞控姿态解算的精度,对无人机的飞行极其重要[3]. 地球磁场的强度约为50~60 μT,多旋翼无人机在飞行中其机载磁力计的测量精度会受到板载电路电磁特性、电机和空间环境磁场的干扰,导致飞控接收到错误的航向信息[4].
当有外部磁场干扰时,磁力计测量数据偏差较大,导致测量精确度下降. 对于磁力计的校准问题有一些学者进行了研究. 有学者针对三轴磁力计校正模型系数之间存在的相关性,提出的基于遗传算法三轴磁力计校正系数求解[5],很好地解决了磁力计校正系数之间的相关性问题,但该方法模型复杂、计算量大,实际效果不明确;有学者提出的一种基于最小二乘的磁力计椭球拟合静态校准方法[6],解决了一类静态校准问题. 有针对其他设备的磁力计的校准问题,提出的 “8”字旋转方式的动态校准方法[7],但是该方法对空中的机载磁力计的校准难以实现. 在已有的研究中,校准主要集中在静态校准,板载电路电磁特性干扰可以通过该方法进行修正校准[8],静态校准之后的磁力计数据会随时间积累产生偏移[9],同时电机和随机出现的环境磁场也将对磁力计产生干扰. 多旋翼无人机在空中飞行时的磁力计校准问题存在严重缺陷,因此动态实时校准的研究对多旋翼无人机安全稳定飞行具有重要意义.
本文针对上述问题,在多旋翼无人机静态校准的基础上提出一种自适应动态校准的方法. 该方法能有效解决多旋翼无人机磁力计的动态实时校准问题,使多旋翼无人机在空中飞行时能根据磁场环境的变化,实时校准磁力计,更新无人机航向信息.
1 小角度最小二乘迭代球心的动态校准多旋翼无人机在空中飞行时,没有外部磁场干扰的理想情况下,机载的磁力计只能感应到一个方向恒定指北的地球磁场[10],将机载磁力计绕三维空间的各个方向旋转360°,地球磁场将均匀分布在X、Y、Z轴上,磁力计的输出可以拟合成一个球心在坐标原点的标准圆球[11]. 由前文对载体周围磁场分析可得磁力计的数学模型:
| $ {{H}}_{{\rm{obs}}}^m = \left( {I + {C_i}} \right)\left( {{{H}}_{\rm{e}}^b + {{H}}_{\rm{p}}^b} \right), $ | (1) |
其中,
| $ \begin{split} &\left( {{{H}}_{{\rm{obs}}}^m} \right)\dfrac{{{{\left[ {{{\left( {I + {C_i}} \right)}^{ - 1}}} \right]}^{\rm{T}}}{{\left( {I + {C_i}} \right)}^{ - 1}}}}{{\left\| {{{H}}{{_{\rm{e}}^b}^2}} \right\|}}{{H}}_{{\rm{obs}}}^m -\\ & 2\dfrac{{{{\left( {{{H}}_{\rm{p}}^b} \right)}^{\rm{T}}}{{\left( {I + {C_i}} \right)}^{ - 1}}}}{{\left\| {{{H}}{{_{\rm{e}}^b}^2}} \right\|}}{{H}}_{{\rm{obs}}}^m +\dfrac{{{{\left( {{{H}}_{\rm{p}}^b} \right)}^{\rm{T}}}{{H}}_{\rm{p}}^b}}{{\left\| {{{H}}{{_{\rm{e}}^b}^2}} \right\|}} = 1. \end{split} $ | (2) |
由此可知,系统误差对磁力计输出的影响在解析几何上表现为使测量数据拟合结果由球体畸变成椭球,同时磁场干扰的影响,会使输出的坐标点发生偏移,拟合出的椭球中心点也对应偏移[13],偏移量大小代表了磁力计因周围磁场干扰产生的误差大小.
最小二乘拟合椭球的具体实现过程为:首先定义磁力计测量的值为
| $ {u_i} = {\left( {{x_i} - {x_0}} \right)^2} + {\left( {{y_i} - {y_0}} \right)^2} + {\left( {{z_i} - {z_0}} \right)^2} - {r^2}. $ | (3) |
令
| $ U = \mathop \sum \limits_{i = 1}^N u_i^2, $ | (4) |
根据最小二乘,将误差的平方和对所有未知量求偏导,并令偏导为0,即
| $ \frac{{\text{∂} U}}{{\text{∂} {X_0}}} = \frac{{\text{∂} U}}{{\text{∂} {y_0}}} = \frac{{\text{∂} U}}{{\text{∂} {z_0}}} = \frac{{\text{∂} U}}{{\text{∂} r}} = 0. $ | (5) |
求解可得拟合后椭球中心mr,即磁力计的零偏,将测量数据减去该零偏,即可完成磁力计的校准[14].
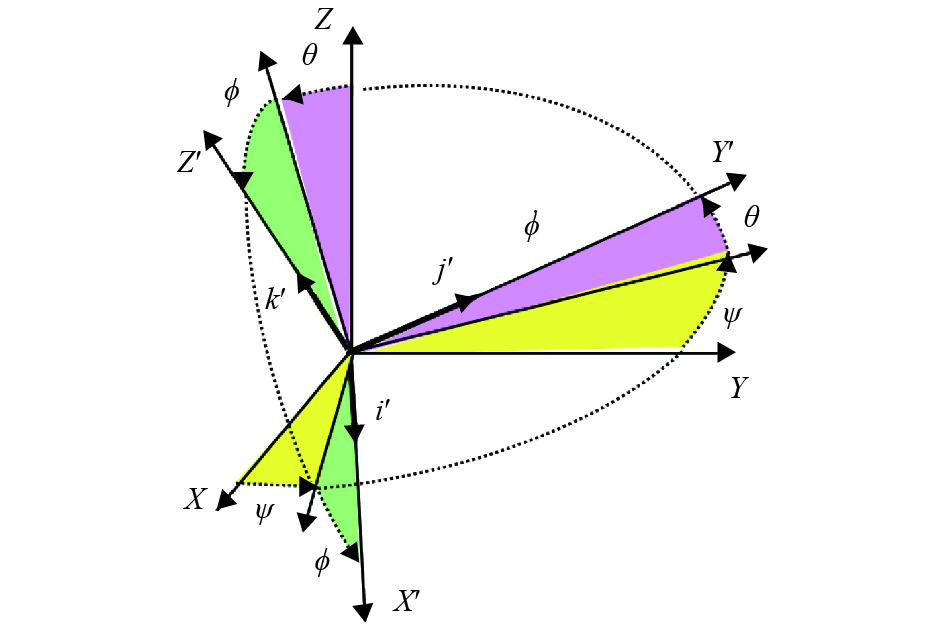
根据多旋翼无人机的飞行原理,其在空中稳定飞行时,机体会发生偏转. 如图1所示,无人机改变航向自旋时,机体坐标系相对于地球坐标系绕Z轴旋转ψ角;向左或右飞行,绕X轴旋转θ角;向前或后飞行时,绕Y轴旋转φ角. 区别于静态校准,无人机在空中稳定飞行过程中不可能实现空间各角度360°旋转,此动态校准过程中机体坐标系均绕X、Y、Z轴完成小角度的偏转. 利用无人机稳定飞行过程中的小角度偏转,磁力计实时生成磁场数据点.
|
图 1 小角度旋转示意图 Figure 1 The diagram of small angle rotation |
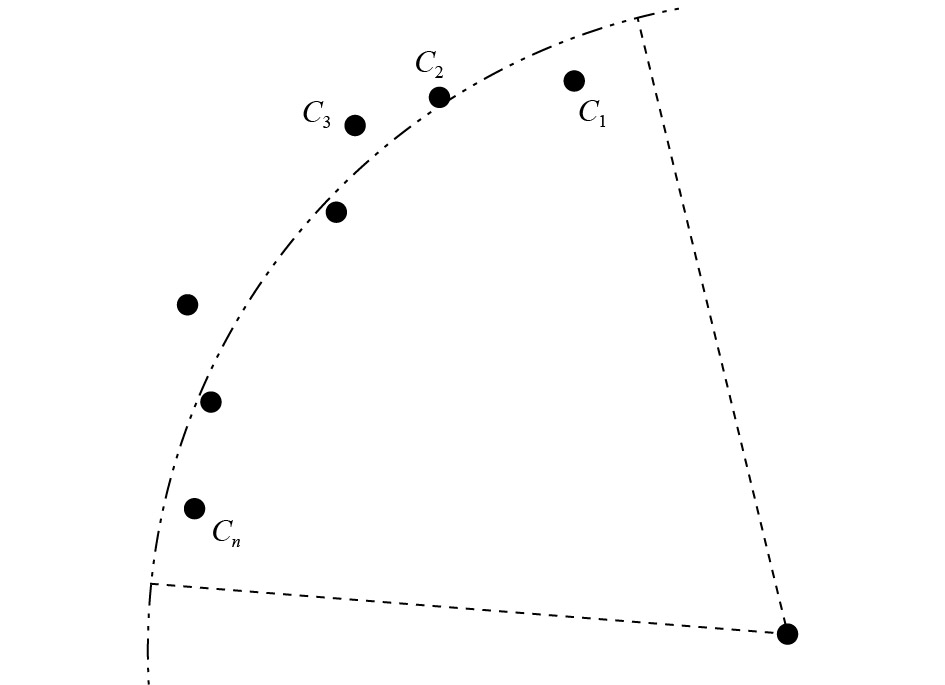
由于动态校准的磁场环境更加复杂,此方法对磁力计数据点的选取比静态校准更加严格,每两个数据点需大于10 μT,以此屏蔽掉合理数据点周围的大量噪声点[15]. 如图2所示,将数据点映射到平面来分析,选取n个合理的数据点C1到Cn,利用最小二乘将其拟合为一段弧,求取圆心. 将此平面拟合过程演绎到无人机机体坐标系中,则可得到拟合的部分球面,根据部分球面解算出球心,将下一时刻选取的n个磁力计合理数据点减去该球心坐标,得到新的数据点,即完成一次校准. 利用新的数据点进行最小二乘拟合,求得球心坐标,即可进行下一次校准.
此动态校准方法采用迭代的思想,每完成一次误差校准,数据点均进行一次更新,再取合理的数据点进行第2次误差校准,从而实现磁力计的实时动态校准.
|
图 2 最小二乘拟合示意图 Figure 2 The diagram of least squares fitting |
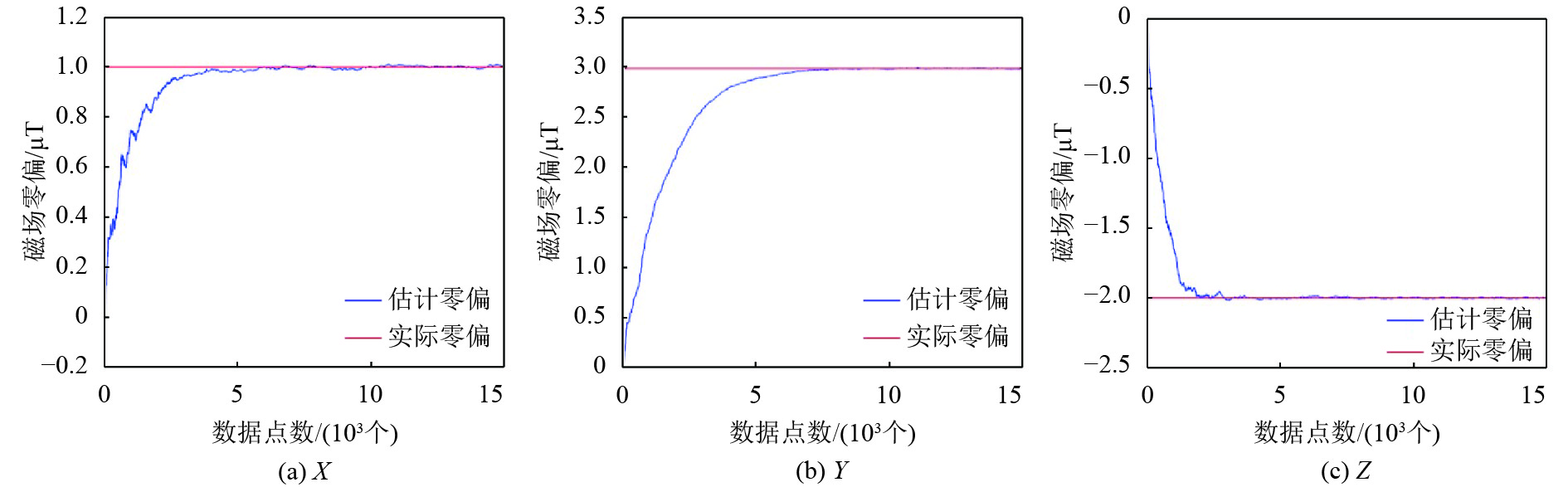
本文利用matlab仿真进行验证. 分别设置半径为20的球体在三维坐标的零偏,并随机生成15 000个数据点. 对这些数据进行加噪,噪声幅度为30%,利用该方法进行动态校准,如表1所示,随机预设置了3种零偏值,在未利用该方法进行动态校准时,matlab结算出的零偏与预设置零偏差距较大,与之对应采用该方法动态校准后,结算零偏和预设置零偏基本对应,且误差较小,可信度高. 图3为其中一组数据点追踪零偏的情况,从图中可看出数据点在3个轴向均能快速响应,准确追踪到对应零偏. 因此在仿真环境下,该方法能准确有效解算出磁力计零偏,从而实现磁力计动态校准.
| 表 1 三轴零偏及误差 Table 1 The zero offset and error of three axis |
|
图 3 三轴估计零偏 Figure 3 The estimated zero offset of three axis |
本实验采用的是以STM32F4系列芯片为主控的无人机飞控平台,磁力计采用的是LSM303DTR,包含一个三轴磁力计和一个三轴加速计,采用数字接口. 磁力计的测量范围从130 μT到810 μT共分7档,用户可以自由选择. 并且在2000 μT以内的磁场环境下都能够保持一致的测量效果和相同的灵敏度[16]. 它的分辨率可以达到0.8 μT,并且内部采用12位ADC,以保证对磁场强度的精确测量. 与采用霍尔效应原理的磁力计相比,LSM303DTR的功耗低,精度高,线性好,并且不需要稳定补偿.
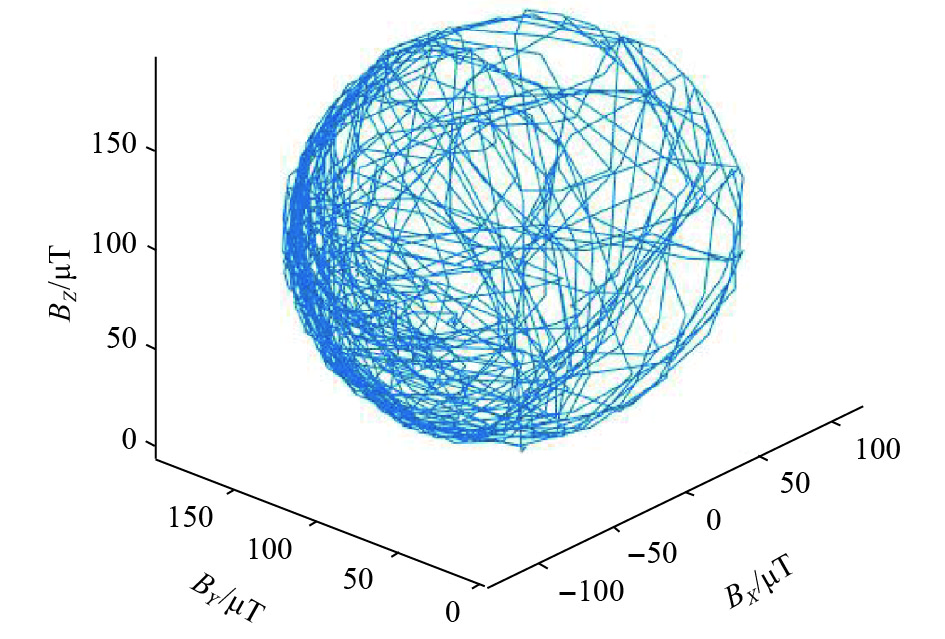
本文选取空旷实验场地,周围磁场环境较为纯净. 采用传统的USB数据线将无人机飞控与电脑端地面站连接,地面站采集飞控收集的磁力计数据,采样频率为10 Hz,并将数据保存于电脑,为避免电脑磁场干扰,数据线长度为2 m以上[17]. 将无人机飞控在空间进行小角度倾转,磁力计的数据通过飞控传输到地面站,收集到10 897个数据点,利用matlab将所有数据点连接起来,其在三维坐标中的分布如图4所示.
|
图 4 磁力计输出数据分布 Figure 4 The data distribution of magnetometer output |
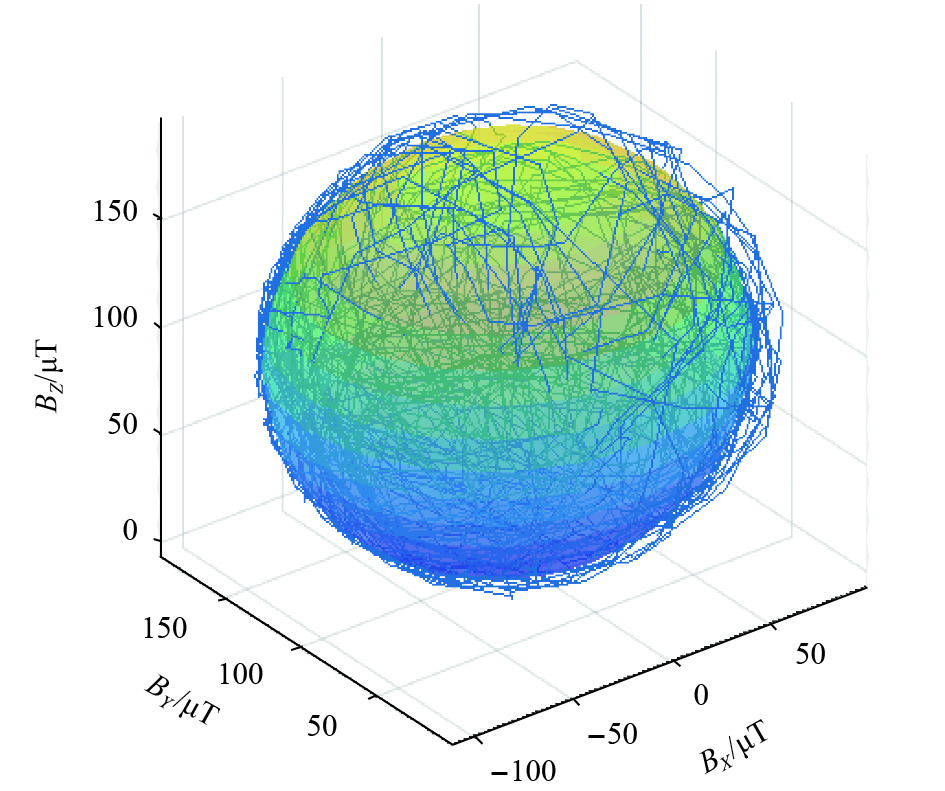
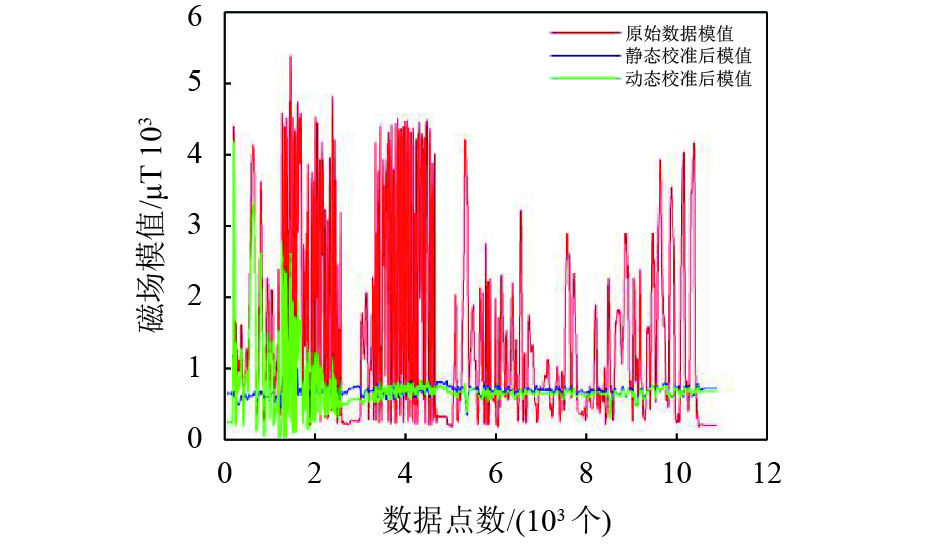
由上文分析知小角度最小二乘拟合迭代算法对合理数据点的选取要求严格,将合理数据点拟合可得椭球体,不满足要求的噪点则杂乱无章地分布在椭球体表明附近,如图5所示. 利用小角度最小二乘拟合迭代的动态校准后可得出球心坐标为(9.89, 959.91, 940.26),即为三轴零偏,符合理论分析及仿真结果. 如图6所示,在多旋翼无人机机载设备及周围磁场的影响下,实际测量磁场模值波动较大,主要表现在2 700个数据点之前,随着数据点的增加,迭代的作用逐渐显现,动态校准后的模制能很好地跟随静态校准的结果,并趋于稳定,并且在3 000数据点附近. 本文将飞控移入另一个环境,此时动态校准仍能很好抵抗噪声干扰,模值保持较低值且未出现波动. 因此多旋翼无人机在空中飞行无法进行三维空间任意旋转校准的情况下,可利用本文提出的小角度最小二乘迭代法实现多旋翼无人机动态实时校准.
|
图 5 椭球拟合结果 Figure 5 The result of ellipsoid fitting |
|
图 6 校准前后磁场模值 Figure 6 The variation of magnetic field modulus before and after calibration |
本文在多旋翼无人机静态校准的基础上,提出了一种小角度最小二乘迭代的动态校准方法. 根据仿真结果,该动态校准方法在3个角度能较好地跟踪预设置的零偏误差,且误差很小. 从实验结果可得出该方法在多旋翼无人机的磁力计动态校准过程中能达到静态校准的效果,动态校准的模值最终趋于稳定与静态校准模值相同. 本文提出的小角度最小二乘迭代法能快捷有效地解决多旋翼无人机的动态校准问题,进一步减少周围磁场环境对磁力计测量数据的影响,从而提高多旋翼无人机磁力计的自适应能力. 该方法校准效果好,易于实现,能广泛应用于多旋翼无人机磁力计的动态校准.
| [1] |
NGUYEN K D, HA C. Development of hardware-in-the-loop simulation based on gazebo and pixhawk for unmanned aerial vehicles[J].
International Journal of Aeronautical and Space Science, 2018, 19(1): 238-249.
DOI: 10.1007/s42405-018-0012-8. |
| [2] |
EZEQUIEL C A F, CUA M, LIBATIQUE N C, et al. UAV aerial imaging applications for post-disaster assessment, environmental management and infrastructure development[C] //Proceedings of International Conference on Unmanned Aircraft Systems. New York: IEEE, 2014: 274-283.
|
| [3] |
LI W, LIU M H, GONG D P, et al. Huber-based divided difference filter with application to relative navigation[J].
Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2013, 228(9): 1475-1486.
|
| [4] |
HEEKWON N, CHO A, KEE C. New compensation method of magnetometer time-varying bias for UAV[J].
Institute of Navigation Technology, 2018, 29(6): 529-541.
|
| [5] |
庞学亮, 林春生. 基于遗传算法三轴磁传感器校正系数求解[J].
探测与控制学报, 2017, 39(1): 42-45.
PANG X L, LIN C S. Calibration coefficients solving of three-axis magnetic sensor based on genetic algorithm[J]. Journal of Detection & Control, 2017, 39(1): 42-45. |
| [6] |
FANG J, SUN H, CAO J, et al. A novel calibration method of magnetic compass based on ellipsoid fitting[J].
IEEE Transactions on Instrumentation & Measurement, 2011, 60(6): 2053-2061.
|
| [7] |
刘宇, 陈永炜, 路永乐. 基于最小二乘的磁力计误差补偿与校准[J].
导航定位与授时, 2018, 1(5): 17-21.
LIU Y, CHEN Y W, LU Y L. Research on error compensation and calibration of magnetometer based on least square method[J]. Navigation Positioning & Timing, 2018, 1(5): 17-21. |
| [8] |
程华富. 磁传感器温度特性校准装置研究[J].
电测与仪表, 2012, 49(10A): 45-49.
CHENG H F. Calibration device for temperature property of magnetic sensors[J]. Electrical Measurement & Instrumentation, 2012, 49(10A): 45-49. |
| [9] |
WU Y X, LUO S T. On misalignment between magnetometer and inertial sensors[J].
IEEE Sensors Journal, 2016, 16(16): 6288-6297.
DOI: 10.1109/JSEN.2016.2582751. |
| [10] |
BONNET S, BASSOMPIERRE C, GODIN C, et al. Calibration methods for inertial and magnetic sensor[J].
Sensors & Actuators A Physical, 2009, 156(2): 302-311.
|
| [11] |
李勇, 刘文怡, 李杰, 等. 基于椭球拟合的三轴磁传感器误差补偿方法[J].
传感器技术学报, 2012, 25(7): 918-920.
LI Y, LIU W Y, LI J, et al. Error compensation method for three-axis magnetic sensor based on ellipsoid fitting[J]. Chinese Journal of Sensors and Actuators, 2012, 25(7): 918-920. |
| [12] |
ROHAC J, SIPOS M, SIMANEK J. Calibration of low-cost triaxial inertial sensors[J].
Instrumentation & Measurement Magazine IEEE, 2015, 18(6): 32-38.
|
| [13] |
郭鹏飞, 华春红, 任章, 等. 基于递推最小二乘的航姿系统罗差校准[J].
中国惯性技术学报, 2008, 16(1): 24-27.
GUO P F, HUA C H, REN Z, et al. Magnetic deviation compensation using recursive least square for AHRS[J]. Journal of Chinese Inertial Technology, 2008, 16(1): 24-27. |
| [14] |
闫蓓, 王斌, 李媛. 基于最小二乘法的椭圆拟合改进算法[J].
北京航空航天大学学报, 2018, 34(3): 295-298.
YAN B, WANG B, LI Y. Optimal ellipse fitting method based on least square principle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 34(3): 295-298. |
| [15] |
WUY X, SHI W. On calibration of three-axis magnetometer[J].
IEEE Sensors Journal, 2015, 15(11): 6424-6431.
DOI: 10.1109/JSEN.2015.2459767. |
| [16] |
刘建敬, 陈丽, 汪冬瑾, 等. 三轴磁传感器的校正方法[J].
现代电子技术, 2018, 41(9): 179-181.
LIU J J, CHEN L, WANG D J, et al. Correction method of 3-axis magnetic sensor[J]. Modern Electronics Technique, 2018, 41(9): 179-181. |
| [17] |
LI X, LI Z. A new calibration method for tri-axial field sensors in strap-down navigation systems[J].
Measurement Science and Technology, 2012, 23(10): 12-16.
|
 2019, Vol. 36
2019, Vol. 36

