经济全球化的发展,使恐怖袭击呈现出全球化的发展态势,其形式、手段等都存在明显的多样化. 恐怖袭击是人类的共同威胁,它不仅会对国际社会的稳定、人们生命财产安全造成严重影响,还会给人们带来巨大的心理压力. 恐怖袭击具有极大的危害性和破坏力,会造成国际社会一定程度的动荡不安,妨碍人们正常的生产和生活秩序,进而阻碍经济建设与发展. 恐怖袭击已成为国际社会和平与安全的最大威胁之一,并成为全球的关注热点,反恐已然成为一项刻不容缓的任务[1]. 数据挖掘技术已经广泛应用于电信[2]、金融[3]、医药[4]等领域,如何将此项技术应用于公共安全领域变得愈加重要.
恐怖袭击具有复杂性,形式、手段等都存在明显多样化的特点,因而决定了反恐是一项长期的复杂工作. 恐怖袭击行为总是有迹可循的,通过对历年来发生的恐怖袭击案件进行梳理和总结,可以发现同一恐怖团伙实施的恐怖袭击案件在细节上存在许多相似之处,而不同恐怖团伙实施的恐怖袭击案件却有显著的不同,这是由恐怖团伙自身的特点决定的[5]. 根据同一恐怖团伙实施的恐怖袭击事件相似度高,不同团伙实施的恐怖袭击事件差异度明显的特点,利用聚类分析算法[6]对反恐情报进行分析,可以提升反恐部门打击恐怖活动的效能.
基于此,本文采用美国马里兰大学搜集并构建的全球恐怖主义数据库[7](Global Terrorism Database,GTD)中的2015年和2016年的恐怖袭击数据,提出了改进的聚类算法,引入深度自编码器,将稀疏和嘈杂的原始数据映射为类内紧凑平滑的数据,提升了聚类分析效果. 实验结果表明,改进后的算法可以提高聚类分析效果,能把相似的恐怖袭击事件进行快速分组归类,从而提高反恐案件的侦破效率,有利于尽早发现新生或者隐藏的恐怖分子.
1 相关工作恐怖袭击的问题由来已久,且有向全球化发展的态势. 为了应对日益严峻的反恐态势,众多学者投身致力于反恐任务的研究. Peter 等[8]于2006年设想搭建全球反恐主义信息网,并通过数据挖掘技术完善其准确度. Chen等[9]则通过自然语言处理技术对生化恐怖主义进行了深入研究. Wang等[10]根据全球恐怖主义数据库中记载的历史恐怖袭击事情数据,提出了一个视觉分析系统,分析人员可以用可视化分析模型去描绘事件的基本信息. Jones J等[11] 为了发现隐藏在全球恐怖主义数据库中的知识和行为模式,建立了一个图相关的线索. 颜峻[12]于2009年利用数据挖掘技术,从时间和空间的维度,对恐怖主义信息进行分析和研究. 彭如香等[13]把恐怖主义数据库中2001年至2016年的数据进行定量分析和可视化分析,呈现出全球恐怖袭击活动的发展现状和蔓延态势,指出了下一步反恐工作需要关注的问题;李勇男等[14]提出了对涉恐情报数据进行ROCK聚类,对未知涉恐人员数据进行预测分组.
综上所述,对恐怖袭击与恐怖主义数据的研究,限于安全等各种因素,对袭击方式与特点分析、风险评估、应急处理的报道较多,但对数据深入分析,把相似的恐怖袭击事件进行分组归类,并对恐怖事件的归属进行标签化的有关文献尚不多见. 基于此,本文首先对数据进行深度自编码表征[15],并尝试应用较为广泛的大众化方法——改进的K-means聚类算法进行分析,以获得较好而又普遍的聚类效果,进而将无标签恐怖袭击数据按概率形式进行标签化. 以便有利于反恐分析人员将相似案件并案分析处理,找到案件的犯罪同伙及团伙. 实验数据表明,相比于传统的K-means聚类算法,改进后的算法可以进一步提高聚类效果,能把相似的恐怖袭击事件进行分组归类,这将为反恐情报部门预警提供支持,从而提高相应部门的决策能力.
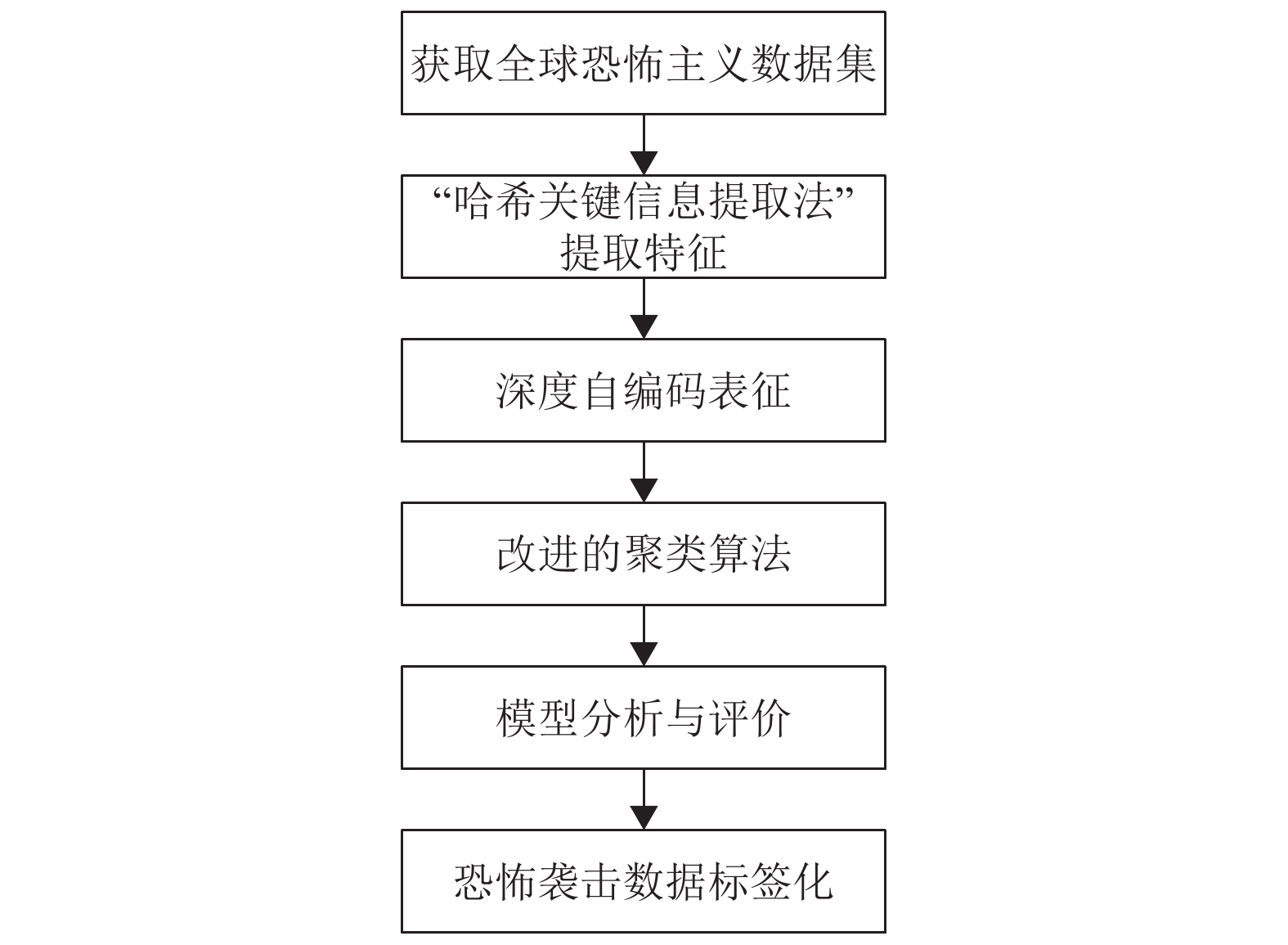
2 深度自编码表征的改进聚类算法本节针对全球恐怖主义数据库,提出了基于深度自编码表征的改进的聚类分析方法,具体分析过程如图1所示.
|
图 1 分析过程 Figure 1 Analytical procedure |
本文采用美国马里兰大学搜集并构建的全球恐怖主义数据库[7]中的2015年和2016年的恐怖袭击数据作为原始的数据集,每条数据有125个属性,记录了其发生地点、时间、运用的武器、袭击事件的伤亡数量、可确定的责任方、袭击目标特点等特征.
2.2 数据提取与整理本文从描述恐怖袭击事件的125个属性中,归纳出32个对恐怖袭击事件起关键性作用的指标. 对于可以量化的指标,直接进行处理. 对于没有量化的指标,为了准确性,寻找本校政法学院相关专业老师、教授对这些指标进行评价,得到的评价标准如表1所示.
| 表 1 哈希指标界定表 Table 1 Hash indicator definition tabl |
本节主要从以下5个关键因素对恐怖袭击事件的特征进行分析、整理和归纳,包括时间要素、危害程度、影响范围、社会影响、武器类型和攻击类型. 下面从中选取4个指标进行简要的说明:(1) 节假日:恐怖袭击倾向于发生在节假日,于是设定其为评价指标,判断条件是“以袭击的发生日期判断是否在节假日”,如果发生日期在节假日,则赋值为1,反之赋值为0. (2) 持续时间:恐怖袭击是有组织、有预谋的活动,往往持续时间比较长,于是把“持续时间”设为评价指标,判断条件是“判断袭击持续时间是否超过24小时”,如果袭击持续时间超过24小时,则赋值为1,反之赋值为0. (3) 绑架人质结果:恐怖组织在发动恐怖袭击的时候往往伴随着人质绑架事件,而且人质的生还率很低. 因此把“绑架人质结果”设为评价指标,判断条件是“以袭击中人质是否成功生还判断”,如果袭击中人质成功生还,则赋值为0,反之赋值为1. (4) 逃脱获释数量:手无寸铁的平民在遭受恐怖组织的挟持或者绑架的时候,往往逃脱的几率是很低的. 于是把“逃脱获释数量”设为评价指标,判断条件是“以袭击中逃脱获释的人质数量多少判断”,如果袭击中逃脱获释的人质数量超过预定的阈值,则赋值为0,反之赋值为1.
在特征处理方面采用“哈希关键信息提取法”,用“0”、“1”记录某个属性的特征,这不仅仅使得后期处理方便,也让模拟过程速度有了极大的提升,运算过程中内存占用极少.
本文根据表1的评价标准将每一条恐怖袭击数据转化成32维、由“0”或“1”组成的向量. 数据库中的“gname”属性记录了凶手所在犯罪集团的名称,若该属性值为“Unknown”,则表示发动此次恐怖袭击的凶手所在的犯罪集团是未知的,而属性值为“Unknown”的数据就是本文中需要标签化的数据,属性值为犯罪集团名称的数据将作为本文恐怖袭击事件的标签数据.
2.3 深度自编码表征传统的聚类算法,如K-means聚类算法,是根据输入数据之间的某种距离来确定出簇. 此外,传统聚类算法的聚类规则缺乏自学习性质. 因此,通过具有自学习能力的算法将各个簇的数据映射得更紧凑,这样相当于提前训练了一个类似于聚类策略的算法,从而有助于改善传统聚类效果. 一般的输入数据具有稀疏和嘈杂的特点,最后是通过自学习算法得到类内更紧凑的更平滑的聚类算法输入数据.
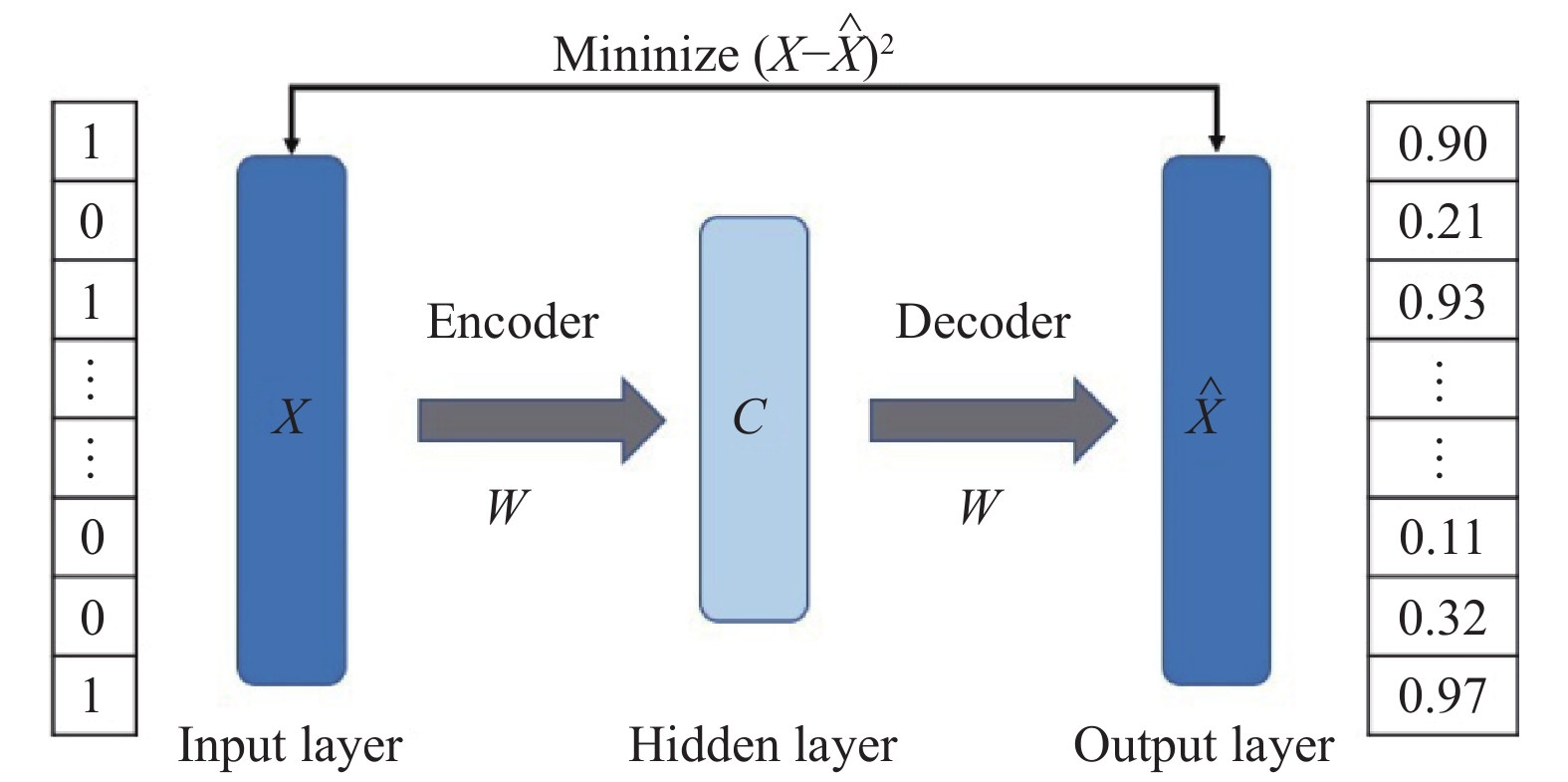
本文提出的深度自编码器将稀疏和嘈杂的原始数据映射为类内紧凑平滑的数据,如图2所示,深度自编码器由编码器(Encoder)和解码器(Decoder)组成,其结构是输入层、隐藏层和输出层的串联结构. 隐藏层一般由全连接层组成. 编码器负责学习输入数据的特征,解码器负责将编码器学习到的特征恢复为原来的样子. 网络在训练的时候最小化输入向量和输出向量的差的平方,网络最终使输入向量和输出向量尽可能相似. 深度自编码算法是一种无监督算法,它能够学习原始数据的内部特征,异化数据之间的特征距离. 图2中最左侧的数据是由“0”或“1”组成的32维向量,这个向量是由原始的恐怖袭击数据经过“哈希关键信息提取法”的评价标准转化得到的,此向量作为深度自编码器的输入数据;而最右侧的数据是深度自编码器的输出数据,也是32维的向量,即为输入数据的深度自编码表征形式.
|
图 2 深度自编码器 Figure 2 Deep self-encoder |
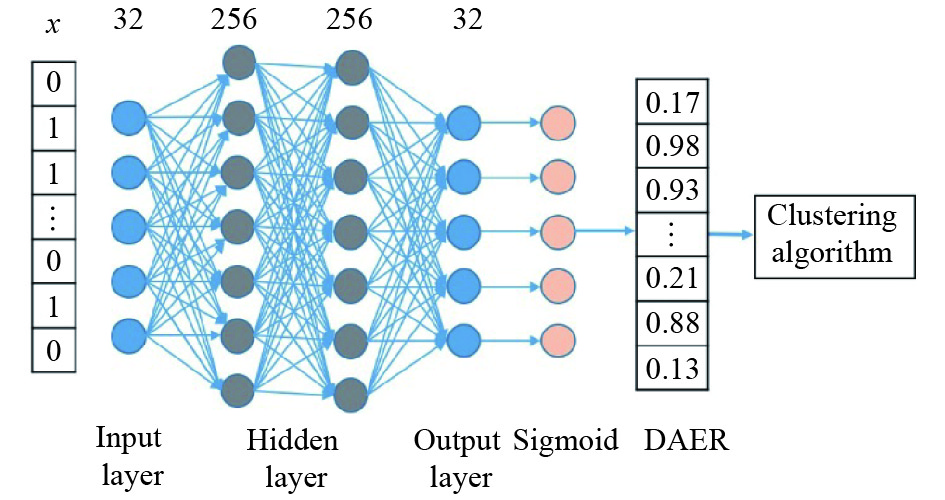
图3展示了自编码器的结构和参数,其由32个节点的输入层、输出层和两层拥有256个节点的隐藏层组成. 输出层由Sigmoid函数激活,其他层则由Relu函数激活. 网络的输出就是原始数据的深度自编码表征形式,作为聚类算法的输入. 图3中最左侧的数据是深度自编码器的输入数据,最右侧的数据是深度自编码器的输出数据,即为输入数据的深度自编码表征形式.
|
图 3 深度自编码器的结构和参数 Figure 3 Structure and parameters of the depth self-encoder |
虽然深度自编码器是使输入向量与输出向量越来越接近,但是,输出向量与输入向量太接近显然是没有多大意义的. 本文提出的深度自编码表征,是通过深度自编码器学习到的具有数据内部结构化且数据间差异化的向量表征. 因此,在数据输入前加入正态化的噪声,即图3中x为x+noisy. 因为训练loss越小,说明输入向量与输出向量越接近,所以在训练网络时,当loss下降到快要平稳前就停止. 这样,模型训练的时候既学习到了原始数据的特征,又不会恢复到原始的粗糙数据,因此原始数据就被映射到一个类内更紧凑的空间.
2.4 改进的聚类算法根据对K-means算法的初始聚类中心的选取和输入数据自编码学习的改进,得到基于深度自编码表征的K-means聚类算法.算法具体流程如下:
输入:经过“哈希关键信息提取法”处理的数据集X.
输出:数据聚类划分.
Step1:将数据集X输入到深度自编码器进行学习,得到数据集Y;
Step2:取数据量大于10的犯罪集团的类别数K作为聚类数目;
Step3:随机选取K个初始聚类中心;
Step4:遍历数据集Y中所有数据,采用欧氏距离,将每个数据划分到最近的中心点中;
Step5:计算每个聚类的平均值,并作为新的中心点;
Step6:重复Step4和Step5,直到聚类中心不再发生变化,算法停止;最终得到K个簇.
3 恐怖数据标签化依据上节的聚类结果按簇对恐怖数据库中的无标签数据进行相似度匹配,然后按概率打分判定其可能归属的犯罪集团. 标签化算法如下:
Step1:随机取出数据库中的无标签数据;
Step2:计算无标签数据与上节聚类出来的每一个簇中心的距离;
Step3:选取距离最小的簇,查看簇中出现的犯罪集团类别和数目,计算每个犯罪集团出现的数目占总数的比率;
Step4:按概率打分判定此条数据可能归属的犯罪集团;
Step5:再次执行上述4个步骤,直到取完所有的无标签数据,过程结束.
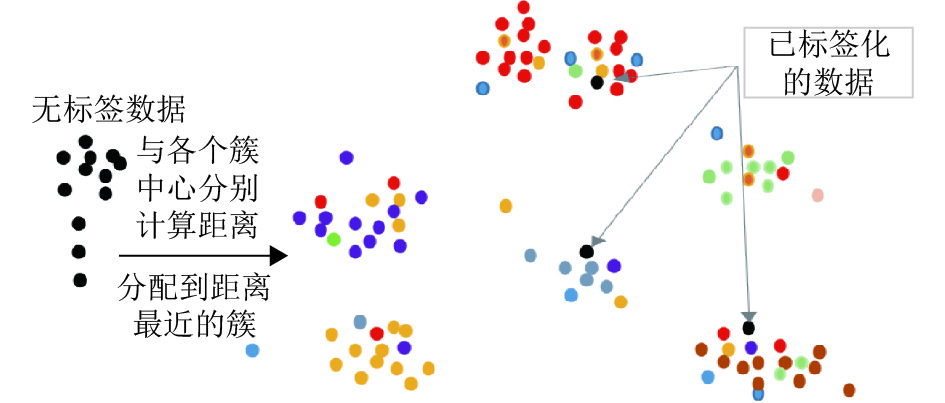
对恐怖数据库的标签化结果示意图参见图4.
|
图 4 无标签数据的相似度匹配 Figure 4 Similarity matching for unlabeled data |
由于本文的数据集标签是犯罪集团名字“gname”,但是聚类是一种无监督方法. 因此,在聚类过程中并未用到标签. 本文聚类结果的标签是在簇上打标签,然后在测试过程中根据这些标签来计算准确率.
本文对簇打标签的方法如下:(1) 统计簇中出现犯罪集团名称的总个数N. (2) 统计每个集团各自出现的个数M. (3) 在这个簇中,以集体出现个数最大为首个基准,计算集体个数排名第二占集体个数排名第一的比例,若比例大于70%,则计算集体个数排名第三占集体个数第二的比例,若比例大于70%,则继续往下类推,最多计算的集体个数排名第五的情况. 在此推算过程中只要比例未达到70%或已到犯罪集团数极限,则停止计算,并记录已计算的集体名称. (4) 在(3) 中记录的集体名称,就是该簇的标签,一个簇至少有1个标签,最多有5个标签.
如果现有测试数据n个,测试方法如下:
Step1:用测试数据逐条与每个簇的中心计算距离,把数据分配给距离最近的簇.
Step2:对比测试数据的标签与簇的标签,只要测试数据标签在簇的标签中,就算正确,否则错误.
Step3:历遍这个测试集,得到正确的数据个数为m.
则准确率计算如公式(1):
| $ {\rm{Accuracy}}=\frac{m}{n} \times 100\,\%. $ | (1) |
为了验证本文提出方法的有效性,本文对两个算法进行了比较实验,包括传统的K-means聚类算法和基于深度自编码表征的改进的聚类算法.
4.1 实验数据本文采用美国马里兰大学搜集并构建的全球恐怖主义数据库中的2015年和2016年的恐怖袭击数据作为原始的数据集,并采用了“哈希关键信息提取法”对原始数据进行了提取和整理.
4.2 评价指标本文采取了以下3种评价指标,包括Silhouette Coefficient,Calinski-Harabasz Index和准确率. 其中,Silhouette Coefficient和Calinski-Harabasz Index作为聚类效果好坏的评价标准,无需先验知识,直接从簇内的稠密程度和簇间的离散程度来评估聚类的效果,分数越高,聚类效果越好.
Silhouette Coefficient[16]的评分越高,聚类效果越好. 假设已经通过聚类算法将数据聚类到k集群. 对于每个数据i,a(i)是两者之间的平均距离i和同一群集中的所有其他数据. 可以解释a(i)作为一种衡量标准i被分配给它的集群(值越小,分配越好). 然后定义点的平均差异i到集群c作为距离的平均值i到了所有的点c.
b(i)是最小的平均距离i到任何其他群集中的所有点,其中i不是成员. 具有这种最小平均差异的群集被称为“邻近群集” i因为它是下一个最适合点的集群i. 现在定义一个轮廓,计算见公式(2):
| $ S(i)=\frac{b(i)-a(i)}{\max \{a(i), b(i)\}}. $ | (2) |
类别内部数据之间的协方差越小,不同类别数据之间的协方差越大,这样的Calinski-Harabasz[17]分数会越高,聚类效果会更好. Calinski-Harabasz分数值的数学计算公式(3):
| $ s(k)=\frac{\operatorname{Tr}\left({ B}_{k}\right)}{\operatorname{Tr}\left({ W}_{k}\right)} \cdot \frac{m-k}{k-1}. $ | (3) |
其中m为训练集样本数,k为类别数. Bk为类别数据之间的协方差矩阵,Wk为类别内部数据之间的协方差矩阵. Tr为矩阵的迹.
4.3 实验结果在实验之前,本文先将数据集分成训练集和测试集. 数据集划分方法是按照每个犯罪集体内的70%的数据为训练集,剩余的为测试集. 由于犯罪集团出现次数差异巨大,出现较少的数据将被视为干扰数据. 本文将犯罪集团出现次数小于10 的数据视为干扰数据,这些数据将不用在实验中. 此时,数据集中的犯罪集团类别个数为144,亦即数据集中标签个数为144.
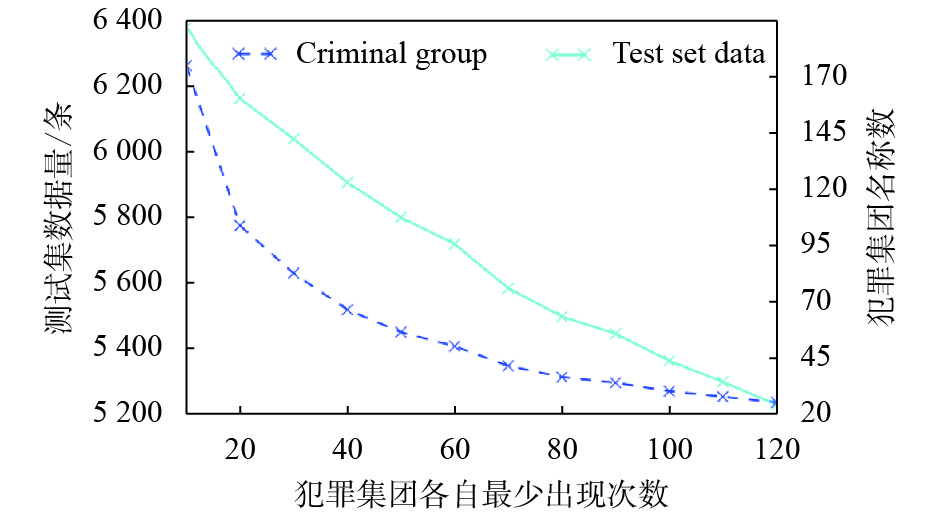
最后训练集数据为15 107条,测试集数据变化如图5所示. 图5中X轴是数据集中犯罪集团各自最少出现次数的变化刻度,左Y轴是测试集数据量变化刻度,右Y轴是犯罪集团个数变化刻度. 由图可以看到,当犯罪集团的最少出现次数从10递增到120时,测试集数据量从6 380条递减到5 227条,而犯罪集团名称个数由144个递减到24个. 可看到,犯罪集团类别个数急剧下降,而数据量比例并没有急剧下降. 由于实际情况并不会有那么少的犯罪集团,因此本文只将犯罪集团的最少出现次数取到120.
|
图 5 测试集数据量和犯罪集团个数变化 Figure 5 The amount of data in the test set and the number of criminal groups |
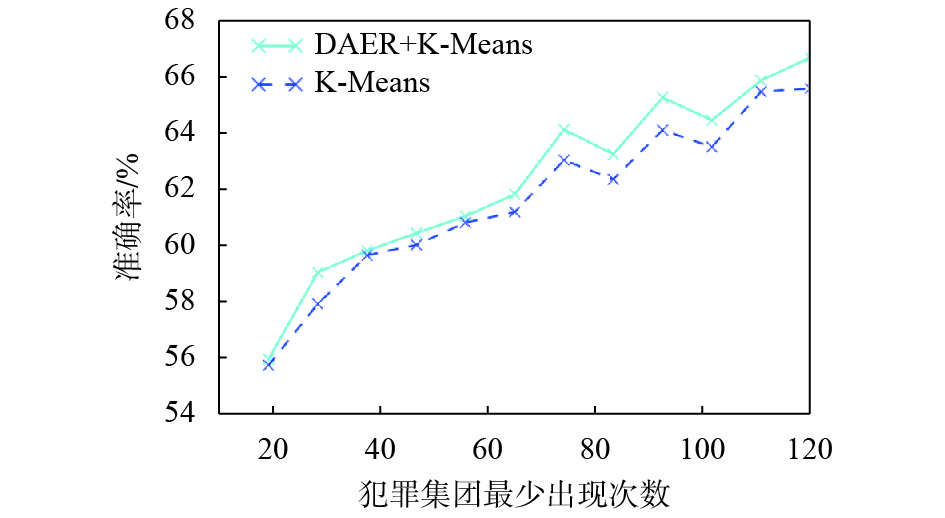
如图6所示,改进算法的准确率都要高于传统K-means聚类算法. 两种算法的准确率都随着犯罪集团最少出现次数增加而增加,其中准确率最高的是犯罪集团最少出现次数为120的时候,此时传统的K-means聚类算法的准确率为65.58%,而基于深度自编码表征的K-means聚类算法的准确率却达到了66.69%,比传统的K-means聚类算法高出了1.11%.
|
图 6 准确率对比 Figure 6 Comparison in accuracy |
因为聚类个数是需要得到的重要指标,同时K-means算法需要预先设定聚类个数,即K值,所以在本实验中我们调节的自变量是聚类个数. 我们将观察不同聚类个数的Calinski-Harabaz Score和Silhouette Score,以寻找到适合的聚类个数.
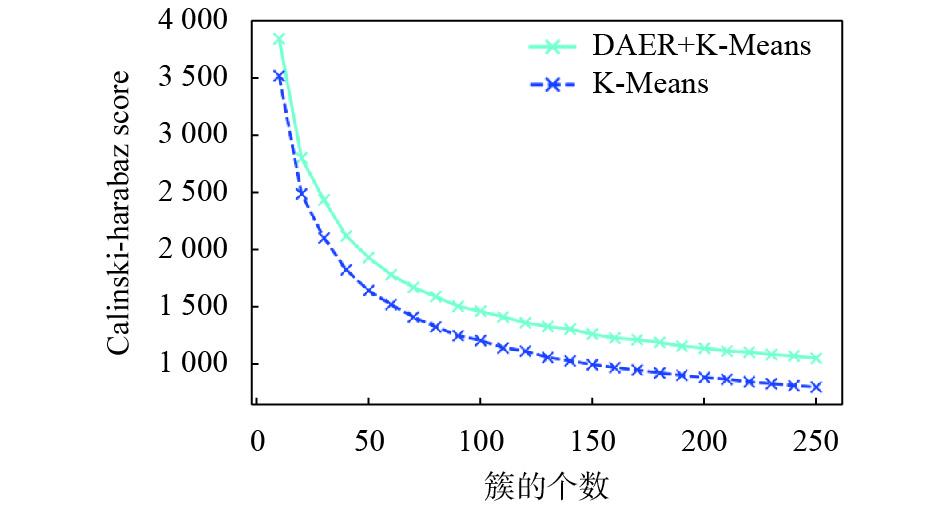
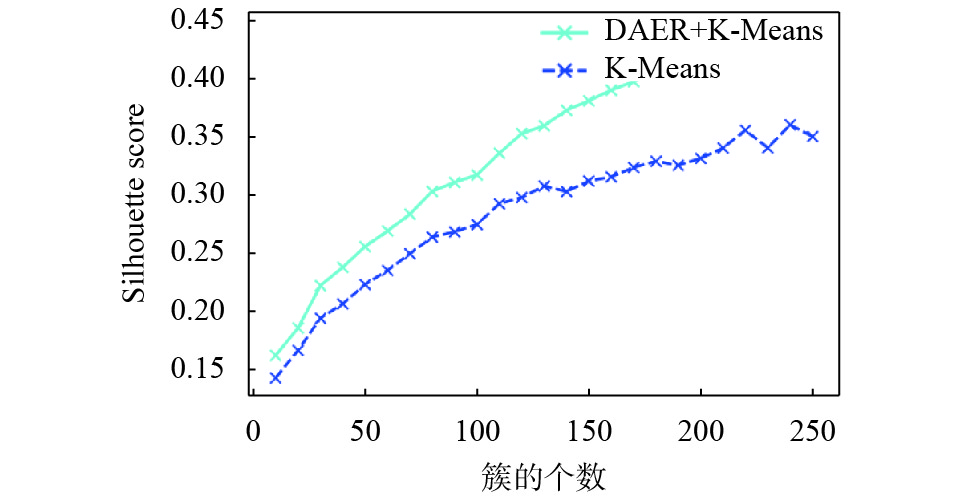
如图7和图8所示,横轴是K值自变量,由于太大和太小的聚类个数对于恐怖案件侦查的实际意义不大. 因此我们取的K值区间为10到250. 纵轴分别是Silhouette Score、Calinski-Harabaz Score. 显而易见,无论是Silhouette Score还是Calinski-Harabaz Score,基于深度自编码表征的K-means聚类算法都比传统的K-means聚类算法高很多. 由图7可以看出,Calinski-Harabaz Score随着簇的个数增加而递减,明显看到聚类效果之间变差. 而从图8可以看出,随着聚类个数增加,Silhouette Score逐渐接近1,表明同类别样本越来越接近,且不同类别样本越来越远. 实验结果显示,基于深度自编码表征的K-means聚类算法具有显著的优越性. 由图8可以看出,当K为250时,基于深度自编码表征的K-means聚类算法得到较高的Silhouette Score.
|
图 7 Calinski_Harabaz评分对比 Figure 7 Calinski Harabaz score comparison |
|
图 8 Silhouette评分对比 Figure 8 Comparison of Silhouette Scores |
在K值等于数据集标签个数(即144)时,基于深度自编码表征的K-means聚类算法的Silhouette Score和Calinski-Harabaz Score都要高于传统K-means聚类算法,结合准确率对比实验,都说明了基于深度自编码表征的K-means聚类算法比传统K-means聚类算法具有更优越的性能.
4.4 恐怖数据的标签化本节从恐怖袭击数据库中随机抽取5条无标签的恐怖袭击数据,执行上述的标签化算法,得到如表2所示的结果:表中第一列表示的是随机抽取出来的无标签数据的编号;第二列表示该无标签数据经过相似度匹配,被分配到的簇的编号;第三列表示该无标签数据被分配到的簇中每一类犯罪集团数目占该簇犯罪集团总数的比率. 如表2的编号为1的无标签数据,它被分配到103号簇中,簇内4号集团、75号集团、45号集团各自所在的比率分别为50%、32%、18%,所以判定编号为1的恐怖袭击事件有50%的概率是4号集团组织的,有32%的概率是75号集团组织,也有18%的概率是45号集团组织的.
| 表 2 标签化结果 Table 2 Labeled result |
本文通过引入深度自编码器,基于全球恐怖主义数据库,提出了一种深度自编码表征(Deep Auto-Encoder Representation)的改进聚类算法,使得与传统K-means聚类算法相比,准确率得到了进一步提升,有助于把相似的恐怖袭击事件进行分组归类,将相似案件并案分析处理,提高反恐分析员侦破案件的效率. 并且,还可以将无标签的恐怖袭击数据标签化,找到案件的犯罪团伙,给反恐分析员侦破案件提供指引.
| [1] |
李国辉. 全球恐怖袭击时空演变及风险分析研究[D].合肥: 中国科学技术大学,2014
|
| [2] |
滕少华, 吴昊, 李日贵, 等. 可调多趟聚类挖掘在电信数据分析中的应用[J].
广东工业大学学报, 2014, 31(3): 1-7.
TENG S H, WU H, LI R G, et al. The application of the adjustable multi-times clustering algorithm in telecom data[J]. Journal of Guangdong University of technology, 2014, 31(3): 1-7. DOI: 10.3969/j.issn.1007-7162.2014.03.001. |
| [3] |
ALTMAN I, HUNTER M M. The employment and income effects of cleaner coal: the case of future gen and rural Illinois[J].
Clean Technologies and Environmental Policy, 2015, 17(6): 1475-1485.
DOI: 10.1007/s10098-014-0872-y. |
| [4] |
BARALIS E, CAGLIERO L, CERQUITELLI T, et al. Digging deep into weighted patient data through multiple-level patterns[J].
Information Sciences, 2015, 322: 51-71.
DOI: 10.1016/j.ins.2015.06.006. |
| [5] |
吴绍忠. 基于聚类分析的反恐情报中潜在恐怖团伙发现技术[J].
警察技术, 2016(6): 18-21.
WU S Z. Potential terrorist gang discovery technology in counter-terrorism intelligence based on cluster analysis[J]. Police Technology, 2016(6): 18-21. DOI: 10.3969/j.issn.1009-9875.2016.06.005. |
| [6] |
张巍, 麦志深. 核模糊谱聚类LOF降噪方法研究[J].
广东工业大学学报, 2018, 35(6): 77-82.
ZHANG W, MAI Z S. Research on LOF noise reduction method based on kernel fuzzy spectral clustering[J]. Journal of Guangdong University of Technology, 2018, 35(6): 77-82. DOI: 10.12052/gdutxb.180053. |
| [7] |
LIBRARY W E. National consortium for the study of terrorism and responses to terrorism[C]// International Symposium on High-power Laser Ablation. Santa Fe, NM: International Society for Optics and Photonics, 2010.
|
| [8] |
PETER K, MICHAEL D I, JOHN P S. Countering terrorism and WMD: creating a global counter-terrorism network[M]. New York: Routledge, 2006.
|
| [9] |
CHEN H, REID E, SINAI J, et al. Terrorism informatics: knowledge management and data mining for homeland security[M]. West Berlin: Springer Publishing Company, 2008.
|
| [10] |
WANG X, MILLER E, SMARICK K, et al. Investigative visual analysis of global terrorism[J].
Computer Graphics Forum, 2008, 27(3): 919-926.
DOI: 10.1111/cgf.2008.27.issue-3. |
| [11] |
JONES J, BUTKIEWICZ T, RIBARSKY W. Visualizing uncertainty for geographical information in the global terrorism database[J].
Proceedings of SPIE - The International Society for Optical Engineering, 2008, 15(9): 1396.
|
| [12] |
颜峻. 基于时空数据挖掘的社会安全(刑事)事件成因研究[D]. 北京清华大学, 2009.
|
| [13] |
彭如香, 张奥博, 杨涛, 等. 基于GTD的全球恐怖主义活动现状与发展趋势研究[J].
计算机应用与软件, 2019, 36(1): 1-5.
DOI: 10.3969/j.issn.1000-386x.2019.01.001. |
| [14] |
李勇男, 梅建明. ROCK聚类在反恐情报分析中的应用研究[J].
情报杂志, 2017(10): 26-29.
LI Y N, MEI J M. Application of ROCK clustering in anti-terrorism intelligence analysis[J]. Journal of Information, 2017(10): 26-29. DOI: 10.3969/j.issn.1002-1965.2017.10.006. |
| [15] |
AYTEKIN C, NI X, CRICRI F, et al. Clustering and unsupervised anomaly detection with L2 normalized deep auto-encoder representations [J]. arXiv preprint arXiv: 1802.00187, 2018.
|
| [16] |
CHANG C J, DAI W L. A grey silhouette coefficient for the small sample forecasting[C]// IEEE International Conference on Grey Systems & Intelligent Services. Macau: IEEE, 2014.
|
| [17] |
LUKASIK S, KOWALSKI P A, CHARYTANOWICZ M, et al. Clustering using flower pollination algorithm and calinski-harabasz index[C]// 2016 IEEE Congress on Evolutionary Computation. Vancouver: IEEE, 2016.
|
 2019, Vol. 36
2019, Vol. 36
