死锁是自动化制造系统(AMS)资源分配问题中的一个严重问题. 它的出现逼使系统出现停顿甚至引发灾难性的后果^[1]. 目前，主要有两种死锁问题的解决方法: 死锁避免(deadlock avoidance)^[2-4]和死锁预防(deadlock prevention)^[5-9]. 二者的主要区别是前者是在线(on-line)策略，后者是离线(off-line)策略. 死锁预防策略的目标是，合成的监督控制器阻止系统陷入不期望的状态，即，防止系统从合法状态(可达的安全状态)向非法状态(可达的不安全状态)演化^[10-11]. 考虑到合成的监控器的性能, 三个问题有待解决: (1) 受控系统的行为许可性^[12-13]；(2) 合成监控器的计算复杂性^[14]；(3) 合成监控器的结构复杂性^[10]. 本文主要关注前两个问题.

一个行为约束(或策略)强加到系统后，得到的系统称为受控系统. 一个约束使得某个标识不可达，或者说该标识不满足添加的约束，称为该标识被约束禁止(forbid). 一个行为约束/策略被称为是最大许可的(maximally permissive)或者最优的(optimal)，如果它至少禁止掉一个不期望的标识，同时没有一个期望的标识被它禁止. (下文中，期望的与不期望的标识，采用Petri网术语，分别定义为合法的与非法的标识.)

考虑到计算复杂性，结构分析技术^[5,15]可以获得计算上易处理(tractable)且被证明是正确的策略^[2]，例如，资源上游策略(resource upstream neighborhood-RUN)、资源排序策略(resource ordering policy-RO)、状态排序策略、银行家算法以及基于信标(siphon)的控制策略^[5,16]. 然而，结构分析策略在通常情况下不能获得最大许可( maximal permissiveness)或者最优(optimality)控制，往往会导致系统过分受到限制，行为许可性低.

最大许可行为的监控器可以使得受控系统拥有较高的资源利用率^[2]. 一个非最大许可的策略可能还存在二级死锁问题^[2]，意味着某些合法的状态在受控系统也变得不可达. 通常，合成自动化系统的最大许可控制器是NP-问题^[11]. 通过计算系统的可达图，可以得到最大许可监控器. 然而，两个挑战性的问题有待解决：(1) 枚举系统的可图状态是困难的，因为系统的可达状态数域系统规模呈指数关系；(2) 为了获取最优控制器，不可避免地要设计和求解混合整数规划(mixed integer linear programming-ILP)问题，目前还没有有效的算法求解该问题.

基于文献[10-11]的工作, 提出了标识覆盖技术去搜寻缩减的首遇坏标识(first-met bad markings–FBM), 在文献[10-11]中称为安全可达的边界标识(“boundary” reachable unsafe states)与缩减的合法标识. 这两个缩减的标识集合分别表示为 $ \mathcal{M}^{\ast}_\mathrm{FBM} $ and $ \mathcal{M}^{\ast}_\mathrm{L} $ . 计算出一个线性约束来最大许可地禁止 $ M_j \in \mathcal{M}^*_\mathrm{FBM} $ 等价于将标识 $ M_j $ 从集合 $ \mathcal{M}^*_\mathrm{L} $ 线性分离开来. 该线性分离器的存在性在文献[17]已经给出. 另外, 在不能线性分离的情况下, 生成最大许可非线性控制的策略在文献[18]已经做过研究. 采用整数规划方法, 假设其最优解存在, 从而合成具有最小结构的最优控制器^[10], 它禁止了所有的 $ \mathcal{M}^{\ast}_\mathrm{FBM} $ 而保留所有的 $ \mathcal{M}^{\ast}_\mathrm{L} $ . 该方法的计算开销巨大, 特别是对于大规模的AMS, 计算耗时非常可观. 在众多后续的研究中, 都在专注如何加速合成最优的控制器，想方设法减少混合整数的的变量个数与约束条件的个数. 遗憾的是, 这些方法均需求解整数规划.

智能制造中的资源分配属于离散事件系统^[19-20]. Petri网(PNs)^[21-23]准确而形象地描述AMS的动态演化过程. Petri网可达图计算与可达状态的分类提取是本文的工作基础，但不属于本文研究范围. 假设 $ \mathcal{M}^{\ast}_\mathrm{FBM} $ 与 $ \mathcal{M}^{\ast}_\mathrm{L} $ 均已由可达性分析计算得出. 具体过程可参阅文献[13].

下一节简单地回顾了与Petri网、带资源简单顺序加工系统(system of simple sequential processes with resources (S³PR^[5]))相关的概念和性质. 概括了标识覆盖技术. 该节最后还给出了最大许可控制的线性规划(LP)方法. 在第2节, 通过结构分析, 具有特定结构的部分非法标识被识别出, 非常简便地构建了这些标识的最大许可约束. 第3节通过两个常见的例子, 展示了本策略的有效性, 比较了本方法与现有方法的优劣. 最后, 第4节对本文的工作进行了总结.

1 预备知识 1.1 Petri网

一个Petri网^[21]被定义为四元组 $ N = (P, T, F, W) $ , 其中 $ P $ 和 $ T $ 分别是有限的非空的库所集和变迁集, 并且满足 $ P\cap T = \varnothing $ . $ F\subseteq(P\times T)\cup(T\times P) $ 是有向弧的集合, 每条弧方向要么从一个库所指向一个变迁, 或者反过来, 从变迁指向库所. $W: (P\times T )\cup(T\times P) \to \mathbb{N} = $ $ \{0,1,2,\cdots\} $ 是一个权值分配函数, 为 $ F $ 中的每条弧指定一个整数权值. $ (N, M) $ 表示一个带有标识 $ M $ 的Petri网系统. 标识也称为状态. 标识 $ M $ 通常被写为多集的形式. $ M(p) $ 是一个非负整数, 给定了在标识 $ M $ 下库所 $ p $ 中令牌(token)的数量. $ M_0 $ 通常用来标识系统的初始标识. 例如, $ M = a_1p_1+ a_2p_2+\cdots + a_np_n $ , 有 $ M(p_i) = a_i, a_i \in \mathbb N \ {\text{且}}\ i \in \mathbb \{1, 2, \cdots, n\} $ . 假设 $ S\subseteq P $ 是库所子集, $ S $ 上的标识表示为 $ S $ 中所有库所令牌数总和, 即 $ M(S) = \sum \limits_{p\in S}M(p) $ . $ ^{\bullet}t $ ( $ ^{\bullet}p $ )用来代表 $ t $ ( $ p $ )的前集(preset). $ t^{\bullet} $ ( $ p^{\bullet} $ )为 $ t $ ( $ p $ )的后集(postset), 即 $ ^{\bullet}t = \{p|(p, t)\in F\} $ , $ t^{\bullet} = \{p|(t, p)\in F\} $ , $ ^{\bullet}p = \{t|(t, p)\in F\} $ , $ p^{\bullet} = \{t|(p, t)\in F\} $ .

一个变迁 $ t\in T $ 在 $ M $ 下被称为使能的(enabled)，如果 $ M(p) \geqslant W(p,t) $ , $ \forall p\in {^{\bullet}t} $ , 表示为 $ M[t\rangle $ . 发射一个使能的变迁 $ t $ 产生一个新的标识 $ M^\prime $ 并且满足 $ M^\prime(p) = $ $M(p)- W(p,t) + W(t,p) $ , 表示为 $ M[t\rangle M^\prime $ . $ R(N, M) $ 代表从 $ M $ 开始按照使能规则可达的所有标识的集合. 当然默认 $ M\in R(N,M) $ 成立. 网系统 $ (N, M_0) $ 所有按发射规则可达的状态表示为 $ R(N, M_0) $ . 一个变迁 $ t $ 被称为在 $ M \in R(N, M_0) $ 下是死锁的(dead)，如果对任意的 $ M^\prime \in R(N, M) $ , $ M^\prime[t\rangle $ 都不成立. 如果对任意的 $ M \in R(N, M_0) $ , $ t $ 在 $ M $ 下都不会死锁, $ t $ 称之为活的(live). 一个标识 $ M \in R(N, M_0) $ 被称为是合法的(legal)，如果 $ M_0 \in R(N, M) $ . 一个标识 $ M \in R(N, M_0) $ 被称为是非法的(illegal)，如果 $ M_0 \notin R(N, M) $ . 所有的合法标识和非法标识的集合分别表示为 $ \mathcal{M}_\mathrm{L} $ 和 $ \mathcal{M}_\mathrm{B} $ . 从而, 下两式成立: $ R(N, M_0) = \mathcal{M}_\mathrm{L} \cup \mathcal{M}_\mathrm{B} $ ; $ \mathcal{M}_\mathrm{L}\cap \mathcal{M}_\mathrm{B} = \emptyset $ . $ M\in \mathcal{M}_\mathrm{B} $ 被称为非法死锁的(deadlock-illegal)，如果存在一个资源库所与变迁构成的回路，其中每个变迁 $ t $ , $ t $ 在 $ M $ 下是死锁的. $ M \in \mathcal{M}_\mathrm{B} $ 被称为非法非死锁的(non-deadlock-illegal)，如果 $ M $ 是非法的，但不是死锁的. 根据状态的区域理论, 非法的标识可以分成两部分: 非法死锁的标识和非法非死锁的标识. 网系统 $ (N, M_0) $ 是活的，如果对任意的变迁 $ t\in T $ , $ t $ 在 $ M_0 $ 下都是活的.

本文研究带有资源的简单顺序加工系统(a system of simple sequential processes with resources-S³PR). 这类系统通常用来为具有柔性路径的单资源分配系统(Disjunctive-Single-Unit AMS)建模. 它是普通(ordinary)守恒(conservative)Petri网的一个子类^[21]. 文献[5]给出了S³PR的详细定义. S³PR类型的网包含三种库所集: 闲置(idle)库所, 行为(activity)库所和资源(resource)库所，分别表示为 $ P^0, P_{\rm A} $ 和 $ P_{\rm R} $ . 或者写成 $ P = P^0\cup P_{\rm A}\cup P_{\rm R} $ . $ M_0(P^0) $ 表明在系统中可以同时被处理的最大作业的数量. 行为库所中的令牌表示工件正在被某个资源加工处理. 在初始状态 $ M_0 $ 下, 所有的行为库所均是没有令牌的. 资源库所通常为AMS中机器、机械手、缓冲器建模, 代表系统中的资源. 其中的令牌数代表目前状态下可用资源的数目. 初始状态下，资源库所中的令牌数表示可利用该资源的最大数目. 假设 $ r $ 是一个资源库所, $ M $ 是S³PR上的标识. 由于不同种类库所上的标识是相互依赖的, 为了简单起见, $ M $ 通常仅用行为库所集 $ P_{\rm A} $ 上的多集表示. 资源 $ r $ 的持有者定义为一些行为库所的集合，记为 $ H(r) = (^\bullet {^\bullet r}) \cap P_{\rm A} $ . $ r $ 在标识 $ M $ 下的当前持有者记为 $ H(r, M) = \{p | p\in H(r), M(p)>0\} $ . 行为库所的指标集写为 $ \mathbb N_{\rm A} = \{i|p_i \in P_{\rm A} \} $ . 在 $ M $ 下, 非空的行为库所的指标集记为 $ \mathbb N_{\rm A}(M) = \{i|i \in \mathbb N_{\rm A}, M(p_i) \neq 0\} $ . 除了 $ ^\bullet P^0\cup {P^0}^\bullet $ 之外, 在 $ M $ 下使能的的变迁集合表示为 $ T_E(M) = $ $ \{t\in{T\setminus (^\bullet\!P^0\cup {P^0}^\bullet)}\ |\, M[t\rangle\} $ . 全部行为库所中所有的令牌总数写成 $ |M|_{\rm A} = \sum \limits_{i\in \mathbb N_{\rm A}}M(p_i) $ . 给定一个库所 $ p\in P_{\rm A} $ , $ p $ 所需要的支撑资源库所集为 ${\rm Req}(p) = $ $ ({p^\bullet} ^\bullet)\cap P_{\rm R} $ . 对于一个变迁 $ t $ , 定义 $ ^{\rm R}t = {^\bullet t}\cap P_{\rm R} $ 为 $ t $ 的资源前集.

一个非空的库所集 $ S\subseteq P $ 称为一个信标(siphon), 如果 $ {^\bullet S}\subseteq S^\bullet $ . 如果一个信标不包含另外一个信标作为其真子集, 它被称为是最小信标. 一个最小信标 $ S $ 被称为严格的(strict), 如果 $ {^\bullet S}\subsetneqq S^\bullet $ , 通常缩写成SMS (Strict Minimal Siphon). 在下文中, 如果提及信标, 均指的是严格最小信标. $ \varPi $ 表示一个Petri网的所有最小信标集. 在S³PR中, $\forall p\in P_{\rm A}, \exists r\in P_{\rm R}, \{r\} =$ $ {\rm Req}(p) $ 成立.

定义1 　在S³PR中, 假定 $ r\in P_{\rm R} $ 为一个资源库所, $ M \in R(N, M_0) $ 是一个可达标识. 资源 $ r $ 在 $ M $ 下被唯一占用，如果 $ |H(r,M)| = 1 $ ; $ r $ 在 $ M $ 下被饱和占用，如果 $ M(r) = 0 $ ; $ r $ 在 $ M $ 下被垄断占用，如果 $ r $ 既被唯一占用又被饱和占用. 假设 $ \mathcal R_M = \{r|r\in P_{\rm R}, M(r) \neq M_0(r)\} $ . $ M $ 是唯一占用/垄断占用的标识, 如果 $ \mathcal R_M\neq \varnothing $ 而且 $ \forall r\in \mathcal R_M $ , $ r $ 在标识 $ M $ 下是被单独占用/垄断占用的.

定义2 　S³PR的一个标识 $ M\in R(N, M_0) $ 称为向前一步死锁的(one-step-ahead deadlock)，如果对于所有 $ t\in T_E(M) $ , $ M[t\rangle M^\prime $ , 并且存在一个信标 $ S\in \varPi $ 满足 $ M^\prime(S) = 0 $ .

定理1^[5] 　假设 $ M $ 是S³PR的一个可达标识. $ M $ 称为非法死锁的，当且仅当存在一个信标 $ S $ 满足 $ M(S) = 0 $ , 即, $ M $ 清空 $S $ .

定理2^[2] 　在S³PR中, 如果对于任意 $ r \in P_{\rm R}, $ $M_0(r) \geqslant 2 $ , 则可达状态 $ R(N, M_0) $ 不含有非法非死锁的标识.

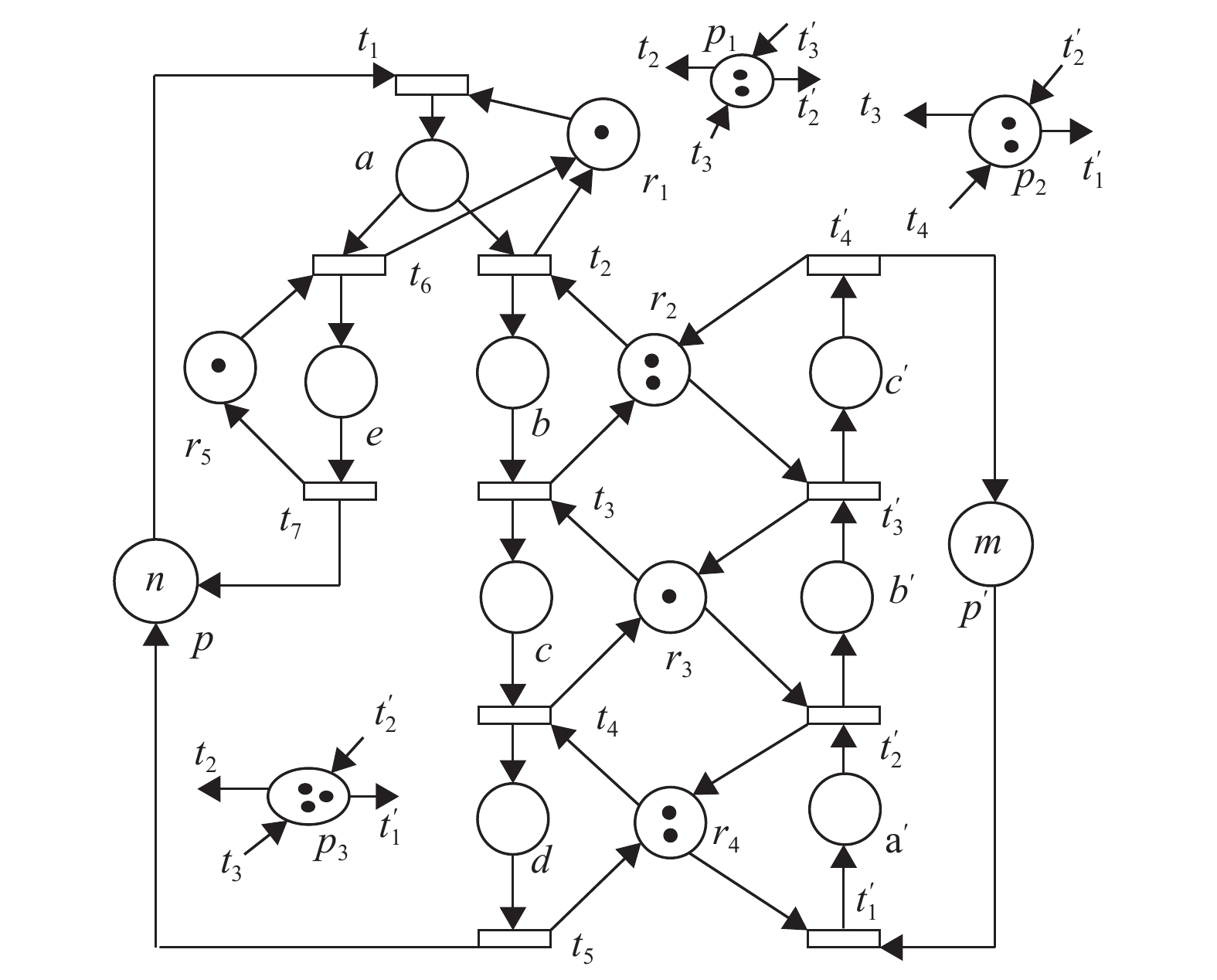
例1 　本例选自文献[5]的一个AMS，其S³PR模型见图1，其中圆圈表示库所，矩形表示变迁. $ P^0 = \{ p, p^\prime\} $ , $ P_{\rm R} = \{r_1, r_2, r_3, r_4, r_5\} $ 与 $ P_{\rm A} =\{a, b, c, d, a^\prime, $ $ b^\prime, c^\prime, e\} $ . 工件A有可选择的柔性加工顺序序列: $ p t_1 a t_6 e t_7 p $ 或者 $ p t_1 a t_2 b t_3 c t_4 d t_5 p $ . 工件B具有确定的加工序列: $ p^\prime t_1^\prime a^\prime t_2^\prime b^\prime t_3^\prime c^\prime t_4^\prime p^\prime $ . 由此可见, $H(r_2) = $ $ \{b, c^\prime\} $ 与 $ {\rm Req}(b) = \{r_2\} $ . $ S = \{r_2, r_3, r_4, d, c^\prime\} $ 是一个最小严格信标. 假设在 $ M $ 下, $ M(a) = M(e) = M(c^\prime) = M(d) = $ $ M(c) = 0 $ , $ M(b) = M(a^\prime) = 2 $ , $ M(b^\prime) = 1 $ , $ H(r_2, M) = \{b\} $ , $ S $ 在 $ M $ 下是被清空的.

1.2 可达图分析与标识覆盖

可达图分析的详细过程，读者可以参阅文献[10-12]. 为了下文阐述之方便，本节仅列出与死锁问题有关的概念与结论. 此外，还将合成最优控制的整数线性规划(ILP)方案改造成线性规划(linear programming-LP)的解决方案. 在规模相近的情况下，求解线性规划复杂度远小于求解整数规划的复杂度.

首遇坏标识(first-met bad marking-FBM)是可达图中位于 $ \mathcal{M}_\mathrm{B} $ 的边界标识, 它可以从 $ \mathcal{M}_\mathrm{L} $ 中的某个标识，通过一步变迁发射到达. 集合FBMs在数学上表示为:

${{\cal M}_{{\rm{FBM}}}} = \{ M \in {{\cal M}_{\rm{B}}}|\exists {M^\prime } \in {{\cal M}_{\rm{L}}},\;t \in T,{M^\prime }[t\rangle M\}. $

死锁预防就是禁止集合 $ \mathcal{M}_\mathrm{B} $ , 系统受控后，这些标识不可达. 显然, 只需要禁止 $ \mathcal{M}_\mathrm{FBM} $ 就达到预防死锁的目的, 因为 $ \mathcal{M}_\mathrm{B} $ 中的任何一个标识必定来自于 $ \mathcal{M}_\mathrm{FBM} $ 中的某个标识. 遗憾的是, 虽然 $ |\mathcal{M}_\mathrm{FBM}|\ll |\mathcal{M}_\mathrm{B}| $ , $ \mathcal{M}_\mathrm{FBM} $ 也可能仍然是一个规模巨大的集合. 标识覆盖技术可以进一步降低需要处理的对象的规模, 从而明显减轻计算工作负担.

定义3 ^[10-12] 　假定 $ M $ 与 $ M^\prime $ 是S³PR的两个标识. 如果 $ M(p)\geqslant M^\prime(p) $ , $ p\in P_{\rm A} $ , 则MA-覆盖(activity-cover) $ M^\prime $ (或者 $ M^\prime $ 被MA-覆盖), 记为 $ M\geqslant_{\rm A} M^\prime $ (或者 $ M^\prime \leqslant_{\rm A} M $ ); 如果 $ M\geqslant_{\rm A} M^\prime $ , $ \exists p\in P_{\rm A} $ 满足 $ M(p)>M^\prime(p) $ , 则 $ M $ 真地A-覆盖 $ M^\prime $ (或者 $ M^\prime $ 被 $ M $ 真地 A-覆盖), 记为 $ M \gneqq_{\rm A} M^\prime $ (or $ M^\prime \lneqq_{\rm A} M $ ).

基于标识覆盖, 一个在规模上更小的子集 $ \mathcal{M}^*_\mathrm{FBM}\subseteq \mathcal{M}_\mathrm{FBM} $ 可以从 $ \mathcal M_\mathrm{FBM} $ 计算得到, 从而进一步降低需要处理问题的规模，降低计算复杂度.

定义4^[10-12] 　标识集 $ \mathcal{M}^*_\mathrm{FBM}\subseteq \mathcal M_\mathrm{FBM} $ 称为首遇坏标识集 $ \mathcal M_\mathrm{FBM} $ 的最小被覆盖集，如果满足下列条件:

(1) $ \forall M\in \mathcal M_\mathrm{FBM}, \exists M^\prime \in \mathcal M^*_\mathrm{FBM}, M \geqslant_{\rm A} M^\prime $ ;

(2) $ \forall M \in \mathcal{M}^*_\mathrm{FBM},\nexists M^\prime \in \mathcal{M}^*_\mathrm{FBM}, M \geqslant_{\rm A} M^\prime $ 且 $ M \neq M^\prime $ .

类似地, $ \mathcal{M}_\mathrm{L} $ 的一个子集 $ \mathcal{M}^*_\mathrm{L} $ 可以由标识覆盖计算得到, 定义如下:

定义5^[10-12] 　假设 $ \mathcal{M}^*_\mathrm{L}\subseteq \mathcal{M}_\mathrm{L} $ 为合法标识集的子集. $ \mathcal{M}^*_\mathrm{L} $ 被称为是集合 $ \mathcal{M}_\mathrm{L} $ 的最小覆盖集, 如果满足下列条件:

(1) $ \forall M\in \mathcal{M}_\mathrm{L}, \exists M^\prime \in \mathcal{M}^*_\mathrm{L}, M^\prime \geqslant_{\rm A} M $ ;

(2) $ \forall M \in \mathcal{M}^*_\mathrm{L},\nexists M^\prime \in \mathcal{M}^*_\mathrm{L}, M^\prime \geqslant_{\rm A} M $ 而且 $ M \neq M^\prime $ .

如果一个线性的代数约束的系数均为非负整数，且该约束最大许可地禁止了标识 $ M \in \mathcal{M}^*_\mathrm{FBM} $ . 那么, 对于任意的满足 $ M^\prime \geqslant_{\rm A} M $ 的 $ M^\prime $ , 均可被该约束最大许可地禁止^[11].

根据上述可达图分析与标识覆盖的概念, 容易导出以下两个结论.

引理1 　假设 $ M $ and $ M^\prime $ 为S³PR $ N $ 的两个标识. 满足 $ M\in R(N, M_0) $ 与 $ M \geqslant _{\rm A} M^\prime $ . 那么, $ M^\prime \in R(N, M_0) $ .

证明 　由于 $ M\in R(N, M_0) $ ，则存在一个变迁发射序列， $ t_{i_1}t_{i_2}\cdots t_{i_k} $ , 使得系统状态从 $ M_0 $ 演化到 $ M $ . 又 $ M \geqslant _{\rm A} M^\prime $ ，在状态 $ M^\prime $ 下， $ p\in P_{\rm A} $ 中的每个令牌都对应位于状态 $ M $ 下同一个库所 $ p $ 中. 状态 $ M^\prime $ 一定可以由 $ M_0 $ 开始，通过发射 $ t_{i_1}t_{i_2}\cdots t_{i_k} $ 的某个子序列而到达. 故 $ M^\prime \in R(N, M_0) $ .

定理3 　在S³PR中，如果任意的标识 $M \in $ $ \mathcal{M}^*_\mathrm{FBM} $ 均被某策略最大许可地禁止，则受控后的网系统是活的.

证明 　根据策略最大许可性的定义，禁止 $ M $ 的时候不禁止任何合法的标识. 一方面，可达图中 $ \mathcal{M}^*_\mathrm{FBM} $ 及其后续标识被禁止了. 另一方面，从任何一个合法标识 $ M_l $ 到达 $ M_0 $ 而途经的中间标识都未能被禁止，即， $ M_0 \in R(N, M_l) $ . 又由于 $ M_0 $ 是良好配置的，即， $ \forall t\in T $ , $ t $ 从 $ M_0 $ 开始必定至少可以发射一次. 受控系统的可达图是强连通的，受控后， $ \forall t \in T $ 是活的，故受控系统也是活的.

以下设计的线性规划算法，可以作为求最大许可线性约束的通用方法. 目标是求出一个超平面，分离开 $ M_j \in \mathcal{M}^*_\mathrm{FBM} $ 与 $ \mathcal{M}^*_\mathrm{L} $ . 如果分离超平面存在，最大许可地禁止 $ M_j $ 的非负整系数线性约束可由超平面方程导出.

$\begin{array}{*{20}{l}} {\max\; \varepsilon. }\qquad\qquad\qquad\quad\qquad{\left( {{\rm{LP1}}} \right)}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\qquad }{\sum\limits_{i \in {\mathbb{N}_{\rm A}}({M_j})} {{l_i}} \cdot {M_j}({p_i}) = 1;}\\ \quad\quad\quad{\sum\limits_{i \in {\mathbb{N}_{\rm A}}({M_j})} {{l_i}} \cdot {M_k}({p_i}) + \varepsilon \leqslant 1,}\quad {\forall {M_k} \in {\cal M}_{\rm{L}}^*};\\ \quad\quad\quad{{l_i} \geqslant 0,}\quad{\forall i \in {\mathbb{N}_{\rm A}}({M_j}).} \end{array}$

显而易见, LP1必定至少含有一个可行解，即可行域非空. 如果目标函数的最优解 $ \varepsilon ^*>0 $ , 构造线性约束 $ \sum \limits_{i \in \mathbb N_{\rm A}(M_j)} l_i \cdot u_{p_i} \leqslant 1-\varepsilon^* $ . 它最大许可地禁止掉标识 $ M_j \in \mathcal{M}^*_\mathrm{FBM} $ , 其中 $ u_{p_i} $ 是与行为库所 $ p_i $ 相关的一个标识变量. 另一方面, 如果LP1得出的最优解 $ \varepsilon ^* \leqslant 0 $ , 则不存在线性约束最大许可地禁止标识 $ M_j \in \mathcal{M}^*_\mathrm{FBM} $ , 因为, 在几何上, 非法标识 $ M_j $ 位于离散点集 $ \mathcal{M}^*_\mathrm{L} $ 的闭包(convex hull)内部, 从而无法线性分离合法标识与非法标识.

众所周知线性规划问题可以被有效地求解. 然而, LP1存在一个问题: 求解出的最优解 $ \varepsilon^* $ 与系数 $ l_i $ 一定不是整数，甚至可能是无理数. 对于任何一个实数，都存在一个有理数序列收敛于该实数. 可以通过在线性约束不等式两边乘以某个整数因子使之变为整系数约束. 该约束为最大许可约束. 第3节的例子将说明这一点.

线性规划LP1方法是一类纯数学的方法来计算最大许可的约束, 文献[11]称之为最优分类器. 这种方法没有考虑到Petri网的结构特性. 如果能够分析非法标识与Petri网结构的关系, 建立最大许可约束, 将进一步减少计算量. 与求解线性规划LP1比较, 基于结构分析的方法更有效. 因此, 本文首先需要识别标识的结构特征, 为满足特定结构特征的标识综合出最优控制器.

2 基于结构分析的最优控制

死锁的产生是由于在系统中待处理的工作大量涌入, 它们竞争有限的资源和资源分配不当造成的. 对于一个S³PR的非法标识 $ M_j $ , 我们迫使所有的合法标识的令牌总数严格少于该标识中的令牌数, 显然, $ M_j $ 被禁止了. 另外，线性约束不等式中的系数必须是整数，这样才能用Petri网的形式合成死锁控制器. 然后验证得出约束的最大许可性. 因此, 构造下列线性约束:

$\sum\limits_{i \in {\mathbb{N}_{\rm A}}({M_j})} {{u_{{p_i}}}} \leqslant |{M_j}{|_{\rm A}} - 1,\forall {M_j} \in {\cal M}_{{\rm{FBM}}}^*.$

(1)

为了验证标识 $ M $ 是否满足构造出的约束(1), 将不等式左侧的 $ u_{p_i} $ 用 $ M(p_i) $ 来代替. 毫无疑问, 约束(1)禁止了特定的标识 $ M_j\in \mathcal M^*_\mathrm{FBM} $ 使得它变得不可达. 然而，将约束(1)加到系统中, 不一定能保证其最大许可性. 一种方法是, 将 $ \mathcal M^*_\mathrm L $ 中的每个标识代入约束不等式, 验证其最大许可性. 然而, 在理论上, $ |\mathcal M^*_\mathrm L| $ 是一个巨大的数字, 是网系统规模的指数型函数. 因此, 在计算复杂性角度，该枚举算法不是一个好方法.

根据文献[11], 如果一个标识 $ M_j\in \mathcal M^*_\mathrm{FBM} $ 清空了一个信标, 也就是说, 它是一个死锁非法标识. 约束(1)禁止了 $ M_j $ , 而且该策略是最大许可的. 并且文献[2]还提供了一个多项式复杂度死锁检测算法(deadlock detection algorithm–DDA), 它的计算复杂度为 $ O(|P_{\rm R}|^2 \cdot K) $ , 其中 $ K $ 为资源的最大容量. 调用DDA, 可以在多项式时间内判定一个给定的非法标识是否死锁非法. 在本文中, 主要关注那些非死锁非法标识, 并且通过结构分析的方法, 推导其最大许可约束. 基于不同的结构特点, 将这些非死锁非法标识划分为不同的情形.

2.1 垄断占用的标识

垄断占用标识的结构特征明显，识别验证较容易. 由定理4归纳的策略，高效，简便，易于执行.

定理4 　如果 $ M_j\in \mathcal M^*_\mathrm{FBM} $ 是S³PR的一个垄断占用标识, 则约束(1)具有最大许可性.

证明 　(反证法). 假设存在一个标识 $ M(\neq M_j)\in$ $ \mathcal{M}_\mathrm{L} $ 并且 $ M $ 被约束(1)禁止. 则公式 $\sum \limits_{i\in \mathbb N_{\rm A}(M_j)}M(p_i)\geqslant $ $ |M_j|_{\rm A} $ 必定成立. 由已知条件 $ \forall i\in \mathbb N_{\rm A}(M_j) $ , $M_j(p_i) = $ $ M_0({\rm Req}(p_i)) $ , 蕴含着, 在标识 $ M_j $ 下, $ p_i $ 容纳了最大数量的令牌数. 因此, 在任意的标识 $ M \in R(N, M_0) $ , $ \sum \limits_{i\in \mathbb N_{\rm A}(M_j)}M(p_i)\ngtr |M_j|_{\rm A} $ 成立; 否则, 与上述结论矛盾. 另外 $ \sum \limits_{i\in \mathbb N_{\rm {\rm A}}(M_j)}M(p_i)\neq |M_j|_{\rm A} $ 也成立; 否则, $ M = M_j $ , 与 $ M \in \mathcal M_\mathrm L $ 相矛盾. 从而, 没有一个合法标识被约束(1)禁止掉.

为了验证一个标识 $ M_j\in \mathcal M^*_\mathrm{FBM} $ 是否属于垄断占用的, 对于每一个 $ p_i\in P_{\rm A} $ 满足 $ M_j(p_i)\neq 0 $ , 需要验证等式 $ M_j(p_i) = M_0({\rm Req}(p_i)) $ 是否成立. 根据 $ p_i \in P_{\rm A} $ 去搜寻 $ {\rm Req}(p_i) $ 的计算复杂度为 $ |P|+|T| $ . 从而, 验证定理4的条件具有的计算复杂度为 $ O(|P|+|T|) $ .

例1中， $ M_3 = 2b+2a^\prime $ 是一个FBM， $ {\rm Req}(b) = \{r_2\} $ , $ {\rm Req}(a^\prime) = \{r_4\} $ , $ M_3(b) = M_0(r_2) = 2 $ , $M_3(a^\prime) = M_0(r_4) = $ 2, 也就是说, 定理4的条件获得满足. 从而, $u_b+u_a^\prime \leqslant $ $ 2+2-1 = 3 $ 是一个最大许可约束. 同理可得, FBMs $ M_1 $ 与 $ M_2 $ 均为垄断占用的标识. 根据定理4, 它们的最大许可策略能够容易地构造. 换句话说, 对于这个系统, 由 $ M_i( i = 1, 2, 3) $ 构造出的具有(1)形式的约束都是最大许可的. 该系统的最大许可监控器由3个控制库所构成, 其相关的连接弧都在图1中画出.

2.2 向前一步死锁标识

向前一步死锁标识属于非死锁非法标识，可以在多项式复杂性下，识别该类标识的结构特征.

定理5 　如果 $ M_j\in \mathcal M^*_\mathrm{FBM} $ 是S³PR 的向前一步死锁标识, 那么, 约束(1)是最大许可的.

证明 　根据向前一步死锁的定义, 下列事实成立.

(1) $ \forall t \in T_E(M_j), |^{\rm R}t | = 1 $ .

如果 $ |^{\rm R}t| > 1 $ , 从S³PR中, 可以抽出一些顶点与弧, 构成一个强连接的子网 $ \Omega $ 满足 $ |^{\rm R}t| = 1 $ . 定义 $ M_j^\prime $ 为标识 $ M_j $ 在 $ \Omega $ 上的投影标识, 即, $ M^\prime_j(p) = M_j(p) $ , 如果 $ p $ 位于 $ \Omega $ 或者 $ p \in P_{\rm R} $ ; $ M^\prime_j(p) = 0 $ , 否则. 可以得出 $ M_j > M_j^\prime $ . 由引理1, $ M_j^\prime $ 是可达的. 另外可得, $ M_j^\prime \in \mathcal M^*_\mathrm{FBM} $ , 这与 $ M_j\in \mathcal M^*_\mathrm{FBM} $ 相矛盾.

(2) $ M_j(^{\rm R}t) = 1 $ .

假设 $ ^{\rm R}t = \{r\} $ . 如果 $ M_j(r) = 0 $ , 则 $ T_E(M_j) = \varnothing $ . 如果 $ M_j(r) \geqslant 2 $ , $ M_j $ 一定不是一个向前一步死锁标识, 因为任意的 $ t \in T_E(M_j) $ 发射后, $ r $ 必定被清空. 然而, 当 $ M_j(r) \geqslant 2 $ 的时候，这是不可能的发生的.

(3) $ M_0(r) = 1 $ .

(反证法)假设 $ M_0(r) \geqslant 2 $ . 将 $ M_0(r_i) = 1 $ 改变为 $ M^\prime_0(r_i) = 2 $ , $ \forall r_i \in P_{\rm R} \setminus \{r\} $ . 则 $ M_j^* $ 是可以从改变后的表示 $ M^\prime_0 $ , 满足

$M_j^*(p) = \left\{ {\begin{array}{*{20}{l}} {2,\quad {\rm{if}}\;p \in {P_{\rm A}},{M_j}(p){\rm{ = }}{M_{\rm{0}}}({\rm Req}(p)){\rm{ = 1}};}&{}\\ {2,\quad {\rm{if}}\;p \in {P_{\rm R}},{M_j}(p){\rm{ = }}{M_{\rm{0}}}(p){\rm{ = 1}};}&{}\\ {{M_j}(p),\quad \quad {\text{其他情形}}\;.}&{} \end{array}} \right.$

$ M_j^* $ 也是一个向前一步的死锁标识. 然而, 由定理2, 这样的标识根本不可能存在.

(4) $ \forall i \in \mathbb N_{\rm A}(M_j) $ , $ M_j({\rm Req}(p_i)) = 0 $ .

根据以上推导出的两个事实1与2, 这个结论是显而易见的.

本文得出以下结论: $ \forall r \in P_{\rm R} $ 满足 $ M_j(r)\ne M_0(r) $ , 资源 $ r $ 在 $ M_j $ 下被饱和占用. 库所集 $ \{p|p\in P_{\rm A}, M_j(p)>$ 0} 在任何状态下能够容纳的令牌总数不超过 $ |M_j|_{\rm A} $ . 对于 $ \forall M_k\in \{M|\sum \limits_{i\in\mathbb N_{\rm A}(M_j)}M(p_i) = |M_j|_{\rm A}\} $ , 存在下述两种情形:

情形1: $ M_k $ 清空某个信标;

情形2: $ M_k $ 是一个向前一步的死锁标识.

不管在什么情形下, 可以得出 $ M_k $ 都是一个非法的标识. 从而, 约束(1)具有最大许可性. 证毕.

对于每个 $ t \in T^E(M_j) $ , 均调用DDA算法, 可以验证 $ M_j\in \mathcal M^*_\mathrm{FBM} $ 是否是一个向前一步死锁标识. 该算法的复杂度为 $ O(|T|\cdot |P_{\rm R}| \cdot\ K) $ , 其中 $ K $ 是资源的最大容量, 为一个常数.

在例1中, $ M_3 = 2b+2a^\prime $ 是一个向前一步死锁标识. 根据定理5, $ u_b+u_a^\prime \leqslant 2+2-1 = 3 $ 是最大许可地禁止了 $ M_3 $ .

2.3 唯一占用的标识

唯一占用的标识的结构特征稍显复杂. 利用下述定理，可以有效地识别出唯一占用的标识中的一个子类，从而最大许可地禁止该子类标识.

定理6 　假设 $ M_j\in \mathcal M^*_\mathrm{FBM} $ 是S³PR的唯一占用非法标识. 满足下列条件:

(1) $ \exists r\in P_{\rm R} $ 满足 $ M_j(r) = 1 $ 与 $ M_0(r) > 1 $ ;

(2) $ $ \forall r_i(\neq r)\in P_{\rm R}\; {\text{而且}}\, M_j(r_i)\neq M_0(r_i) $ , $ r_i $ 是被唯一占用的;

(3) $ 假设 $ \{p_l\} = H(r,M_j) $ . 定义一个基于 $ r $ 由 $ M_j $ 更改而得到的标识 $ M_j^r $ :

$M_j^r(p) = \left\{ {\begin{array}{*{20}{l}} {{M_j}(p) + 1,}&{{\rm{if}}\;p{\rm{ = }}{p_l};}\\ {{M_j}(p) - 1,}&{{\rm{if}}\;p{\rm{ = }}r;}\\ {{M_j}(p),}&{{\rm{if}}\;p \in P{\rm{\backslash }}\{ r,{p_l}\} .} \end{array}} \right.$

选取一个行为库所 $ p_i ( \neq p_l )\in P_{\rm A} $ 满足 $ M_j^r(p_i)>0 $ , 根据下述更改规则构造新的标识 $ M_{j_{p_i}} $ :

${M_{{j_{{p_i}}}}}(p) = \left\{ {\begin{array}{*{20}{l}} {M_j^r(p) - 1,}&{{\rm{if}}\;p{\rm{ = }}{p_i};}\\ {M_j^r(p) + 1,}&{{\rm{if}}\;p \in {\rm Req}({p_i});}\\ {M_j^r(p),}&{{\rm{if}}\;p \in P\backslash (\{ {p_i}\} \cup {\rm Req}({p_i})).} \end{array}} \right.$

令 $ \mathcal M^d = \{M_{j_{p_i}}|p_i \in P_{\rm A} $ , $ p_i \notin H(r, M_j) $ , $ M_j^r(p_i)>0\} $ 是由 $ M^r_j $ 更改库所 $ p_i\ (i\in \mathbb N_{\rm A}{(M_j^r)} \setminus \{l\}) $ 中令牌数而得到的标识集合. 如果对于任意的标识 $ M\in \mathcal M^d $ , 有 $ M \in \mathcal M_\mathrm B $ , 则约束(1)最大许可的.

证明 　假设 $ M_j = a_1p_1+a_2p_2+ \cdots +a_kp_k $ , $p_i\in P_{\rm A}, $ $ a_i\neq 0, i\in \{1,2,\cdots, k\} $ . 禁止 $ M_j $ 的约束(1)为 $u_{p_1} + u_{p_2} + $ $ \cdots + u_{p_k} \leqslant |M_j|_{\rm A} - 1 $ 的形式. 根据假设, 需要证明如下结论: 所有满足不等式 $ u_{p_1} + u_{p_2} + \cdots + u_{p_k} \geqslant |M_j|_{\rm A} $ 的可达标识均为非法标识. 分两种情形证明之.

情形1: $ u_{p_1} + u_{p_2} + \cdots + u_{p_k} > |M_j|_{\rm A} $ . 根据条件1和2, 可得 $ u_{p_1} + u_{p_2} + \cdots + u_{p_k} \leqslant |M_j|_{\rm A} +1 $ . 因此, 仅存在一个可达的标识， $ M_j^r = a_1p_1+a_2p_2+ \cdots +(a_l+1)p_l+\cdots $ $ a_kp_k $ ，即为条件3中构造出的 $ M_j^r $ ，满足条件 $ u_{p_1} + u_{p_2} + \cdots + u_{p_k} > |M_j|_{\rm A} $ , $ p_i\in P_{\rm A} $ , $ i\in \{1,2,\cdots, l, \cdots, k\} $ . 显然, 由于 $ M_j^r \geqslant_{\rm A} M_j $ , 可知 $ M_j^r \in \mathcal{M}_\mathrm{B} $ .

情形2: $ u_{p_1} + u_{p_2} + \ldots + u_{p_k} = |M_j|_{\rm A} $ . 任何满足该等式的可达标识可以如此获得: 从库所 $ p_i, i\in \mathbb N_{\rm A}(M_j^r) $ 中移走一个令牌. 从而，可以得到一个新的标识 $ M_{j_{p_k}} $ . 根据定理中条件3的末尾部分可得, $ M_{j_{p_k}} \in \mathcal M_B $ .

基于上述两种情形, 约束(1)禁止非法标识的同时没有禁止掉合法标识, 从而是最大许可的. 证毕.

运用定理6识别标识，需要验证给定的3个条件. 前两个条件比较容易验证. 在验证第3个条件的时候, 需要基于 $ M_j $ 构造标识集合 $ \mathcal M^d $ , 基本操作为向某个库所添加令牌或者移走令牌. 这样的操作复杂度为 $ O(|P|) $ . 尽管, 在一般情况下, 验证一个标识是否是非法属于NP-困难的. 然而, 如果 $ \mathcal M^d $ 只包含死锁非法标识与向前一步死锁标识, 可以获得具有多项式复杂度的死锁预防策略. 在下文第3节的例子中将会讨论这类标识.

针对具有不同的结构特性的非法标识，提出了构建最大许可约束的方法. 需要注意的是, 定理4~6给出的结构分析方法比采用LP1给出的线性规划方法更有效. 因此, 首先采用结构分析方法, 识别出具有定理中给定的结构的标识, 相应地设计出对应的控制方法. 至于目前还未能识别出具有特殊结构的非法标识 $ M_j\in \mathcal M^*_\mathrm{FBM} $ , 姑且采用线性规划的算法寻求最大许可约束. 算法1给出了设计最大许可控制器的工作流程. 注意到验证上述定理中给定的条件的可满足性具有不同的复杂性，具有较低复杂性的策略总是优先考虑. 算法1按照从易到难的顺序去识别非法标识的结构特性. 综上所述, 对于任意 $ M \in \mathcal{M}_\mathrm{FBM}^\ast $ , 如果 $ M $ 是线性可控的, 本文都可以有效地得到最大许可控制策略, 避免目前文献中求解混合整数规划.

算法1　计算禁止 $ M_j\in \mathcal{M}_\mathrm{FBM}^\ast $ 最优约束流程

输入：S³PR $ N = (P^0\cup P_{\rm A}\cup P_{\rm R}, T, F) $ , $ M_j\in \mathcal{M}_\mathrm{FBM}^\ast $

输出： $ c(M_j) $ // $ c(M_j) $ 是禁止 $ M_j $ 的最优约束.

1: if $ M_j $ 满足定理4 then goto 7;

2: else if $ M_j $ 是非法死锁的(by DDA) then goto 7;

3: else if $ M_j $ 满足定理5 then goto 7;

4: else if $ M_j $ 满足定理6 then goto 7;

5: else LP1最优解 $ \varepsilon^* > 0 $ 时，得到约束 $ c(M_j) $ ，goto 8;

6: endif

7: $ c(M_j)\leftarrow $ 约束 (1);

8: return $ c(M_j) $ ;

3 两个规模稍大的范例

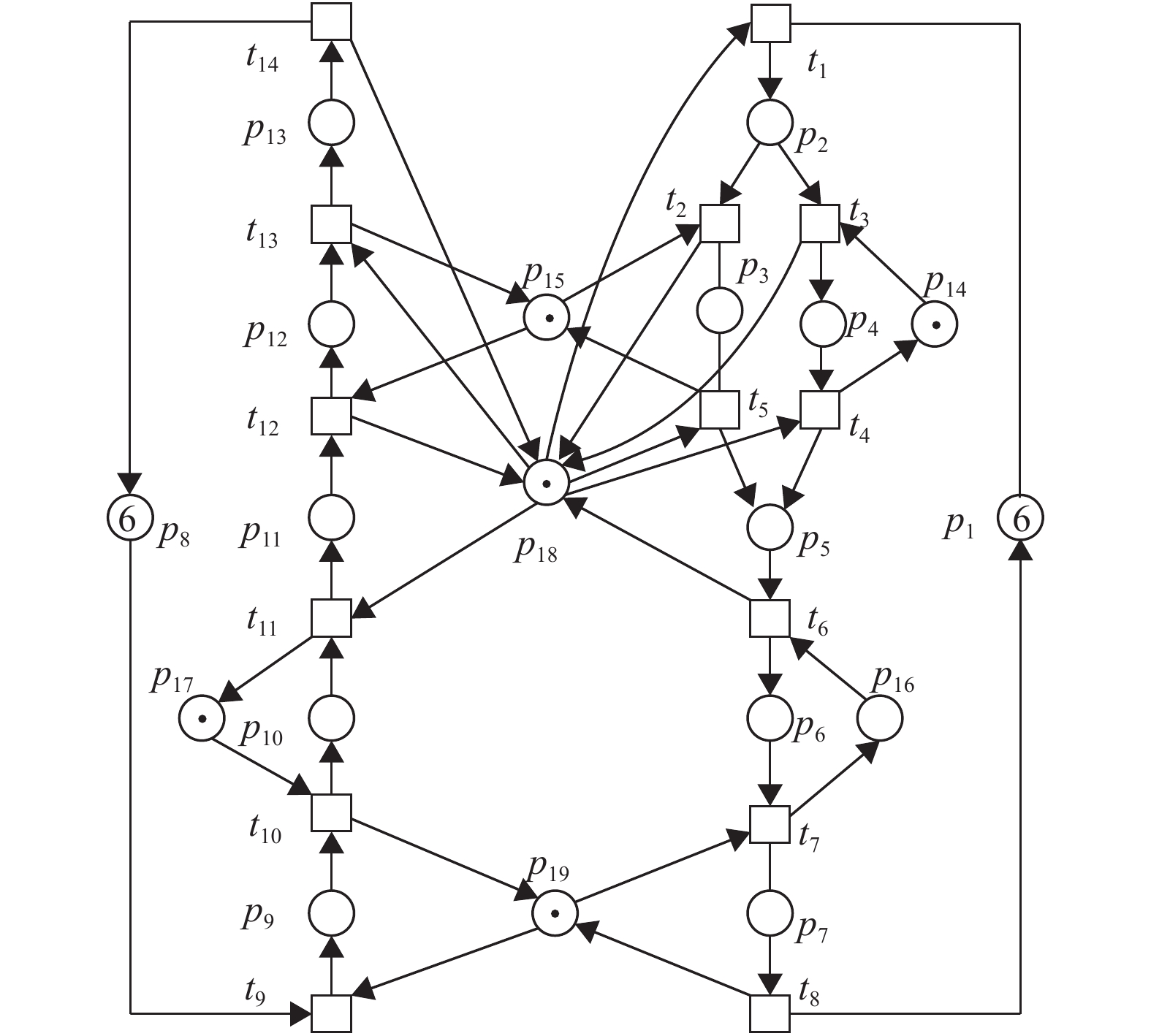
例2 　本系统选取自文献[24], 其S³PR显示于图2, 其中 $ p_1 $ , $ p_8 $ 为闲置库所; $ p_{14}-\,p_{19} $ 为资源库所; 其余的库所为行为库所. 工件 $ A $ 的加工工序： $ p_8t_{9}p_9t_{10}p_{10}t_{11}$ $p_{11}t_{12}p_{12}t_{13}p_{13}t_{14}p_8 $ . 工件 $ B $ 的具有可选的加工工序： $ p_1t_{1}p_2t_{2}p_3t_{5}p_5t_{6}p_6t_7p_{7}t_8p_1 $ 或者 $ p_1t_{1}p_2t_{3}p_4t_{4}p_5t_{6}p_6t_7p_{7}$ $ t_8p_1 $ .

该系统加工两种类型的工件. 计算可得 $ |\mathcal{M}_\mathrm{FBM}^\ast| = 8 $ . 可以看出, $ \forall r\in P_{\rm R}, M_0(r) = 1 $ . 因而, 每个可达标识均为垄断占用的, 满足定理4的条件. $ \forall M_j\in \mathcal{M}_\mathrm{FBM}^\ast $ , $ c(M_j) $ 均为最大许可的. 8个添加的库所构成了该系统的控制器. 所有的205个合法标记在受控系统中都可达. 该策略是最大许可的. 在 $ \mathcal M_\mathrm{FBM} $ 计算出来后, 本策略具有多项式复杂性. 然而, 如果采用文献[25]提出的方法, 需要求解8个ILP问题. 如果采用区域理论方法, 需要求解59个不等式组, 每个不等式组包含的不等式个数高达205个^[24].

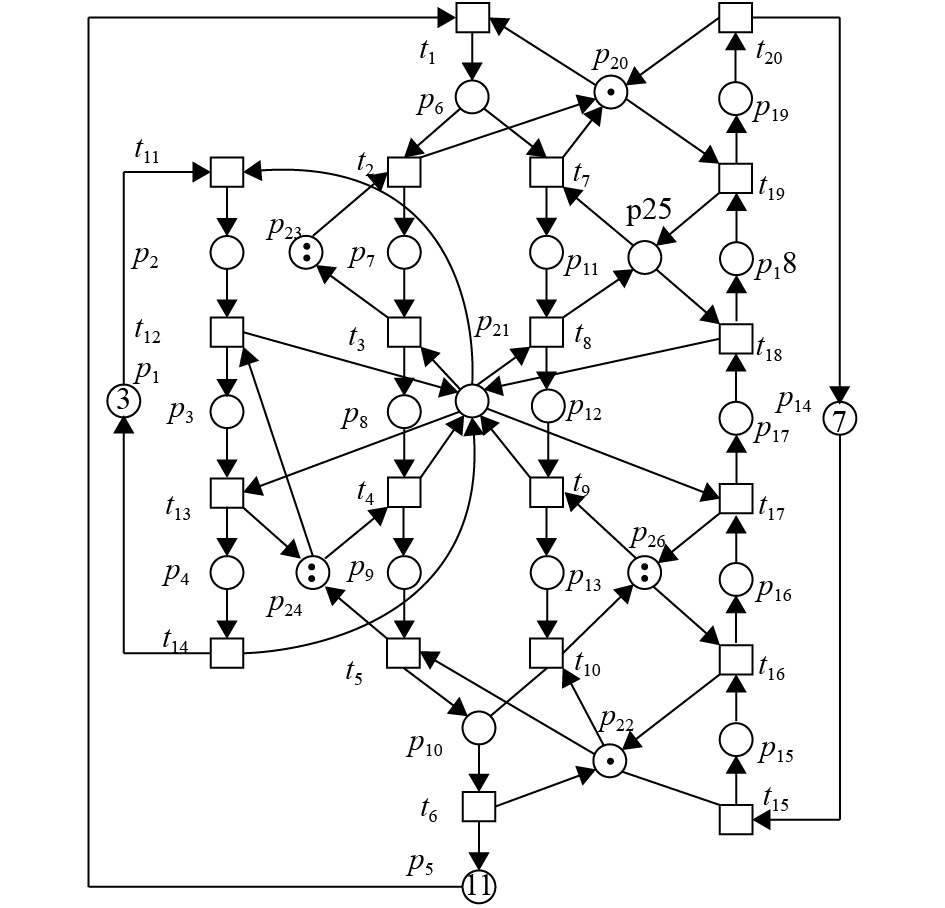
例3 　本例子选取自文献[5], 图3显示了其S³PR模型，其中闲置库所 $ P^0 = \{p_1, p_5, p_{14}\} $ , 资源库所 $P_{\rm R} = $ $ \{p_{20}, \cdots, p_{26}\} $ , 行为库所 $ P_{\rm A} = \{p_2, \cdots, p_4, p_6, \cdots , p_{13}, p_{15}, $ $ \cdots , p_{19}\} $ . 工件 $ A $ 的加工工序： $ p_1t_{11}p_2t_{12}p_3t_{13}p_4t_{14}p_1 $ . 工件 $ B $ 的具有可选的加工工序： $p_5t_{1}p_6t_{2}p_7t_{3}p_8t_{4}p_9t_5 $ $ p_{10}t_6p_5 $ 或者 $ p_5t_{1}p_6t_{7}p_{11}t_{8}p_{12}t_{9}p_{13}t_{10}p_{10}t_6p_5 $ . 工件 $ C $ 的加工序列: $ p_{14}t_{15}p_{15}t_{16}p_{16}t_{17}p_{17}t_{18}p_{18}t_{19}p_{19}t_{20}p_{14} $ .

本系统有 $ 26\;750 $ 个可达状态, 其中 $ |\mathcal M_\mathrm L| = 21\;581 $ , $ |\mathcal M_\mathrm{FBM}| = 4\;211 $ . 采用标识覆盖技术后, $ |\mathcal M^*_\mathrm L| = 393 $ , $ |\mathcal M^*_\mathrm{FBM}| = 34 $ . 由于数目的过大, 本文无法给出这些标识的详细信息和 $ \mathcal M^*_\mathrm{FBM} $ 中每个标识的许可约束. 就该系统而言, $ \mathcal M^*_\mathrm{FBM} $ 中的每个标识都可以最大许可地被禁止. $ \mathcal M^*_\mathrm{FBM} $ 中有 $ 18 $ 个属于非死锁非法的标识. 据作者所知, 目前的研究中还没有有效的方法处理这类非死锁非法的标识. 这 $ 18 $ 个标识中, $ 10 $ 个可以由定理4~6提出的方法实现最大许可控制, 也就是说, 对于这 $ 10 $ 个标识, 其对应的约束(1)是最优的. 例如, 在 $ \mathcal M^*_\mathrm{FBM} $ 中, 下列三个标识 $ 2p_{11} + 2p_{16} $ , $ 2p_{11}+ p_{13} + p_{15} + $ $p_{16},\; 2p_{11}+ p_{12} + p_{15} + p_{16} $ 分别满足据定理4~6的条件, 易获得其最优控制策略. 对于另外剩下的 $ 8 $ 个标识, 目前还没有更好的结构控制策略. 如果采用(LP1), 能够获得它们的最优控制策略. 例如, 对于标识 $ p_6 + 2p_7 + p_8 + p_9 +$ $ p_{11} + p_{13} + p_{15} + p_{16} + p_{18} $ , 无法用文中的定理识别出它的结构特征，采用线性规划的方法, 计算出约束

$ \begin{split} &0.076\;9u_{p_6} + 0.076\;9u_{p_7}+ 0.076\;9u_{p_8} + 0.076\;9u_{p_9} +\\ &0.076\;9u_{p_{11}}+ 0.153\;8u_{p_{13}} + 0.153\;8u_{p_{15}} + 0.153\;8u_{p_{16}} + \\ &0.076\;9u_{p_{18}}+0.076\;9 \leqslant 1. \end{split} $

为了合成控制器, 将其等价变形整系数约束

$ \begin{split} &u_{p_6} + u_{p_7} + u_{p_8} + u_{p_9} + u_{p_{11}} + 2u_{p_{13}} + 2u_{p_{15}} +\\ &2u_{p_{16}} + u_{p_{18}} \leqslant 12. \end{split} $

它是一个最优约束. 尽管很多学者基于不同的方法也给出本例的最大许可控制策略, 这些策略不可避免地需要求解混合整数规划. 本文提出的方案不需要求解整数规划, 从计算复杂性的角度, 具有一定的优势.

4 结论

合成自动化制造系统最大许可死锁控制器, 不但保证系统的正常运行, 还确保系统的优化运行. 本工作的目的是, 在合成最优控制器时, 尽可能减少计算开销. 基于S³PR模型, 首先, 通过标记覆盖技术, 缩小待处理问题的规模. 其次, 分析利用网结构的特点, 结合标识本身的特性, 揭示二者之间的联系. 识别出标识的特定结构, 避免了求解混合整数规划这一高复杂性的算法. 实验结果表明, 对于绝大数标识, 仅仅利用结构分析就可以获得最大许可控制. 特别是对于那些非死锁非法标识, 本策略也是有效的. 该问题是目前本领域的研究难点.

探索更多结构分析技术, 处理更多的非法标识具有现实意义. 比如, 对文中只能采用线性规划方法处理的非法标识, 转而采用结构分析来处理, 计算量会进一步降低. 此外，当将线性约束转换为具有整数系数的约束时，可能产生监督控制器难以实现的大乘数. 此外，决定如何最小化监督控制器结构仍然是一个重要问题. 本研究中关注S³PR, 并在未来的工作中将结果扩展到更一般的Petri网模型.