双三相永磁同步电机(DTP-PMSM)能以较小功率器件实现大功率化,具有较小的输出转矩脉动、较强的容错能力和较高的效率等特点,正逐步应用于对功率和可靠性等性能有较高要求的场合[1]. 矢量控制以其良好的控制效果成为设计DTP-PMSM高性能控制系统的重要思想和方法,但是其需要实时检测电机速度及转子位置信号,引入速度传感器是优先的选择.
随着现代电机控制理论、电力电子和数字信号处理器等技术的发展,在难以使用速度传感器的场合,DTP-PMSM的无速度传感器控制得到了广泛关注,其方案主要分为基于基波激励数学模型的无传感器法[2-4]和基于高频信号注入的无传感器法[5-7]两大类.
基于基波激励数学模型的无传感器法主要有滑模观测器法[8-10]、模型参考自适应法[11]及卡尔曼滤波法[12]等类型. 本文采用的是滑模观测器法,它具有较强的鲁棒性、较快的响应速度、较简单的实现算法及较少的模型依赖等特点.
本文研究的DTP-PMSM具有两套对应相相差30°电角度的定子绕组,且其两个中性点彼此独立,而每套绕组在空间呈对称分布. 采用矢量空间解耦坐标变换方法,可以将DTP-PMSM的各变量分别映射到几个彼此正交的子空间[13],即参与机电能量转换的
对于基于矢量空间解耦的DTP-PMSM无速度传感器控制系统,其常规滑模观测器一般用符号函数作为开关函数获得反电动势信号,用低通滤波器进行滤波,再加入相位补偿模块,进而才得所需转速和位置信号,这使得整个观测器的结构变得较为复杂[15].
DTP-PMSM控制系统的电流控制部分一般采用旋转参考坐标系下的滞环电流控制或者比例积分(PI)电流控制. 滞环电流控制的输出电流脉动和噪声较大,PI电流控制由于增益和带宽限制,难以对交流信号实现无静差跟踪控制. 而静止参考坐标系下的比例谐振(PR)电流控制不含与电机参数有关的项,能够减少复杂的旋转坐标变换计算,能够无稳态误差地跟踪特定频率的正弦交流信号[16],故可用其代替滞环或PI电流控制.
综上所述,本文提出一种基于自适应滑模观测器(SMO)和多重比例谐振(PR)控制器的DTP-PMSM无速度传感器控制方案,并利用理论分析和仿真实验来表明所提控制方案的可行性和有效性.
1 数学模型和无速度传感器控制系统根据DTP-PMSM的电磁原理可以得到在自然坐标系下的各相绕组的电压、电流及磁链之间的关系表达式,进而得到它的原始数学模型. 为了方便后面的分析和设计,可以采用矢量空间解耦坐标变换方法对此数学模型进行简化.
为了便于简化分析,在此忽略零序子空间的影响,这样将DTP-PMSM在自然坐标系下的各个变量转换到静止坐标系的变换方程为
| ${\left[ {{f_\alpha }}\;\;{{f_\beta }}\;\;{{f_x}}\;\;{{f_y}} \right]^{\rm{T}}} = {{{T}}_{\alpha \beta }}\left[ {{f_A}}\;\;{{f_B}}\;\;{{f_C}}\;\;{{f_U}}\;\;{{f_V}}\;\;{{f_W}} \right],$ | (1) |
其中,变换矩阵
| ${{{T}}_{\alpha \beta }} = \displaystyle\frac{1}{3}\left[{\begin{array}{*{20}{c}} 1&{-\displaystyle\frac{1}{2}}&{-\displaystyle\frac{1}{2}}&{\displaystyle\frac{{\sqrt 3 }}{2}}&{-\displaystyle\frac{{\sqrt 3 }}{2}}&0 \\ 0&{\displaystyle\frac{{\sqrt 3 }}{2}}&{ - \displaystyle\frac{{\sqrt 3 }}{2}}&{\displaystyle\frac{1}{2}}&{\displaystyle\frac{1}{2}}&{ - 1} \\ 1&{ - \displaystyle\frac{1}{2}}&{ - \displaystyle\frac{1}{2}}&{ - \displaystyle\frac{{\sqrt 3 }}{2}}&{\displaystyle\frac{{\sqrt 3 }}{2}}&0 \\ 0&{ - \displaystyle\frac{{\sqrt 3 }}{2}}&{\displaystyle\frac{{\sqrt 3 }}{2}}&{\displaystyle\frac{1}{2}}&{\displaystyle\frac{1}{2}}&{ - 1} \end{array}} \right].$ | (2) |
通过计算可得表贴式DTP-PMSM在静止坐标系下
| $\left[{\begin{array}{*{20}{c}} {{u_\alpha }} \\ {{u_\beta }} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} R&0 \\ 0&R \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{i_\alpha }} \\ {{i_\beta }} \end{array}} \right] + \left[{\begin{array}{*{20}{c}} {{L_{\rm{s}}}}&0 \\ 0&{{L_{\rm{s}}}} \end{array}} \right]\frac{{\rm{d}}}{{{\rm{d}}t}}\left[{\begin{array}{*{20}{c}} {{i_\alpha }} \\ {{i_\beta }} \end{array}} \right] + \left[{\begin{array}{*{20}{c}} {{e_\alpha }} \\ {{e_\beta }} \end{array}} \right],$ | (3) |
| $\left[{\begin{array}{*{20}{c}} {{u_x}} \\ {{u_y}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} R&0 \\ 0&R \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{i_x}} \\ {{i_y}} \end{array}} \right] + \left[{\begin{array}{*{20}{c}} {{L_{\rm{z}}}}&0 \\ 0&{{L_{\rm{z}}}} \end{array}} \right]\frac{{\rm{d}}}{{{\rm{d}}t}}\left[{\begin{array}{*{20}{c}} {{i_x}} \\ {{i_y}} \end{array}} \right],$ | (4) |
其中,
| ${e_\alpha } = - {\psi _{\rm{f}}}{\omega _{\rm{e}}}\sin {\theta _{\rm{e}}}{\rm{, }}\;\;\;\;{e_\beta } = {\psi _{\rm{f}}}{\omega _{\rm{e}}}\cos {\theta _{\rm{e}}}.$ | (5) |
式(5)中,
由式(3)和式(4)可知DTP-PMSM的数学模型实现了完全的解耦,从而可以将应用于三相PMSM的矢量控制策略推广到DTP-PMSM. 另外由式(5)可知反电动势分量蕴含有电机转速和转子位置信息.
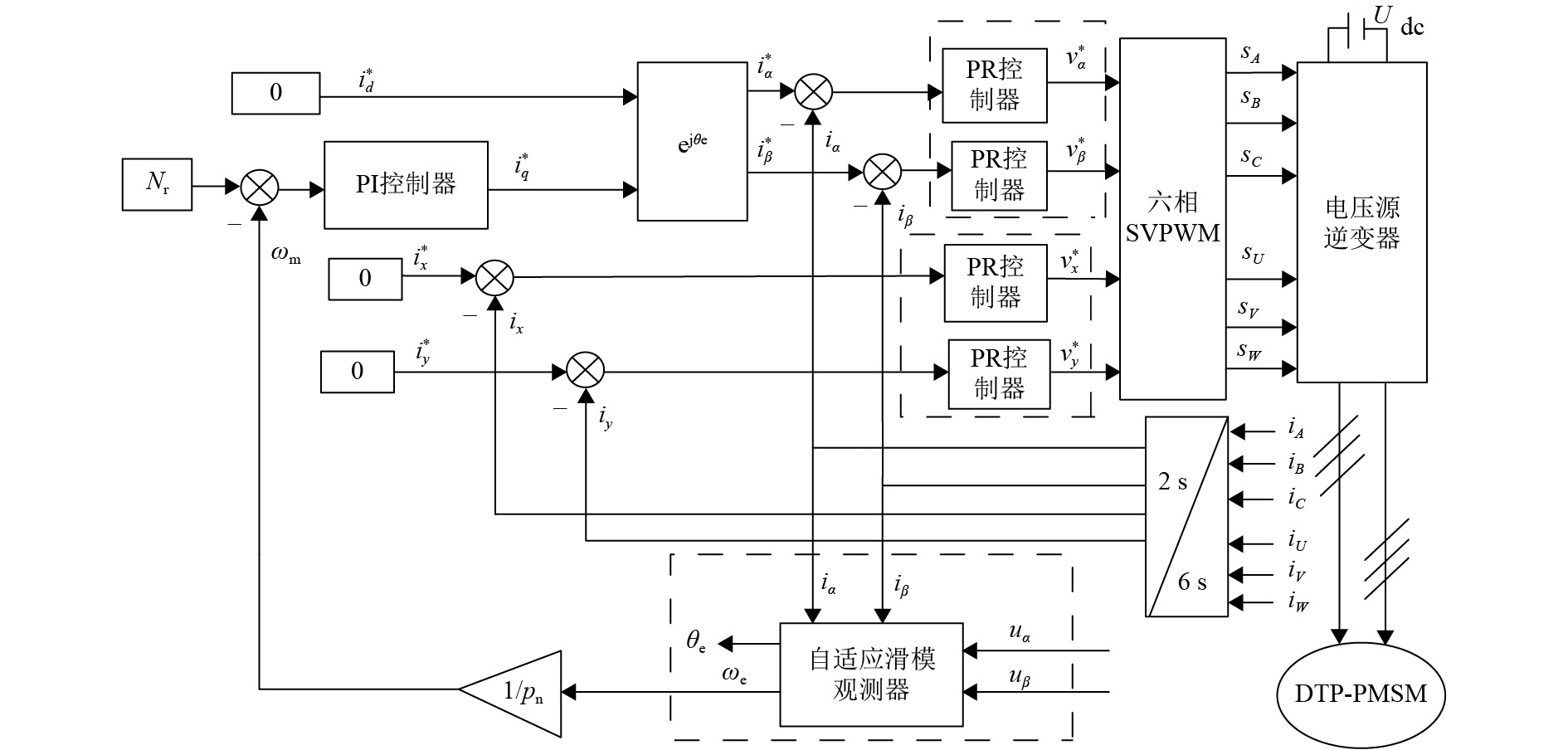
基于自适应滑模观测器和多重比例谐振控制器的DTP-PMSM无速度传感器控制系统的原理框图如图1所示。其中,
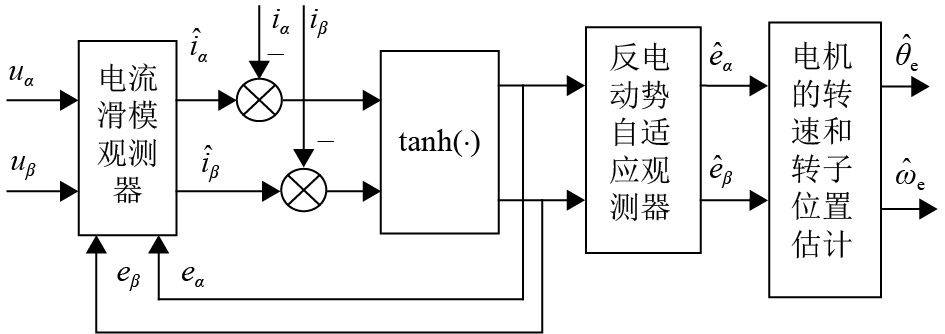
需要指出,用于观测电机转速和转子位置的自适应滑模观测器是实现无速度传感器控制的核心单元,而由4个PR控制器构成的多重比例谐振控制器则是进一步提升控制性能的核心部分. 对于图1中的自适应滑模观测器(图中最下面的虚线框内部分),其原理框图如图2所示. 该观测器包括电流滑模观测器和反电动势自适应观测器两部分,其中电流滑模观测器采用双曲正切函数(tanh)作为开关函数来代替符号函数. 因为双曲正切函数具有连续光滑性,故其可以有效地削弱自适应滑模观测器的滑模抖动. 电流滑模观测器的后一级采用的反电动势自适应观测器能够有效地估计和提取反电动势信号,免除了低通滤波器和相位补偿模块,并进而实现电机转速和转子位置的估计.
|
图 1 DTP-PMSM无速度传感器控制系统原理框图 Figure 1 Block diagram of speed sensorless control system for DTP-PMSM |
|
图 2 自适应滑模观测器原理框图 Figure 2 Block diagram of the adaptive SMO strategy |
前已述及,DTP-PMSM数学模型经过矢量空间解耦坐标变换后,自适应滑模观测器的设计和分析可以在静止坐标系下的
为了方便设计和分析DTP-PMSM控制系统,以及为了方便仿真模型的搭建,现将DTP-PMSM数学模型写为状态方程的形式. 选用电流分量作为状态变量,根据式(3)可得表贴式DTP-PMSM的状态空间表达式为
| $\left\{ {\begin{array}{*{20}{c}} {\displaystyle\frac{{{\rm{d}}{i_\alpha }}}{{{\rm{d}}t}} = - \displaystyle\frac{R}{{{L_{\rm{s}}}}}{i_\alpha } + \displaystyle\frac{1}{{{L_{\rm{s}}}}}{u_\alpha } - \displaystyle\frac{1}{{{L_{\rm{s}}}}}{e_\alpha }}, \\ {\displaystyle\frac{{{\rm{d}}{i_\beta }}}{{{\rm{d}}t}} = - \displaystyle\frac{R}{{{L_{\rm{s}}}}}{i_\beta } + \displaystyle\frac{1}{{{L_{\rm{s}}}}}{u_\beta } - \displaystyle\frac{1}{{{L_{\rm{s}}}}}{e_\beta }}. \end{array}} \right.$ | (6) |
根据滑模变结构控制理论,考虑将DTP-PMSM的电流滑模观测器设计为
| $\left\{ {\begin{array}{*{20}{c}} {\displaystyle\frac{{{\rm{d}}{{\hat i}_\alpha }}}{{{\rm{d}}t}} = - \displaystyle\frac{R}{{{L_{\rm{s}}}}}{{\hat i}_\alpha } + \displaystyle\frac{1}{{{L_{\rm{s}}}}}{u_\alpha } - \displaystyle\frac{1}{{{L_{\rm{s}}}}}{k_1}\tanh \left( {{{\hat i}_\alpha } - {i_\alpha }} \right)}, \\ {\displaystyle\frac{{{\rm{d}}{{\hat i}_\beta }}}{{{\rm{d}}t}} = - \displaystyle\frac{R}{{{L_{\rm{s}}}}}{{\hat i}_\beta } + \displaystyle\frac{1}{{{L_{\rm{s}}}}}{u_\beta } - \displaystyle\frac{1}{{{L_{\rm{s}}}}}{k_2}\tanh \left( {{{\hat i}_\beta } - {i_\beta }} \right)}. \end{array}} \right.$ | (7) |
其中,
| $\tanh \left( {ax} \right) = \frac{{\exp \left( {ax} \right) - \exp \left( { - ax} \right)}}{{\exp \left( {ax} \right) + \exp \left( { - ax} \right)}}.$ | (8) |
式(8)中,
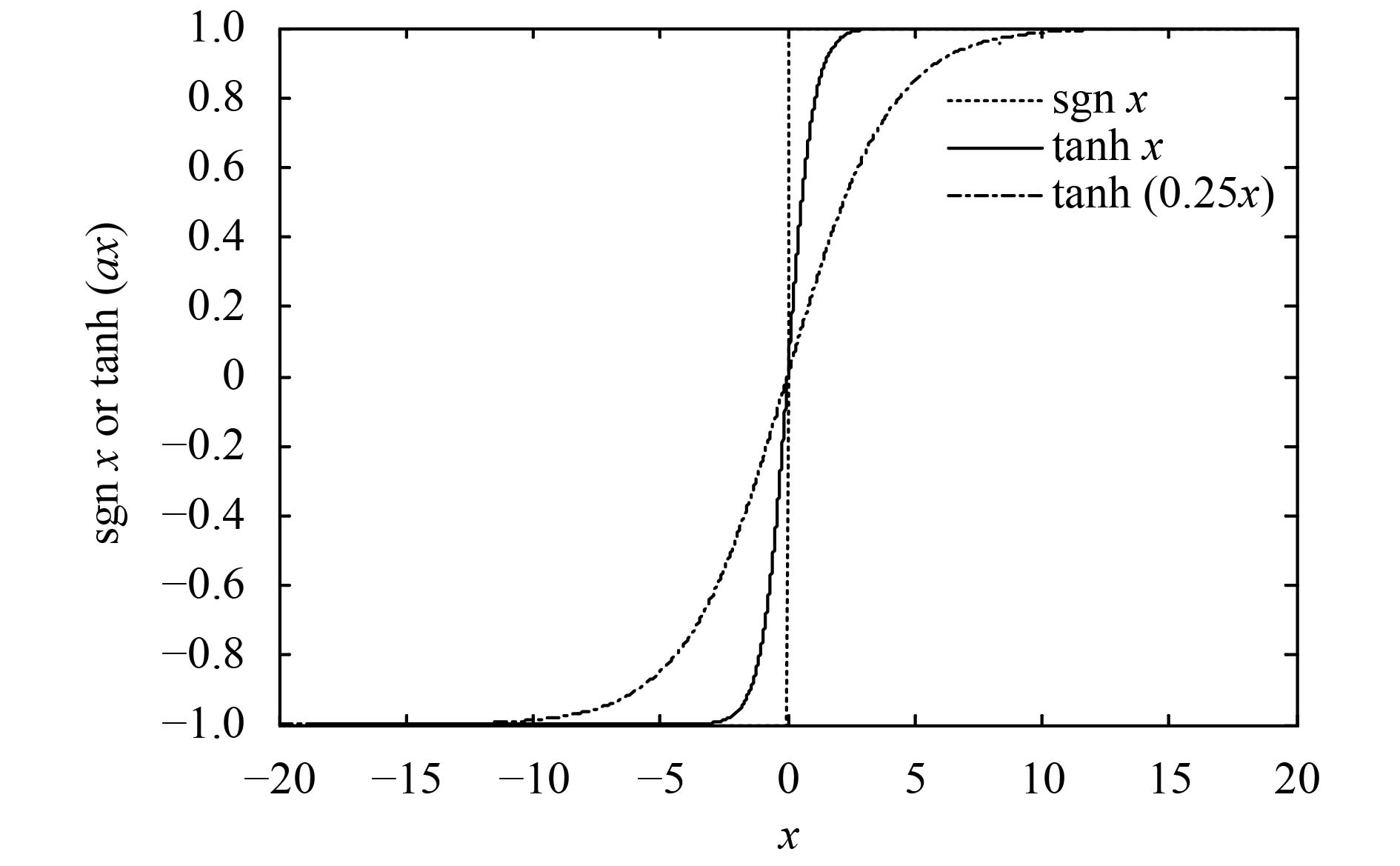
双曲正切函数的形状特性如图3所示,其中列出了
|
图 3 符号函数及双曲正切函数的曲线形状 Figure 3 Curves of signum function and hyperbolic tangent function |
为了证明所设计的电流滑模观测器的稳定性,先给出其滑模面以及有关的李雅普诺夫函数的定义. 定义电流滑模观测器的滑模面为
| ${{s}} = \left[{\begin{array}{*{20}{c}} {{{\tilde i}_\alpha }} \\ {{{\tilde i}_\beta }} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{{\hat i}_\alpha }-{i_\alpha }} \\ {{{\hat i}_\beta }-{i_\beta }} \end{array}} \right].$ | (9) |
式(9)中,
| $V = \frac{1}{2}{{{s}}^{\rm{T}}}{{s}} = \frac{1}{2}\left( {{{\tilde i}_\alpha }^2 + {{\tilde i}_\beta }^2} \right).$ | (10) |
显然,李氏函数式(10)是正定的,下面证明其导数还是负定的. 对式(10)求导,有
| $\dot V = {{{s}}^{\rm{T}}}{\dot{ s}} = {\tilde i_\alpha }{{\dot{\tilde{i}}}_{\alpha }} + {\tilde i_\beta }{{\dot{\tilde{i}}}_{\beta }}.$ | (11) |
其中,
将式(7)减去式(6),可得
| $\left\{ {\begin{array}{*{20}{c}} {\displaystyle\frac{{\rm{d}}}{{{\rm{d}}t}}{{\tilde i}_\alpha } = - \displaystyle\frac{R}{{{L_{\rm{s}}}}}{{\tilde i}_\alpha } + \displaystyle\frac{1}{{{L_{\rm{s}}}}}{e_\alpha } - \displaystyle\frac{1}{{{L_{\rm{s}}}}}{k_1}\tanh \left( {{{\tilde i}_\alpha }} \right)}, \\ {\displaystyle\frac{{\rm{d}}}{{{\rm{d}}t}}{{\tilde i}_\beta } = - \displaystyle\frac{R}{{{L_{\rm{s}}}}}{{\tilde i}_\beta } + \displaystyle\frac{1}{{{L_{\rm{s}}}}}{e_\beta } - \displaystyle\frac{1}{{{L_{\rm{s}}}}}{k_2}\tanh \left( {{{\tilde i}_\beta }} \right)} . \end{array}} \right.$ | (12) |
将式(12)代入式(11)中,可得
| $\begin{split} &\dot V = - \displaystyle\frac{R}{{{L_{\rm{s}}}}}\left( {{{\tilde i}_\alpha }^2 + {{\tilde i}_\beta }^2} \right) + \displaystyle\frac{1}{{{L_{\rm{s}}}}}\left\{ {{{\tilde i}_\alpha }{e_\alpha } - {k_1}{{\tilde i}_\alpha }{\rm tanh}\left( {{{\tilde i}_\alpha }} \right)} \right.+\\ &\left. { {{\tilde i}_\beta }{e_\beta } - {k_2}{{\tilde i}_\beta }{\rm tanh}\left( {{{\tilde i}_\beta }} \right)} \right\}. \end{split}$ | (13) |
当取
| ${{s}} = {\left[{\begin{array}{*{20}{c}} {{{\tilde i}_\alpha }}&{{{\tilde i}_\beta }} \end{array}} \right]^{\rm{T}}} = 0{\rm{, }}\;\;\;\;{\dot{ s}} = {\left[{\begin{array}{*{20}{c}} {{\dot{\tilde{i}}_\alpha }}&{{\dot{\tilde{i}}_\beta }} \end{array}} \right]^{\rm{T}}} = 0.$ | (14) |
将式(14)代入式(12),可得
| ${e_\alpha } = {k_1}\tanh \left( {{{\tilde i}_\alpha }} \right){\rm{, }}\;\;\;\;{e_\beta } = {k_2}\tanh \left( {{{\tilde i}_\beta }} \right).$ | (15) |
考虑前述的表贴式DTP-PMSM数学模型中的反电动势表达式(5),可得其估计值表达式为
| ${\hat e_\alpha } = - {\psi _{\rm{f}}}{\hat \omega _{\rm{e}}}\sin {\hat \theta _{\rm{e}}}{\rm{, }}\;\;\;\;{\hat e_\beta } = {\psi _{\rm{f}}}{\hat \omega _{\rm{e}}}\cos {\hat \theta _{\rm{e}}}.$ | (16) |
另外,对式(5)两边分别求导,并考虑到电机的机械时间常数远大于电气时间常数,故可认为电机的电角速度在一个估算周期内不变,即
| $\left\{\!\!\!\begin{array}{l} {{\dot e}_\alpha } = - {\psi _{\rm{f}}}{{\dot \omega }_{\rm{e}}}\sin {\theta _{\rm{e}}} + \left( { - {\psi _{\rm{f}}}{\omega _{\rm{e}}}\cos {\theta _{\rm{e}}}} \right) \cdot {{\dot \theta }_{\rm{e}}} = - {\omega _{\rm{e}}}{e_\beta },\\ {{\dot e}_\beta } = {\psi _{\rm{f}}}{{\dot \omega }_{\rm{e}}}\cos {\theta _{\rm{e}}} + \left( { - {\psi _{\rm{f}}}{\omega _{\rm{e}}}\sin {\theta _{\rm{e}}}} \right) \cdot {{\dot \theta }_{\rm{e}}} = {\omega _{\rm{e}}}{e_\alpha }. \end{array} \right.$ | (17) |
根据自适应观测器设计方法,并考虑到反电动势微分表达式(17),可以将反电动势自适应观测器设计为
| $\left\{ \begin{array}{l} {\dot{\hat{e}}_\alpha } = - {{\hat \omega }_{\rm{e}}}{{\hat e}_\beta } - {k_1}\left( {{{\hat e}_\alpha } - {e_\alpha }} \right) = - {{\hat \omega }_{\rm{e}}}{{\hat e}_\beta } - {k_1}{{\tilde e}_\alpha },\\ {\dot{\hat{e}}_\beta } = {{\hat \omega }_{\rm{e}}}{{\hat e}_\alpha } - {k_2}\left( {{{\hat e}_\beta } - {e_\beta }} \right) = {{\hat \omega }_{\rm{e}}}{{\hat e}_\alpha } - {k_2}{{\tilde e}_\beta },\\ {\dot{\hat{\omega }}_{\rm{e}}} = {{\tilde e}_\alpha }{{\hat e}_\beta } - {{\hat e}_\alpha }{{\tilde e}_\beta } - {k_3}{{\tilde \omega }_{\rm{e}}}. \end{array} \right.$ | (18) |
其中,
为了证明所设计的反电动势自适应观测器的稳定性,构造相应的的李雅普诺夫函数如下
| $V = \frac{1}{2}{\tilde e_\alpha }^2 + \frac{1}{2}{\tilde e_\beta }^2 + \frac{1}{2}{\tilde \omega _{\rm{e}}}^2.$ | (19) |
显然,所构造的李氏函数式(19)是正定的. 现在对式(19)求导,考虑到
| $\begin{split} &\dot V = {{\tilde e}_\alpha }{{\dot {\tilde e}}_\alpha } + {{\tilde e}_\beta }{{\dot {\tilde e}}_\beta } + {{\tilde \omega }_{\rm{e}}}{{\dot {\tilde \omega} }_{\rm{e}}}=\\ &{{\tilde e}_\alpha }\left( {{{\dot {\hat e}}_\alpha } - {{\dot e}_\alpha }} \right) + {{\tilde e}_\beta }\left( {{{\dot {\hat e}}_\beta } - {{\dot e}_\beta }} \right) + {{\tilde \omega }_{\rm{e}}}\left( {{{\dot {\hat \omega} }_{\rm{e}}} - {{\dot \omega }_{\rm{e}}}} \right)=\\ &- \left( {{k_1}{{\tilde e}_\alpha }^2 + {k_2}{{\tilde e}_\beta }^2 + {k_3}{{\tilde \omega }_{\rm{e}}}^2} \right). \end{split}$ | (20) |
取
| $\dot V \leqslant - k\left( {{{\tilde e}_\alpha }^2 + {{\tilde e}_\beta }^2 + {{\tilde \omega }_{\rm{e}}}^2} \right) = - 2kV.$ | (21) |
由式(21)可得
| $V\left( t \right) \leqslant {{\rm{e}}^{ - 2k\left( {t - {t_0}} \right)}}V\left( {{t_0}} \right).$ | (22) |
因
至此,可以直接由反电动势的估计值得到电机的电角速度和转子位置. 根据反电动势
| ${\hat \theta _{\rm{e}}} = - \arctan \left( {\frac{{{{\hat e}_\alpha }}}{{{{\hat e}_\beta }}}} \right){\rm{, }}\;\;\;\;{\hat \omega _{\rm{e}}} = \frac{{\sqrt {{{\hat e}_\alpha }^2 + {{\hat e}_\beta }^2} }}{{{\psi _{\rm{f}}}}}.$ | (23) |
考虑到实际运行过程中电机的永磁体磁链
理想的PR控制器由比例调节器和谐振调节器组成,因为其在谐振频率处具有无穷大增益,故能够实现无静差地跟踪控制特定频率的交流输入信号,但是其高增益频带过窄,从而对输入信号的频率变化会十分敏感,进而造成系统波动. 在实际应用中,为了拓宽系统频带,增强系统稳定性,一般采用改进的准PR控制器[17],其传递函数为
| ${G_{{\rm{PR}}}}\left( s \right) = {K_{\rm{p}}} + \frac{{2{K_{\rm{i}}}{\omega _{\rm{c}}}s}}{{{s^2} + 2{\omega _{\rm{c}}}s + {\omega _0}^2}}.$ | (24) |
其中,
若非特别说明,本文后面提到的PR控制器皆是指准PR控制器,两者之间不再加以区分.
3.1因为静止参考坐标系下的PR电流控制器能够减少复杂的旋转坐标变换计算,能够无稳态误差地跟踪特定频率的正弦交流输入信号,加之基于矢量空间解耦的DTP-PMSM模型的3个子空间实现了完全解耦,故可以在静止坐标系下的
受到谐波磁链、互漏感等因素的影响,双三相永磁同步电机容易产生大量的
谐波电流不但增加电机损耗和额外增大逆变器容量,还影响电机的控制性能,需要被有效地抑制. 根据矢量空间解耦理论,不参与机电能量转换的
对于所设计的的DTP-PMSM无速度传感器控制系统,为了验证所提出的自适应滑模观测器和多重PR控制器的有效性,利用Matlab/Simulink仿真软件,根据如图1所示的原理框图搭建仿真模型.
所用电机的参数为:定子交、直轴的电感为
仿真参数设置为:直流侧电压为
基于速度传感器和PI电流控制器的DTP-PMSM速度控制系统(简称为SensorPI系统)能够较好地实现速度或位置控制,是一种成熟的解决方案,广泛应用于实际的工程场合,但是其电机相电流中的谐波成份较多. 为了表明本文所提出的自适应滑模观测器和多重PR控制器的有效性,本文将此成熟方案的实验结果一并给出以作为对比,所用的电机参数和仿真参数与基于自适应滑模观测器和多重PR控制器的DTP-PMSM无速度传感器控制系统(简称为SensorlessPR系统)相同.
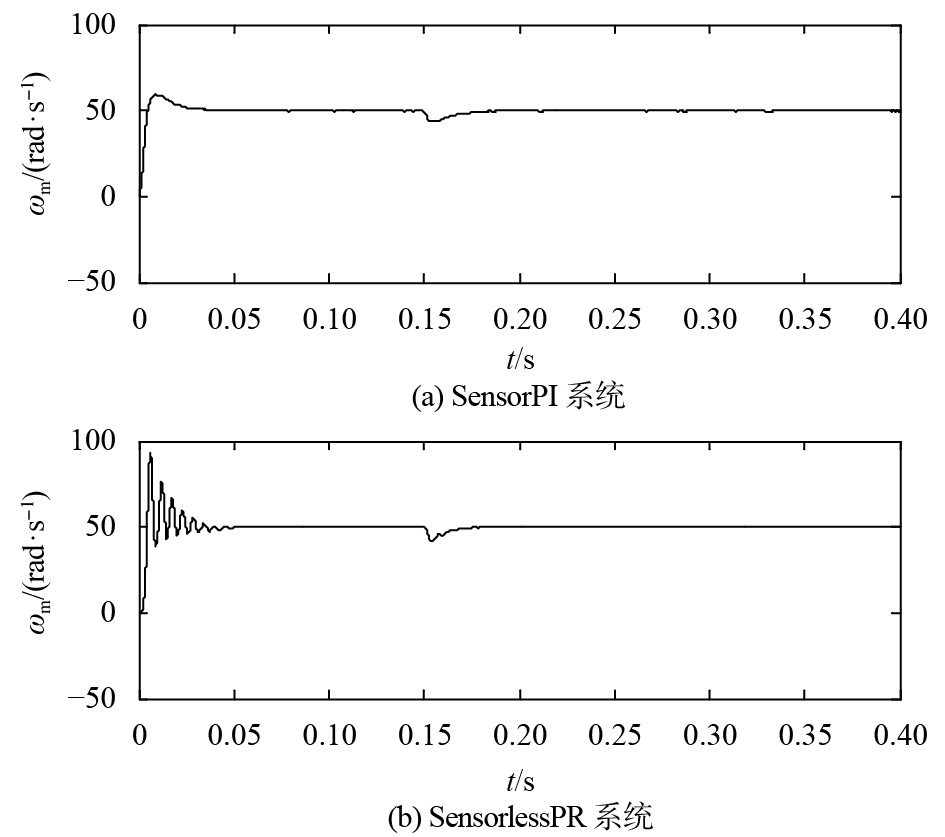
在额定转速以及随后突加负载转矩的条件下,仿真实验结果如图4~10所示,其中图4、图5、图7和图8的上半部分是SensorPI系统的实验结果,而相应的下半部分是SensorlessPR系统的实验结果. 需要指出,因自适应滑模观测器依赖电机转速,故在电机的起始的零低速阶段会失效,需要借助其他技术手段予以解决,由于篇幅所限,本文不予赘述.
|
图 4 转子速度
|
|
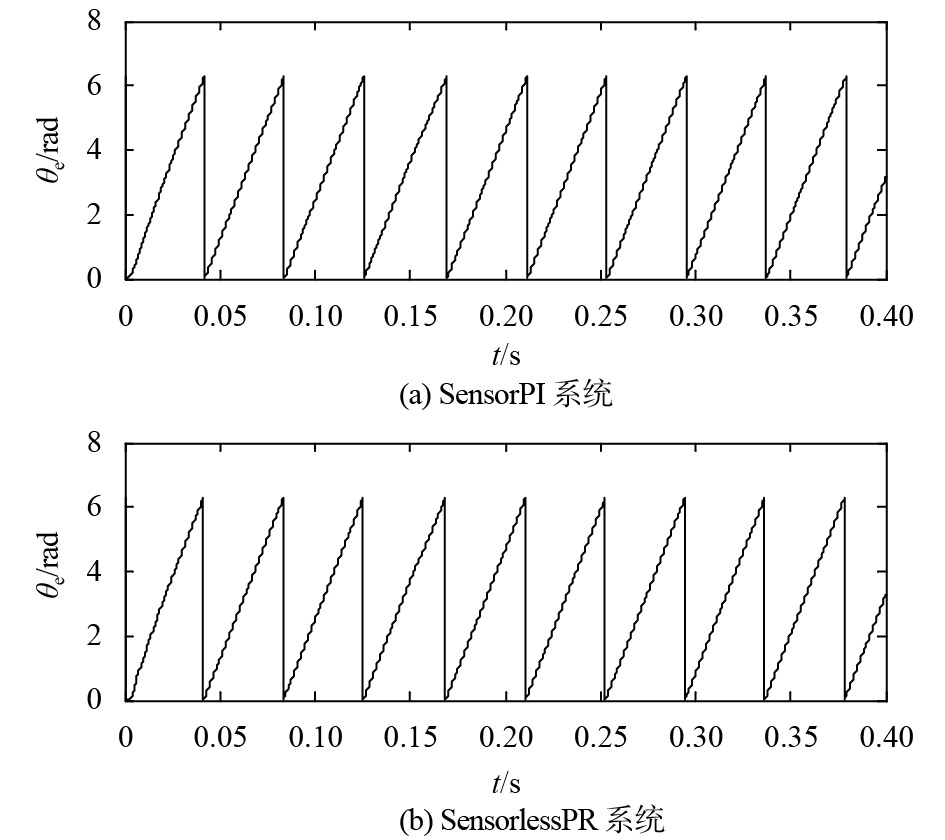
图 5 转子位置
|
|
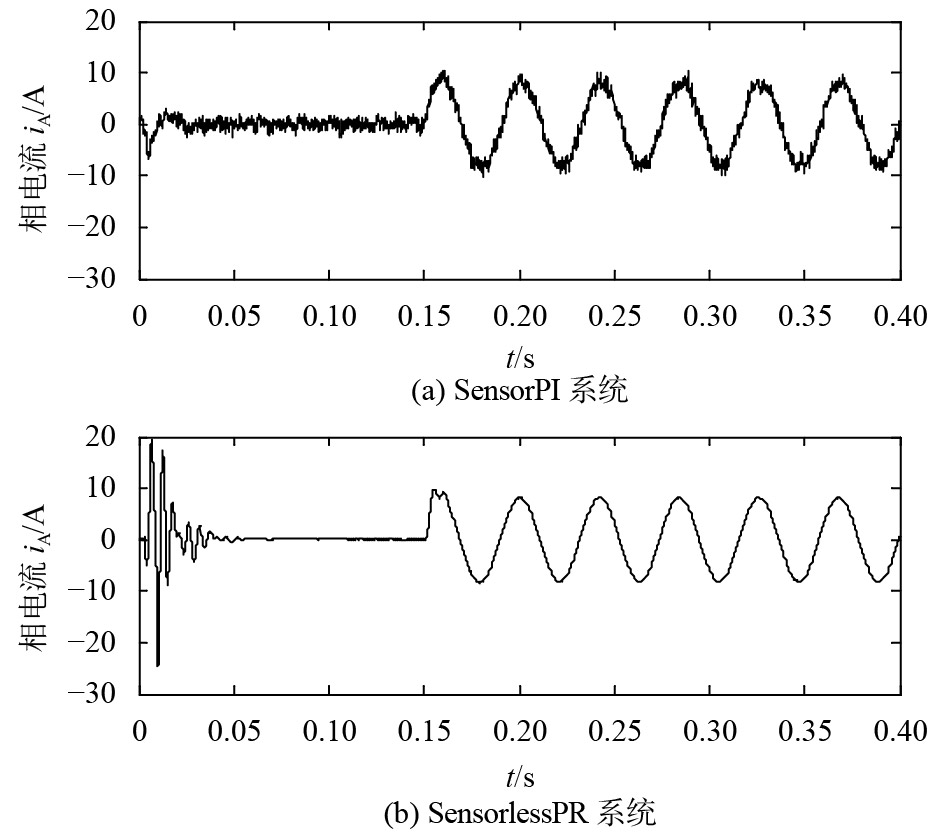
图 7 相电流
|
|
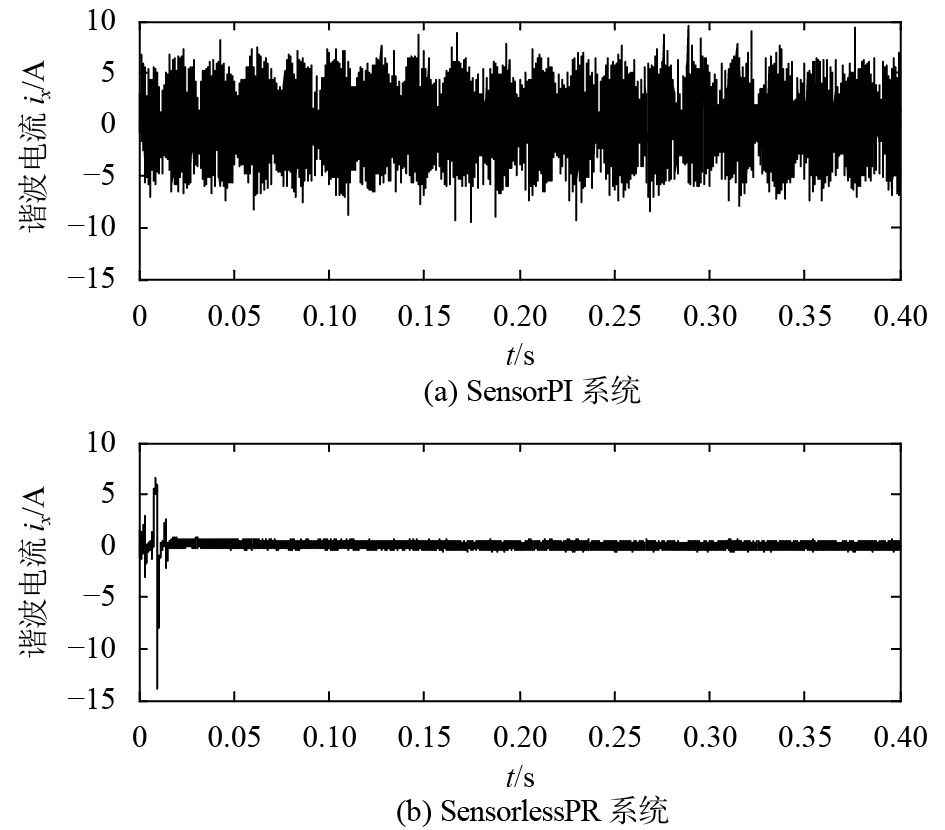
图 8 谐波电流
|
图4和图5给出了SensorPI系统和SensorlessPR系统中电机的转速及转子位置的对比情况. 图4中,除了起始的零低速阶段,两者的转速图形较为吻合,都能有效地跟踪给定转速,都能克服在
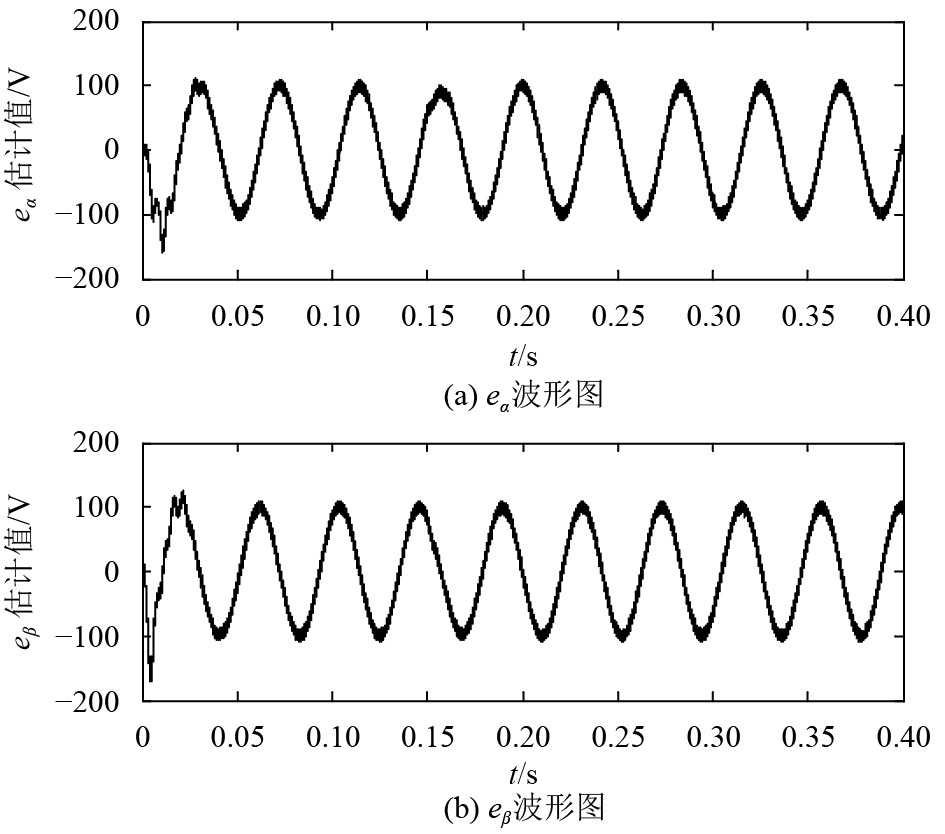
图6给出了SensorlessPR系统的自适应滑模观测器对反电动势
|
图 6 反电动势波形图
Figure 6 Estimated value of back EMF
|
图7是SensorPI系统和SensorlessPR系统中电机的相电流波形的对比情形. 图中,除了起始的零低速阶段,两者的相电流波形总体上较为相似,两者对
图8是SensorPI系统和SensorlessPR系统中电机的
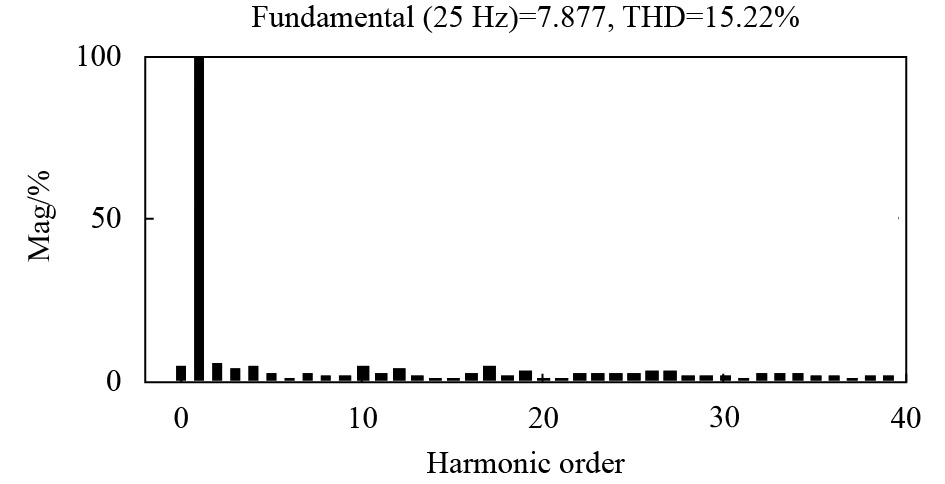
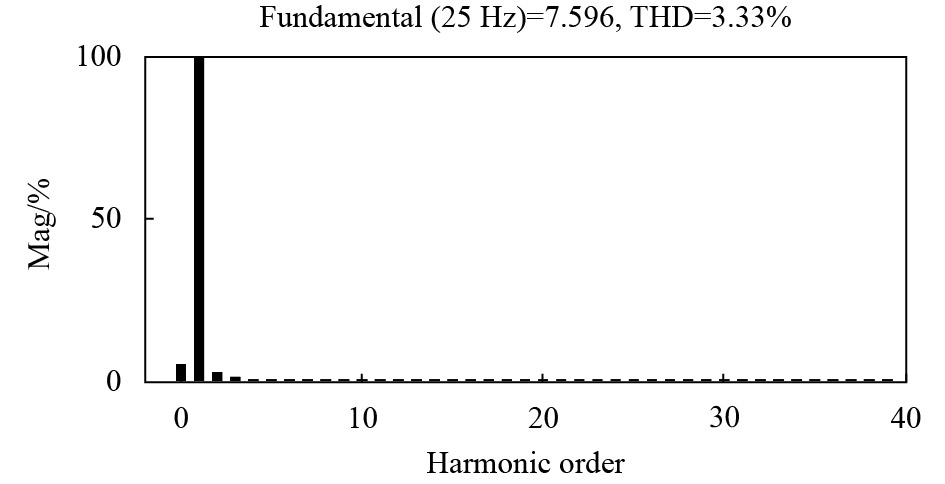
图9~10分别给出了SensorPI系统以及SensorlessPR系统中电机相电流的FFT分析图. 由图可知,相较于前者,后者的电机相电流中的
|
图 9 SensorPI系统中电机相电流的FFT分析图 Figure 9 FFT analysis of phase current of motor for SensorPI system |
综合图7~10可知,SensorlessPR系统中电机的
|
图 10 SensorlessPR系统中电机相电流的FFT分析图 Figure 10 FFT analysis of phase current of motor for SensorlessPR system |
基于矢量空间解耦理论,本文对DTP-PMSM无速度传感器控制系统设计了自适应滑模观测器和多重PR控制器. 除了起始的零低速阶段,所设计的自适应滑模观测器能够有效地观测反电动势信号,能够有效地跟踪实际电机转速和转子位置,且具有较好的抗扰性,此外其稳定性通过构造的李雅普诺夫函数也得到证明. 对于所设计的多重比例谐振控制器,
| [1] |
KARTTUNEN J, KALLIO S, PELTONIEMI P, et al. Decoupled vector control scheme for dual three-phase permanent magnet synchronous machines[J].
IEEE Transactions on Industrial Electronics, 2014, 61(5): 2185-2196.
DOI: 10.1109/TIE.2013.2270219. |
| [2] |
WANG G, LI T, ZHANG G, et al. Position estimation error reduction using recursive-least-square adaptive filter for model-based sensorless interior permanent-magnet synchronous motor drives[J].
IEEE Transactions on Industrial Electronics, 2014, 61(9): 5115-5125.
DOI: 10.1109/TIE.2013.2264791. |
| [3] |
WANG G, ZHAN H, ZHANG G, et al. Adaptive compensation method of position estimation harmonic error for eMF-based observer in sensorless IPMSM drives[J].
IEEE Transactions on Power Electronics, 2014, 29(6): 3055-3064.
DOI: 10.1109/TPEL.2013.2276613. |
| [4] |
LIN S, ZHANG W. An adaptive sliding-mode observer with a tangent function-based PLL structure for position sensorless PMSM drives[J].
International Journal of Electrical Power & Energy Systems, 2017, 88: 63-74.
|
| [5] |
刘海东, 周波, 郭鸿浩, 等. 脉振高频信号注入法误差分析[J].
电工技术学报, 2015, 30(6): 38-44.
LIU H D, ZHOU B, GUO H H, et al. Error analysis of high frequency pulsating signal injection method[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 38-44. DOI: 10.3969/j.issn.1000-6753.2015.06.005. |
| [6] |
RAMEZANI M, OJO J. The modeling and position sensor-less estimation technique for a nine-phase interior permanent magnet machine using high frequency injections[J].
IEEE Transactions on Industry Applications, 2016, 52(2): 1555-1565.
|
| [7] |
LIU J M, ZHU Z Q. Novel sensorless control strategy with injection of high-frequency pulsating carrier signal into stationary reference frame[J].
IEEE Transactions on Industry Applications, 2014, 50(4): 2574-2583.
DOI: 10.1109/TIA.2013.2293000. |
| [8] |
KIM H, SON J, LEE J. A high-speed sliding-mode observer for the sensorless speed control of a PMSM[J].
IEEE Transactions on Industrial Electronics, 2011, 58(9): 4069-4077.
DOI: 10.1109/TIE.2010.2098357. |
| [9] |
LEE H, LEE J. Design of iterative sliding mode observer for sensorless PMSM control[J].
IEEE Transactions on Control Systems Technology, 2013, 21(4): 1394-1399.
DOI: 10.1109/TCST.2012.2199493. |
| [10] |
QIAO Z, SHI T, WANG Y, et al. New sliding-mode observer for position sensorless control of permanent-magnet synchronous motor[J].
IEEE Transactions on Industrial Electronics, 2013, 60(2): 710-719.
DOI: 10.1109/TIE.2012.2206359. |
| [11] |
胡维昊, 王跃, 李明烜, 等. 基于MRAS的多相永磁直驱型风力发电系统无速度传感器控制策略研究[J].
电力系统保护与控制, 2014(23): 118-124.
HU W H, WANG Y, LI M X, et al. Research on sensorless control strategy of direct drive multi-phase PMSG wind power generation system based on MRAS[J]. Power System Protection and Control, 2014(23): 118-124. DOI: 10.7667/j.issn.1674-3415.2014.23.019. |
| [12] |
QUANG N K, HIEU N T, HA Q P. FPGA-based sensorless PMSM speed control using reduced-order extended kalman filters[J].
IEEE Transactions on Industrial Electronics, 2014, 61(12): 6574-6582.
DOI: 10.1109/TIE.2014.2320215. |
| [13] |
CHE H S, LEVI E, JONES M, et al. Current control methods for an asymmetrical six-phase induction motor drive[J].
IEEE Transactions on Power Electronics, 2014, 29(1): 407-417.
DOI: 10.1109/TPEL.2013.2248170. |
| [14] |
YUAN L, CHEN M L, SHEN J Q, et al. Current harmonics elimination control method for six-phase PM synchronous motor drives[J].
Isa Transactions, 2015, 59: 443-449.
DOI: 10.1016/j.isatra.2015.09.013. |
| [15] |
REN J J, LIU Y C, WANG N, et al. Sensorless control of ship propulsion interior permanent magnet synchronous motor based on a new sliding mode observer[J].
Isa Transactions, 2015, 54(2): 15-26.
|
| [16] |
ZMOOD D N, HOLMES D G, BODE G H. Frequency domain analysis of three-phase linear current regulator[J].
IEEE Transactions on Industry Applications, 2001, 37(2): 601-610.
DOI: 10.1109/28.913727. |
| [17] |
张淼, 苏协飞. 基于比例谐振和谐波补偿控制技术的单相逆变并网研究[J].
广东工业大学学报, 2016, 33(5): 59-64.
ZHANG M, SU X F. Research on proportional-resonant controller and harmonic compensation for grid-connected inverter[J]. Journal of Guangdong University of Technology, 2016, 33(5): 59-64. DOI: 10.3969/j.issn.1007-7162.2016.05.011. |
| [18] |
HU Y, ZHU Z Q, LIU K. Current control for dual three-phase permanent magnet synchronous motors accounting for current unbalance and harmonics[J].
IEEE Journal of Emerging & Selected Topics in Power Electronics, 2014, 2(2): 272-284.
|
 2019, Vol. 36
2019, Vol. 36

