随着竞争越来越激烈,企业自身的能力是有限的,为了更好地发展,往往需要通过市场融资的方式筹集资金解决发展问题. 常见的融资方式有银行贷款、股权筹资、债券融资和融资租赁等等,而本文只考虑银行贷款融资. 银行向企业的商业贷款是在货币政策的指引下进行的. 货币政策可以分为扩张性货币政策与收缩性货币政策,下面简称货币宽松政策与货币紧缩政策. 企业对融资具有3种不同的风险偏好态度,分别是风险规避、风险中性与风险追求. 这3种不同的态度会影响企业的融资策略与发展战略.
根据Caldentey R[1]、Kouveils P[2]和Li Y[3]的研究,证明银行融资可以提高供应链的绩效,即最优采购量与利润都提高了. 它们是在不考虑竞争的条件下得出的结论. 本文在此基础上进行延伸,探究在非合作竞争条件下,3家旅行社在采取不同的银行融资策略后利润与绩效的表现. 本文的绩效指的是旅行社产品的质量、数量和个性化. 因为融资可以为企业注入新的活力,通过融资,企业可以利用融资得到资金提高产品的质量,增加产品的个性化以及提高产品的产量,所以融资最终会影响企业的收益状况,因此本文构建了包含收益效用与融资效用的效用函数. 还考虑了融资的效用是受企业管理者的风险偏好程度的影响.
本文认为,旅行社之间的竞争是符合严格的博弈论框架的,通过使用变分不等式理论构建这样的框架,用于制定控制纳什均衡的条件,计算均衡数量、质量和个性化. 有关变分不等式方法的背景与适用于有关质量的供应链竞争,请参考Nagurney 和Li D[4-5]的文献. 博弈论通常被用来探究企业之间的合作与竞争关系,朱莹等[6]构建博弈模型探究企业的合作与竞争的策略选择. 最近有几篇有关通过拉格朗日乘数法模拟均衡问题来分析变分不等式的解. 例如,在运筹学中,Barbagallo等[7]提出财务均衡问题的论文. Saberi S等[8]提出了具有多功能供应链的货运运营网络模型. Nagurney和Yu M等[9]提出了供应链网络博弈论框架为了最大限度地实现多个制造商与制造工厂在非合作竞争下的利润最大化.
本文的结构如下. 第1节构建纳什收益模型,并给出了非合作竞争纳什均衡的定义和提出了变分不等式,还证明了均衡解的存在性. 第2节介绍了通过使用拉格朗日乘数构建变分不等式的替换公式,并对旅行社的产品质量、产品个性化和产品数量进行边际效用分析. 第3节实例分析3家旅行社的两种旅游产品的非合作竞争,并运用Python的软件包SymPy进行仿真分析. 第4节总结结论.
1 收益纳什均衡模型本文主要运用纳什均衡定理对竞争模型进行探究. 假设有
假设旅行社
| ${{\mathop q\limits^{\smile}} _{ij}} \leqslant {q_{ij}} \leqslant {{\mathop q\limits^{\frown}} _{ij}}.$ |
另外,相关的质量水平是有界的. 通常本文会设置最低的质量标准,这里本文用
| ${{\mathop Q\limits^{\smile}} _{ij}} \leqslant {Q_{ij}} \leqslant {{\mathop Q\limits^{\frown}} _{ij}}.$ |
产品的个性化是指旅行社会根据消费者的偏好制定各种个性化旅游产品,为消费者提高个性化服务. 以云南旅游为例,哪怕是在同一个旅行社,它都会为消费者提供各种各样去云南游玩的旅游产品,即云南旅游只是这些旅游产品的统称. 旅行社
| ${{\mathop s\limits^{\smile}} _{ij}} < {s_{ij}} < {{\mathop s\limits^{\frown}} _{ij}}.$ |
本文设旅行社
| $ \begin{array}{l} {{ K}_i} \equiv \left\{ {\left. {\left( {{{ q}_i},{{ Q}_i},{{ s}_i}} \right)} \right|{{{\mathop { q}\limits^{\smile}} }_i} \leqslant {{ q}_i} \leqslant {{{\mathop { q}\limits^{\frown}} }_i}} \right.,\\ {{\mathop { Q}\limits^{\smile}} _i} \leqslant {{ Q}_i} \leqslant {{\mathop { Q}\limits^{\frown}} _i},\;\;\left. {{{{\mathop { s}\limits^{\smile}} }_i} \leqslant {{ s}_i} \leqslant {{{\mathop { s}\limits^{\frown}} }_i}} \right\}. \end{array} $ |
用
| ${p_{ij}} = {p_{ij}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ij}}} \right),$ |
其中
用
| ${c_{ij}} = {c_{ij}}\left( {{ Q},{ s},{{{\beta }}_{ij}}} \right),$ |
其中
旅行社
| ${{ B}_i}\left( {{ q},{ Q},{ s},{{{\rho }}_i}} \right){{ = }}\sum\limits_{j = 1}^n {{b_{_{ij}}}\left( {{ Q},{ s},{{{\rho }}_{ij}}} \right){q_{ij}}} ,$ |
其中
旅行社
| ${{ u}_i} = {{\tilde{\omega }_i}}{{ B}_i}\left( {{ q},{ Q},{ s},{{{\rho }}_{ij}}} \right),$ |
其中
旅行社
| ${v_{ij}} = \left[ {{p_{ij}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ij}}} \right) - {c_{ij}}\left( {{ Q},{ s},{{{\beta }}_{ij}}} \right)} \right]{{q}_{ij}}.$ |
旅行社
| ${V_i} = \sum\limits_{j = 1}^n {\left[ {{p_{ij}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ij}}} \right) - {c_{ij}}\left( {{ Q},{ s},{{{\beta }}_{ij}}} \right)} \right]} {q_{ij}}.$ |
本文假设以上函数都是连续可微的.
因此,旅行社
| $ \begin{array}{l} {{ U}_i} = \displaystyle\sum\limits_{j = 1}^n {{p_{_{ij}}}} \left( {{ q},{ Q},{ s},{{{\alpha }}_{ij}}} \right){q_{ij}} - \displaystyle\sum\limits_{j = 1}^n {{c_{ij}}\left( {{ Q},{ s},{{{\beta }}_{ij}}} \right)} {q_{ij}} +\\ {{\tilde{\omega }_i}}\displaystyle\sum\limits_{j = 1}^n {{b_{_{ij}}}\left( {{ Q},{ s},{{{\rho }}_{ij}}} \right){q_{ij}}} . \end{array} $ |
本文假设以上函数都是连续可微的,所有的旅行社都是非合作竞争关系,如图1所示,竞争模型符合纳什均衡模型的. (可参考Nash的文献[10-11])
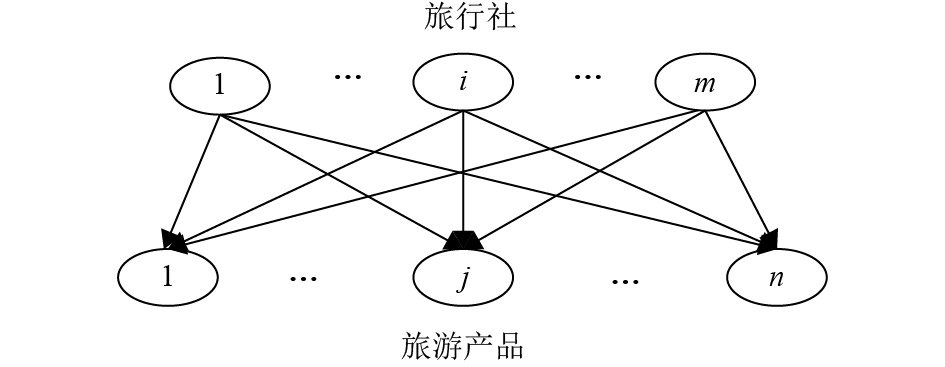
|
图 1 有关旅行社竞争的博弈论网络模型 Figure 1 The network structure of the game theory model for the competition of the travel agencies |
定义1(纳什均衡的定义) 设可行集为
| $\!\!\!\! \begin{split} &{{ U}_i}\left( {{{ q}_i}^*,{{{\mathop { q}\limits^{\frown}} }_i}^*,{{ Q}_i}^*,{{{\mathop { Q}\limits^{\frown}} }_i}^*,{ s}_i^*,{\mathop { s}\limits^{\frown}} _i^*,{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right) \geqslant \\ &{{ U}_i}\left( {{{ q}_i},{{{\mathop { q}\limits^{\frown}} }_i}^*,{{ Q}_i},{{{\mathop { Q}\limits^{\frown}} }_i}^*,{{ s}_i},{\mathop { s}\limits^{\frown}} _i^*,{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right), \forall \left( {{{ q}_i},{{ Q}_i},{{ s}_i}} \right) \in {{ K}_i}, \end{split} $ | (1) |
其中,
| $ \begin{split} &{{\mathop { q}\limits^{\frown}} _i}^* \equiv \left( {{{ q}_1}^*, \cdots ,{{ q}_{i - 1}}^*,{{ q}_{i + 1}}^* \cdots ,{{ q}_m}^*} \right), \\ &{{\mathop { Q}\limits^{\frown}} _i}^* \equiv \left( {{{ Q}_1}^*, \cdots ,{{ Q}_{i - 1}}^*,{{ Q}_{i + 1}}^* \cdots ,{{ Q}_m}^*} \right), \\ &{{\mathop { s}\limits^{\frown}} _i}^* \equiv \left( {{{ s}_1}^*, \cdots ,{{ s}_{i - 1}}^*,{{ s}_{i + 1}}^* \cdots ,{{ s}_m}^*} \right). \end{split} $ | (2) |
根据式(2),如果没有旅行社可以通过选择数量、质量和个性化的替代向量单方面来改善其效用,则建立了纳什均衡.
定理1(纳什均衡变分不等式) 设对于企业
| $ \begin{split} &- \displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^m {\dfrac{{{\text{∂}} {{ U}_i}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {q_{ij}}}}} } \times \left( {{q_{ij}} - q_{ij}^*} \right) - \\ &\displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^m {\dfrac{{{\text{∂}} {{ U}_i}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {Q_{ij}}}}} } \times \left( {{Q_{ij}} - Q_{ij}^*} \right) - \\ &\displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^m {\dfrac{{{\text{∂}} {{ U}_i}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {{s}_{ij}}}}} } \times \left( {{{s}_{ij}} - {s}_{ij}^*} \right) \geqslant 0, \\ &\forall \left( {{ q},{ Q},{ s}} \right) \in { K}. \end{split} $ | (3) |
等价于
| $ \begin{split} &-\! \displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^m {\left( {{p_{ij}}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ij}}} \right) \!+\!\! \displaystyle\sum\limits_{k = 1}^n {{q}_{ik}^*\dfrac{{{\text{∂}} {p_{ik}}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {q_{ij}}}}} } \right.} } -\\ & \left. { \displaystyle\sum\limits_{k = 1}^n {{c_{ik}}\left( {{{ Q}^*},{{ s}^*},{{{\beta }}_{ik}}} \right) + {{\tilde{\omega }_i}}\displaystyle\sum\limits_{k = 1}^n {{b_{ik}}\left( {{{ Q}^*},{{ s}^*},{{{\rho }}_{ik}}} \right)} } } \right) \times \\ & \left( {{q_{ij}} - q_{ij}^*} \right) - \displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^m {\left( {\displaystyle\sum\limits_{k = 1}^n {q_{ik}^*\dfrac{{{\text{∂}} {p_{ik}}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} -}\right.}} \\ &{{\left.{\displaystyle\sum\limits_{k = 1}^n {q_{ik}^*\dfrac{{{\text{∂}} {c_{ik}}\left( {{{ Q}^*},{{ s}^*},{{{\beta }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} } \right.} } + \left. { {{\tilde{\omega }_i}}\displaystyle\sum\limits_{k = 1}^n {q_{ik}^*\dfrac{{{\text{∂}} {b_{ik}}\left( {{{ Q}^*},{{ s}^*},{{{\rho }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} } \right) \times \\ &\left( {{Q_{ij}} - Q_{ij}^*} \right) - \displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^m {\left( {\displaystyle\sum\limits_{k = 1}^n {q_{ik}^*\dfrac{{{\text{∂}} {p_{ik}}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} -} \right.}}\\ & {{\left.{ \displaystyle\sum\limits_{k = 1}^n {q_{ik}^*\dfrac{{{\text{∂}} {c_{ik}}\left( {{{ Q}^*},{{ s}^*},{{{\beta }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} } \right.} } +\left. { {{\tilde{\omega }_i}}\displaystyle\sum\limits_{k = 1}^n {q_{ik}^*\dfrac{{{\text{∂}} {b_{ik}}\left( {{{ Q}^*},{{ s}^*},{{{\rho }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} } \right)\times \\ & \left( {{s_{ij}} - s_{ij}^*} \right) \geqslant 0,\forall \left({{ q},{ Q},{ s}} \right) \in { K}. \end{split} $ | (4) |
证明 由于可行集
根据
| $\begin{split}&\dfrac{{{\text{∂}} {{ U}_i}}}{{{\text{∂}} {q_{ij}}}} = {p_{ij}}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ij}}} \right) + \displaystyle\sum\limits_{k = 1}^n {q_{ik}^*\dfrac{{{\text{∂}} {p_{ik}}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {q_{ij}}}}} -\\ & \displaystyle\sum\limits_{k = 1}^n {{c_{ik}}\left( {{{ Q}^*},{{ s}^*},{{{\beta }}_{ik}}} \right) + {{\tilde{\omega }_i}}\displaystyle\sum\limits_{k = 1}^n {{b_{ik}}\left( {{{ Q}^*},{{ s}^*},{{{\rho }}_{ik}}} \right)} } , \end{split}$ |
| $\begin{split}&\dfrac{{{\text{∂}} {{ U}_i}}}{{{\text{∂}} {Q_{ij}}}} = {p_{ij}}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ij}}} \right) + \sum\limits_{k = 1}^n {q_{ik}^*\dfrac{{{\text{∂}} {p_{ik}}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {q_{ij}}}}} -\\ & \sum\limits_{k = 1}^n {{c_{ik}}\left( {{{ Q}^*},{{ s}^*},{{{\beta }}_{ik}}} \right) + {{\tilde{\omega }_i}}\sum\limits_{k = 1}^n {{b_{ik}}\left( {{{ Q}^*},{{ s}^*},{{{\rho }}_{ik}}} \right)} } ,\end{split} $ |
| $\begin{split}&\dfrac{{{\text{∂}} {{ U}_i}}}{{{\text{∂}} {s_{ij}}}} \!=\! \sum\limits_{k = 1}^n {q_{ik}^*\dfrac{{{\text{∂}} {p_{ik}}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} \! -\!\! \sum\limits_{k = 1}^n {q_{ik}^*\dfrac{{{\text{∂}} {c_{ik}}\left( {{{ Q}^*},{{ s}^*},{{{\beta }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} +\\ &{{\tilde{\omega }_i}}\sum\limits_{k = 1}^n {q_{ik}^*\dfrac{{{\text{∂}} {b_{ik}}\left( {{{ Q}^*},{{ s}^*},{{{\rho }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} .\end{split} $ |
代入不等式(3)可得不等式(4).
将变分不等式(4)构造成一个标准的变分不等式,即存在
| $\left\langle {F\left( {{{ X}^*}} \right),{ X} - {{ X}^*}} \right\rangle \geqslant 0,\;\forall { X} \in { \kappa} ,$ | (5) |
其中
根据式(4),令
用给定的
| $ \begin{split}&F_{ij}^1\left( { X} \right) = - \frac{{{\text{∂}} {{ U}_i}\left( {{ q},{ Q},{ s},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {q_{ij}}}} =\\ &- {p_{ij}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ij}}} \right) - \sum\limits_{k = 1}^n {{q_{ik}}\frac{{{\text{∂}} {p_{ik}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ij}}} \right)}}{{{\text{∂}} {q_{ij}}}}} +\\ &\sum\limits_{k = 1}^n {{c_{ik}}\left( {{ Q},{ s},{{{\beta }}_{ij}}} \right) - {{\tilde{\omega }_i}}\sum\limits_{k = 1}^n {{b_{ik}}\left( {{ Q},{ s},{{{\rho }}_{ij}}} \right)} } , \end{split} $ |
| $\begin{split}& F_{ij}^2\left( { X} \right) = - \frac{{{\text{∂}} {{ U}_i}\left( {{ q},{ Q},{ s},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {Q_{ij}}}}=\\ &- \sum\limits_{k = 1}^n {{q_{ik}}\frac{{{\text{∂}} {p_{ik}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} +{q_{ik}}\sum\limits_{k = 1}^n {\frac{{{\text{∂}} {c_{ik}}\left( {{ Q},{ s},{{{\beta }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} -\\ & {{\tilde{\omega }_i}}\sum\limits_{k = 1}^n {\frac{{{q_{ik}}{\text{∂}} {b_{ik}}\left( {{ Q},{ s},{{{\rho }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} , \end{split} $ |
| $\begin{split} &F_{ij}^3\left( X \right) = - \frac{{{\text{∂}} {U_i}\left( {{ q},{ Q},{ s},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {s_{ij}}}} =\\ & - \sum\limits_{k = 1}^n {{q_{ik}}\frac{{{\text{∂}} {p_{ik}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} +{q_{ik}}\sum\limits_{k = 1}^n {\frac{{{\text{∂}} {c_{ik}}\left( {{ Q},{ s},{{{\beta }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} -\\ &{{\tilde{\omega }_i}}{q_{ik}}\sum\limits_{k = 1}^n {\frac{{{\text{∂}} {b_{ik}}\left( {{ Q},{ s},{{{\rho }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} . \end{split} $ |
显然,变分不等式(3)(和(4))可转化为标准不等式(5).
另外,有关变分不等式问题的额外背景,可参考Naugurney的文献[13].
定理2(解的存在性) 变分不等式(3)一定存在一个解
证明 根据 Kinderlehrer 和 Stampacchia[14]的变分不等式的结论,由于价格与质量都是有界的,边际效用函数都是连续的,所以可行集
为了分析旅行社竞争性的纳什均衡,本文提供了变分不等式(2)和(3)进行替代公式,进一步分析边际效用,可参考Nagurney的文献[15].
可行集
| $ \begin{split} &{ K} = \left.\Big\{ {\left( {{ q},{ Q},{ s}} \right) \in {R^{3mn}}:} \right. - {q_{ij}} + {{\mathop q\limits^{\smile}} _{ij}} \leqslant 0,{q_{ij}} - {{\mathop q\limits^{\frown}} _{ij}} \leqslant 0, \\ & -\! {Q_{ij}} \!+\! {{\mathop Q\limits^{\smile}} _{ij}} \leqslant 0,{Q_{ij}} - {{\mathop Q\limits^{\frown}} _{ij}} \leqslant 0, - {s_{ij}} +\! {{\mathop s\limits^{\smile}} _{ij}} \leqslant 0,{s_{ij}} - \!{{\mathop s\limits^{\frown}} _{ij}} \leqslant 0,\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\ &\left. {i = 1, \cdots ,m,j = 1, \cdots ,n} \right.\Big\}. \end{split} $ | (6) |
变分不等式(3)重新构造等价于最小值问题,如下:
| $ \begin{split} &V\left( {{ q},{ Q},{ s}} \right) = - \displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^m {\dfrac{{{\text{∂}} {{ U}_i}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ij}},{{{\beta }}_{ij}},{{{\rho }}_{ij}}} \right)}}{{{\text{∂}} {q_{ij}}}}} } \times \\ &\left( {{q_{ij}} - q_{ij}^*} \right)- \displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^m {\dfrac{{{\text{∂}} {{ U}_i}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ij}},{{{\beta }}_{ij}},{{{\rho }}_{ij}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} } \times \\ & \left( {{Q_{ij}} - Q_{ij}^*} \right)-\displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^m {\dfrac{{{\text{∂}} {{ U}_i}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ij}},{{{\beta }}_{ij}},{{{\rho }}_{ij}}} \right)}}{{{\text{∂}} {s_{ij}}}}} } \times\\ &\left( {{s_{ij}} - s_{ij}^*} \right). \end{split} $ | (7) |
在
| $ \mathop {\min }\limits_{ K} V\left( {{ q},{ Q},{ s}} \right) = V\left( {{{ q}^*},{{ Q}^*},{{ s}^*}} \right) = 0. $ | (8) |
现在构造拉格朗日函数
| $ \begin{split} &L\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{ \lambda} ^1},{{ \lambda} ^2},{{ \mu} ^1},{{ \mu} ^2},{{ \gamma} ^1},{{ \gamma} ^2}} \right)=\\ &- \displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {\dfrac{{{\text{∂}} {{ U}_i}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ij}},{{{\beta }}_{ij}},{{{\rho }}_{ij}}} \right)}}{{{\text{∂}} {q_{ij}}}}} \times } \left( {{q_{ij}} - {q_{ij}}^*} \right)-\!\!\!\!\!\! \\ & \displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {\dfrac{{{\text{∂}} {{ U}_i}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ij}},{{{\beta }}_{ij}},{{{\rho }}_{ij}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} \times \left( {{Q_{ij}} - {Q_{ij}}^*} \right)} -\!\!\!\!\!\! \\ &\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {\dfrac{{{\text{∂}} {{ U}_i}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_{ij}},{{{\beta }}_{ij}},{{{\rho }}_{ij}}} \right)}}{{{\text{∂}} {s_{ij}}}}} \times \left( {{s_{ij}} - {s_{ij}}^*} \right)} + \\ &\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {\lambda _{ij}^1\left( { - {q_{ij}} + {{{\mathop q\limits^{\smile}} }_{ij}}} \right) + } } \displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {\lambda _{ij}^2\left( {{q_{ij}} - {{{\mathop q\limits^{\frown}} }_{ij}}} \right)} } + \\ &\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {\mu _{ij}^1\left( { - {Q_{ij}} + {{{\mathop Q\limits^{\smile}} }_{ij}}} \right) + } } \displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {\mu _{ij}^2\left( {{Q_{ij}} - {{{\mathop Q\limits^{\frown}} }_{ij}}} \right)} } + \\ & \displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {\gamma _{ij}^1\left( { - {s_{ij}} + {{{\mathop s\limits^{\smile}} }_{ij}}} \right) + } } \displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {\gamma _{ij}^2\left( {{s_{ij}} - {{{\mathop s\limits^{\frown}} }_{ij}}} \right)} } , \end{split} $ | (9) |
其中,
根据Jahn[16]所提出的最小点存在定理,由于集合
| $ \begin{split} &{ L}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{ \lambda} ^1},{{ \lambda} ^2},{{ \mu} ^1},{{ \mu} ^2},{{ \gamma} ^1},{{ \gamma} ^2}} \right) \leqslant \\ &{ L}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{\bar { \lambda} }^1},{{\bar { \lambda} }^2},{{\bar { \mu} }^1},{{\bar { \mu} }^2},{{\bar { \gamma} }^1},{{\bar { \gamma} }^2}} \right) \leqslant \\ &{ L}\left( {{ q},{ Q},{ s},{{\bar { \lambda} }^1},{{\bar { \lambda} }^2},{{\bar { \mu} }^1},{{\bar { \mu} }^2},{{\bar { \gamma} }^1},{{\bar { \gamma} }^2}} \right). \end{split} $ | (10) |
对于所有的
| $ \begin{split} &\bar \lambda _{ij}^1\left( {{{{\mathop q\limits^{\smile}} }_{ij}} - q_{ij}^*} \right) = 0, \; \bar \lambda _{ij}^2\left( {{q^*}_{ij} - {{{\mathop q\limits^{\frown}} }_{ij}}} \right) = 0, \\ &\bar \mu _{ij}^1\left( {{{{\mathop Q\limits^{\smile}} }_{ij}} - Q_{ij}^*} \right) = 0, \; \bar \mu _{ij}^2\left( {{Q^*}_{ij} - {{{\mathop Q\limits^{\frown}} }_{ij}}} \right) = 0, \\ &\bar \gamma _{ij}^1\left( {{{{\mathop s\limits^{\smile}} }_{ij}} - s_{ij}^*} \right) = 0, \; \bar \gamma _{ij}^2\left( {{s^*}_{ij} - {{{\mathop s\limits^{\frown}} }_{ij}}} \right) = 0. \end{split} $ | (11) |
从式(10)可得,
| $ \begin{split} &\dfrac{{{\text{∂}} { L}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{ \lambda} ^1},{{ \lambda} ^2},{{ \mu} ^1},{{ \mu} ^2},{{ \gamma} ^1},{{ \gamma} ^2}} \right)}}{{{\text{∂}} {q_{ij}}}} = \\ &- \dfrac{{{\text{∂}} {{ U}_i}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {q_{ij}}}} - \bar \lambda _{ij}^1 + \bar \lambda _{ij}^2 = 0, \end{split} $ | (12) |
| $ \begin{split} &\dfrac{{{\text{∂}} { L}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{ \lambda} ^1},{{ \lambda} ^2},{{ \mu} ^1},{{ \mu} ^2},{{ \gamma} ^1},{{ \gamma} ^2}} \right)}}{{{\text{∂}} {Q_{ij}}}} = \\ &- \dfrac{{{\text{∂}} {{ U}_i}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {Q_{ij}}}} - \bar \mu _{ij}^1 + \bar \mu _{ij}^2 = 0, \end{split} $ | (13) |
| $ \begin{split} &\dfrac{{{\text{∂}} { L}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{ \lambda} ^1},{{ \lambda} ^2},{{ \mu} ^1},{{ \mu} ^2},{{ \gamma} ^1},{{ \gamma} ^2}} \right)}}{{{\text{∂}} {s_{ij}}}} = \\ & - \dfrac{{{\text{∂}} {{ U}_i}\left( {{{ q}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {s_{ij}}}} - \bar \gamma _{ij}^1 + \bar \gamma _{ij}^2 = 0. \end{split} $ | (14) |
对式(12)进行分析,根据式(11)可以得到:如果
| $ \begin{split} & - \frac{{{\text{∂}} {{ U}_i}\left( {{{ p}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {p_{ij}}}} = \\ &- {p_{ij}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ij}}} \right) - \sum\limits_{k = 1}^n {{q_{ik}}\frac{{{\text{∂}} {p_{ik}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {q_{ij}}}}} +\\ &\sum\limits_{k = 1}^n {{c_{ik}}\left( {{ Q},{ s},{{{\beta }}_{ik}}} \right) - {{\tilde{\omega }_i}}\sum\limits_{k = 1}^n {{b_{ik}}\left( {{ Q},{ s},{{{\rho }}_{ik}}} \right)} } = 0. \end{split} $ |
如果
| $ \begin{split} &- \dfrac{{{\text{∂}} {{ U}_i}\left( {{{ p}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {p_{ij}}}} = \\ &- {p_{ij}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ij}}} \right) - \sum\limits_{k = 1}^n {{q_{ik}}\dfrac{{{\text{∂}} {p_{ik}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {q_{ij}}}}} +\\ &\sum\limits_{k = 1}^n {{c_{ik}}\left( {{ Q},{ s},{{{\beta }}_{ik}}} \right) - {{\tilde{\omega }_i}}\sum\limits_{k = 1}^n {{b_{ik}}\left( {{ Q},{ s},{{{\rho }}_{ik}}} \right)} } = \bar \lambda _{ij}^1. \end{split}$ |
如果
| $ \begin{split}&- \dfrac{{{\text{∂}} {{ U}_i}\left( {{{ p}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {p_{ij}}}} =\\ &{p_{ij}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ij}}} \right) - \sum\limits_{k = 1}^n {{q_{ik}}\dfrac{{{\text{∂}} {p_{ik}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {q_{ij}}}}} +\\ & \sum\limits_{k = 1}^n {{c_{ik}}\left( {{ Q},{ s},{{{\beta }}_{ik}}} \right) - {{\tilde{\omega }_i}}\sum\limits_{k = 1}^n {{b_{ik}}\left( {{ Q},{ s},{{{\rho }}_{ik}}} \right)} } = - \bar \lambda _{ij}^2. \end{split} $ |
对式(13)进行分析,又根据式(11)可得:如果
| $ \begin{split} &-\dfrac{{{\text{∂}} {{ U}_i}\left( {{{ p}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {Q_{ij}}}} =\\ &- \sum\limits_{k = 1}^n {{q_{ik}}\dfrac{{{\text{∂}} {p_{ik}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ij}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} + {q_{ik}}\sum\limits_{k = 1}^n {\dfrac{{{\text{∂}} {c_{ik}}\left( {{ Q},{ s},{{{\beta }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} -\\ &{{\tilde{\omega }_i}}\sum\limits_{k = 1}^n {\dfrac{{{q_{ik}}{\text{∂}} {b_{ik}}\left( {{ Q},{ s},{{{\rho }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} = 0. \end{split} $ |
如果
| $ \begin{split} &- \frac{{{\text{∂}} {{ U}_i}\left( {{{ p}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {Q_{ij}}}} = \\ & - \sum\limits_{k = 1}^n {{q_{ik}}\frac{{{\text{∂}} {p_{ik}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} + {q_{ik}}\sum\limits_{k = 1}^n {\frac{{{\text{∂}} {c_{ik}}\left( {{ Q},{ s},{{{\beta }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} - \\ & {{\tilde{\omega }_i}}\sum\limits_{k = 1}^n {\frac{{{q_{ik}}{\text{∂}} {b_{ik}}\left( {{ Q},{ s},{{{\rho }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} = \bar \mu _{ij}^1. \end{split} $ |
如果
| $ \begin{split} &- \frac{{{\text{∂}} {{ U}_i}\left( {{{ p}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {Q_{ij}}}} =\\ &- \sum\limits_{k = 1}^n {{q_{ik}}\frac{{{\text{∂}} {p_{ik}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} + {q_{ik}}\sum\limits_{k = 1}^n {\frac{{{\text{∂}} {c_{ik}}\left( {{ Q},{ s},{{{\beta }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}}-\\ & {{\tilde{\omega }_i}}\sum\limits_{k = 1}^n {\frac{{{q_{ik}}{\text{∂}} {b_{ik}}\left( {{ Q},{ s},{{{\rho }}_{ik}}} \right)}}{{{\text{∂}} {Q_{ij}}}}} = - \bar \mu _{ij}^2. \end{split} $ |
对式(14)进行分析,又根据式(11)可得:如果
| $ \begin{split}&- \dfrac{{{\text{∂}} {{ U}_i}\left( {{{ p}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {s_{ij}}}} = \\ & - \sum\limits_{k = 1}^n {{q_{ik}}\frac{{{\text{∂}} {p_{ik}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} + {q_{ik}}\sum\limits_{k = 1}^n {\frac{{{\text{∂}} {c_{ik}}\left( {{ Q},{ s},{{{\beta }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} - \\ & {{\tilde{\omega }_i}}{q_{ik}}\sum\limits_{k = 1}^n {\frac{{{\text{∂}} {b_{ik}}\left( {{ Q},{ s},{{{\rho }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} = 0. \end{split} $ |
如果
| $\begin{split}& - \dfrac{{{\text{∂}} {{ U}_i}\left( {{{ p}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {s_{ij}}}} =\\ & - \sum\limits_{k = 1}^n {{q_{ik}}\frac{{{\text{∂}} {p_{ik}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} + {q_{ik}}\sum\limits_{k = 1}^n {\frac{{{\text{∂}} {c_{ik}}\left( {{ Q},{ s},{{{\beta }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} - \\ &{{\tilde{\omega }_i}}{q_{ik}}\sum\limits_{k = 1}^n {\frac{{{\text{∂}} {b_{ik}}\left( {{ Q},{ s},{{{\rho }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} = \bar \gamma _{ij}^1. \end{split} $ |
如果
| $\begin{split} & - \frac{{{\text{∂}} {{ U}_i}\left( {{{ p}^*},{{ Q}^*},{{ s}^*},{{{\alpha }}_i},{{{\beta }}_i},{{{\rho }}_i}} \right)}}{{{\text{∂}} {s_{ij}}}} = \\ & - \sum\limits_{k = 1}^n {{q_{ik}}\frac{{{\text{∂}} {p_{ik}}\left( {{ q},{ Q},{ s},{{{\alpha }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} + {q_{ik}}\sum\limits_{k = 1}^n {\frac{{{\text{∂}} {c_{ik}}\left( {{ Q},{ s},{{{\beta }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} -\\ & {{\tilde{\omega }_i}}{q_{ik}}\sum\limits_{k = 1}^n {\frac{{{\text{∂}} {b_{ik}}\left( {{ Q},{ s},{{{\rho }}_{ik}}} \right)}}{{{\text{∂}} {s_{ij}}}}} = - \bar \gamma _{ij}^2. \end{split} $ |
本节进行实例分析,运用Python的软件包SymPy进行仿真. 在案例中只讨论3个线上销售旅游产品的公司,分别为飞猪旅游、携程旅游和途牛旅游,分别用旅行社1、旅行社2和旅行社3表示. 下面仅探究这3家旅行社的两种处于非合作竞争的旅游产品,分别为云南旅游和摩洛哥旅游,分别用产品1和产品2来表示. 如图2. 无论是云南旅游产品还是摩洛哥旅游产品,3家旅行社都会为消费者提供不同的旅游方案. 每一项旅游产品都是旅行社与它们的合作商共同完成,本文不考虑它们与合作商的成本与利润分配问题,而每一项产品的决策应该为旅行社与它们的合作商共同决定的,但本文简单规划为由旅行社决定. 本文设置产品质量范围为:
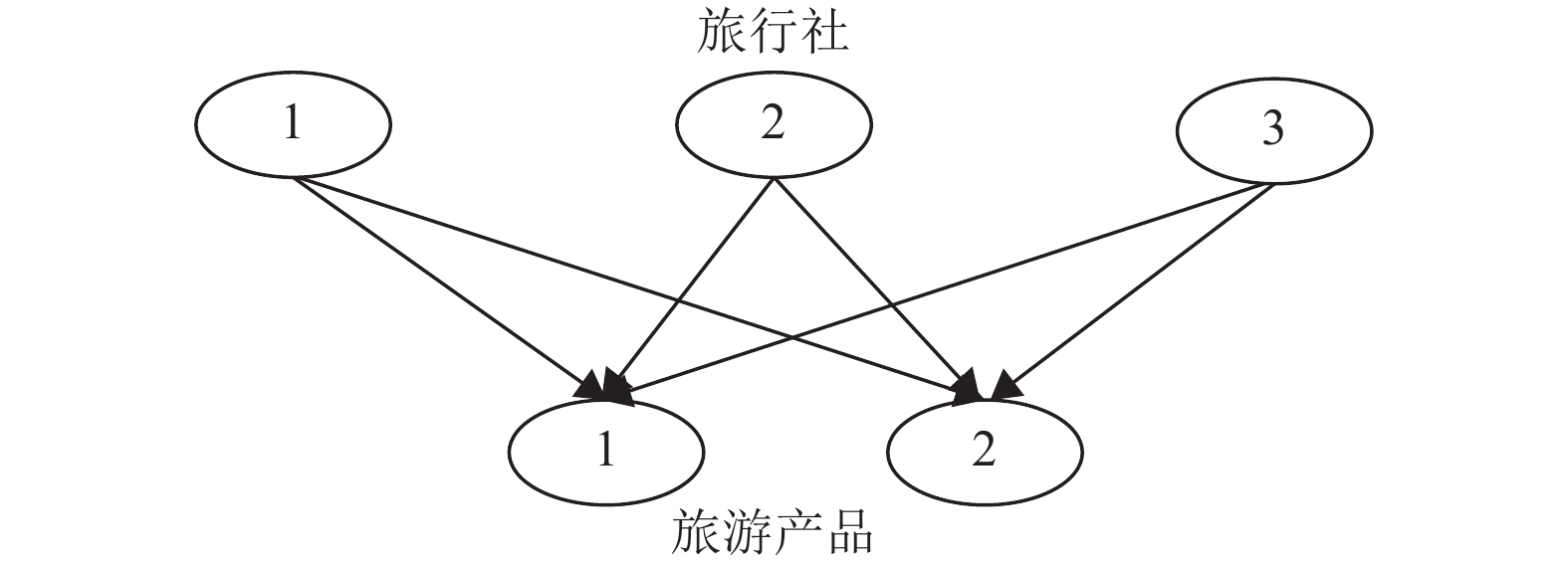
|
图 2 3家旅行社的竞争网络模型 Figure 2 The network structure for the competition of three travel agencies |
在本文中每一家旅行社对融资具有3种不同的态度,分别是风险规避、风险中性和风险追求,旅行社对风险的偏好程度影响旅行社的融资效用,并且
本文探究两种货币政策下的两种不同的融资模型. 在货币宽松政策的指引下,银行仅考虑申请贷款旅行社的营运情况. 在货币紧缩政策的指引下,银行不仅考虑申请贷款的营运情况,还考虑了它的竞争者对它的影响,在本文融资模型中仅考虑竞争者质量对申请贷款旅行社的影响. 风险偏好程度在一定程度上代表着旅行社为了提高服务质量与增加产品多样性所承担的营运风险与向银行融资贷款风险的决心. 而融资金额在一定程度上代表了旅行社的融资能力.
例1 以下分别是3家旅行社产品1的价格模型、成本模型与货币宽松政策下的融资模型. 本文用
价格模型:
| $ \begin{split} &{p_{11}}\left( {{ q},{ Q},{ s}} \right) = - 1.1{q_{11}} + 10{Q_{11}} + 10{s_{11}} + {q_{21}} - 0.1{Q_{21}} -\\ &0.2{s_{21}} + {q_{31}} - 0.1{Q_{31}} - 0.2{s_{31}}, \end{split}$ |
| $\begin{split}& {p_{21}}\left( {{ q},{ Q},{ s}} \right) = - 1.5{q_{21}} + 8.4{Q_{21}} + 6{s_{21}} + {q_{11}} - 0.2{Q_{11}} - \\ &0.1{s_{11}} + {q_{31}} - 0.2{Q_{31}} - 0.1{s_{31}}, \end{split}$ |
| $\begin{split} &{p_{31}}\left( {{ q},{ Q},{ s}} \right) = - 1{q_{31}} + 7.4{Q_{31}} + 10.5{s_{31}} + {q_{11}} - 0.1{Q_{11}} - \\ & 0.1{s_{11}} + {q_{21}} - 0.2{Q_{21}} - 0.2{s_{21}}. \end{split} $ |
成本模型:
| ${c_{11}}\left( {{ Q},{ s}} \right) = 0.01Q_{11}^2 + 0.2{Q_{11}}{s_{11}},$ |
| ${c_{21}}\left( {{ Q},{ s}} \right) = 0.02Q_{21}^2 + 0.1{Q_{21}}{s_{21}},$ |
| ${c_{31}}\left( {{ Q},{ s}} \right) = 0.01Q_{31}^2 + 0.15{Q_{31}}{s_{31}}.$ |
在货币宽松政策条件下的融资模型:
| ${B_{11}}\left( {{ q},{ Q},{ s}} \right) = \left( {0.4{Q_{11}} + 0.6{s_{11}}} \right){q_{11}},$ |
| ${B_{21}}\left( {{ q},{ Q},{ s}} \right) = \left( {0.2{Q_{21}} + 0.8{s_{21}}} \right){q_{21}},$ |
| $\;\;\;\;{B_{31}}\left( {{ q},{ Q},{ s}} \right) = \left( {0.25{Q_{31}} + 0.75{s_{31}}} \right){q_{31}}.$ |
| 表 1 例1的均衡解 Table 1 The equilibrium solutions of Eg. 1 |
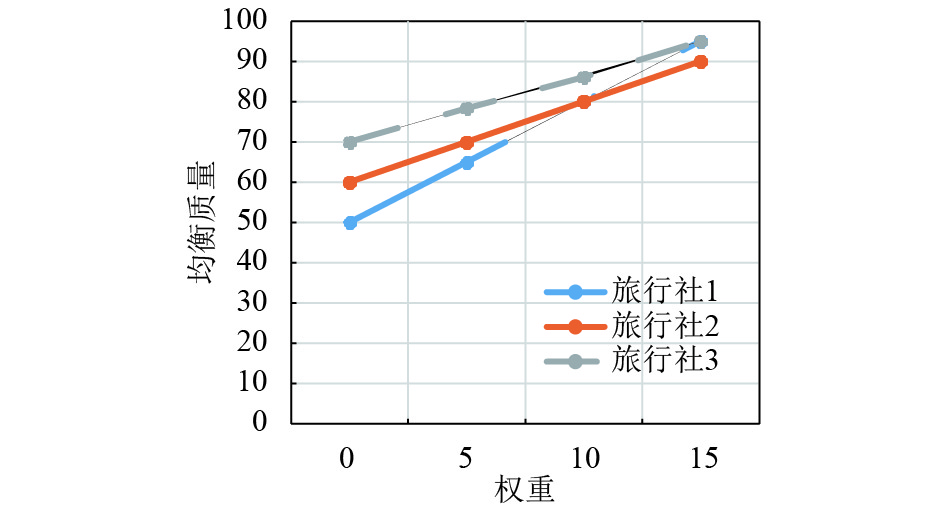
|
图 3 产品1的均衡质量折线图 Figure 3 The broken line diagram of the equilibrium quality of product 1 |
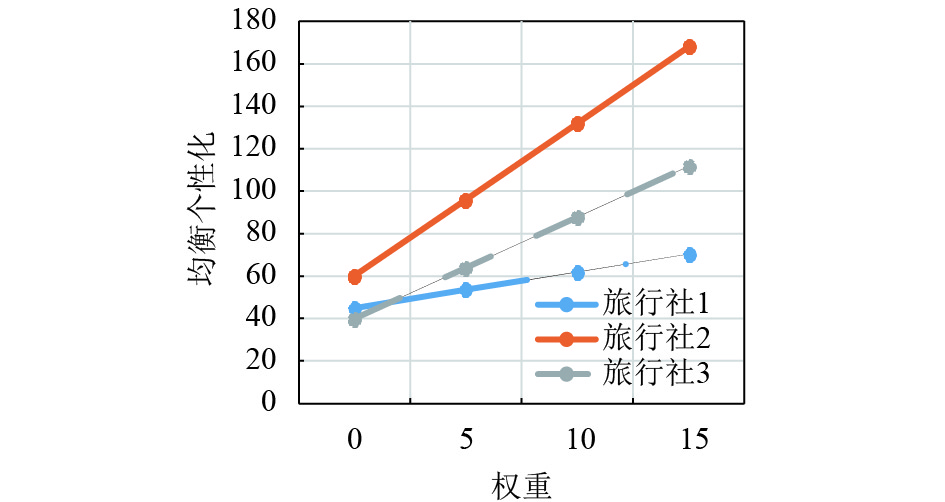
|
图 4 产品1的均衡个性化折线 Figure 4 The broken line diagram of Equilibrium individuation of product 1 |
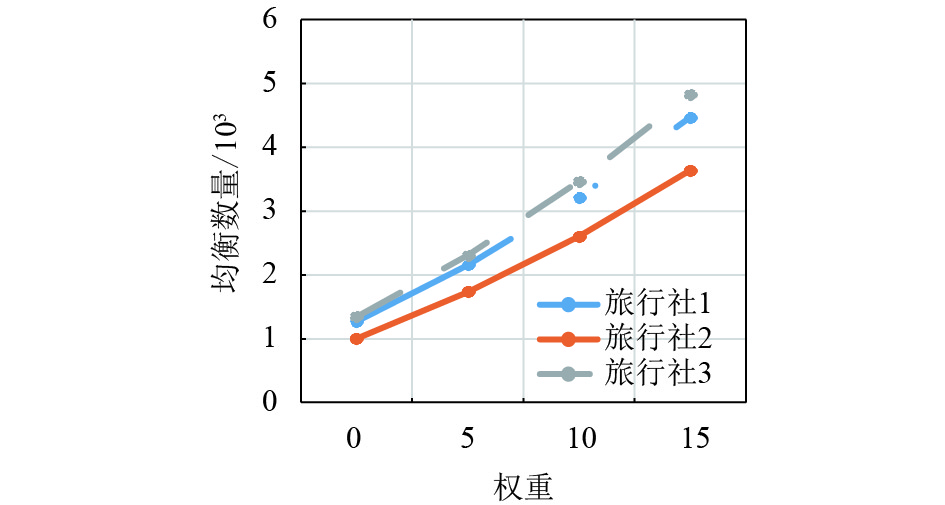
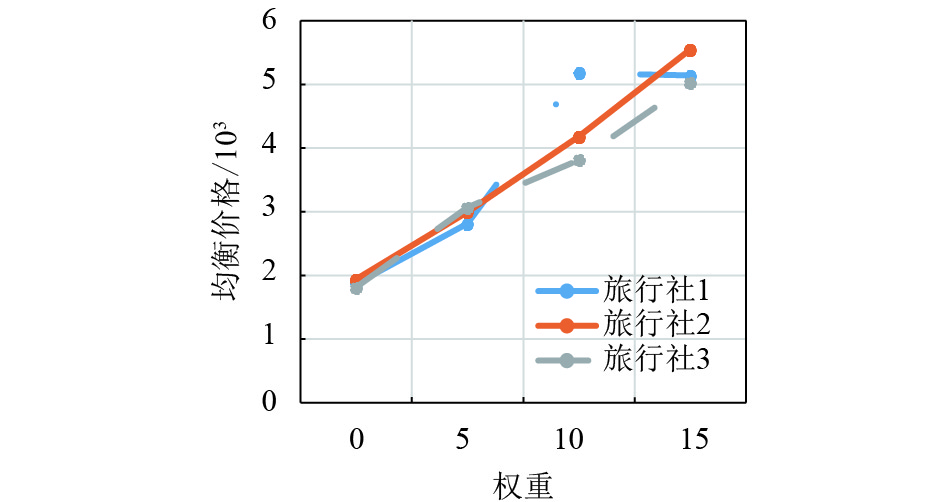
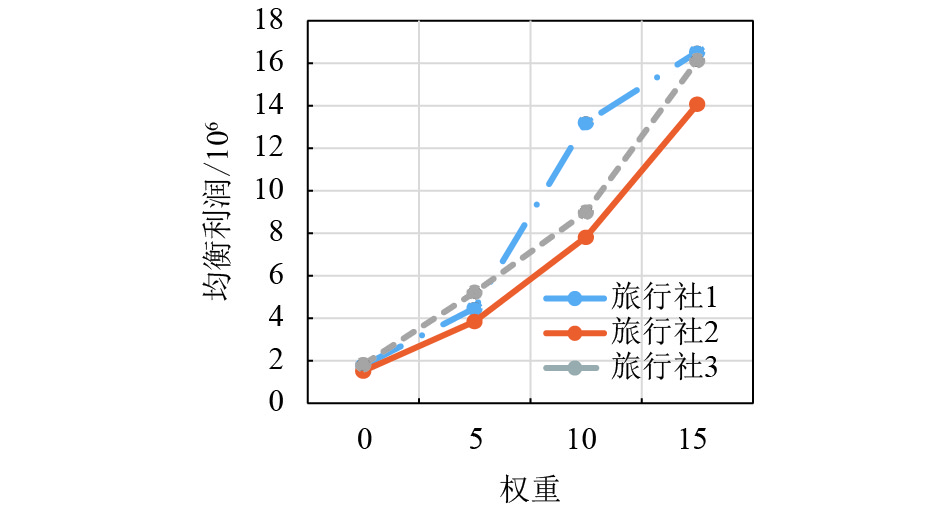
通过表1与图3~图7的分析,本文可以得到随着风险偏好程度的增加,3家旅行社的产品1即云南旅游产品的均衡质量、均衡数量和均衡个性化都增加了,以至由它们产生的均衡单位成本、均衡价格与利润也基本随之增加了.
|
图 5 产品1的均衡数量折线图 Figure 5 The broken line diagram of the equilibrium quantity of product 1 |
|
图 6 产品1的均衡价格折线图 Figure 6 The broken line diagram of the equilibrium price of product 1 |
|
图 7 产品1的均衡利润折线图 Figure 7 The broken line diagram of the equilibrium revenue of product 1 |
这里值得注意的是旅行社1的产品1的价格变化,
例2 与例1中的价格模型和成本模型相同,融资模型采取货币紧缩政策条件下的融资策略,其中
这里的
| 表 2 例2的均衡解 Table 2 The equilibrium solutions of Eg. 2 |
货币紧缩政策条件下的融资模型:
| ${B_{11}}\left( {{ q},{ Q},{ s}} \right) = \left( {0.4{Q_{11}} + 0.6{s_{11}}} \right.\left. { - 0.1 \times \left( {{Q_{21}} + {Q_{31}}} \right)} \right){q_{11}},\;$ |
| ${B_{21}}\left( {{ q},{ Q},{ s}} \right) = \left( {0.2{Q_{21}} + 0.8{s_{21}}} \right.\left. { - 0.1 \times \left( {{Q_{11}} + {Q_{31}}} \right)} \right){q_{21}},\;\;$ |
| ${B_{31}}\left( {{ q},{ Q},{ s}} \right) = \left( {0.25{Q_{31}} + 0.75{s_{31}}} \right.\left. { - 0.1 \times \left( {{Q_{11}} + {Q_{21}}} \right)} \right){q_{31}}.$ |
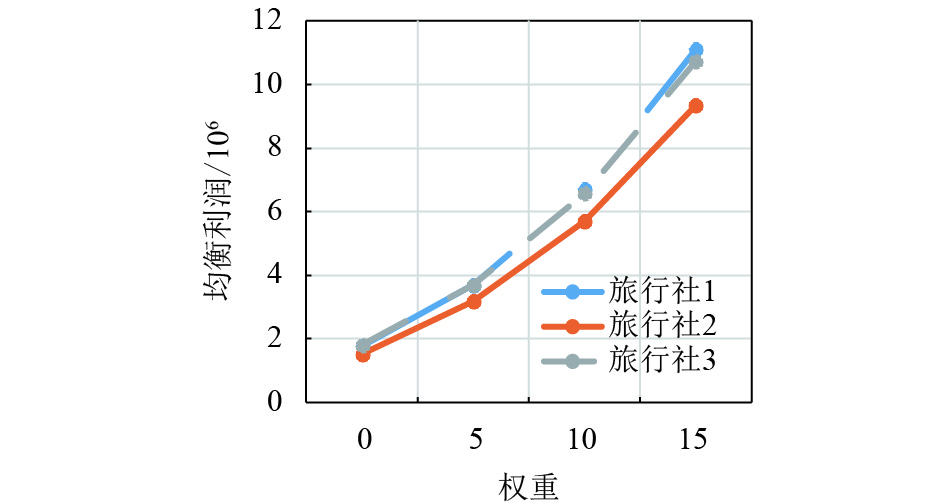
通过表1和表2的分析,本文发现融资模型改变后,相同的风险偏好程度所对应的均衡质量、均衡个性化与均衡单位成本相同,所以本文可以得到均衡质量与均衡个性化随风险偏好程度的改变而改变,而均衡数量由融资模型与风险偏好共同影响. 在相同的风险偏好程度下对应的所有旅行社的均衡数量都比例1中的下降,利润也比例1中的相应地减少了. 这是因为当风险偏好增加时,均衡质量与均衡个性化也增加,而在货币紧缩政策的情况下旅行社到银行贷款融资的难度增大,为了保证预期的均衡质量与个性化,在有限资金的情况下所能保证的均衡数量必定有所下降. 所以通过比较可以得到,在相同的风险偏好程度下,图8的3家旅行社的利润与图7的相比都有所下降.
|
图 8 改变融资模型后产品1的均衡利润折线图 Figure 8 The revenue line diagram of product 1 after changing the financing model |
这也是符合事实的. 以云南旅游其中一个项目拉市海为例,该项目已经包含了午餐,但由于人流过大,吃饭与拉市海划艇都是要排队的,虽然导游建议先排队吃饭,在吃饭前边划艇边等号,但由于该景区的设备落后,游客在划艇时是听不到广播的,容易错过叫号,所以为了提高服务质量景点应该引入二维码扫码排号系统,同时只有一个项目分流在客流量较大时是不够的,但再添加新的项目,旅行社的经营成本必定上升,愿不愿意承担这样的经营风险主要是看决策者的风险偏好程度. 同时,本文通过纳什均衡定理分析可以得到,已经确定均衡价格的前提下,如果旅行社卖出的产品数量比均衡数量还要大时,就会超出景区所能承受的服务能力范围,这样质量必定下降而不利于旅行社与景区的持续发展,说明景区不能为了眼前的利润而放弃长期的发展.
近年来云南旅游热持续升温,选择去云南的旅客也越来越多,而人们也越来越注重品质,通过模型发现均衡质量与均衡个性化的提高,融资用于营运提高均衡质量与均衡个性化的单位成本越多,在保证均衡质量与个性化的基础上,融资金额越高则均衡数量就越大即能够服务更多的消费者,那么旅行社的利润就越大.
例3 以下分别为3家旅行社的产品2的价格模型、成本模型与货币宽松政策下的融资模型. 本文用
| 表 3 例3的均衡解 Table 3 The equilibrium solutions of Eg. 3 |

|
图 9 产品2的均衡质量折线图 Figure 9 The broken line diagram of the equilibrium quality of product 2 |
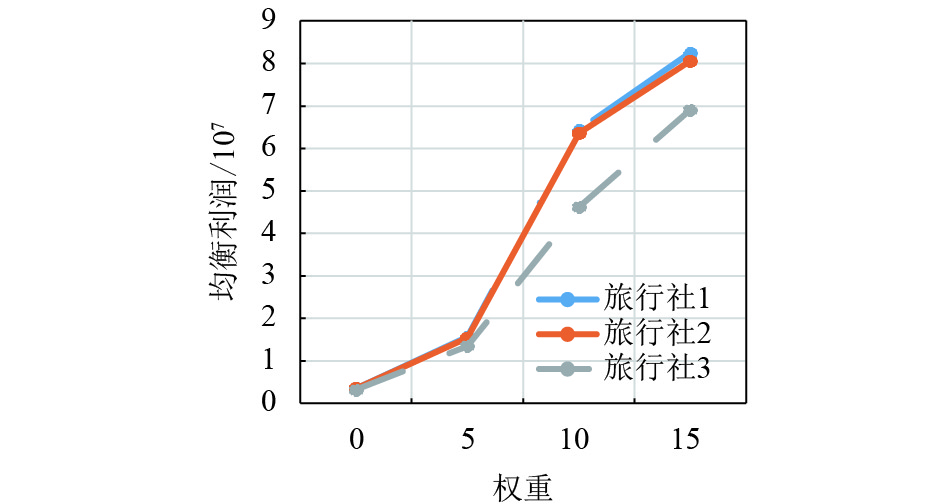
|
图 13 产品2的均衡利润折线图 Figure 13 The broken line diagram of the equilibrium revenue of product 2 |
价格模型:
| $\begin{split}&{p_{12}}\left( {{ q},{ Q},{ s}} \right) = - 1.5{q_{12}} + 16.8{Q_{12}} + 48{s_{12}} + 1.2{q_{22}} - \\ & 0.1{Q_{22}} - 0.5{s_{22}} + {q_{32}} - 0.3{Q_{32}} - 0.2{s_{32}},\end{split}$ |
| $\begin{split}&{p_{22}}\left( {{ q},{ Q},{ s}} \right) = - 1.2{q_{22}} + 12.8{Q_{22}} + 70{s_{22}} + 1.1{q_{12}} - \\ &0.5{Q_{12}} - 0.1{s_{12}} + {q_{32}} - 0.3{Q_{32}} - 0.2{s_{32}}, \end{split} $ |
| $\begin{split}&{p_{32}}\left( {{ q},{ Q},{ s}} \right) = - 1.1{q_{32}} + 16.5{Q_{32}} + 32.5{s_{32}} - 0.1{Q_{12}} +\\ &{q_{12}} - 0.1{s_{12}} + 0.8{q_{22}} - 0.2{Q_{22}} - 0.15{s_{22}}. \end{split} $ |
成本模型:
| ${c_{12}}\left( {{ Q},{ s}} \right) = 0.04Q_{12}^2 + 0.8{Q_{12}}{s_{12}},$ |
| ${c_{22}}\left( {{ Q},{ s}} \right) = 0.02Q_{22}^2 + {Q_{22}}{s_{22}},\quad$ |
| ${c_{32}}\left( {{ Q},{ s}} \right) = 0.05Q_{32}^2 + 0.5{Q_{32}}{s_{32}}.$ |
货币宽松政策条件下的融资模型:
| ${B_{12}}\left( {{ q},{ Q},{ s}} \right) = \left( {3{Q_{12}} + 1.6{s_{12}}} \right){q_{12}},$ |
| ${B_{22}}\left( {{ q},{ Q},{ s}} \right) = \left( {3{Q_{22}} + 1.8{s_{22}}} \right){q_{22}},$ |
| ${B_{32}}\left( {{ q},{ Q},{ s}} \right) = \left( {2.5{Q_{32}} + {s_{32}}} \right){q_{32}}.$ |
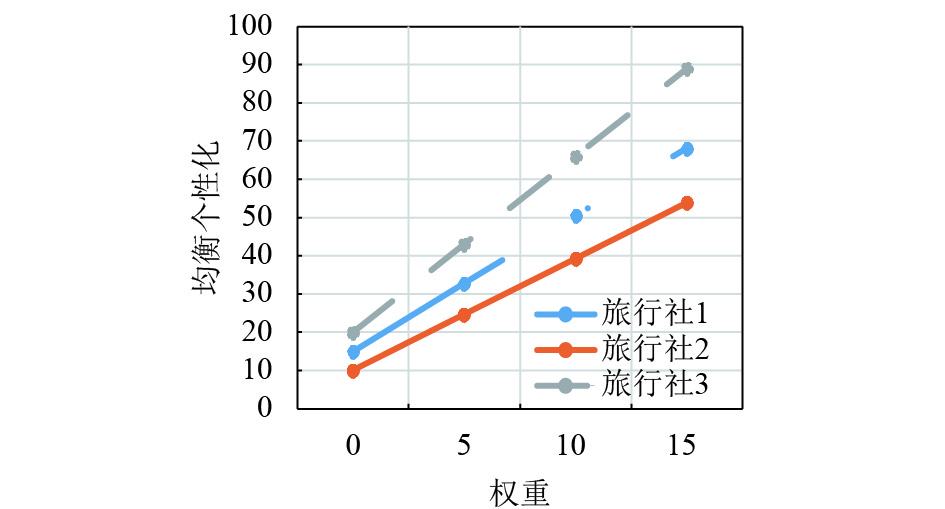
|
图 10 产品2的均衡个性化折线图 Figure 10 The broken line diagram of the equilibrium individuation of product 2 |
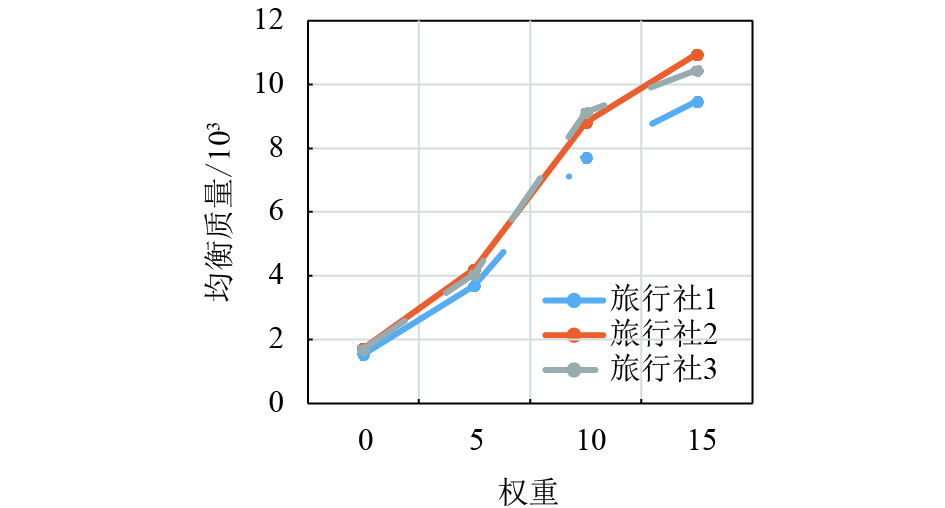
|
图 11 产品2的均衡数量折线图 Figure 11 The broken line diagram of the equilibrium quantity of product 2 |
通过表3与图9~图13的分析,本文可以得到随着风险偏好程度的增加,3家旅行社的产品2即摩洛哥旅游产品的均衡质量、均衡数量和均衡个性化都增加了,以至由它们产生的均衡单位成本、均衡价格与利润也基本随之增加.
这里值得注意的是旅行社3的产品,在相同的风险偏好程度下,旅行社3的产品均衡质量与均衡个性化都比旅行社1的好,并且旅行社3均衡单位成本基本比旅行社1的低. 由于旅行社3的定价模型决定了旅行社3均衡的价格比旅行社1的低,虽然旅行社3的均衡数量比旅行社1的高,但均衡总利润不如旅行社1. 这说明旅行社3的产品2的潜力被低估了,随着时间的推移,旅行社3的价格会有升价的可能,利润会相应提高.
在相同的风险偏好程度下,旅行社2的均衡质量比旅行社1的好,但旅行社2的均衡个性化不如旅行社1的多,所以均衡单位成本相差不大,旅行社2的均衡数量比旅行社1的大,但均衡价格不如旅行社1的高,所以最后它们的均衡利润也相差不大. 说明了旅行社可以通过提高质量或者增加产品个性化、制定合理的产品数量与价格,从而可以提高它们的利润.
例4 与例3中的价格模型和成本模型相同,融资模型采取货币紧缩政策条件下的融资策略,本文令
这里的
货币紧缩政策条件下的融资模型:
| ${B_{12}}\left( {{ q},{ Q},{ s}} \right) = \left( {3{Q_{12}} + 1.6{s_{12}}} \right.\left. { - 0.1 \times \left( {{Q_{22}} + {Q_{32}}} \right)} \right){q_{12}},$ |
| ${B_{22}}\left( {{ q},{ Q},{ s}} \right) = \left( {3{Q_{22}} + 1.8{s_{22}}} \right.\left. { - 0.1 \times \left( {{Q_{12}} + {Q_{32}}} \right)} \right){q_{22}},$ |
| ${B_{32}}\left( {{ q},{ Q},{ s}} \right) = \left( {2.5{Q_{32}} + {s_{32}}} \right.\left. { - 0.1 \times \left( {{Q_{12}} + {Q_{22}}} \right)} \right){q_{32}}.\;$ |
| 表 4 例4的均衡解 Table 4 The equilibrium solutions of Eg. 4 |
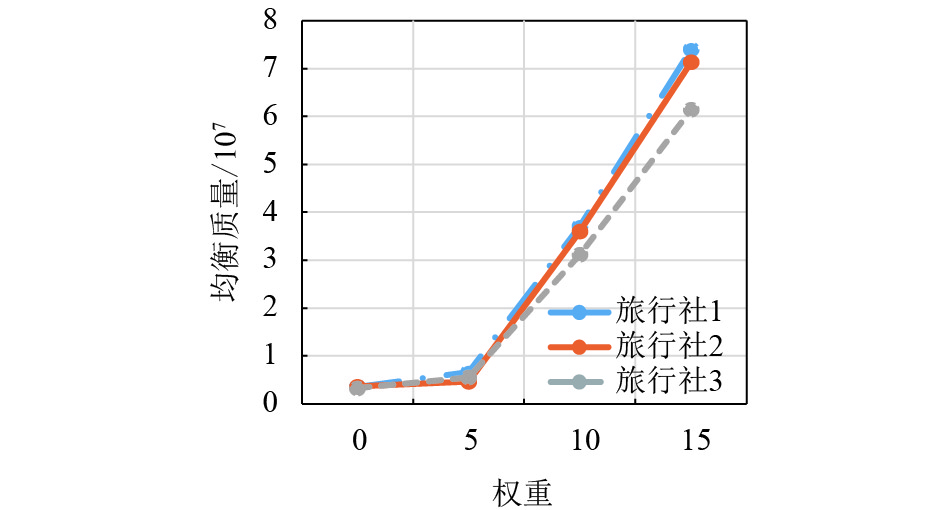
|
图 14 改变融资模型后产品2的均衡利润折线图 Figure 14 The revenue line diagram of product 2 after changing the financing model |
通过表3和表4的分析,本文同样发现与产品1的情况相似,融资模型改变后,相同的风险偏好度所对应的均衡质量、均衡个性化与均衡单位成本相同,所以本文可以得到均衡质量与均衡个性化随风险偏好程度的改变而改变,而均衡数量是由融资模型与风险偏好共同决定. 旅行社提高质量与增加产品个性化虽然能够提高消费者的满意度,但同时也会增加它们的营运成本与融资成本,是否愿意承担风险取决于管理者对风险的偏好程度,而融资金额多则可满足相应的均衡质量与均衡个性化的同时提高更多的产品均衡数量. 通过图13与图14,本文可以得到融资金额越高,风险偏好越大,利润就越大.
通过表1和表3,本文可以得到在货币宽松政策融资策略下旅行社的总利润,如表5所示.
| 表 5 旅行社的总利润表 Table 5 The total revenue statement of travel agencies |
通过表2和表4,本文可以得到在货币紧缩政策融资策略下旅行社的总利润,如表6所示.
| 表 6 改变融资模型后旅行社的总利润 Table 6 The total revenue statement of travel agencies after financing model |
通过表5与表6,本文可以发现随着风险偏好程度的增加,无论在宽松货币融资策略下还是货币紧缩政策融资策略下,旅行社的均衡利润都整数倍增加. 而在相同风险偏好程度下,在货币紧缩条件下的旅行社的利润比在货币宽松条件下的利润要低很多.
4 结果与结论本文构建了在两种不同的货币政策指引下和旅行社受风险偏好程度影响而采取不同的融资策略下的收益纳什均衡模型. 两种货币政策分别为货币宽松政策与货币紧缩政策. 风险偏好类型有3种分别为风险规避、风险中性与风险追求. 本文对风险偏好程度进行敏感性分析并将它分为4个程度:其中,当
本文通过分析在不同风险偏好程度影响下的融资效用对旅行社均衡质量、个性化和数量以及由它们得出的均衡价格与利润的作用,探究3家旅行社的两种产品的竞争模型. 为此本文构建了包含收益效用与融资效用的效用函数. 本文将均衡条件转化为变分不等式问题并且证明了均衡解的存在性. 通过拉格朗日分析,运用KKT求解,并通过运用Python的软件包SymPy进行仿真.
通过数据分析,本文可以得出如下结论. 随着旅行社的风险偏好程度的增加,旅行社的均衡质量、个性化和数量也会随之增大,而由它们产生的均衡价格、成本与利润也随之增大. 其中,产品的均衡数量是受风险偏好程度与融资金额共同决定的. 所以本文得出的结论是风险偏好程度越高,在货币宽松的政策下,旅行社越容易向银行贷款融资则利润越大. 这是不考虑旅行社还本付息的前提下成立的,如果考虑了还本付息,那必定会冲减旅行社的利润.
本文的创新点是在Nagurney A等的研究基础上进行延伸,探究在纳什均衡条件下,银行融资对3家旅行社收益与绩效的影响,同时还探讨了风险偏好对融资效用的影响.
| [1] |
CALDENTEY R, CHEN X. The role of financial services in procurement contracts[C]//KOUVELIS P. Handbook of Integrated Risk Mange Global Supply Chains. Canada: Wiley, 2010: 289-326.
|
| [2] |
KOUVELIS P, ZHAO W. Financing the news vendor: suppler vs. bank, and the structure of optimal trade credit contracts[J].
Operations Research, 2012, 60(3): 566-580.
DOI: 10.1287/opre.1120.1040. |
| [3] |
LI Y, ZHEN X, QI X, et al. Penalty and financial assistance in a supply chain with supply disruption[J].
Omega, 2016, 61: 167-181.
DOI: 10.1016/j.omega.2015.12.011. |
| [4] |
NAGURNEY A, LI D. A dynamic network oligopoly model with transportation costs, product differentiation, and quality competition[J].
Computational Economics, 2014, 44(2): 201-229.
DOI: 10.1007/s10614-013-9387-6. |
| [5] |
NAGURNEY A, LI D. A supply chain network game theory model with product differentiation, outsourcing of production and distribution, and quality and price competition[J].
Annals of Operations Research, 2015, 228(1): 479-503.
|
| [6] |
朱莹, 张成科, 朱怀念. 基于演化博弈的供应链成员间研发竞争与合作分析[J].
广东工业大学学报, 2015, 32(3): 46-50.
ZHU Y, ZHANG C K, ZHU H N. R & D competition and cooperation among members in supply chain based on evolutionary game[J]. Journal of Guangdong University of technology, 2015, 32(3): 46-50. DOI: 10.3969/j.issn.1007-7162.2015.03.009. |
| [7] |
BARBAGALLO A, DANIELE P, GIUFFRE S, et al. Varitiational approach for a general financial equilibrium problem: the deficit formula, the balance law and the liability formula. A path to economy recovery my recovery[J].
European Journal Operational Research, 2014, 237(1): 231-244.
DOI: 10.1016/j.ejor.2014.01.033. |
| [8] |
SABERI S, CRUZ J M, SARKIS J. A competitive multiperiod supply chain network model with freight carriers and green technology investment option[J].
European Journal of Operational Research, 2018, 226(3): 934-949.
|
| [9] |
NAGURNEY A, YU M, BESIK D. Supply chain capacity competition with outsourcing: a variational equilibrium framework[J].
Journal of Global optimization, 2017, 69(1): 231-254.
DOI: 10.1007/s10898-017-0497-x. |
| [10] |
NASH J F. Equilibrium points in n-person games[J].
Proceeding of National Academy of Sciences of the United States of America (PNAS), 1950, 36(1): 48-49.
DOI: 10.1073/pnas.36.1.48. |
| [11] |
NASH J F. Non-cooperative games[J].
Annals of Mathematics, 1951, 54(2): 286-298.
DOI: 10.2307/1969529. |
| [12] |
GABAY D, H MOULIN. On the uniqueness and stability of nashi equilibria in Non-cooperative games[J].
Applied Stochastic Control in Econome trics and Management Science, 1980, 9: 271-294.
|
| [13] |
NAGURNEY A, LI D. Competing on Supply Chain Quality: A Network Economics Perspective[M]. Switzerland: Springer International Publishing, 2016: 27-42.
|
| [14] |
KINDERLEHRER D. STAMPACCHIA G. Introduction to Vartiational Inequalities and their application[M]. New York: Academic Press, 1980: 8-18.
|
| [15] |
NAGURNEY A, KAREN LI. Hospital competition in prices and quality: a variational inequality framework[J].
Operations Research for Health Care, 2017, 15: 91-101.
DOI: 10.1016/j.orhc.2017.10.002. |
| [16] |
JAHN J. Introduction to the theory of Nonlinear Optimization[M]. Berlin, Germany: Springer Verlag, 1994: 7-29.
|
 2019, Vol. 36
2019, Vol. 36