近年来，许多客户在面对各类爆炸增长的互联网信息和新兴多变的电子商务项目时感到无所适从. 既多样又复杂的服务项目不仅不会为商户带来经济效益，反而会降低客户的满意度和忠诚度. 实践表明，推荐系统是一种解决信息过载问题的有效方法和工具. 因此推荐系统已成为大多数电子商务和社交网络系统发展中的重要模块^[1].

目前，在电子商务领域和社交网络市场的激烈竞争中，探索客户的真正需求显得至关重要^[2]. 社交网络推荐系统主要针对社交媒体领域，通过计算客户及其社会关系成员在社交网络发布的信息来模拟其行为偏好，涉及个体的心理行为和组织的氛围环境^[3]. 该系统利用好友关系、社群成员、关注或被关注者等社会关系来对客户进行分析和推送，以此提高客户满意率和留存率^[4]，其主要目标是通过向客户呈现与其最具相关性的或对其最具吸引性的项目来解决社会信息过载问题^[5].

然而，推荐系统目前面临着各种各样的挑战，例如数据稀疏(Data Sparsity)和冷启动(Cold Start)等问题，这造成了效率低下和推荐精度不尽人意的后果. 此外，推荐系统还面临着推荐项目的多样性和新颖性不足等问题. 过去实验表明，将隐式的社会关系(如潜在的好友)作为隐式信息去改进推荐系统能够取得较好的效果^[6]. 其实，在社交网络中，不但有强联系(Strong Ties)，还有弱联系(Weak Ties). Granovetter认为，与强联系相比，弱联系更能接触到各式各样的社交圈子，所以将会触及更广泛的人，有传播更长的社会距离^[7]. 三元闭包原则认为在相同社交网络中，如果互不相识的两人有同一好友，则这两人会由于某些因素(如信任、情感、机遇、动机等)在未来成为好友的概率将会提高^[8]. 另外，两个陌生人有越多的共同好友，则他们在未来成为好友的可能性越大^[9]. Granovetter强调，在社交网络中从弱联系获得的人脉关系价值往往比强联系更高，理由是强联系的信息传递存在严重的主观性和冗余性，信息量少且单一；相反，弱联系能把不同的社交圈子连接起来，是社交网络的集大成者，提供的信息更加广泛、客观和可靠^[7]. 尽管最初强弱联系是以交流的频率而划分，但其本质是强联系传播更深而弱联系传播更广.

在社交网络中，有学者提出以联系程度的强弱来区分强弱关系并识别有价值的弱联系^[10]：由于网络中存在的大量无用弱联系很容易造成信息冗余进而降低有益信息的传播效率，所以将有价值的弱关系识别出来显得很有必要. 从上述传播距离的角度来看，可以把一级人脉关系看作强联系(社交信息的深度传播)，把二级人脉关系看作弱联系(社交信息的广泛传播)，其好处是：(1) 因为弱联系在社交网络中是广泛存在的，通过现有强联系拓展而来的弱联系会显得更有价值，避免浪费过多资源去过滤价值不高的弱联系. (2) 强联系作用是维系社交联系，弱联系作用是扩大信息传播范围和维护网络结构. 弱联系传播价值的本质是其“桥梁”的角色^[11]. 从强联系拓展出来的弱联系正好实现了这座“桥梁”的建造. (3) 绝大多数具有传播价值的弱联系度数都是少于3个，因为信息的传播或多或少存在失真，过长的传播路径会急剧降低信息的传播效率^[10]. 这是不选择三级及以后社交关系的依据. (4) 强联系保证了信息传播的接受性和高效性，弱联系是在强联系的基础上使信息传播更具广泛性和多样性，因此，强联系和弱联系是相辅相成、相互作用的^[12].

回顾以往相关研究：国内学者认为社交网络中的链路预测很少考虑路径的权重，故考虑弱联系去计算局部相似性而得到权重，并在问答布告系统(Question-Answer Bulletin Boards System)中进行实验，结果表明在某些社交网络中，考虑其中的弱联系能够显著提高链路预测质量^[13]. 此外，国外学者也在信息交互加权系统(Weighted Mutual Information Model)中计算路径权重时引入一个可调节的弱联系系数，并在USAir、Celegans、Baywet、Bible等多个数据集中进行实验，结果表明如果权重与节点的相似性是负相关的话，更应该考虑用弱联系去分析网络^[14]. 还有研究在基于共同好友和相似标签去进行好友推荐时，通过加入弱联系因素去丰富原来的稀疏矩阵(但没有通过弱联系去分析网络中的路径权重)，实验结果表明在社交网络考虑了弱联系的推荐系统的性能是强于单指标协同过滤推荐系统^[15]. 总的来说，目前在链路预测领域考虑弱联系的相关研究是较多的，而在推荐系统领域考虑弱联系的相关研究是较少的. 基于此，本推荐系统将会涉及链路预测，并在同时考虑强弱联系因素.

除此之外，国内外也有不少学者在推荐系统中考虑兴趣因素，以此提高系统的准确性、多样性和新颖性. 一种基于客户兴趣的协同过滤推荐算法将兴趣权重引入到客户项目评分矩阵，通过聚类分析改进相似度计算并得到推荐列表，最后实验证明考虑了兴趣的推荐系统准确率优于参照系统^[16]；一种基于兴趣的推荐系统基于客户的使用标签扩展了其兴趣，然后通过增加与客户扩展兴趣的新项目，最后以扩展的客户交互项目作为协同过滤系统的输入变量^[17]. 实验结果表明，该算法显著提升了系统的准确性、多样性和新颖性；基于客户兴趣变化和类别关联度的推荐系统依据客户的评分对项目进行分类，再量化客户对各个类别的兴趣爱好，同时认为客户兴趣随时间的变化类似艾宾浩斯遗忘曲线，此外，还在相似度计算前对客户进行聚类，最后匹配相近的客户群和项目集^[18]. 基于前人研究，本算法也考虑兴趣爱好因素，旨在提高推荐结果的多样性和新颖性，进而增加客户的满意度.

此研究以客户在社交网络的强弱联系和兴趣爱好为基础，力图合理地计算出客户之间的社交和兴趣相近程度，并以此为权重对目标客户进行个性化推荐. 客户社交关系的建立传播过程可以简化成一个马尔科夫链^[19]，即认为一个客户未来结识的对象与目前已结识的对象存在关联性. 更进一步，将目标客户的一二级社交对象去重复之后构建邻接矩阵，计算任意两个对象的支持度和置信度，以此作为对象之间社交传递的权重，得到此社交网络的概率转移矩阵. 同时，将此矩阵替换经典PageRank算法中的概率转移矩阵. 由于经典PageRank算法中的概率转移矩阵只对出度的数目进行简单平均(即目标客户与每个对象的社交紧密程度是相等的)，合理性比不上改进后的模型. 接着，根据改进的概率矩阵重新求极限，得出在此社交网络中每个客户对应的改进PR值. 同时，还依据各自喜欢的标签数，即兴趣爱好，计算目标客户与参考对象(一二级社交对象)之间的Jaccard系数. 然后，以PR值和Jaccard系数作为各个参考对象为候选项目进行投票的权重，对候选项目进行评分. 使用Jaccard系数去计算兴趣爱好相似度，目的是摆脱计算客户相似度时严重依赖足量共同评分的限制，有效地缓解了稀疏矩阵带来的负面影响. 此外，Jaccard系数能够提高相似性度量中共同评分项目所占的比例，获得各个项目之间的关联信息，进而克服许多相似度指标难以计算，缺乏共同评分的客户间的相似度的问题，能够较好地度量客户兴趣爱好之间的相似程度^[20]. 最后，算出各个候选项目的最终得分，再将其进行降序排序，从前往后选取N个项目对目标客户进行推荐(Top-N过滤). 下文给出了该算法的详细计算过程，并设计实验进行评估，验证其相对于其他传统算法具有有效性和合理性.

1 结合强弱联系和兴趣的改进PageRank推荐算法

本算法结合强弱联系旨在全面地观察客户之间潜在的关联性和相似性，克服了部分客户来自好友的参考信息过少以及降低了部分来自强联系的主观信息对结果的不良影响，同时也避免无价值的弱联系信息对系统的干扰，有效地缓解了数据稀疏和冷启动在个性化推荐中的不良影响. 此外，融入兴趣权重也增加了系统的多样性和新颖性. 本算法适用于社交网络中含有社交关系和兴趣标签的个性化推荐场景，推荐的对象包括具体或抽象项目，如图书或标签等. 衡量客户与不同对象的社交紧密程度是重要的：社交网络中的待评估实体是不断动态变化的，一般其上一个状态会直接影响下一个状态，所以，有研究通过考虑信任的时间相关性，依据连续时间的隐马尔可夫模型建立社交关系评估模型，并证明了其合理性^[21]. 据此，本算法假定客户未来与不同对象建立社交关系的过程符合马尔科夫过程，也就是说，客户未来的社交关系主要受到当前社交关系影响，即前一过程和紧接的后一过程具有很强的关联性.

1.1 结合强弱联系的改进

说明1 　在一个社交网络中，任取一个客户并记为u，其社交关系集为 $U = \left\{ {{u_1},{u_2}, \cdots ,{u_n}} \right\}$ ，且任取n个递增的非负整数作为时间序列数(t_i $\geqslant$ 0; t_i+1 $\geqslant$ t_i; i=1, $2, \cdots,n $ ). 在t_i时刻u建立的社交关系对象记为U(t_i)=u_i，满足无后效性，即u在t_i+1建立的社交关系u_i+1仅仅依赖于t_i已建立的社交关系u_i.

$ \begin{split} &P\{ U({t_{i + 1}}) = {u_{i + 1}}|U({t_i}) = {u_i}\} = \\ &P\{ U({t_{i + 1}}) = {u_{i + 1}}|U({t_i}) = {u_i}, \cdots ,U({t_1}) = {u_1}\}\text{，} \end{split} $

(1)

式(1)中， $P\left( {U({t_{i + 1}}) = {u_{i + 1}}|U({t_i}) = {u_i}} \right)$ 属于条件概率，是状态转移矩阵的元素，表示u在t_i已有社交关系u_i的条件下，在t_i+1建立社交关系u_i+1的可能性.

在社交网络G=(U, E)中，顶点集合 $ U\! \!=\! \{ {u_1},{u_2}, \cdots ,{u_n}\} $ 表示该网络中的客户，有向边集合E表示客户之间的社交关系，其对应权重 $P({u_j}|{u_i}) = {p_{ij}}$ 是状态转移概率，表示u在当前状态已建立社交关系u_i的条件下，下一承接状态建立社交关系u_j的概率. 由此，构成状态转移矩阵.

说明2 　记状态转移矩阵为P=[p_ij]_n×n，其中 ${p_{ij}} = P\left( {{u_j}|{u_i}} \right)$ ，且必须同时满足3个条件：(1) 随机性：任意 $i=1 ,2, \cdots ,n$ 和 $j=1 , 2, \cdots ,n$ 都有 $p_{ij} \geqslant 0$ ，且任意 $i=1 , 2, \cdots ,n$ 都有 $\mathop \sum \nolimits_{j = 1}^n {p_{ij}}{\rm{ = }}1$ ；(2) 不可约性：方阵P是不可约的充要条件是方阵P对应的有向图是强连通的，即对于 $\forall $ i, j∈U，都存在从i到j的路径；(3) 非周期性：状态i是周期性的定义是存在一个最小的大于1的正整数k，使得从i出发又回到状态i的所有路径的长度都是k的整数倍. 若不存在这样的k或者k=1，则认为此状态是非周期的. 一个非周期的马尔科夫链要求其包含的所有状态都是非周期的.

${ P} = \left( {\begin{array}{*{20}{c}} 0&{p({u_2}|{u_1})}& \cdots &{p({u_n}|{u_1})} \\ {p({u_1}|{u_2})}&0& \cdots &{p({u_n}|{u_2})} \\ \vdots & \vdots & \ddots & \vdots \\ {p({u_1}|{u_n})}&{p({u_2}|{u_n})}& \cdots &0 \end{array}} \right)\text{。}$

记u对客户集U中的各个对象的初始概率分布为 ${{\pi}} = {(p_1^0,p_2^0, \cdots ,p_h^0)^{\rm{T}}}$ ，式中， $p_i^0$ 要求所有元素大于等于零且所有元素之和为1，表示 $u$ 在初始时刻对u_i的社交紧密程度；经过第一次迭代， $u$ 对U中各个对象的概率分布变为 ${{\pi} _1} = ({{ P}^{\rm T}}){{\pi} _0} = {(p_1^1,p_2^1, \cdots ,p_h^1)^{\rm{T}}}$ ；类推可知，经过第h次的迭代，u对U中的各个对象的概率分布变为 ${{\pi} _h} = {({{ P}^{\rm T}})^h}{{\pi} _0} = {(p_1^h,p_2^h, \cdots ,p_h^h)^{\rm{T}}}$ . 当h→+∞时，π_h就会趋向于其极限，即一个常向量. 上文提到状态转移矩阵必须满足的3个条件，目的是保证3个效果：(1) 的极限一定存在；(2) 该极限与π₀的选取无关；(3) 该极限的大小用来表示u对U中各个对象的(潜在)社交紧密程度是合理的 .

如果矩阵P满足这3个条件，则此推荐算法就属于一个马尔科夫链. π_h是其中的状态，P是其中的状态转移矩阵，而马尔科夫链的遍历性及其极限分布在前人的许多研究中都已经得到证明，即前段中的(1)和(2)是能够保证的. 此处将对(3)进行详细分析. 当客户遇到其他悬挂客户(别人当他是朋友，但他不当别人是朋友，其出度为零)时，绝不会停止在此人身上，而是会尝试与其他人建立社交关系. 针对个人，与任何人建立社交关系与其个体因素有关；然而，针对社交网络的巨大客户群，随机观察一个客户未来将会与何人建立社交关系则是随机的. 所以，遇到悬挂客户时，则将其对应的零向量修正成e/n(e是所有元素均为1的列向量，n是社交网络中客户的总数). 此外，网络中存在如社会化视角、安全视角等诸多显著影响客户建立社交关系的因素^[22]. 所以，客户不会完全受其当前社交关系限制，不只会单一地从当前社交关系中挖掘新社交对象. 换句话说，u每一次增加新社交关系时，既以d(0<d<1)的概率从当前社交关系去寻找新的社交对象，也以(1–d)的概率不受此限制，随机地与网络中任意一个对象去建立新的社交关系.

说明3 　PageRank改进型社交关系传递矩阵T=[t_ij]_n×n的计算方法：

$ {t_{ij}} = \frac{{{C}{_{ij}}}}{{{\rm{rowSums}}{(C)_j}}}\text{，} $

(2)

式(2)中，C_ij表示矩阵C=[C_ij]_n×n位置为i行j列对应的元素；rowSums(C)_j表示C各行求和而成的新向量，j表示新向量的第j个元素.

矩阵C=[c_ij]_n×n的计算方法：

$ {{C}}{_{ij}} = \frac{{{\rm{suppor}}{{\rm{t}}_{ij}}}}{{{\rm{suppor}}{{\rm{t}}_i}}}\text{，} $

(3)

式(3)中，C_ij表示u_i→u_j的置信度，support_ij表示u_i和u_j的支持度，support_i表示u_i的支持度.

说明4 　改进型状态转移矩阵为P=[p_ij]_n×n的计算方法：

$ { P} = {\rm{d}}{ T} + \frac{{(1 - d)}}{n}{{ e}^{\rm{T}}}{ e}\text{，} $

(4)

式(4)中，T为本文算法创新性提出地PageRank改进型社交关系传递矩阵.

1.2 结合兴趣的改进

另外，还需考虑客户之间共同喜爱项目占他们所有喜爱项目的比例，即用Jaccard系数去衡量用户之间的兴趣爱好相似程度，其优势已经在前言部分作出详细说明，此处不再赘述.

说明5 　用户之间兴趣相似度的计算方法：

$ {\rm{Jaccar}}{{\rm{d}}_{ij}} = \frac{{{\rm{Count(Ite}}{{\rm{m}}_i} \cap {\rm{Ite}}{{\rm{m}}_j}{\rm{)}}}}{{{\rm{Count(Ite}}{{\rm{m}}_i} \cup {\rm{Ite}}{{\rm{m}}_j}{\rm{)}}}}, $

(5)

式(5)中，Jaccard_ij表示u_i和u_j之间的兴趣相似度. 若两个客户之间的共同爱好项目数越多，该系数值越大，表示他们之间的兴趣紧密程度越大.

然后，根据目标客户u的一二级社交关系集合U给所有项目进行投票并计算得分.

说明6 　目标客户u的候选项目集的各个成分计算方法：

${\rm{Scor}}{{\rm{e}}_i} = \alpha \cdot\!\!\!\!\!\!\! \sum\limits_{m \in Ij,j \in U}\!\!\!\!\!\!\! {{\rm{PageRan}}{{\rm{k}}_j}} + \beta \cdot \!\!\!\!\!\!\!\sum\limits_{m \in Ij,j \in U} \!\!\!\!\!\!\!{{\rm{Jaccar}}{{\rm{d}}_{uj}}}\text{，}$

(6)

式(6)中，Score_i表示候选项目i的推荐得分值，得分越高则越值得推荐；i∈I_j表示u_j喜爱的项目集合I_j包含候选项目i；u_j∈U表示U包含u_j；PageRank_j表示u_j在u的一二级社交网络G=(U, E)中使用改进PageRank算法计算的得分值；Jaccard_uj表示u和u_j之间的Jaccard系数；α和β为对应两个得分值的权重，满足条件0 $\leqslant$ α $\leqslant$ 1; 0 $\leqslant$ β $\leqslant$ 1; α+β=1.

最后，将所有候选项目根据得分进行降序排序，再利用Top-N过滤法对目标客户实施推荐. 由于每个客户的一二级社交关系是不相同的，所以推荐是个性化的，能够更加接近客户的真实诉求和实际情况.

1.3 实现过程

设目标客户为u，将其社交关系记为一级客户，一级客户延伸出的社交关系记为二级客户，将一级客户和二级客户合并成一个新的客户集合 $U = \{ {u_1},{u_2}, \cdots ,{u_n}\} $ ，其对应的社交网络为G=(U, E)，E是存储社交关系的有向边集合.

详细实现过程：(1) 构建客户之间的社交关系网络：从U中任取2个不同的客户u_i和u_j，若存在u_k∈U且k≠i，k≠j，满足有向边e(u_k, u_i)∈E和e(u_k, u_j)∈E，则称u_i有指向u_j的社交关系，记为蕴含式u_i→u_j. 据此，遍历U中的全部客户，记录所有的社交指向关系，就能构建以 $u$ 的一二级社交关系为对象的网络. (2) 计算支持度和置信度：先计算支持度support_i和support_ij，进而得到置信度C_ij. 据此，遍历U中的全部客户，记录所有蕴含式的置信度，得到该网络有向边的传递权重. (3) 基于关联规则改进状态转移矩阵：承上计算改进型社交关系传递矩阵T=[t_ij]_n×n，其中t_ij=t(u_j|u_i)，再增加阻尼因子得到状态转移矩阵P=[p_ij]_n×n. (4) 计算各个客户的改进PageRank分值：任取初始值PageRank₀= ${\pi _0} \!=\! {(p_1^0,p_2^0, \cdots ,p_h^0)^{\rm{T}}}$ ，经过足够数量的h次迭代计算得到 $ {\rm{PageRan}}{{\rm{k}}_h} \!=\! {\pi _h} \!=\! {({{{P}}^{\rm{T}}})^h}{\pi _0} \!=\!{(p_1^h,p_2^h, \cdots ,p_h^h)^{\rm{T}}}$ . 由定义知，PageRank_h+1=(P^T)PageRank_h，令h→∞则有PageRank=(P^T)PageRank. 因此，PageRank是状态转移矩阵的转置矩阵P^T特征值为1对应的特征向量. (5) 计算目标客户与其社交对象的Jaccard系数. (6) 计算候选项目的得分，得分越高越值得推荐. (7) 进行Top-N过滤得到候选项目：根据得分对项目集进行降序排序，并选取前N个项目对目标客户 $u$ 进行个性化推荐.

2 实验

为了验证本文提出的推荐算法的合理性和有效性，将对本文改进算法、PageRank算法、基于用户的最近邻推荐算法和基于物品的最近邻推荐算法进行对比实验分析.

2.1 数据集和实验环境

实验数据来源是GroupLens项目组(https://group-lens.org)的hetrec2011-delicious-2k数据集，其介绍见表1. Delicious(Delicious website, http://www.delicious.com.)是当今全球最大的书签类网站，其用途是帮助客户存储、分享和发现其他的书签. 此数据集具有高度稀疏的特点，客户与客户之间的关系列表数据稀疏率高达99.56%，客户与项目之间的关系列表数据稀疏率高达99.70%，非常适合测评算法是否能够有效缓解数据稀疏和冷启动对推荐结果的干扰. 本文算法属于非监督式机器学习，在不划分训练集和测试集的情况下，也可以根据目标客户现有的强联系去寻找相应的弱联系并进行赋权，最后得到有序的项目推荐列表.

实验平台的中央处理器为Intel(R) Core(TM) i7-8550U CPU@1.80 GHz(1 992 MHz)，内存为8.00 GB (2 400 MHz)，固态硬盘为SanDisk X400 M.2 2280 128 GB，操作系统为Microsoft Windows 10，所有算法都通过R语言编译实现.

2.2 评测指标

在信息检索和项目个性化推荐领域中，比较常用的评测指标包括平均绝对误差(Mean Absolute Error, MAE)、均方根误差(Root Mean Square Error, RMSE)、准确率(Precision)、召回率(Recall)和F度量(F-Measure). MAE和RMSE的评价效果类似，主要是用于度量预测值与真实值的远近程度，是目前最常用的定量衡量方法，而RMSE更曾作为Netflix Prize智能推荐大赛的官方指定评价指标而风靡一时. MAE和RMSE的数值越小，则表明推荐系统的性能越好. 准确率表示正确推荐(所推荐项目在实际被客户喜欢)数和所有推荐数的比值；召回率表示表示正确推荐(所推荐项目为客户喜欢)数和客户所有喜欢项目数的比值. 尽管准确率和召回率没有必然的联系，但在大规模项目集中，这两个指标是相互制约的：在一般情况下，准确率越高，则召回率就越低；准确率越低，则召回率就越高. 所以，还需要引进二分类模型的常用评价指标F-Measure：使用调和平均值以整合精确度和回溯精确度.

$ {\rm{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^n {|({\rm{observe}}{{\rm{d}}_i} - {\rm{predicte}}{{\rm{d}}_i})} {\rm{|}}\text{，} $

$ {\rm{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({\rm{observe}}{{\rm{d}}_i} - {\rm{predicte}}{{\rm{d}}_i})}^2}} }\text{，} $

$ {\rm{Precision}} = \frac{{{\text{正确推荐的数量}}}}{{{\text{所有推荐的数量}}}}\text{，} $

$ {\rm{Recall}} = \frac{{{\text{正确推荐的数量}}}}{{{\text{所有喜欢的数量}}}}\text{，} $

$ F{\rm{ - Measure}} = \frac{{2\times{\rm{precision}}\times{\rm{recall}}}}{{\operatorname{precision} + {\rm{recall}}}}\text{。} $

2.3 实验设计与结果分析

在本算法中，参数α和β的选取将会对推荐系统的质量造成重要影响. 因此，有必要先分析参数的不同取值会如何影响推荐结果. 不同α和β得到的MAE和RMSE值见表2.

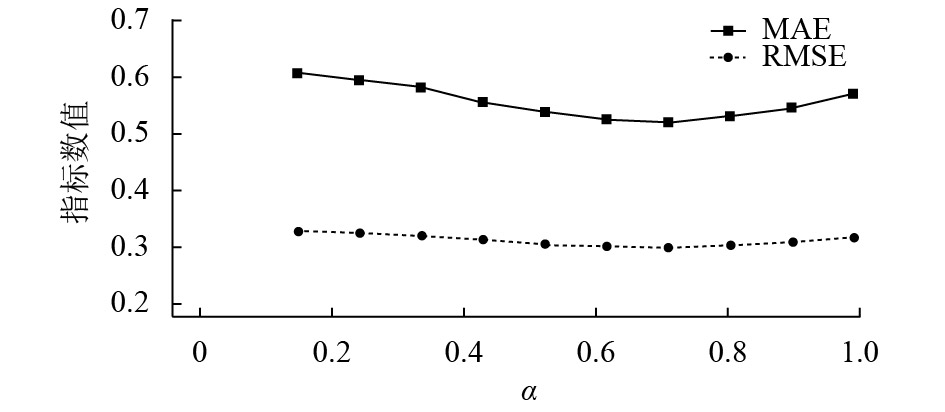
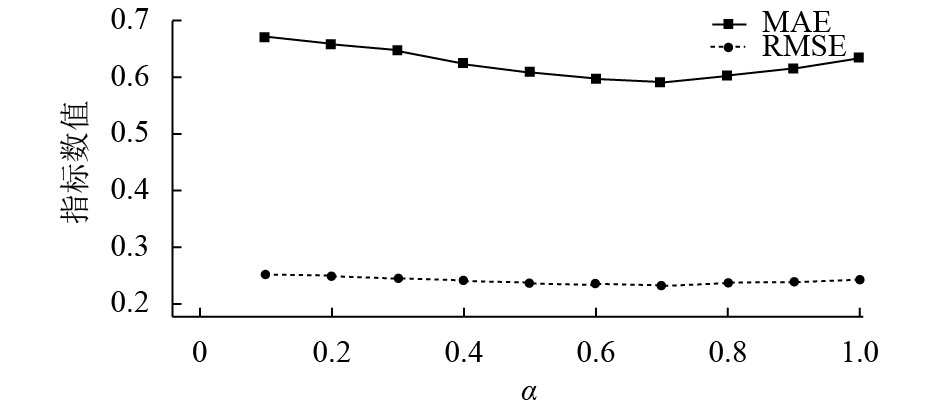
图1和图2分别给出了当N=5和N=10时，α和β的不同取值(α+β=1)对推荐系统的MAE和RMSE造成的不同影响. 由图1和图2可知，刚开始随着α取值的变大β取值的变小，MAE和RMSE的数值都在变小，表明此时推荐系统的性能在提高；在α=0.7且β=0.3的位置附近，推荐系统的性能达到最高值，其在推荐个数为5和10对应的MAE分别为0.538 1和0.589 9，对应的RMSE分别为0.302 7和0.233 7；之后，随着α取值的变大β取值的变小，MAE和RMSE的数值都在变大，表明此时推荐系统的性能在降低. 根据此实验结果，将近似认为当参数α=0.7且β=0.3时，本文提出的推荐系统将达到最优，并将其值固定下来，作为在下文与其他推荐算法做比较时的选定值.

当α=1.0时，推荐系统仅受PageRank_j的结果影响，其在推荐个数为5和10对应的MAE分别为0.590 7和0.633 9，对应的RMSE分别为0.321 9和0.243 5；相反，当β=1.0时，推荐系统仅受Jaccard_ij的计算结果影响，其在推荐个数为5和10对应的MAE分别为0.650 7和0.685 8，对应的RMSE分别为0.342 4和0.254 5. 由此可见，前者的推荐性能优于后者，即单纯考虑社交网络中强弱关系的推荐系统性能是优于单纯考虑兴趣相似度的. 因为，如果客户其社交网络中彼此紧密联系或者相互关联，则他们有相近的兴趣爱好和积极互动的可能性会明显变大^[23]. 此外，当将两者以合适的权重进行并行式投票，能够各自取长补短，提升推荐系统的性能，这与其他学者将社交网络和标签结合形成普适性推荐系统^[24]有异曲同工之妙，因为标签之间也有存在关系，能传达与客户兴趣爱好相关的高度个性化信息，进而就能通过分析标签之后，又能进一步更加准确地区分不同用户之间的相似程度.

在确定了参数α和β的取值之后，将继续探讨本文推荐系统与其他推荐系统的比较.

基于传统PageRank算法的过滤(简称对比算法1)：与本文改进的推荐系统相比，缺少使用关联规则去改进状态转移矩阵. 此外，对候选项目进行投票的环节中，不考虑Jaccard系数，其他推荐环节与本文算法一致.

基于用户的最近邻过滤(简称对比算法2)：此处将不采用传统的Pearson相关系数，而采用Jaccard系数去计算用户之间的相似系数，其他与经典算法一致.

基于项目的最近邻过滤(简称对比算法3)：传统的过滤方法，主要利用项目之间的余弦相似性系数来对目标客户进行项目推荐.

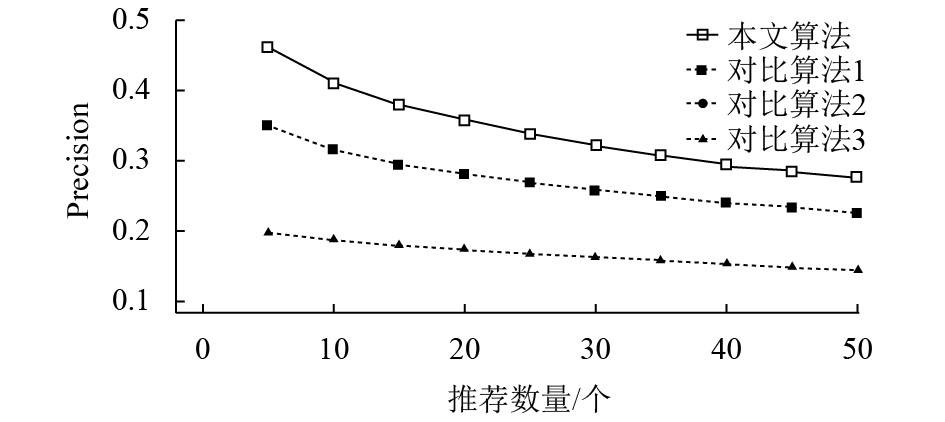
本实验将对目标客户推荐不同数目的候选项目，以此观测各个算法的准确率、召回率和F-measure的变化情况，其实验结果如图3、4和5所示.

图3表明，在推荐个数范围为5~50个的情况下，本文算法的准确率优于其他3种算法. 对比算法1和对比算法2的准确率非常接近，所以两条曲线几乎重合起来. 对比算法3的准确率水平最低. 可以推测，本文算法由于通过调整系数权重结合了传统PageRank算法和基于用户的最近邻过滤的优势，此外，还考虑了客户之间的强弱联系关系，所以，能够更真实客观地反映客户的社交关系和兴趣爱好，进而能够做出更精确的推荐.

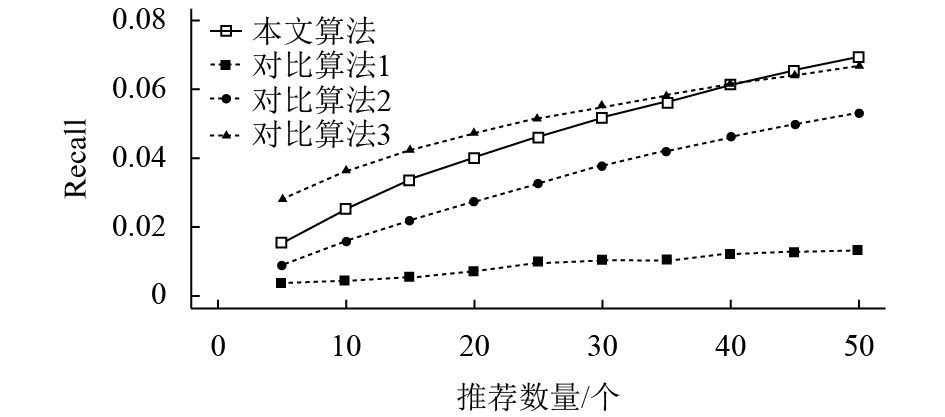
图4表明，在推荐个数范围为5~50个的情况下，本文算法的召回率优于对比算法2和对比算法1. 对比算法1的召回率一直都处于较低水平，随着推荐个数的增加，其值增大不明显；对比算法2的召回率在推荐个数较少时也处于较低水平，可是随着推荐个数的增加，其回溯精确的迅速增大，其增长速度是4种算法中最快的. 由此可见，尽管对比算法1的准确率较高，但是其针对目标客户做出有效推荐的平均覆盖程度并不佳，即平均覆盖范围较小；而对比算法2，当推荐个数较多时，其召回率水平较高，即其推荐结果能够较大范围地覆盖客户真实喜欢的项目. 本文算法和对比算法3的召回率都优于前面两种算法，在此方面表现出较好的性能水平. 在推荐个数范围为5~40个时，对比算法3的召回率优于本文算法. 当推荐个数大于40个时，本文算法的召回率优于其他3种对比算法. 其实，准确率和召回率是没有必然联系的，尽管对比算法3准确率性能水平较低，但是其召回率性能水平却可以表现得更好. 事实上，当推荐个数为50个时，本文算法和对比算法3准确推荐的个数分别为2407 7和1348 6，但是，对比算法3却能较均匀地分配到各个客户，所以其召回率能表现出更优异的水平. 综上所述，本文算法在召回率方面的性能水平也有较佳的表现. 在现实生活表现其推荐结果为对于不同的客户都能均匀较高比例地覆盖其爱好的项目，而不是对于一些客户能够很好地覆盖其爱好项目而对于另外一些客户却显得无能为力.

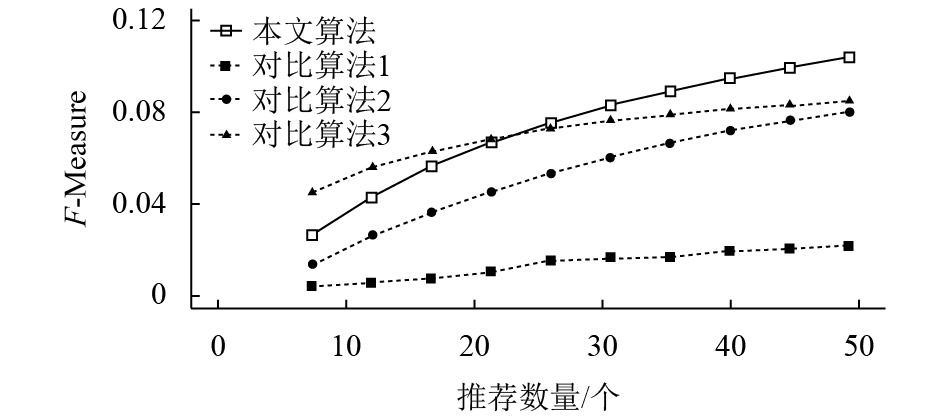
图5表明，在推荐个数范围为5~50个的情况下，4种算法F-measure值的表现类似图4的结果，即本文算法和对比算法1的性能水平优于对比算法2和对比算法3，而本文算法在推荐个数超过25个时，其性能水平才优于对比算法1.

综上所述，基于项目的最近邻过滤算法由于缺乏对客户之间社交关系的考虑，所以准确率性能水平表现不好；基于传统PageRank算法的过滤算法其中一个环节是认为客户对其每一个好友的社交紧密程度是均匀相同的，太过于粗糙，与现实情况不符。此外，其召回率水平一直很低，非常影响其性能表现；基于用户的最近邻过滤，在推荐项目数较少时，其表现并不太好，而只有当推荐项目较多时，可能由于某些因素降低了上述限制性带来的负面影响，提高了表现水平. 本文算法通过关联规则更合理地考虑了客户之间社交紧密程度的差异，还利用了客户之间的兴趣爱好相似度，此外，还通过强联系和弱联系之间两种社交关系的优势互补，既表现了客户之间的相似程度，又合理地补充了客户在强联系中缺乏的部分信息，因此，在准确率、召回率和F-measure值都具有较佳表现，尤其适合推荐数目较多的情景.

3 结束语

在信息技术快速发展和互联网广泛普及的时代，快速准确地为客户找到令人满意的项目显得尤为重要. 在此背景下，本文提出一种结合强弱联系和兴趣的社交网络推荐个性化算法.

为了验证本文提出的推荐算法的合理性和有效性，将对本文改进算法、PageRank算法、基于用户的最近邻推荐算法和基于物品的最近邻推荐算法进行对比实验分析，评估指标选用准确率、召回率和F-measure值，实验结果表明，本文算法的性能水平表现较佳.

由于实验环境的限制，本研究难以选取较大的数据集进行测试，因此，对于大数据试验，本文算法可能具有一定的未知局限性. 此外，本文原先计划将实验数据划分为训练集和测试集，融合监督式学习，通过遗传算法在训练集中计算α和β的最佳组合，但是其计算量实在过于庞大，一般计算机无法实现，将来可作进一步研究.