在计算机图形学中,与传统的基于过程的流体模拟方法相比,基于物理的模拟技术[1]通过直接求解流体运动的控制方程,能够获得更逼真的模拟结果. 其核心是对控制方程纳维—斯托克斯方程组(简称NS方程组)[2]的数值求解与更新,再通过图形渲染技术将动画效果逐帧渲染. 该方法近年取得显著进步,但仍主要存在两方面不足:第一,求解过程中易产生数值耗散导致部分细节丢失[3];第二,相比传统方法其计算量更大,难以得到实时应用.
涡度(Vorticity)[4]是表征流体旋转度的物理量,部分流体模拟工作[5-12]将其作为一种辅助工具用以添加流体细节. 涡粒子(Vortex Particle)[4-5]是模拟涡度的一种重要工具,由其产生的速度场具有良好的无散(Divergence-free)特性. 本文提出一种完全基于涡粒子的模拟框架,结合涡度形式的流体控制方程动态求解,与直接求解NS方程组得到速度场的方法相比,本文方法能够降低数值耗散并更好保持涡旋细节,从而获得真实感更强的流体动画效果.
此外,虽然本文方法避免了直接求解NS方程组时最费时的压力步骤[2],但需要将求得的涡度场转换为速度场,涉及到求解泊松方程组. 该方程组的求解占据了整个流体求解的大部分时间,为突破此性能瓶颈,针对GPU(graphics processing unit,图形处理器)特性和算法特点,基于CUDA(Compute Unified Device Architecture)平台[13]设计提出一种基于GPU的预条件共轭梯度法快速求解,可保证模拟质量不受损的前提下大幅提升模拟速度.
1 相关工作 1.1 基于涡度的细节增强直接基于速度场的流体模拟需对压力求解来保证流体的不可压特性[2],此过程必然存在数值耗散造成细节丢失. 由于涡度转换成速度后有良好的不可压属性,部分研究者通过给速度场添加涡度来补充丢失的流体细节,增强流体真实感.
Selle等[5]在常规的欧拉网格上释放随机涡粒子模拟动态的烟雾和水流效果,但涡粒子只用于辅助添加流体细节,其模拟架构仍存在较大数值耗散. Pfaff等[6]在高分辨率三角网格上模拟了涡流层来合成湍流细节. Mauricio等[7]在固体表面合成涡度模拟了更具真实感的流固耦合效果. Zhang等[8]提出一种有效方法用于处理求解涡度方程时的边界问题. Eberhardt等[9]则提出从速度场逐层提取涡旋丝(Vortex Filament)以增强流体细节. Zhu等[10]通过人工合成流体细节补偿对流过程中的涡度损失,增强了烟雾模拟的真实感. 此外,涡度也被用于基于光滑粒子动力学(SPH)的流体模拟方法以提升模拟质量[11-12]. 与上述方法不同,本文方法完全基于涡粒子,不依赖于传统的速度求解架构.
1.2 流体模拟硬件加速传统的GPU因图形计算而产生,早期采用汇编语言、Cg语言等图形渲染开发语言编写与图形渲染流水线相关联的计算流程,基于GPU的通用计算编程门槛较高. 自2006年NVIDIA公司推出CUDA平台[13]后,通用并行计算难度大幅降低,CUDA也成为一个重要的并行计算平台,可用以解决基于物理的流体模拟中的巨量计算问题.
2008年Tolke和Krafczyk[14]在普通的桌面机上利用CUDA 成功实现了一个有效的三维LBM求解器. 2010年G. McAdams等[15]在多核GPU系统上实现了求解多网格(Multi-grid)方法的线性系统. 2015年Bailey 等[16]利用计算机集群设计了一种并行求解器. 2016年Yang等[17]通过修改迭代正交投影(Iterated Orthogonal Projection,IOP)框架加快了迭代法求解泊松方程的收敛速度. 同年Liu等[18]针对异构平台基于区域划分的方法设计了一种流体模拟的压力求解器. 在此基础上,2017年Chu等[19]在多核系统上设计了一种能更快收敛的求解器,但该计算平台更适应于CPU而非GPU. 除常规网格法外,GPU加速也被应用到其他非常规网格法,如SPH[20]、MPM (物质点方法)[21],本文则利用GPU加速求解涡度到速度的转换过程.
2 基于涡粒子的流体模拟基于物理的流体模拟技术的核心是对以下NS方程组的数值求解与更新,其计算精度对最终模拟效果有重要影响.
| $\frac{{{\text{∂}} { u}}}{{{\text{∂}} t}} + { u} \cdot \nabla { u} + \frac{1}{\rho }\nabla p = { g} + \nu \nabla \cdot \nabla { u}.$ | (1) |
| $\nabla \cdot { u} = 0.$ | (2) |
式中
直接基于速度场求解上述NS方程组容易产生数值耗散而丢失部分细节,为解决此问题,本文提出用涡粒子来模拟流体,通过保持流体模拟过程中的涡旋,以获得更好的流体模拟细节. 对式(1)两边求旋度,结合式(2)整理得
| $\frac{{{\text{∂}} { \omega }}}{{{\text{∂}} t}} + ({ u} \cdot \nabla ){ \omega } = (\nabla { u}) \cdot { \omega } + \nu {\nabla ^2}{ \omega } + \frac{1}{\rho }\nabla \times { g}.$ | (3) |
式(3)即为涡度形式的NS方程,相比式(1)压力项由于对梯度场求旋度而消失(
类似于求解常规NS方程组,本文采取分裂的方法将式(3)依次拆分为以下对流项、伸展项、扩散项和外力项逐项迭代求解.
| $\frac{{{\text{∂}} { \omega }}}{{{\text{∂}} t}} + ({ u} \cdot \nabla ){ \omega } = 0.$ | (4) |
| $\frac{{{\text{∂}} { \omega }}}{{{\text{∂}} t}} = (\nabla { u}) \cdot { \omega }.$ | (5) |
| $\frac{{{\text{∂}} { \omega }}}{{{\text{∂}} t}} = \nu {\nabla ^2}{ \omega }.$ | (6) |
| $\frac{{{\text{∂}} { \omega }}}{{{\text{∂}} t}} = \frac{1}{\rho }\nabla \times { g}.$ | (7) |
式(4)为对流项,描述涡粒子如何随速度场移动. 由于涡粒子的拉格朗日属性,求解对流项时方程左边当做整体,采用积分求解. 无需像基于速度的求解算法中利用半拉格朗日等方法回退求解,可避免回退算法本身严重的数值损耗. 式(5)为伸展项,描述涡粒子在单一时间步下伸展度和倾斜度的变化,可直接计算式中右边项再结合离散数值方法更新粒子的旋度. 式(6)为扩散项,描述流体粘性对流体的影响,当模拟无粘流体时可将粘性系数
整体模拟流程如图1所示,该方法由于直接使用涡度模拟流场,能够保持更多涡旋,同时可避免直接基于速度场方法求解对流以及压力步骤时产生的数值耗散,以捕捉更丰富的流体细节.

|
图 1 基于涡粒子的烟雾模拟流程 Figure 1 The workflow of vortex particle based smoke simulation |
求解式(3)需速度场
亥姆霍兹分解定理[4]表明任意向量场
| ${{U}} = \nabla \times {{V}} - \nabla \varphi .$ | (8) |
等式右边两项分别为无散和无旋部分,其中
| $\nabla \cdot {{V}} = 0.$ | (9) |
| $\nabla \times \nabla \varphi = 0.$ | (10) |
对式(8)求旋度(即施加算子
| ${ \omega } = \nabla \times (\nabla \times { V} ).$ | (11) |
此外,有以下向量恒等式:
| $\nabla \times (\nabla \times {{V}} ) = \nabla (\nabla \cdot {{V}} ) - {\nabla ^2}{{V}}. $ | (12) |
综合式(9),(11)和(12),得到
| ${\nabla ^2} {{V}} = - { \omega }.$ | (13) |
式(13)是一个泊松方程组,求解方程组得到
| ${ u} = \nabla \times {{V}}. $ | (14) |
数值求解泊松方程组(式(13))时,先采用有限差分离散左边的拉普拉斯算子
CUDA是GPU上的一种通用并行计算平台和编程模型[13],可利用GPU上远多于CPU的计算核心有效解决多个大型复杂计算的并行化问题,在流体模拟中也被广泛应用[14-21]. 本文算法即在CUDA架构上进行优化和加速.
如上文所述,在涡粒子模拟流体的过程中,整个计算流程速度场的求解(式(13))最为耗时. 离散后的泊松方程的系数矩阵为一大型稀疏对称正定矩阵,本文采用预条件共轭梯度法(Preconditioned Conjugate Gradient method,下文简称PCG)[2]迭代求解. PCG方法具有存储空间小且收敛速度快等优点. 针对线性方程组
算法1:预条件共轭梯度法(PCG method)
初始化:x=0, r=b, z=M-1r, s=z,
Loop until done:
1: 辅助向量z=As
2:
3: 更新
4: If
5:
6:
7:
8: 搜索向量
9:
算法1中
首先,CUDA对于稀疏矩阵的存储主要有稀疏行压缩(Compressed Sparse Row,CSR)、坐标格式(Coordinate Format,COO)、稀疏列压缩格式(Compressed Sparse Column Format,CSC)等,本文算法采用较为常用的CSR格式。存储后的矩阵由变量nnz和三个一维数组csrValA、csrRowPtrA、csrColIndA组成,其中nnz存储矩阵中非零元素的个数,csrValA以行优先顺序存储所有非零元素值,csrRowPtrA存储每行非零元素在csrValA中的索引和整数nz。若索引从0开始,nz的值为nnz;若从1开始,则nz的值为nnz+1。csrColIndA存储csrValA数组中对应元素在矩阵中的列索引。举例如下:
若A=
| $\begin{split} &{\rm nnz} = 9;\\ &{\rm csrValA} = \left[ {1.0\;\;4.0\;\;2.0\;\;3.0\;\;5.0\;\;7.0\;\;8.0\;\;9.0\;\;6.0} \right];\\ &{\rm csrRowPtrA} = \left[ {0\;\;2\;\;4\;\;7\;\;9} \right];\\ &{\rm csrColIndA} = \left[ {0\;\;1\;\;1\;\;2\;\;0\;\;3\;\;4\;\;2\;\;4} \right]. \end{split}$ |
其次,PCG方法每次迭代都需要两次矩阵向量乘,此操作时耗较高,本文结合系数矩阵的特点采用CUDA对其进行并行优化。三维泊松方程离散后系数矩阵每行非零元素恰为7个,如图2所示(矩阵中字母代表非零常量)。

|
图 2 三维泊松方程系数矩阵 Figure 2 The coefficient matrix of three-dimensional Poisson equation |
根据CUDA以线程束为调度单位的特点,32个线程为一个线程束,即每次均为32个线程在不同的数据上执行相同指令,采取每半个线程束计算两个结果向量的元素的策略,可最大程度减少闲置线程束;并根据数据复用特点在每个线程块中分配适当共享内存提高计算效率. 具体优化步骤见伪代码形式的算法2. 为简要阐述,算法2和下文的算法3中部分计算步骤采用函数表示(如算法2中的f,h,u以及g),其功能作用会在算法中对应的注释中进行说明.
算法2: CUDA矩阵向量乘算法
输入:矩阵A[m][n],向量x
输出:结果向量r
1: 分配共享内存数组cache;// f:根据cuda函数内置变量计算出此线程所对应的cache索引cid、线程索引tid和偏移量offset.
2: cid、tid、offset=f(threadIdx.x, blockIdx.x, lockDim.x)
3: row =h(tid) //初始行数
4: tidInWrap=u(threadIdx.x)//线程在半个线程束中的偏移量
5: For i=row to m
6: col=g(row, tidInWrap); //计算线程所要计算元素对应矩阵的列索引
7: If (矩阵对应元素不为零)
8: cache[cid]=A[i][col]*x[col];//共享内存
9: _syncthreads(); //线程同步
10: If (col为此行第一个非零元素的列索引)
11: r[i]=sum(cache[cid…]); //此行所对应cache数组求和写入结果向量r
12: If (col为下一行第一个非零元素的列索引)
13: r[i+1]=sum(cache[cid…]);//此行所对应cache数组求和写入结果向量r
14: i+=offset;
15: End For
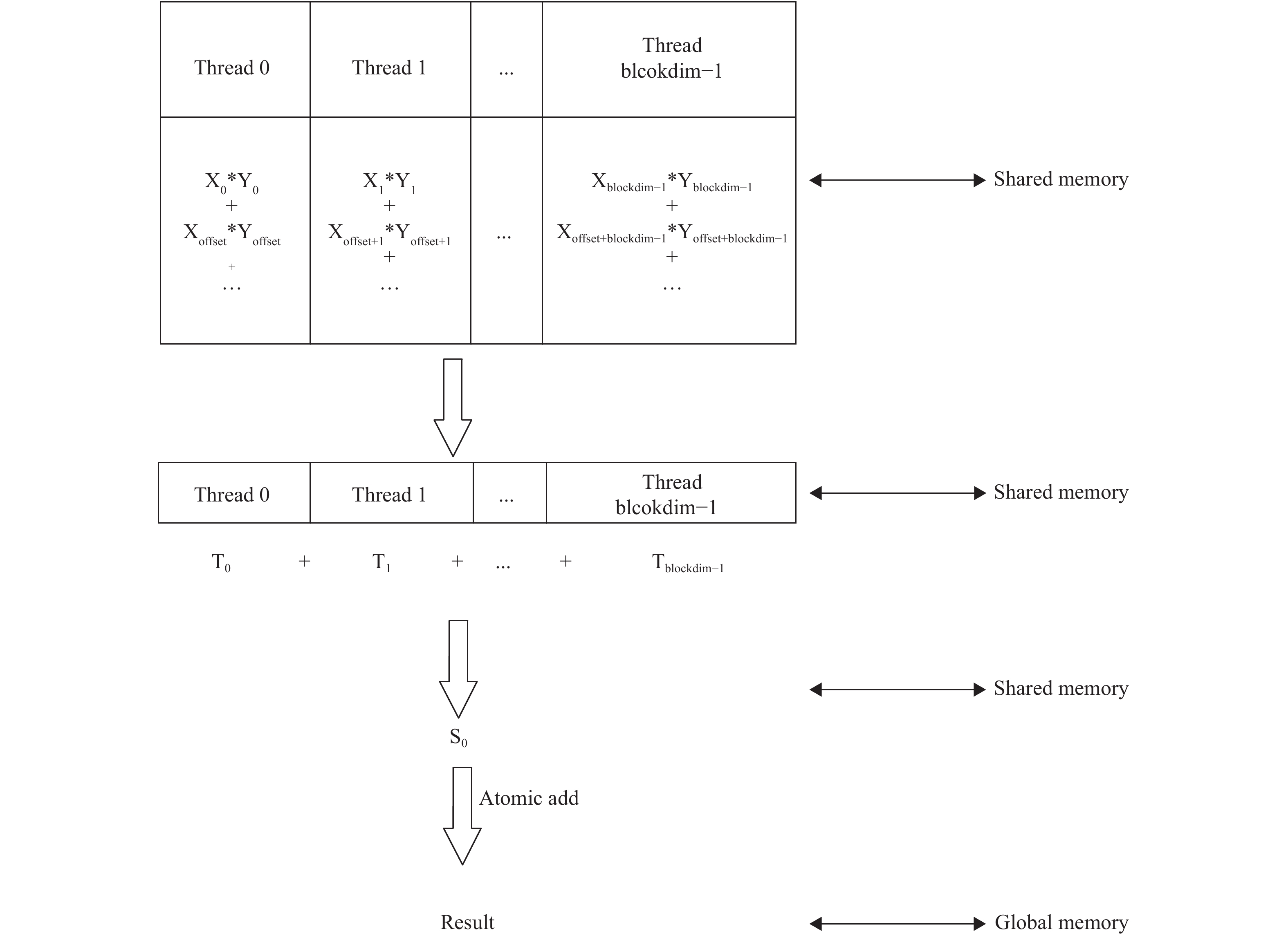
再次,每次迭代均需进行两次向量乘操作,向量乘操作的优化策略为block内归约和block间归约两步. 由于向量维度较大,每个线程需进行多个乘法运算,为使线程合并访存减小访存时间,每个线程进行“跳跃式”运算. 计算完一对向量内元素的乘积后,对向量元素相对于现在位置偏移整个grid的距离,以达到相邻的线程可连续访问相邻的全局内存,实现合并访存. 此外,每个block分配一定的共享内存保存中间变量存储多次乘积后的和. Block间由于无法通信,用原子操作进行归约,最终将计算结果存储于目标位置. 图3演示了向量内积操作中一个线程块中的计算过程,其中Blockdim为线程块中的线程数,offset为总线程数,Atomic Add为原子加操作.
|
图 3 一个线程块中向量内积的计算过程 Figure 3 Vector inner product calculation in a thread block |
内积运算对应的优化步骤详见算法3,其他kernel函数调用此函数优化相应计算.
算法3: CUDA向量乘算法
输入:向量x, y和长度n
输出:相乘结果r
1: 分配共享内存数组cache;
2: cid、tid、offset=f(threadIdx.x, blockIdx.x, blockDim.x) //f:根据cuda函数内置变量计算出此线程所对应的cache索引cid、线程索引tid和偏移量offset.
3: clear(cache,cid,r); //重置cache和r
4: For i=tid to n
5: cache[cid]+=x[tid]*y[tid];
6: tid+=offset;
7: End For
8: _syncthreads(); //线程同步
9: half=g(threadIdx.x) //块内总线程
10: While (half/2 !=0) do //归约求和
11: If (cid<half)
12: cache[cid]+=cache[cid+half];
13: _syncthreads();
14: atomicAdd(r,cache) //原子加操作
最后,针对数据传输耗时的问题,提出采用分页锁定(page locked)的方式申请内存,可降低传输时间. CPU端的收敛判断通常采用剩余向量中最大元素小于特定值的判读方法,而本文GPU执行则采取了更适合并行的剩余向量长度小于阈值的方法,调整阈值的大小可得到相近的计算精度. CUDA流(stream)技术改进了GPU上的算法,即CUDA显卡有独立引擎分别处理kernel计算和数据传输. 本文利用此技术在判断收敛同时传输结果,使数据传输和计算在一定程度上并行以提升计算效率.
5 实验结果和分析本文算法测试硬件平台为:i7-7700k CPU,8 G内存,GTX-1060 GPU(显存6 G),软件平台为:Visual Studio 2015,CUDA9.0. 求解泊松方程时,收敛条件设为剩余向量元素最大绝对值低于10–6. 为保证公平性,所有对比实验均在同样配置的软硬件平台进行. 从图4可见,本文方法模拟结果与真实烟雾场景相似度较高.

|
图 4 本文方法烟雾模拟效果(左)与真实图片对比(右) Figure 4 Comparison of the smoke simulation result (left) with real image (right) |
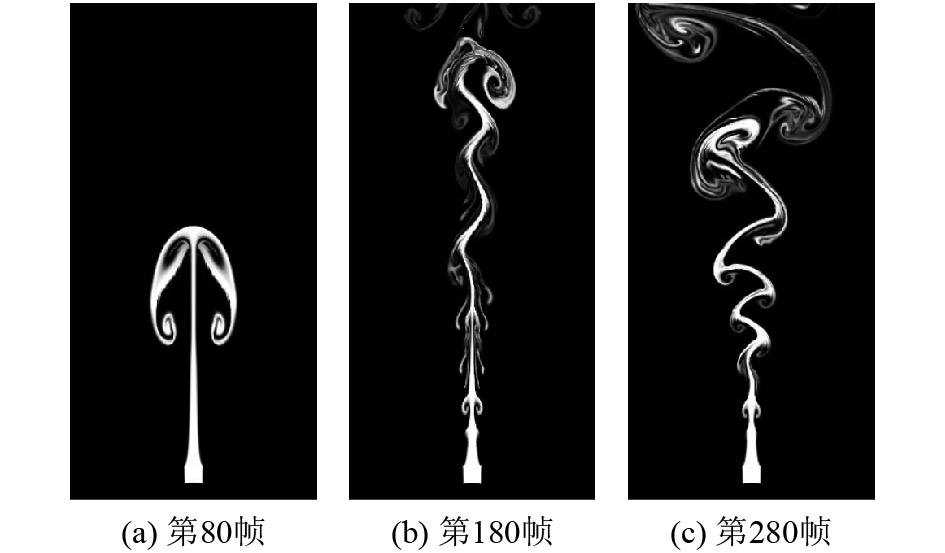
将传统的基于速度场的直接模拟方法与本文的完全基于涡粒子的方法对比. 首先,测试算法在二维烟雾模拟上的效果. 网格分辨率为256×512,采用OpenGL渲染模拟结果. 抽取第80帧、180帧和280帧,模拟效果对比见图5、图6. 可见本文方法能够捕捉更多流体细节(见图6(a)和(b)),保持更多涡旋效果(见图6(c)),流体真实感更强.
|
图 5 基于速度的方法二维烟雾模拟效果 Figure 5 2D smoke simulation results of velocity based method |
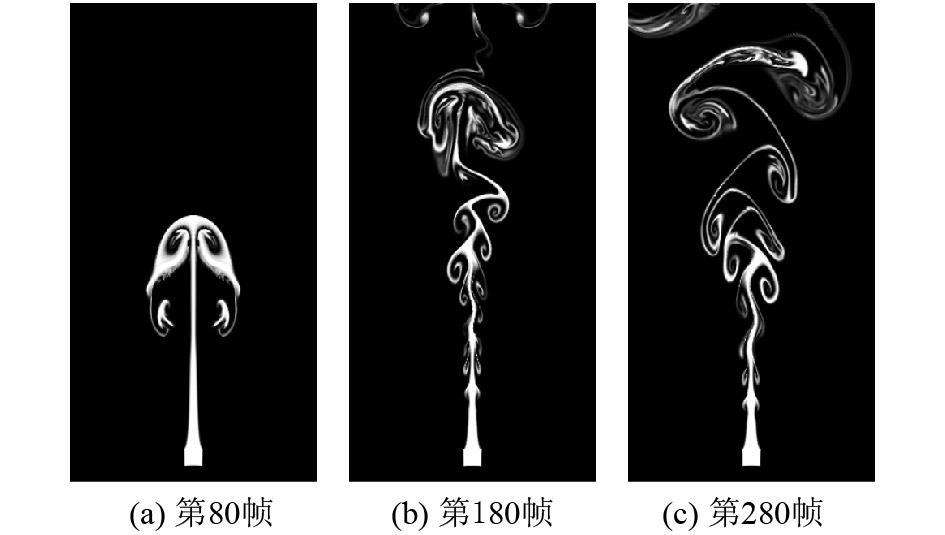
|
图 6 本文方法的二维烟雾模拟效果 Figure 6 2D smoke simulation results of the method |
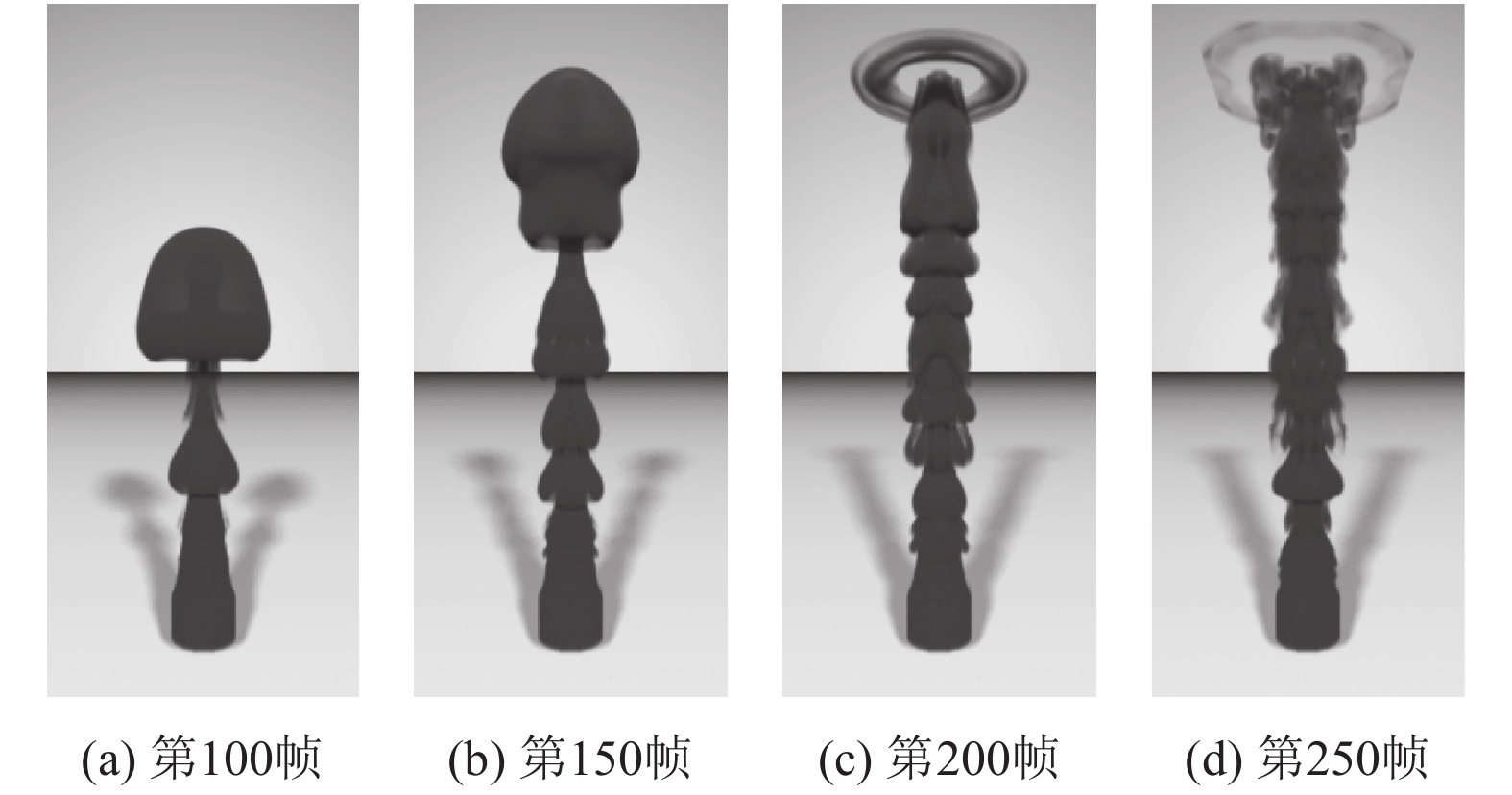
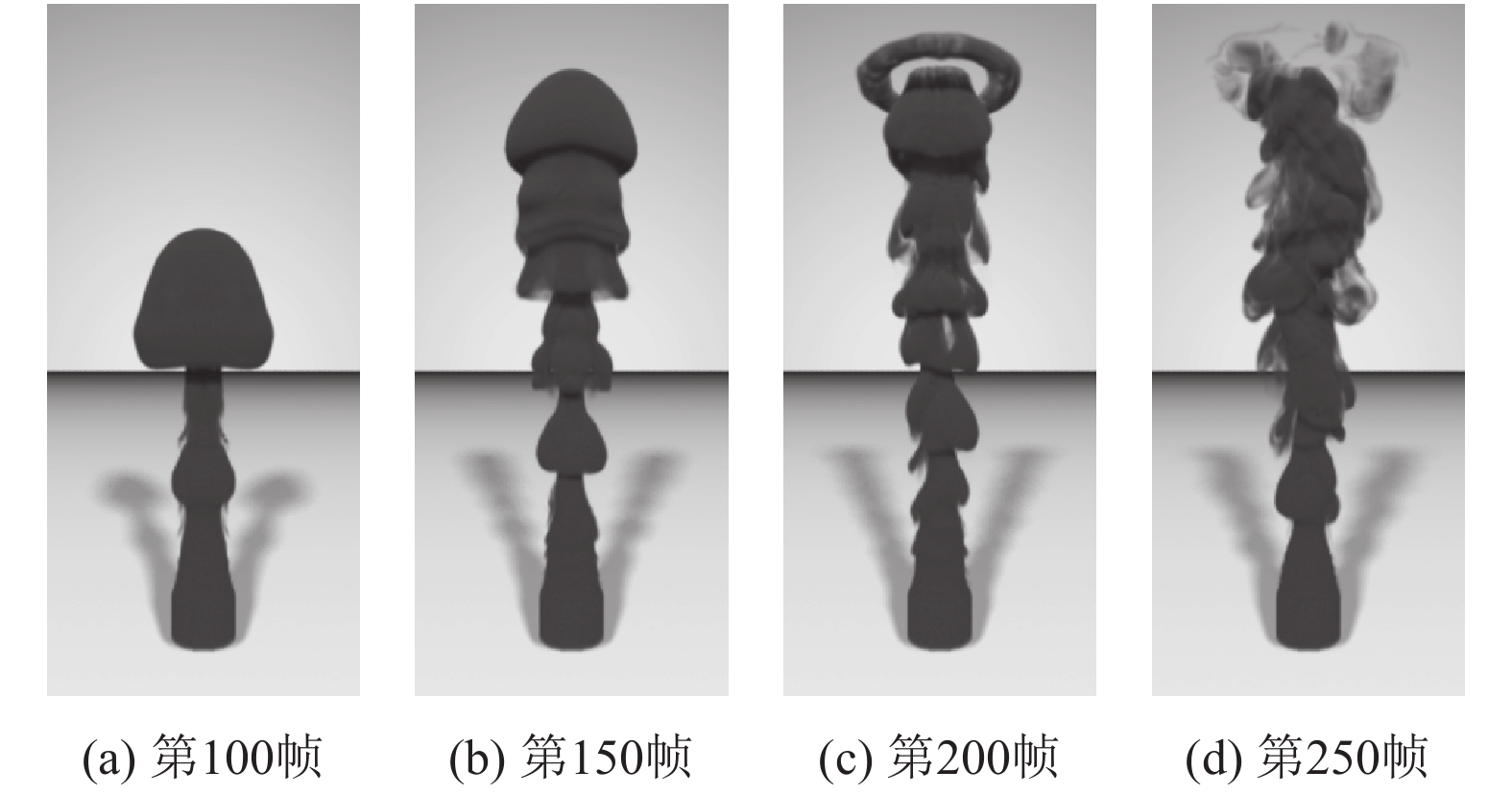
其次,测试算法在三维烟雾模拟上的效果对比. 网格分辨率为96×192×96,采用开源离线渲染器PBRT渲染模拟结果. 抽取第100帧、150帧,200帧和250帧,模拟效果对比见图7、图8. 同样可见本文算法在捕捉细节和保持涡旋上具有明显优势.
|
图 7 基于速度的方法三维烟雾模拟效果 Figure 7 3D smoke simulation results of velocity based method |
因涡粒子方法产生的速度场为无散的,虽可避免基于速度的方法中费时的压力求解步骤,但涡度转为速度时涉及到泊松方程组的求解,又将额外增加计算量. 为此,在GPU上实现了PCG算法快速求解离散后的泊松方程,加快模拟速度. 需注意,本文仅对涡粒子模拟方法中最为耗时的泊松求解步进行了GPU加速,若将整个算法移植到GPU上执行,可获得更快的模拟速度. 表1列出了每个时间步的平均时耗对比.
|
图 8 本文方法的三维烟雾模拟效果 Figure 8 3D smoke simulation results of the method |
| 表 1 各方法单个时间步的平均耗时 Table 1 The average time cost of each method in each time step |
在二维模拟中,涡粒子方法(见图6)整体平均时耗约为基于速度方法(见图5)的1.35倍,其中泊松方程组求解耗时占比34.78%,经GPU加速后,该步耗时仅0.04秒,加速比达8倍. 加速后的整体时耗为0.64秒,减少到基于速度方法的94.12%.
在三维模拟中,涡粒子方法(见图8)整体平均时耗约为基于速度方法(见图7)的1.38倍,其中泊松方程组求解耗时占比50.42%,经GPU加速后,该步耗时仅0.54秒,加速比达12倍. 加速后整体时耗7.02秒,仅为基于速度方法的74.28%.
此外,针对上述的三维烟雾模拟,除PCG方法外,GPU端还实现了雅克比迭代法(下文称Jacobi方法). Jacobi方法是一种求解大型稀疏矩阵方程组的经典方法[2, 22],但其收敛较慢. 表2列出了GPU端两种方法耗时对比. 前100帧速度PCG方法是Jacobi的3.8倍;第200到300帧,由于流体运动复杂化,求解时PCG收敛得更快,达到Jacobi算法的5.3倍,充分说明本文PCG算法的性能优势.
| 表 2 GPU端两种方法耗时对比 Table 2 Comparison of two GPU-based solvers on average simulation time |
本文针对流体模拟中传统的基于速度场方法存在的数值耗散以及难以保持涡旋细节等问题,提出一种完全基于涡粒子的流体模拟算法. 涡粒子运动通过求解涡度形式的NS方程计算更新,网格点的涡度通过周围涡粒子插值得到,再转换成速度场. 对流项通过积分求解,可避免速度场方法对流时存在的严重数值耗散,且涡粒子转换的速度场具有无散的特点,更能保持流场的涡流细节. 此外,针对涡粒子方法模拟需求解泊松方程组的性能瓶颈,在GPU平台实现了一种高效的PCG算法提升求解速度,在三维模拟时加速比超过10倍,最终的模拟速度低于传统算法的75%. 可见在模拟质量和模拟速度上本文算法均优于传统的基于速度场算法.
本文方法还可应用于自由表面的流体,后续研究计划采用本文算法模拟动态的真实感水流效果. 此外,本文只针对流体模拟中耗时的泊松方程求解过程采用GPU加速,后续计划将整个模拟流程移植到GPU端执行,计算任务分配到多个GPU中协同计算,预计可实现大规模的高度真实感流体模拟.
| [1] |
HUANG Z P, GONG G H, HAN L. Physically-based smoke simulation for computer graphics: a survey[J].
Multimedia Tools and Applications, 2015, 74(18): 7569-7594.
DOI: 10.1007/s11042-014-1992-4. |
| [2] |
BRIDSON R. Fluid simulation for computer graphics [M]. New York, America: A K Peters/CRC Press, 2015: 21-28.
|
| [3] |
HUANG Z P, KAVAN L, LI W K, et al. Reducing numerical dissipation in smoke simulation[J].
Graphical Models, 2015, 78: 10-25.
DOI: 10.1016/j.gmod.2014.12.002. |
| [4] |
COTTET G H, KOUMOUTSAKOS P D. Vortex methods: theory and practice [M]. Cambridge, UK: Cambridge University Press, 2000.
|
| [5] |
SELLE A, RASMUSSEN N, FEDKIW R. A vortex particle method for smoke, water and explosions[J].
ACM Transactions on Graphics, 2005, 24(3): 910-914.
DOI: 10.1145/1073204. |
| [6] |
PFAFF T, THUEREY N, GROSS M. Lagrangian vortex sheets for animating fluids[J].
ACM Transactions on Graphics, 2012, 31(4): 1-8.
|
| [7] |
MAURICIO V, BEN H, LANG J, et al. Vortical inviscid flows with two-way solid-fluid coupling[J].
IEEE Transaction on Visualization and Computer Graphics, 2014, 20(2): 303-315.
DOI: 10.1109/TVCG.2013.95. |
| [8] |
ZHANG X X, LI M C, BRIDSON R. Resolving fluid boundary layers with particle strength exchange and weak adaptivity[J].
ACM Transactions on Graphics, 2016, 35(4): 1-8.
|
| [9] |
EBERHARDT S, WEISSMANN S, PINKALL U, et al. Hierarchical vorticity skeletons [C]//Proceedings of the ACM SIGGRAPH/ Eurographics Symposium on Computer Animation. NY, USA: ACM Press, 2017: 1-11.
|
| [10] |
ZHU J, LUO Y, REN X H, et al. Synthetic fluid details for the vorticity loss in advection[J].
Computer Animation and Virtual Worlds, 2018, 29(3-4): 1-11.
|
| [11] |
JANG T, BLANCO I RIBERA R, BAE J, et al. Simulating SPH fluid with multi-level vorticity[J].
International Journal of Virtual Reality, 2011, 10(1): 17-23.
|
| [12] |
PEER A, TESCHNER M. Prescribed velocity gradients for highly viscous SPH fluids with vorticity diffusion[J].
IEEE Transactions on Visualization and Computer Graphics, 2017, 23(12): 2656-2662.
DOI: 10.1109/TVCG.2016.2636144. |
| [13] |
COOK S. CUDA Programming: a developer's guide to parallel computing with GPUs[M]. Waltham, USA: Elsevier, 2013: 106-205.
|
| [14] |
TOLKE J, KRAFCZYK M. Teraflop computing on a desktop pc with gpus for 3d cfd[J].
International Journal of Computational Fluid Dynamics, 2008, 22(7): 443-456.
DOI: 10.1080/10618560802238275. |
| [15] |
MCADAMS A, SIFAKIS E, TERAN J. A parallel multigrid Poisson solver for fluids simulation on large grids [C]//ACM SIGGRAPH Symposium on Computer Animation. Madrid, Spain: Eurographics Association Aire-la-Ville, 2010: 65-74.
|
| [16] |
BAILEY D, BIDDLE H, AVRAMOUSSIS N, et al. Distributing liquids using OpenVDB [C]//ACM SIGGRAPH 2015 Talks. Los Angeles: ACM Press, 2015: 1.
|
| [17] |
YANG Y, YANG X B, YANG S C. A fast iterated orthogonal projection framework for smoke simulation[J].
IEEE Transactions on Visualization and Computer Graphics, 2016, 22(5): 1492-1502.
DOI: 10.1109/TVCG.2015.2446474. |
| [18] |
LIU H X, MITCHELL N, AANJANEYA M, et al. A scalable Schur–complement fluids solver for heterogeneous compute platforms[J].
ACM Transactions on Graphics, 2016, 35(6): 1-12.
|
| [19] |
CHU J Y, ZAFAR N B, YANG X B. A schur complement preconditioner for scalable parallel fluid simulation[J].
ACM Transactions on Graphics, 2017, 36(5): 1-10.
|
| [20] |
TAKADA K, NITTA T, OHNO K. Acceleration of SPH-based fluid simulation on GPU[C]//High Performance Computing Symposium. Los Angeles, USA: ACM Press, 2017: 26-35.
|
| [21] |
GAO M, WANG X L, WU K, et al. GPU optimization of material point methods[J].
ACM Transactions on Graphics, 2018, 37(6): 1-12.
|
| [22] |
AMADOR G, GOMES A. CUDA-based linear solvers for stable fluids[C]//ICISA 2010: 2010 International Conference on Information Science and Applications. Seoul: IEEE, 2010: 279-286.
|
 2019, Vol. 36
2019, Vol. 36

