近年来,经济增长问题一直是许多专家学者研究的热点问题[1]. 自改革开放以来,我国的经济发展一直处于突飞猛进的状态,地区生产总值逐年增高. 但是,随着经济的增长,在追求经济发展的过程中必然会引发很多问题,其中的负面因素必将对我国的经济发展产生不良的影响. 因此对经济增长的评价尤为重要,通过对不同省份经济增长的评价可以明确各个省份所存在的影响因素及差异程度[2].
可拓学[3]是由我国学者蔡文于1983年提出的一门横跨数学、哲学和工程学交叉的原创性横断学科,它以形式化的模型,探讨事物拓展的可能性以及开拓创新的规律和方法,并用于解决现有的条件下无法实现人们要达到的目标的问题. 目前,可拓学已经广泛应用于计算机科学、工程、管理和经济等诸多领域[4-10].
突变理论是一门新兴的现代数学分支,1972年,法国数学家托姆(R.Thom)的《结构稳定性和形态发生学》的出版标志着突变理论的诞生[11]. 突变论结合了奇点理论、拓扑学和结构稳定性等数学工具,以系统结构稳定性为基础,处理现实世界具有矛盾性的不连续现象. 因此,突变理论的本质就是揭示事物的质变方式是如何依赖条件变化的[12]. 突变理论是突变级数法的理论基础,是一种对评价目标进行多层次矛盾分解,然后利用突变理论与模糊数学相结合产生突变模糊隶属函数,再由归一公式进行综合量化计算,最后归一为一个参数,即求出总的隶属函数,从而对评价目标进行排序分析的一种综合评价方法[13]. 由于该方法考虑了评价指标的相对重要性但却没有对指标采用权重,从而减少了主观性又不失科学性及合理性,而且计算相对简易准确,因此应用范围极为广泛.
为了更科学性地评价国内各地区的经济增长状况,本文根据专业的指标建立原则,借鉴国内外专家学者的经验,从《中国统计年鉴》[14]中选取了与经济增长影响因素最大的若干指标,建立了经济增长的指标评价体系[15]. 根据各指标重要性的不同,确定出矛盾的主要方面和次要方面以及指标体系所对应的突变模型的类别. 原始的突变级数法是将突变理论和模糊数学将结合,本文将可拓学理论与突变理论相结合,用可拓学中的关联函数代替原有突变级数法中的模糊隶属函数,求出指标的关联度进而得出各指标的突变指数值并将其转化为一般意义上的综合值进行评价. 该方法将可拓理论和突变级数法结合,经过对比分析,评价结果真实地反映了我国部分省、市、自治区经济增长的快慢,对经济增长的综合评价起到积极作用.
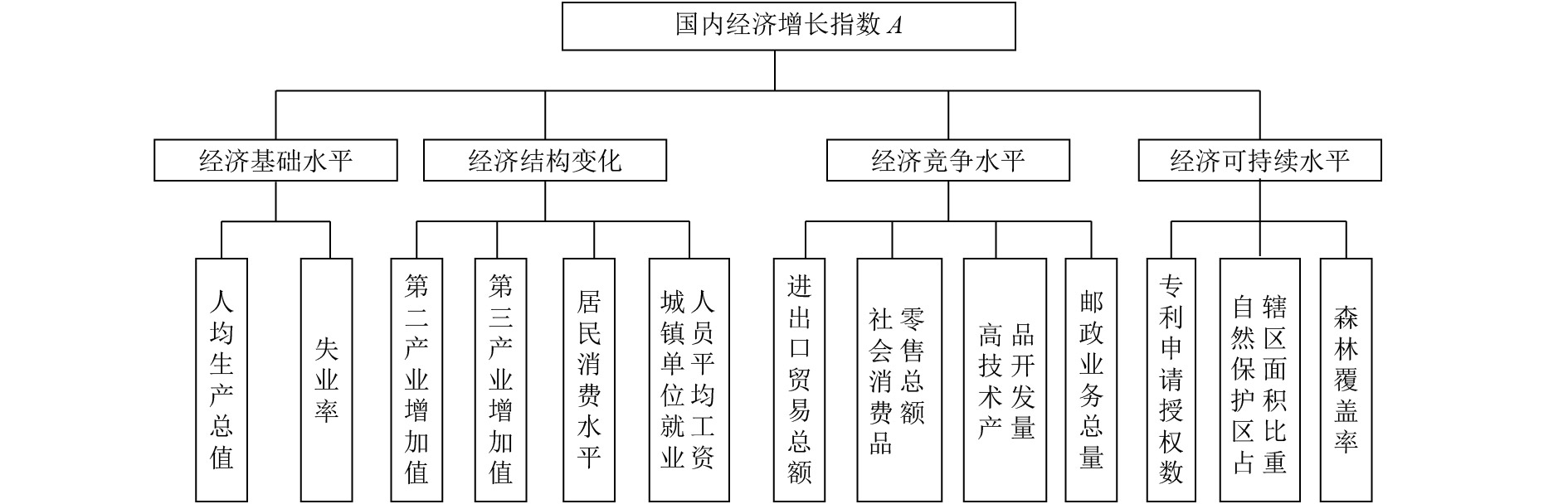
1 经济增长评价体系基于国内外专家学者研究的基础上,本文选取了经济基础水平、经济结构变化、经济竞争力水平,经济可持续发展水平这4个指标作为经济增长评价的一级指标,并根据中国统计年鉴中的经济基础数据分别选取了若干二级指标[16],各子系统指标之间相互独立,又彼此联系. 经济增长指标体系如表1.
| 表 1 经济增长指标体系 Table 1 Economic growth indicator system |
经济基础水平,即经济的基础发展水平,包括区域内的经济发展基础,产业类型等有关因素. 影响经济基础水平的因素有人均生产总值GDP和失业率,二者都是衡量经济增长的最重要指标之一,看似相互独立,却又存在关联. 失业率高,人均收入少,相应的人均可支配收入下降,消费减少,生产萎缩,生产总值也相应下降.
1.2 经济结构变化经济结构变化,即各产业结构的变化,我国产业结构纷杂,划分为农业、工业和服务业的一、二、三产业. 影响经济结构变化的二级指标有:第二产业增加值、第三产业增加值、居民消费水平和城镇单位就业人员平均工资构成. 平均工资越高,可支出金额比例越高,居民消费水平越高,随之,以工业为主的第二产业和餐饮服务业为代表性的第三产业的增加值也必将大幅度提升.
1.3 经济竞争力水平经济竞争水平,即各地区参与竞争的经济实力. 本文选取了对经济竞争力水平影响较大的4个因素:进出口贸易总额、社会消费品零售总额、高技术产品开发量和邮政业务总量作为经济竞争力水平指标下的二级指标. 进出口总额体现了对外贸易方面的总规模,社会消费品零售额反应了消费品总额,即城乡居民和社会集团的消费品总支出,代表了一定的购买力,而购买力必定影响贸易额,随着购买力的增加也必将推动邮政业务的增加和高新技术产业的提升.
1.4 经济可持续发展水平经济可持续发展水平,即是一种能够长远发展的经济模式,在保持经济发展的同时,环境及科技等多方面共同进步才会导致整体发展水平呈上升趋势. 影响经济可持续发展水平的二级指标有:专利申请授权数、自然保护区占辖区面积比重和森林覆盖率. 环境方面,后两者都是特定的土地面积比重,且某些特殊的森林区域也属于自然保护区.
2 计算关联度 2.1 确定关联函数由于本文涉及的各评价因子量值域不相同,各指标最优点情况亦不同,故选取的关联函数也有差别[17]. 对于负向指标,即期望值越小越好的指标,其最优点在量值域左端. 对于正向指标,即期望值越大越好的指标,其最优点在量值域右端. 基于以上指标的最优点分析,各指标满足可拓理论中的简单关联函数如下.
正域为有限区间
当
| $k(x) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{x - a}}{{b - a}},}&{x < a};\\ {\dfrac{{b - x}}{{b - a}},}&{x > a};\\ {k(a) = 1,}&{x = a} . \end{array}} \right.$ | (1) |
当
| $k(x) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{x - a}}{{b - a}},}&{x < b};\\ {\dfrac{{b - x}}{{b - a}},}&{x > b};\\ {k(b) = 1,}&{x = b}. \end{array}} \right.$ | (2) |
本文中,各评价特征的数量化的量值域分别为表2所示. 对于评价指标
根据关联函数的计算公式(1)和(2),可以计算出各个指标的关联函数值,即关联度.
| 表 2 评价指标的量值域 Table 2 The value domain of indicators |
由于本文涉及的各评价因子量值域不相同,而且有的期望值越大越好,有的则期望值越小越好,故选取的关联函数也有差别.
在确立了指标的关联度之后,将各省份的指标值对应到关联函数中,求出对应的关联度,本文以广东省为例,其关联度如表3所示.
| 表 3 评价指标的关联度 Table 3 The relating degree of indicators |
首先,根据突变级数法确定各指标之间的相对重要性,建立经济增长指标体系如图1所示. 然后,采用突变级数法对各个指标进行综合评价. 根据突变理论建立逐级的突变模型,然后再对指标进行标准化处理,根据极值法公式将原始数据全部统一至0~1之间. 根据各指标在其子系统内的先后顺序对应相应的归一公式计算,最后根据各指标间的“互补”或者“非互补”关系来判定使用“平均值”原则或者“大中取小”原则. 最后得出各年度的经济增长指数. 现以广东省为例计算经济增长指数.
|
图 1 经济增长指标体系 Figure 1 Economic growth indicator system |
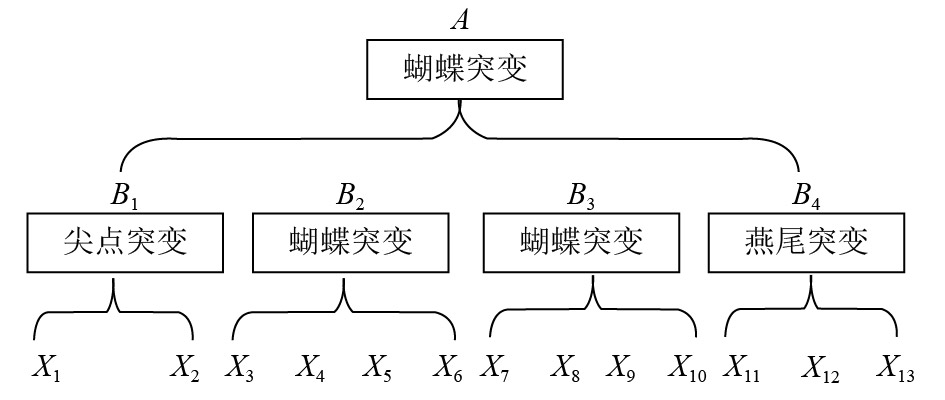
初等突变系统类型一共有7种,分别为折叠突变系统、尖点突变系统、燕尾突变系统、蝴蝶突变系统、椭圆脐突变系统和抛物脐型突变系统. 其中最常见的类型有尖点突变系统、燕尾突变系统和蝴蝶型突变系统. 若一个指标仅分解为2个子指标,该系统可视为尖点突变系统;若一个指标仅分解为3个子指标,该系统可视为燕尾突变系统;若一个指标仅分解为4个子指标,该系统可视为蝴蝶突变系统. 本文中各指标层构成尖点、燕尾和蝴蝶突变模型,经济增长评价的逐级突变模型如图2所示.
|
图 2 经济增长评价的逐级突变模型 Figure 2 Step catastrophe model of economic growth |
利用归一公式对同一对象各个控制变量(即指标)计算出的相应的
由于指标层的各指标之间互补,因此对于各子系统中的指标采用“平均值”原则. 准则层B1、B2、B3、B4之间非互补,采用“大中取小”原则,且重要性排序为
准则层
| $\begin{split} {B_1} = &( {{X_1}^{1/2} + {X_2}^{1/3}} ){\rm{/2}}=\\ &( {{\rm{0}}{\rm{.488}}\;{{\rm{1}}^{{\rm{1/2}}}} + {\rm{0}}{\rm{.620}}\;{{\rm{1}}^{{\rm{1/3}}}}} ){\rm{/2}}=\\ & ( {{\rm{0}}{\rm{.698}}\;{\rm{6}} + {\rm{0}}{\rm{.852}}\;{\rm{7}}} ){\rm{/2}}= 0.{\rm{775}}\;{\rm{7}}. \end{split}$ |
同理:
目标层
| $\begin{split} A =& \min \{ {B_1}^{1/2},{B_2}^{1/3},{B_3}^{1/4},{B_4}^{1/5}\} =\\ & \min \{ 0.775\;{7^{1/2}},0.893\;{6^{1/3}},0.984\;{4^{1/4}},0.814\;{7^{1/5}}\} =\\ & \min \{ 0.880\;7,0.964\;9,0.996\;1,0.959\;8\} = 0.880\;7. \end{split}$ |
因此,广东省2016年的经济增长突变评价指数为0.880 7.
4 经济增长等级划分及结果转换 4.1 经济增长水平等级划分这里将经济增长发展水平在0~1之间划分为几个等级,分别为极弱水平、弱水平、一般水平、较强水平和强水平,具体划分如表4所示.
| 表 4 经济增长水平程度划分等级 Table 4 The level of economic growth grade |
为了准确表达突变的评估结果,采用分数转换法对突变评价的结果进行转换,使其变成一般意义上的综合值. 即假设所有指标的相关从属度都为n,相关的高层次关联从属度也是n,而在所有的指标相关从属度为n时的突变评价结果为m. 通过这种方法,将每个突变评价值都换成一般意义上的综合值[18]. 分别计算指标标准化后为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9时相对应的突变结果,以0.5为例,具体计算如下.
假设所有的底层指标
(1) 指标层,C1、C2构成尖点突变模型,按照互补原则有
| $ {X_{B_1}} = ({X_{C_1}}^{1/2} + {X_{C_2}}^{1/3})/{\rm{2}}= ({0.5^{1/2}} + {0.5^{1/3}})/{\rm{2}} = 0.{\rm{750}}. $ |
C3、C4、C5、C6构成蝴蝶突变模型,按照互补原则有
| $\begin{split} {X_{B_2}} =& ({X_{C_5}}^{1/2} + {X_{C_6}}^{1/3} + {X_{C_7}}^{1/4} + {X_{C_8}}^{1/5})/4 =\\ & ({0.5^{1/2}} + {0.5^{1/3}} + {0.5^{1/4}} + {0.5^{1/5}})/4 = 0.803. \end{split}$ |
C7、C8、C9、C10构成蝴蝶突变模型,按照互补原则有
| $\begin{split} {X_{B_3}} =& ({X_{C_9}}^{1/2} + {X_{C_{{10}}}}^{1/3} + {X_{C_{11}}}^{1/4} + {X_{C_{{2}}}}^{1/5})/4=\\ &({0.5^{1/2}} + {0.5^{1/3}} + {0.5^{1/4}} + {0.5^{1/5}})/4 = 0.803. \end{split}$ |
C11、C12、C13构成燕尾突变模型,按照互补原则有
| $\begin{split} {X_{B_{{4}}}} =& ({X_{C_{{13}}}}^{1/2} + {X_{C_{{14}}}}^{1/3} + {X_{C_{{15}}}}^{1/4})/{\rm{3}}=\\ & ({0.5^{1/2}} + {0.5^{1/3}} + {0.5^{1/4}})/{\rm{3}} = {\rm{0}}{\rm{.781}}. \end{split}$ |
(2) 准则层,B1、B2、B3构成蝴蝶突变模型,按照非互补原则有
| $\begin{split} {X_A} =& \min \{ {X_{{B_1}}}^{1/2},{X_{{B_2}}}^{1/3},{X_{{B_3}}}^{1/4},{X_{{B_4}}}^{1/5}\} =\\ &\min \{ 0.{\rm{75}}{{\rm{0}}^{1/2}},{0.803^{1/3}},{0.803^{1/4}},{0.781^{1/5}}\}= 0.8{\rm{66}.} \end{split}$ |
按照同样的方法步骤,可以求出所有底层的指标
| 表 5 一般相对隶属度水平等级对应突变评价值 Table 5 General relative membership degree value level corresponding mutations |
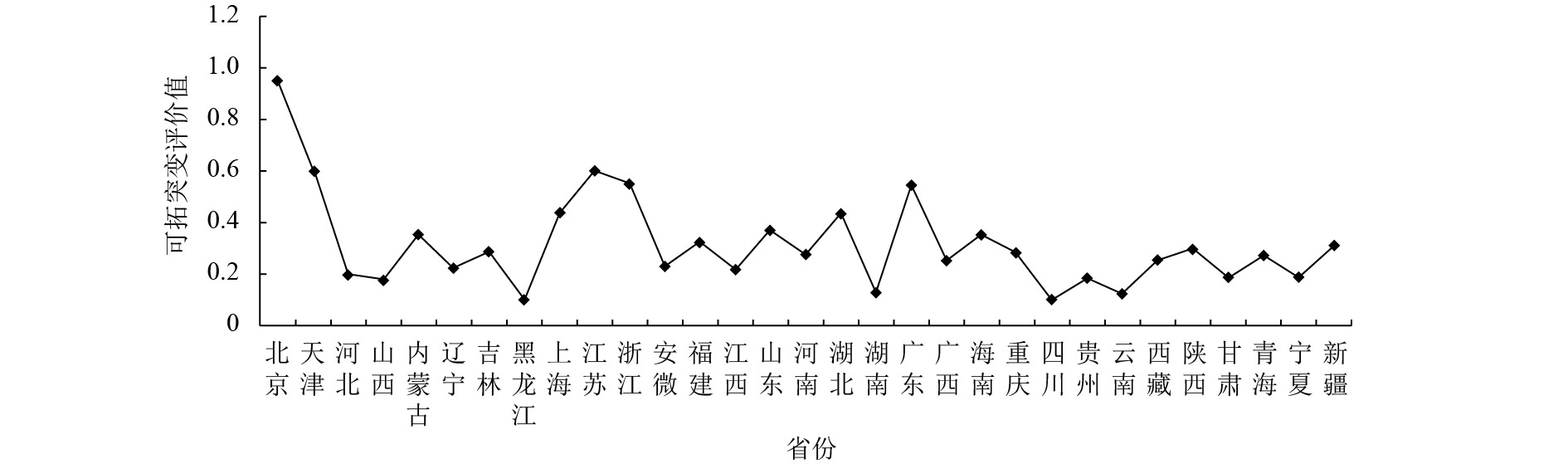
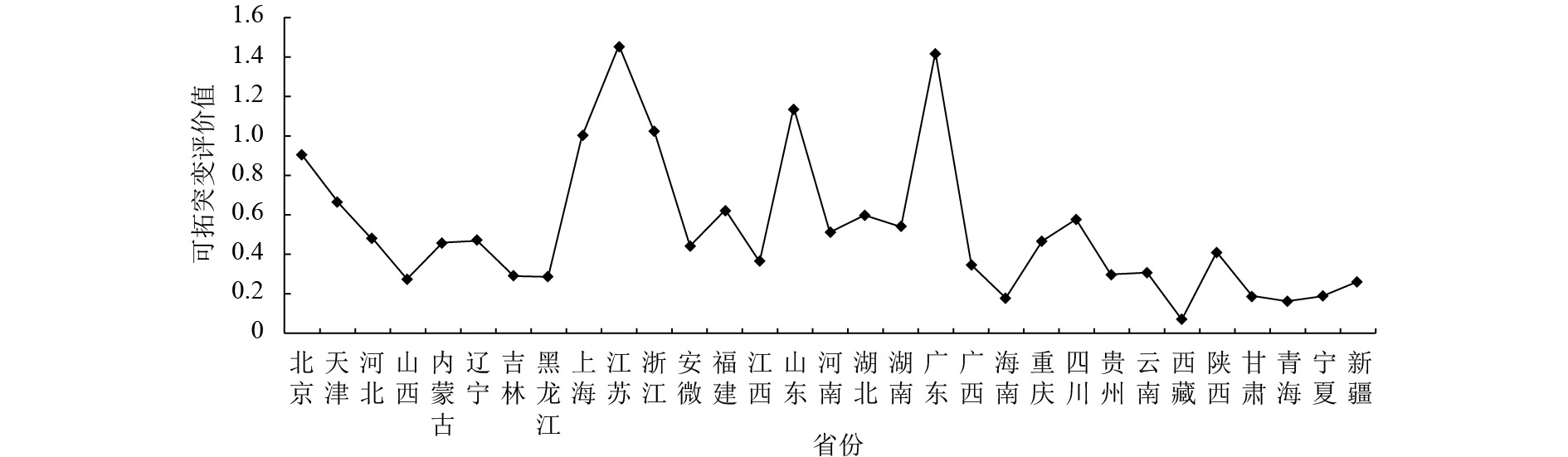
在经济增长指标体系建立的基础之上,通过建立逐级突变模型、指标关联函数、归一公式等突变评价数据处理方法,对原始数据进行分析处理,得出经济基础水平、经济结构水平、经济竞争力水平、经济可持续水平及全国各地区经济增长的可拓突变评价结果,并通过突变级数法结果转换方式,将评价结果对应到表中一般相对隶属度等级对应的突变评价值,我国部分省、市、自治区的可拓突变值如图3~7所示.
|
图 3 经济基础水平可拓突变评价值 Figure 3 The extension catastrophe value of economic base level |
|
图 4 经济结构水平可拓突变评价值 Figure 4 The extension catastrophe value of economic structure level |
|
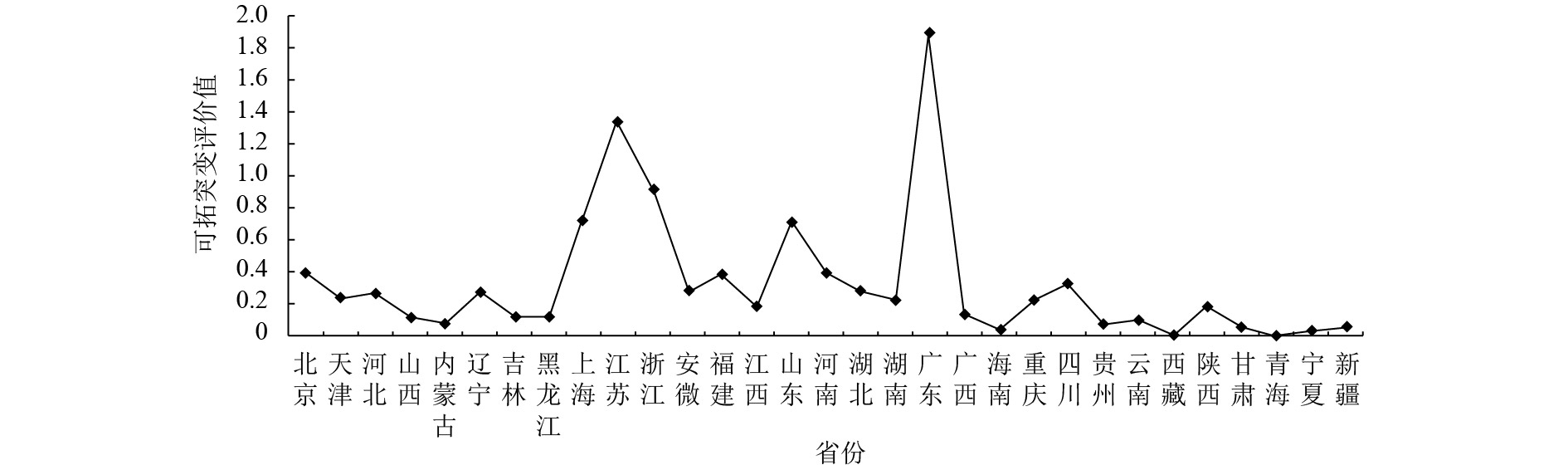
图 5 经济竞争力水平可拓突变评价值 Figure 5 The extension catastrophe value of economic competitiveness level |

|
图 6 经济可持续水平可拓突变评价值 Figure 6 The extension catastrophe value of economic sustainable level |
|
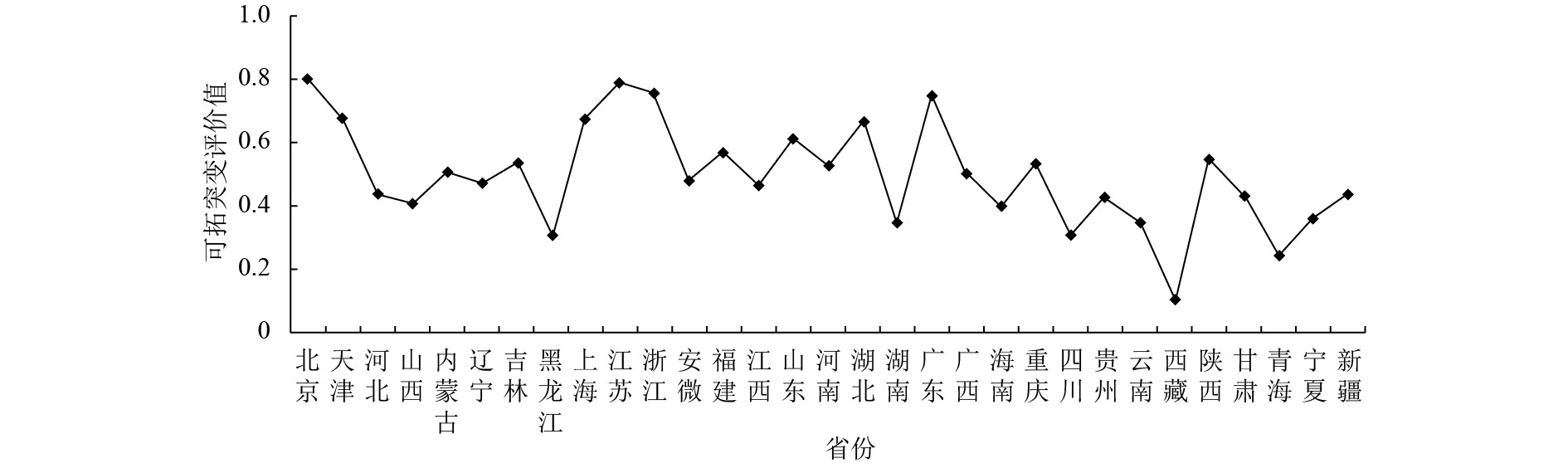
图 7 经济增长可拓突变评价值 Figure 7 The extension catastrophe value of economic growth |
(1) 经济基础水平. 由图3可知,四川省的经济基础水平处于最低水平,其可拓突变评价值为0.101,属于极弱水平;北京市的经济基础水平处于最高水平,其可拓突变评价值为0.955,属于强水平;此外,天津市,浙江省,江苏省和广东省四个地区位于一般水平. 经计算,各地区的经济基础水平值为0.317,各省平均处于弱水平状态.
从经济基础水平系统指标的角度分析变化原因,北京市的人均生产总值在所有地区中居于首位,负向指标失业率在所有省份中也为最低值,所以北京市的经济基础水平在所有省份中居于最高水平. 而四川省的人均生产总值处于末位,其失业率高达4.2%,是所有省份中的最高值,所以四川省的经济基础水平最低.
(2) 经济结构水平. 由图4可知,西藏的经济结构水平处于最低水平,其可拓突变评价值为0.062,属于极弱水平;江苏省的经济结构水平处于最高水平,其可拓突变评价值为1.445,属于强水平;上海市、浙江省、山东省及广东省仅次于江苏省也位于强水平,北京市的经济结构水平处于较强水平. 经计算,各地区的经济结构水平值为0.519,各省平均处于一般水平状态.
从经济结构水平系统指标的角度分析变化原因,虽然西藏的就业人员平均工资很高,仅次于北京和上海,但是其第二产业增加值、第三产业增加值及居民消费水平的指标值在所有省份中都处于最低值,所以位于最低水平. 而江苏省虽然在居民消费水平和城镇单位就业人员平均工资两个指标值上落后于北京和上海,但其在二、三产业增加值上却遥遥领先,所以奠定了其高水平的基础.
(3) 经济竞争力水平. 由图5可知,西藏的经济竞争力水平处于最低水平,其可拓突变评价值为0,属于极弱水平;广东省的经济竞争力水平处于最高水平,其可拓突变评价值为1.892,属于强水平;江苏省和浙江省也位于强水平,上海市的经济竞争力水平处于较强水平. 经计算,各地区的经济竞争力水平值为0.318,各省平均处于弱水平状态.
从经济竞争力水平系统指标的角度分析变化原因,广东省由于其珠三角的优势,所有指标值均属于最高值,尤其影响最大的进出口贸易总额,已达470 284 515千美元. 而西藏因为地域原因,其指标值在所有省份中均处于最低状态.
(4) 经济可持续水平. 由图6可知,各省份的经济可持续水平普遍偏低,广东省以0.564的可拓突变评价值居于首位,但仍处于一般水平,新疆的经济可持续水平处于最低状态,可拓突变评价值为0.05. 经计算,各省平均可持续竞争力水平值0.21,处于弱水平状态.
从经济可持续水平系统指标的角度分析变化原因,甘肃、西藏、四川、内蒙古以及东三省的自然保护区占辖区面积比重远大于广东省,但是广东省的专利申请授权数达259 032件,更由其为主要影响因素,所以广东省在经济可持续水平方面居于首位. 而新疆的所有指标值均处于最下层,所以其在经济可持续水平方面并不乐观.
5.2 经济增长水平分析通过对比分析,各地区的综合可拓突变评价值相较子系统的值要高,经过计算各地区综合评价值为0.499,各省平均水平处于一般状态. 由图7可以看出,北京市的经济增长水平位于最高状态,其值为0.786,为较强水平. 江苏省、浙江省、广东省、天津市和上海市等5个城市也处于中上水平. 但西藏和青海的综合可拓突变评价值均小于0.3,在所有省份中处于最弱情况,而黑龙江省和四川省的评价值也位于0.3左右,处于较低水平.
从子系统的角度分析变化的原因,综合来看,北京市、上海市、广东省、江苏省、浙江省和天津市的经济基础水平、经济结构水平、经济竞争力水平和经济可持续水平均处于中上状态,北京市强水平的经济基础水平为其经济增长奠定了坚实的基础,而天津作为港口城市,其优越的地理位置为其经济增长带来了强大的优势.
6 结论本文将可拓学理论与突变理论相结合,用可拓关联函数代替原始突变级数法中的模糊隶属函数,用关联度代替模糊隶属度的方法,从中国统计年鉴中提取了国内2016年各省份的经济增长相关指标数据进行评价,得到了各省、市、自治区的经济增长综合评价值. 其数值所表现的经济增长水平等级与传统的突变级数法所得到的结果相似,都基本符合各地区的实际经济增长情况. 因此,验证了本文可拓突变级数法的正确有效性. 但目前只是在经济增长领域使用了此方法,后续可以在更多领域使用并继续验证此方法.
| [1] |
MARIE J, CHRISTOPHER F. Models of doom: a critique of the limits to growth[M].New York: Chatto & Windus for Sussex University Press, 1973: 1-244.
|
| [2] |
IMOISI A I, ABUO M, SOGULES I W. Domestic investment and economic growth in nigeria from 1970-2013: an econometric analysis[J].
Canadian Social Science, 2015, 11(6): 70-79.
|
| [3] |
杨春燕, 蔡文. 可拓学[M]. 北京: 科学出版社, 2014, 92-108.
|
| [4] |
邓群钊, 郭艳清, 李莎莎. 可拓学在管理领域中的应用研究进展[J].
数学实践与认识, 2009, 39(4): 89-93.
DENG Q Z, GUO Y Q, LI S S. Research progress of Extension Theory application in management[J]. Mathematics in Practice and Theory, 2009, 39(4): 89-93. |
| [5] |
邱绍维, 刘力川, 刘于嘉. 可拓评判在试卷质量分析的计算机程式应用[J].
广东工业大学学报, 2001, 18(1): 42-47.
QIU S W, LIU L C, LIU Y J. The computer program application of extension evaluation to qualitative analysis for an examination paper[J]. Journal of Guangdong University of Technology, 2001, 18(1): 42-47. DOI: 10.3969/j.issn.1007-7162.2001.01.010. |
| [6] |
李桥兴, 张婷. 网络环境下服务系统绩效的指标体系和可拓评价[J].
广东工业大学学报, 2016, 33(6): 1-17.
LI Q X, ZHANG T. An indicator system and extension assessment of service performance in a network context[J]. Journal of Guangdong University of Technology, 2016, 33(6): 1-17. |
| [7] |
蔡国梁. 可拓学及其经济应用[J].
河南科学, 1998, 16(3): 330-338.
CAI G L. Extension subject and its application in economic field[J]. Henan Science, 1998, 16(3): 330-338. |
| [8] |
花黄伟, 杨春燕. 可拓识别方法及其在无人车识别障碍物中的应用研究[J].
广东工业大学学报, 2016, 33(4): 1-6.
HUA H W, YANG C Y. Research on Extension recognition method and its application on obstacles recognition of self-driving car[J]. Journal of Guangdong University of Technology, 2016, 33(4): 1-6. DOI: 10.3969/j.issn.1007-7162.2016.04.001. |
| [9] |
高洁, 唐国庆. 基于关联函数的电网规划优度评价法[J].
系统工程理论方法应用, 2000, 9(4): 341-344.
GAO J, TANG G Q. The superiority evaluation method of power network planning based on the dependent function[J]. Application of System Engineering Theory and Method, 2000, 9(4): 341-344. |
| [10] |
张家宾, 张金春, 李日华, 等. 基于可拓学的故障诊断及预防方法研究[J].
广东工业大学学报, 2015, 32(1): 11-15.
ZHANG J B, ZHANG J C, LI R H, et al. Research on fault diagnosis and prevention based on extension[J]. Journal of Guangdong University of Technology, 2015, 32(1): 11-15. DOI: 10.3969/j.issn.1007-7162.2015.01.003. |
| [11] |
都兴富. 图突变理论在经济领域下的应用(下)[M]. 成都: 电子科技大学出版社, 1994.
|
| [12] |
POSTON T, STEWART I. Catastrophe theory[M]. Cambridge: Cambridge University Press, 1980.
|
| [13] |
ZEEMAN E C. Catastrophe theory: Selected papers, 1972–1977[J].
Addison-Wesley Pub. Co. Advanced Book Program, 1978.
|
| [14] |
国家统计局. 中国统计年鉴[M]. 北京: 中国统计出版社, 2017.
|
| [15] |
梁亚民. 经济增长质量评价指标体系研究[J].
西北师大学报, 2002, 39(2): 15-118.
LIANG Y M. A study of the index system for evaluating the quality of economic growth[J]. Journal of Northwest Normal University, 2002, 39(2): 15-118. |
| [16] |
WANG X M, SUN J F, WANG X M, et al. Study on evolution of 3E system in different economic growth speed—taking Shandong as an example[C]// International Conference on Information Management. Beijing:IEEE, 2012.
|
| [17] |
杨春燕, 蔡文. 可拓工程[M]. 北京: 科学出版社, 2007, 89-120.
|
| [18] |
SU S L, LI D, YU X, et al. Assessing land ecological security in shanghai (China) based on catastrophe theory[J].
Stochastic Environment Research and Assessment, 2011, 25(6): 737-746.
DOI: 10.1007/s00477-011-0457-9. |
 2019, Vol. 36
2019, Vol. 36

