近年来随着计算机技术的迅速发展，多智能体协调控制问题引起了社会各界越来越多的关注^[1-3]，在分布式编队控制^[4]、神经系统稳定控制^[5]、脉冲控制^[6]等领域都得到了广泛应用. 多智能体系统一致性是协调控制的重要组成部分. 多智能体一致性指的是系统中所有智能体的信息最终趋于相同. 为实现多智能体的一致性，需要设计出能使各个智能体相互交换彼此信息从而实现所有智能体信息最终趋于相同的规则，即一致性协议.

目前，在多智能体系统一致性问题的研究中，许多学者已经取得了丰硕的成果. Vicsek等^[7]从统计学角度出发，建立了经典离散时间模型. Olfati等^[8]则对无向联通并且权值对称的多智能体系统进行研究，认为只要系统强联通，则多智能体系统就能实现一致性. 而Ren等^[9]在文献[8]的基础上得到了有向拓扑的多智能体系统收敛条件.

然而在实际应用中，系统不可避免地遇到各种外界影响，例如网络堵塞或者其他因素等，造成通信延迟，从而导致智能体之间的信息传递存在一定时延. 针对这种现象，文献[10-13]对含有时延的多智能体系统一致性进行了广泛研究. 由于环境的复杂性，多智能体系统中智能体之间输入时延随机存在更具有普遍性. 本文受文献[14]的启发，研究系统中存在随机时延的情形. 文献中对含有时延的多智能体系统的分析一般利用线性矩阵不等式给出系统一致性的条件，但线性矩阵不等式法计算量大且复杂，不便于分析含有随机时延的多智能体系统. 本文将采用文献[15]提出的模型简化法对含有随机时延的的多智能体系统的一致性进行讨论.

1 预备知识 1.1 图论

令 $G(\nu ,\varepsilon ,A)$ 表示具有n个节点的有向图， $\nu = \{ {\nu _1},{\nu _2}, \cdots ,{\nu _n}\} $ 表示图 $G$ 顶点集， $\varepsilon \subseteq \nu \times \nu $ 表示图 $G$ 边集， $A = [{a_{ij}}]$ 表示图 $G$ 的邻接矩阵，若存在由节点 ${\nu _i}$ 到 ${\nu _j}$ 的有向边 ${e_{ij}} \in \varepsilon $ ，则 ${a_{ij}} > 0$ ，否则 ${a_{ij}} = 0$ . 令矩阵 ${{D}} = {\rm diag}\{ {d_i},i = 1,2, \cdots ,n\} $ ，其中 ${d_i} = \displaystyle\sum\limits_{j = 1}^n {{a_{ij}}} $ 为节点 $i$ 的出度，则Laplacian矩阵L可定义为L=D–A.

假设1 　Laplacian矩阵的0特征值是一个单一特征值.

对于网络连接，这个情形代表了这个网络存在一个生成树从而连接任意两个子系统，对于一致性协议的设计，只需考虑0特征值是单一特征值^[16].

1.2 模型

本文考虑具有n个智能体的一阶多智能体系统，智能体之间的拓扑图用图 $G$ 表示，每个智能体可看作图 $G$ 的一个节点，且满足以下动态方程

${\dot x_i}(t) = {{A}}{x_i}(t) + {{B}} {{\delta }} (t) {u_i}(t) + {{B}}(1 - {{\delta}} (t)){u_i}(t - h).$

(1)

其中x_i表示智能体 $i$ 的状态，u_i则表示控制输入，A, B表示常数可控矩阵，h>0表示系统输入时延，同时为了表征系统时延可能存在也可能不存在，引入变量δ(t)，当δ(t)=1时表示系统不存在时延，而δ(t)=0表示系统存在时延，其中δ(t)满足如下分布变换：

$\left\{\!\!\begin{array}{l} {\rm prob}\{ \delta (t) = 1\} = E\{ \delta (t)\} = \bar \delta , \\ {\rm prob}\{ \delta (t) = 0\} = 1 - E\{ \delta (t)\} = 1 - \bar \delta . \end{array}\right.$

(2)

引理1 　一个含输入时延的系统：

$\dot x (t) = {{A}}x(t) + {{{B}}_{{0}}}u(t) + {{{B}}_{{1}}}u(t - h).$

(3)

令

$y(t) = x(t) + \int_{t - h}^t {{{\rm e}^{{{A}}(t - s - h)}}{{{B}}_{{1}}}} u(s){\rm d}s,$

(4)

则原系统(3)稳定性与如下系统(5)相同,

$\dot y(t) = {{A}}y(t) + ({{{B}}_{{0}}} + {{D}})u(t),\;\;\;{{D}} = {{\rm e}^{ - {{A}}h}}{{{B}}_{{1}}}.$

(5)

证明

$\left\{\! \begin{split}& y(t) \!=\! x(t) + \displaystyle\int_{t - h}^t {{{\rm e}^{{{A}}(t - s - h)}}{{{B}}_{{1}}}} u(s){\rm d}s;\\ &\dot y(t) \!=\! \dot x(t) \!+\! {{A}}\displaystyle\int_{t - h}^t {{{\rm e}^{{{A}}(t - s - h)}}{{{B}}_{{1}}}u(s){\rm d}s \!+\! {{\rm e}^{ - {{A}}h}}{{{B}}_{{1}}}u(t)} -\\ & {{{{B}}_{{1}}}u(t - h)}\!=\! {{A}}x(t) \!+\! {{{B}}_{{0}}}u(t) \!+\! {{A}}\displaystyle\int_{t - h}^t {{{\rm e}^{{{A}}(t - s - h)}}}\times\\ & { {{{B}}_{{1}}}u(s){\rm d}s} \!+\! {{\rm e}^{ - {{A}}h}}{{{B}}_{{1}}}u(t)\!=\!{{A}}y(t) + ({{{B}}_{{0}}} \!+\! {{\rm e}^{ - {{A}}h}}{{{B}}_{{1}}})u(t).\!\!\! \end{split}\right.\!\!\! $

(6)

对系统(3)，提出以下控制器

$u(t) = {{K}}y(t).$

(7)

如果控制器(7)能使得系统(5)达到稳定，则原系统(3)也能用相同控制器达到稳定^[17-18].

引理2^[16] 　如果Laplacian矩阵L只含有一个0特征值，其余特征值均大于0，则存在一个相似变换T，同时T的第一列 ${{{T}}_{(1)}} = {\phi}$ , ${\phi}=[1,\cdots, 1]^{\rm T} $ 使得

${{{T}}^{ - 1}}{{LT}} = {{J}}.$

(8)

${{J}} = {\left[ {\begin{array}{*{20}{c}} 0&{}&{}&{}&{}&{}&{} \\ {}&{{{{J}}_{{2}}}}&{}&{}&{}&{}&{} \\ {}&{}& \ddots &{}&{}&{}&{} \\ {}&{}&{}&{{{{J}}_{{p}}}}&{}&{}&{} \\ {}&{}&{}&{}&{{{{J}}_{{{p + 1}}}}}&{}&{} \\ {}&{}&{}&{}&{}& \ddots &{} \\ {}&{}&{}&{}&{}&{}&{{{{J}}_{{q}}}} \end{array}} \right]_{N \times N}}.$

(9)

当 ${{{J}}_{{k}}} \in {R^{{n_k} \times {n_k}}}$ , $k = 2,3, \cdots ,p$ ，是Jordan块中的 ${n_k}$ 重实数特征值 ${\lambda _k} > 0$ 的形式，即

${{{J}}_{{k}}} = {\left[ {\begin{array}{*{20}{c}} {{\lambda _k}}&1&{}&{} \\ {}&{{\lambda _k}}& \ddots &{} \\ {}&{}& \ddots &1 \\ {}&{}&{}&{{\lambda _k}} \end{array}} \right]_{{n_k} \times {n_k}}}.$

而 ${{{J}}_{{k}}} \in {R^{2{N_k} \times 2{N_k}}}$ ， $k = p + 1,p + 2, \cdots ,q$ ，是Jordan块中的 ${n_k}$ 重复数特征值 ${\alpha _k} \pm j{\beta _k}$ ，且 ${\alpha _k} > 0,{\beta _k} > 0$ 的形式如下：

${{{J}}_k} = {\left[ {\begin{array}{*{20}{c}} {{{\nu }}({{{\alpha }}_k},{{{\beta }}_k})} & {{{{I}}_2}} & {} & {}\\ {} & {{{\nu }}({{{\alpha }}_k},{{{\beta }}_k})} & \ddots & {}\\ {} & {} & \ddots & {{{{I}}_2}}\\ {} & {} & {} & {{{\nu }}({{{\alpha }}_k},{{{\beta }}_k})} \end{array}} \right]_{2{n_k} \times 2{n_k}}}.$

I₂是 ${R^{2 \times 2}}$ 的单位矩阵且

${{{\nu }}({{{\alpha }}_k},{{{\beta }}_k})} = {\left[ {\begin{array}{*{20}{c}} {{\alpha _i}}&{{\beta _i}} \\ { - {\beta _i}}&{{\alpha _i}} \end{array}} \right]_{2 \times 2}}.$

2 主要结果

根据引理1，对多智能体系统(1)，使用变换(4)作简化. 令

${y_i}(t) = {x_i}(t) + \displaystyle\int_{t - h}^t {{{\rm e}^{{{A}}(t - s - h)}}{{{B}}_{{1}}}} {u_i}(s){\rm d}s$ ，

则系统(1)可转化为

${\dot y _i}(t) = {{A}}{y_i}(t) + {{B}} {{\delta}} (t){u_i}(t) + {{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta}} (t)){u_i}(t).$

(10)

针对简化后的系统(10)，采用如下控制协议

${u_i}(t) = - {{K}}\sum\limits_{j = 1}^N {{q_{ij}}[{y_i}(t) - {y_j}(t)]} = - {{K}}\sum\limits_{j = 1}^N {{l_{ij}}{y_j}(t)}, $

(11)

其中，K表示控制增益.

定理1 　当控制增益K满足

${{K}} > \frac{{{{A}} + {{{A}}^{\rm{T}}}}}{{2\underline \lambda \overline \delta {{B}} + 2\underline \lambda (1 - \overline \delta ){{\rm e}^{ - {{A}}h}}{{B}}}},$

(12)

$\underline \lambda = \min \{ {\lambda _2}, \cdots ,{\lambda _n},{\alpha _1}, \cdots {\alpha _n}\}, $

系统(1)可达到一致性.

证明 　令

　　　　 $y(t) = {\left[ {\begin{array}{*{20}{c}} {{y_1}}&{{y_2}}& \cdots &{{y_N}} \end{array}} \right]^{\rm{T}}},$

则系统(10)可写成

$\begin{split} &\dot y(t) = ({{{I}}_N} \otimes {{A}})y(t) - ({{L}} \otimes {{BK}}){{\delta }}(t)y(t)-\\ &({{L}} \otimes {{\rm e}^{ - {{A}}h}}{{BK}})(1 - {{\delta }}(t))y(t). \end{split}$

(13)

定义 ${{r}} \in {R^N}$ 为矩阵L的0特征值对应的左特征值向量，即 ${{{r}}^{\rm{T}}}{{L}} = {{0}}$ ，同时使之单位化，即 ${{{r}}^{\rm{T}}}{{\phi}} = {{\phi}} $ , ${\phi}=[1,\cdots ,1]^{\rm T}$ . 从引理2可知存在矩阵T使得 ${{{T}}^{{{ - 1}}}}{{LT}} = {{J}}$ .

定义

${e_i}(t) = {y_i}(t) - \sum\limits_{j = 1}^N {{{{r}}_{{j}}}{y_j}(t)}. $

(14)

令 $e(t) = {\left[ {\begin{array}{*{20}{c}} {{e_1}(t)}&{{e_2}(t)}& \cdots &{{e_N}(t)} \end{array}} \right]^{\rm{T}}}$ ，则

$e(t) = y(t) - [({{\phi}}{{{r}}^{\rm{T}}}) \otimes {{{I}}_{{n}}}]y(t) = ({{M}} \otimes {{{I}}_{{n}}})y(t).$

(15)

此时 ${{M}} = {{{I}}_{{N}}} - {{\phi}}{{{r}}^{\rm{T}}}$ . 由于 ${{{r}}^{\rm{T}}}{{\phi}} = {{\phi}}$ 即 ${{M}}{\phi} = {{0}}$ ，因此系统(13)的稳定性相当于e=0，因为此时相当于 ${y_1} = $ $ {y_2} = \cdots = {y_N}$ ，则一致性问题转化成了系统稳定性问题.

$\begin{split} &\dot e(t) = ({{{I}}_N} \otimes {{A}})e(t) - ({{L}} \otimes {{BK}}){{\delta }}(t)e(t)-\\ &({{L}} \otimes {e^{ - {{A}}h}}{{BK}})(1 - {{\delta }}(t))e(t), \end{split}$

(16)

定义

$\sigma (t) = ({{{T}}^{{{ - 1}}}} \otimes {{{I}}_{{n}}})e(t),$

(17)

则

$\begin{split} &\dot \sigma (t) = ({{{I}}_N} \otimes {{A}})\sigma (t) - ({{J}} \otimes {{BK}}){{\delta }}(t)\sigma (t)-\\ & ({{J}} \otimes {e^{ - {{A}}h}}{{BK}})(1 - {{\delta }}(t))\sigma (t). \end{split}$

(18)

根据转化式(14)和(17)，

${\sigma _1}(t) = ({{{r}}^{\rm{T}}} \otimes {{{I}}_{{n}}})e(t) = [({{{r}}^{\rm{T}}}{{M}} \otimes {{{I}}_{{n}}})]z(t) \equiv {{0}}.$

(19)

因此只需要证明 ${\sigma _i}$ 收敛到0，则可以证明一致性可达成基于laplacian矩阵的结构，可以发现

${N_k} = {n_1} + \sum\limits_{j = 2}^k {{n_j}}. $

(20)

同时，n₁=1, N_q=N，且 $k=2,3,\cdots,q $ .

当J_k为实数特征值，即 $2 \leqslant k \leqslant p$ ，

$\begin{split} &{{\dot \sigma }_i}(t) = ({{A}} - {\lambda _i}{{B}} {{\delta }}(t){{K}} - {\lambda _i}{{\rm e}^{ - {{A}}h}}B(1 - {{\delta }}(t)){{K}}){\sigma _i}(t)-\\ & ({{B}} {{\delta }}(t){{K}} + {{\rm e}^{ - {{A}}h}}B(1 - {{\delta }}(t)){{K}}){\sigma _{i + 1}}(t),\\ & i = {N_{k - 1}} + 1,{N_{k - 1}} + 2, \cdots ,{N_k} - 1. \end{split}$

(21)

$\begin{split}& {{\dot \sigma }_i}(t) = ({{A}} - {\lambda _i}{{B}}{{\delta }}(t){{K}} - {\lambda _i}{e^{ - {{A}}h}}B(1 - {{\delta }}(t)){{K}}){\sigma _i}(t),\\ & i = {N_k}. \end{split}$

(22)

当J_k为复数特征值，即k>p，可考虑一对动态状态方程，为方便，让

$ \begin{split} &{i_1}(j) = {N_{k - 1}} + 2j - 1,\;\;\;\;{i_2}(j) = {N_{k - 1}} + 2j,\\ &j = 1,2, \cdots ,{n_k}/2. \end{split} $

则当 $j = 1,2, \cdots ,{n_k}/2 - 1$ ， ${\sigma _{i1(j)}}$ 和 ${\sigma _{i2(j)}}$ 的动态方程为

$\left\{\!\!\begin{split} &{{\dot \sigma }_{i1(j)}}(t) = ({{A}} \!-\! {\alpha _k}{{B}}{{\delta }}(t){{K}} \!-\! {\alpha _k}{{\rm e}^{ - {{A}}h}}B(1 \!-\! {{\delta }}(t)){{K}})\times\\ & {\sigma _{i1(j)}}(t)\!-\! ({\beta _k}{{B}}{{\delta }}(t){{K}} \!+\! {\beta _k}{{\rm e}^{ - {{A}}h}}{{B}}(1 \!-\! {{\delta }}(t)){{K}}){\sigma _{i2(j)}}(t)-\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\ & ({{B}}{{\delta }}(t){{K}} \!+\! {{\rm e}^{ - {{A}}h}}{{B}}(1 \!-\! {{\delta }}(t)){{K}}){\sigma _{i1(j) \!+\! 2}}(t),\\ &{{\dot \sigma }_{i2(j)}}(t) \!=\! (A \!-\! {\alpha _k}{{B}}{{\delta }}(t){{K}} \!-\! {\alpha _k}{{\rm e}^{ - {{A}}h}}{{B}}(1 \!-\! {{\delta }}(t)){{K}})\times\\ & {\sigma _{i2(j)}}(t)\!+\!({\beta _k}{{B}}{{\delta }}(t){{K}} \!+\! {\beta _k}{{\rm e}^{ - {{A}}h}}B(1 \!-\! {{\delta }}(t)){{K}}){\sigma _{i1(j)}}(t)-\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\ &({{B}}{{\delta }}(t){{K}} \!+\! {{\rm e}^{ - {{A}}h}}{{B}}(1\! -\! {{\delta }}(t)){{K}}){\sigma _{i2(j) \!+\! 2}}(t). \end{split}\right.$

(23)

当 $j = {n_k}/2$ ,

$\,\!\!\left\{\!\!\begin{split} &{{\dot \sigma }_{i1(j)}}(t) = ({{A}} - {\alpha _k}{{B}}{{\delta }}(t){{K}} - {\alpha _k}{{\rm e}^{ - {{A}}h}}B(1 - {{\delta }}(t)){{K}})\times\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\ & {\sigma _{i1(j)}}(t)\!-\!({\beta _k}{{B}}{{\delta }}(t){{K}} \!+\! {\beta _k}{{\rm e}^{ - {{A}}h}}{{B}}(1 \!-\! {{\delta }}(t)){{K}}){\sigma _{i2(j)}}(t),\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\ &{{\dot \sigma }_{i2(j)}}(t) \!=\! ({{A}} \!-\! {\alpha _k}{{B}}{{\delta }}(t){{K}} \!-\! {\alpha _k}{{\rm e}^{ - {{A}}h}}{{B}}(1 \!-\! {{\delta }}(t)){{K}})\times\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\ & {\sigma _{i2(j)}}(t)\!+\! ({\beta _k}{{B}}{{\delta }}(t){{K}} \!+\! {\beta _k}{{\rm e}^{ - {{A}}h}}{{B}}(1 \!-\! {{\delta }}(t)){{K}}){\sigma _{i1(j)}}(t).\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \end{split}\right.$

(24)

对于系统(8)构造如下Lyapunov函数

$V = {\sigma _i}^{\rm{T}}(t){{P}}{\sigma _i}(t).$

(25)

当i=N_k，V的导数为

$ \begin{split} &\dot V = {\sigma _i}^{\rm{T}}(t){{P}}{{\dot \sigma }_i}(t) + \dot \sigma _i^{\rm{T}}(t){{P}}{\sigma _i}(t)=\\ & {\sigma _i}^{\rm{T}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}}){\sigma _i}(t) - 2{\lambda _k}{\sigma _i}^{\rm{T}}(t){{P}}{{\delta }}(t){{BK}}{\sigma _i}(t) -\\ & 2{\lambda _k}{\sigma _i}^{\rm{T}}(t){{P}}(1 - {{\delta }}(t)){{\rm e}^{ - {{A}}h}}{{BK}}{\sigma _i}(t)=\\ & {\sigma _i}^{\rm{T}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\lambda _k}{{P}} {{\delta }}(t){{BK}}-\\ & 2{\lambda _k}{{P}}(1 - {{\delta }}(t)){{\rm e}^{ - {{A}}h}}{{BK}}){\sigma _i}(t). \end{split} $

(26)

对等式两边求解期望，

$\begin{split} &E(\dot V) = E({\sigma _i}^{\rm{T}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\lambda _k}{{P}}{{\delta }}(t){{BK}}-\\ & 2{\lambda _k}{{P}}(1 - {{\delta }}(t)){{\rm e}^{ - {{A}}h}}{{BK}}){\sigma _i}(t))=\\ & {\sigma _i}^{\rm{T}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\lambda _k}{{P}}\overline \delta {{BK}}-\\ & 2{\lambda _k}{{P}}(1 - \overline \delta ){{\rm e}^{ - {{A}}h}}{{BK}}){\sigma _i}(t). \end{split}$

所以 $\dot V < 0$ 的充要条件即是

$ \begin{split} &{{{A}}^{\rm {T}}}{{P}} + {{PA}} - 2{\lambda _k}{{P}}\overline \delta {{BK}} - 2{\lambda _k}{{P}}(1 - \overline \delta ){{\rm e}^{ - {{A}}h}}{{BK}} < 0,\\ &k = 2,3, \cdots n. \end{split} $

(27)

存在某个K值使得(9)恒成立. 由于 ${{P}} > 0$ ，即需要

$ \begin{split}& \max ({{{A}}^{\rm {T}}} + {{A}} - 2{\lambda _k}\overline \delta {{BK}} - 2{\lambda _k}(1 - \overline \delta ){{\rm e}^{ - {{A}}h}}{{BK}}) < 0,\\ &k = 2,3, \cdots n, \end{split} $

所以

${{K}} > \frac{{{{A}} + {{{A}}^{\rm{T}}}}}{{2{\lambda _{\min }}\overline \delta {{B}} + 2{\lambda _{\min }}(1 - \overline \delta ){{\rm e}^{ - {{A}}h}}{{B}}}}.$

(28)

当 $i = {N_{k - 1}} + 1,{N_{k - 1}} + 2, \cdots ,{N_k} - 1$ ，V的导数为

$ \begin{split}& \dot V = {\sigma _i^{\rm{T}}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\lambda _k}{{P}}{{\delta }}(t){{BK}}- \\ & 2{\lambda _k}{{P}}(1 - {{\delta }}(t)){{\rm e}^{ - {{A}}h}}{{BK}}){\sigma _i}(t)- \\ & 2\sigma _i^{\rm{T}}(t)({{PB}}{{\delta }}(t){{K}} + {{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i + 1}}(t)\leqslant\\ & {\sigma _i^{\rm{T}}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\lambda _k}{{P}}{{\delta }}(t){{BK}}-\\ & 2{\lambda _k}{{P}}(1 - {{\delta }}(t)){{\rm e}^{ - {{A}}h}}{{BK}}){\sigma _i}(t). \end{split} $

(29)

所以 $\dot V < 0$ 的充要条件与式(28)一致，即

${{K}} > \frac{{{{A}} + {{{A}}^{\rm{T}}}}}{{2{\lambda _{\min }}\overline \delta {{B}} + 2{\lambda _{\min }}(1 - \overline \delta ){{\rm{e}}^{ - {{A}}h}}{{B}}}}.$

(30)

当 $j = {n_k}/2$ ,

$ \begin{split} &{{\dot V}_{i1}} + {{\dot V}_{i2}}=\\ & \sigma _{i1}^{\rm{T}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\alpha _k}{{PB}}{{\delta }}(t){{K}} - \\ & 2{\alpha _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i1}}(t)-\sigma _{i1}^{\rm{T}}(t)({\beta _k}{{PB}}{{\delta }}(t){{K}}+ \\ & {\beta _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i2}}(t)- \sigma _{i2}^{\rm{T}}(t)({\beta _k}{{PB}}{{\delta }}(t){{K}} + \\ & {\beta _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i1}}(t)+\sigma _{i2}^{\rm{T}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - \\ & 2{\alpha _k}{{PB}}{{\delta }}(t){{K}} - 2{\alpha _k}{{P}}{{\rm e}^{ - {{A}}h}}B(1 - {{\delta }}(t)){{K}}){\sigma _{i2}}(t)+ \\ & \sigma _{i2}^{\rm{T}}(t)({\beta _k}{{PB}}{{\delta }}(t){{K}} + {\beta _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i1}}(t)+ \\ &\sigma _{i1}^{\rm{T}}(t)({\beta _k}{{PB}}{{\delta }}(t){{K}} + {\beta _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i2}}(t) = \\ & \sigma _{i1}^{\rm{T}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\alpha _k}{{PB}}{{\delta }}(t){{K}} -\\ &2{\alpha _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i1}}(t) +\sigma _{i2}^{\rm{T}}(t)({{{A}}^{\rm{T}}}{{P}} +\\ & {{PA}} - 2{\alpha _k}{{PB}}{{\delta }}(t){{K}} - 2{\alpha _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i2}}(t). \end{split} $

(31)

对两边求期望

$ \begin{split} &E(\dot V) = E(\sigma _{i1}^{\rm{T}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\alpha _k}{{PB}}{{\delta }}(t){{K}}-\\ & 2{\alpha _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i1}}(t))+\\ & E(\sigma _{i2}^{\rm{T}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\alpha _k}{{PB}}{{\delta }}(t){{K}} -\\ & 2{\alpha _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i2}}(t)) =\\ & \sigma _{i1}^{\rm{T}}(t)({{{A}}^{\rm{T}}}{{P}} \!+\! {{PA}} \!-\! 2{\alpha _k}{{PB}}\overline \delta {{K}} \!-\! 2{\alpha _k}{{P}}{{\rm e}^{ \!-\! {{A}}h}}{{B}}(1 \!-\! \overline \delta ){{K}}){\sigma _{i1}}(t)+\\ & \sigma _{i2}^{\rm{T}}(t)({{{A}}^{\rm{T}}}{{P}} \!+\! {{PA}} \!-\! 2{\alpha _k}{{PB}}\overline \delta {{K}} \!-\! 2{\alpha _k}{{P}}{{\rm e}^{ \!-\! {{A}}h}}{{B}}(1 \!-\! \overline \delta ){{K}}){\sigma _{i2}}(t)\!=\\ & ({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\alpha _k}{{PB}}\overline \delta {{K}} - 2{\alpha _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - \overline \delta ){{K}})\\ &(\sigma _{i1}^{\rm{T}}(t){\sigma _{i1}}(t) + \sigma _{i2}^{\rm{T}}(t){\sigma _{i2}}(t)). \end{split} $

(32)

所以 $\dot V < 0$ 的充要条件即是

$ \begin{split} &{{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\alpha _k}{{P}}\overline \delta {{BK}} - 2{\alpha _k}{{P}}(1 - \overline \delta ){{\rm e}^{ - {{A}}h}}{{BK}} < 0,\\ &k = 2,3, \cdots n. \end{split} $

(33)

存在某个K值使得式(33)恒成立. 由于 ${{P}} > 0$ ，即

$ \begin{array}{l} \max ({{{A}}^{\rm{T}}} + {{A}} - 2{\alpha _k}\overline \delta {{BK}} - 2{\alpha _k}(1 - \overline \delta ){{\rm e}^{ - {{A}}h}}{{BK}}) < 0,\\ k = 2,3, \cdots n. \end{array} $

所以

${{K}} > \frac{{{{A}} + {{{A}}^{\rm{T}}}}}{{2{\alpha _{\min }}\overline \delta {{B}} + 2{\alpha _{\min }}(1 - \overline \delta ){e^{ - {{A}}h}}{{B}}}}.$

(34)

当 $j = 1,2, \cdots ,{n_k}/2 - 1$ ，

$ \begin{split} &{{\dot V}_{i1}} + {{\dot V}_{i2}} =\\ & {\sigma _{i1}^{\rm{T}}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\alpha _k}{{PB}}{{\delta }}(t){{K}}-\\ & 2{\alpha _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i1}}(t)+\\ & {\sigma _{i2}^{\rm{T}}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\alpha _k}{{PB}}{{\delta }}(t){{K}}-\\ & 2{\alpha _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i2}}(t)-\\ & 2\sigma _{i1}^{\rm{T}}(t)({{B}}{{\delta }}(t){{K}} + {{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i1 + 2}}(t)-\\ & 2\sigma _{i2}^{\rm{T}}(t)({{B}}{{\delta }}(t){{K}} + {{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i2 + 2}}(t)\leqslant\\ & {\sigma _{i1}^{\rm{T}}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\alpha _k}{{PB}}{{\delta }}(t){{K}}-\\ & 2{\alpha _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i1}}(t)+\\ & {\sigma _{i2}^{\rm{T}}}(t)({{{A}}^{\rm{T}}}{{P}} + {{PA}} - 2{\alpha _k}{{PB}}{{\delta }}(t){{K}}-\\ & 2{\alpha _k}{{P}}{{\rm e}^{ - {{A}}h}}{{B}}(1 - {{\delta }}(t)){{K}}){\sigma _{i2}}(t). \end{split} $

(35)

所以 ${\dot V_{i1}} + {\dot V_{i2}} < 0$ 充要条件与式(33)一致,

${{K}} > \frac{{{{A}} + {{{A}}^{\rm{T}}}}}{{2{\alpha _{\min }}\overline \delta {{B}} + 2{\alpha _{\min }}(1 - \overline \delta ){{\rm{e}}^{ - {{A}}h}}{{B}}}}.$

(36)

因此结合式(28)、式(30)、式(34)和式(36)，只要满足

${{K}} > \frac{{{{A}} + {{{A}}^{\rm{T}}}}}{{2\underline \lambda \overline \delta {{B}} + 2\underline \lambda (1 - \overline \delta ){{\rm{e}}^{ - {{A}}h}}{{B}}}},$

$\underline \lambda = \min \{ {\lambda _2}, \cdots ,{\lambda _n},{\alpha _1}, \cdots {\alpha _n}\} ,$

多智能体系统(1)可达到一致性.

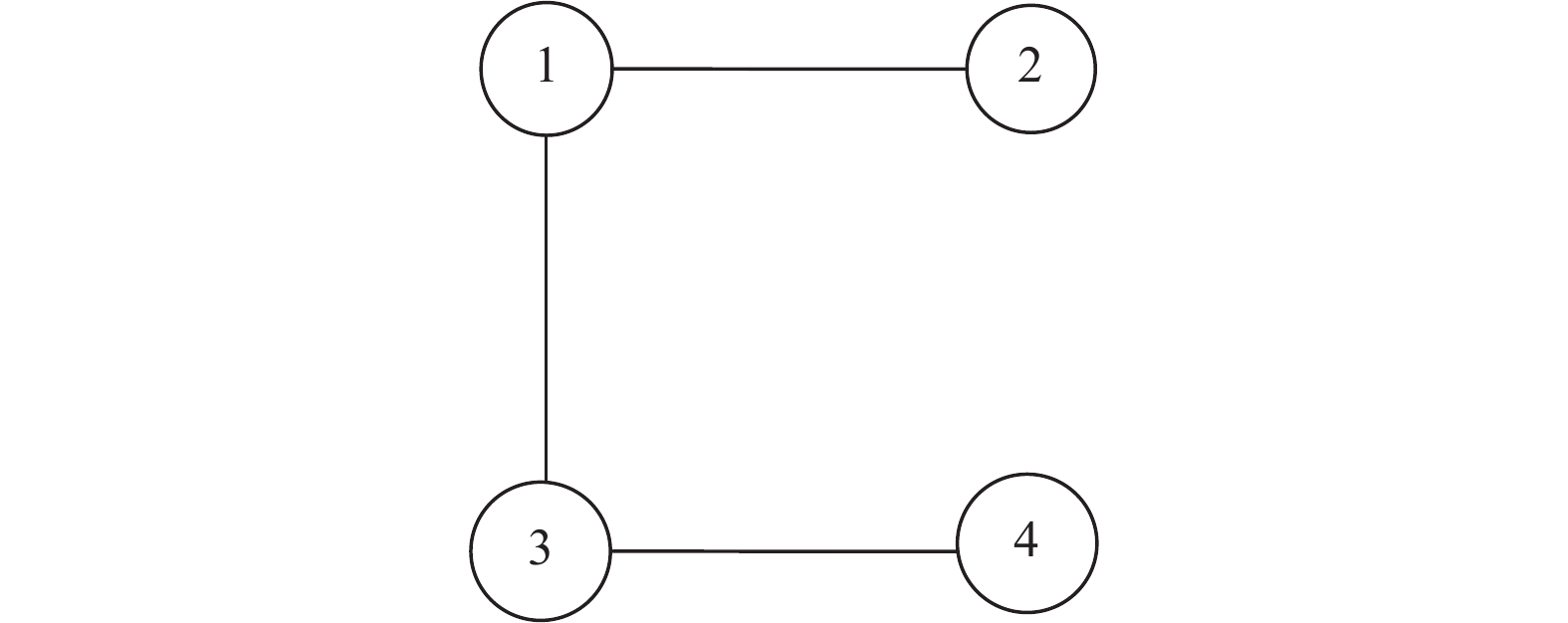
3 仿真验证

如图1所示，假设多智能体系统拓扑图包含以下4个节点，分别记作节点1、2、3、4，令A=1，B=3任意选择初始状态 ${x_1}(0) = - 20$ ， ${x_2}(0) = - 5$ ， ${x_3}(0) = 15$ ， ${x_4}(0) = $ 30， $\overline \delta = 0.8$ ，时延h=0, 03，各智能体连接权重为1.

根据该拓扑图可写出Laplacian矩阵L，

${{L}} = \left[ {\begin{array}{*{20}{c}} 2&{ - 1}&{ - 1}&0 \\ { - 1}&1&0&0 \\ { - 1}&0&2&{ - 1} \\ 0&0&{ - 1}&1 \end{array}} \right].$

可求得最小非0特征值 $\underline \lambda = 0.5858$ ,

${{{r}}^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{1}{4}}&{\displaystyle\frac{1}{4}}&{\displaystyle\frac{1}{4}}&{\displaystyle\frac{1}{4}} \end{array}} \right].$

代入式(12)可得K >0.5724.

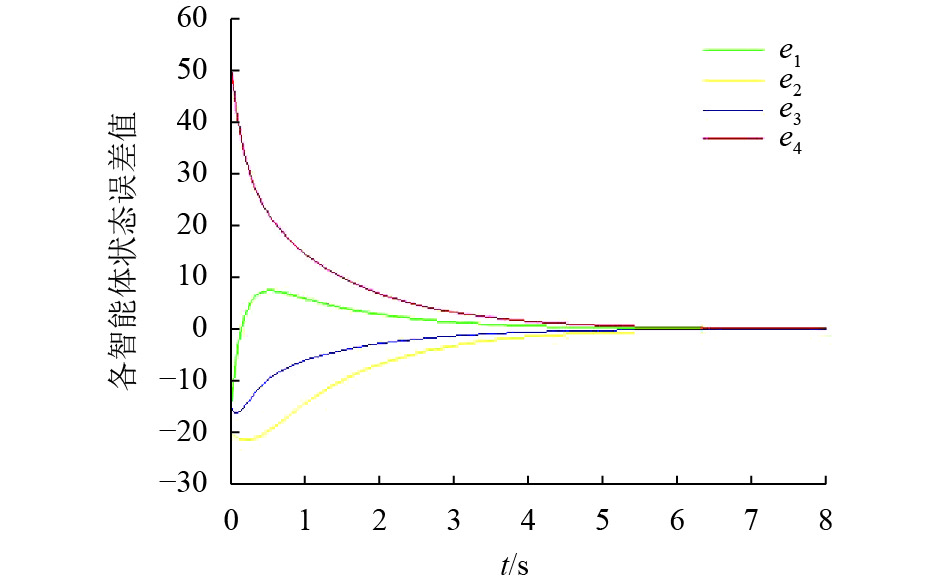
令 ${{K}} = 1$ ，系统误差曲线如图2所示. 可看到各智能体之间误差均趋于0，系统在协议(12)的控制下达到一致.

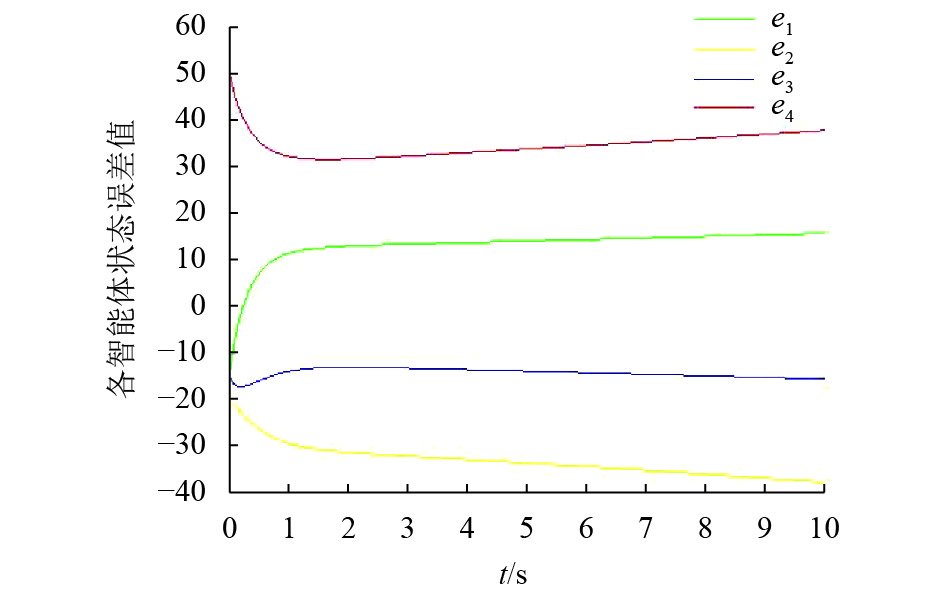
当K=0.562略小于临界值，如图3所示. 可以看出当K值小于临界值时，各智能体误差曲线呈发散趋势，无法收敛于0，各智能体无法达到一致性.

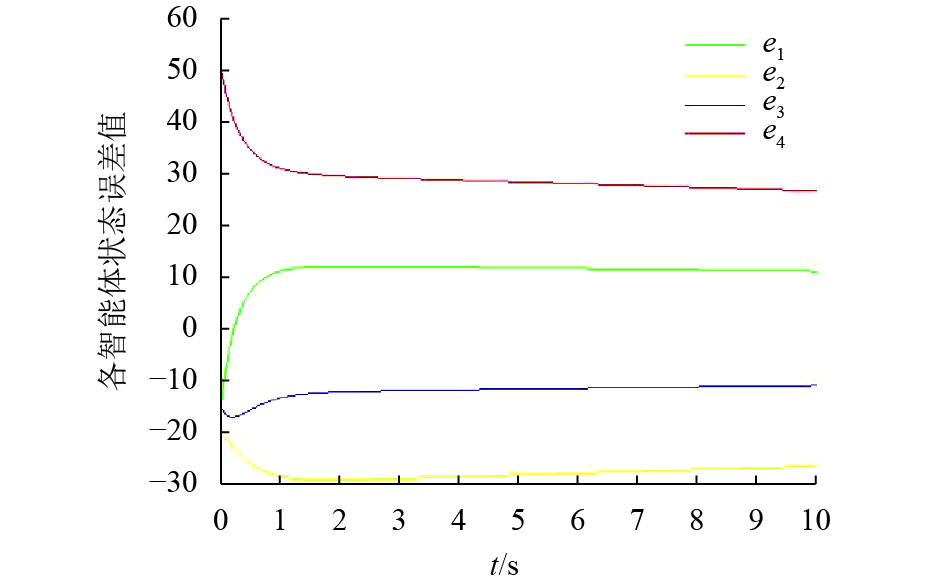
当K=0.582略大于临界值，如图4所示. 可以看出当K值大于临界值时，各智能体误差曲线呈收敛趋势，经过一定时间能够收敛于0，各智能体能够达到一致性.

4 结束语

本文研究了一阶含随机时延的多智能体一致性问题，并通过模型简化法，引入一个新变量，将原本含有时延的系统转化为一个不含时延的系统，并提出一个一致性算法，使用Lyapunov函数，找出多智能体系统在这个算法下达到一致的充分必要条件. 最后给出模型仿真，验证出这个结论的正确性以及通过模型简化法对含有随机时延的多智能体系统分析的可行性.