机器人在复杂环境中执行任务时,比如救灾、探测、巡检等环境中,不可避免地会遇到障碍物. 因此,机器人往往需要具备跨越大尺度障碍物的能力. 而该性能既是机器人运动性能好坏的体现,也是机器人能否适应复杂环境并且进行有效的人机协作的基础之一. 特别是,当前服务类机器人逐步融入到人们的工作生活环境中,越障能力对机器人越来越重要.
机器人一般是由多个关节和连杆所组成的复杂的非线性系统,这也意味着很高的控制难度. 尤其是在跨越大尺度障碍物时,如果机器人仅仅依靠自身关节驱动和姿态调整来保持平衡,那么机器人的重心在地面的投影很容易偏离出脚底的支撑多边形,从而导致机器人不稳定,发生倾倒[1]. 目前,已有不少相关的研究重点集中在仿人机器人自身关节结构设计、跨越足工作空间的优化和通过借助环境来实现大尺度障碍物的跨越. 程刚等[2]利用3次均匀B样条曲线的方法规划出机器人越障的轨迹. 通过选择适当的参数,实现了良好的仿生越障步态. 当然,也有人通过多足的结构或足轮结合的方式[3-4],在保证机器人稳定的前提下,实现越障. Kalamian N等[5]提出使用预测控制器,实现双足的机器人动态的越障,该方法不需要规划越障轨迹,便能找到最优的步长,而且具有闭环稳定性. Zhou C X等[6]通过增加机器人髋关节处的冗余关节,扩大了仿人机器人跨越时的工作空间,最终跨越的长度超过其腿长20%的大尺度障碍物. Fu C L等[7]用步态合成和传感控制的方法,能够让32个自由度的机器人实现上下楼梯运动. Koch K H等[8]通过全身优化控制算法,解耦了弹性踝关节和稳定控制算法间的关系,最终使HRP-2跨越了高20cm宽11cm的障碍物. 管贻生等[9-11]通过建立仿人机器人越障时的无碰撞和平衡稳定等非线性约束优化模型,分析了仿人机器人的灵活性,然后再对机器人的越障动作进行规划,最终在HRP-2上验证了其方法的可行性. Stasse O等[12]从时间维度上出发,通过规划确定的质心运动轨迹和减小着陆时的冲击等,使得机器人能在4s内完成越障,极大地缩短了越障时间. 于薇薇等[13]提出一种基于模糊Q学习算法的路径规划策略,能通过在线学习跨越不可预期的障碍物. Guo F Y等[14]解决了连续两个障碍物的跨越问题. 当然,上述的研究主要是基于机器人自身的驱动装置以及调整姿态来实现越障的. 然而,机器人越障时不可避免地要与环境发生接触. 因此,还有其他方法也可以实现大尺度越障. Doubliez P F[15]提出控制后脚能量喷射装置的方法,实现双足机器人动态的越障. 该方法主要是通过后脚的喷射装置,给整个机器人提供一个前上方的冲力,帮助双足机器人踩上障碍物,实现越障. 与本文所用的借助外力保持平衡实现越障类似. Kojio Y等[16]研究了机器人在水中受到水流的拖拽力影响下的行走和越障能力,通过基于捕获点的步态生成方法,实现了水中平地行走和上下楼梯等动作. 该研究在外力干扰的情况下,实现了机器人的移动与越障功能. 当然,也有人提出了借助环境来实现越障的方法. Farnioli E等[17]提出通过多点接触的方式,来克服机器人因跨出一大步导致的重心失稳问题. 因此,机器人不仅可以通过手扶墙壁站立在不平整的地面上,还可以双手扶着水泥砖跨越障碍物.
本文在机器人借助涵道风机提供额外推力,跨越一条宽沟渠的研究基础上进行进一步拓展与推广[18],把障碍物作为一个非线性的约束,添加到冗余机器人跨越的优化模型中,着重解决之前未考虑的凸出地面的大尺度障碍物跨越及避障问题.
1 机器人建模机器人往往是多自由度复杂的非线性系统,为了能准确地描述并分析该系统,一般需要建立机器人的模型. 同时,为了避免DH(Denavit Hartenberg)法建模时,因连杆局部坐标运动而造成的累积误差,以及能直观地读取双足机器人各连杆间的位姿关系[1],本文采用基于旋量理论的运动学建模方法.
1.1 机器人连杆的数据结构机器人连杆数据是指在机器人建模时用于存放机器人初始位置、姿态以及连杆长度等信息的集合,可用一个结构体来表示. 而机器人各个连杆之间也存在的连接关系,决定机器人的运动方式. 常用的有串行连接和并行连接. 本文的研究对象是每条腿有六个自由度的双足机器人,两条腿均采用串行连接,并通过腰部连杆连接构成一个完整的双足机器人.
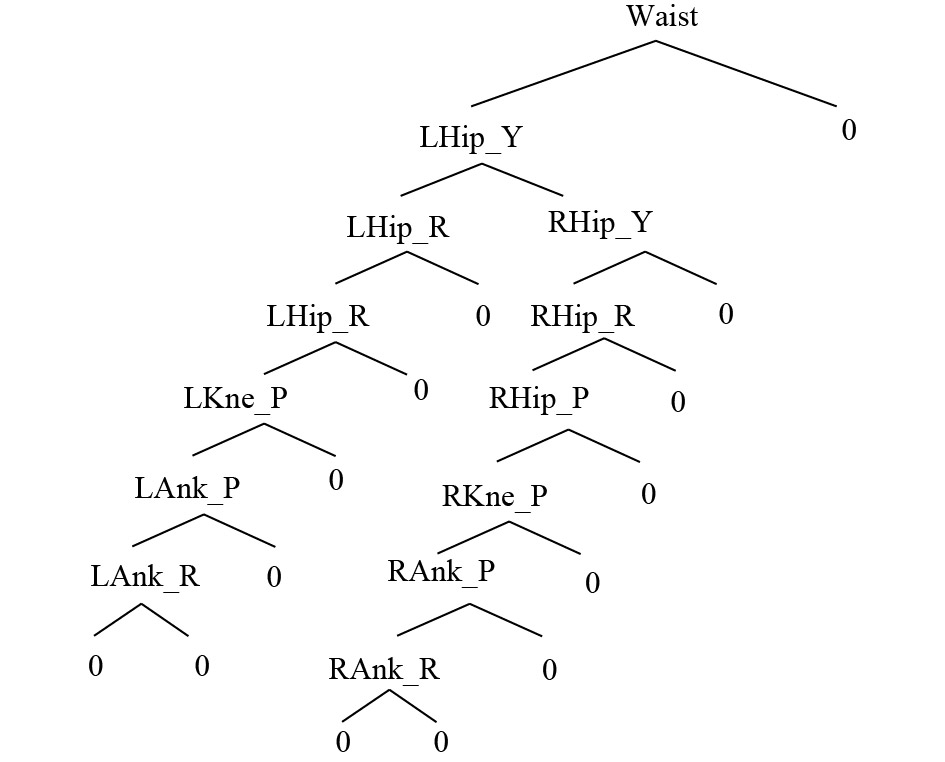
为方便描述各个关节的之间的关系,机器人连杆采用类似家谱结构(也称树形结构)的数据结构形式,从初始节点开始,每个节点都有左右两个分支,左分支为“子女”节点,右分支为“姊妹”节点,都没有的话以“0”标记,用字母“L”和“R”前缀来区分左右[1]. 通过这种连接,将机器人的关节之间的连接表示出来,如图1所示.
|
图 1 机器人连杆的数据结构 Figure 1 The data structure of robot links |
一般地,本文选取双足机器人站立姿态为其初始姿态. 其中,选择双足机器人腰部连杆作为机器人建模原点,建立第一个与世界坐标系平行的局部坐标系,然后其他局部坐标系按照这种方式在机器人的每个关节处建立[1].
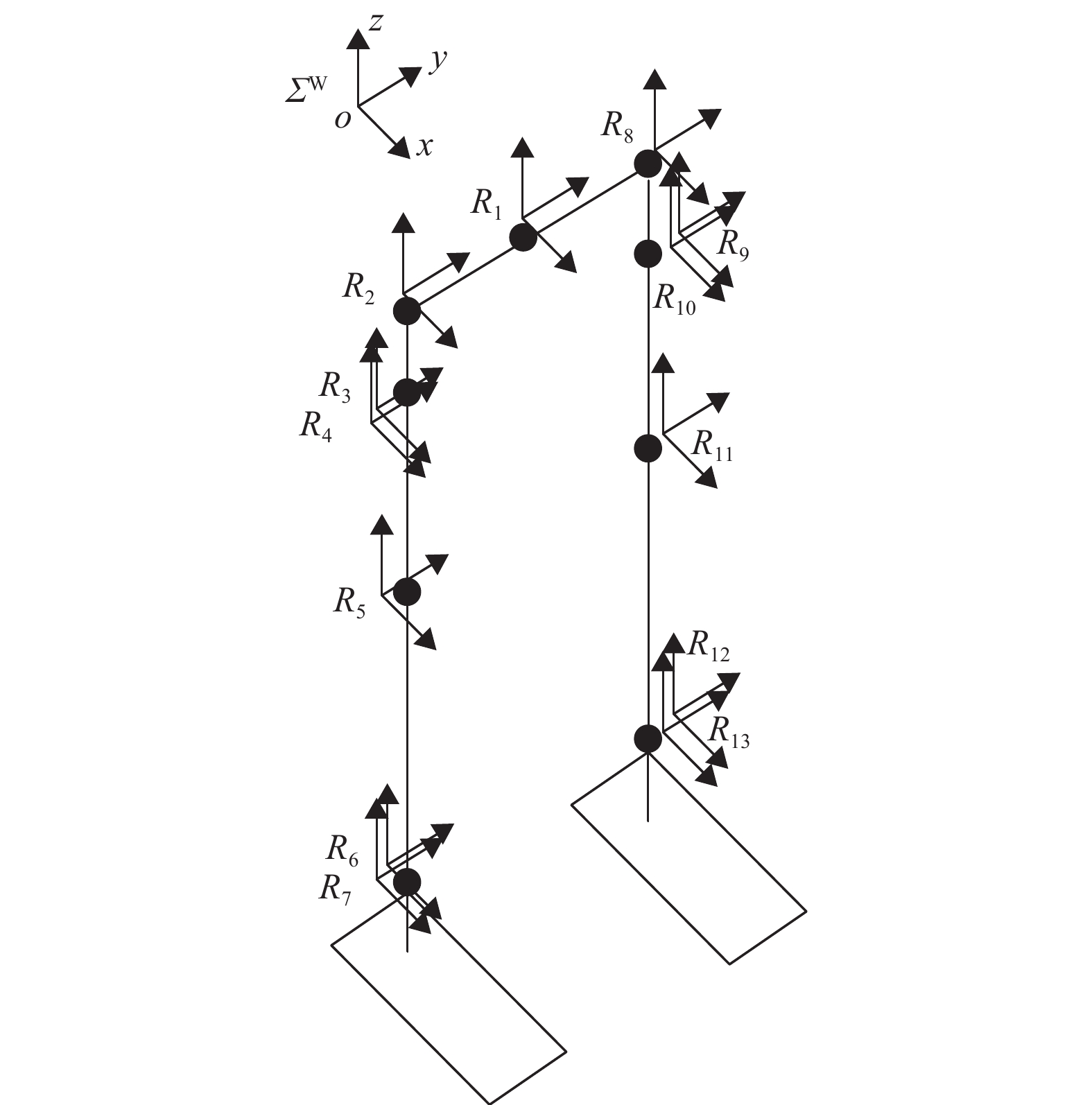
双足机器人的局部坐标系确定如图2所示,各个局部坐标系的原点落在机器人关节的旋转轴上. 图2中Ri(i=
| ${{R}_i} = {E},i = 1,\cdots,13.$ | (1) |
此处,E为3阶单位矩阵.
|
图 2 局部坐标系的选取 Figure 2 The choosing of local frames |
关节轴矢量即为机器人旋转关节转动轴的轴向,该方向满足右手定则,即右手四指沿着转动的正方向握拳弯曲,此时拇指所指向的方向. 相对位置矢量是指相邻的两个局部坐标系原点之间的位置关系,由于局部坐标系固连在机器人关节处,因而相对位置矢量也反映出机器人连杆的参数.
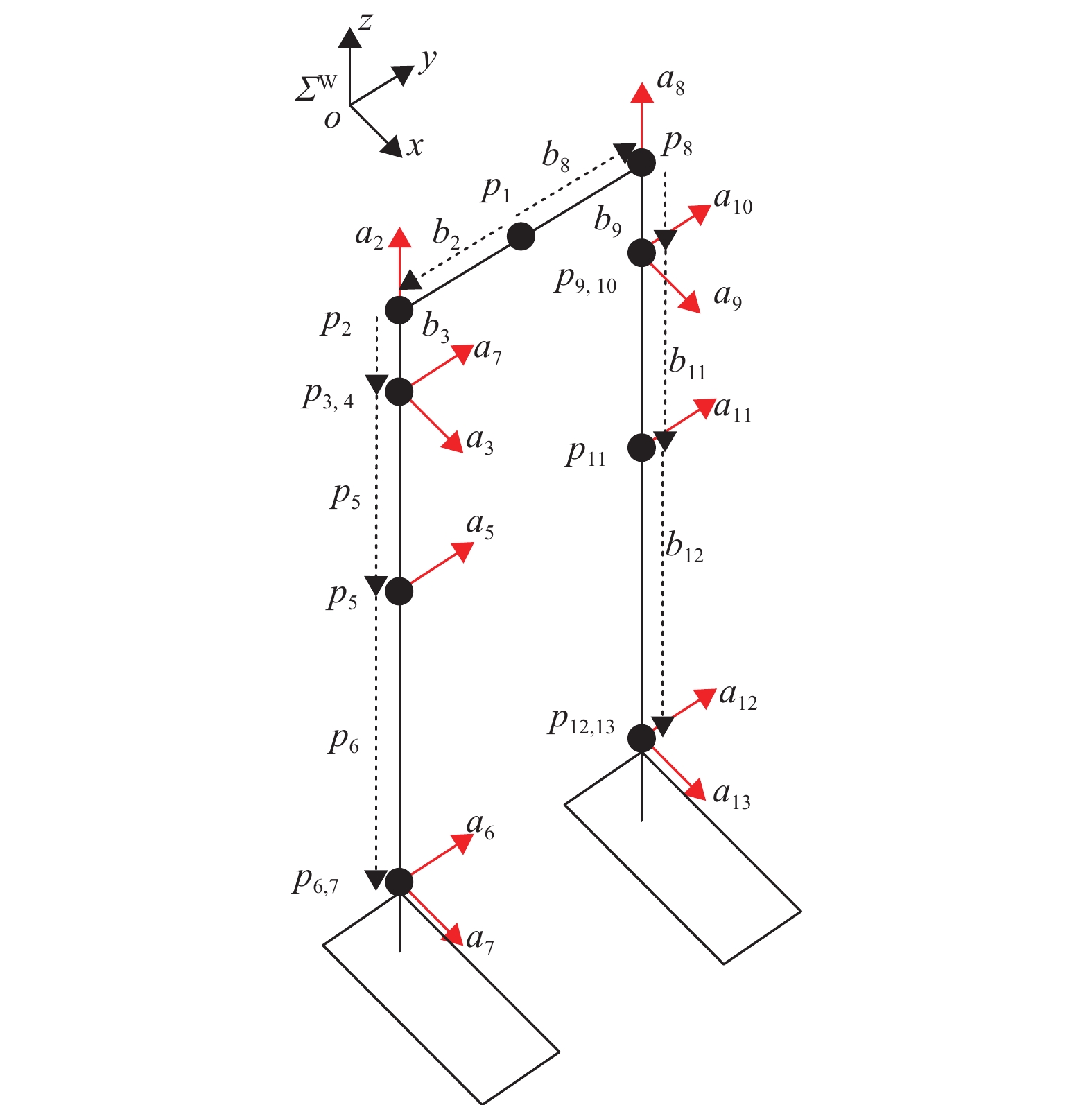
在图3中,ai(i=
根据罗德里格指数映射公式[1],可得相邻关节之间的齐次变换矩阵:
| ${}^i{{A}_j} = \left[ {\begin{array}{*{20}{c}} {{{\rm e}^{{\hat{ a}}_j}{\theta _j}}}&{{{b}_j}} \\ {\begin{array}{*{20}{c}} 0&0&0 \end{array}}&1 \end{array}} \right].$ | (2) |
|
图 3 关节轴矢量与相对位置矢量 Figure 3 Axis vector of joints and relative position vector |
此处bj为相邻关节间的相对位置矢量,θj为关节转动的角度,
若
通过相邻关节之间的变换关系,可以求得通过机器人腰部参考点到机器人末端的变换关系:
| $\begin{split} & ^1{{A}_7}{ = ^1}{{A}_2}{ \cdot ^2}{{A}_3}{ \cdot ^3}{{A}_4}{ \cdot ^4}{{A}_5}{ \cdot ^5}{{A}_6}{ \cdot ^6}{{A}_7},\\ & ^1{{A}_{13}}{ = ^1}{{A}_8}{ \cdot ^8}{{A}_9}{ \cdot ^9}{{A}_{10}}{ \cdot ^{10}}{{A}_{11}}{ \cdot ^{11}}{{A}_{12}}{ \cdot ^{12}}{{A}_{13}}. \end{split}$ | (3) |
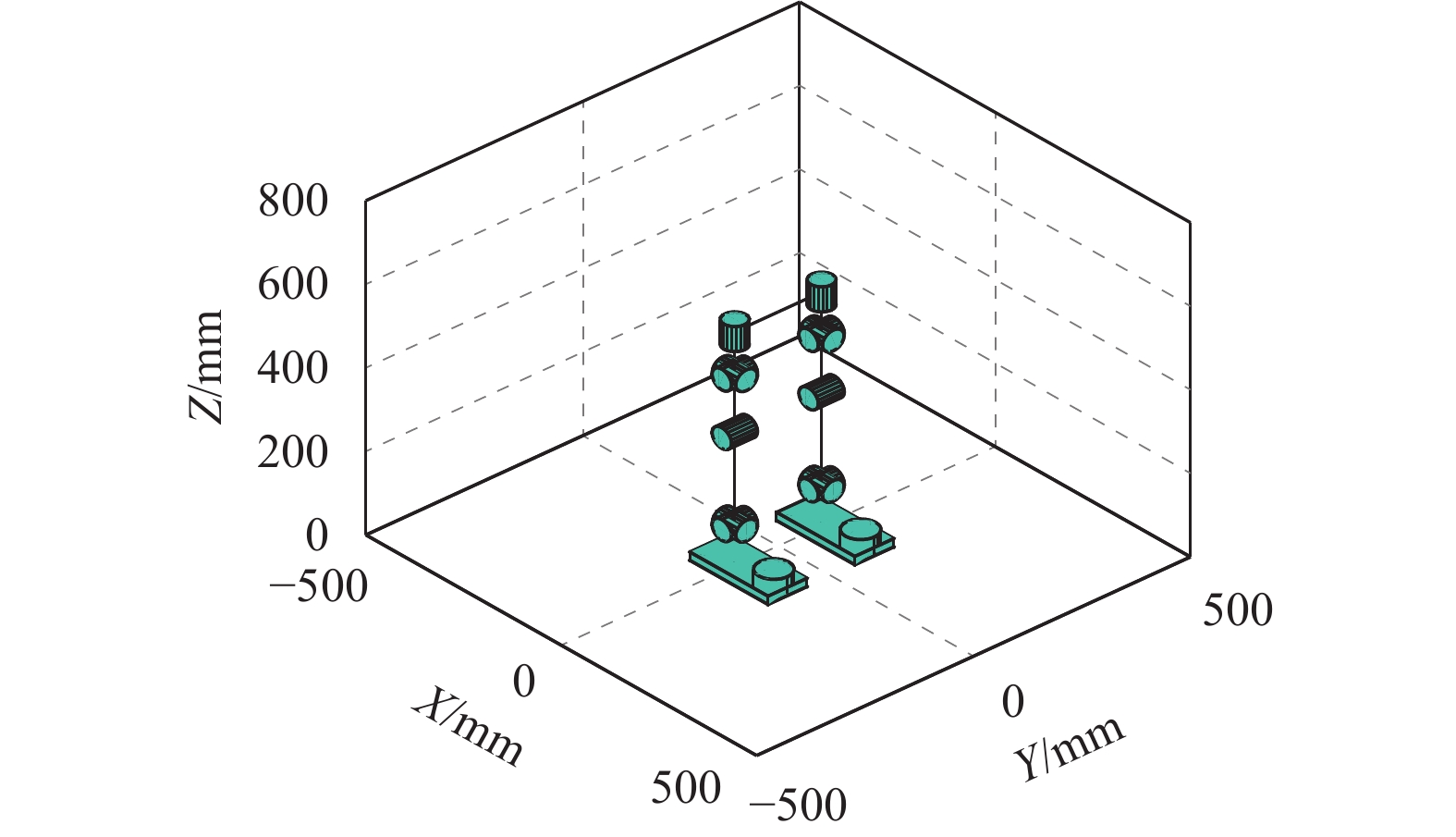
最终,通过上述的齐次变换关系,在MATLAB环境下建立起了双足机器人的3D模型(如图4所示). 图中机器人脚掌上的圆柱体表示给机器人提供额外推力的装置,比如涵道推进系统、喷气助推系统等. 其余圆柱体表示对应的12个转动关节.
|
图 4 双足机器人3维模型 Figure 4 The 3D model of the bipedal robot |
本文针对双足机器人在借助外力的基础上,跨越一个大尺度的障碍物. 因此,整个跨越过程需要3个步骤来实现:(1) 需要规划合理的跨越脚运动轨迹;(2) 需要对双足机器人跨越过程中进行受力分析,并且建立避免碰撞的同时保持平衡稳定的优化模型;(3) 优化求解出机器人整个跨越过程的关节角空间和脚掌端需要的推力变化.
2.1 跨越轨迹规划在规划双足机器人的跨越轨迹前,需要确定双足机器人的跨越步态,即机器人通过几个步骤,从障碍物一边运动到障碍物的另一边. 由于机器人跨越凸出的障碍与跨越沟渠类似,故拟采用之前研究所提出的跨越—滑动—跨越2D步态[18]:
(1) 前脚跨越:双足机器人重心后移,落在后脚支撑脚上,前脚跨出;
(2) 前脚到达障碍物另一侧,继续借助外力向前滑行一段距离;
(3) 重心切换,前脚为支撑脚,后脚为跨越脚,跨越脚向障碍物方向滑行一段距离;
(4) 后脚借助外力,收回到障碍物的另一侧,完成跨越.
跨越轨迹的规划,需要考虑双足机器人初始位置、机器人脚掌的长度以及障碍物的大小等. 然后通过曲线拟合的方式,生成合适的多次样条曲线轨迹,多次样条曲线能有效地平滑机器人的关节角,保证运动的平稳性[19]. 文本中的规划条件给出如下:
(1) 机器人前脚的跨越足初始位置为Pini= (0, 100, 0)T;
(2) 机器人脚掌的长度为200 mm,脚后跟的位置为轨迹所在点,到脚尖的距离为Lfoot=135 mm;
(3) 障碍物的形状为长方体,机器人所需跨越的障碍物的截面为宽50 mm,高200 mm的矩形;
(4) 跨越时,轨迹和障碍物之间需保持一定的安全距离Hsafe=100 mm.
由于跨越动作的对称性,根据上述给出的条件,可以确定5个关键的位置点,拟合出一条合适的4次曲线(如图5):
| $\begin{split} & z = {p_4^{}}{y^4} + {p_3^{}}{y^3} + {p_2^{}}{y^2} + {p_1^{}}y + {p_0^{}}, \\ &{p_0^{}} = {\rm{ - 1}}{\rm{.357976853623562}}\times 10^3, \\ &{p_1^{}} = {\rm{2}}{\rm{2.848901267640077}}, \\ &{p_2^{}} = {\rm{0.1}}{\rm{16719650402620}}, \\ &{p_3^{}} = {\rm{2}}{\rm{.621271609662897}}\times 10^{-4} , \\ &{p_4^{}} = {\rm{ - 2}}{\rm{.184393008052421}}\times 10^{-7}. \end{split} $ | (4) |

|
图 5 跨越轨迹规划 Figure 5 Planning stepping trajectory |
本文中的双足机器人不同于传统的双足机器人,在本文中,通过引入额外的外力,可以让机器人在跨出较大步幅的情况下,保持机器人不倾倒. 而且,相比较于其他动态的越障动作,本文中的机器人能以准静态的方式实现跨越,这样可以有效地减小机器人跨越脚着陆时的冲击,增加机器人的稳定性,同时,也能减小对机器人的损害.
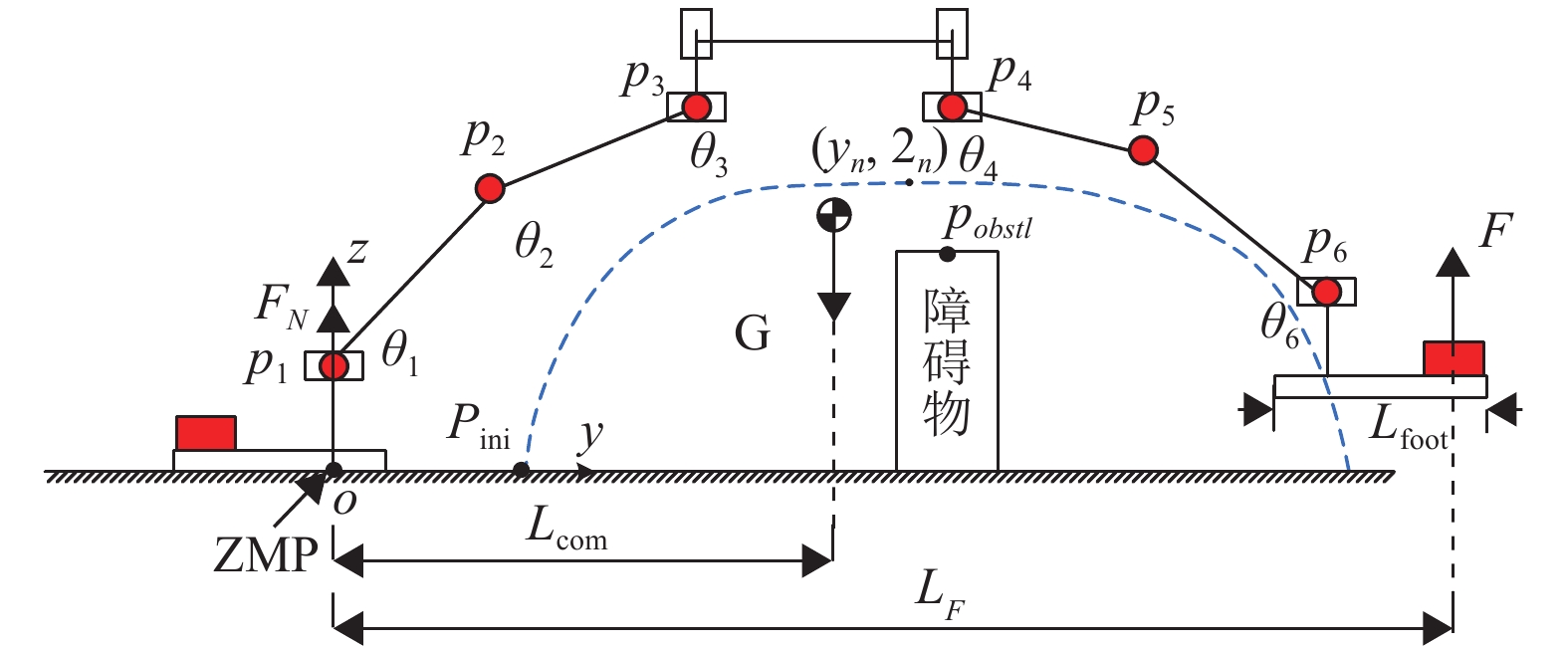
双足机器人要通过准静态方式越障,首先,需要对机器人进行受力分析,由于采用2D步态,故双足机器人可以简化成在跨越平面内运动的6自由冗余平面机器人,机器人的准静态受力分析如图6所示.
|
图 6 双足机器人准静态模型受力分析 Figure 6 Force analysis of quasi-static model of bipedal robot |
图6中,红色的关节表示实际活动的关节,其余关节是锁定不变的. F、FN和G分别为额外的外力、地面的支撑力和重力. Lfoot和Lcom分别为外力和重力对支撑点,即机器人参考的零力矩点(ZMP)的力臂. 红色矩形表示提供额外外力的助推装置.
由于双足机器人在跨越的过程中,每个姿态都视为准静态,即机器人的速度和加速度都是0. 因此,每个姿态都满足力和力矩平衡:
| $\left\{ {\begin{array}{*{20}{l}} {{F_N} + G + F = 0}, \\ {{F_N} \cdot 0 + G \cdot {L_{\rm com}} + F \cdot {L_{\rm foot}} = 0}. \end{array}} \right.$ | (5) |
由于双足机器人采用2D步态跨越障碍物,其模型简化为平面6自由度的冗余机器人. 对于确定的末端位置和姿态,具有无穷多解. 因此,在机器人无穷解中,存在满足跨越过程中外力最小的最优解.
双足机器人在跨越过程中达到额外外力最小时,必须满足一定的约束条件:
(1) 机器人的腰部连杆和跨越脚的脚掌都与地面保持水平,主要是为了增加外力的作用力臂和保证外力竖直向上;
(2) 机器人跨越足末端沿着规划轨迹运动;
(3) 跨越过程中机器人的机体不与障碍物发生碰撞.
根据上述的约束条件,结合机器人自身关节角度的限制,得到如下优化模型:
| $\begin{array}{l} \min \;F({\theta }) = G \cdot {L_{\rm com}}({\theta })/{L_{\rm foot}}({\theta }),\\ {\theta } = {\left[ {{\theta _1}}\quad{{\theta _2}}\quad{{\theta _3}} \quad{{\theta _4}}\quad{{\theta _5}}\quad{{\theta _6}} \right]^{\rm T}}. \end{array}$ | (6) |
| ${\rm s.t.}\;\;\;\;{{\theta }_{\rm lb}} \leqslant {\theta } \leqslant {{\theta }_{\rm ub}},\;\;\;\;\;\;{{\theta }_{\rm lb}},{{\theta }_{\rm ub}} \in {{R}^{6 \times 1}}.$ | (7) |
| $\left\{ {\begin{array}{*{20}{c}} {{\theta _1} + {\theta _2} + {\theta _3} = 0}, \\ {{\theta _4} + {\theta _5} + {\theta _6} = 0}. \end{array}} \right.$ | (8) |
| $\left\{ {\begin{array}{*{20}{l}} {{y_n} = {L_F}({\theta }) - {L_{\rm foot}}}, \\ {{z_n} = {H_F}({\theta })}. \end{array}} \right.$ | (9) |
| $\left\{\!\!{\begin{array}{*{20}{c}} {\delta (\left| {{p_{\rm obstl}}(y) - {p_5}(y)} \right| < 80) \cdot ({p_5}(z) - {p_{\rm obstl}}(z) > 0)}, \!\!\!\!\\ {\delta (\left| {{p_{\rm obstl}}(y) - {p_4}(y)} \right| < 80) \cdot ({p_4}(z) - {p_{\rm obstl}}(z) > 0)}. \!\!\!\! \end{array}} \right.$ | (10) |
优化模型中,式(6)是求优化问题的代价函数,即机器人保持平衡时的所需外力大小;式(7)为机器人6个对应关节角度的上下限约束. 式(8)表示机器人脚掌和腰部连杆与地面保持平行的约束;式(9)表示机器人跨越足沿着规划的轨迹运动的位置约束,(yn, zn)为规划轨迹上离散的序列点;式(10)为避障约束,表示机器人的跨越脚的膝关节和臀关节进入到避障区域时,所需满足的避障约束条件,pobstl、p4和p5分别表示障碍物的位置,跨越脚臀关节的位置和膝关节的位置. 其中
| $\delta \left( x \right) \buildrel \Delta \over = \left\{ {\begin{array}{*{20}{l}} {1,\;\;\;\;x\text{为真}};\\ {0,\;\;\;\;x\text{为假}}. \end{array}} \right.$ | (11) |
由于上述的优化模型是典型的多变量多约束的非线性优化问题,可以通过MATLBA工具箱进行优化求解. 最终可以优化求解沿着规划轨迹,而且满足各个约束条件的机器人关节角度空间和所需外力.
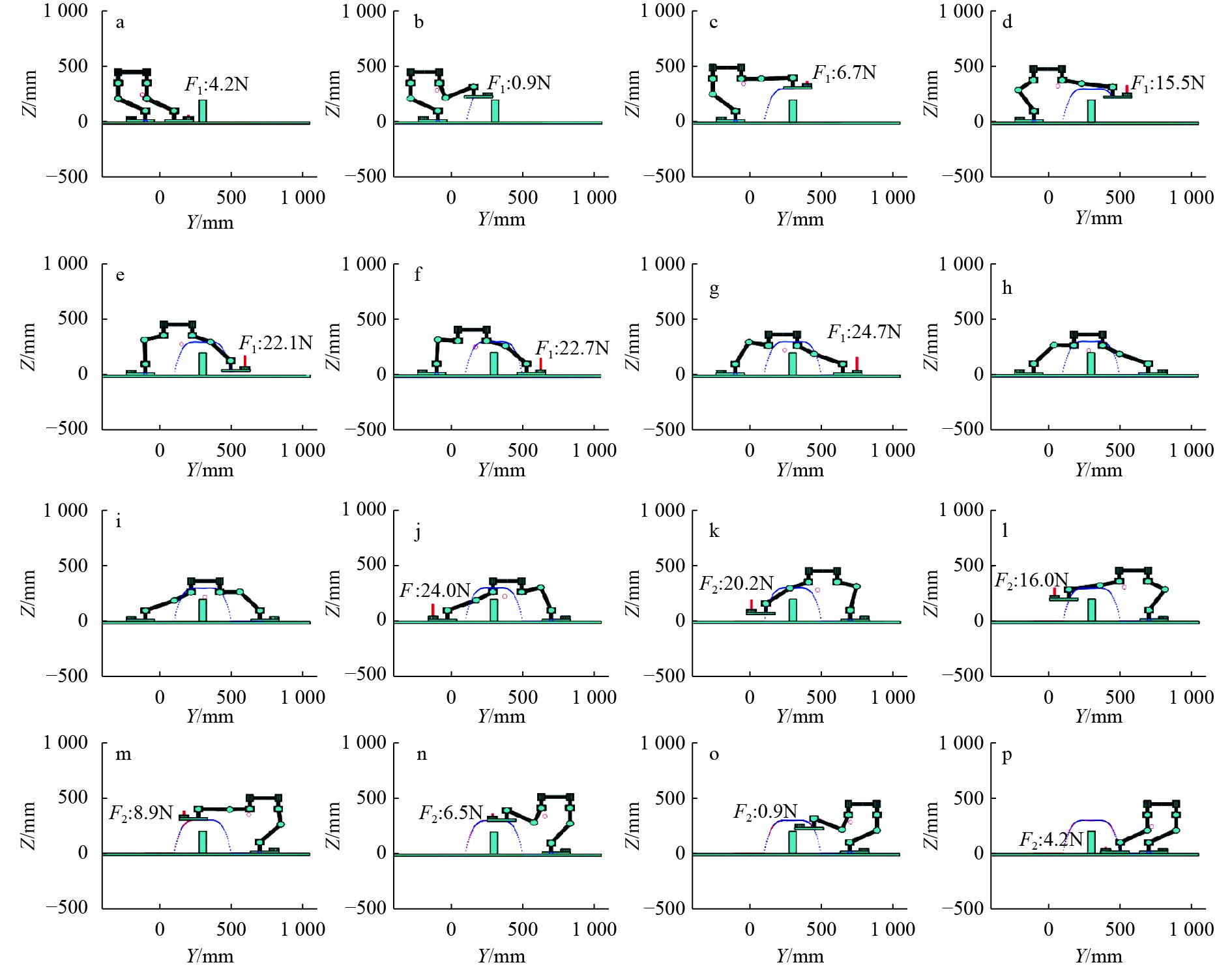
3 实验验证 3.1 仿真结果通过越障优化模型,依次遍历求解规划轨迹上离散的位置点,最终能求取出机器人跨越动作的6个关节角度空间和对应跨越姿态下的推力大小. 同时,由于是在水平面上进行跨越,而且障碍物形状对称,因此,机器人前脚跨过障碍物的动作实际上和后脚收脚的动作镜像对称,因此,只需要求解前脚跨出一步的动作,后脚的收腿的动作可由前脚镜像变换得到. 完整的跨越障碍物的仿真结果如图7所示.
|
图 7 双足机器人越障仿真结果 Figure 7 The results of the bipedal robot stepping over the obstacle |
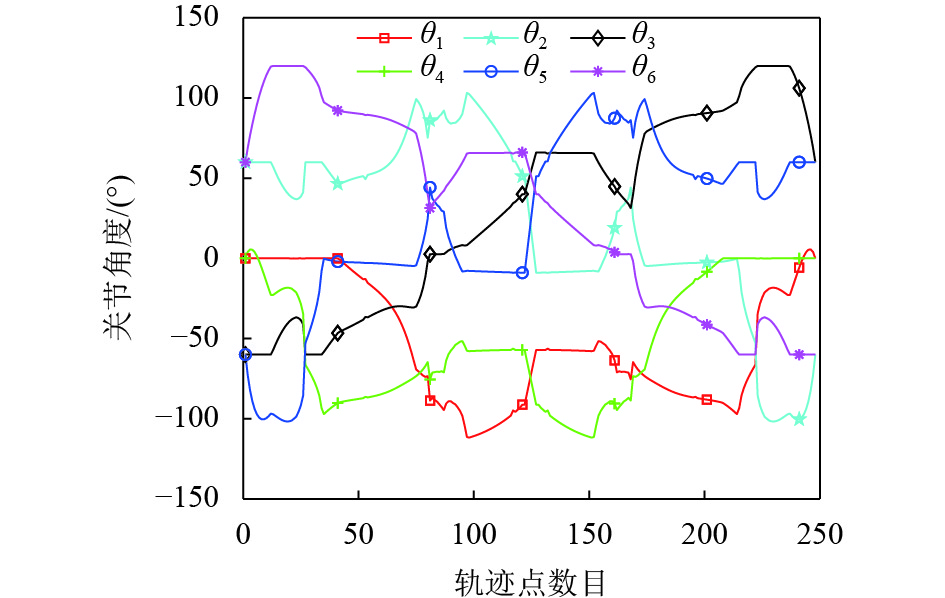
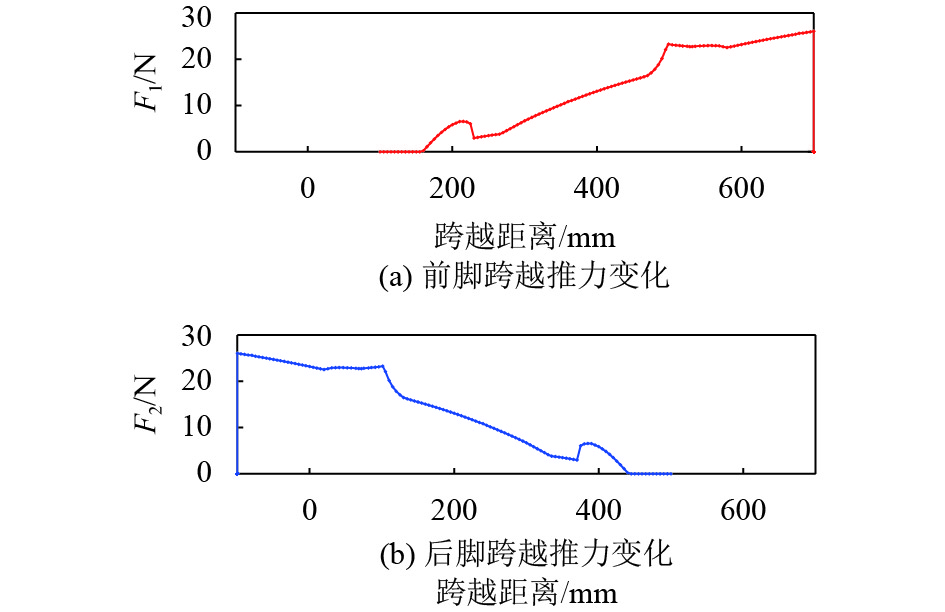
在图7中,双足机器人跨越了高200 mm,宽50 mm的矩形截面的障碍物,其中跨越高度约为其腿长的43%. 图7(i)和图7(k)显示了其避障时的效果,通过向上凸出,避免与障碍物碰撞,整个越障过程中的6个关节角度变化和所需的推力变化如图8和图9所示.
|
图 8 机器人越障的关节角空间 Figure 8 Joints angles space of stepping over obstacle |
|
图 9 机器人越障所需的外力 Figure 9 The required extra force for the robot stepping over the obstacle |
由于在求解优化跨越姿态过程中,引入了避障的非线性约束,使得相同的越障轨迹,机器人有无避障的跨越姿态和推力会不同.
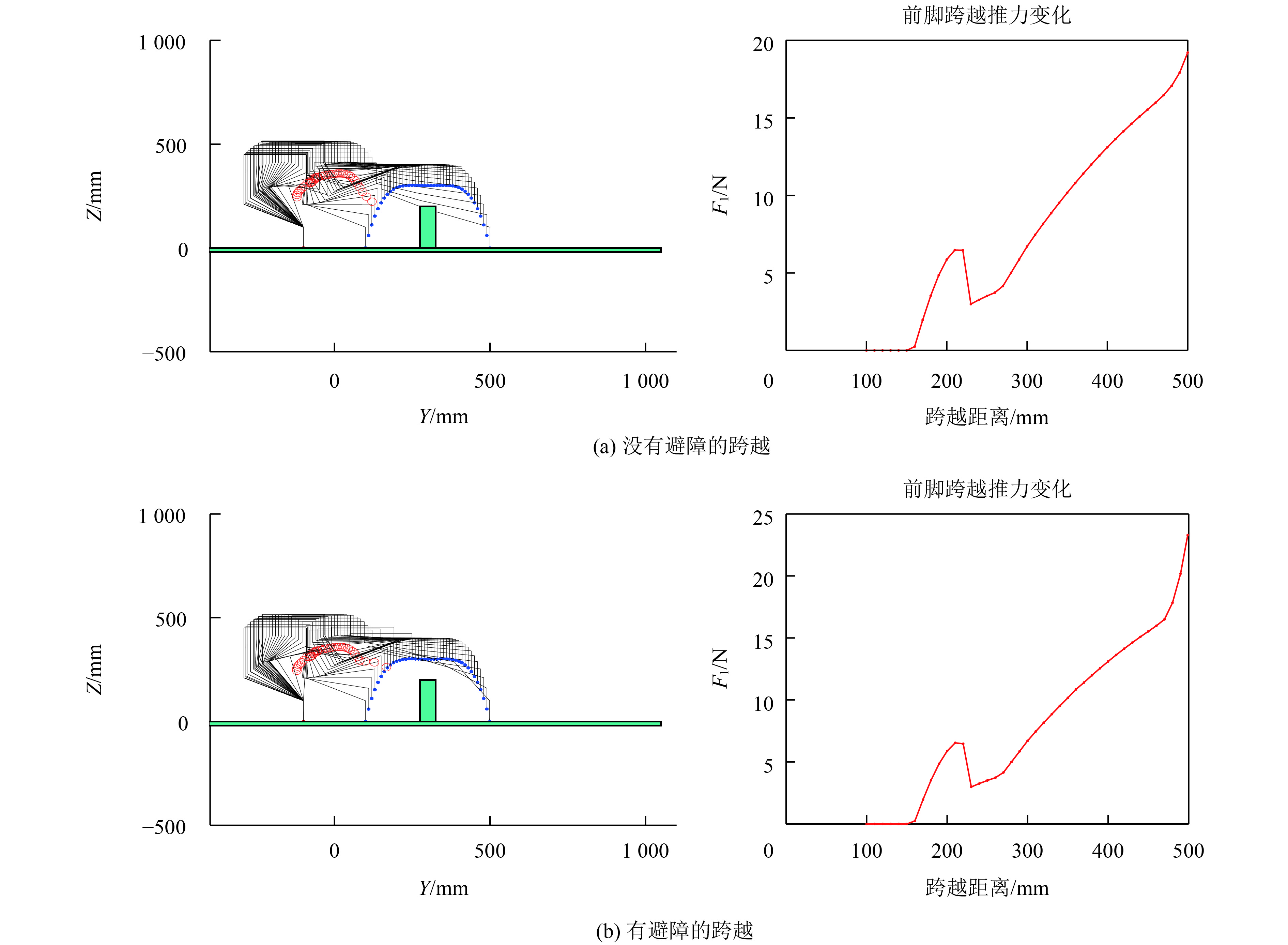
没有考虑避障情况下(见图10(a)),机器人在着陆时机体明显与障碍物发生了碰撞. 这样,在实际实验时,很可能会导致机器人失去平衡,进而越障任务失败. 从图10(b)可以发现机器人在有考虑避障的情况下,机器人机体能与障碍物保持一定的安全距离,避免跨越过程中与障碍物发生碰撞.
|
图 10 避障跨越仿真结果及外力变化对比 Figure 10 Comparison of stepping simulation and extra force variation |
对比发现,考虑避障时,由于机器人需要把重心(见图10左图红色圆圈)更加前移,从而,也需要更大的外力来保持机器人的准静态平衡. 因此,避障跨越时推力变化比没有考虑避障时要更大.
3.3 样机实验双足机器人越障算法是否有效,需要用实际的样机实验来验证. 根据前面规划的步态与轨迹和假定的障碍物,在样机喷射仿人机器人1号(Jet-HR1)平台上进行验证:
如图11所示,样机实验测试了双足机器人前脚跨越障碍物的步态,根据跨越动作的对称性,双足机器人可以根据跨越障碍物的逆动作,收回后腿,完成越障. 由于双足机器人跨越时关节的角度存在较大的误差. 因此,影响了双足机器人可跨越的障碍物高度. 实验样机最终可跨越15cm高5cm宽的障碍物.

|
图 11 样机实验 Figure 11 Prototype experiment |
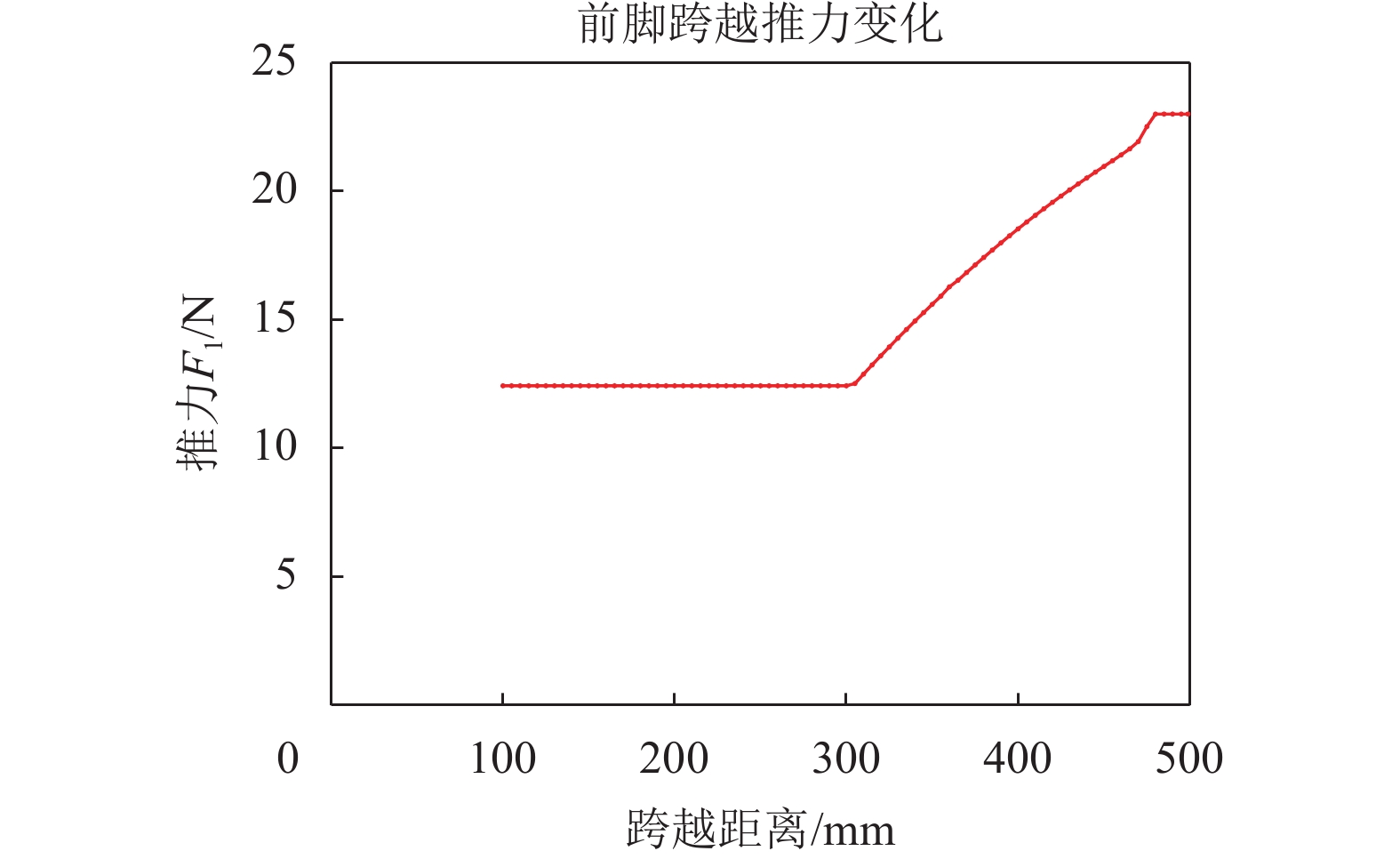
由于涵道风机存在物理死区,刚开始启动时,设定为一恒定的值,而且,由于双足机器人质量模型的理论计算值与实际值之间存在误差,实际实验时,需要在理论计算值的基础上,将输入PWM控制信号提高14%. 推力助推器涵道风机输出值存在上限,最大输出值为23 N. 所以,最终得到双足机器人跨越时的推力变化如图12所示.
|
图 12 推力变化 Figure 12 Experimental thrust change |
本文主要研究双足机器人借助外力,来实现跨越大尺度障碍物的任务,通过对双足机器人越障时的准静态模型进行分析,建立起姿态优化模型. 最终,在仿真情况下,双足机器人可跨越障碍物的高度为20 cm,达到机器人腿长的43%. 实际样机实验,机器人跨越了高15 cm的障碍物,到达其腿长的32%.
仿真和样机实验的结果说明,本文所提出的双足机器人通过引入额外的外力来跨越凸出地面的大尺度障碍物的方法是可行的.
| [1] |
梶田秀司. 仿人机器人[M]. 北京: 清华大学出版社, 2007.
|
| [2] |
程刚, 竺长安, 沈连婠, 等. 基于b样条曲线的两足机器人仿生越障步行模式实现方法[J].
图学学报, 2006, 27(4): 1-7.
CHENG G, ZHU C A, SHEN L W, et al. A method of planning bionic over-obstacle walking mode for biped robot based on b-spline curves[J]. Journal of Engineering Graphics, 2006, 27(4): 1-7. DOI: 10.3969/j.issn.1003-0158.2006.04.001. |
| [3] |
苏磊, 侯宇, 吴飞, 等. 轮足式机器人机构设计及越障性能分析[J].
机械设计与制造, 2016, 1(8): 46-48+53.
SU L, HOU Y, WU F, et al. Design and analysis of wheel foot type robot mechanism and the obstacle-surmounting performance[J]. Machinery Design & Manufacture, 2016, 1(8): 46-48+53. DOI: 10.3969/j.issn.1001-3997.2016.08.013. |
| [4] |
叶献伟, 陈樊, 高建华. 六足仿生机器人越障步态方法研究[J].
浙江理工大学学报, 2008, 25(5): 611-614.
YE X W, CHEN F, GAO J H. Obstacle-crossing gait research on hexapod robot[J]. Journal of Zhejiang Sci-Tech University, 2008, 25(5): 611-614. DOI: 10.3969/j.issn.1673-3851.2008.05.025. |
| [5] |
KALAMIAN N, FARROKHI M. Dynamic walking of biped robots with obstacles using predictive controller[C]//20111st International Econference on Computer and Knowledge Engineering (ICCKE). Iran, Mashhad: IEEE, 2011: 105-110.
|
| [6] |
ZHOU C X, WANG X, LI Z B, et al. Exploiting the redundancy for humanoid robots to dynamically step over a large obstacle[C]//2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Germany, Hamburg: IEEE, 2015: 1599-1604.
|
| [7] |
FU C L, CHEN K. Gait synthesis and sensory control of stair climbing for a humanoid robot[J].
IEEE Transactions on Industrial Electronics, 2008, 55(5): 2111-2120.
DOI: 10.1109/TIE.2008.921205. |
| [8] |
KOCH K H, MOMBAUR K, STASSE O, et al. Optimization based exploitation of the ankle elasticity of hrp-2 for overstepping large obstacles[C]//201414th IEEE-RAS International Conference on Humanoid Robots (Humanoids). Spain, Madrid: IEEE, 2014: 733-740.
|
| [9] |
GUAN Y H, NEO E S, YOKOI K, et al. Stepping over obstacles with humanoid robots[J].
IEEE Transactions on Robotics, 2006, 22(5): 958-973.
DOI: 10.1109/TRO.2006.878962. |
| [10] |
GUAN Y S, SIAN N E, YOKOI K. Motion planning for humanoid robots stepping over obstacles[C]//2005 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Canada, Edmonton: IEEE, 2005: 364-370.
|
| [11] |
GUAN Y S, YOKOI K, TANIE K. Feasibility: Can humanoid robots overcome given obstacles?[C]//2005 IEEE International Conference on Robotics and Automation (ICRA). Spain, Barcelona: IEEE, 2005: 1054-1059.
|
| [12] |
STASSE O, VERRELST B, VANDERBORGHT B, et al. Strategies for humanoid robots to dynamically walk over large obstacles[J].
IEEE Transactions on Robotics, 2009, 25(4): 960-967.
DOI: 10.1109/TRO.2009.2020354. |
| [13] |
于薇薇, SABOURIN C, MADANI K, 等. 基于adams和matlab联合仿真的双足机器人越障研究[J].
计算机测量与控制, 2008, 16(11): 1741-1743+1769.
YU W W, SABOURIN C, MADANI K, et al. Approach of biped robot to step over obstacle based on adams and matlab united simulation[J]. Computer Measurement & Control, 2008, 16(11): 1741-1743+1769. |
| [14] |
GUO F Y, MEI T, LUO M Z, et al. Motion planning for humanoid robot dynamically stepping over consecutive large obstacles[J].
Industrial Robot-an International Journal, 2016, 43(2): 204-220.
DOI: 10.1108/IR-08-2015-0157. |
| [15] |
DOUBLIEZ P F, BRUNEAU O, BEN OUEZDOU F. Dynamic obstacle crossing by a biped robot, based on control of the propulsion energy[C]//IEEE/RSJ 2010 International Conference on Intelligent Robots and Systems (IROS 2010). Taipei: IEEE, 2010: 3144-3149.
|
| [16] |
KOJIO Y, KARASAWA T, KOJIMA K, et al. Walking control in water considering reaction forces from water for humanoid robots with a waterproof suit[C]//2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2016). South Korea, Daejeon: IEEE, 2016: 658-665.
|
| [17] |
FARNIOLI E, GABICCINI M, BICCHI A. Toward whole-body loco-manipulation: Experimental results on multi-contact interaction with the walk-man robot[C]//2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2016). South Korea, Daejeon: IEEE, 2016: 1372-1379.
|
| [18] |
HUANG Z F, LIU B, WEI J P, et al. Jet-hr1: Two-dimensional bipedal robot step over large obstacle based on a ducted-fan propulsion system[C]//2017 IEEE-RAS 17th International Conference on Humanoid Robotics (Humanoids). UK, Birmingham: IEEE, 2017: 406-411.
|
| [19] |
杜玉红, 李兴, 赵地, 等. 仿人机器人越障步态控制研究[J].
中国工程机械学报, 2017, 15(1): 10-14.
DU Y H, LI X, ZHAO D, et al. Gait control on humanoid obstacle-crossing robots[J]. Chinese Journal of Construction Machinery, 2017, 15(1): 10-14. |
 2019, Vol. 36
2019, Vol. 36

