2. 广东海洋大学 机械与动力工程学院,广东 湛江 524088
2. School of Mechanical and Power Engineering, Guangdong Ocean University, Zhanjiang 524088, China
伴随着人工智能技术的飞速发展和广泛应用,模式识别和机器学习等基于数据处理的研究领域变得比以往任何时期都更具有重要意义,而分类是处理数据挖掘问题无法避免的基础操作[1]. 决策树是解决分类问题的一种经典算法,相比于神经网络、支持向量机和逻辑回归算法,决策树算法更容易理解和操作,尤其是在处理多分类问题和离散型数值分类问题中具有较高的自主学习能力和较低的先验知识要求,因而在很多领域都有着广泛的应用. 决策树算法是一种逼近离散值目标函数的方法,这种方法通过对训练集的学习,找到特定样本环境下样本类别属性和单个特征属性的集合关系,并提取出该特定环境和集合关系作为分类规则,把所有的分类规则构建为一棵决策树,从而达到预测模型的目的. 决策树方法以其速度快、精度高、生成的模式简单等优点,在数据挖掘中受到许多研究者和软件公司的关注[2].
单标签分类问题是一类典型的矛盾问题,因为样本不可能同时属于两种类别,因而造成了分类结果“是”与“不是”的单一描述,和“对”或“不对”的评价标准[3]. 可拓学是以矛盾问题为研究对象、以矛盾问题的智能化处理为主要内容、以可拓方法论为主要研究方法的一门学科,对矛盾问题的解决有着横跨哲学、数学和工程学领域的逻辑思维模式. 所以不同于其他学者从正确率、泛化能力和分类效率等方面对决策树进行分析和改进,从数学推导和计算的方式来评价该算法,文章尝试从可拓逻辑和可拓思维模式的角度对决策树分类算法的各个步骤进行逻辑和理论分析,从全新视角下验证决策树算法的可行性和优劣性,并根据可拓集理论以关联函数为参考,建立一套关于决策树分类结果的评价体系.
1 决策树算法简介决策树学习算法是一种归纳算法,它采用自上而下、阈值区分的方法将样本集划分为若干个互不相交的子集,并将每个子集按层层递进的规则提取出来作为一个分枝,并建立决策树,用来形成分类器和预测模型,可以对未知数据进行分类、预测和数据预处理等. 每一层选择哪个属性作为子节点,以及怎样对子节点进行分枝将决定决策树的规模和分类精度[2]. 设训练集为S,其类别集包含
Step1 把全体样本集作为根节点,计算所有属性的信息增益值,并找到信息增益值最大的属性作为分枝的子节点.
(1) 根据类别集划分样本集S所得信息熵为
| $I(C) = - \sum\limits_{i = 1}^k {{P_i}{{\log }_2}} {P_i}, $ | (1) |
其中,
(2) 假设所有样本的第
| $ E\left( {{A_m}} \right) = \sum\limits_{j = 1}^q {\frac{{\left| {{S_j}} \right|}}{{\left| S \right|}}I\left( {{C^j}} \right)} , $ | (2) |
| $I({C^j}) = - \sum\limits_{i = 1}^k {{p_{ij}}{{\log }_2}{p_{ij}}} , $ | (3) |
其中,
| ${\rm{Gain}}({A_m}) = I(C) - E({A_m}). $ | (4) |
(3) 属性
| ${\rm{Split}}({A_m}) = - \sum\limits_{j = 1}^q {\frac{{\left| {{S_j}} \right|}}{{\left| S \right|}}} \log \left(\frac{{\left| {{S_j}} \right|}}{{\left| S \right|}}\right). $ | (5) |
根据式(4)~(5)可得信息增益率
| ${\rm{Gain\_Ratio}}({A_m}) = \frac{{{\rm{Gain}}({A_m})}}{{{\rm{Split}}({A_m})}}. $ | (6) |
Step2 选择信息增益率最大的属性作为子节点对根节点进行分类,把样本集分为若干子集,然后采用与step1相同的方法递归地对子集进行分类,建立树的分枝,一直循环到所有分枝节点中的样本都属于同一类别,则该子节点就成为叶子节点,该分枝停止生长.
Step3 对构建好的决策树进行剪枝,消除噪声和孤立点等随机因素的影响,以得到简化的决策树,其中剪枝方法可分为预剪枝和后剪枝两种类型.
Step4 根据修剪好的决策树,提取分类规则,对新的样本进行逐层分类,一直到叶子结点,从而预测样本的类别.
2 可拓学视角下的决策树算法分析可拓学理论认为解决矛盾问题的工具是变换和推理,若不考虑事物的内涵和外延,就不能表达物、事、关系和特征变换以及变换所引起的其他物、事、关系和特征变换的传导变换. 所以可拓学处理矛盾问题的过程就是把物、事、关系看成是可以拓展的,并根据物、事、关系的可拓性,变换问题的目标或条件,使得目标得以实现[7].
决策树算法是解决分类问题这一典型矛盾问题的有效方法,其解决问题的过程符合可拓学处理矛盾问题的理论,样本的属性和类别就是事物的内涵,样本的属性和类别之间的关系就是事物的外延,而样本某一或某些属性值的变化导致类别发生变化,就是事物的传导变换. 文章从可拓思维模式中的菱形思维模式的角度分析决策树算法每个节点的选择,以可拓逻辑中基元变换理论来评价决策树算法的规则提取,以可拓逻辑中的基元发散规则来解释决策树算法的预测步骤,验证了决策树算法和可拓学理论的契合程度.
2.1 菱形思维模式菱形思维模式是一种先发散后收敛的思维方式,它包括了发散思维和收敛思维两个阶段. 利用菱形思维模式解决问题,首先对问题进行拓展分析,提出解决问题的尽可能多的信息和丰富资料,这个过程就是发散;然后从可行性、优劣性、相容性等角度出发对信息进行整合,向最佳的解决方案聚焦,这个过程就是收敛[8-10]. 在构建决策树的过程中,找到每个节点,即每个子集的最优的分类属性,我们要拓展出所有会影响分类效果的信息,不仅要考虑每个属性分类的精度和分类的集中度,为了构建更简单有效的决策树,还要考虑子集的类别复杂度和属性复杂度;在找到所有影响因素之后,还需要对这些因素进行综合考虑,使得决策树在精度和复杂度两个方面达到平衡. 利用可拓思维模式中的菱形思维模式来解决这一问题的模型如图1所示[11-12].
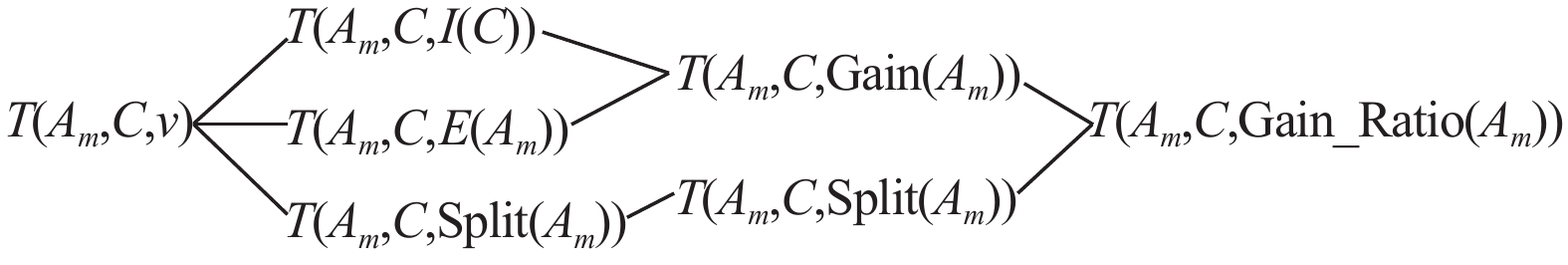
|
图 1 决策树的菱形思维模式 Figure 1 The rhombus thought model of Decision Tree |
在图1子集
(1) 在菱形思维模式的第一阶段进行发散思维,发现对分类效果有影响的因素有:根据类别集
(2) 在菱形思维模式的第二阶段进行收敛思维,根据式(4)把
(3) 在菱形思维模式的第三阶段继续对第二阶段的两个因素进行收敛思维,根据式(6)把
可拓逻辑不同于经典数理逻辑和模糊逻辑,是通过变换和推理将矛盾问题转换为不矛盾问题的逻辑思维方法. 在数理逻辑和模糊逻辑中,事物是否属于某种类别,命题为“真”或“假”是对立的,但在可拓逻辑中,由于引入了变换,事物属于某类别的程度或者说命题的“真假”程度是会随着事物某些属性的改变而改变的,比如性别“男”和“女”是对立的,但在生活中我们经常会有“很男人”或者某人比另外一人“更男人”的说法. 所以,数理逻辑是从静态的角度研究事物的特征和命题的真假,而可拓逻辑从变换的角度研究事物的动态和变化的特征[13].
决策树分类规则的提取是基于属性的分类方法,在每一个节点都根据该节点的属性,把具有相同属性值的样本分到同一个子集,然后在对所有子集使用同样的方法递归处理,直到子集里的样本全都属于同一类,则该分枝就是一个分类规则. 把样本看作基元,样本的属性和类别就是基元的要素,样本某一属性的取值不同可能会使得样本的类别不同,就相当于基元内部的某一属性要素的变化导致了类别要素的传导变换.
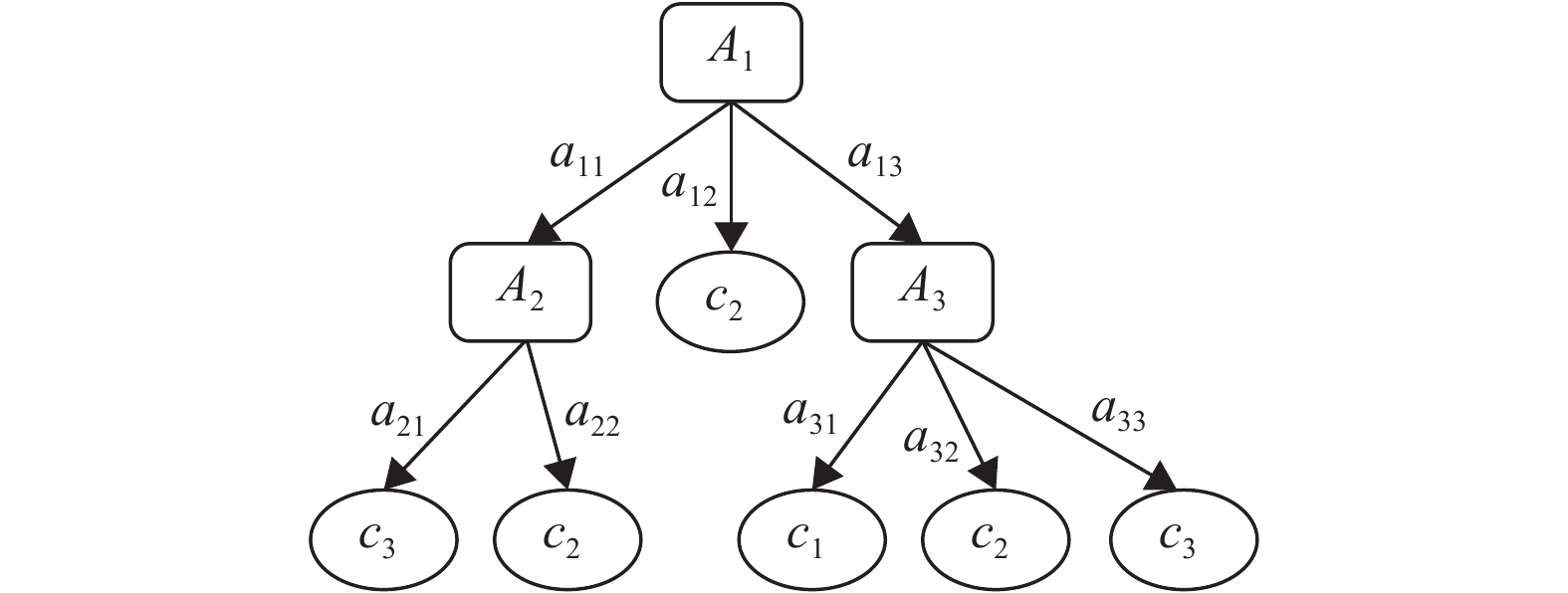
图2为一棵简单的决策树,首先根据属性
|
图 2 简单决策树 Figure 2 A simple decision tree |
根据可拓学基元变换的理论,图2决策树的分类规则可以理解为对于具有多个属性的基元,即使仅仅改变其中一个重要属性,也有可能会对基元的性质产生影响,而相反的,改变多个无关属性,也有可能对基元的性质没有影响. 文本将可拓化的样本
| $\begin{split} ({T_O}O \in C)\vDash& {(_O}{T_{{A_1}}}{A_1} = {a_{12}})\vDash\\ &((O, {A_1}, {a_{12}}) \in {c_1}), \end{split}$ | (7) |
即若基元O的
| $\begin{split} ({{T}_{O}}O=C)&\vDash \left( _{O}\left[ \begin{matrix} {{T}_{{{A}_{1}}}}{{A}_{1}} \\ {{T}_{{{A}_{2}}}}{{A}_{2}} \\ \end{matrix} \right]=({{a}_{11}},{{a}_{21}}) \right)\vDash \\ & \left( \left( \begin{array}{l} O,{{A}_{1}},{{a}_{12}} \\ \quad{{A}_{2}},{{a}_{21}} \\ \end{array} \right) \right)\in {{c}_{3}}, \end{split}$ | (8) |
即若基元O的
| $\begin{split} ({{T}_{O}}O=&C)\vDash \left( _{O}\left[ \begin{matrix} {{T}_{{{A}_{1}}}}{{A}_{1}} \\ {{T}_{{{A}_{3}}}}{{A}_{3}} \\ \end{matrix} \right]=({{a}_{13}},{{a}_{32}}) \right) \vDash\\ & \left( \left( \left[ \begin{matrix} O, & {{A}_{1}}, & {{a}_{13}} \\ {} & {{A}_{3}}, & {{a}_{32}} \\ \end{matrix} \right] \right)\in {{c}_{2}} \right). \end{split}$ | (9) |
对基元
决策树构建完成以后,就可以用来预测新样本的类别. 根据样本在决策树中根节点属性的取值,把样本划分到不同的子集,然后再根据子节点的属性取值继续划分,直到把样本划分到叶子结点,就得到样本类别的预测结果. 这种预测方法和可拓学中基元的发散过程推理是一致的. 基元发散是基元拓展推理中的一种,可以利用基元的发散推理,结合决策树的分类规则,对已知类别的样本进行发散,把某些属性和该已知样本的取值相同的未知样本分类到该类别中[14-15]. 如图2所示的决策树,根据训练得到的
| $\begin{split} S&\dashv \left\{ {{c}_{1}}|{S}'=\left[ \begin{matrix} O, & {{A}_{1}}, & {{a}_{12}} \\ {} & \cdots , & \cdots \\ \end{matrix} \right] \right\}\dashv \\ & \left\{ {{c}_{1}}|{S}''=\left[ \begin{matrix} O, & {{A}_{1}}, & {{a}_{13}} \\ {} & {{A}_{2}}, & * \\ {} & {{A}_{3}}, & {{a}_{31}} \\ {} & \cdots , & \cdots \end{matrix} \right] \right\}. \end{split}$ | (10) |
根据
| $\begin{split} S&\dashv \left\{ {{c}_{2}}|{S}'=\left[ \begin{matrix} O, & {{A}_{1}}, & {{a}_{11}} \\ {} & {{A}_{2}}, & {{a}_{22}} \\ {} & \cdots , & \cdots \end{matrix} \right] \right\}\dashv \\ & \left\{ {{c}_{2}}|{S}''=\left[ \begin{matrix} O, & {{A}_{1}}, & {{a}_{13}} \\ {} & {{A}_{2}}, & * \\ {} & {{A}_{3}}, & {{a}_{32}} \\ {} & \cdots , & \cdots \end{matrix} \right] \right\}. \end{split}$ | (11) |
在构建决策树的过程中,不同的分类规则也有可能得到同样的分类结果,如图2所示的决策树中,
当样本根据决策树的某一分枝的预测规则被预测为某一类别时,找到训练集中所有符合该规则的样本,求得其每个属性的平均取值,最大取值和最小取值,把每个属性都取平均值的样本视为该分枝的标准枝,把每个属性的最大值的和最小值的作为样本取值区间的上下限. 然后计算预测样本与标准枝的可拓距,以此来反映样本属于该类别的程度.
假设数据集中样本共有5个属性,其决策树规则如图2所示,某样本
| $\begin{gathered} {\rho _{{A_3}}}(S, {c_2}) = \left| {{a_3} - \frac{{{\partial _1}+{\partial _2}}}{2}} \right| - \frac{{{\partial _1} - {\partial _2}}}{2} - \left| {{a_3} - \bar \partial } \right|. \end{gathered} $ | (12) |
同理,该样本在属性
| $\begin{gathered} {\rho _{{A_4}}}(S, {c_2}) = \left| {{a_4} - \frac{{{\beta _1} + {\beta _2}}}{2}} \right| - \frac{{{\beta _1} - {\beta _2}}}{2} - \left| {{a_4} - \bar \beta } \right|, \end{gathered} $ | (13) |
| $\begin{gathered} {\rho _{{A_5}}}(S, {c_2}) = \left| {{a_5} - \frac{{{\lambda _1} + {\lambda _2}}}{2}} \right| - \frac{{{\lambda _1} - {\lambda _2}}}{2} - \left| {{a_5} - \bar \lambda } \right|. \end{gathered} $ | (14) |
根据式(12-14),把样本
| $\begin{gathered} \rho (S, {c_2}) = {\rho _{{A_3}}}(S, {c_2}) + {\rho _{{A_4}}}(S, {c_2}) + {\rho _{{A_5}}}(S, {c_2}). \end{gathered} $ | (15) |
可拓距越小,则表示该样本属于
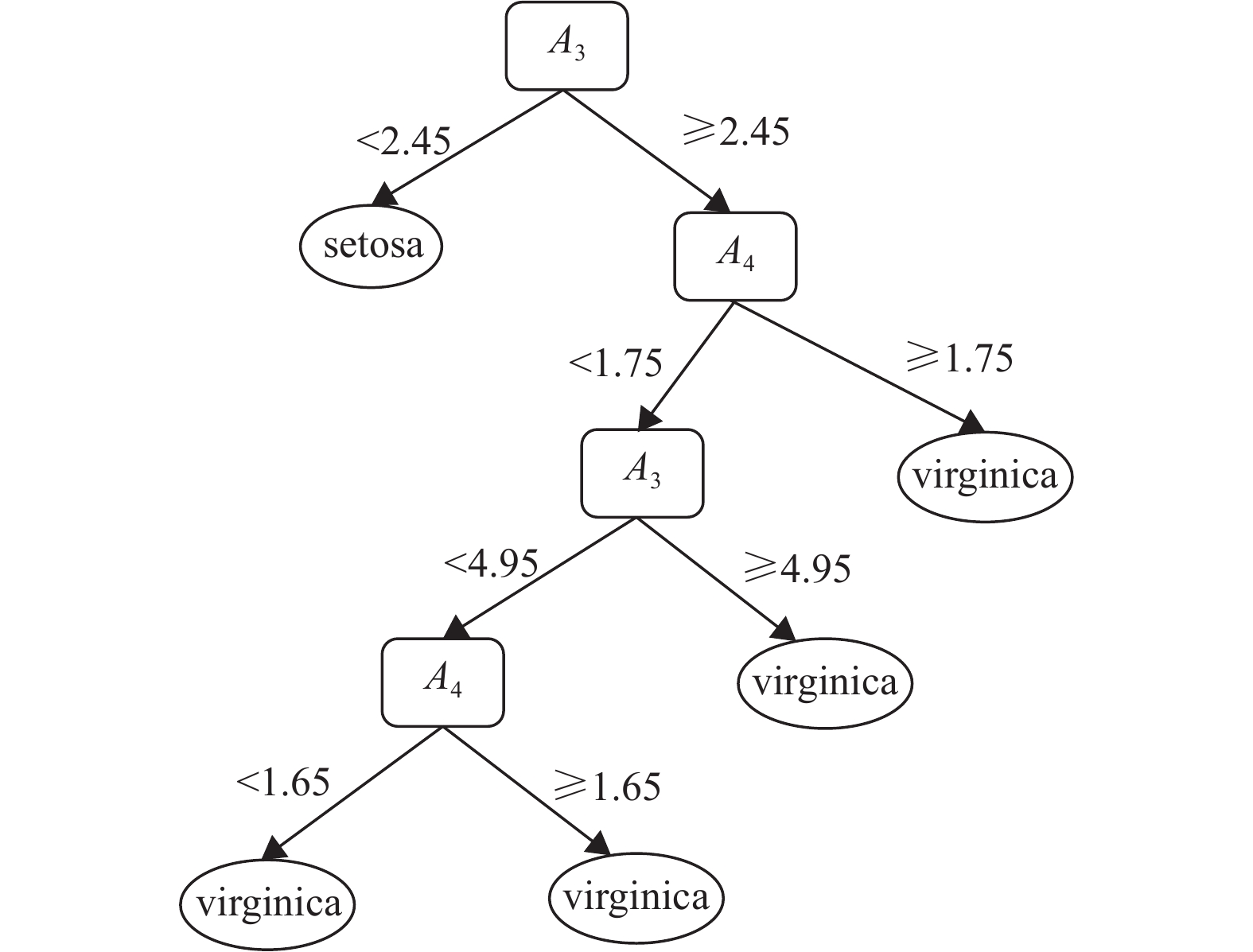
若样本的特征量化值是连续的,需要对某分枝上所有样本找到每个属性的最大值和最小值,并求得平均值,作为该分枝的标准枝. 以fisher iris数据为例,我们建立一套基于可拓距的决策树分类评价体系,因为该数据的特征量化值是连续的,因此得到如图3所示的二叉树.
|
图 3 fisher iris的决策树 Figure 3 Tree of fisher iris |
以图3中
| $\begin{array}{l} \rho (S, {\rm{virginica}}) = \\ (\left| {{a_1} - \displaystyle\frac{{7.9+5.6}}{2}} \right| - \displaystyle\frac{{7.9 - 5.6}}{2} - \left| {{a_1} - 6.626\;1} \right|)+ \\ (\left| {{a_2} - \displaystyle\frac{{3.8+ 2.5}}{2}} \right| - \displaystyle\frac{{3.8 - 2.5}}{2} - \left| {{a_2} - 3.017\;4} \right|)+ \\ (\left| {{a_3} - \displaystyle\frac{{6.9+4.8}}{2}} \right| - \displaystyle\frac{{6.9 - 4.8}}{2} - \left| {{a_3} - 5.573\;9} \right|)+ \\ (\left| {{a_4} - \displaystyle\frac{{2.5+1.8}}{2}} \right| - \displaystyle\frac{{2.5 - 1.8}}{2} - \left| {{a_4} - 2.073\;} \right|). \end{array} $ |
可拓学以形式化的模型,探讨事物拓展的可能性以及开拓创新的规律与方法,并用于解决矛盾问题,其理论价值或应用价值在各个领域都能得到体现. 本文以可拓学的视角去解析决策树分类算法的逻辑推理过程,不仅证明了决策树算法和可拓学理论的契合性,还对决策树算法的预测结果建立基于可拓距的评价标准.
| [1] |
拉维 莱美, 阿卡里氏 阿帕德, 尼噶. 人类行为解释与转换系统的多通道进化框架研究[J].
广东工业大学学报, 2016, 33(2): 5-14.
RAVI LIMAYE, AKHILESH UPADHYAY, NIGAM S R. Evolving multimodal frameworks for human behavior interpretation and transformation system[J]. Journal of Guangdong University of Technology, 2016, 33(2): 5-14. DOI: 10.3969/j.issn.1007-7162.2016.02.002. |
| [2] |
罗良维, 杨春燕. 基于基因可拓模块化设计的陶瓷物流包装设计研究[J].
广东工业大学学报, 2015, 32(2): 11-16.
LUO L W, YANG C Y. Study on ceramic logistics packaging design based on gene extension modular design[J]. Journal of Guangdong University of Technology, 2015, 32(2): 11-16. |
| [3] |
朱弘扬, 高红, 刘巍, 等. 可拓AdaBoost算法对预测结果的改进[J].
辽宁工程技术大学学报(自然科学版), 2016, 35(9): 993-997.
ZHU H Y, GAO H, LIU W, et al. Extenics AdaBoost for modifying the prediction of classification algorithm[J]. Journal of Liaoning Technical University (Natural Science), 2016, 35(9): 993-997. |
| [4] |
MASZCZYK T, DUCH W. Comparison of Shannon, Renyi and Tsallis entropy used in decision trees[C]//International Conference on Artificial Intelligence and Soft Computing.[s.n.]: Springer, 2008: 643−651.
|
| [5] |
HAYKIN S. Neural networks and learning machines[M]. Beijing: China Machine Press, 2009: 1−7.
|
| [6] |
余志伟, 李兴森. 基元库构建模型及其应用研究[J].
广东工业大学学报, 2015, 32(3): 5-9.
YU Z W, LI X S. Modeling of basic-element and its application[J]. Journal of Guangdong University of Technology, 2015, 32(3): 5-9. DOI: 10.3969/j.issn.1007-7162.2015.03.002. |
| [7] |
杨春燕, 蔡文. 可拓学[M]. 北京:科学出版社, 2014.
|
| [8] |
郭强, 邹广天. 基于决策树分类的可拓建筑策划预测方法[J].
智能系统学报, 2017, 12(1): 117-123.
GUO Q, ZOU G T. Prediction methods for extension architecture programming based on decision tree classification[J]. CAAI Transactions on Intelligent Systems, 2017, 12(1): 117-123. |
| [9] |
陈晓华, 刘大莲, 田英杰, 等. 可拓支持向量分类机[J].
智能系统学报, 2018(1): 147-151.
CHEN X H, LIU D L, TIAN Y J, et al. Extension support vector classification machine[J]. CAAI Transactions on Intelligent Systems, 2018(1): 147-151. |
| [10] |
郭韧, 李红, 陈福集. 基于可拓聚类的网络舆情演化预测研究[J].
情报理论与实践, 2017(1): 83-87.
|
| [11] |
DING Y, GAO H, LIU W. A personalized recommendation algorithm based on Extenics[C]// The International Symposium on Extenics and Innovation Methods. Beijing: CAAI, 2013.
|
| [12] |
杨春燕, 蔡文. 基于可拓学的创意生成与生产研究[J].
广东工业大学学报, 2016, 33(1): 12-16.
YANG C Y, CAI W. Generating creative ideas for production based on Extenics[J]. Journal of Guangdong University of Technology, 2016, 33(1): 12-16. DOI: 10.3969/j.issn.1007-7162.2016.01.002. |
| [13] |
弗罗仁汀 司马仁达齐. 可拓逻辑与中智逻辑的内在关联初探[J].
广东工业大学学报, 2014, 31(4): 1-5.
FLORENTIN S. Connections between extension logic and refined neutrosophic logic[J]. Journal of Guangdong University of Technology, 2014, 31(4): 1-5. DOI: 10.3969/j.issn.1007-7162.2014.04.001. |
| [14] |
王丰, 顾佼佼, 孙江, 等. 传导过程元与过程元可拓集及其工程应用[J].
广东工业大学学报, 2018, 35(5): 1-4.
WANG F, GU J J, SUN J, et al. Transmission process element and process element Extension set and its engineering application[J]. Journal of Guangdong University of Technology, 2018, 35(5): 1-4. |
| [15] |
范锐, 颜思伟, 彭中煌, 等. 可拓策略生成软件架构及其应用研究[J].
广东工业大学学报, 2017, 34(2): 1-5.
FAN R, YAN S W, PENG Z H, et al. A research on software architecture and its application for ESGS[J]. Journal of Guangdong University of Technology, 2017, 34(2): 1-5. DOI: 10.12052/gdutxb.160146. |
| [16] |
鄞汉藩, 周彦, 韩丽平, 等. 特征分析与可拓创新四步法在发明专利法律保护中的运用[J].
广东工业大学学报, 2017, 34(2): 12-16.
YIN H F, ZHOU Y, HAN L P, et al. Feature analysis and application of the four-step Extenics innovation method in patent law protection of the inventions[J]. Journal of Guangdong University of Technology, 2017, 34(2): 12-16. DOI: 10.12052/gdutxb.160143. |
 2019, Vol. 36
2019, Vol. 36

