TRIZ(Theory of Inventive Problem Solving)和可拓学均是当今重要的创新方法。TRIZ由苏联的Genrich Altshuller于1946年所创立,主要用于解决工程矛盾问题[1];可拓学由我国著名学者蔡文于1983年创立,是致力于解决矛盾冲突问题的原创新横断学科,被认定成为人工智能下的二级学科[2]。二者均以矛盾问题作为研究对象,并给出了比较成熟的矛盾问题解决理论和方法体系。
有研究学者发现单一设计理论存在较大局限性,并察觉出TRIZ和可拓学存在的某些异同点,认为二者的理论和应用具有很好的互补作用[3]。同时随着创新方法研究与应用的发展,人们开始着力研究不同创新方法的融合应用。TRIZ和可拓学的融合机制研究正是在这个背景下产生的,研究内容主要包括理论差异对比、模型转换、融合机制以及理论应用。
自2004年开始,才逐渐有学者将TRIZ理论与可拓方法融合起来研究,如张祥唐等[4]采用可拓方法与TRIZ方法来进行产品创新设计,仇成等[5]进行了TRIZ理论与可拓学的比较研究,宋守许等[6]进行了融合可拓与TRIZ理论的可拆卸性结构设计方法及应用研究,李苏洋等[7]也将TRIZ与可拓学融合应用到结构或方案设计中,江帆等[8]研究融合两种创新方法的集成创新方法,并将研究成果应用在手推车的改进设计中,周贤永等[9]研究了TRIZ 40条发明原理的可拓变换表达形式、格论与TRIZ技术进化理论融合的理想化水平表达方式。
现阶段所提出的TRIZ理论与可拓学的结合求解方式通常是顺次使用,如先采用可拓学方法分析问题并获得矛盾,再由TRIZ理论求解矛盾。顺次使用方式流程固定,不够灵活,无法处理复杂问题,而且没有使用可拓学中的拓展和变换方法,两种方法的结合不够深入。
1 TRIZ与可拓学融合方法研究 1.1 TRIZ理论冲突求解流程TRIZ解决问题的过程包含4个步骤:定义问题、分析问题、分析解以及选择最优解。定义问题指将待解决问题转化为问题模型;分析问题指针对不同问题模型,应用相应的TRIZ求解工具。分析解则指将上一步获得的解决方案转化为领域解,并在最后一步进行解的筛选及择优。
TRIZ有4种问题模型:技术矛盾、物理矛盾、物质−场模型、知识与效应库。针对这4种问题模型,TRIZ提供了相应的求解工具:矛盾矩阵、分离原理、76个标准解、标准解法系统。其中,以技术矛盾和物理矛盾模型的应用最为普遍,二者被一同归纳在TRIZ矛盾问题求解体系中,其求解流程如图1所示。

|
图 1 TRIZ理论矛盾求解流程 Figure 1 TRIZ theoretical contradiction solving process |
矛盾矩阵主要用于解决技术系统中两个参数之间存在相互制约的矛盾问题,即技术矛盾。分离原理主要用于解决技术系统中某一个参数无法满足子系统内具有相反要求的矛盾问题,即物理矛盾。
1.2 可拓学求解流程可拓学的求解流程相对固定,主要通过4个步骤获得解决方案,包括建立模型、拓展分析、可拓变换和优度评价。其分析求解过程通过符号化、模型化的描述和运算等操作实现,具有可操作性强的特点,便于人和计算机利用程序提出解决问题的方案。
拓展解决的是创意从何而来的问题。通过4种拓展方法,对问题的目标或条件进行拓展,能够找到解决矛盾问题的创意。拓展分析是可拓变换的前提,提供了变换的路径。
变换是把一个对象变为另一个对象或者分解为若干对象,是实现创新或获得解决矛盾问题的创意的关键。通过变换及其运算,可以得到多种方案。
优度评价法是可拓学中评价一个对象,包括事物、策略、方法等的优劣的基本方法。本文通过计算来定量判别各个方案的优度,从而选择出合适的方案。
1.3 融合TRIZ与可拓学的求解流程TRIZ相对成熟,应用广泛。但TRIZ理论的问题通解具体化时通常需要深厚的领域背景知识。另外,TRIZ理论没有严格的形式化描述,在计算机上实现比较困难。可拓学相对于TRIZ理论,其研究的矛盾更具一般性,并在研究对象和研究目标上具有更为宽广和系统化的理论基础,易于计算机实现[10]。TRIZ和可拓学在问题解决流程上存在相似性,若将二者结合,发挥各自的优势,将有利于提升复杂问题的求解效率[11]。本文结合TRIZ解决问题的实用性和可拓学分析问题的规范性和可操作性,提出一种二者的结合求解方法。该方法的基本思路为:将问题的解决过程流程化为问题描述、问题分析、问题求解和方评价4个阶段,各阶段优先使用可拓学的工具,而将TRIZ作为拓展思路的辅助工具。
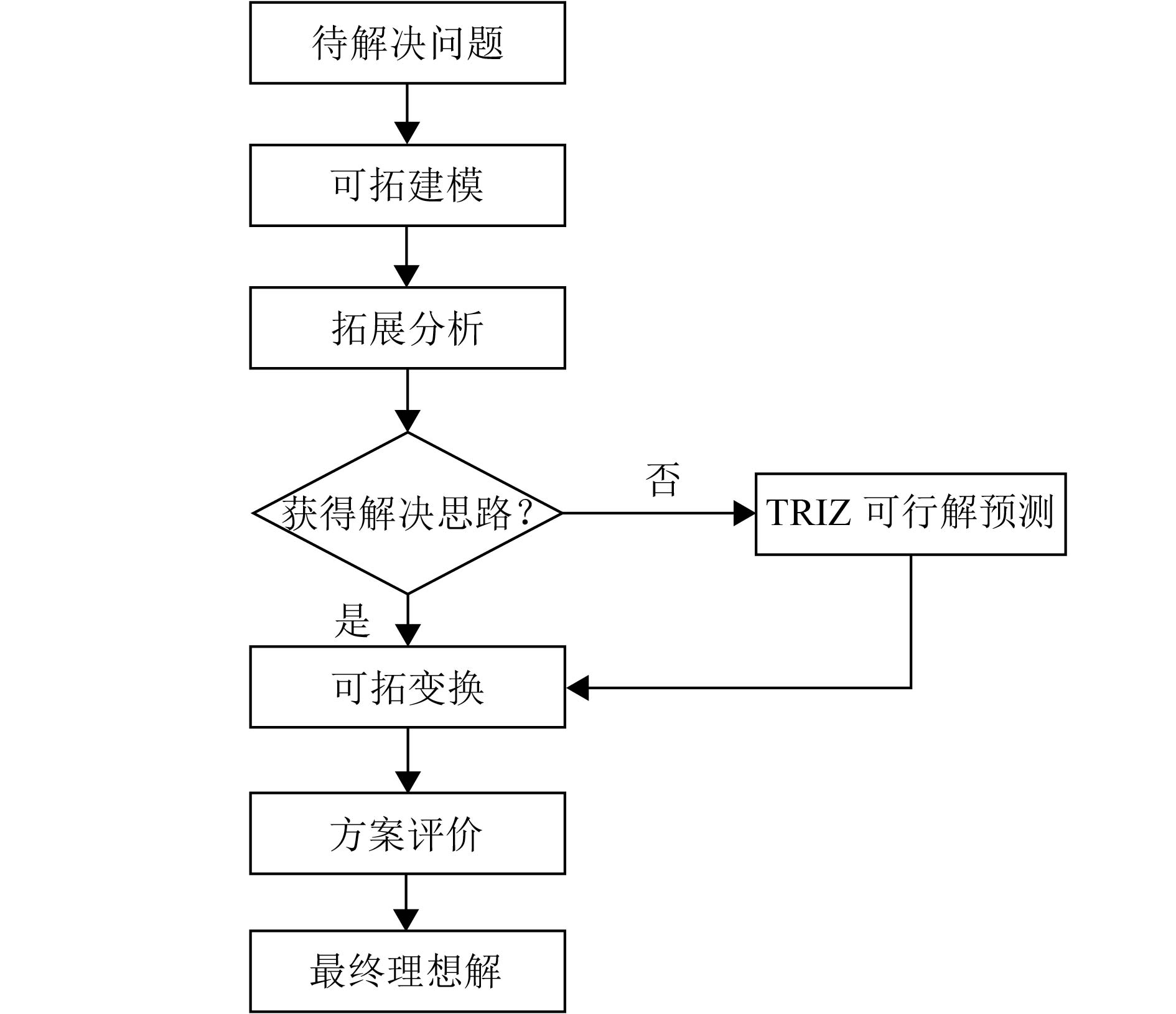
其基本流程包括:在问题描述阶段,主要针对待解决问题,利用可拓基元模型进行矛盾的分析和提取,并归纳问题类别[12];接着,尝试使用可拓学的拓展分析获得解决问题的思路,若直接使用可拓学的基元变换很难获得有效的可能解,则寻求TRIZ创新原理中的工具对问题进行可行解的预测,再根据TRIZ原理解的提示,进行可行解的基元变换[13];最后进行方案的优度评价,以获得方案的最终理想解。TRIZ在该求解流程中的任务是在拓展分析的基础上进行可行解预测。其解决问题的流程如图2所示。
|
图 2 融合方法解决问题的流程 Figure 2 Process of fusion method solving the problem |
在铸件清理中,铸件的磨削占了很大比重,对铸件的质量起到非常关键的作用。现有的盘类铸件磨削设备,主要是单机小功率圆盘磨削设备,只能对圆盘的端面进行磨削,需要配合其他打磨工具才能完成圆盘的整个磨削工艺,如图3所示。若要进行盘类铸件自动磨削工作,则打磨设备一般需采用打磨流水线原理设计,这种做法提高了清理效率和自动化程度,但设备复杂度和成本却大幅增加。

|
图 3 单机圆盘打磨设备示意图 Figure 3 Schematic diagram of single disc grinding equipment |
打磨方案设计的最终期望目标为简化铸件清理流程,提高自动化程度,而现有的打磨设备只能磨削铸件的端面,内表面则通过人工打磨实现。先对该问题进行可拓基元建模。
设盘类零件待打磨端面面积占总的待打磨面积的60%。改进前打磨设备只能打磨端面,则清理效率为0.6。根据可拓学形式化描述,其条件物元为
| $L = \left[ {\begin{array}{*{20}{c}} {\text{打磨设备},}& {\text{磨具类型},}& {\text{砂轮}}\\ {}& {\text{磨削方式},}& {\text{端面}}\\ {}& {\text{清除效率},}&{0.6} \end{array}} \right],$ |
目标事元为
| $G = \left[ {\begin{array}{*{20}{c}} {\text{提高},}& {\text{支配对象},}& {\text{清理效率}}\\ {}& {\text{接受对象},}& {\text{打磨设备}}\\ {}& {\text{程度},}&{1} \end{array}} \right],$ |
则该问题属于一个不相容问题,可以描述为
| $P = G*L.$ |
应用发散树,对“磨削设备”进行分析,以生成解决问题的思路。根据“一特征多量值”的发散分析原理[14],按照磨削设备的磨具类型进行发散分析得
| $ L\dashv\left\{ \begin{array}{l} L_1 = \left[ {\begin{array}{*{20}{c}} {\text{磨削设备},}& {\text{磨具类型},}& {\text{砂带}}\\ {}& {\text{磨削方式},}& {\text{外表面}}\\ {}& {\text{清理效率},}&{0.6} \end{array}} \right],\\ L_2 = \left[ {\begin{array}{*{20}{c}} {\text{磨削设备},}& {\text{磨具类型},}& {\text{抛光头}}\\ {}& {\text{磨削方式},}& {\text{内表面}}\\ {}& {\text{清理效率},}&{0.4} \end{array}} \right],\\ L_3 = \left[ {\begin{array}{*{20}{c}} {\text{磨削设备},}& {\text{磨具类型},}& {\text{改进抛光头}}\\ {}& {\text{磨削方式},}& {\text{内、外表面}}\\ {}& {\text{清理效率},}&{1} \end{array}} \right]. \end{array} \right. $ |
根据发散结果,可作如下变换:
(1)
(2)
(3)
(4)
(5)
(6)
T3变换,指使用一种改进的抛光头,其柱面和底面都能够用于磨削,因此,磨削设备可以磨削盘类铸件的内外缘,现将该方案记为A1,方案A1的改进抛光头工作原理如图4所示。T4变换结果不能实现端面和内圆的磨削。而经过T5或T6的变换后,磨削设备同时具备磨削端面和内圆的磨抛工具,将这两个方案分别记为A2和A3。
2.3 基于TRIZ创新原理进一步拓展思维经过上一步拓展和变换,获得A1、A2、A3 3种方案。其中方案A2和A3均需增设另一套主轴设备,系统复杂性增加。在TRIZ中,当改善技术系统某一特性时,引起系统另一特性的恶化,这种矛盾被定义为技术矛盾。因此,可尝试使用TRIZ矛盾矩阵求解该技术矛盾[15]。通过对上述不相容问题模型分析,提取出一个矛盾:如果提高打磨设备的自动化程度,则会导致打磨系统复杂性增大。

|
图 4 改进打磨头示意图 Figure 4 Sketch map for improving grinding head |
将该冲突采用标准参数描述[11]。待改善的参数为:自动化程度(38号);导致恶化的参数为:系统的复杂性(36号)。
根据上一步得到的改善参数和恶化参数,查询经典的TRIZ矛盾矩阵表,得到3个推荐的发明原理,分别为:15号动态化原理;24号中介物原理;10号预操作原理。矛盾矩阵简表如表1所示。
| 表 1 矛盾矩阵简表 Table 1 Contradiction matrix |
这些发明原理具体内容如下:
15号动态化原理:(1) 改变物体的性质或外部环境,使其工作的每一阶段都取得最佳效果;(2) 将物体分成彼此相对移动的几个部分;(3) 使不动的物体成为可动的。
24号中介物原理:(1) 利用可以迁移或有传送作用的中间物体;(2) 把另一个(易分开的)物体暂时附加给某一物体。
10号预操作原理:(1) 预先完成要求的作用(整个的或部分的),如加工成半成品;(2) 预先将物体安放妥当,使它们能在现场和所需地点立即完成需要的功能。
根据TRIZ原理——动态化原理的提示,现考虑能否在不引入另一套动力设备的条件下,增加打磨工具的功能,使之既能够加工盘类零件端面,又能够加工内表面。为了能够同时加工盘类零件的不同部位,打磨工具应能够变换工具头,以适应不同部位的打磨。而打磨工具头是固定在安装架上的,因此可对打磨头的安装架进行变换,即
| $M = \left[ {\begin{array}{*{20}{c}} {\text{安装架},}& {\text{工具种类},}& {1}\\ {}& {\text{位置},}& {\text{夹具上方}}\\ {}& {\text{状态},}& {\text{固定}} \end{array}} \right].$ |
可做置换变换T2,使
| ${T_2}M = {M'},$ |
其中,
| $T_2 = \left[ {\begin{array}{*{20}{c}} {\text{置换},}& {b_1,}& {M}\\ {}& { {b_2},}& {M}\\ \end{array}} \right],$ |
| $M' = \left[ {\begin{array}{*{20}{c}} {\text{安装架},}& {\text{工具种类},}& {2}\\ {}& {\text{位置},}& {\text{工件上方}}\\ {}& {\text{状态},}& {\text{可动}} \end{array}} \right].$ |
根据基元要素间的传导变换,安装架的变换将导致打磨设备发生传导变换,于是有
| $L_7 = \left[ {\begin{array}{*{20}{c}} {\text{磨削设备},}& {\text{磨具类型},}& {M'}\\ {}& {\text{磨削方式},}& {\text{内外缘}}\\ {}& {\text{清理效率},}&{1} \end{array}} \right].$ |
最终获得了一种新的方案A4,即将磨削刀具的安装架设计成可动的,能够根据需要变换磨削刀具。改进后的打磨机构能够打磨盘类铸件的端面及内表面,简化了铸件清理工序。
打磨机构的三维模型如图5所示,图5(a)为端面打磨工况;图5(b)为内表面打磨工况。其安装架位于导轨上的平台,并且本身可以相对平台进行旋转,以切换打磨工具。安装架上的砂轮和抛光头,共用一套主轴,解决了打磨设备的自动化和系统复杂性之间的矛盾。
2.4 优度评价根据分析共获得4种解决方案。方案A1使用一种改进的抛光头;方案A2和方案A3均使用两套主轴,为磨削内缘和外缘的刀具提供动力;方案A4使用一种可切换磨削装置的安装架。4种方案的清理效率均符合要求,现采用优度评价进行择优。
(1) 确定衡量条件.
选择打磨方案的简便性c1、可靠性c2和成本c3 3个因素作为衡量条件,得衡量条件集:
| $O = \{ ({c_1},{V_1}),({c_2},{V_2}),({c_3},{V_3})\} ,$ |
其中,
(2) 确定权系数.
采用AHP法,根据各因素重要程度的差别,确定两两因素间的相互比率,使用1-9比率标度法。由于装置的可靠性比其他两个因素明显重要,装置的成本比装置的简便性略重要[16],因此采用AHP法构造出的判别矩阵H为
| $H = \left[ {\begin{array}{*{20}{c}} 1&5&3 \\ {1/5}&1&{1/5} \\ {1/3}&5&1 \end{array}} \right].$ |
采用AHP的和积法求得权系数
| $\alpha = (0.607\;00,\;0.089\;65,\;0.303\;34).$ |
(3) 建立关联函数,计算规范关联度.
设装置的简便性、可靠性和质量的量级均在1~5级,则可建立简单的离散型关联函数
| ${K_i}\left( x \right) = \left\{ \begin{array}{l} 5,x= {\text{极简便/极可靠/极低}};\\ 4,x= {\text{简便/可靠/低}};\\ 3,x= {\text{一般}};\\ 2,x= {\text{复杂/不可靠/高}};\\ 1,x= {\text{极复杂/极不可靠/极高}}. \end{array} \right.$ |

|
图 5 改进的单机圆盘打磨设备示意图 Figure 5 Schematic diagram of improved single disc grinding equipment |
比较4种方案:对于指标c1,方案A2和A3均安装两套主轴设备,结构复杂;方案A1使用同一工具打磨内外缘,极简便;A4简便性一般。故有
综上所述,方案A1、A2、A3和A4关于衡量指标:简便性c1、可靠性c2和成本c3的关联度分别为
| $ \begin{array}{*{20}{c}} {{K_{{c_1}}} = \left( {{K_{{c_1}}}({O_{\rm{1}}}),{K_{{c_1}}}({O_2}),{K_{{c_1}}}({O_{\rm{3}}}),{K_{{c_1}}}({O_{\rm{4}}})} \right) = \left( {{\rm{5}},2,1,3} \right),}\\ {{K_{{c_{\rm{2}}}}} = \left( {{K_{{c_{\rm{2}}}}}({O_{\rm{1}}}),{K_{{c_{\rm{2}}}}}({O_2}),{K_{{c_{\rm{2}}}}}({O_{\rm{3}}}),{K_{{c_{\rm{2}}}}}({O_{\rm{4}}})} \right) = \left( {{\rm{3}},5,5,4} \right)},\\ {{K_{{c_{\rm{3}}}}} = \left( {{K_{{c_{\rm{3}}}}}({O_{\rm{1}}}),{K_{{c_{\rm{3}}}}}({O_2}),{K_{{c_{\rm{3}}}}}({O_{\rm{3}}}),{K_{{c_{\rm{3}}}}}({O_{\rm{4}}})} \right) = \left( {{\rm{5}},1,1,3} \right).} \end{array} $ |
根据规范关联度公式
| ${k_i}({O_j}) = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{{K_i}({O_j})}}{{\mathop {\max }\limits_{x \in {X_0}} {K_i}(x)}},{K_i}({O_j}) > 0} ,\\ {\dfrac{{{K_i}({O_j})}}{{\mathop {\max }\limits_{x \notin {X_0}} {K_i}(x)}},{K_i}({O_j}) < 0,} \end{array}} \right.$ |
则它们的规范关联度分别为
| $\begin{split} & {k_{{c_1}}} = (1,0.25,0.2,0.6) , \\ & {k_{{c_2}}} = (0.6,1,1,0.8), \\ & {k_{{c_3}}} = (1,0.2,0.2,0.6) . \end{split} $ |
(4) 计算优度.
各方案关于衡量条件O的规范关联度为
| $\begin{split} & K({O_1}) = {\left( {1,0.6,1} \right)^{\rm{T}}} , \\ & K({O_{2}}) = {\left( {0{{.25}},{1},0{{.2}}} \right)^{\rm{T}}} , \\ & K({O_{3}}) = {\left( {0{{.2}},{1},0{{.2}}} \right)^{\rm{T}}} , \\ & K({O_{4}}) = {\left( {0{{.6}},0.{{8}},0{{.6}}} \right)^{\rm{T}}} , \end{split} $ |
因此,各方案的优度分别为
| $\begin{gathered} C({O_1}) = \alpha K({O_1}) = 0{{.964\;1}}, \\ C({O_{2}}) = \alpha K({O_2}) = 0{{.302\;1}} , \\ C({O_{3}}) = \alpha K({O_3}) = 0{{.271\;7}} , \\ C({O_{4}}) = \alpha K({O_4}) = 0{{.617\;9}} . \end{gathered} $ |
由于
(1) 通过对TRIZ理论和可拓学的融合机制研究,得到了解决矛盾问题的一般方法:利用可拓学分析矛盾,归纳问题类型;基于TRIZ相应的解决工具进行可行解预测,得到可行的原理解;结合设计问题的实际背景,实施可行的基元变换;运用优度评价方法对各方案进行比较分析,得到最理想的解决方案。
(2) 采用融合可拓学与TRIZ的方法对盘类铸件打磨设备进行分析和改进设计,方便地获得了理想的解决方案。证明了TRIZ理论和可拓方法的融合能够提升设计问题求解时的效率和求解稳定性。
(3) 在问题求解的4个阶段,优先使用可拓学的工具,虽在求解效率上不是最优的,但其简化了TRIZ与可拓学的结合使用。若能够为每个求解阶段制定一种选择机制,将进一步提高问题解决的效率,这是后续研究的重点。
| [1] |
SAVRANSKY S D. Engineering of Creativity[M]. Boca Raton: Crc Press, 2002.
|
| [2] |
杨春燕,蔡文. 可拓学[M]. 北京: 科学出版社, 2014.
|
| [3] |
江帆. TRIZ与可拓学比较及融合机制研究[M]. 北京: 北京理工大学出版社, 2015.
|
| [4] |
张祥唐, 陈家豪. 可拓方法与TRIZ方法在产品创新设计上的应用[J].
工业工程, 2004, 7(2): 33-37.
ZHANG X T, CHEN J H. Application of extension method and TRIZ method in product innovation design[J]. Industrial Engineering, 2004, 7(2): 33-37. DOI: 10.3969/j.issn.1007-7375.2004.02.010. |
| [5] |
仇成, 冯俊文, 郭春明. TRIZ与可拓学的较研究[J].
工业技术经济, 2007, 26(10): 105-107.
QIU C, FENG J W, GUO C M. A comparative study of TRIZ and Extension[J]. Industrial Technology Economy, 2007, 26(10): 105-107. DOI: 10.3969/j.issn.1004-910X.2007.10.029. |
| [6] |
宋守许, 袁小鹤, 刘涛, 等. 基于可拓与TRIZ理论的可拆卸性结构设计方法及应用[J].
机械设计与制造, 2011(10): 61-63.
SONG S X, YUAN X H, LIU T, et al. Design method and application of detachable structure based on extension and TRIZ theory[J]. Mechanical Design and Manufacturing, 2011(10): 61-63. DOI: 10.3969/j.issn.1001-3997.2011.10.025. |
| [7] |
李苏洋, 杨春燕, 张晓伟, 等. 运用可拓学与TRIZ方法解决矛盾问题[J].
广东工业大学学报, 2013, 30(1): 7-12.
LI S Y, YANG C Y, ZHANG X W, et al. Using Extension and TRIZ to solve contradictions[J]. Journal of Guangdong University of Technology, 2013, 30(1): 7-12. DOI: 10.3969/j.issn.1007-7162.2013.01.002. |
| [8] |
江帆, 方伟中, 岳鹏飞, 等. 基于TRIZ与可拓学的半自动手推叉车设计[J].
广州大学学报(自然科学版), 2016, 15(2): 76-80.
JIANG F, FANG W Z, YUE P F, et al. Semi-automatic forklift truck design based on TRIZ and Extenics[J]. Journal of Guangzhou University (Natural Science Edition), 2016, 15(2): 76-80. |
| [9] |
周贤永, 陈光. TRIZ40条发明原理的可拓变换表述形式研究[J].
科技进步与对策, 2011, 28(5): 107-115.
ZHOU X Y, CHEN G. Research on Extension transform form of 40 invention principles of TRIZ40[J]. Science & Technology Progress and Policy, 2011, 28(5): 107-115. DOI: 10.3969/j.issn.1001-7348.2011.05.023. |
| [10] |
江帆, 杨鹏海. TRIZ理论与可拓学的融合方法研究[J].
广州大学学报(自然科学版), 2014, 13(6): 59-64.
JIANG F, YANG P H. Research on the fusion method of TRIZ theory and extenics[J]. Journal of Guangzhou University (Natural Science Edition), 2014, 13(6): 59-64. |
| [11] |
蔡文, 杨春燕, 何斌. 可拓学研究中的若干问题[J].
广东工业大学学报, 2001, 18(1): 1-5.
CAI W, YANG C Y, HE B. Some problems in extension studies[J]. Journal of Guangdong University of Technology, 2001, 18(1): 1-5. DOI: 10.3969/j.issn.1007-7162.2001.01.001. |
| [12] |
李延伟, 王璐, 王芳. 基于可拓的E-SURF图像识别算法[J].
计算机应用与软件, 2014, 31(7): 221-225.
LI Y W, WANG L, WANG F. Extension-based E-SURF image recognition algorithm[J]. Computer Applications and Software, 2014, 31(7): 221-225. DOI: 10.3969/j.issn.1000-386x.2014.07.056. |
| [13] |
杨春燕, 蔡文. 可拓集中关联函数的研究进展[J].
广东工业大学学报, 2012, 29(2): 7-14.
YANG C Y, CAI W. Research progress of extension set association function[J]. Journal of Guangdong University of Technology, 2012, 29(2): 7-14. DOI: 10.3969/j.issn.1007-7162.2012.02.002. |
| [14] |
谢蓝, 曾韬, 余永权, 等. 可拓检测的可拓变换机理[J].
计算机工程与应用, 2011, 47(5): 149-151.
XIE L, ZENG T, YU Y Q, et al. Extension transformation mechanism of extension detection[J]. Computer Engineering and Application, 2011, 47(5): 149-151. DOI: 10.3778/j.issn.1002-8331.2011.05.044. |
| [15] |
杨春燕, 蔡文. 可拓工程[M]. 北京: 科学出版社, 2007.
|
| [16] |
张雷, 彭宏伟, 刘志峰, 等. 绿色产品概念设计中的知识重用[J].
机械工程学报, 2013, 49(7): 72-79.
ZHANG L, PENG H W, LIU Z F, et al. Knowledge reuse in conceptual design of green products[J]. Journal of Mechanical Engineering, 2013, 49(7): 72-79. |
 2019, Vol. 36
2019, Vol. 36