在经济全球化、市场国际化、技术进步加快的背景下，我国制造业企业面临着严峻的形势^[1]. 制造企业的竞争策略也从成本领先，发展成为交货时间、质量、成本、服务等综合因素的竞争^[2]. 这些限制迫使企业必须要转变落后的制造模式，思考如何提高车间系统的性能.

精益生产是二战后丰田汽车公司为了追赶发达国家汽车制造业的过程中创建的一种不同于西方的批量生产的全新的生产方式^[3]. 精益生产以客户的角度定义价值，识别整个价值流，合理利用人力、设备等资源，推动价值的流动并持续不断地推进整个价值流的改善^[4]，提高整个生产系统性能. 徐文杰等^[5]基于整流化思想，通过工序拆分、瓶颈改善等精益改善方法对DMA(Digital Away Module)生产线物流路径进行优化提升；江欣昊等^[6]运用工业工程、TOC(Theory of Constraints)、SLP(Systematic Layout Plonning)、精益生产等知识，在现有生产系统基础上优化了车间布局和物流搬运系统，提高了生产线利用率. 周高峰^[7]通过对生产线节拍的精益优化方法研究，分析了影响生产线节拍的关键因素，并以MTM(Method Time Measurement)分析方法、生产线平衡分析等方法对生产节拍进行精益优化. 王秀红等^[8]利用价值流图分析技术对生产现场进行了改进，取消了不增值部分，提高了产品生产线效率. 但是在精益改善过程中，只能找到生产中浪费问题，具体浪费的程度却不能测算；在改善过程中由于领导层制定了较高的目标，但是缺少具体改善的逻辑体系和方法去改善生产流程，使得改善过程较为复杂并且对员工有一定的能力要求.

可拓创新方法原称可拓方法^[9]，是用于对研究对象进行建模、拓展、变换、评价等，以生成解决各种矛盾问题的方法. 可拓方法特别适用于解决各种类型的创新和优化设计中遇到的矛盾问题，如产品创新、技术创新、管理创新等^[10]. 杨春燕等^[11]通过对可拓创新方法及其应用的研究，说明了可拓创新方法具有普适性和可操作性，并对技术创新、发明创造的定式化研究有非常重要的价值. 张华伟等^[12]以石油机械产品为例，运用可拓创新方法中的可拓变换获得了创新方案，得到了满意的创新产品，实证了可拓创新方法的科学性和有效性. 杜洋^[13]把可拓创新方法与物流成本控制相结合开展研究，运用可拓创新方法创建可拓模型，并利用优度评价法，从而获得物流成本控制策略.

本文将生产中的浪费转换成矛盾问题，在精益改善的基础上结合可拓创新方法以解决生产中的各种矛盾问题，并借助案例对可拓创新方法应用于生产线优化的有效性进行验证，表明可拓方法可以高效地解决生产中的矛盾问题^[14].

1 相关理论

可拓创新方法包括可拓模型建立方法、拓展分析方法、共轭对方法、可拓变换方法、可拓集合方法、优度评价方法等. 为了更好地揭示事物发展变化的本质，可拓学从事物的物质性、系统性、动态性、对立性出发，提出了虚实、软硬、潜显、负正四对共轭属性，利用共轭属性对事物进行全面分析，并用于解决矛盾问题，该方法称为共轭对方法. 从物的系统性考虑事物的结构，把物的组成部分的全体称为物的硬部，物与它的组成部分之间及与该物以外的物之间的关系称为物的软部，这种分析方法称为软硬共轭对分析法.

精益生产基本思想是通过生产过程整体优化，改进技术，理顺物流，杜绝超量生产，消除无效劳动与浪费，有效利用资源，降低成本，改善质量，达到用最少的投入实现最大产出的目的^[15]. 在对生产线进行精益改善中，通过对价值流图的绘制会发现生产中存在的矛盾问题，从而可以发现需要改善的地方. 但是在解决这些问题的时候往往是根据经验，缺少相应逻辑体系和工具方法，使得在改善过程中遇到阻碍. 生产中的矛盾问题可以通过对生产系统进行共轭分析，从而找到有效解决矛盾问题的途径. 事物的共轭属性在一定条件下可以相互转化，利用这种性质，为相关矛盾问题的解决寻求思路和方法，这就是利用可拓学特有的共轭思维模式进行创新的探索. 利用共轭思维模式可以使我们全面深入地了解事物的信息和结构，从而整体把握优势和劣势，有针对性地化解矛盾、解决问题.

矛盾问题是可拓学的研究对象，当问题的诱因是因为主观和客观矛盾引起时，这类问题称为不相容问题，利用可拓创新方法解决不相容问题的方法称为可拓策略生成方法^[16]. 可拓策略生成方法基本思路一般是：首先界定目标和条件并建立问题的核模型；再建立该矛盾问题的相容度函数并判断不相容程度；然后对目标或条件进行可拓变换；最后对变换后形成问题再次计算相容度函数，选取最优的方案^[17].

在生产中出现的问题为目标与条件的不相容问题，用软硬共轭对分析方法解决生产中的矛盾问题的可拓策略生成方法步骤如下：

(1) 收集工作现场信息和数据绘制现状价值流图. 价值流图主要绘制的是产品从原材料到到达顾客手中的生产流程，在绘制过程中收集产品生产的数据，并找出那些不产生价值的非增值活动，精益生产的目的就是为了消除这些非增值活动.

(2) 找出现状价值流图出现的矛盾问题. 通过对收集到的数据进行分析，例如库存量、员工数和增值时间占比等具体数据找到产品生产过程中存在的矛盾问题.

(3) 建立核问题的可拓模型，并确定该模型中硬部条件和软部条件. 用基元表示实际问题的目标和条件，建立问题的可拓模型，然后根据实际问题提供的指标和要达到的目标所需要的相应指标的取值，确定问题的核问题，并建立可拓模型.

(4) 建立问题的相容度函数，判定是否为不相容问题. 如果是不相容问题，则需要对生产过程进行分析，对不相容的问题进行共轭对变换，使矛盾问题得以解决；然后通过评价优选，确定较优策略.

(5) 将最优的策略具化成为设计方案，并绘制未来价值流图.

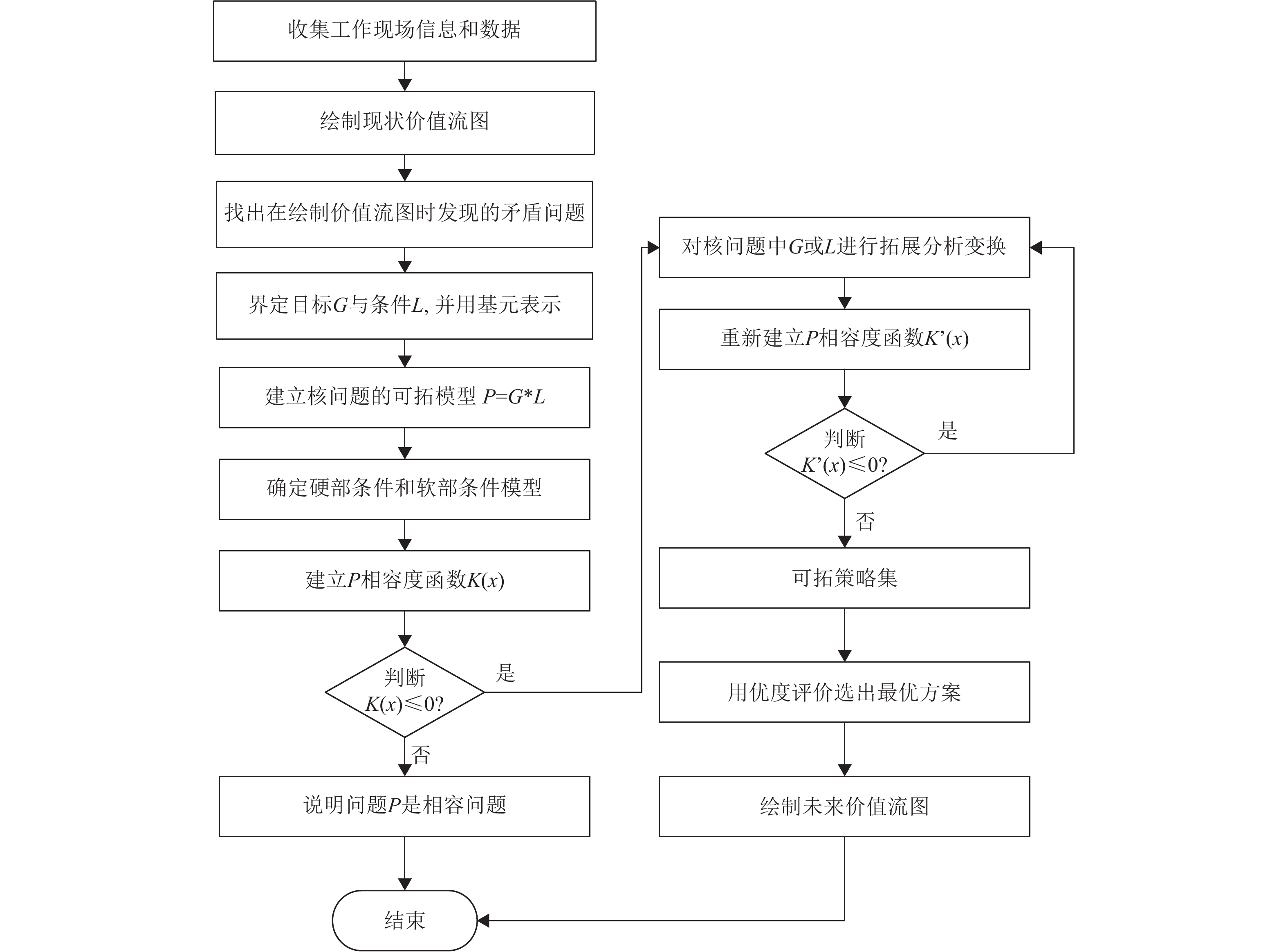
可拓创新在精益生产的应用框架如图1所示.

2 案例分析

国内某电子工厂生产一种汽车电子模块B，主要用于对汽车发生碰撞等事故过程中的信息计算和处理，然后判断是否需要激活安全保护系统. 由于生产这种电子模块的生产线建立较早，没有仔细研究工艺需求与生产线配置，而只是简单满足电子模块装配生产线生产能力，这就造成了生产线生产效率低下、前后工序干涉严重、浪费严重的现象. B电子模块生产线共有6个工序分别是：电容组装(工序1)、压接(工序2)、打螺丝钉(工序3)、震动测试(工序4)、功能测试(工序5)、发货前检测(工序6). 具体人员配置、工序时间以及库存情况见表1.

2.1 问题分析

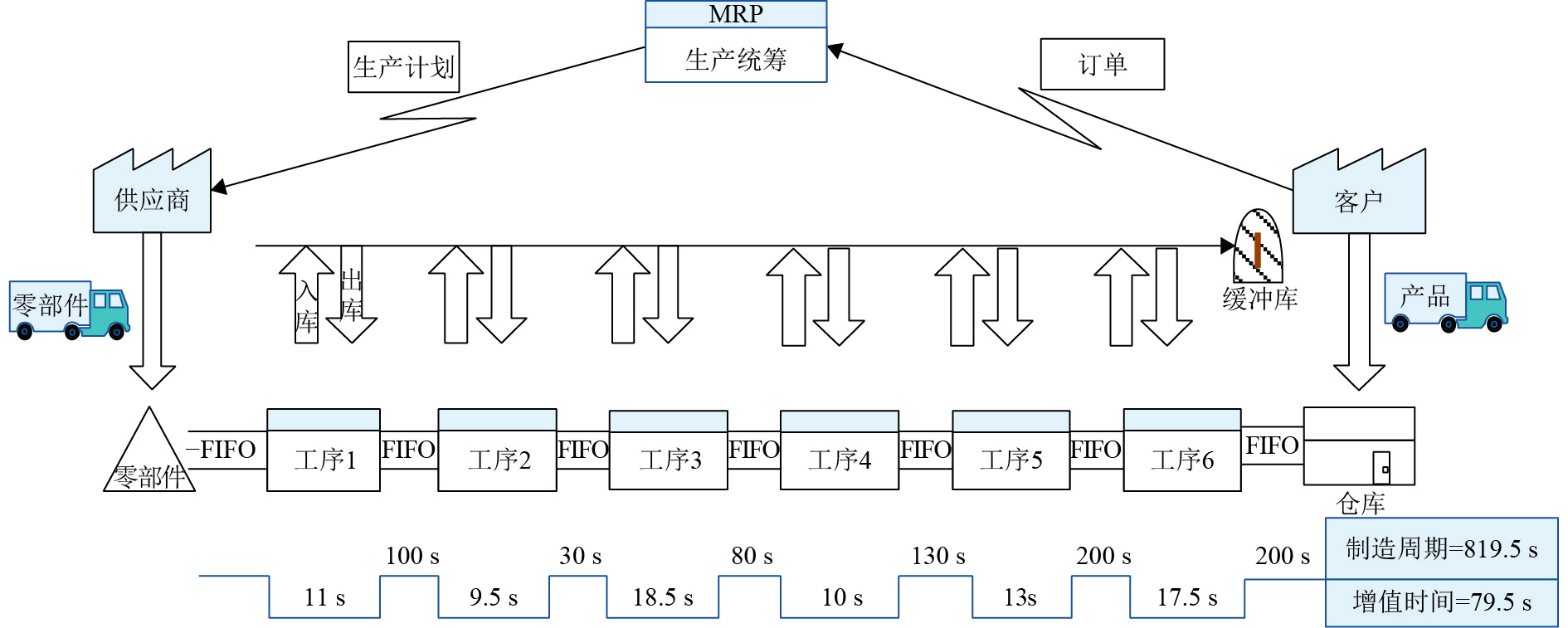
对现有的生产线流程进行调研，沿着生产顺序对各个工序进行计时，收集数据，绘制现状价值流图，如图2所示.

在绘制完成现状价值流图之后，具体分析B电子模块价值流图出现的矛盾问题如下:

(1) 产能过剩. 每道工序都会过量生产，导致有大量在制品只能运输到缓冲库中，造成了库存浪费. (2) 工序6设计成“孤岛”. 在整个生产过程中工序6作为一个“孤岛”游离于生产线之外的，员工需要不断地从上道工序搬运在制品至工序6；同时每道工序多余的在制品不断地搬运至缓冲库，这就造成了运输浪费^[18]. (3) 员工作业不平衡. 在对6名员工作业进行分析后，发现员工生产节奏不平衡，有的员工几乎没有休息，而有的员工却有大量时间等待，这就造成了员工浪费. (4) 工序作业时间不合理. 在对B产品半年需求量以及计划作业时间分析之后，可以计算出该产品的生产节拍. 生产节拍=有效工作时间/订单量=460 800/28 800=16 s，取宽放系数为5%，则生产节拍为15.2~16.8 s，但是发现生产中的6道工序时间与生产节拍时间相差较大，这就导致过多的库存以及人力浪费.

2.2 可拓创新变换

现有的B产品生产过程中存在诸多不合理的问题，造成了大量浪费. 从客户需求以及企业自身出发，对 ${\rm B}$ 生产线有了新的要求，列出前后参数对照数据，如表2所示. 设原有生产线为 ${N_0}$ ，目标生产线为 ${N_1}$ ，其目标生产线是基于制定目标数据的管理者要求的进行优化改善后的生产线. 根据可拓创新的步骤分析，B产品生产线核问题非常明确，直接建立核问题的可拓模型为 $P = G*L$ .

该核问题模型是用软硬共轭方法建立的. 其条件 $L = {L_1} \wedge {L_2}$ ，其中 ${L_1}$ 是硬部条件，即生产线系统中各个工序； ${L_2}$ 是软部条件，即各个工序之间的在制品运输联系.

(1) 建立矛盾问题的简单相容度函数.

① 对于节拍时间. 以最大值点 ${x_1} = 16$ ，正域 ${X_1} = $ $ \left[ {15.2,16.8} \right]$ 建立简单相容度函数为

$ k\left( {{x_1}} \right) = \left\{ \begin{array}{l} \dfrac{{{x_1} - 15.2}}{{0.8}},\;\;\;\;\;\;{x_1} \leqslant 16;\\ \dfrac{{16.8 - {x_1}}}{{0.8}},\;\;\;\;\;\;{x_1} > 16. \end{array} \right. $

② 对于在制品件数. 以最大值点 ${x_2} = 10$ ，正域 ${X_2} = \left[ {0,10} \right]$ 建立简单相容度函数为

$k\left( {{x_2}} \right) = \left\{ \begin{array}{l} \dfrac{{{x_2}}}{{10}},\;\;\;\;\;\;\;\;\;\;\;\;{x_2} \leqslant 10;\\ \dfrac{{10 - {x_2}}}{{10}},\;\;\;\;\;\;{x_2} > 10. \end{array} \right.$

③ 对于工人数. 以最大值点 ${x_3} = 5$ ，正域 ${X_3} = \left[ {2,5} \right]$ 建立简单相容度函数为

$ k\left( {{x_3}} \right) = \left\{ \begin{array}{l} \dfrac{{{x_3} - 2}}{3},\;\;\;\;\;\;\;{x_3} \leqslant 5;\\ \dfrac{{5 - {x_3}}}{3},\;\;\;\;\;\;\;{x_3} > 5. \end{array} \right. $

则由实际问题的综合相容度函数为： $K\left( P \right) = $ ${k_1}\left( {{x_1}} \right) \wedge {k_2}\left( {{x_2}} \right) \wedge {k_3}\left( {{x_3}} \right)$ . 将观测数据代入到相容度函数中可以得到，

$ \begin{array}{l} {k_1}\left( {{x_1}} \right) = {k_1}\left( {11} \right) \wedge {k_1}\left( {9.5} \right) \wedge {k_1}\left( {18.5} \right) \wedge {k_1}\left( {10} \right) \wedge \\ {k_1}\left( {13} \right) \wedge {k_1}\left( {17.5} \right) = - 7.125, \end{array} $

$ \begin{array}{l} {k_2}\left( {{x_2}} \right) = {k_2}\left( {50} \right) \wedge {k_2}\left( {15} \right) \wedge {k_2}\left( {40} \right) \wedge {k_2}\left( {65} \right) \wedge \\ {k_2}\left( {50} \right) \wedge {k_2}\left( {50} \right) = - 5.5, \end{array}\;\;\;\; $

${k_3}\left( {{x_3}} \right) = {k_3}\left( 6 \right) = - 0.333.\quad\quad\quad\;\;\quad\quad\quad\quad\quad$

则实际问题的综合相容度函数 $K\left( P \right) = {k_1}\left( {{x_1}} \right) \wedge $ ${k_2}\left( {{x_2}} \right) \wedge {k_3}\left( {{x_3}} \right) = - 7.125 $ ，即问题 $P = G*L$ 是不相容问题.

(2) 对问题进行拓展分析变换.

由上述分析可知，现有的生产线中，由于员工动作不标准导致各工序的作业时间与预期节拍差距较大；上下工序劳动强度相差较大，在忙碌的生产过程中会出现员工闲置，这非常不合理；而库存则是由于该生产过程中工序作业时间与节拍不同和生产线布局不合理产生的，也就是工序作业时间和在制品运输是库存产生的主要原因. 当未来生产计划确定时，则可拓模型中的目标不能改变. 因此必须利用条件 ${l_0}$ 的变换来解决矛盾问题.

① 为了实现目标G，首先实施对硬部物元的变化. 例如，以 ${L_{11}}$ 为例实施主动变换：

$ {\varphi _{11}}{L_{11}} ={\varphi _{11}} \left[ {\begin{array}{*{20}{c}} {{\text{工序}}1,} & {{\text{时间}},} & {11\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {50{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{内}}} \end{array}} \right] =\\ \left[ {\begin{array}{*{20}{c}} {{\text{工序}}1,} & {{\text{时间}},} & {8.0\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {50{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{内}}} \end{array}} \right] = L{'_{11}}. $

在对工序1进行动作分析后，发现工人的操作熟练度不高，并且有些动作多余. 针对这些问题对工人进行熟练度培训并减少操作人员的目视检查产品动作，由此工序1的工序时间减少到8 s. 依次对其他工序进行类似的主动变换，则有主动变换 ${\varphi _1} = {\varphi _{11}} \wedge {\varphi _{12}} $ $ \wedge {\varphi _{13}} \wedge {\varphi _{14}} \wedge {\varphi _{15}} \wedge {\varphi _{16}}$ 使得

$ \begin{array}{l} {\varphi _1}{L_1} = \left[ {\begin{array}{*{20}{c}} {{\text{工序}}1,} & {{\text{时间}},} & {8.0\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {50{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{内}}} \end{array}} \right] \wedge \left[ {\begin{array}{*{20}{c}} {{\text{工序}}2,} & {{\text{时间}},} & {7.5\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {15{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{内}}} \end{array}} \right] \wedge \left[ {\begin{array}{*{20}{c}} {{\text{工序}}3,} & {{\text{时间}},} & {16.5\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {40{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{内}}} \end{array}} \right]\wedge\\ \quad\quad\quad \left[ {\begin{array}{*{20}{c}} {{\text{工序}}4,} & {{\text{时间}},} & {7.0\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {65{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{内}}} \end{array}} \right] \wedge \left[ {\begin{array}{*{20}{c}} {{\text{工序}}5,} & {{\text{时间}},} & {9.0\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {50{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{内}}} \end{array}} \right] \wedge \left[ {\begin{array}{*{20}{c}} {{\text{工序}}6,} & {{\text{时间}},} & {15.5\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {50{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{外}}} \end{array}} \right]=\\ \quad\quad\quad{\rm{ }}L{'_{10}} \wedge L{'_{11}} \wedge L{'_{12}} \wedge L{'_{13}} \wedge L{'_{14}} \wedge L{'_{15}} \wedge L{'_{16}}. \end{array} $

由上可见，可以实施主动变换 ${\varphi _1}$ ，对生产线6道工序实施标准化作业分析，将现行作业的操作和动作进行分解，然后对作业过程进行改善，可以将员工操作周期减少.

② 从条件 ${l_0}$ 看出第6个工序与其他工序不同，它并没有位于生产线上，而是作为“孤立”的工序游离于生产线之外，工作人员需要不断地从工序5将在制品搬运到工序6，这就产生了不必要的浪费和库存. 在对生产线布局进行研究后，发现可以通过调整位置，将工序6搬移到生产线内. 因此对工序6位置实施主动变换.

$ \begin{split} {\varphi _{2}}{L{'_{16}}} =& {\varphi _{2}} \left[ {\begin{array}{*{20}{c}} {{\text{工序}}6,} & {{\text{时间}},} & {15.5\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {50{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{外}}} \end{array}} \right]= \\ & \left[ {\begin{array}{*{20}{c}} {{\text{工序}}6,} & {{\text{时间}},} & {15.5\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {50{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{内}}} \end{array}} \right] = L{'_{16}}. \end{split}$

在对工序6的位置进行调整后，则导致生产线的软部 ${L_{25}}$ 、 ${L_{26}}$ 中连接关系发生改变，发生共轭变换，即有： ${\varphi _2}{ = _{{\varphi _2}}}{T_1}$ ，使得

$ \begin{array}{*{20}{c}} _{{\varphi _2}}{T_1}{L_2} ={L_{21}} \wedge {L_{22}} \wedge {L_{23}} \wedge {L_{24}} \wedge L{'_{25}} \wedge L{'_{26}} = \\ \left[ {\begin{array}{*{20}{c}} {{\text{连接}}1,} & {{\text{前项}},} & {{\text{工序}}1}\\ {} & {{\text{后项}},} & {{\text{工序}}2}\\ {} & {{\text{运输距离}},} & {2\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {100\;{\rm{s}}} \end{array}} \right]\wedge\\ \left[ {\begin{array}{*{20}{c}} \\ {{\text{连接}}2,} & {{\text{前项}},} & {{\text{工序}}2}\\ {} & {{\text{后项}},} & {{\text{工序}}3}\\ {} & {{\text{运输距离}},} & {2\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {30\;{\rm{s}}} \end{array}} \right]\wedge \\ \left[ {\begin{array}{*{20}{c}} \\ {{\text{连接}}3,} & {{\text{前项}},} & {{\text{工序}}3}\\ {} & {{\text{后项}},} & {{\text{工序}}4}\\ {} & {{\text{运输距离}},} & {2\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {80\;{\rm{s}}} \end{array}} \right]\wedge\\ \left[ {\begin{array}{*{20}{c}} \\ {{\text{连接}}4,} & {{\text{前项}},} & {{\text{工序}}4}\\ {} & {{\text{后项}},} & {{\text{工序}}5}\\ {} & {{\text{运输距离}},} & {2\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {130\;{\rm{s}}} \end{array}} \right] \wedge \\ \left[ {\begin{array}{*{20}{c}}\\ {{\text{连接}}5,} & {{\text{前项}},} & {{\text{工序}}5}\\ {} & {{\text{后项}},} & {{\text{工序}}6}\\ {} & {{\text{运输距离}},} & {2\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {100\;{\rm{s}}} \end{array}} \right]\wedge\\ \left[ {\begin{array}{*{20}{c}} \\ {{\text{连接}}6,} & {{\text{前项}},} & {{\text{工序}}6}\\ {} & {{\text{后项}},} & {{\text{仓库}}}\\ {} & {{\text{运输距离}},} & {4\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {200\;{\rm{s}}} \end{array}} \right]. \end{array} $

③ 在对工序进行标准化作业分析后发现工序作业时间远小于节拍时间，因此可以将相邻工序整合成一个系统. 记硬部条件：

$L{'_{1m}} = \left[ \begin{array}{l} {O_{m1}},{c_{m1}},{c_{m1}}({O_{m1}})\\ \;\;\;\;\;\;\;\;\;\;{c_{m2}},{c_{m2}}({O_{m1}})\\ \;\;\;\;\;\;\;\;\;\;{c_{m3}},{c_{m3}}({O_{m1}})\\ \;\;\;\;\;\;\;\;\;\;{c_{m4}},{c_{m4}}({O_{m1}}) \end{array} \right],\;\;\;\;(m \in \left[ {1,6} \right]).$

则根据可积分析原理^[17]，将工序1和工序2整合成新的工序1，将原工序4和工序5整合成新工序3. 即

$ \begin{array}{l} L{'_1} = L{'_{11}} \otimes L{'_{12}} \wedge L{'_{13}} \wedge L{'_{14}} \otimes L{'_{15}} \wedge L{'_{16}}= \\ \left[ {\begin{array}{*{20}{c}} {{\text{工序}}1,} & {{\text{时间}},} & {15.5\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {65{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{内}}} \end{array}} \right] \wedge \\ \left[ {\begin{array}{*{20}{c}}\\ {{\text{工序}}2,} & {{\text{时间}},} & {16.5\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {40{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{内}}} \end{array}} \right]\wedge\\ \left[ {\begin{array}{*{20}{c}}\\ {{\text{工序}}3,} & {{\text{时间}},} & {16.0\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {115{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{内}}} \end{array}} \right]\wedge\\ \left[ {\begin{array}{*{20}{c}}\\ {{\text{工序}}4,} & {{\text{时间}},} & {15.5\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {50{\text{件}}}\\ {} & {{\text{位置}},} & {{N_0}{\text{外}}} \end{array}} \right] . \end{array} $

在硬部条件进行可积变换进行调整后，则导致生产线的软部变化，即必存在共轭变换，即有 ${\varphi _3}{{\rm{ = }}_{{\varphi _3}}}{T_2}$ ，使得

$ \begin{array}{l} _{{\varphi _3}}{T_2}{L_2} = L{'_{21}} \wedge L{'_{22}} \wedge L{'_{23}} \wedge L{'_{24}}= \\ \left[ {\begin{array}{*{20}{c}} {{\text{连接}}1,} & {{\text{前项}},} & {{\text{工序}}1}\\ {} & {{\text{后项}},} & {{\text{工序}}2}\\ {} & {{\text{运输距离}},} & {2\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {130\;{\rm{s}}} \end{array}} \right]\wedge\\ \left[ {\begin{array}{*{20}{c}}\\ {{\text{连接}}2,} & {{\text{前项}},} & {{\text{工序}}2}\\ {} & {{\text{后项}},} & {{\text{工序}}3}\\ {} & {{\text{运输距离}},} & {2\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {80\;{\rm{s}}} \end{array}} \right]\wedge\\ \left[ {\begin{array}{*{20}{c}}\\ {{\text{连接}}3,} & {{\text{前项}},} & {{\text{工序}}3}\\ {} & {{\text{后项}},} & {{\text{工序}}4}\\ {} & {{\text{运输距离}},} & {2\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {230\;{\rm{s}}} \end{array}} \right]\wedge\\ \left[ {\begin{array}{*{20}{c}}\\ {{\text{连接}}4,} & {{\text{前项}},} & {{\text{工序}}4}\\ {} & {{\text{后项}},} & {{\text{仓库}}}\\ {} & {{\text{运输距离}},} & {4\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {200\;{\rm{s}}} \end{array}} \right]. \end{array} $

④ 根据相关分析和传导变换可知，工序作业时间变换、工序位置变换和工序的整合变换都会改变库存. 旧生产线 ${N_0}$ 通过主动变换 $\varphi = {\varphi _1} \wedge {\varphi _2} \wedge {\varphi _3}$ ，则必有如下传导变换 $\varphi {{\rm{ = }}_\varphi }{T_1}{ \Rightarrow _1}{T_2}{ \Rightarrow _2}{T_3}{ \Rightarrow _3}{T_4}$ . 则形成新的生产线 ${N_1}$ ，其硬部条件为

$ \begin{array}{l} L'{'_1}{{\rm{ = }}_3}{T_4}{L_1} = \;\;\; \left[ {\begin{array}{*{20}{c}} {{\text{工序}}1,} & {{\text{时间}},} & {15.5\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {1{\text{件}}}\\ {} & {{\text{位置}},} & {{N_1}{\text{内}}} \end{array}}\right] \wedge\end{array} $

$ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\text{工序}}2,} & {{\text{时间}},} & {16.5\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {3{\text{件}}}\\ {} & {{\text{位置}},} & {{N_1}{\text{内}}} \end{array}}\right]\wedge \end{array} $

$ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\text{工序}}3,} & {{\text{时间}},} & {16.0\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {7{\text{件}}}\\ {} & {{\text{位置}},} & {{N_1}{\text{内}}} \end{array}} \right]\wedge \end{array} $

$ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\text{工序}}4,} & {{\text{时间}},} & {15.5\;{\rm{s}}}\\ {} & {{\text{员工数}},} & {1{\text{人}}}\\ {} & {{\text{库存}},} & {8{\text{件}}}\\ {} & {{\text{位置}},} & {{N_1}{\text{内}}} \end{array}} \right] =\\ \;\;\;\; L'{'_{11}} \wedge L'{'_{12}} \wedge L'{'_{13}} \wedge L'{'_{14}}. \end{array} $

其软部条件为

$ \begin{array}{l} L'{'_2} =\left[ {\begin{array}{*{20}{c}} {{\text{连接}}1,} & {{\text{前项}},} & {{\text{工序}}1}\\ {} & {{\text{后项}},} & {{\text{工序}}2}\\ {} & {{\text{运输距离}},} & {2\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {2\;{\rm{s}}} \end{array}} \right] \wedge\end{array} $

$\quad\quad \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\text{连接}}2,} & {{\text{前项}},} & {{\text{工序}}2}\\ {} & {{\text{后项}},} & {{\text{工序}}3}\\ {} & {{\text{运输距离}},} & {2\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {6\;{\rm{s}}} \end{array}} \right]\wedge\end{array} $

$\quad\quad \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\text{连接}}3,} & {{\text{前项}},} & {{\text{工序}}3}\\ {} & {{\text{后项}},} & {{\text{工序}}4}\\ {} & {{\text{运输距离}},} & {2\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {14\;{\rm{s}}} \end{array}} \right]\wedge\end{array} $

$ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\text{连接}}4,} & {{\text{前项}},} & {{\text{工序}}4}\\ {} & {{\text{后项}},} & {{\text{仓库}}}\\ {} & {{\text{运输距离}},} & {4\;{\rm{m}}}\\ {} & {{\text{运输时间}},} & {32\;{\rm{s}}} \end{array}} \right]= \\ \;\;\;\;L'{'_{21}} \wedge L'{'_{22}} \wedge L'{'_{23}} \wedge L'{'_{24}}. \end{array} $

对原有生产线进行拓展变换后的具体数据如表3所示.

⑤对问题进行拓展变换，并判断其相容性. 生产线 ${N_0}$ 需要同时满足上述变换整合成新生产线 ${N_1}$ ，单一的变换并不能解决矛盾问题，因此需要将上述拓展变换综合运用才能使综合相容度满足要求. 计算优化后的综合相容度为： $K\left( {P'} \right) = 0.1 > 0$ . 说明实施变换之后不相容问题 $P$ 转化为相容问题. 本文只生成了一个策略方案，若在其他问题中得到多个方案，则可用优度评价选出最优方案，具体评选过程见文献[19].

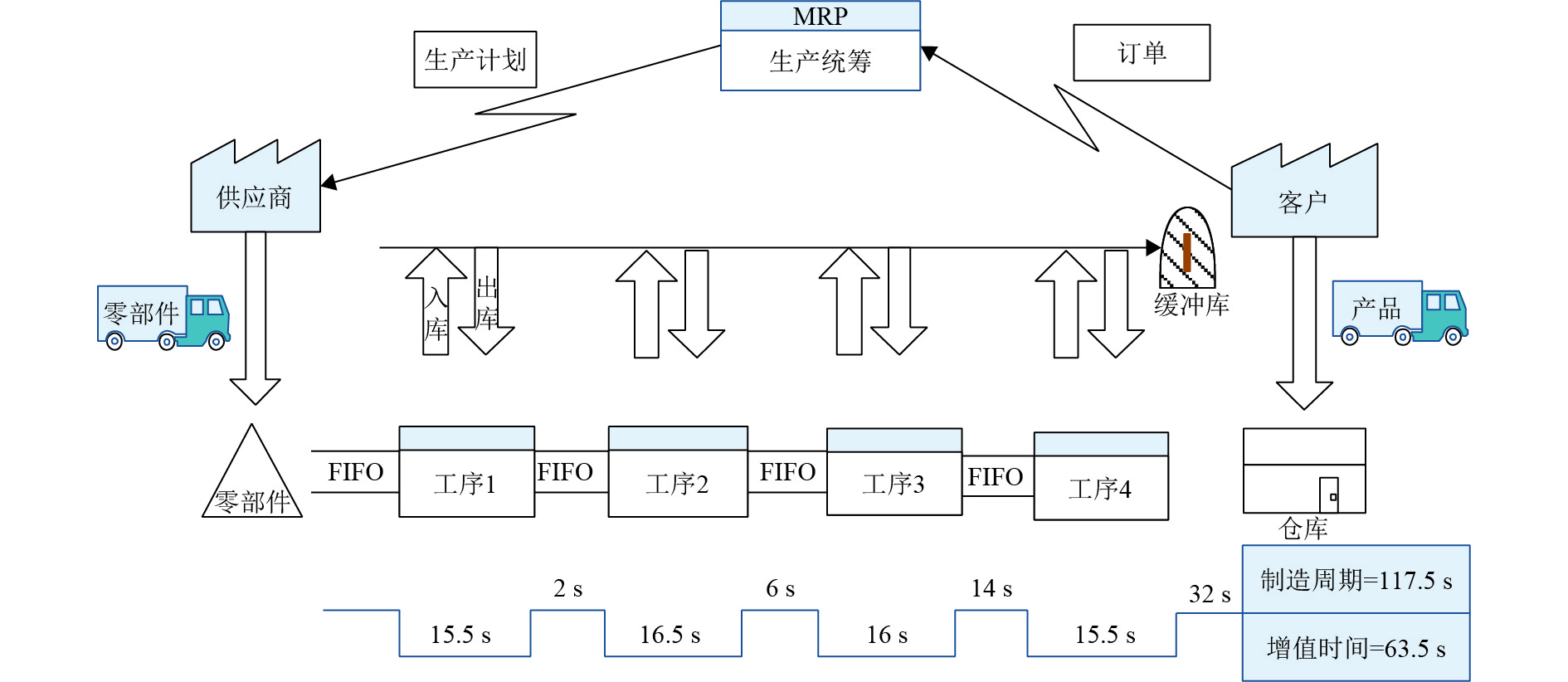
(3) 形成设计方案，并绘制未来价值流图，如图3所示.

在对B产品生产线进行可拓创新后可以看出，该产品制造周期大大缩短，员工数降至4人，在在制品库存方面，各个工序都较之前有了很大的减少，线上库存总数降至19件，增值比增至54.04%^[20]，生产线得到了大幅度优化.

3 结论

精益生产是以消除浪费、消灭库存为核心的一种生产方式，它追求整个价值流都要实现精益. 可拓创新方法是对创新过程中遇到矛盾问题进行拓展变换，最终生成解决矛盾问题的创新方法. 本文基于共轭对分析方法对精益生产中出现的矛盾问题提出了特定的逻辑架构，为精益生产提供了一套逻辑体系和解决方法. 通过价值流图找出矛盾问题，把目标与条件形式化、定量化，将矛盾问题建立可拓模型，再利用可拓创新方法解决矛盾问题，可以让管理者更好地调配生产中的人、财、物.