随着互联网以及各类视觉设备的普及,存储的图像和视频早已不计其数,从而使得在海量图片中检索出与目标图片相似的图像变得极为困难. 因为这不仅需要考虑检索的准确度,还需要考虑检索所需的时间. 传统的图像检索方法主要分两种:一种是基于标签的图像检索(Text-Based Image Retrieval,TBIR),另一种是基于内容的图像检索(Content Based Image Retrieval,CBIR). TBIR方法主要是通过图像的关键字和标题等标签信息进行图像的检索,而CBIR主要是通过提取图像的特征,通过相似性度量、排序得出目标结果. CBIR一直是图像检索领域内的重心,而影响其检索效果的关键在于其提取的图像特征. 好的特征不仅对图像检索精确度有很大的帮助,在检索速度上面也有极大的提升. 主要的特征提取方式有:基于颜色的,一般采用颜色直方图实现检索;基于纹理方面的,有PHOG、LBP、Gabor等方式;基于形状、轮廓方面的,一般使用形状上下文描述子,这种不仅适合刚性物体,也对非刚性物体有较好的鲁棒性[1-4]. 这些经典的传统算法虽然很实用,但提取的特征一般比较简单和粗糙.
近年来,随着深度学习的兴起和发展,利用深度学习方法来提取图像的复杂特征成了研究的热点. 深度学习提取的特征属于高层语义特征,它能更好地表达图像的内容和细节. 最近,研究者们提出了一种专门为计算图像之间相似度而设计的一种深度学习框架——孪生卷积网络(Siamese CNN),它在实际应用中取得了很好的效果. 由于此网络是监督性网络,需要大量的标签样本,因此它存在着一定的局限性[5-7]. 为了改进这种需要监督的局限性,Mallat S等[8]提出来了一种新的小波散射卷积神经网络. 它已经在理论上证明了通过此方法提取的特征具有平移不变性和形变稳定性,而且这种网络为非监督的前馈式神经网络. 它的识别效果在小数据集上表现良好,已经被成功运用到图像识别和语音识别等领域[9-13]. 因为小波卷积神经网络优越的性能和完美的数学理论性质,为了拓广其应用背景,类比经典的卷积神经网络的思路,所以Wiatowski T等人不断完善并扩展延伸了小波散射卷积网络的理论及其网络结构,使得非线性化和池化在网络中得以运用. 这在一定程度上使得提取的特征实现了降维[14].
针对图像检索的复杂背景、大规模图像检索消耗的时间过长以及深度神经网络需要固定输入尺寸等问题,本文主要利用小波散射卷积神经网络做了以下工作:(1) 将小波散射卷积神经网络运用到图像检索领域;(2) 对每张图片构造对应大小的小波核,解决任意尺度输入问题;(3) 对小波散射提取的特征进行加工,以特征系数的均值和方差作为新的特征,从而降低特征维度来满足大规模图像检索在时间上的需求.
1 小波散射卷积神经网络图像检索的先决条件就是提取图像的特征,而特征的好坏直接关系到图像检索的准确度和检索时间. 有一种做法就是将其转化到时频域,然后求其特征. 早期使用的方法是傅里叶变换,该方法是频域分析法,只能描述全局特征,且提取出来的特征只有平移不变性不具备形变稳定性. 而由傅里叶变换改进的小波变换,提取的特征满足形变稳定性,在时域和频域都有很好的表现. 但是,单纯的小波变换对特征并没有平移不变性,最新提出的小波散射卷积神经网络恰好弥补了这一不足[5]. 本节将具体介绍如何利用小波散射卷积神经网络提取图像的特征.
小波散射实际上是二维方向母小波通过缩放、旋转得到一组小波簇,在不同尺度的情况下对信号源进行滤波,然后通过尺度函数不断提取其高频信息的过程. 具体过程如下.
设尺度函数
因为小波变换不具有平移不变性,所以维持其不变性需要加入非线性的度量. 这里取小波变换的模算子
| ${{{U}}_\lambda }{{f}}(x) = \rho ({{f}} * {{{\psi}} _\lambda }(x)),$ | (1) |
其中
| ${{{U}}_\lambda }{{f}}(x) = {{P}}\left( {\rho \left( {{{f}} * {{{\psi}} _\lambda }(x)} \right)} \right), $ | (2) |
其中
为了更好地分类,本文采用局部低通滤波器——Gabor小波作为尺度函数来提取细节,即
| ${{{S}}_J}(q){{f}} = {{P}}(\rho ({{f}} * {{{\psi}} _\lambda }(x))) * {{{\varphi}} _J}(q {\text{为路径}}),$ | (3) |
其中
| $\begin{array}{c}{{{S}}_J}(q){{f}} = {{P}}(\rho ([{{P}}(\rho ({{f}} * {{{\psi}} _{{\lambda _1}}}))] * {{{\psi}} _{{\lambda _2}}})) *\\ {{{\varphi}} _J} \;\; (\lambda \in ([{j_1},{\gamma _1}],[{j_2},{\gamma _2}][{j_3},{\gamma _3}] ,\cdots )) . \end{array}$ |
由此可得小波传播算子为
| $\overline {{{{U}}_\lambda }{{f}}} = \left\{ {{{{U}}_\lambda }{{f}},\left. {{{{S}}_J}{\rm{(q)}}{{f}}} \right\} = } \right.\left\{ {{{P}}(\rho ({{f}} * {{{\psi}} _\lambda })),{{P}}(\rho ({{f}} * {{{\psi}} _\lambda })) * {{{\varphi}} _\lambda }} \right\},$ | (4) |
其中前一个分量表达的是信号不变的高频特征,后一个分量为稳定的低频特征(散射算子).
每做一次低频散射,都会伴随着高频的丢失. 因此,在下一步操作时又得恢复高频. 通过路径
| ${{U}}[q]{{f}} = {{U}}[({\lambda _1},{\lambda _2}, \cdots ,{\lambda _n})]{{f}} = {{{U}}_{{n}}}[{\lambda _n}] \cdots {{{U}}_{\rm{2}}}[{\lambda _2}]{{{U}}_{\rm{1}}}[{\lambda _1}]f,$ | (5) |
| ${{S}}[q]{{f}} = {{U}}[q]{{f}} * {{{\varphi}} _J}.$ | (6) |
这样,可得小波散射的网络结构,见图1所示.
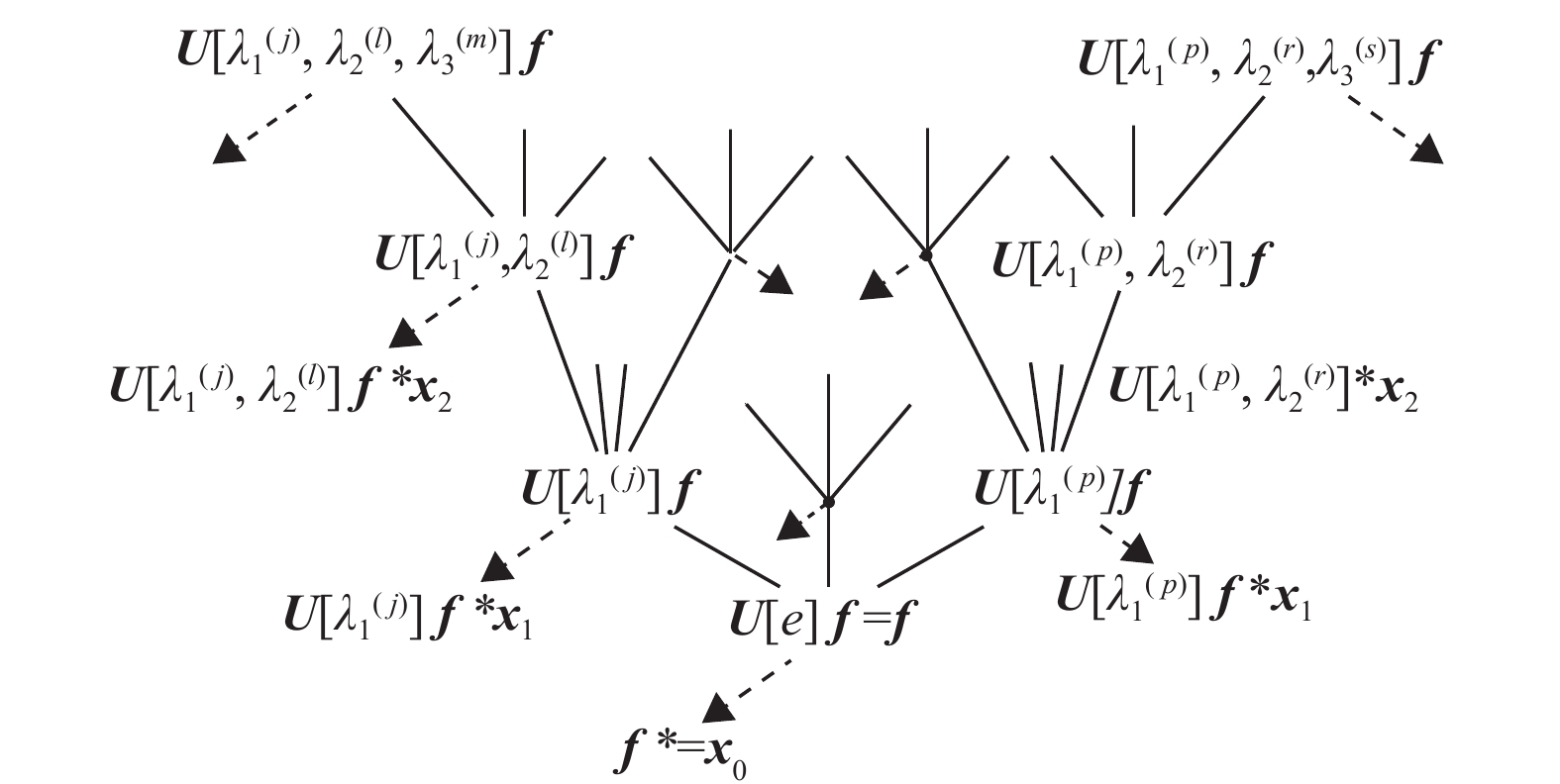
|
图 1 小波散射卷积网络结构图 Figure 1 Structure diagram of wavelet scattering convolution network |
因为在网络的每一层都有低频稳定的特征输出,故其特征集合为
| $\begin{split}&{{{S}}_J}\left[ {{P_j}} \right]{{f}} = \left\{ \begin{array}{c}{{{S}}_J}\left[ \varphi \right]{{f}}\\{{{S}}_J}\left[ { \wedge _J^1} \right]{{f}}\\{{{S}}_J}\left[ { \wedge _J^2} \right]{{f}}\\{{{S}}_J}\left[ { \wedge _J^3} \right]{{f}}\\ \cdots\end{array} \right\} =\\& {\left\{ \begin{array}{c}f * {{{\varphi}} _{{2^J}}}\\\left| {{{f}} * {\psi _{{\lambda _1}}}} \right| * {{{\varphi}} _{{2^J}}}\\\left| {\left| {{{f}} * {{{\psi}} _{{\lambda _1}}}} \right| * {{{\psi}} _{{\lambda _2}}}} \right| * {{{\varphi}} _{{2^J}}}\\\left| {\left| {\left| {{{f}} * {{{\psi}} _{{\lambda _1}}}} \right| * {{{\psi}} _{{\lambda _2}}}} \right| * {{{\psi}} _{{\lambda _3}}}} \right| * {{{\varphi}} _{{2^J}}}\\ \cdots \end{array} \right\}_{{\lambda _1},{\lambda _2},{\lambda _3}}}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!. \end{split}$ |
Mallat S等[8]在实验中已经得到当网络深度达到3层时,散射能量可达到99%以上. 因此本文所取的网络深度为M=3.
2 基于小波散射卷积神经网络的图像检索算法流程 2.1 算法思路图像检索的思路是提取图像库的特征,存储在数据库中以建立索引. 然后对查询图像也提取特征,与数据库中特征进行匹配,计算相似度,最后返回相似结果(算法流程见图2). 本文算法是基于小波散射卷积神经网络提取小波散射特征矩阵. 这些特征矩阵是满足平移不变性和形变稳定性,然后再对这些特征矩阵进行均值和方差化. 此举不仅能解决任意尺度输入问题,同时也具有降维的效果. 因此,本文将采用这种做法以得到图像的特征向量,然后进行匹配,返回相似度最大的N个图像作为检索结果.
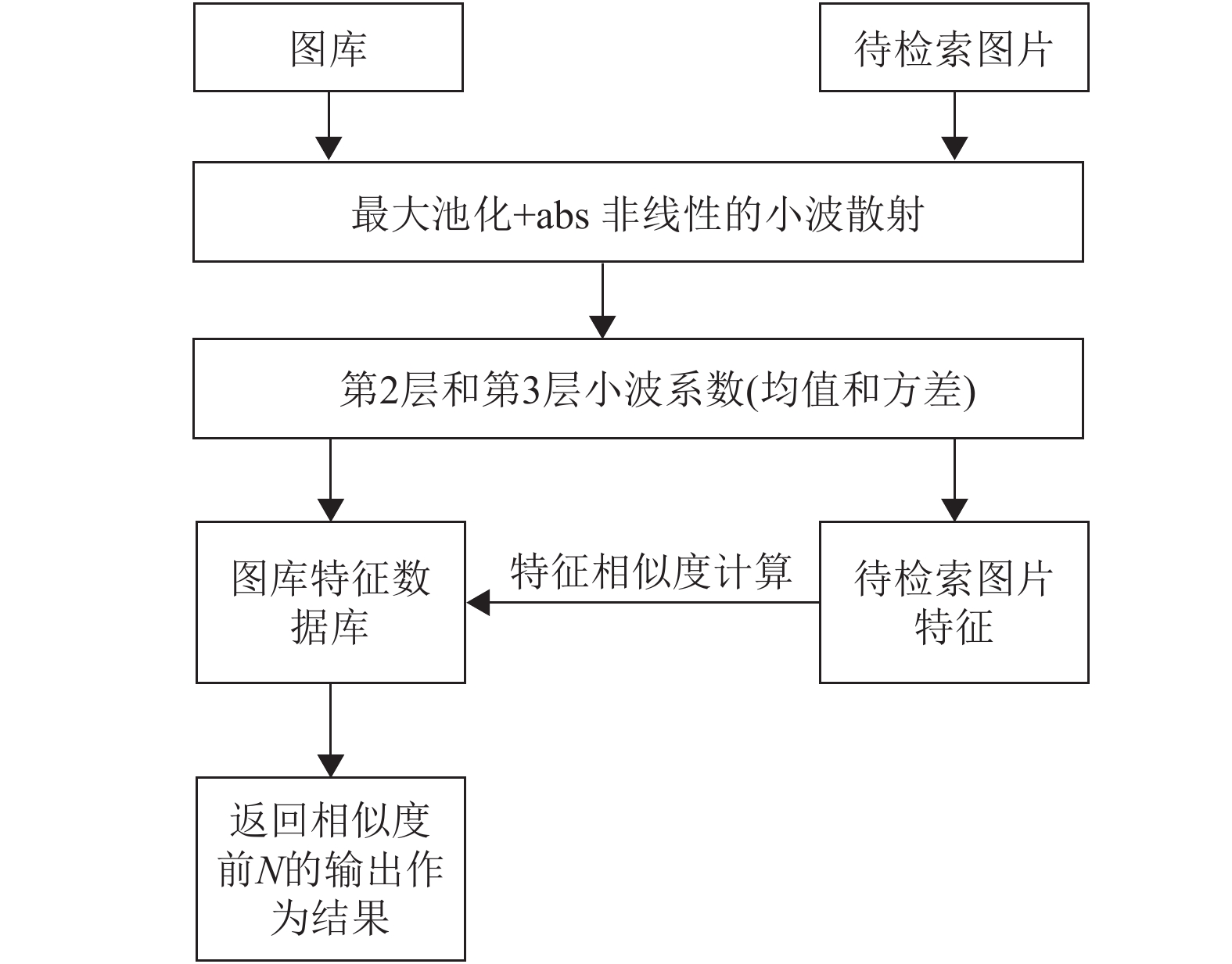
|
图 2 检索流程 Figure 2 the retrieval process |
本文算法小波散射结果如图1. 图像先通过小波散射卷积神经网络提取小波散射特征系数,此处设置网络深度M=3,方向L=4,尺度J=3,这样可提取出散射网络在不同尺度和不同方向上对应的3层特征系数矩阵:第1层为1个,第2层为12个,第3层为48个. 所有特征集合在一起为
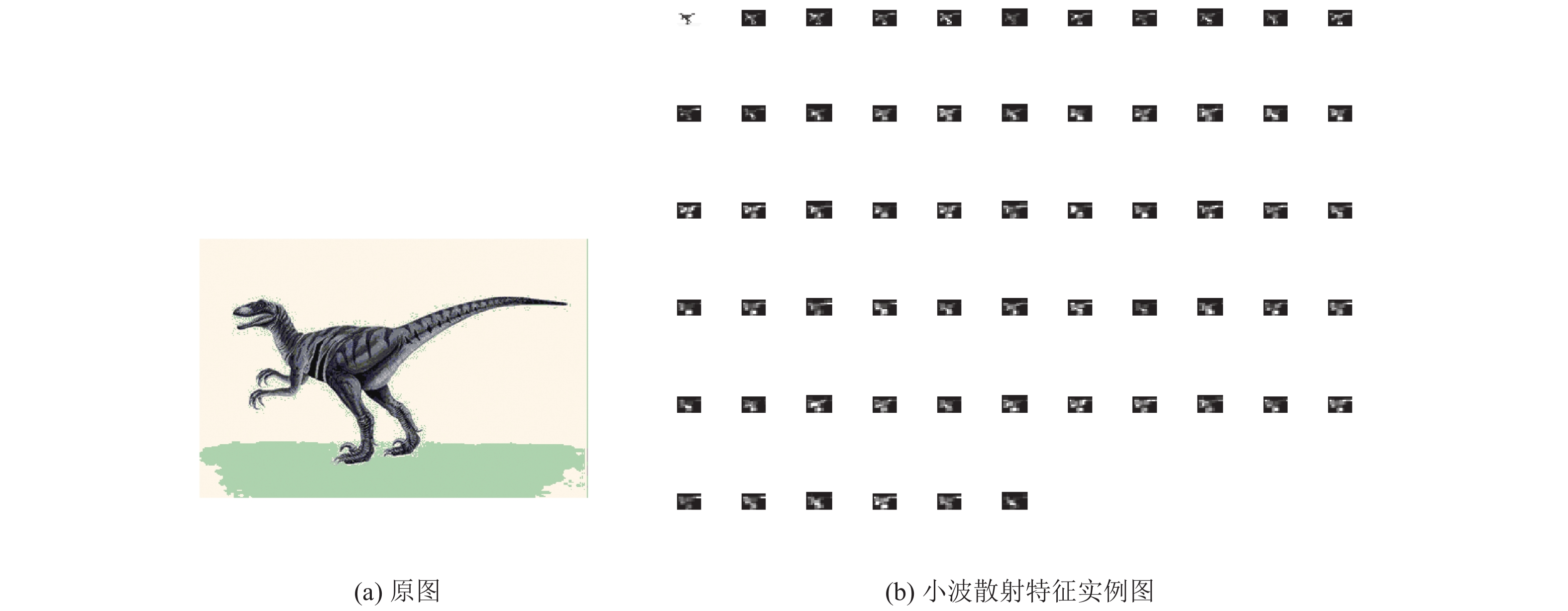
|
图 3 恐龙及其小波散射特征实例图 Figure 3 The original image and its wavelet scattering feature example |
根据小波散射的性质,已知第1层特征系数矩阵为全局特征,能量最大,但噪声也最大. 第2层、第3层特征系数矩阵为局部特征,突出细节. 本文主要是通过分析小波散射特征系数矩阵的第2层和第3层,并计算其特征系数矩阵对应的平均值(
| ${\mu _{s,k}} = \frac{1}{{M \times N}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{{S}}_{s,k}}(i,j)} } ,$ | (7) |
| ${\sigma _{s,k}} = \sqrt {\frac{1}{{M \times N}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left( {{{{S}}_{s,k}}(i,j) - {\mu _{s,k}}} \right)}^2}} } }, $ | (8) |
其中
本文采用的欧氏距离来计算相似度,即特征向量之间的距离来计算相似度. 根据式(7)、(8)的计算方式,可以得到每张图片的特征向量
| $S \!=\! \alpha \sqrt {{{\left( {{{{f}}_{2Q}} \!-\! {{f}}_2} \right)}^2}} \!+\! \left( {1 \!-\! \alpha } \right)\sqrt {{{\left( {{{{f}}_{3Q}} \!-\!{{f}}_3} \right)}^2}} \;\;\;\; 0 \leqslant \alpha \leqslant 1. $ | (9) |
其中
本文采用电脑配置Windows 7,i5-6600cpu,8 G内存,MATLAB R2014a编程实现. 本文使用的数据库为图像检索中常用的corel-1000图像库作为实验数据库,其中包含了土著人、沙滩、大巴车、恐龙等10类图像,每个类别为100张图片,其大小为384×256像素或者256×384像素. 本文使用查全率(recall)P作为评价指标.
| $P = \frac{{\sum {{m_i}} }}{M},$ | (10) |
式(10)中M表示返回的检索图片数量,
图4(a)、(b)分别为恐龙和公共汽车在本文算法上检索的结果.

|
图 4 恐龙和公交图片的检索结果 Figure 4 The dinosaur and the bus image retrieval results |
基于小波散射变换的图像检索算法步骤为:(1) 图片统一进行预处理,归一化. (2) 对图库和待检索的图片进行小波散射变换,提取其小波散射系数特征(此处用的最大池化和绝对值的非线性变换). (3) 针对第2层和第3层的小波散射系数特征矩阵,求其均值和方差. (4) 利用式(9),对图库中每张图片和待检测图片进行特征欧氏相似距离计算. (5) 利用下面3.2寻找最优的超参
本文在非洲居民类(其余类别背景相对简单)中随机选取10张图片,每张图片检索并返回这10张图片的结果. 在遍历
图5横坐标为系数权重
表1为结果返回10张图片本文算法和文献[15-16]的所有图片平均查全率.
由表1可知,本文算法在corel-1000图像库上的图像检索效果总体上优于另外两种算法,尤其是在公共汽车和花等轮廓和纹理特征比较明显的图像上检索效果尤为明显. 其中,在文献[15]中,它用到的方法是对图片的HSV3个通道分别做小波变换,级联3个通道的小波特征. 文献[16]是图像的颜色矩和小波变换相结合. 两者都为小波变换的纹理特征和颜色特征结合,相当于多特征的融合. 本文算法仅仅是基于灰度图的小波散射系数特征(单一特征),但效果却更好,这也验证了本文算法的可行性和优越性.
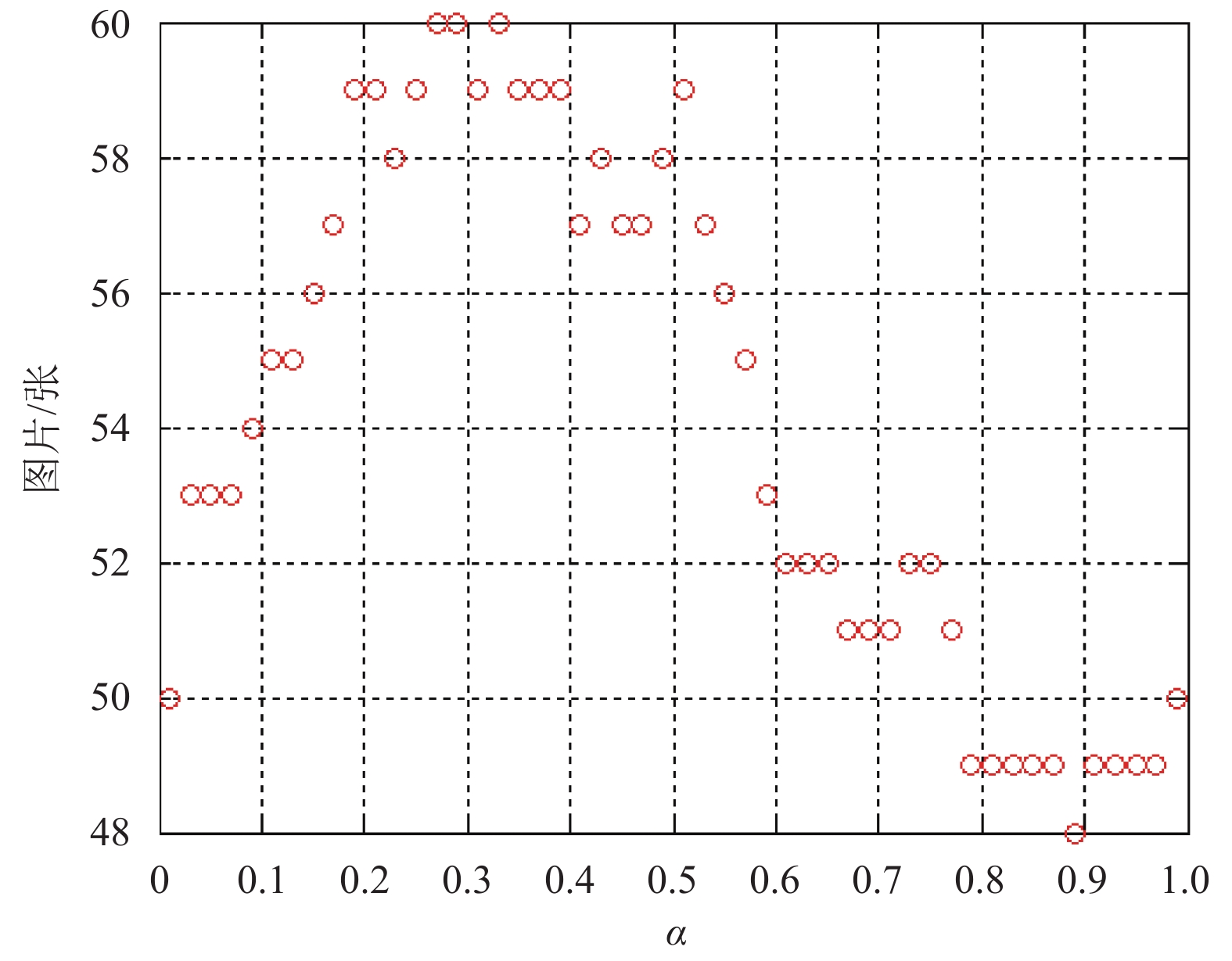
|
图 5 不同
|
| 表 1 3种算法平均查全率比较 Table 1 Comparison of average precision of three algorithms |
本文算法是利用小波散射卷积网络方法来提取图片特征并进行加工以实现在图像检索方面的应用,实验表明了我们方法的有效性和优越性. 但此方法仅从图像的灰度图的纹理特性着手,用到的特征较为单一,并不能完美地检索出所有图片,同时在寻找超参
| [1] |
AKGUI C B, RUBIN D L, NAPEL S. Content-based image retrieval in radiology: current status and future directions[J].
Journal of Digital Imaging, 2011, 24(2): 208-222.
DOI: 10.1007/s10278-010-9290-9. |
| [2] |
KHODASKAR A, LADHAKE S. A novel approach for content based image retrieval in context of combination S C techniques[C]//LADHAKE S. International Conference on Computer Communication and Informatics. Coimbatore: IEEE, 2015: 1-6.
|
| [3] |
张克军, 窦建君. 基于小波方向波变换和灰度共生矩阵的纹理图像检索[J].
徐州工程学院学报(自然科学版), 2016, 31(4): 65-69.
ZHANG K J, DU J J. Texture image retrieval based on wavelet directional wave transform and gray level co-occurrence matrix[J]. Journal of Xuzhou Institute of Technology(Natural Sciences Edition), 2016, 31(4): 65-69. |
| [4] |
叶志坚, 王福龙. 一种改进的FREAK算法的图像特征点匹配[J].
广东工业大学学报, 2017, 34(6): 37-42.
YE Z J, WANG F L. An improved FREAK algorithm for image feature point matching[J]. Journal of Guangdong University of Technology, 2017, 34(6): 37-42. DOI: 10.12052/gdutxb.170034. |
| [5] |
ZAGORUYKO S, KOMODAKIS N. Learning to compare image patches via convolutional neural networks[C]// Computer Vision and Pattern Recognition. Boston: IEEE , 2015: 4353-4361.
|
| [6] |
HE K, ZHANG X, REN S. Spatial pyramid pooling in deep convolutional networks for visual recognition[J].
IEEE Transactions on Pattern Analysis & Machine Intelligence, 2015, 37(9): 1904-1916.
|
| [7] |
LECUN Y, BOTTOU L. Gradient-based learning applied to document recognition[J].
Proceedings of the IEEE, 1998, 86(11): 2278-2324.
DOI: 10.1109/5.726791. |
| [8] |
MALLAT S. Group invariant scattering[J].
Communications on Pure & Applied Mathematics, 2012, 65(10): 1331-1398.
|
| [9] |
JOAKIM A, VINCENT L, STEPHANE M. Joint time-frequency scattering for Audio classification[C]// IEEE International Workshop on Machine Learning for Signal Processing (MLSP). Boston:IEEE, 2015: 1-6.
|
| [10] |
BRUNA J, MALLAT S, BACRY E. Intermittent process analysis with scattering moments[J].
Annals of Statistics, 2015, 43(1): 1-1.
DOI: 10.1214/14-AOS1259. |
| [11] |
SIFRE L, MALLAT S. Rotation, scaling and deformation invariant scattering for texture discrimination[C]// Computer Vision and Pattern Recognition. Portland: IEEE , 2013: 1233-1240.
|
| [12] |
吴华娟, 张明新, 郑金龙. 基于小波散射卷积网络的纹理分割方法[J].
微电子学与计算机, 2013, 30(5): 31-34.
WU H J, ZHANG M X, ZHEN J L. Texture segmentation based on wavelet scattering convolution network[J]. Microelectronics & Computer, 2013, 30(5): 31-34. |
| [13] |
伍家松, 姜龙玉, 韩旭. 小波散射网络在各种彩色空间进行图像纹理分类的性能比较[J].
东南大学学报(英文版), 2015, 31(1): 46-50.
WU J S, JIANG L Y, HAN X. Performance evaluation of wavelet scattering network in image texture classification in various color spaces[J]. Journal of Southeast University, 2015, 31(1): 46-50. DOI: 10.3969/j.issn.1003-7985.2015.01.008. |
| [14] |
WIATOWSKI T, BÖLCSKEI H. A mathematical theory of deep convolutional neural networks for feature extraction[J].
IEEE Transactions on Information Theory, 2015, 64(3): 1845-1866.
|
| [15] |
金汉均, 曾婷. 小波变换在HSV颜色空间上的图像检索应用研究[J].
电子测量技术, 2016, 39(7): 106-109.
JIN H J, ZENG T. Application of wavelet transform to image retrieval in HSV color space[J]. Electronic Measurement Technology, 2016, 39(7): 106-109. DOI: 10.3969/j.issn.1002-7300.2016.07.022. |
| [16] |
SINGH S M, HEMACHANDRAN K. Content-based image retrieval using color moment and gabor texture feature[J].
International Journal of Computer Science Issues, 2012, 9(5): 719-724.
|
 2019, Vol. 36
2019, Vol. 36
