移动机器人正朝着具有自组织、自学习、自适应的智能化方向发展，随着应用领域日益广泛，如何使移动机器人决策系统在无需人为干预下，对未知复杂动态环境下具备环境感知、局部路径规划、轨迹跟踪和动态避障功能^[1-2]，且能保证决策系统稳定性、平滑性和泛化性，是移动机器人领域研究的关键课题.

移动机器人轨迹跟踪和动态避障定义为机器人在非线性动态环境条件下，以期望的速度沿着一条给定起点到目标点的轨迹，通过传感器局部感知以最小偏离轨迹安全无碰地绕过动态障碍物到达目的地. 这是典型的非线性动态局部可观测环境的多任务决策问题，要求决策系统具备实时性、适应性和对机器人状态的泛化性. 然而在机器人对非线性动态环境不存在任何先验信息情况下，依赖激光雷达或摄像头等传感器感知的信息构建出的环境模型必然存在噪声和不确定性，依据有噪声的环境模型进行局部路径规划和动态避障必将产生具有传递性的不确定性. 而且机器人在非线性动态环境中极易受到墨菲定律的影响^[3]，即任何可能出错的场景都会出错. 通过人工编码设计出的专家系统来适应机器人可能遇到的各种状态以对抗墨菲定律是不现实的，而选择容纳这种错误并让机器人从中学习应对策略以适应将来可能出现的相似状态空间，并纠正这些错误是一个创新.

传统移动机器人局部路径规划动态避障算法主要有：(1) Koren Y等^[4]提出人工势场法，视目标点产生引力，障碍物产生斥力，引力和斥力的合力引导机器人运动方向. 然而引力势场相对斥力势场作用范围更大，当机器人和障碍物的距离超过障碍物影响范围时，机器人会不受斥力势场的影响，在某些区域会受到多个引力或斥力势场的联合分布，而陷入局部极小陷阱区域，在障碍物前产生振荡或在狭窄通道中徘徊，在障碍物群中不能识别路径，导致目标不可达等问题. (2) Yang S X等^[5]提出神经网络方法，该算法将优化目标函数定义为轨迹点集的碰撞能量函数与距离函数的和. 通过迭代求解优化目标函数极值，使路径能避障同时趋向于最短，然而权值训练不理想导致算法效果不理想. (3) Castillo O等^[6]提出遗传算法根据自然选择、遗传操作抽象出算子，将二维路径规划编码问题简化为一维编码问题，并把动态避障和最短路径生成要求融合成适应度函数，通过对代表可行解的参数编码字符串进行遗传操作，并且并行对可行解空间进行搜索求解，进而得到全局最优解. (4) Clerc M等^[7]提出粒子群优化算法，将粒子群个体位置代表优化问题的搜索空间潜在的解，该算法每一步寻优方向和步伐大小依据当前群体中某些个体处于最优位置以及这些个体自身曾经到达的最优位置来调整. 但该算法易陷于局部最优，参数选择不当造成早熟收敛问题.

为了解决移动机器人在非线性动态环境的多任务决策问题，本文提出了基于深度强化学习的环境视觉感知和多任务决策方法^[8]. 该算法采用端对端的学习方式，将深度卷积神经网络的特征提取能力与强化学习的决策能力相结合^[9]，通过视觉感知移动机器人周围局部动态环境作为网络输入，网络输出为机器人的动作，并采用卷积网络拟合基于值的非模型时间差Q学习算法，该算法使用经验回机制，在线处理强化学习智能体与动态仿真环境的交互状态转移样本，随机抽取状态转换序列以缓解训练时数据相关和算法不稳定问题，为加快网络模型收敛，动作选择策略使用小概率和低于阈值回报时随机选择动作的搜索策略，并运用已知最大Q值所对应动作的利用策略，平衡算法的搜索与利用策略可加快网络模型的收敛速度. 仿真环境使用400×400像素二维环境地图来描述机器人所处的非线性动态环境模型，在该环境模型下机器人每时刻可通过视觉感知，获取以其为中心的80×80像素环境图像，以及机器人做出动作后的即时奖惩回报. 机器人决策系统根据与环境交互获得的奖惩不断地迭代优化网络模型，从一系列状态动作序列中学习出最优策略.

1 相关研究 1.1 深度卷积神经网络

深度卷积神经网络由多层非线性运算单元组成，通过特征提取器的自我学习完成图像特征提取任务，自动地从大量训练数据中学习复杂的、高维的非线性特征映射，以发现数据的分布式特征^[10]，进而通过分类器将这些特征进行分类，解决移动机器人在某个状态下动作选择的回归预测问题.

本文运用深度卷积神经网络对视觉感知图像信息进行特征提取，具有对图像发生位移、缩放、形变时保持特征不变性特点，第n层卷积神经网络的第i个特征图计算定义为

$x_i^n = f\left( {0,\sum\limits_{j \in {M_i}} {x_j^{n - 1}k_{ji}^n} + b_i^n} \right).$

(1)

式(1)中， ${M_i}$ 是特征图的集合， $k_{ji}^n$ 为第n层的第i个卷积核，b_iⁿ为第n层第i个编置，f()为激活函数，本文采用纠正线性单元作为激活函数(Rectified Linear Unit，ReLU).

1.2 强化学习

强化学习相较于其他经典机器学习算法，其最大特点是在交互中学习，可解决序列多步决策问题，通过策略迭代学习获得最大累积回报的最优策略π^[11]. 强化学习智能体在t时刻感知到的环境状态为s_t，它采取某种动作a_t达到另一状态s_t+1，同时获得环境评判一次交互动作好坏的立即奖惩回报r_t，而完成任务的最终奖赏标记在多步动作之后才能观察到，是一种标记延迟的监督学习，整个交互过程是部分可观测马尔科夫决策序列过程，表示为 $\left\langle {{s_t},{a_t},{r_t},{s_{t + 1}}} \right\rangle $ .

强化学习智能体遵循策略从t₁时刻状态开始到t₂时刻状态结束时，状态累积奖赏回报之和定义为

${R_t} = \sum\nolimits_{t' = {t_1}}^{{t_2}} {{\gamma ^{t' - {t_1}}}{r_{t'}}} .$

(2)

引入折扣衰减系数γ是为了避免陷入无限循环，其取值为 $\gamma \in \left[ {0,1} \right]$ ，它权衡未来回报在当前时刻的价值比例.

状态动作值函数 ${Q^{\pi} }\left( {s,a} \right)$ 定义强化学习智能体遵循策略π在状态s下，采取动作a直到状态结束的这一过程最大累计回报，表示为

${Q^{\pi} }(s,a) = E\left[ {{R_t}\left| {{s_t} = s,{a_t} = a,\pi } \right.} \right].$

(3)

如果对于所有的状态动作空间的期望回报达到最大值，对应的策略π^*为最优策略. 最优策略的状态动作值函数定义为

${Q^*}(s,a) = {\max _\pi }E\left[ {{R_t}\left| {{s_t} = s,{a_t} = a,\pi } \right.} \right].$

(4)

而且最优状态动作值函数遵循贝尔曼最优方程，即

${Q^*}(s,a) = {E_{s'\sim S}}\left[ {r + \gamma {{\max }_{a'}}Q(s',a')\left| {s,a} \right.} \right].$

(5)

传统求解强化学习算法Q值函数方法一般通过迭代贝尔曼方程，即

${Q_{i + 1}}(s,a) = {E_{s'\sim S}}\left[ {r + \gamma {{\max }_{a'}}{Q_i}(s',a')\left| {s,a} \right.} \right].$

(6)

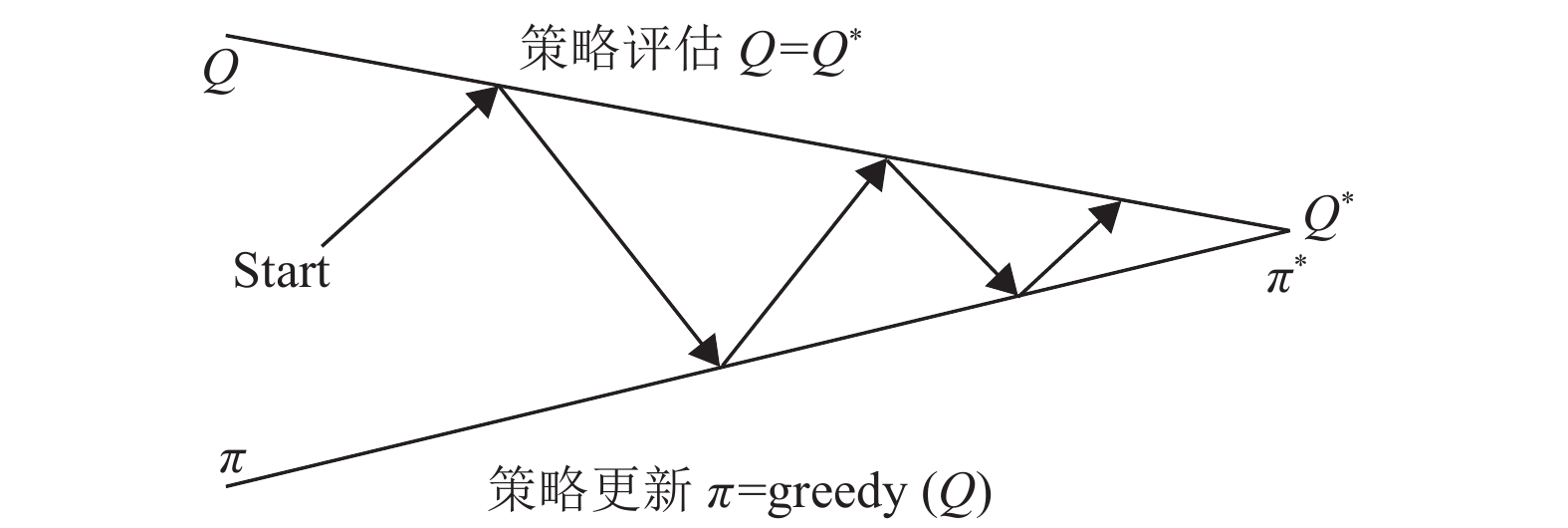
如图1所示，当 $i \to \infty $ 时，强化学习通过策略评估和策略更新求解最优策略，使状态动作值函数最终收敛 ${Q_i} \to {Q^*}$ .

然而，对于采用表格存储策略的传统强化学习算法，当状态动作空间规模较大或动作空间连续时，将会出现维数灾难的问题，通过迭代式(6)求解最优策略计算代价太大，通常使用线性回归模型或非线性的深度卷积神经网络模型，通过函数逼近方法拟合状态动作值函数，以增强算法泛化性，即 $ Q\left( {s,a\left| \theta \right.} \right) \approx $ ${Q^*}\left( {s,a\left| \theta \right.} \right)$ .

1.3 深度强化学习

早期的深度强化学习算法由于训练数据的缺乏和计算能力的不足以及算法结合存在不稳定等问题，只适用于维度较小状态空间的控制决策问题. Mnih等^[12]开创性提出基于视觉感知控制的深度Q网络(Deep Q-Network，DQN)模型算法，将卷积神经网络与基于Q学习的强化学习算法相结合^[13]；Hasselt等^[14]提出了有2套不同参数θ和θ^–的深度双Q网络 (Deep Double Q-Network，DDQN)模型^[15]，该算法的提出是为了降低过高估计Q值的风险，将动作选择和策略评估分别用两个不同参数的网络分离开；Bellemare等^[16]重新定义贝尔曼方程，该算法为了缓和模型因每次选取下一状态的最大Q值对应动作所带来的评估误差，而采用增大最优动作值和次优动作值之间的差别.

2 基于深度强化学习的移动机器人轨迹跟踪和动态避障

本文提出基于深度强化学习的移动机器人轨迹跟踪和动态避障方法，该方法中智能体不需了解环境动力学模型如何工作，而仅聚焦于价值函数，先评估每个状态动作的Q值，再根据Q值求解最优策略 $\pi \left( {a\left| s \right.} \right)$ ，策略函数由价值函数间接求解得到. 网络模型训练数据来源于强化学习智能体与环境动力学模型交互，使得机器人态势感知和决策控制之间形成一个闭环. 强化学习智能体依据策略在状态s_t时，采取动作a_t后的状态s_t+1和及时收益r_t只与当前状态和动作有关，而与历史状态无关，观测到的当前状态信息完整地决定了决策需要的特征，是一个部分可观测马尔可夫决策过程，即

$P\left( {{s_{t + 1}},{r_{t + 1}}\left| {{s_0},{a_0}, \cdots ,{s_t},{a_t}} \right.} \right) = P\left( {{s_{t + 1}},{r_{t + 1}}\left| {{s_t},{a_t}} \right.} \right).$

(7)

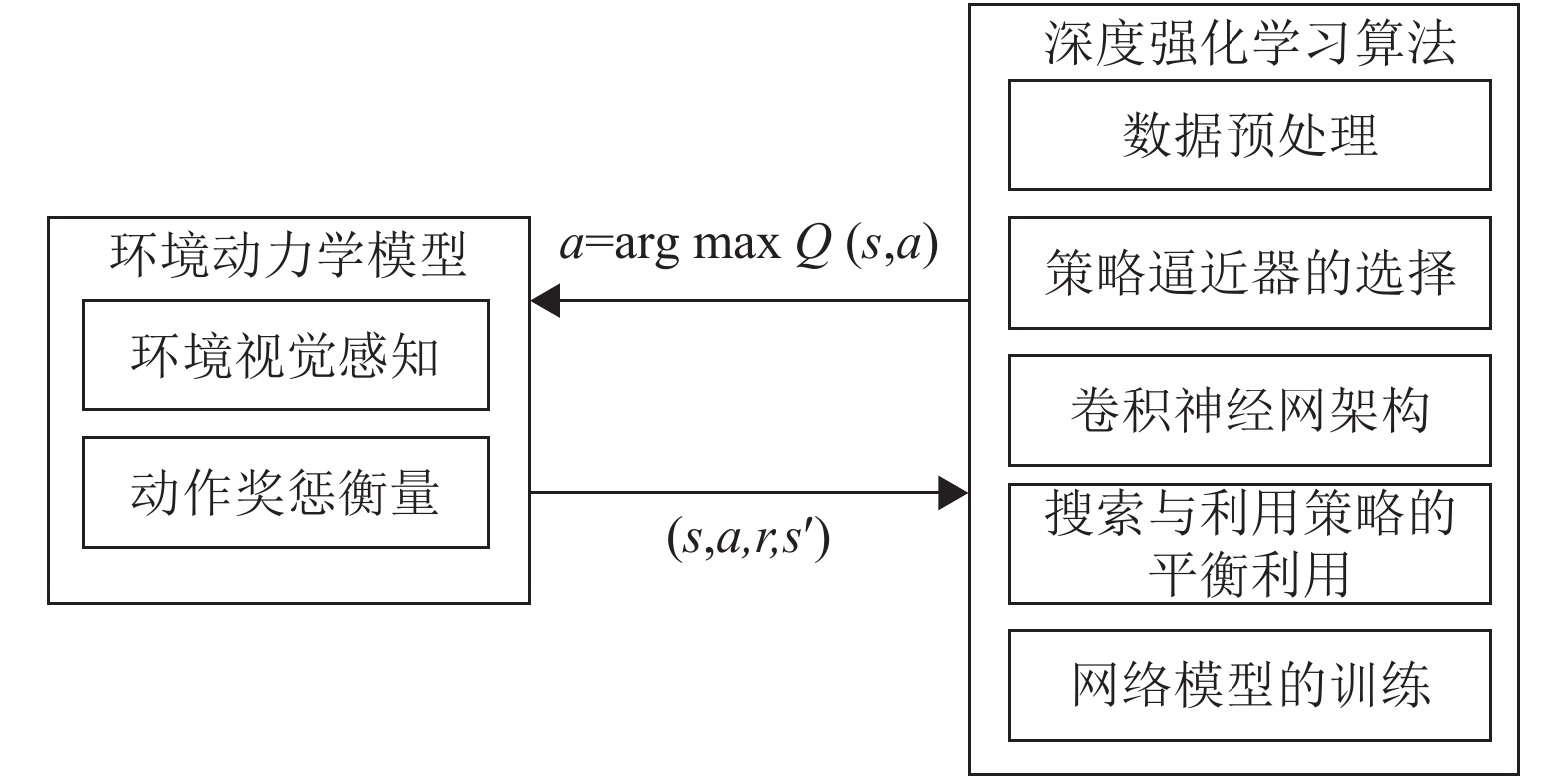
该方法称为基于异策略时间差分Q-learning方法，产生行动数据的动作策略和需要评估的策略不是同一个策略. 动作策略使用小概率随机策略(ε)和低于阈值时使用随机动作的引导性策略，而要评估和改进的策略是每次都选取最大值函数对应动作的贪婪策略. 基于深度强化学习的移动机器人轨迹跟踪和动态避障算法系统结构如图2所示.

2.1 数据预处理

移动机器人轨迹跟踪和动态避障算法主要运用深度卷积神经网络对机器人态势感知的图像数据进行特征提取，即使图像信息发生位移、缩放、形变时，还能保持机器人对障碍物和轨迹相对位置特征不变性，故网络输入先将RGB图像进行灰度化预处理，旨在减少输入数据维数.

2.2 策略的逼近器选择

制约传统强化学习算法的瓶颈在于Q-learning是一种表格方法，根据过去出现过的状态动作空间，更新和迭代Q值，使得其适用的状态和动作空间非常小，如果一个状态从未出现过，强化学习是无法处理的，模型几乎就没有泛化能力，为增强模型预测能力，通常使用回归函数拟合Q值： $Q\left( {s,a\left| \theta \right.} \right) \approx {Q^*}\left( {s,a} \right)$ ，θ代表的是模型参数，模型有线性的和非线性的. 传统强化学习逼近器的策略更多采用是人工特征加线性模型来拟合值函数或策略. 深度卷积神经网的兴起，以强大非线性抽象表达能力，直接从输入的图像数据中自动提取特征，端到端地拟合Q值，通常可以学到比手工设计特征更好的泛化能力，故本算法值函数或策略的逼近器选择采用深度卷积神经网络，其模型的优化目标函数为

$L(\theta ) = E\left[ {{{\left( {r + \gamma \mathop {\max }\limits_{a'} Q(s',a'{\rm{|}}\theta ) - Q(s,a|\theta )} \right)}^2}} \right].$

(8)

卷积神经网络模型权重参数(θ)的更新使用小批量数据随机梯度下降(Stochastic Gradient Descent，SGD)算法，公式为

$\nabla L(\theta ) = E\left[ {\left( {r + \gamma \mathop {\max Q(s',a'{\rm{|}}\theta )}\limits_{a'} - Q(s,a|\theta )} \right)\nabla Q(s,a|\theta )} \right].$

(9)

2.3 卷积神经网络架构

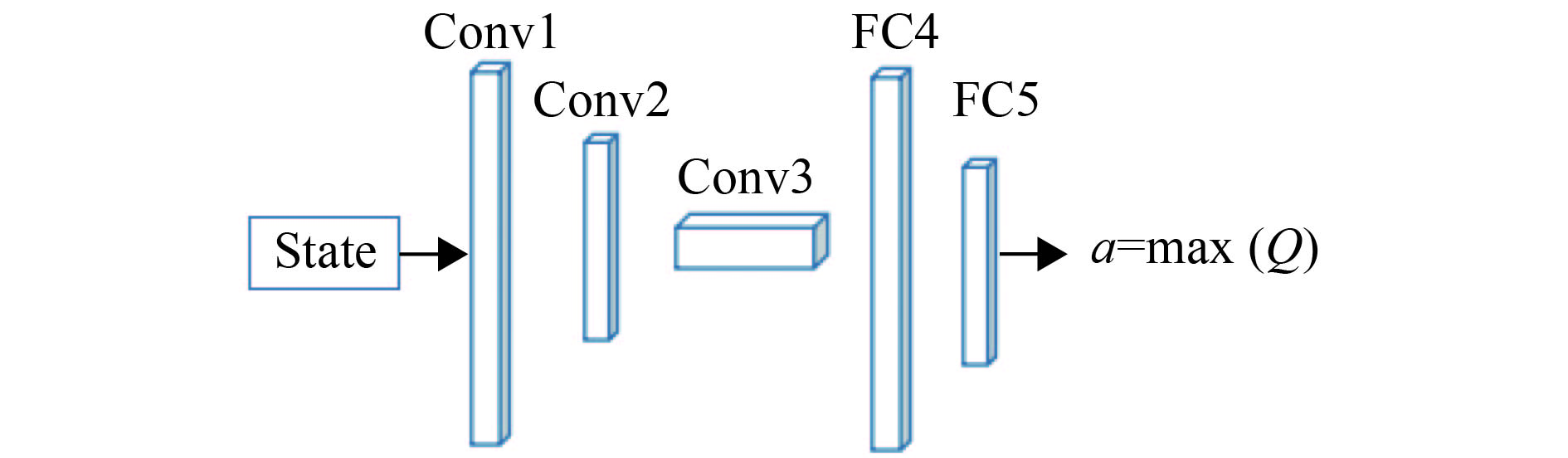
网络模型设计采用3层卷积层(Conv)，2层全连接层(Fc)，网络输入为状态state，网络输出为各个动作对应的Q值，选择对应最大Q值的动作与环境交互，网络计算成本与动作空间成正比，网络模型如图3所示，网络模型参数设置如表1所示.

2.4 搜索与利用策略的平衡利用

强化学习是一个试错的学习过程，采用探索和利用两种策略. 强化学习智能体的利用策略，是指当得到当前最大期望回报的动作策略，就直接利用当前最好的策略动作；强化学习智能体探索策略^[17]，是指即使得到了当前期望最高的奖励，但是它仍然是以一定概率去选择随机动作，以获取各个动作回报的期望奖励值，以搜索获取更好结果. 为了使强化学习智能体与环境的交互中学习一个好的策略，同时又不至于在试错的过程中丢失太多的奖励，本文算法平衡运用探索和利用策略，搜索策略定义为小概率随机搜索策略和及时回报小于设定阈值进行随机动作搜索的引导式(δ)策略，增加强化学习智能体对Q值的选择，加快神经网络模型收敛速度，小概率策略ε值更新公式为

$\varepsilon = \varepsilon - \left( {{\rm{Ini}}\_\varepsilon - {\rm{Fin}}\_\varepsilon } \right)/{{\rm explore}} .$

(10)

其中Ini_ε为初始ε值，Fin_ε为ε衰减终止值，explore为ε衰减的总步数. 小概率随机搜索策略及引导式策略搜索定义为

${\rm{flag}} = (r < {\rm{threshold}})\& ({\rm{rand}}() < \varepsilon ).$

(11)

当flag为True时，使用随机动作，为false时使用利用策略选择动作，其中r为及时奖励回报threshold为阈值，rand() $ \in \left[ {0,1} \right]$ 为随机数.

利用策略定义为

$\pi = {\arg \max }_a Q(s,a).$

(12)

2.5 模型的训练

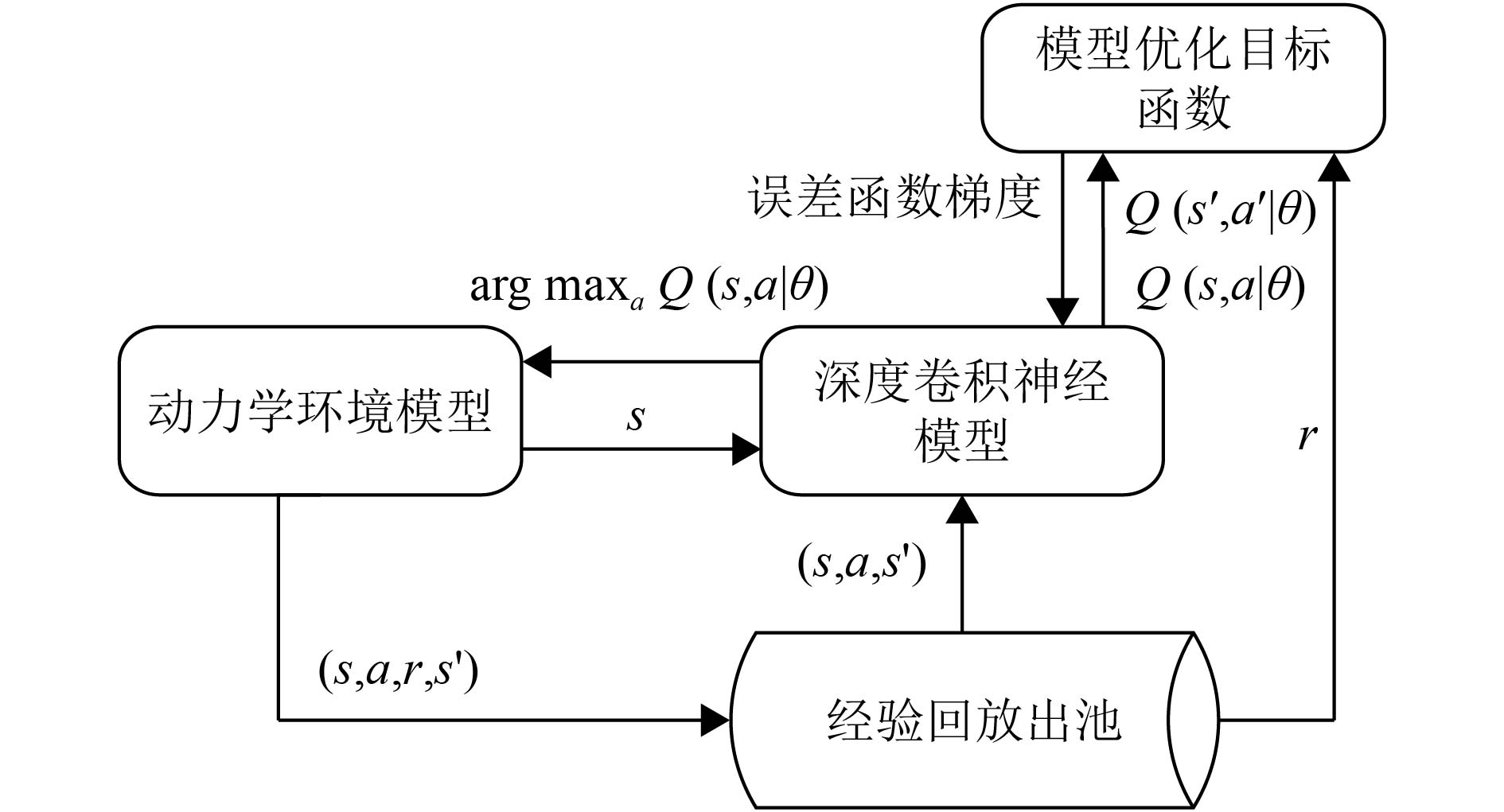
深度卷积神经网络进行训练时存在的假设是训练数据是独立同分布，而从环境中采集到的数据之间存在着关联性，利用这些数据进行顺序训练，算法模型将存在不稳定问题. 通过经验回放的方式可以令训练出的模型收敛且稳定^[18]. 在强化学习智能体与动力学环境交互过程中，同时将一部分状态动作序列数据存储起来，然后利用均匀随机采样的方法从存储数据库中抽取数据，卷积神经网络通过模型优化目标函数进行梯度调参训练. 训练出的模型行为分布的平均值超过了它以前的许多状态，平滑了学习，避免了参数中的振荡或发散，网络模型训练流程如图4所示.

2.6 环境动力学模型的视觉感知和行为奖惩函数

深度卷积神经网络的输入是机器人为中心截取环境地图80×80RGB的原始图像感知区域，该区域符合移动机器人采用激光雷达和深度摄像机的探测范围，移动机器人作出决策也是基于移动机器人可感知的局部环境而非全局环境.

在机器人的轨迹跟踪、局部路径规划和实时动态避障的多任务中，设计易于训练且能优化智能体作出正确决策的奖罚函数是很困难的. 假设想要机器人学习如何进行轨迹跟踪，其最自然的奖罚函数是让智能体在达到所需的最终轨迹配置时得到奖励1，得到其他结果的奖励为–1. 对于不同的任务来说，环境给出的及时回报密度不一样，其中采用随机选择动作的策略对训练有价值的及时回报是比较稀疏的，有些任务的及时回报可能只有在任务最后成功或失败的时候才会有非零的回报，其余时候及时回报都是0的稀疏奖励设置下，强化学习无法训练机器人完成以期望速度沿着轨迹前进且进行局部路径规划与动态避障等多任务，强化学习的初始随机探索策略不能为这一目标任务获取过多有价值正向回报. 为此环境动力学模型定义机器人沿着轨迹行走及时奖惩函数定义为

$r = 10 - {\rm{dis}}\_{p^{1.2}},$

(13)

其中dis_p^1.2表示对移动机器人与轨迹偏离的直线距离的1.2次方惩罚值. 当移动机器人与障碍物相遇进行动态避障时，奖罚函数定义改为

$r = 10 - {({\rm{abs}}({\rm{dis}}\_o - 8))^{1.2}},$

(14)

其中dis_o定义为移动机器人与障碍物的距离，abs()表示取绝对值，移动机器人进行轨迹跟踪和动态避障同时能够不断向目标点靠近，在奖惩函数基础上增加靠近目标的激励，定义为

$r = r + 3 - {\rm{dis}}\_b,$

(15)

其中dis_b定义为移动机器人与最优动作位置的距离，数字3表示为对兼顾速度的动作进行奖励.

2.7 深度强化学习算法伪代码

深度强化学习算法计算流程，S为状态空间，A(s)为状态空间可执行的动作，D(N)为经验回放池，θ为模型参数，min_bach为小批量数据，ϕ()为卷积神经网络特征提取操作， $\varepsilon \left| \delta \right.$ 为搜索策略，greedy()为利用策略， $(s,r) \leftarrow {\rm{env}}(a)$ 为环境动力学执行动作a返状态s和回报r.

[1] Init $\forall s \in S$ ， $a \in A(s)$ ， $Q(s,a) \leftarrow \theta $ , $D(N)$ ，e=1，t=1，j=1，min_bach=64

[2] for e<M do

[3] ${s_1} = \{ {x_1}\} ,{\phi _1} = \phi ({s_1})$

[4] for t<T do

[5] if $\varepsilon |\delta $ >0 than

[6] a=rand()

[7] else

[8] a=greedy( ${\phi _1}$ )

[9] $\left( {s,a} \right) \leftarrow {\rm{env}}\left( a \right)$

[10] ${s_{t + 1}} = ({x_t},{a_t},{x_{t + 1}}){\phi _{t + 1}} = \phi ({s_{t + 1}})$

[11] $D \leftarrow ({\phi _t},{a_t},{r_t},{\phi _{t + 1}})$

[12] for j<min_bach do

[13] $D \to ({\phi _j},{a_j},{r_j},{\phi _{j + 1}})$

[14] if Terminal then

[15] ${y_j} = {r_j}$

[16] else

[17] ${y_j} = {r_j} + \gamma {\max _d}Q({\phi _{j + 1}},a'|\theta )$

[18] $\Delta \theta = \alpha \left[ {{y_j} - Q(\phi ,a|\theta )} \right] \nabla Q(\phi ,a|\theta )$

[19] $\theta = \theta + \Delta \theta $

[20] end for

[21] end for

[22] end for

3 实验结果与分析

本文为了验证以上方法的有效性，在二维环境下进行了移动机器人轨迹跟踪和动态避障仿真实验，所有实验均运行在为i7处理器，主频3.40 GHz，内存为8 G的电脑上，系统为Ubuntu16.04.

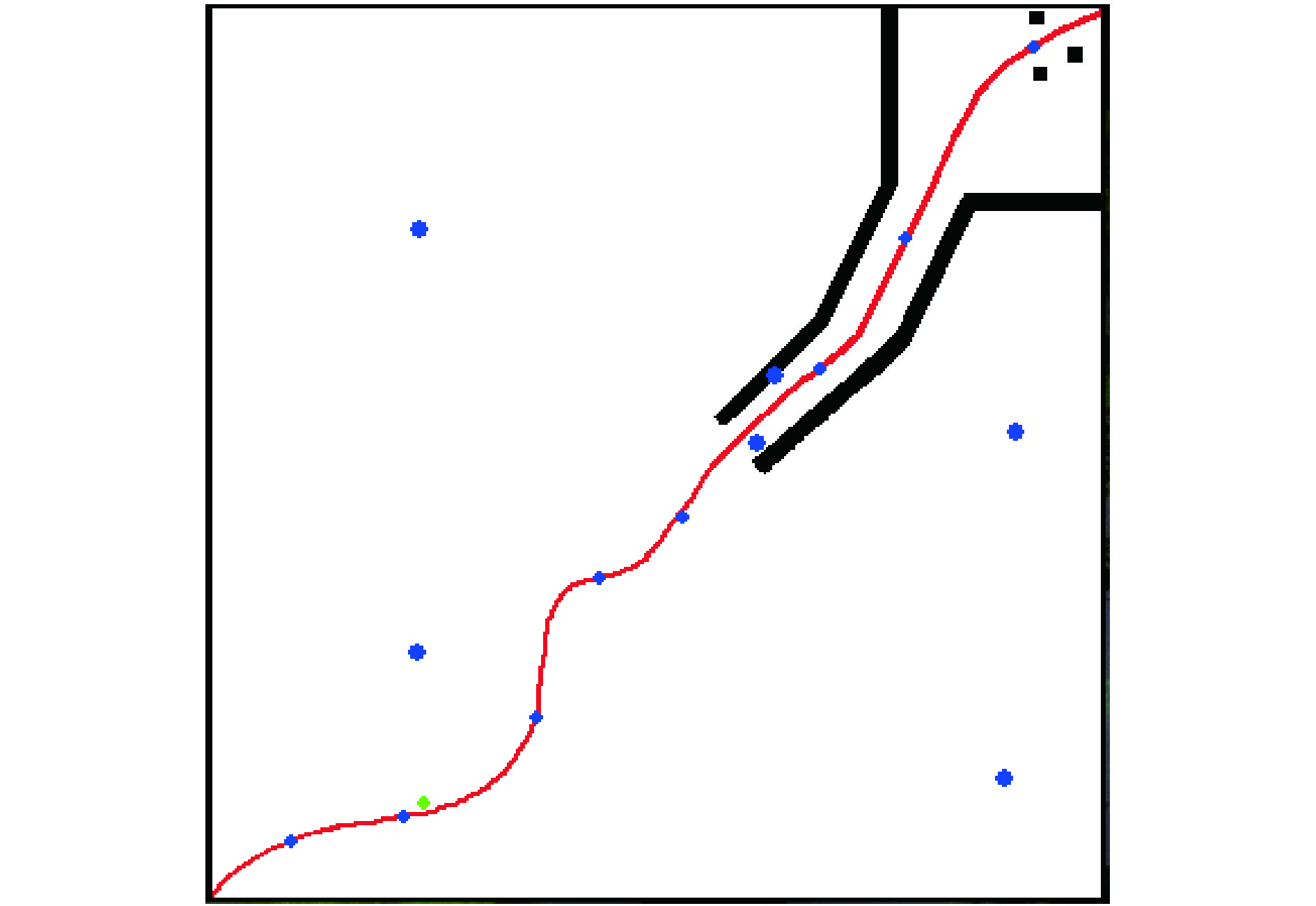
3.1 实验平台描述

移动机器人动力学仿真环境如图5所示，在该环境下，强化学习智能体控制的移动机器人为图中的绿色小球表示，从左下角沿轨迹到达右上角，期间将有5个随机运动的障碍物，以及沿轨迹从右上角向左下角运动的8个动态障碍物. 用深度卷积神经网络构建强化学习智能体，运用深度卷积神经网络模型输出最大Q值对应动作控制移动机器人，实现移动机器人动态避开沿着轨迹行走的动态障碍物同时沿着轨迹从起始点快速到达目的地. 深度卷积神经网络输入是以机器人为中心局部环境感知图像，训练强化学习智能体，根据轨迹跟踪和动态避障设定的奖惩函数自我交互学习. 奖励函数范围10~–6，当及时回报为最低时，需重置场景，以这种方式奖励限制了错误衍生品的规模，使其更容易训练，自动趋向于不同量级的高回报奖励.

3.2 实验参数设置

目标函数使用基于梯度下降的Adam 优化算法，根据损失函数对每个参数的梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习速率，算法的epsilon参数设置为10⁻⁴. 每次随机抽取经验回放池64个小批量(mini-batch)数据进行随机梯度下降算法更新网络权重，训练过程中的行为策略是小概率(ε)和引导式(δ)−贪婪搜索(greedy)算法，搜索因子ε从0.1下降到0.000 1，引导式阈值δ为5，当及时回报小于5时，进行大概率随机动作加搜索最优策略，强化学习的折扣回报衰减系数γ为0.9，网络模型训练分为180个阶段(Epoch)，每个阶段训练实时更新迭代20 000次同时保存一次模型，经验回放池(experience replay)容纳20万个序列转移样本，实验开始阶段经验回放池并没有足够训练数据，因此先使用小概率和引导策略随机选取动作进行观测(observe)1 000个样本，网络模型训练参数如表2所示.

3.3 实验结果

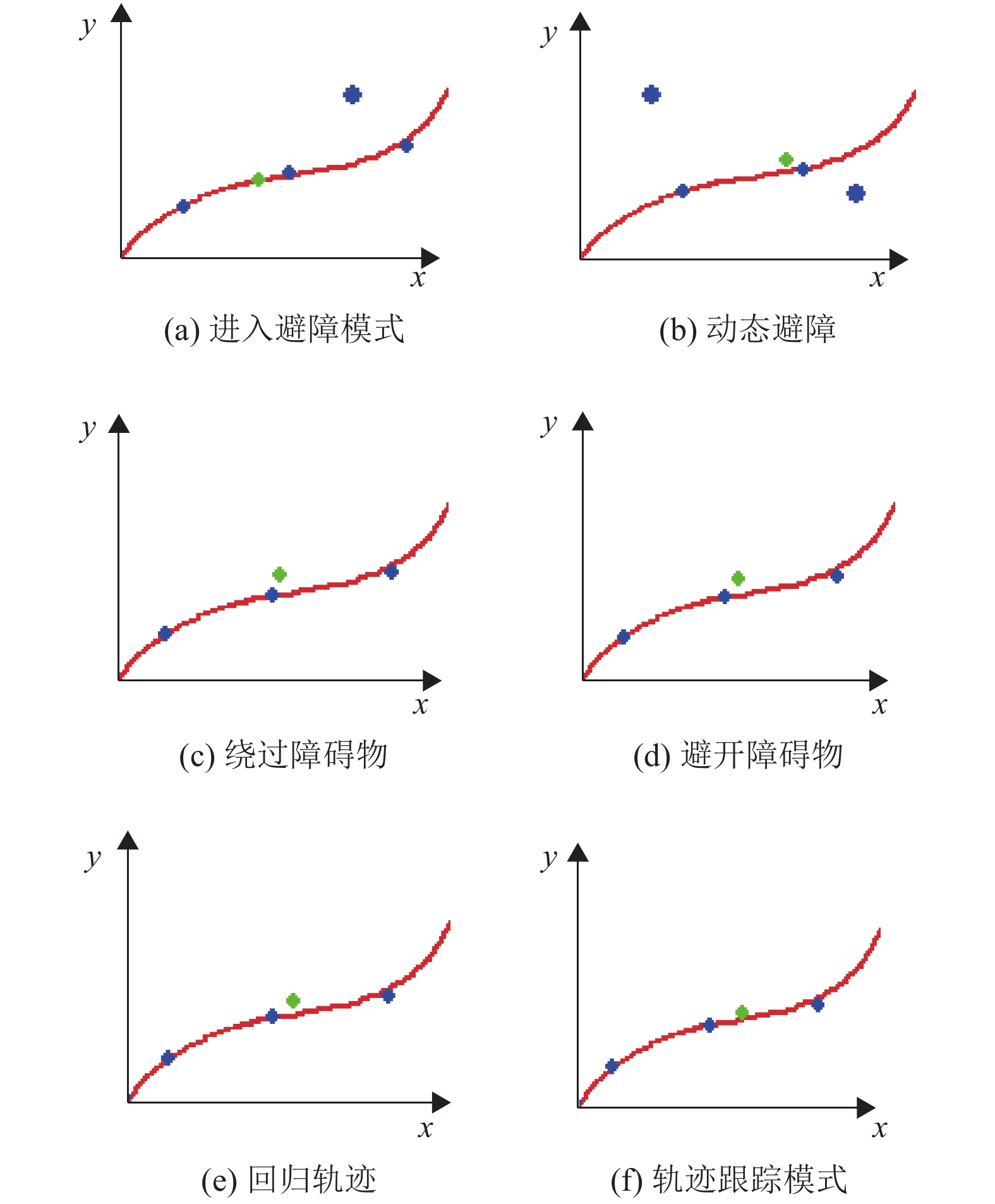
移动机器人的轨迹跟踪和动态避障实验结果如图6的局部截图所示，绿色的移动机器人小球从左下角的起始位置沿着轨迹向右上角的目标点运动，较大的蓝色障碍物小球在环境中进行非线性运动，较小的蓝色障碍物小球沿着轨迹从右上角向左下角运动. 如图6(a)~(c)所示，当移动机器人沿着轨迹向目标点运动与障碍物相遇时，深度强化学习算法满足最小偏离轨迹和动态避障要求选择最优动作作为机器人运动方向，在避障后选择回归轨迹的动作继续向目标点运动，如图6(d)~(f)所示，图中x和y代表坐标方向.

3.4 实验分析

深度卷积神经训练过程在线处理状态动作转换样本 $\left\langle {{s_t},{a_t},{r_t},{s_{t + 1}}} \right\rangle $ ，每一时刻将强化学习智能体与环境交互得到的转移样本存储在经验回放池，对卷积神经网络模型训练评估是通过定期计算损失函数值. 对强化学习算法评估通过计算一个情节开始到结束的状态动作值及某一状态下执行动作的及时回报值来衡量.

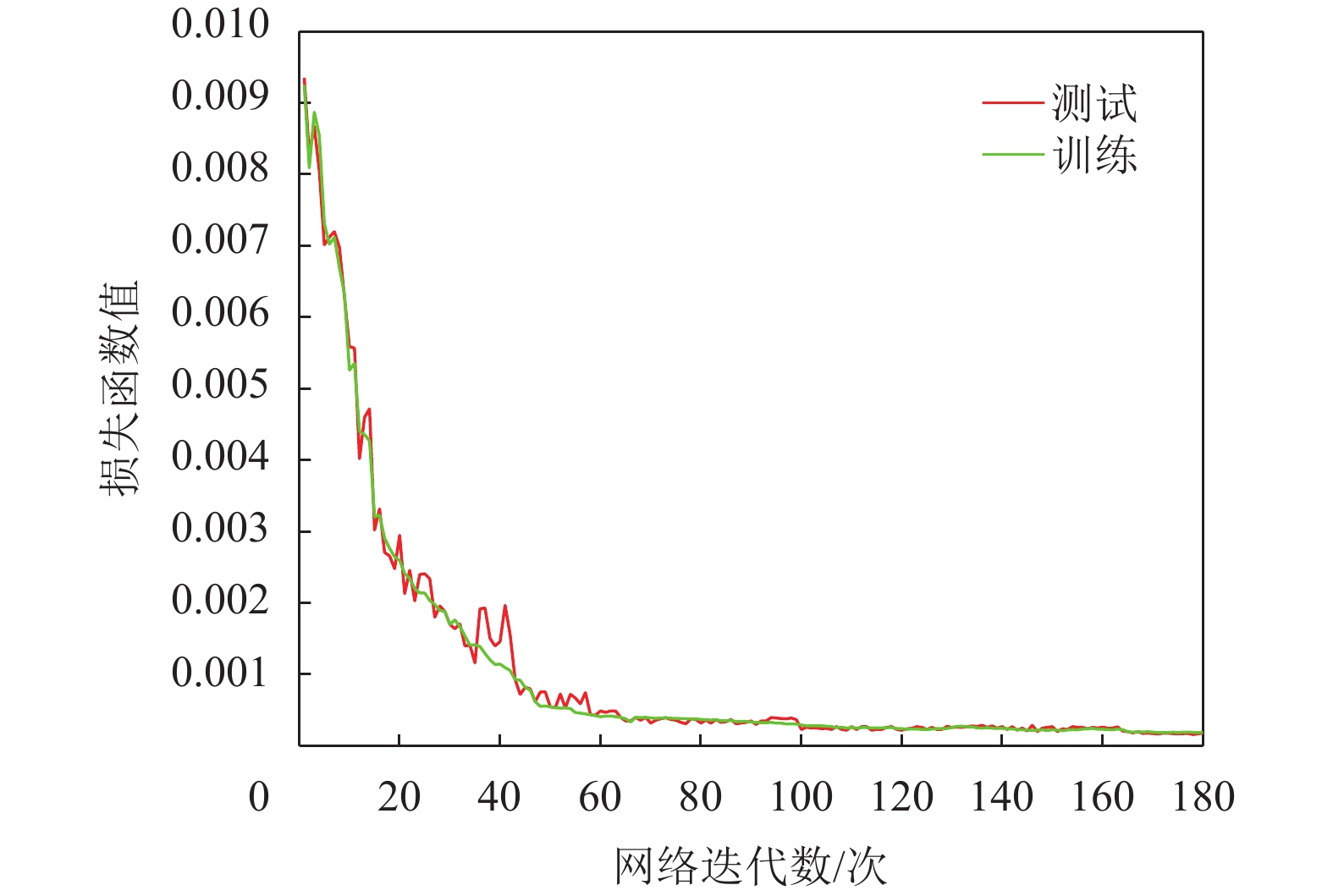
图7显示网络模型训练时损失函数值变化趋势，从图中可看到在神经网络训练60个阶段后，网络开始趋于收敛且相对平稳，在实验中没有遇到任何发散问题.

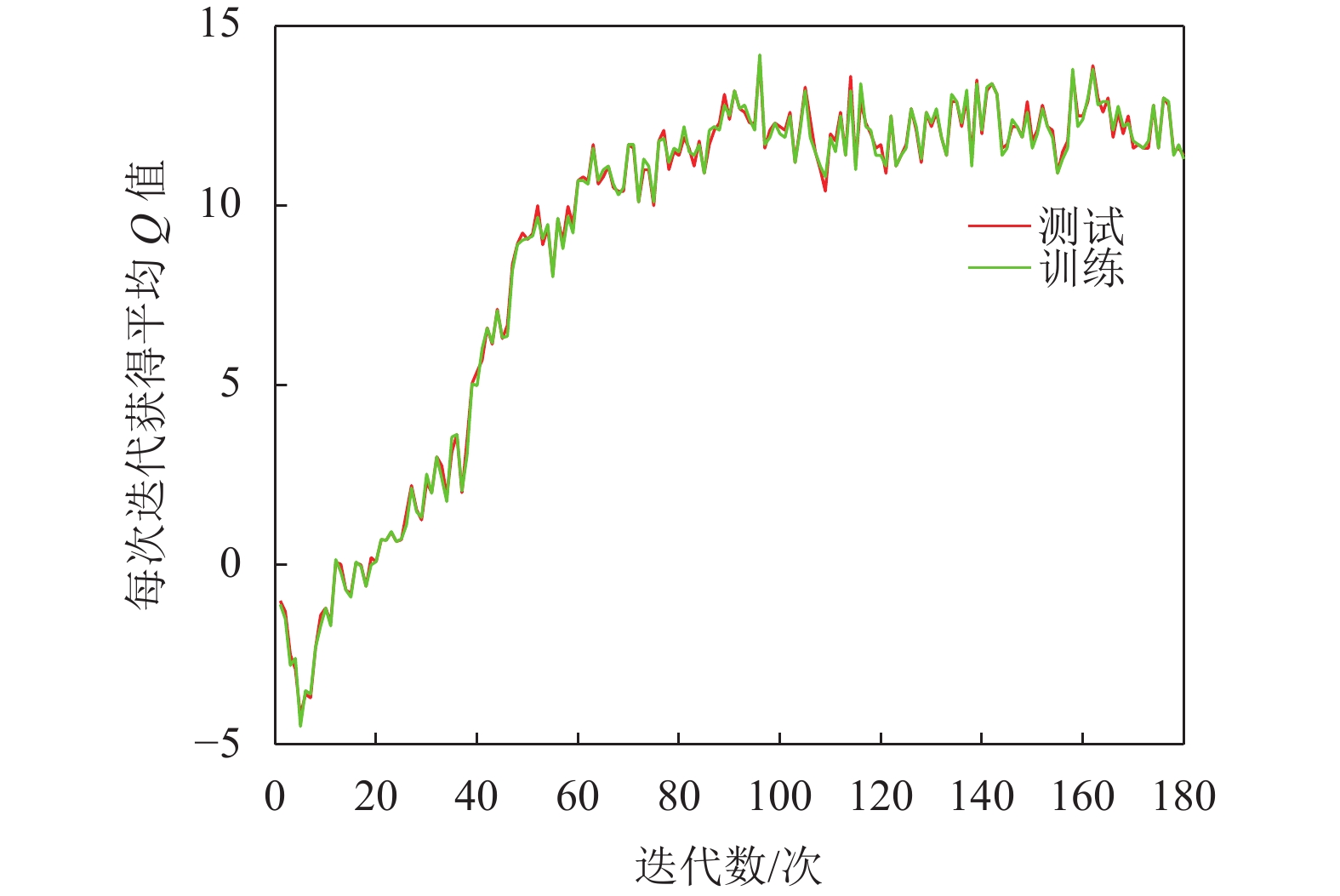
图8显示强化学习平均状态动作值随网络模型训练而变化的情况，它提供强化学习智能体从任何给定状态下执行其策略获得的最大累积回报的估计值. 通过在训练开始前运行一个随机的策略来收集一组固定的状态，并跟踪这些状态的最大预测值的平均值. 图中显示由于策略权重的微小变化会导致策略访问各状态的分配发生巨大变化，状态动作值指标往往是噪声的，强化学习智能体得到的平均回报要比平均Q值平滑得多.

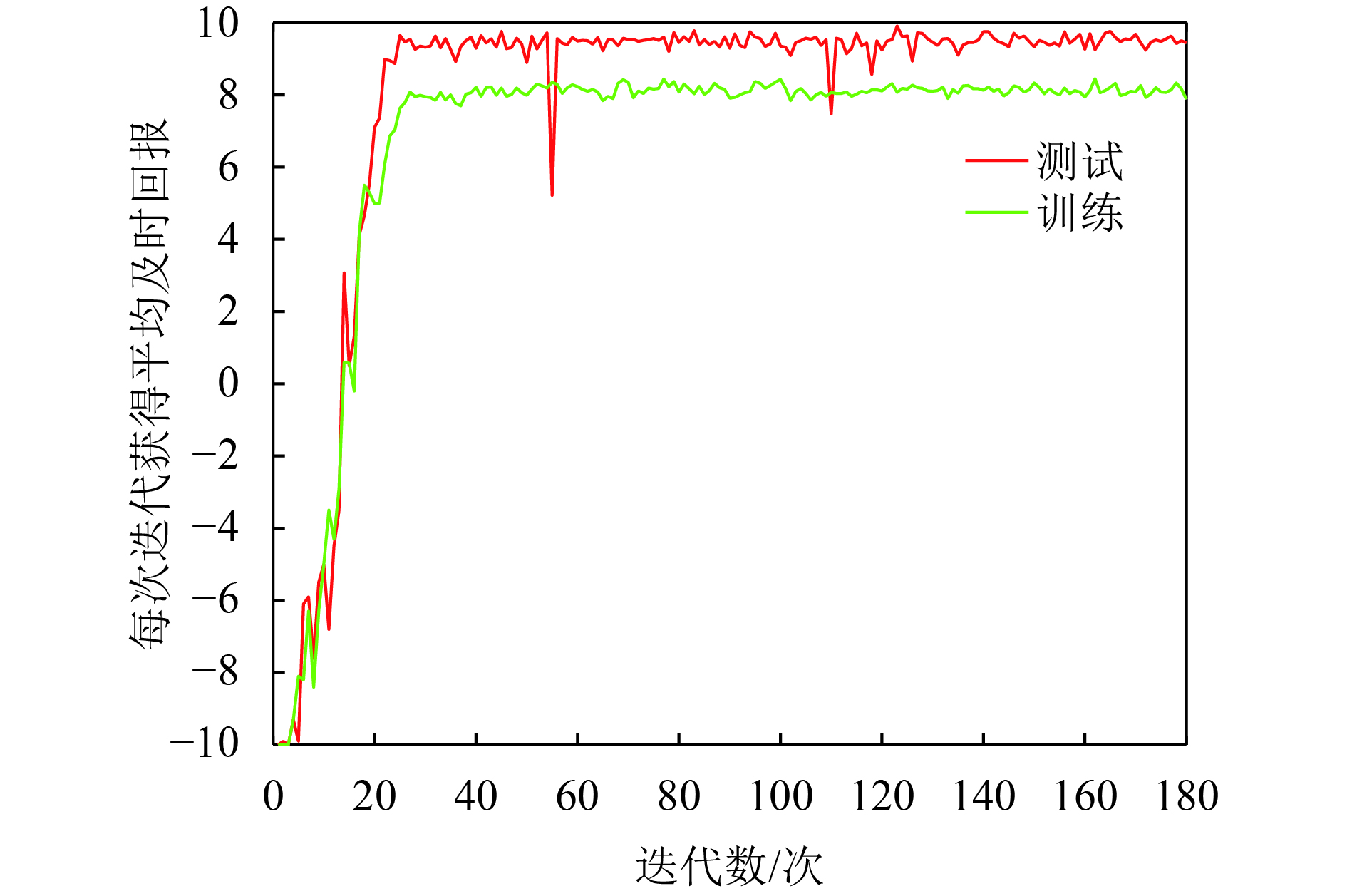
图9显示强化学习智能体随网络模型训练迭代获得的及时回报值的变化情况，图中显示卷积神经网络模型在训练30个阶段及时回报值趋于最优，偶尔出现模型不稳定，策略选择动作产生回报值震荡.

3.5 实验比较

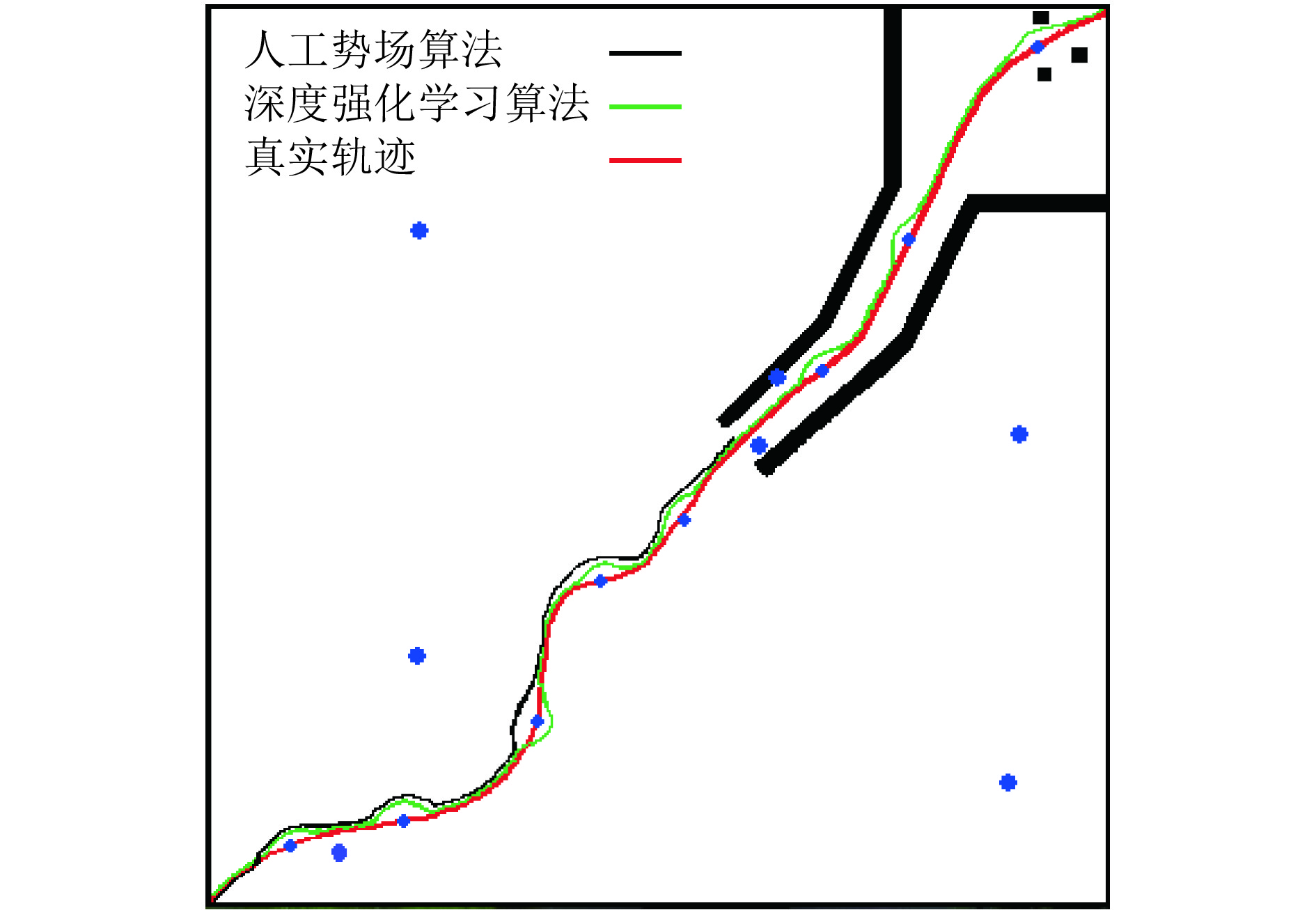
图10为人工势场法(Artifical Potential Field, APF)和深度强化学习算法(Deep Reinforcement Learning, DRL)在仿真平台实验的结果对比图.

本文采用以下因素对比两种算法：(1) 根均值平方误差(ATE.RMSE)用于比较轨迹跟踪时真实轨迹与算法估计的偏离程度；(2) 衡量局部路径规划优劣采用算法规划轨迹长度与真实轨迹长度比值；(3) 移动机器人目标是否可到达；(4) 移动机器人与障碍物是否发生碰撞；(5) 算法在局部路径规划处理时间. 算法对比实验结果如表4所示，通过表4得出本文的深度强化学习算法，实现了动态避障和轨迹跟踪，安全通过狭窄通道和障碍物附近的目标点，在动态避障时进行局部路径规划的长度比人工势场法算法更短，路径更优，而人工势场法由于在狭窄通道存在震荡问题而产生目标点不可达的问题.

4 结语

针对移动机器人兼顾速度性能的动态避障和轨迹跟踪多任务智能决策控制问题，本文提出基于深度强化学习的移动机器人轨迹跟踪动态避障算法，该算法实现了策略自动生成和优化闭环迭代，加强了系统的环境适应性，具有良好的实时避障性能和平滑的轨迹控制. 解决诸如带有非刚体对象的环境或任务参数不确定的情况下，经典运动规划算法难以解决的问题. 但该算法通过求每个动作的最大Q值，适用范围还是在低维、离散动作空间，而且寻找优良的奖惩函数需要相当多的专业知识和实验. 训练一个能够从任何起始状态达成目标的智能体，而无需专家来塑造奖惩函数是未来的发展方向.