离散事件系统(discrete event system, DES)是由离散事件触发而引起状态迁移的一类动态系统,其运行是由离散事件错综复杂地相互作用所决定的,在现代工业控制系统中有着广泛应用[1]. 为了保证系统的可靠性,通常要求能够在有限时间内判断系统运行是否安全可靠. 因此,故障诊断研究一直是离散事件系统的研究热点[2-9].
自1994年Lin F[2]提出基于状态的离散事件系统在线诊断和离线诊断方法以来,Meera S等[3]相继发表了用基于事件的方式研究DES对动态系统进行故障诊断的方法,它以自动机为系统建模[4],通过构建一个诊断器并根据诊断器的状态信息实现对系统是否可诊断的判断. 但是这种方法的复杂度是关于系统状态数的指数时间,这对于一个复杂系统来说,该故障诊断方法将耗费大量时间和空间. 为此,Jian S B和Yoo T S等[5-6]相继提出了并行自动机故障诊断方法,通过自同步来构造系统的全局twin-plant模型−验证器,从而可以由验证器直接判定系统的可诊断性. 胡芹等[7]使用了离散事件系统来优化控制云资源的分配问题,这是后来不断有人使用DES来解决实际问题的例子.
然而,上述方法只适合于处理规模较小的系统的故障诊断,一旦系统规模较大时,这种通过验证器直接判断其可诊断性的方法相当困难. 为此,许多学者将离散事件系统按照一定规则划分为多个子系统,每个子系统对应为全局系统的一个局部模型,通过对各局部模型构建局部诊断器实现对全局复杂系统的故障诊断. 这种方法最具代表性的有Debouk R等[8]提出的分散式诊断方法和Pencolé Y [9]提出的分步式诊断方法. 分散式诊断方法中各个子系统之间不存在任何信息交互,先对每个子系统建模并得到相应的局部诊断结果,再通过一个协调器来处理各个子系统的局部诊断结果,从而得到整个系统的可诊断性. 而分布式诊断方法的各个局部模型之间有通信事件进行连接,对各个局部模型构建诊断器和检测器并进行可诊断性判定,通过对检测器进行剪枝操作进行同步,得出全局系统的故障诊断结果.
尽管在工业应用中的离散事件系统大多数是经典DES,其状态和事件等信息都是十分明确,得到的故障诊断结果也是一个精确结果. 但是在许多实际应用中,特别是生物医学领域,往往得到的数据具有一定程度的模糊性和不精确性. 例如,将人的身体状况分为“好”“中”“差”是具有一定程度的模糊性,身体好到什么程度就属于“好”、差到什么程度就一定属于“差”,往往不同的人有着不同的观点. 于是,2001年Lin F等[10]将模糊数学与经典DES相结合,提出了一种模糊离散事件系统(Fuzzy Discrete Event System, FDES)[11].
从提出FDES以来,国内外许多学者致力于FDES的研究[12-21]. Cao Y Z[12]首先做了基于FDES的分布式控制的研究,Cao Y Z和Qiu D W[13-14]开始做了基于FDES的监督控制的研究,这时Huq R等[15]则做了用FDES的方式研究移动机器人的行为调制技术的研究. Cao Y Z等[16]然后从基于事件的方式推广到了基于状态控制的FDES的研究,Liu J P[17]紧接着又做了对DES和FDES在能控性上的关联的研究. 在此期间Liu F相继发表了FDES在分布式系统的监督控制[18]和故障诊断[19],然后又有了对FDES集中式诊断的研究[20],最后又有了把FDES的安全诊断的时间复杂度降低到了多项式[21].
本文继续文献[19-20]的研究工作,研究模糊离散事件系统基于模式的故障诊断问题. 在文献[19-20]中,将故障定义为单个事件,所以这种故障诊断方法只要求对单个特定事件(即故障)是否发生做出判断. 但是,在许多情况下,不是单个事件的发生导致系统陷入故障,而是一个事件序列(即模式)的发生才会导致系统发生故障. 例如,在图1所示的并联电路中,只有A开关断开,系统仍然处于正常状态,并且系统不会发出警报,但是会使B开关断开的触发条件成立,这时如果B开关也断开,那么系统就会停止工作. 而只有B开关断开的时候,系统也仍然处于正常状态,但是系统的警报会触发,并且不会使A开关断开的触发条件成立,这时可以及时处理问题,确保系统后面不会陷入异常. 这里的开关A和B都有触发器,只有触发器打开才操作,报警装置和机器分别是C和D.
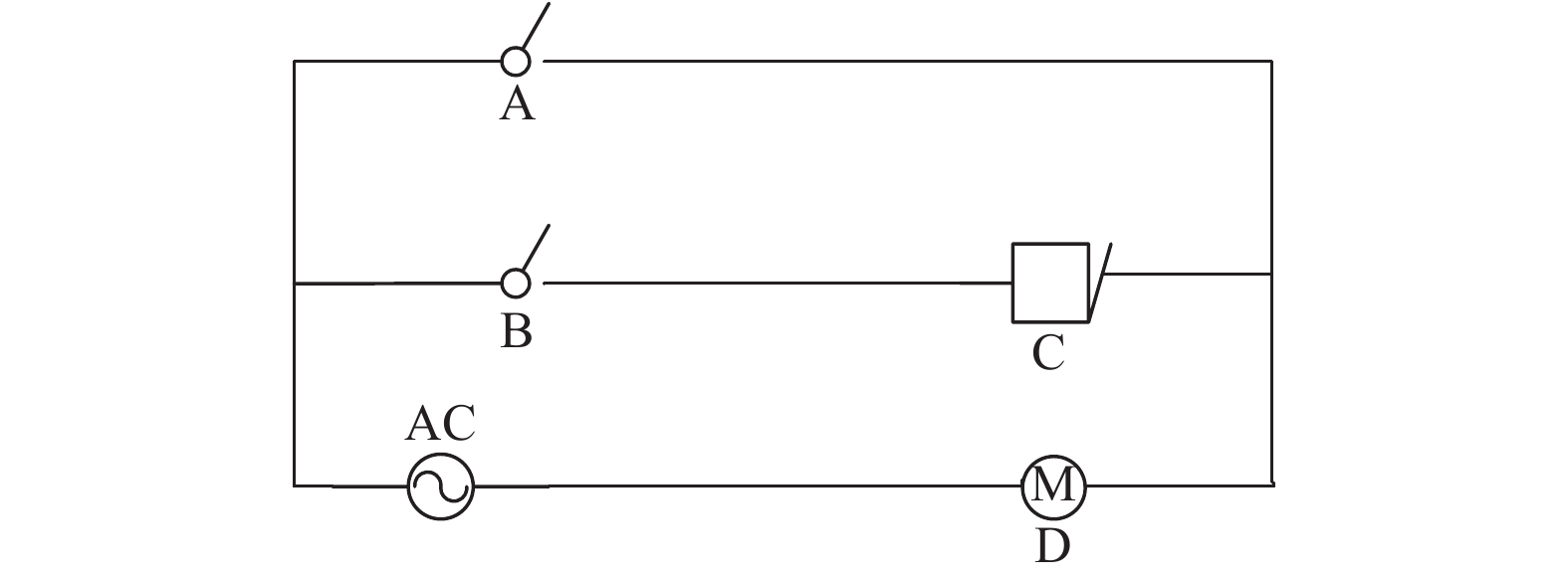
|
图 1 举例中的电路图 Figure 1 The circuit diagram in the example |
对于经典DES的基于模式故障诊断问题,Genc S和Jéron T等[22-23]都提出了通过构造各自不同的诊断器,实现了经典DES基于模式的可诊断性的判断. Ye L等[24-25]则分别对分布式经典DES的基于模式故障诊断进行了探讨,得到了具有多项式时间复杂度的模式诊断方法. 吉林大学欧阳丹彤教授[26]也对基于模式的经典DES故障诊断的算法实现进行了深入研究.
本文以模糊自动机为模型,研究FDES基于模式的故障诊断问题. 先引入两种故障模式:S类型模式和T类型模式. 然后分别对FDES的S类型模式可诊断性和T类型模式可诊断性进行形式化. 通过构造S类型模式诊断器和T类型模式诊断器,分别得到FDES关于S类型模式和T类型模式可诊断性的充分必要条件,从而实现对FDES基于模式的故障诊断的判断.
1 模糊离散事件系统有穷状态自动机(Finite State Automaton,FSA)[4]是指一个5元组
| $G = (Q,\varSigma ,\delta ,{q_0},{Q_m}),$ |
其中Q是有限状态集,
| $\delta :Q \times \varSigma \to Q. $ |
对于给定状态
事件集
如果经典DES状态集
| $\tilde {{G}} = (\tilde {{Q}},\tilde {{\varSigma}} ,\tilde {{\delta}} ,{\tilde {{q}}_0}),$ |
其中
| $L = \{ \tilde {{s}} \in {\tilde {{\varSigma}} ^ * }:(\exists \tilde {{q}} \in \tilde {{Q}})\tilde {{\delta}} ({\tilde {{q}}_0},\tilde {{s}}) = \tilde {{q}}\} .$ |
串
| $L/\tilde {{s}} = \{ \tilde {{t}} \in {\tilde {{\varSigma}} ^ * }:(\exists \tilde {{q}} \in \tilde {{Q}})\tilde {{\delta}} ({\tilde {{q}}_0},\tilde {{s}}\tilde {{t}}) = \tilde {{q}}\} .$ |
定义不可观事件模糊集为
| ${\tilde {{\varSigma}} _{\rm o}}(\tilde {{\sigma}} ) + {\tilde {{\varSigma}} _{\rm uo}}(\tilde {{\sigma}} ) = 1.$ |
并且,最大可观测事件定义为
| ${\tilde {{\varSigma}} _{\max - \rm o}} = \{ \tilde {{\sigma}} \in \tilde {{\varSigma}} :(\forall \tilde {{\alpha}} \in \tilde {{\varSigma}} ){\tilde {{\varSigma}} _{\rm o}}(\tilde {{\sigma}} ) \geqslant {\tilde {{\varSigma}} _{\rm o}}(\tilde {{\alpha}} )\} .$ |
对于
| ${P_{\tilde {{\sigma}} }}(\tilde {{a}}) = \left\{ \begin{array}{l}\tilde {{a}}{\rm{, }}\text{如果}\tilde {{a}} \in {{\tilde {{\varSigma}} }_{{\rm{max - o}}}}\text{或者}{{\tilde {{\varSigma}} }_{\rm o}}(\tilde a) > {{\tilde {{\varSigma}} }_{\rm o}}(\tilde {{\sigma}} );\\\varepsilon ,\text{否则}.\end{array} \right.$ |
其逆映射定义为
| $P_{_{\tilde {{\sigma}} }}^{{\rm{ - }}1}(\tilde {{t}}) = \{ \tilde {{s}} \in {\tilde {{\varSigma}} ^ * }:(\exists \tilde {{q}} \in \tilde {{Q}})\tilde {{\delta}} ({\tilde {{q}}_0},\tilde {{s}}) = \tilde {{q}} \wedge {P_{\tilde {{\sigma}} }}(\tilde {{s}}) = \tilde {{t}}\}. $ |
给定一个语言L和事件集
| $S = \{ \tilde {{s}} \in L:(\exists \tilde {{u}} \in K)(\tilde {{u}}\text{是}\tilde {{s}}\text{的子序列})\}, $ |
| $T = \{ \tilde {{s}} \in L:(\exists \tilde {{u}} \in K)(\tilde {{u}}\text{是}\tilde {{s}}\text{的子串})\}. $ |
定义集合
| ${\varPsi _S}(K) = \{ \tilde {{s}}\tilde {{\sigma}} \in S:(\exists \tilde {{u}}\tilde {{\sigma}} \in K)(\tilde {{u}}\tilde {{\sigma}} \text{是}\tilde {{s}}\tilde {{\sigma}} \text{的子序列})\}, $ |
| ${\varPsi _T}(K) = \{ \tilde {{s}}\tilde {{\sigma}} \in T:(\exists \tilde {{u}}\tilde {{\sigma}} \in K)(\tilde {{u}}\tilde {{\sigma}} \text{是}\tilde {{s}}\tilde {{\sigma}} \text{的子串})\}. $ |
由此可见,这两种类型的区别就是S类型是发生某一特定件事之后,再发生另一特定事件,但是中间可以有其他的事件发生;而T类型要求这几个特定的事件必须是紧接着的,中间不可以再发生其他事件.
定义1(S类型模式可诊断性) 设
| $(\exists n \in \mathbb{N})(\forall \tilde {{s}} \in {\Psi _S}(K))(\forall \tilde {{t}} \in L/\tilde {{s}})(\left\| {\tilde {{t}}} \right\| > n \Rightarrow D_P^S),$ |
这里
直观上,L是关于模式K是S类型模式可诊断的表示,对任意发生的S类型的模式故障,都能够在有限步之内将其诊断出来.
例1 考虑图2给定的FDES的
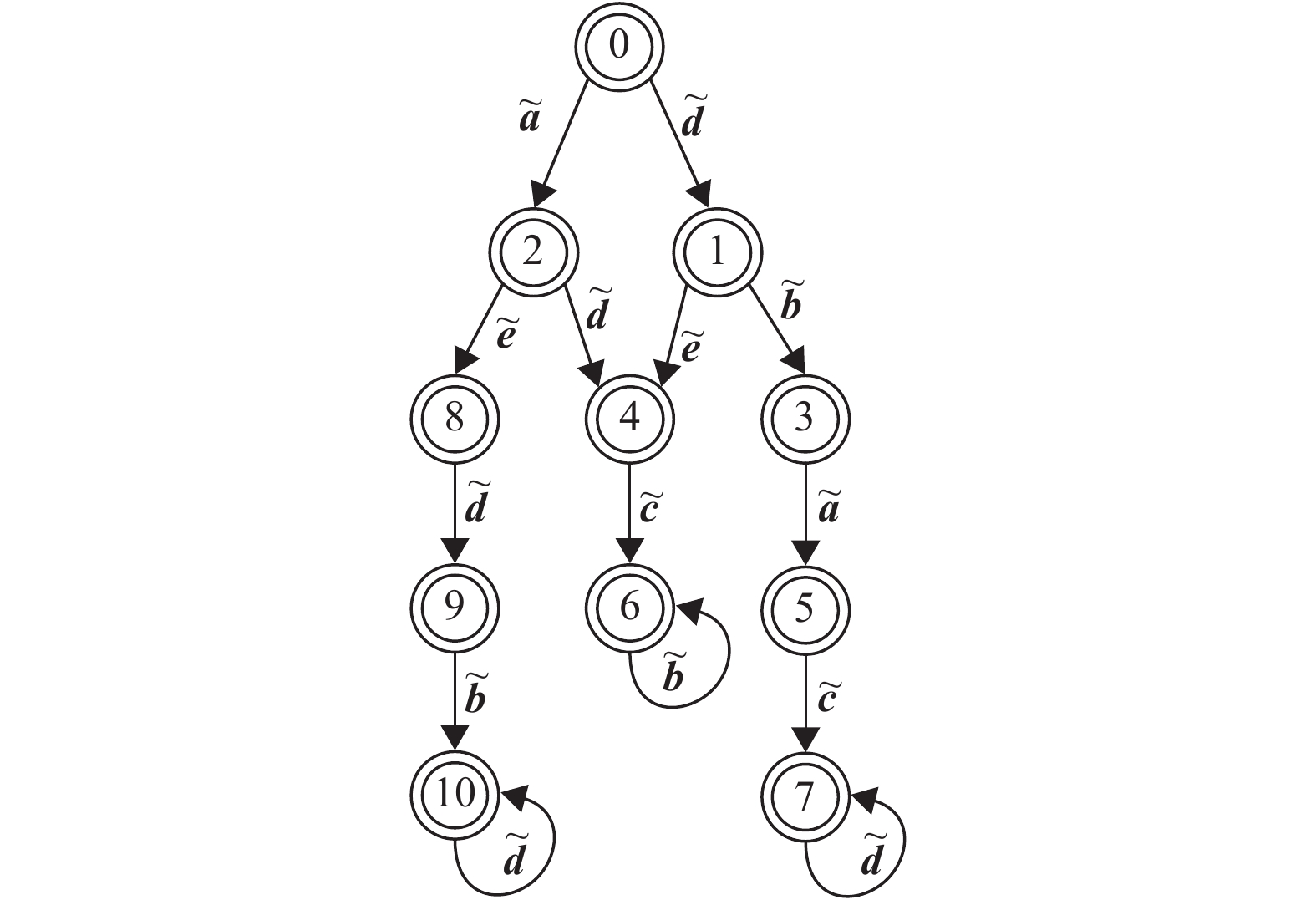
|
图 2 例1中的逻辑自动机 Figure 2 The logical automaton in example 1 |
假设初始状态为
可以得到各个状态为
并且各种事件的可观程度分别为
各种事件可能的故障程度分别为
假设给定的故障模式为
| $S = \{ \tilde {{a}}\tilde {{e}}\tilde {{d}}\tilde {{b}}{\tilde {{d}}^l},\tilde {{a}}\tilde {{d}}\tilde {{c}}{\tilde {{b}}^m},\tilde {{d}}\tilde {{e}}\tilde {{c}}{\tilde {{b}}^p},\tilde {{d}}\tilde {{b}}\tilde {{a}}\tilde {{c}}{\tilde {{d}}^r}:l,m,p,r \geqslant 0\}, $ |
那么
下面判断L是否关于模式K的S类型模式可诊断的.
根据定义1,先验证
当
当
当
当
因此,根据定义1得,L是关于模式K是S类型模式可诊断. 但是,如果将模式改为
当
定义2(T类型模式可诊断性) 设
| $(\exists n \in \mathbb{N})(\forall \tilde {{s}} \in {\Psi _T}(K))(\forall \tilde {{t}} \in L/\tilde {{s}})(\left\| {\tilde {{t}}} \right\| > n \Rightarrow D_P^T),$ |
这里
例2 考虑图3给定的FDES的
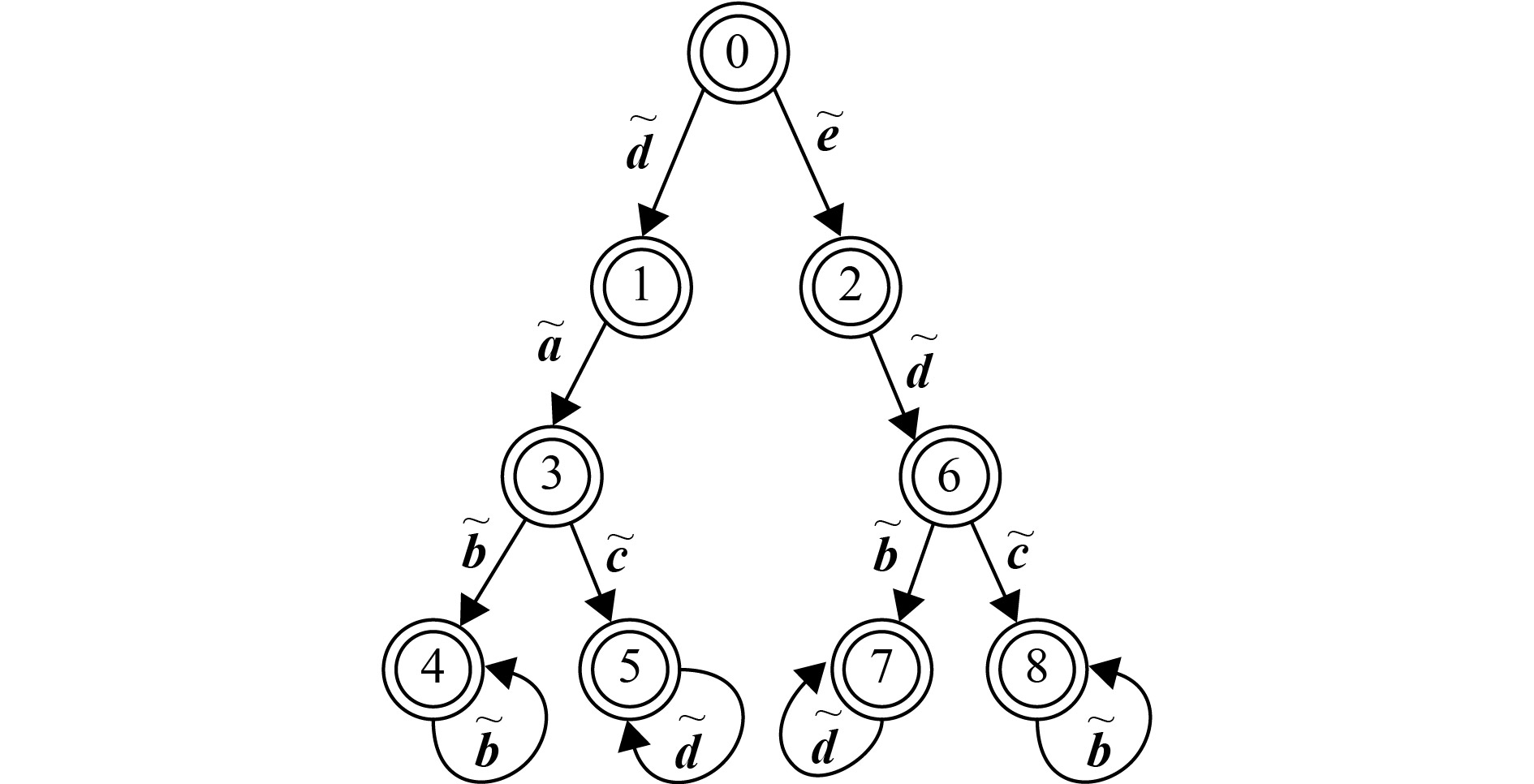
|
图 3 例2中的逻辑自动机 Figure 3 The logical automaton in example 2 |
假设初始状态为

|
图 3 例2中的逻辑自动机 Figure 3 The logical automaton in example 2 |
可以得到各个状态分别为
并且各种事件的可观程度分别为
各种事件可能的故障程度分别为
假设给定模式为
下面判断L是否关于模式K的T类型模式可诊断的.
根据定义2,先验证
当
当
因此,根据定义2得,L是关于模式K是T类型模式可诊断. 但是,如果将模式改为
当
注记1 由定义1和定义2可知,如果一个FDES关于模式K的T类型模式可诊断的,则L关于模式K一定是S类型模式可诊断的. 反之,则不一定成立.
注记2 如果
假设
根据S类型模式和T类型模式,本文先构造2个FSA.
对于给定FDES
| ${H_S}(\tilde {{\varSigma}} ,\tilde {{s}}) = ({\tilde {{Q}}_S},\tilde {{\varSigma}} ,{\tilde {{\delta}} _S},q_0^S,{\tilde {{F}}_S}),$ |
其中
| ${\tilde {{\delta}} _S}(q,\tilde {{\sigma}} ) = \left\{ \begin{array}{l}q + 1,\;\;\;\tilde {{\sigma}} = {{\tilde {{\sigma}} }_{q + 1}},\\q,\;\;\;\;\;\;\;\text{否则},\end{array} \right.$ |
并且
以类似方法,构造一个T类型FSA如下:
| ${H_T}(\tilde {{\varSigma}} ,\tilde {{s}}) = ({\tilde {{Q}}_T},\tilde {{\varSigma}} ,{\tilde {{\delta}} _T},q_0^T,{\tilde {{F}}_T}),$ |
其中
| ${\tilde {{\delta}} _S}(q,\tilde {{\sigma}} ) = \left\{ \begin{array}{l}q + 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\tilde {{\sigma}} = {{\tilde {{\sigma}} }_{q + 1}}\\{\max _{i \in {\rm{match}}(q)}}i,\;\;\;\;{\rm{match}}(q) \ne \emptyset ,\\0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{否则},\end{array} \right.$ |
其中
| $\begin{gathered} {\rm{match}}(q){\rm{ = }}\{ i:[(i = 1) \wedge ({{\tilde {{\sigma}} }_1} = \tilde {{\sigma}} )] \vee \\ [(1 < i \leqslant q) \wedge ({{\tilde {{\sigma}} }_1} \cdots {{\tilde {{\sigma}} }_i} = {{\tilde {{\sigma}} }_{q - i + 1}} \cdots {{\tilde {{\sigma}} }_q})]\},\end{gathered}$ |
并且
给定两个FSA
| ${\tilde {{G}}_1} \times {\tilde {{G}}_2} = {\rm{(}}\tilde {{Q}},\tilde {{\varSigma}} ,\tilde {{\delta}} ,{\tilde {{q}}_0},\tilde F{\rm{)}},$ |
其中
对于
| ${\rm{Obs}}(\tilde {{G}}) = (\tilde {{X}},{\tilde {{\varSigma}} _0},{\tilde {{\delta}} _0},{\tilde {{x}}_0}),$ |
其中
如果
定义3 (不确定环) 如果状态集
(1)
(2)
| $\begin{gathered} \tilde {{q}}_1^1\xrightarrow{{{{\tilde {\sigma} }_{{\rm o},1}}t_1^1}}\tilde {{q}}_2^1 \cdots \xrightarrow{{{{\tilde {\sigma }}_{{\rm o},m - 1}}t_{m - 1}^1}}\tilde {{q}}_m^1\xrightarrow{{{{\tilde {\sigma} }_{{\rm o},m}}t_m^1}} \\ \tilde {{q}}_2^2\xrightarrow{{{{\tilde {\sigma} }_{{\rm o},m - 1}}t_{m - 1}^2}}\tilde {{q}}_m^2 \cdots \tilde {{q}}_1^M\xrightarrow{{{{\tilde {\sigma} }_{{\rm o},1}}t_1^M}} \\ \tilde {{q}}_2^M\xrightarrow{{{{\tilde {\sigma} }_{{\rm o},m - 1}}t_{m - 1}^M}}\tilde {{q}}_m^M\xrightarrow{{{{\tilde {\sigma} }_{{\rm o},m}}t_m^M}}\tilde {{q}}_1^1 \\ \end{gathered} $ |
和
| $\begin{gathered} \tilde {{r}}_1^1\xrightarrow{{{{\tilde {\sigma} }_{{\rm o},1}}u_1^1}}\tilde {{r}}_2^1 \cdots \xrightarrow{{{{\tilde {\sigma }}_{{\rm o},m - 1}}u_{m - 1}^1}}\tilde {{r}}_m^1\xrightarrow{{{{\tilde {\sigma} }_{{\rm o},m}}u_m^1}} \\ \tilde {{r}}_2^2\xrightarrow{{{{\tilde {\sigma} }_{{\rm o},m - 1}}u_{m - 1}^2}}\tilde {{r}}_m^2 \cdots \tilde {{r}}_1^N\xrightarrow{{{{\tilde {\sigma} }_{{\rm o},1}}u_1^N}} \\ \tilde {{r}}_2^N\xrightarrow{{{{\tilde {\sigma} }_{{\rm o},m - 1}}u_{m - 1}^M}}\tilde {{r}}_m^N\xrightarrow{{{{\tilde {\sigma} }_{{\rm o},m}}u_m^M}}\tilde {{r}}_1^1, \\ \end{gathered} $ |
这里对于所有的
定理1 (S类型模式可诊断性充分必要条件) 设
证明 先证明充分性,假设
下面再证明必要性,假设语言L是关于模式K和映射P的S类型的模式可诊断,则根据定义1有
定理2 (T类型模式可诊断性充分必要条件) 设
证明 先证明充分性,假设
下面再证明必要性,假设语言L是关于模式K和映射P的T类型的模式可诊断,则根据定义2有
注记3 由定理1和定理2知,通过构造
下面将例1、2使用定理的方式进行证明.
例3 考虑例1中给定的FDES
(1) 如果模式
将S类型模式诊断器
由于
(2) 如果模式
尽管构造
例4 考虑例2中给定的FDES
(1) 如果模式
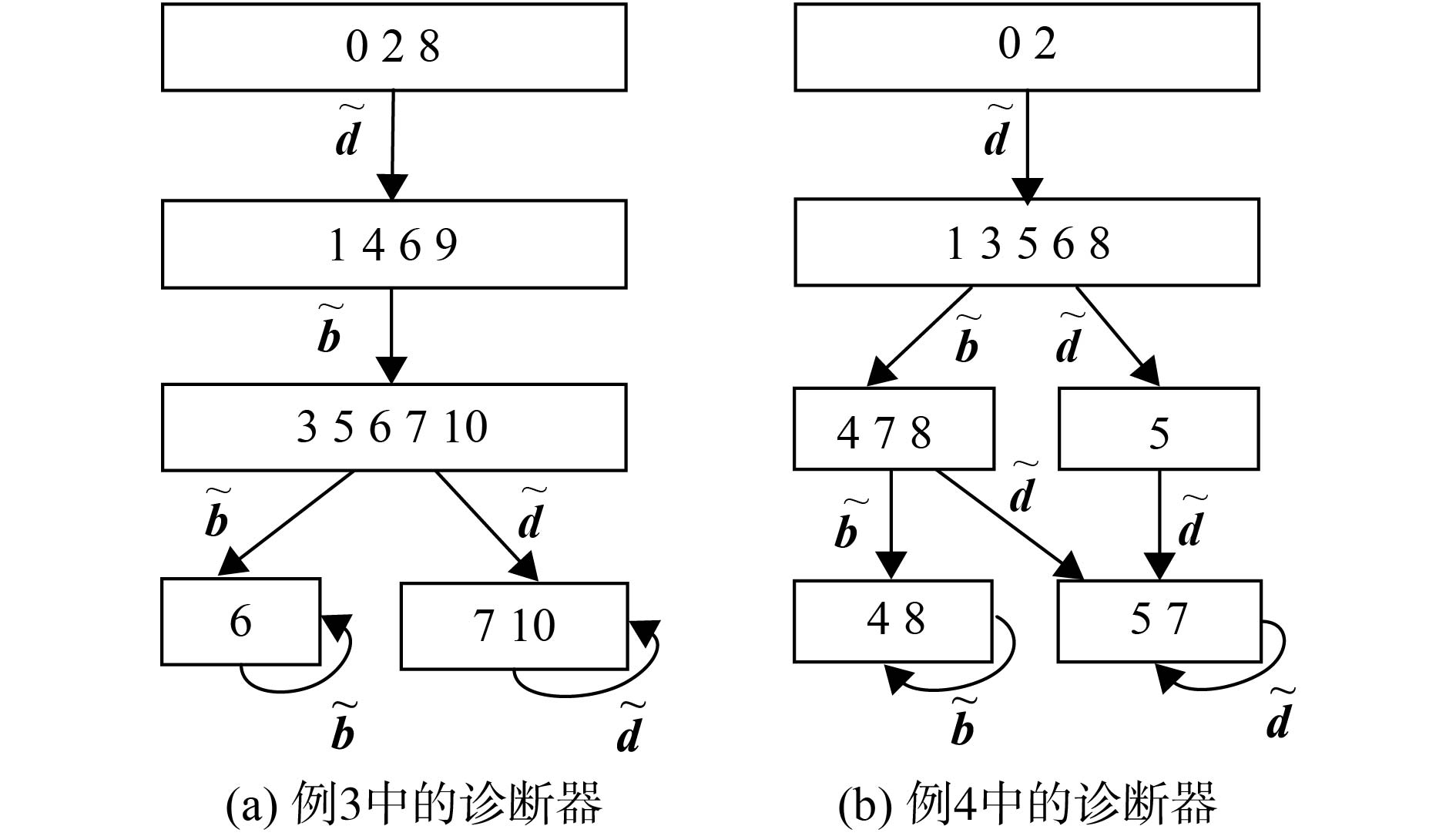
|
图 4 例3与例4中的诊断器 Figure 4 The diagnoser in example 3 and example 4 |
由于
(2) 如果模式
尽管构造
本文以模糊离散事件系统为模型,提出了基于S类型和T类型两种模式的故障诊断方法. 先对模糊离散事件系统的S类型模式可诊断性和T类型模式可诊断性进行了形式化,再通过构造S类型模式诊断器和T类型模式诊断器,分别得到了模糊离散事件系统关于S类型模式可诊断性和T类型模式可诊断性的充分必要条件,实现了模糊离散事件系统基于模式的故障诊断. 在后续工作中,将在本文的基础上将这两种故障模式推广到分布式模糊系统,考虑分布式FDES基于模式的故障诊断问题.
| [1] |
CASSANDRAS C, LAFORTUNE S. Introduction to discrete event systems 2ed[M]. New York: Springer, 2008.
|
| [2] |
LIN F. Diagnosability of discrete event systems and its applications[J].
Discrete Event Dynamic Systems: Theory and Applications, 1994, 4(2): 197-212.
DOI: 10.1007/BF01441211. |
| [3] |
SAMPATH M, SENGUPTA R, LAFORTUNE S, et al. Diagnosability of discrete event system[J].
Automatic Control IEEE Transactions on, 1995, 40(9): 1555-1575.
DOI: 10.1109/9.412626. |
| [4] |
HOPCROFT J E, MOTWANI R, ULLMAN J D. Introduction to automata theory, Languages, and Computation 2ed[M]. Boston: Addison Wesley, 2001.
|
| [5] |
JIANG S, HUANG Z, CHANDRA V, et al. A polynomial algorithm for testing diagnosability of discrete-event systems[J].
Automatic Control IEEE Transactions on, 2001, 46(8): 1318-1321.
DOI: 10.1109/9.940942. |
| [6] |
YOO T S, LAFORTUNE S. Polynomial-time verification of diagnosability of partially observed discrete-event systems[J].
Automatic Control IEEE Transactions on, 2002, 47(9): 1491-1495.
DOI: 10.1109/TAC.2002.802763. |
| [7] |
胡芹, 刘富春. 基于离散事件系统的云资源分配优化控制[J].
广东工业大学学报, 2016, 33(1): 29-35.
HU Q, LIU F C. Optimization control of cloud resource allocation based on DES[J]. Journal of Guangdong University of Technology, 2016, 33(1): 29-35. DOI: 10.3969/j.issn.1007-7162.2016.01.006. |
| [8] |
DEBOUK R, LAFORTUNE S, TENEKETZIS D. Coordinated decentralized protocols for failure diagnosis of discrete event systems[J].
Discrete Event Dynamic Systems: Theory and Applications, 2000, 10(1): 33-86.
|
| [9] |
PENCOLÉ Y. Diagnosability analysis of distributed discrete event systems[C]//ECAI 2004 16th European Conference on Artificial Intelligence. Spain, Valencia: IEEE, 2008: 43-47.
|
| [10] |
DUBOIS D, PRADE H. Fuzzy sets and systems: theory and applications[M]. New York: Academic Press, 1980.
|
| [11] |
LIN F, YING H. Fuzzy discrete event systems and their observability[C]//Joint 9th Ifsa World Congress and 20th Nafips International Conference. Canada, Vancouver: IEEE, 2001: 1271-1276.
|
| [12] |
CAO Y, YING M. Observability and decentralized control of fuzzy discrete-event systems[J].
IEEE Transactions on Fuzzy Systems, 2004, 14(2): 202-216.
|
| [13] |
CAO Y, YING M. Supervisory control of fuzzy discrete event systems[J].
IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics, 2005, 35(2): 366-371.
|
| [14] |
QIU D. Supervisory control of fuzzy discrete event systems: a formal approach[J].
IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics, 2005, 35(1): 72-88.
|
| [15] |
HUQ R, MANN G K I, GOSINE R G. Behavior-modulation technique in mobile robotics using fuzzy discrete event system[J].
IEEE Transactions on Robotics, 2006, 22(5): 903-916.
DOI: 10.1109/TRO.2006.878937. |
| [16] |
CAO Y, YING M, CHEN G. State-based control of fuzzy discrete-event systems[J].
IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics, 2007, 37(2): 410.
|
| [17] |
LIU J, LI Y. The relationship of controllability between classical and fuzzy discrete-event systems[J].
Basic Sciences Journal of Textile Universities, 2007, 178(21): 4142-4151.
|
| [18] |
LIU F, QIU D. Decentralized supervisory control of fuzzy discrete event systems[J].
European Journal of Control, 2008, 14(3): 234-243.
DOI: 10.3166/ejc.14.234-243. |
| [19] |
LIU F, QIU D. Diagnosability of fuzzy discrete-event systems: a fuzzy approach[J].
IEEE Transactions on Fuzzy Systems, 2009, 17(2): 372-384.
DOI: 10.1109/TFUZZ.2009.2013840. |
| [20] |
LIU F, DZIONG Z. Decentralized diagnosis of fuzzy discrete-event systems[J].
European Journal of Control, 2012, 18(3): 304-315.
DOI: 10.3166/ejc.18.304-315. |
| [21] |
LIU F. Safe diagnosability of fuzzy discrete-event systems and a polynomial-time verification[J].
IEEE Transactions on Fuzzy Systems, 2015, 23(5): 1534-1544.
DOI: 10.1109/TFUZZ.2014.2362767. |
| [22] |
GENC S, LAFORTUNE S. Diagnosis of patterns in partially-observed discrete-event systems[C]//IEEE Conference on Decision and Control. California, San Diego: IEEE, 2007: 422-427.
|
| [23] |
JERON T, MARCHAND H, PINCHINAT S, et al. Supervision patterns in discrete event systems diagnosis[C]//International Workshop on Discrete Event Systems. Germany, Berlin: IEEE, 2010: 262-268.
|
| [24] |
YE L, DAGUE P, YAN Y. An incremental approach for pattern diagnosability in distributed discrete event systems[C]//IEEE International Conference on Tools with Artificial Intelligence. New Jersey, Newark: IEEE, 2009: 123-130.
|
| [25] |
YE L, DAGUE P. A general algorithm for pattern diagnosability of distributed discrete event systems[C]//IEEE International Conference on Tools with Artificial Intelligence. Washington: IEEE, 2013: 130-137.
|
| [26] |
崔海春. 基于模式的离散事件系统故障诊断方法[D]. 长春: 吉林大学计算机科学与技术学院, 2013.
|
 2019, Vol. 36
2019, Vol. 36

