随着互联网技术和云技术的发展,电子文件的通信以及云端存储已经成为日常工作的一部分. 然而在复杂的网络环境中,电子文件的安全隐患不容忽视,其主要风险是文件窃取,内容篡改和信息泄露等,从而导致电子文件数据的真实性、完整性、可读性和保密性等安全属性遭受破坏[1-2]. 近年来大型的信息安全事故频发,典型的有2017年黑客入侵雅虎的用户账号,2016年美国遭遇希拉里邮件门,2015年网易邮箱数据泄密等[3].
为了提高电子文件的信息安全,人们提出了多种文件加密方法. 其中有基于DES (Date Encryption Algorithm)及其改进算法的文件加密方法,综合利用了三重DES算法与独立子密钥算法的优点,把原来的64位密钥扩展为128位,通过双重加密,同时采用局部密钥独立的特性提升了加密强度和效率[4];基于Xposed框架的透明文件加解密方法,其以SharedUserId和开发者签名信息为标识自动生成密钥,将各个APP的数据以不同的密钥加密处理,这样即使在恶意APP获取到了Root权限,仍能保护各APP的隐私数据不被非法获取,从而提升了Android设备的安全性[5];一种基于安全局域网分级文件分发的方法,实现了网络文件的分级可控管理,除了能够防范来自系统外部的普通网络攻击行为外,确保了对系统合法用户操作行为的控制,有效阻断了内部人员信息泄露的基本途径,能够提高各类共享数据的安全性[6];基于混沌理论的加密方法,利用混沌对参数和初始位置的敏感性、类随机特性和遍历性的属性进行加密[7-9].
本文基于混沌反控制理论[10-11],提出一种新的混沌加密算法对电子文件进行加密. 其一般原理是基于渐近稳定的
为了避免加密算法对文件格式造成破坏导致文件打开失败或者格式不兼容的问题[4],本文采用选择性加密的方法,其思想是加密文件的数据部分,保留格式部分不加密处理[13]. 本文选取一类格式相对简单的文件比如wav和bmp等多媒体文件进行实验测试,分析出文件的格式和数据两部分,只选取数据部分进行加密处理. 通过理论证明、软件仿真和硬件测试等手段验证了加密算法具有良好的安全性和技术可行性.
1 混沌加密算法 1.1 混沌系统的设计本文采用混沌反控制理论设计三维离散时间混沌系统. 目前在工程应用中被广泛采用的混沌判据主要有两条,即具有正的李氏指数和轨道全局有界[14-15]. 根据以上两条判据,给出混沌系统的具体设计步骤如下。
(1) 设计渐近稳定的标称系统的一般形式为
| $x(k + 1) = {{C}}x(k),$ | (1) |
式中
(2) 为了对标称系统实施有效控制,需要对标称矩阵
| ${{A }}={{{PCP}}^{ - 1}},$ | (2) |
其中
| $x(k + 1) = {{A}}x(k),$ | (3) |
满足式(1)和式(3)具有相同的特征根和稳定性.
(3) 设计一致有界反控制器
| $ x\left( {k{\rm{ + }}1} \right) = {{A}}x(k) + {{B}}g(\sigma x(k),\varepsilon ). $ | (4) |
(4) 利用控制矩阵
选取三维系统作为典型实例,根据式(1)~(4),得对应混沌系统迭代方程的一般形式为
| $\left\{ \begin{array}{l} {x_1}(k + 1) = {a_{11}}{x_1}(k) + {a_{12}}{x_2}(k) + {a_{13}}{x_3}(k) , \\ {x_2}(k + 1) = {a_{21}}{x_1}(k) + {a_{22}}{x_2}(k) + {a_{23}}{x_3}(k) , \\ {x_3}(k + 1) = {a_{31}}{x_1}(k) + {a_{32}}{x_2}(k) + {a_{33}}{x_3}(k) + \\ \quad\quad\varepsilon \sin (\sigma {x_1}(k)) .\end{array} \right.$ | (5) |
其中标称矩阵
| ${{A}} = \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}} \\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}} \\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0.09}&{ - 0.37}&{0.1} \\ { - 0.1}&{ - 0.18}&{0.37} \\ {0.27}&{ - 0.27}&{0.19} \end{array}} \right),$ | (6) |
对应的特征根均位于单位圆内,标称系统渐近稳定.
参照式(5)和式(6)的形式,为混沌系统选取第二组密钥参数,得
| ${{{B}}'} = \left( {\begin{array}{*{20}{c}} {{b_{11}}}&{{b_{12}}}&{{b_{13}}} \\ {{b_{21}}}&{{b_{22}}}&{{b_{23}}} \\ {{b_{31}}}&{{b_{32}}}&{{b_{33}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0.205}&{ - 0.595}&{0.265} \\ { - 0.265}&{ - 0.125}&{0.595} \\ {0.33}&{ - 0.33}&{0.47} \end{array}} \right),$ | (7) |
经计算得到李氏指数为
对式(5)和式(6)的混沌系统进行仿真,得到吸引子相图如图1所示,图1(a)为相平面
根据式(5)~(7)进一步设计混沌加密和解密算法,算法对应的混沌加密迭代方程的数学表达式为
| $\left\{ \begin{array}{l} x_1^{(e)}(k + 1) = {a_{11}}x_1^{(e)}(k) + {a_{12}}x_2^{(e)}(k) + {a_{13}}x_3^{(e)}(k) , \\ x_2^{(e)}(k + 1) = {a_{21}}p(k) + {a_{22}}x_2^{(e)}(k) + {a_{23}}x_3^{(e)}(k) , \\ x_3^{(e)}(k + 1) = {a_{31}}p(k) + {a_{32}}x_2^{(e)}(k) + {a_{33}}x_3^{(e)}(k) + \\\quad\quad\varepsilon \times \sin (\sigma \times p(k)) , \\ x_4^{(e)}(k + 1) = {b_{11}}x_4^{(e)}(k) + {b_{12}}x_5^{(e)}(k) + {b_{13}}x_6^{(e)}(k) , \\ x_5^{(e)}(k + 1) = {b_{21}}p(k) + {b_{22}}x_5^{(e)}(k) + {b_{23}}x_6^{(e)}(k) ,\\ x_6^{(e)}(k + 1) = {b_{31}}p(k) + {b_{32}}x_5^{(e)}(k) + {b_{33}}x_6^{(e)}(k) +\\\quad\quad \varepsilon \times \sin (\sigma \times p(k)) .\end{array} \right.$ | (8) |

|
图 1 三维离散时间混沌系统的吸引子相图 Figure 1 The attractor of the 3-D discrete time chaos system |
由于采用对称密码体制,混沌解密算法是加密算法的逆运算过程,算法对应的混沌解密迭代方程的数学表达式为
| $\left\{ \begin{array}{l} x_1^{(d)}(k + 1) = {\widehat a_{11}}x_1^{(d)}(k) + {\widehat a_{12}}x_2^{(d)}(k) + {\widehat a_{13}}x_3^{(d)}(k) , \\ x_2^{(d)}(k + 1) = {\widehat a_{21}}p(k) + {\widehat a_{22}}x_2^{(d)}(k) + {\widehat a_{23}}x_3^{(d)}(k) , \\ x_3^{(d)}(k + 1) = {\widehat a_{31}}p(k) + {\widehat a_{32}}x_2^{(d)}(k) + {\widehat a_{33}}x_3^{(d)}(k) +\\\quad\quad \widehat \varepsilon \times \sin (\widehat \sigma \times p(k)) , \\ x_4^{(d)}(k + 1) = {\widehat b_{11}}x_4^{(d)}(k) + {\widehat b_{12}}x_5^{(d)}(k) + {\widehat b_{13}}x_6^{(d)}(k) , \\ x_5^{(d)}(k + 1) = {\widehat b_{21}}p(k) + {\widehat b_{22}}x_5^{(d)}(k) + {\widehat b_{23}}x_6^{(d)}(k) , \\ x_6^{(d)}(k + 1) = {\widehat b_{31}}p(k) + {\widehat b_{32}}x_5^{(d)}(k) + {\widehat b_{33}}x_6^{(d)}(k) + \\\quad\quad \widehat \varepsilon \times \sin (\widehat \sigma \times p(k)) .\end{array} \right.$ | (9) |
其中加密信号
| $p(k) = \left( {od (\left\lfloor {x_1^{(e)}(k) \times x_4^{(e)}(k)} \right\rfloor ,256} \right) \oplus m(k) = c(k) \oplus m(k),$ | (10) |
其中符号
文件的通信过程可能受数据丢失和损坏等实际问题的干扰造成解密失败,在密钥匹配的条件下,解密算法能够在数据受到干扰之后迅速恢复正确的解密功能,我们称之为自同步. 假设加密和解密的密钥参数匹配为
| ${\widehat a_{ij}} = \;{a_{ij}},{\widehat b_{ij}} = \;{b_{ij}}(1 \leqslant i,j \leqslant 3),\widehat \varepsilon = \varepsilon ,\widehat \delta = \delta .$ |
同时由于加密数据
| $\left( {\begin{array}{*{20}{c}} {\Delta {x_2}(k + 1)} \\ {\Delta {x_3}(k + 1)} \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {{a_{22}}}&{{a_{23}}} \\ {{a_{32}}}&{{a_{33}}} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {\Delta {x_2}(k)} \\ {\Delta {x_3}(k)} \end{array}} \right),$ |
进一步得到
| $\left( {\begin{array}{*{20}{c}} {\Delta {x_2}(k)} \\ {\Delta {x_3}(k)} \end{array}} \right)={\left( {\begin{array}{*{20}{c}} {{a_{22}}}&{{a_{23}}} \\ {{a_{32}}}&{{a_{33}}} \end{array}} \right)^k} \cdot \left( {\begin{array}{*{20}{c}} {\Delta {x_2}(0)} \\ {\Delta {x_3}(0)} \end{array}} \right),$ | (11) |
其中
| $\left\| {\left( {\begin{array}{*{20}{c}} {\Delta {x_2}(k)} \\ {\Delta {x_3}(k)} \end{array}} \right)} \right\| \leqslant {\left\| {\left( {\begin{array}{*{20}{c}} {{a_{22}}}&{{a_{23}}} \\ {{a_{32}}}&{{a_{33}}} \end{array}} \right)} \right\|^k} \cdot \left\| {\left( {\begin{array}{*{20}{c}} {\Delta {x_2}(0)} \\ {\Delta {x_3}(0)} \end{array}} \right)} \right\|.$ | (12) |
已知系数矩阵
| $\mathop {\lim }\limits_{k \to \infty } \left\| {\Delta {x_i}(k)} \right\| = \mathop {\lim }\limits_{k \to \infty } \left\| {x_i^{(d)}(k) - x_i^{(e)}(k)} \right\| = 0,$ | (13) |
其中
根据式(8)~(13),可得式(8)第一个方程的误差迭代方程
| $\Delta {x_1}(k+1)={a_{11}}\Delta {x_1}(k) + {a_{12}}\Delta {x_2}(k) + {a_{13}}\Delta {x_3}(k),$ | (14) |
其中
| $\mathop {\lim }\limits_{k \to \infty } \left\| {\Delta {x_1}(k)} \right\| = \mathop {\lim }\limits_{k \to \infty } \left\| {x_1^{(d)}(k) - x_1^{(e)}(k)} \right\| = 0.$ | (15) |
同理可证明
根据式(11)~(15)的理论分析,对加密算法和解密算法的自同步过程进行仿真,在密钥匹配的条件下,当密文
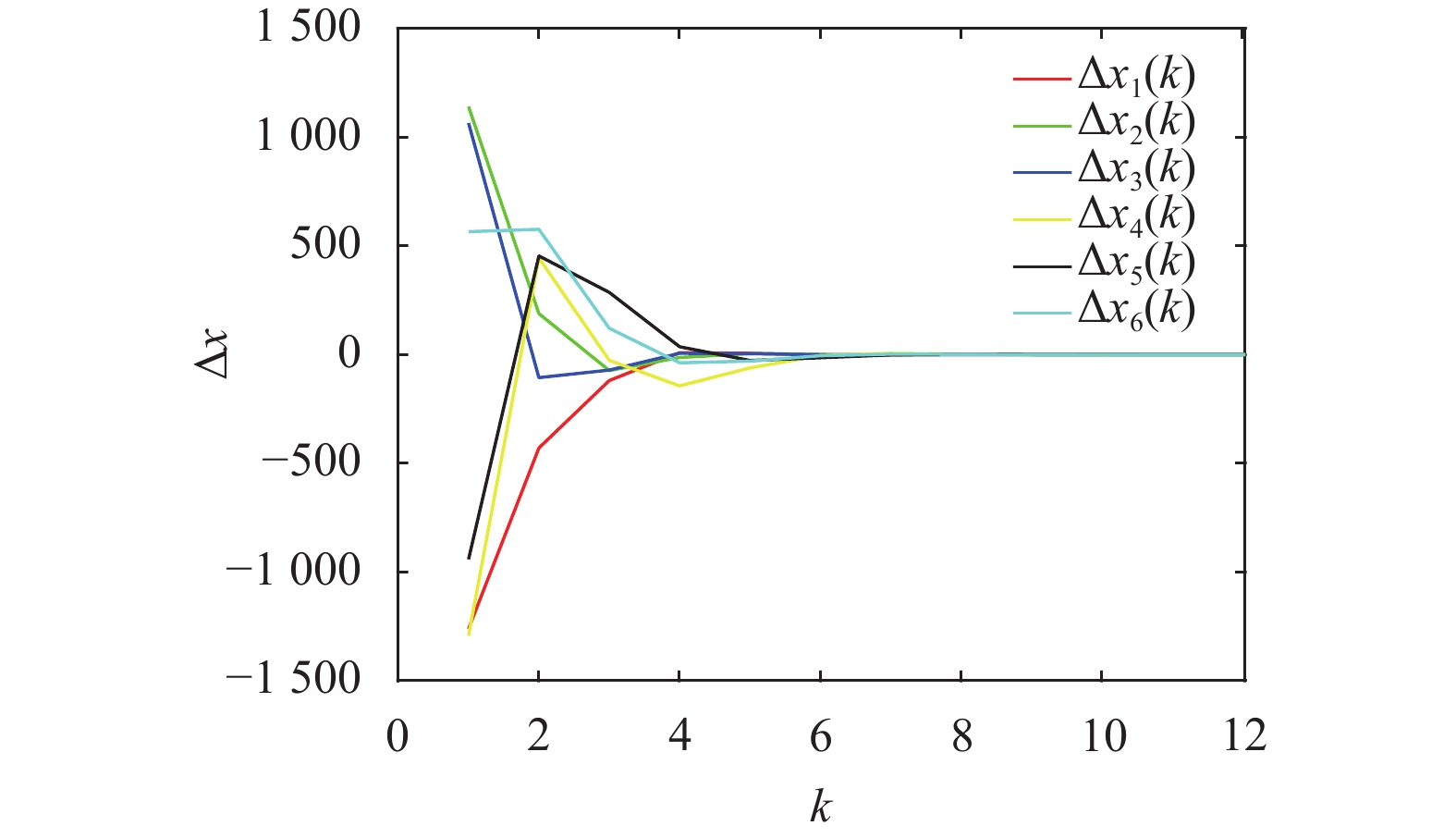
|
图 2 自同步迭代过程仿真图 Figure 2 The simulation figure of self synchronization |
本文从密钥敏感度、攻击复杂度和差分分析3个方面对加密算法的安全性进行分析.
(1) 密钥敏感度分析.
密钥敏感度主要测试密钥参数对解密的敏感性,解密算法中一个密钥参数发生微小的失配能够导致解密失败. 参数敏感性测试数据如表1所示.
| 表 1 参数敏感度测试 Table 1 Keys sensitivity test |
从表1可知加密算法具有良好的敏感度,密钥参数微小的失配能够引起解密失败.
(2) 攻击复杂度分析.
根据密钥参数以及敏感度可计算攻击复杂度
| $\begin{split}& {{{O}}({\rm{Deducing}}\;{a_{ij}},{b_{ij}}) =}\\&{ {{O}}\left\{ {\prod\limits_{i = 1}^{3} {\left( {\prod\limits_{j = 1}^{3} {\displaystyle\frac{{|{a_{ij}}|}}{{|\Delta {a_{ij}}|}}} } \right)} \cdot \prod\limits_{i = 1}^{3} {\left( {\prod\limits_{j = 1}^{3} {\displaystyle\frac{{|{b_{ij}}|}}{{|\Delta {b_{ij}}|}}} } \right)} } \right\}}= \\& { {{O}}({{10}^{{167}}}) > {{O}}({2^{128}})} .\end{split} $ | (16) |
从式(16)可知加密算法具备良好的攻击复杂度.
(3) 差分分析.
差分分析主要测试密文对明文的“雪崩效应”,明文微小变化对密文产生的影响. 一般采用NPCR (Number of Pixels Change Rate) 和UACI (Unified Average Changing Intensity)两个指标来表征. 以图像加密为例,UPCR和UACI的数学表达为
| $\left\{\!\!{\begin{array}{*{20}{l}} {{\rm{NPCR}}\! =\! \displaystyle\frac{{\displaystyle\sum\limits_{i,j} {{{D}}(i,j)} }}{{W \times H}} \times 100\% }, \\ {{\rm{UACI}} \!=\! \displaystyle\frac{1}{{W \times H}} \times \displaystyle\sum\limits_{i,j} {\displaystyle\frac{{\left| {{{C}}(i,j) - {{{C}}'}(i,j)} \right|}}{{255}} \times 100\% } .} \end{array} } \right.$ | (17) |
其中
| ${{C}} = \left( {\begin{array}{*{20}{c}} {{C_{11}}}&{{C_{12}}}&{\; \cdots }&{{C_{1W}}} \\ {{C_{21}}}&{{C_{22}}}& \cdots &{{C_{2W}}} \\ \vdots & \vdots & & \vdots \\ {{C_{H1}}}&{{C_{H2}}}& \cdots &{{C_{HW}}} \end{array}} \right),$ |
| ${{{C}}'} = \left( {\begin{array}{*{20}{c}} {C_{11}'}&{C_{12}'}&{\; \cdots }&{C_{1W}'} \\ {C_{21}'}&{C_{22}'}& \cdots &{C_{2W}'} \\ \vdots & \vdots & & \vdots \\ {C_{H1}'}&{C_{H1}'}& \cdots &{C_{HW}'} \end{array}} \right),$ |
| ${{D}}(i,j) = \left\{ {\begin{array}{*{20}{c}} 1,&\;{{C}}(i,j) \ne {{{C}}'} (i,j); \\ 0,&\;{{C}}(i,j) = {{{C}}'} (i,j) .\end{array}} \right.$ |
NPCR和UACI最理想的理论值分别为0.996 094和0.334 635,经过测试,加密算法的NPCR为0.995 9,UACI为0.334 4,达到了良好的效果.
2 文件格式分析将加密算法应用到wav音频和bmp图像两类文件中. 为了避免破坏文件的格式,在加密之前先进行文件格式分析,并且只针对文件的数据部分进行加密,保留格式部分不作任何加密处理.
wav音频文件格式以及加密方式如图3所示,其中数据块为音频数据,数据块大小由数据总长度的值标示出来.

|
图 3 wav文件格式 Figure 3 The file format of the wav file |
bmp图像文件格式以及加密方式如图4所示,其中图片点阵数据为像素数据,数据大小由图片尺寸以及调色板的表项值共同决定,调色板大小

|
图 4 bmp文件格式 Figure 4 The file format of the bmp file |
文件加密系统的硬件方案如图5所示,系统硬件包括上位机,路由和SOPC (System on a Programmable Chip)平台3部分. 其中上位机实现文件数据部分的网络通信,SOPC平台实现数据的网络通信,加密和解密功能. 图5中,通道1为加密通道,通道2为解密通道,开关k1和k2受上位机的控制同时切换到1通道或者2通道;
系统软件包括上位机软件和ARM软件两部分. 上位机软件执行流程图如图6(a)所示,其中格式分离是指上位机从文件的数据部分开始发送;数据合成是指将接收到的数据按顺序从文件的格式之后存入. ARM的软件执行流程图如图6(b)所示,通道1为加密通道,通道2为解密通道,根据上位机的控制,SOPC同时切换k1和k2进入加密模式或者解密模式.
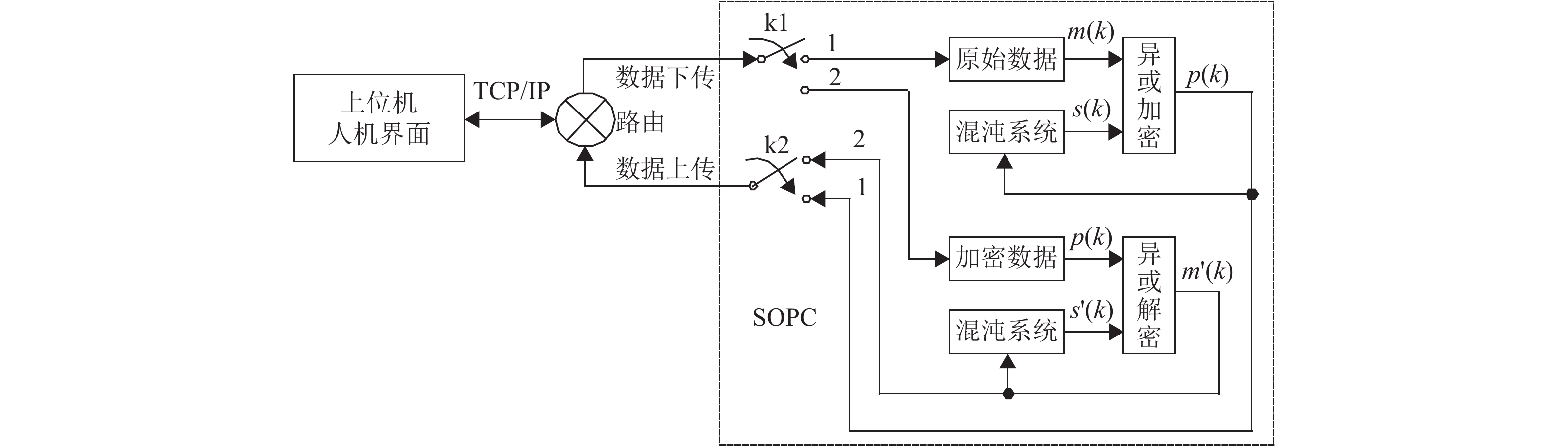
|
图 5 文件加密系统的原理框图 Figure 5 The block diagram of the file encryption system |
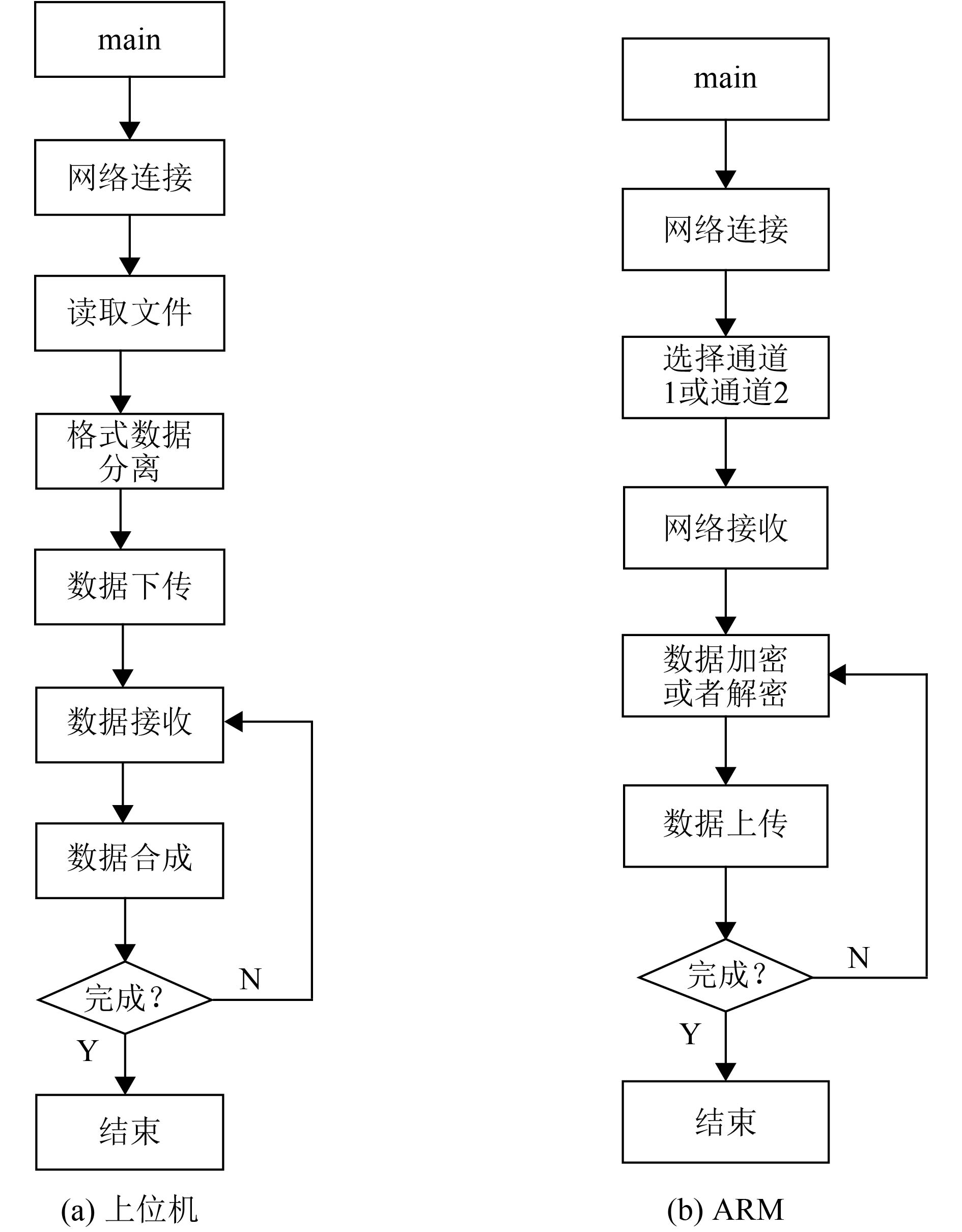
|
图 6 系统的软件执行流程图 Figure 6 Software execution flow chart of the system |
以PC作为上位机,以Xilinx ZC7020开发板作为下位机,上位机和下位机通过路由器连接,配置上位机IP地址为:192.168.1.100,下位机的IP地址为:192.168.1.101,端口为8080. 通过Vivado 2014.1软件编写加密算法和解密算法,并下载程序到下位机并运行. 采用Network软件编写上位机软件,人机界面如图7所示,填写IP和端口信息,选择加密或者解密模式,点击连接按钮进行网络连接,点击打开文件按钮选择需要处理的文件,点击发送和接收按钮开始下传,加密或者解密和上传等操作.
4.2 实验结果及分析分别对wav音频文件和bmp图像文件进行实验测试,wav文件测试结果如图8所示. 从实验结果可知,加密算法能够有效加密音频数据,形成均匀分布的统计特性,在密钥匹配的情况下解密算法能够正确解密音频数据,否则解密失败,解密数据仍然均匀分布.
bmp图像的实验测试结果如图9所示. 由实验结果可知,加密算法能够有效加密原始图片,在密钥匹配的条件下解密算法能够正确解密图像数据,否则解密失败,解密图像为雪花点状.

|
图 7 上位机人机界面 Figure 7 The user interface of the host computer |

|
图 8 wav文件实验测试结果 Figure 8 The tset result of the wav file |

|
图 9 bmp文件实验测试结果 Figure 9 The test result of the bmp file |
本文采用混沌反控制理论设计三维混沌系统,利用2个三维混沌系统联合生成加密序列对文件数据进行加密,经过安全测试证明加密算法具有良好的安全性能,并通过自同步的设计解决了信道干扰影响解密的问题. 为了避免破坏文件格式导致格式不兼容的问题,加密算法只加密文件的数据部分,格式部分保持不变. 最后对文件加密系统进行硬件和软件设计,实验结果证明了算法的技术可行性. 研究工作不足之处在于文件加密系统只能应用于wav和bmp等格式简单的文件,对于诸如JPEG和H.264具有复杂格式的文件无法适用,未来的研究工作是继续分析其他文件的格式,进一步提高文件加密系统的适用范围.
| [1] |
韩英. 浅谈电子文件信息安全与保障措施[J].
档案管理, 2014, 4: 80-81.
HAN Y. Talking about the information security and safeguard measures of electronic documents[J]. Archives Management, 2014, 4: 80-81. DOI: 10.3969/j.issn.1005-9458.2014.06.034. |
| [2] |
贾宗璞, 田肖, 李贺. 一种聚合签名认证的私有云文件加密系统[J].
计算机工程与应用, 2015, 51(24): 114-119.
JIA Z P, TIAN X, LI H. Private cloud files encryption system based on aggregate signature authentication[J]. Computer Engineering and Applications, 2015, 51(24): 114-119. DOI: 10.3778/j.issn.1002-8331.1312-0326. |
| [3] |
王晓妮, 韩建刚. 云计算面临的信息安全威胁及防御策略研究[J].
航空计算技术, 2018, 48(2): 113-117.
WANG X N, HAN J G. Research on information security threats and defense strategies of cloud computing[J]. Aeronautical Computing Technique, 2018, 48(2): 113-117. DOI: 10.3969/j.issn.1671-654X.2018.02.028. |
| [4] |
爨玉伟, 阮晓宏. 基于DES及其改进算法的文件加密系统[J].
计算机技术与发展, 2014, 24(7): 166-169.
CUAN Y W, RUAN X H. Encrypted file system based on DES algorithm and its improved algorithm[J]. Computer Technology and Development, 2014, 24(7): 166-169. |
| [5] |
朱天楠, 施勇, 薛质. 基于Xposed的Android透明文件加密系统的研究[J].
计算机技术与发展, 2017, 27(2): 64-68.
ZHU T N, SHI Y, XUE Z. Research on Android transparent encryption file system based on Xposed[J]. Computer Technology and Development, 2017, 27(2): 64-68. |
| [6] |
许肖威, 刘雄, 戴一奇. 基于安全局域网分级文件分发系统设计与实现[J].
计算机应用研究, 2012, 29(11): 4246-4249.
XU X W, LIU X, DAI Y Q. Gradable file distribution system design and implementation based on security LAN[J]. Application Research of Compute, 2012, 29(11): 4246-4249. DOI: 10.3969/j.issn.1001-3695.2012.11.062. |
| [7] |
万荣泽, 莫洪武, 余思东. 基于超混沌DNA计算优化OTP算法的文本图像加密算法[J].
计算机测量与控制, 2014, 22(10): 3278-3284.
WAN R Z, MO H W, YU S D. Document and image encryption based on OTP optimized by hyper-chaos mapping DNA computing[J]. Computer Measurement & Control, 2014, 22(10): 3278-3284. DOI: 10.3969/j.issn.1671-4598.2014.10.060. |
| [8] |
杨明极, 范希冀, 于舒春. 基于三维混沌映射的HSV空间图像加密算法研究[J].
哈尔滨理工大学学报, 2015, 20(6): 103-106.
YANG M J, FAN X J, YU S C. Encryption algorithm based on 3D chaotic mapping in HSV space[J]. Journal of Harbin University of Science and Technology, 2015, 20(6): 103-106. |
| [9] |
韩庆龙, 吕洁, 王凤芹. 基于混合加密的移动存储文件安全系统设计与实现[J].
海军航空工程学院学报, 2017, 32(6): 576-680.
HAN Q L, LYU J, WANG F Q. Design and implementation of a security system of files on removable sorage devices based on Hybrid encryption[J]. Journal of Naval Aeronautical and Astronautical University, 2017, 32(6): 576-680. |
| [10] |
CHEN G R, LAI D J. Feedback control of lyapunov exponents for discrete-time dynamical systems[J].
International Journal of Bifurcation and Chaos, 1996, 6(7): 1341-1349.
DOI: 10.1142/S021812749600076X. |
| [11] |
WANG X F, CHEN G R. Chaotification via arbitrarily small feedback controls: theory, method, and applications[J].
International Journal of Bifurcation and Chaos, 2000, 10(3): 549-570.
DOI: 10.1142/S0218127400000372. |
| [12] |
GAN Q Y, YU S M, LI C Q, et al. Design and ARM-embedded implementation of a chaotic map-based multicast scheme for multiuser speech wireless communication[J].
International Journal of Circuit Theory and Applications, 2017, 45: 1849-1872.
DOI: 10.1002/cta.v45.11. |
| [13] |
ZHANG X Y, YU S M, CHEN P, et al. Design and ARM-embedded implementation of a chaotic secure communication scheme based on H.264 selective encryption[J].
Nonlinear Dynamics, 2017, 89: 1949-1965.
DOI: 10.1007/s11071-017-3563-5. |
| [14] |
SHEN C W, YU S M, LU J H, et al. A systematic methodology for constructing hyperchaotic systems with multiple positive Lyapunov exponents and circuit implementation[J].
IEEE Transactions on Circuits and Systems-I, 2014, 61(3): 854-864.
DOI: 10.1109/TCSI.2013.2283994. |
| [15] |
SHEN C W, YU S M, LU J H. et al. Constructing hyperchaotic systems at will[J].
International Journal of Circuit Theory and Applications, 2015, 43(12): 2039-2056.
DOI: 10.1002/cta.2062. |
| [16] |
WOLF A, SWIFT J B, SWINNEY H L, et al. Determining Lyapunov exponents from a time series[J].
Physica D, 1985, 16(3): 285-327.
DOI: 10.1016/0167-2789(85)90011-9. |
 2019, Vol. 36
2019, Vol. 36