近年来,离散事件系统的故障检测研究引起了国内外许多学者的广泛关注. 尽管目前关于系统故障检测的方法有很多,包括基于数学模型的定量分析方法和专家系统等人工智能方法,但由Sampath等[1]提出的基于诊断器方法是离散事件系统故障诊断研究中最被广泛使用的方法[2]. Qiu和Kumar[3]将这种基于诊断器方法由集中式系统推广至分布式系统,提出了一种分布式系统故障诊断方法. Chen和Lin[4] 等将故障诊断与系统监控相结合,提出了一种活性诊断方法,并将其应用于电池能源系统的故障诊断. Kwong和Yonge-Mallo[5]研究了一类不完备离散事件系统的故障诊断问题,提出了一种通过构造具有自我学习功能诊断器的故障诊断方法. 欧阳丹彤等[6]也探讨了不完备模型下离散事件系统的故障诊断问题. 李志武等[7]对分布式离散事件系统发生故障后的可重构性进行了深入研究,提出了一种通过设计虚拟协调器与子系统之间的通信协议实现最优协调控制的动态重构方法. 本文作者则对模糊离散事件系统提出了一种模糊故障诊断方法[8].
上述故障诊断是一种“事后诊断”,即在故障已经发生的情况下,判断系统是否能够将该故障及时诊断出来. 显然,这种故障诊断对进一步采取相应的故障隔离或系统修复等补救措施具有重要作用. 但是,对于严重影响系统运行甚至导致系统不可逆转的故障,这种“事后诊断”存在很大的局限性,因为它无法提前阻止该故障的发生. 为此,故障预测方法就应运而生. 故障预测是在故障尚未发生的情况下,预测系统在未来是否会有故障发生. 显然,故障预测能对系统故障进行提前预报和事先维护,对增强系统稳定性、消除系统安全隐患极为重要[9].
在离散事件系统的故障预测方面,Genc和Lafortune[9]对基于正则语言模型的离散事件系统提出了一种故障预测方法. Takai和Kumar[10]针对一类带有界时延通讯的离散事件系统,提出了一种基于推理的分布式故障预测方法. Khoumsi和Chakib[11]运用局部预测信息融合技术提出了一种基于合取与析取逻辑模式的分散预测方法. Sanchez等[12]探讨了一类在初始状态和初始输出信息均未知的情况下 Petri 网结构序列检测问题. 舒少龙等[13]用状态估计方法分别对系统的不可分辨性、强可检测性、强周期可检测性进行了深入研究. 本文作者也对分布式离散事件系统提出了一种分散故障预测方法[14]和一个相应的多项式时间算法[15].
本文研究随机离散事件系统的故障预测问题. 虽然离散事件系统研究在过去数十年内取得了一大批研究成果,但大多数系统模型还是局限于以经典自动机为模型的逻辑离散事件系统[16]. 随着计算机等相关领域的迅猛发展,数据的计算和处理能力越来越强大,对数据处理后得到的数据结果的精确度要求也越来越高. 仅仅使用逻辑离散事件系统来进行数据建模,已经很难满足相关要求. 为了能够更加精确地描述一个数据模型,人们开始引入了随机自动机的概念. 随机离散事件系统将逻辑离散事件系统和随机自动机进行有效结合,通过增加概率描述的方式,可以更加精确地描述一个事件系统. 针对随机离散事件系统,David Thorsley[17]提出了一种基于随机自动机理论的随机离散事件系统的故障诊断方法,通过构造随机诊断器模型实现对故障事件的实时诊断. 笔者也对随机离散事件系统提出了一种分散故障诊断方法[18]和一种安全诊断方法[19].
本文继续笔者在文献[14-15, 18-19]的工作,研究基于随机自动机模型的随机离散事件系统的故障预测方法. 先对随机离散事件系统的故障可预测性进行形式化,要求具有可预测性的系统能确保对无法预测故障事件发生的概率充分小(即能够预测故障事件发生的概率足够大). 再通过引入概率转移矩阵,构建一个故障预测器自动机,得到关于随机离散事件系统的故障可预测性的充分必要条件. 因此,在所构建的故障预测器的基础上,通过计算其扩展马尔可夫矩阵,根据该充分必要条件,可判定随机离散事件系统是否具有故障可预测性,从而实现对故障事件在其发生之前的准确预测. 值得指出的是,本文与文献[20-21]有明显不同,主要在于文献[20]是一种基于状态估计的预测方法,文献[21]是一种带有固定转移步数的预测方法,而本文是一种基于事件的预测方法,提出的通过构建预测器自动机实现对故障事件的预测也是本文的创新之处.
1 随机离散事件系统一个随机离散事件系统是指一个四元组有限状态自动机[17-19]
| $G = (\varSigma ,{ X},p,x{}_0),$ |
其中Σ是有限事件集,X是有限状态集,
一个由
| ${s_f} = \{ {s_f} \in \varSigma ,s \in L,t \in s:s = t{s_f}\}; $ |
| $\varPsi (\sigma ,L) = \{ s\sigma \in L:s \in {\varSigma ^*},\sigma \in \varSigma \} ;$ |
| ${L_{\rm{o}}}(G,x) = \{ s \in L(G,x):s = u\sigma ,u \in \varSigma _{{\rm{uo}}}^*,\sigma \in {\varSigma _{\rm{o}}}\}; $ |
在随机离散事件系统
| $\begin{array}{l}\delta :{X} \times \varSigma \to {X},\\\delta (x,e) = {x'} \Rightarrow p({x'},e|x) > 0.\end{array}$ |
其中,
| $\delta (x,se) = \delta (\delta (x,s),e). $ |
假设1 随机离散事件系统
| $\mathop \varSigma \limits_{{x'} \in { X}} \mathop \varSigma \limits_{e \in \varSigma } p({x'},e|x) = 1.$ |
它表示
假设2 随机离散事件系统
通常有限事件集
| $\begin{array}{l}{P_j}(\varepsilon ) = \varepsilon, \\{P_j}(\sigma ) = \left\{ {\begin{array}{*{20}{l}}{\sigma ,{\text{若}}\sigma \in {\varSigma _{\rm{o}}}};\\{\varepsilon ,{\text{若}}\sigma \in {\varSigma _{{\rm{uo}}}}}.\end{array}} \right.\end{array}$ |
对于
| $P_{jL}^{ - 1}({s_{\rm{o}}}) = \{ s \in L:{P_j}(s) = {s_{\rm{o}}}\} ,\;s \in {\varSigma ^*},{s_{\rm{o}}} \in \varSigma _{\rm{o}}^*.$ |
为进一步简化,上述
| $P_r (es|x) = p(e|x)p(s|\delta (x,e)). $ |
定义1(逻辑可预测性)[9] 设
| $(\exists n \in {\rm N})(\forall s \in \varPsi ({\sigma _p},L))(\exists t \in \bar s)[({\sigma _p} \notin t) \wedge P],$ |
其中P为
| $\begin{array}{l}P:(\forall u \in L)(\forall v \in L/u)[({P_j}(u) = {P_j}(t)) \wedge \\({\sigma _p} \notin u) \wedge (\left\| v \right\| \geqslant n) \Rightarrow ({\sigma _p} \in v)].\end{array}$ |
直观上,它表示对任意一个故障事件串
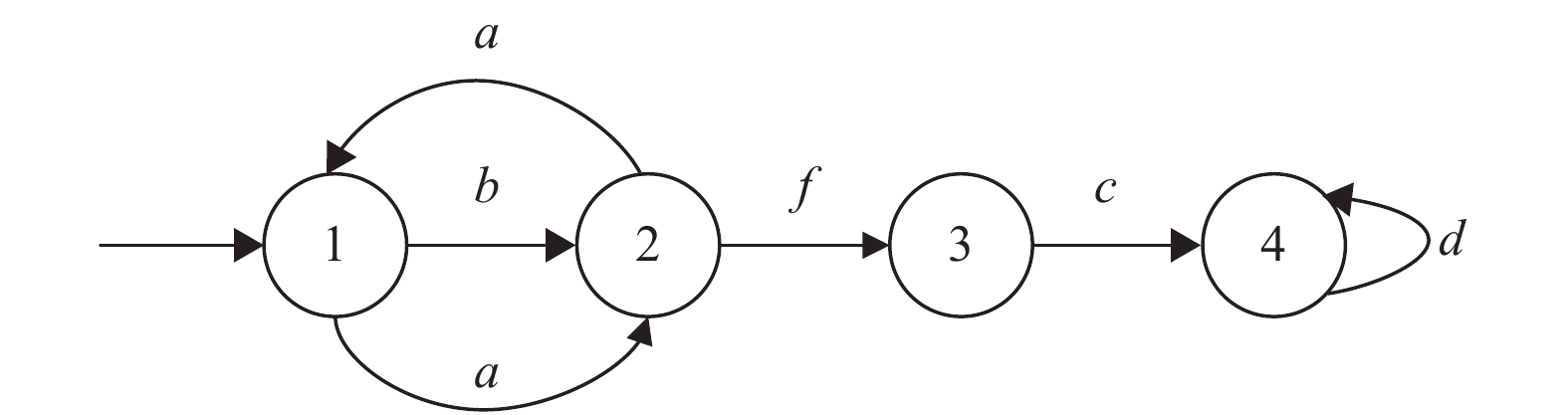
例1 考虑逻辑自动机
|
图 1 例1中的逻辑自动机 Figure 1 The logical automaton in example 1 |
定义2(随机可预测性) 设
| $\begin{array}{l}(\forall \varepsilon > 0)(\exists I \in {\rm N})(\forall s \in \Psi ({\sigma _p},L)),\\(\exists t \in (\bar s \cap {L_{{{\tilde \sigma }_p}}}) \wedge n \geqslant N),\\\{ {P_r}(t:P(t) = 0|t \in (\bar s \cap {L_{{{\tilde \sigma }_p}}})) < \varepsilon \} .\end{array}$ |
其中,
| $P(t) = \left\{ {\begin{array}{*{20}{l}}{1, \;{\text{如果}}(\forall v \in L/{L_u}(t))[\left\| v \right\| \geqslant n \Rightarrow {\sigma _p} \in v]};\\{0, \; {\text{否则}}}.\end{array}} \right.$ |
这里
直观上,它表示对任意一个故障事件串
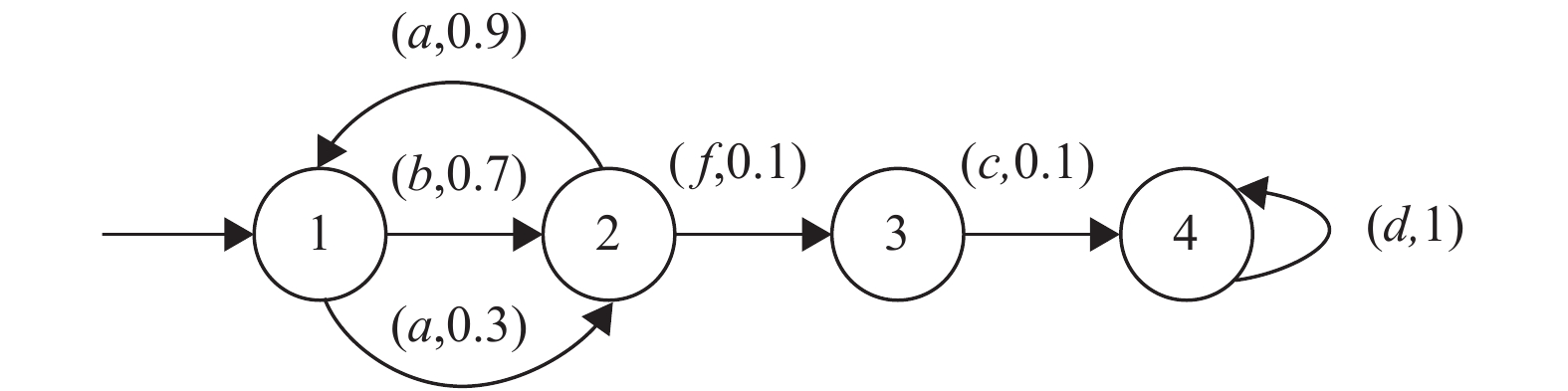
例2 考虑随机自动机
| ${P_r}(b{a^{n/2}}{a^{n/2}}) = 0.7 \times {(0.9)^{n/2}}{(0.3)^{n/2}}. $ |
|
图 2 例2中的随机自动机 Figure 2 The stochastic automaton in example 2 |
显然,随着
为执行随机系统框架下的故障预测,将随机离散事件系统
| ${D_G} = ({Q_d},{\varSigma _{\rm{o}}},{\delta _d},{q_0},{{\varPhi}} ,{\phi _0},{\sigma _p}).$ |
其中
| ${q_d} = \{ ({x_1},{l_1}),({x_2},{l_2}), \cdots ,({x_n},{l_n})\} ({x_i} \in {X_0},{l_i} \in \varOmega ).$ |
在逻辑元素
| $\begin{array}{l}x \in {{X}_{\rm{o}}} \Rightarrow (x = {x_0}) \vee (\exists s \in L:\delta \left( {{x_0},s} \right) = \\x \wedge {s_f} \in {\varSigma _{\rm{o}}}).\end{array}$ |
在预测器中,标签传递函数
| $LP(x,l,s) = \left\{ {\begin{array}{*{20}{l}}{\{ N\} , \; {\text{如果}}l = \{ N\} \wedge \forall i[{\varSigma _{{f_i}}} \notin s]};\\{\{ {F_i}:{F_i} \in l \vee {\varSigma _{{f_i}}} \in s\} ,{\text{否则}}}.\end{array}} \right.$ |
预测器转移函数定义为
| ${\delta _d}(q,\sigma ) = \mathop \cup \limits_{(x,l) \in q} \mathop \cup \limits_{s \in {L_\sigma }(G,x)} \{ (\delta (x,s),LP(x,l,s))\}. $ |
逻辑元素中组件间的转移函数:
| ${\delta _{{\rm comp}}}(q,x,l,s) = ({\delta _d}(q,{P_j}(s)),\delta (x,s),LP(x,l,s)).$ |
定义逻辑元素概率转移矩阵集
| $\begin{array}{l}{{{\varPhi}} _{ij}}(q,{\sigma _{\rm{o}}}) = \sum\limits_{s \in {L_{{\sigma _{\rm{o}}}}}(G,{x_i}):(\delta ({x_i},s),LP({x_i},{l_i},s)) = ({x_i},{l_j})} {P_r (s)}= \\P_r ({c_{{\delta _d}(q,{\sigma _{\rm{o}}}),j}},{\sigma _{\rm{o}}}|{c_{q,i}})\end{array}$ |
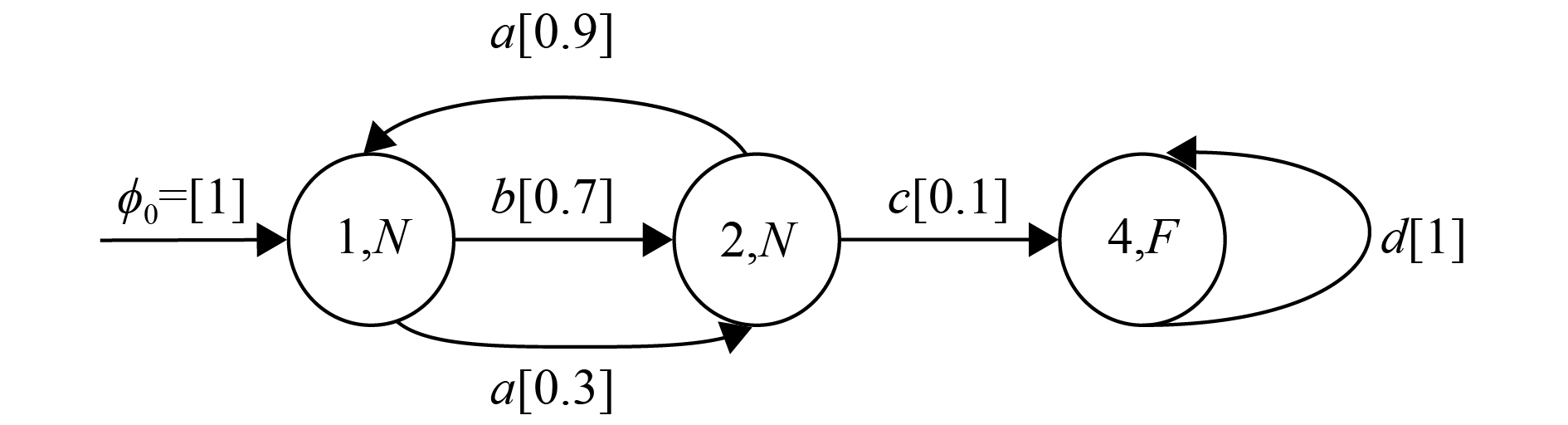
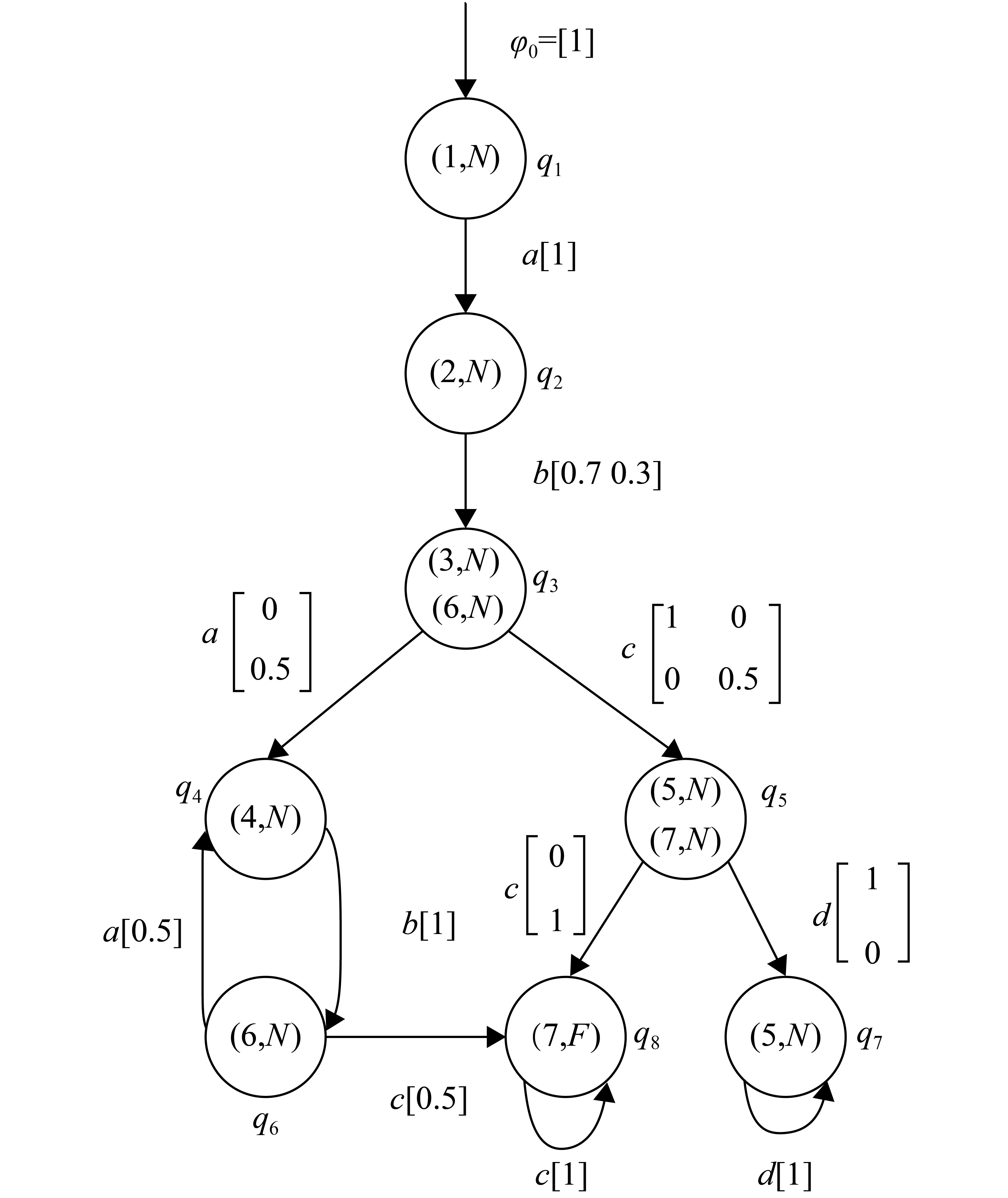
例3 例2中给出的随机自动机
|
图 3 随机自动机
|
|
图 4 随机自动机
|
|
图 5 随机自动机
|
令
| $\begin{array}{l}{F_D} = \{ {x_D} \in Q_D^N:\exists {y_D} = {\delta _D}({x_D},{\sigma _{\rm{o}}}),\\({\sigma _{\rm{o}}} \in {\varSigma _{\rm{o}}},{y_D} \notin Q_D^N)\}.\end{array} $ |
定义3 设
显然,如果
这里还需要马尔可夫链的一些相关概念. 假设
引理1[17] 设
| $P_r (t:\delta \left( {x,t} \right) \in {\rm T}|t \in L(G,x) \wedge \left\| t \right\| = n) < \varepsilon .$ |
下面将给出随机离散事件系统故障事件可预测性的充分必要条件.
定理1 设
证明 先证明必要性. 设
假设存在
1) 若逻辑元素
| ${P_r}(t:P(t) = 0|t \in (\bar s \cap {L_{{{\tilde \sigma }_p}}})) = 1. $ |
所以,
根据定义2得,
2) 若逻辑元素
再证明充分性. 设对于任一
设
| $P_r (t:{\delta _{\rm comp}}\left( {c,t} \right) \in {{\rm T}_c}|t \in L(G,x) \wedge \left\| t \right\| = n) < \varepsilon, $ | (1) |
即在系统
| ${P_r}(t:P(t) = 1|t \in (\bar s \cap {L_{{{\tilde \sigma }_p}}})) > 1 - \varepsilon ,$ |
即
根据定理1可知,判断故障事件的随机可预测性只需要考虑包含有重复态组件的逻辑元素是否满足定理1条件. 为了计算随机离散事件系统
| ${{\varGamma}} ({q_i},{q_j}) = \sum\limits_{{e_{\rm{o}}} \in {\varSigma _{\rm{o}}}:\delta ({q_i},{e_{\rm{o}}}) = {q_j}} {{{\varPhi}} ({q_i},{e_{\rm{o}}})} ,$ |
其中矩阵
| ${{\varPi}} ({D_G}) = \left[ {\begin{array}{*{20}{c}} {{{\varGamma}} ({q_1},{q_1})}& \cdots &{{{\varGamma}} ({q_1},{q_n})} \\ \vdots & {\rm{}} & \vdots \\ {{{\varGamma}} ({q_n},{q_1})}& \cdots &{{{\varGamma}} ({q_n},{q_n})} \end{array}} \right].$ |
例如,图3中随机自动机
| $\begin{array}{*{20}{c}} {}&{({q_1},1,N)}&{({q_2},2,N)}&{({q_3},4,F)} \\ {({q_1},1,N)}&0&1&0 \\ {({q_2},2,N)}&{0.9}&0&{0.1} \\ {({q_3},4,F)}&0&0&1 \end{array}$ |
即
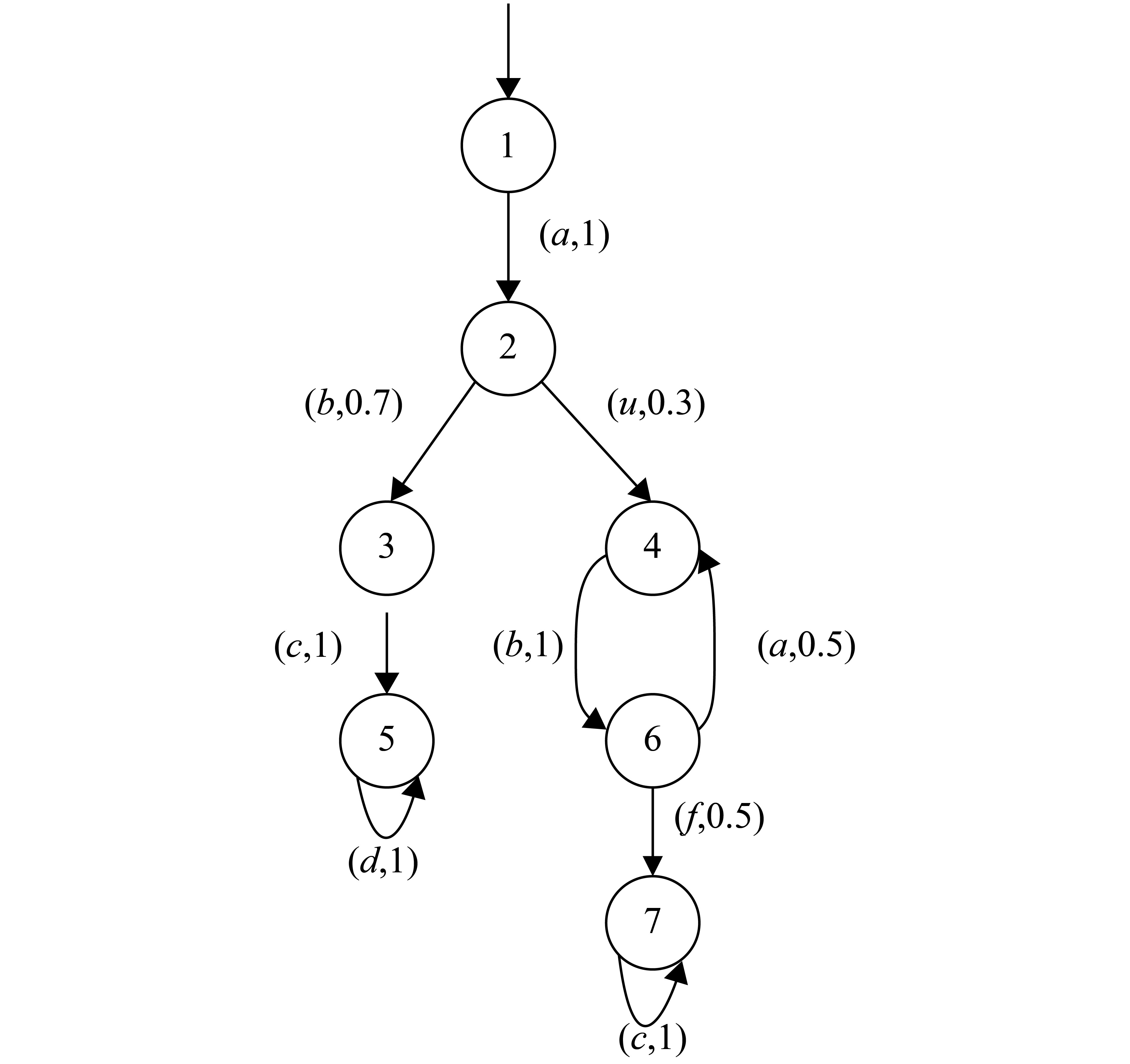
例4 考虑例3中的随机自动机
| ${{\varPi}} ({D_{{G_3}}}) \!=\! \left[\!\! {\begin{array}{*{20}{c}} 0\!&\!1\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0 \\ 0\!&\!0\!&\!{0.7}\!&\!{0.3}\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0 \\ 0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!1\!&\!0\!&\!0\!&\!0\!&\!0 \\ 0\!&\!0\!&\!0\!&\!0\!&\!{0.5}\!&\!0\!&\!{0.5}\!&\!0\!&\!0\!&\!0 \\ 0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!1\!&\!0\!&\!0 \\ 0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!1\!&\!0 \\ 0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!1 \\ 0\!&\!0\!&\!0\!&\!0\!&\!{0.5}\!&\!0\!&\!0\!&\!0\!&\!0\!&\!{0.5} \\ 0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!1\!&\!0 \\ 0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!1 \end{array}} \!\!\right].$ |
从
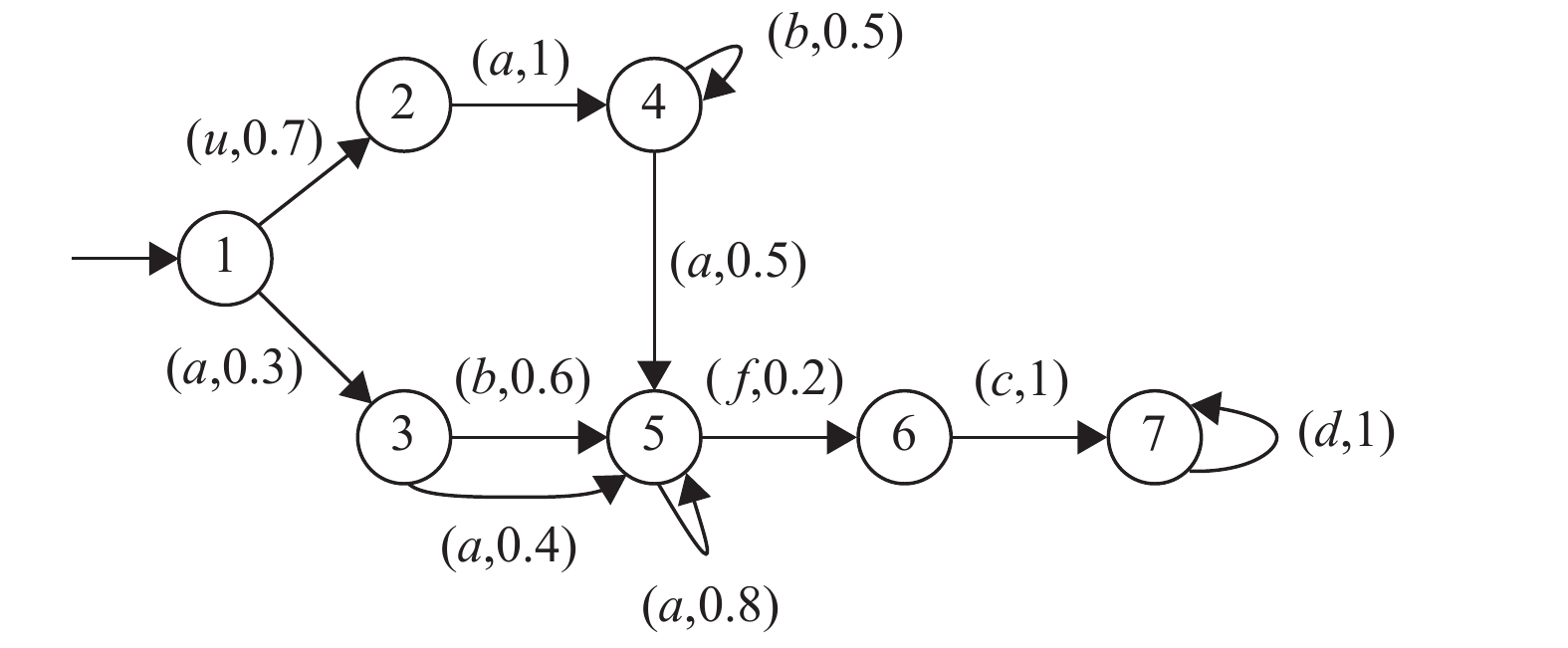
例5 考虑随机自动机
|
图 6 例5中的随机自动机
|
设随机自动机
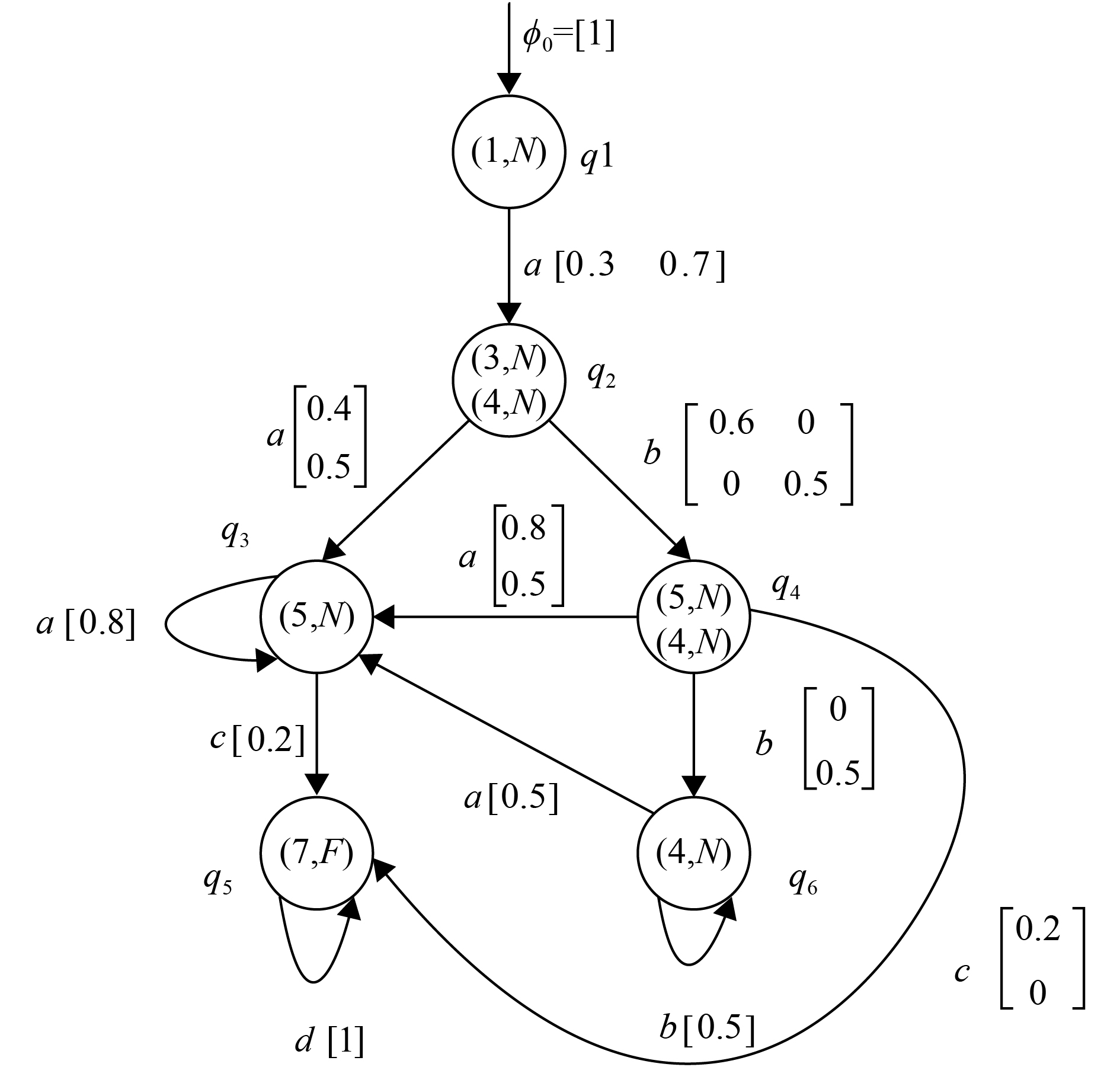
|
图 7 随机自动机
|
由预测器
| ${{\varPi}} ({D_{{G_4}}}) = \left[ {\begin{array}{*{20}{c}} 0&{0.3}&{0.7}&0&0&0&0&0 \\ 0&0&0&{0.4}&{0.6}&0&0&0 \\ 0&0&0&{0.5}&0&{0.5}&0&0 \\ 0&0&0&{0.8}&0&0&{0.2}&0 \\ 0&0&0&{0.8}&0&0&{0.2}&0 \\ 0&0&0&{0.5}&0&0&0&{0.5} \\ 0&0&0&0&0&0&1&0 \\ 0&0&0&{0.5}&0&0&0&{0.5} \end{array}} \right].$ |
从
本文针对随机离散事件系统模型,提出了一种相应的故障预测方法,该方法将逻辑离散事件系统的故障预测方法拓展到带有概率结构的离散事件系统. 通过对随机离散事件系统的故障可预测性的形式化,并引入概率转移矩阵构建了一个故障预测器自动机,得到了一个关于随机离散事件系统的故障可预测性的充分必要条件. 由此得到了判定随机离散事件系统是否具有故障可预测性的方法,从而实现对故障事件在其发生之前的准确预测.
在本文研究的基础上,可以将集中型系统拓展至分布式系统,进一步考虑分布式随机离散事件系统的故障预测问题. 同时,如何对本文提出的故障预测方法应用到实际应用系统中,并通过相关算法编程和应用MATLAB等仿真工具,解决故障预测编程语言的算法实现与算法优化等也是非常有意义的问题. 在后续研究中,笔者将在本文的基础上进一步深入探讨.
| [1] |
SAMPATH M, SENGUPTA R, LAFORTUNE S, et al. Diagnosability of discrete-event systems[J].
IEEE Transactions on Automatic Control, 1995, 40(9): 1555-1575.
DOI: 10.1109/9.412626. |
| [2] |
ZAYTOON J, LAFORTUNE S. Overview of fault diagnosis methods for discrete event systems[J].
Annual Reviews in Control, 2013, 37(2): 308-320.
DOI: 10.1016/j.arcontrol.2013.09.009. |
| [3] |
QIU W, KUMAR R. Decentralized failure diagnosis of discrete event systems[J].
IEEE Transactions on Systems, Man, and Cybernetics - Part A: Systems and Humans, 2006, 36(2): 384-395.
DOI: 10.1109/TSMCA.2005.853503. |
| [4] |
CHEN Z, LIN F, WANG C, et al. Active diagnosability of discrete event systems and its application to battery fault diagnosis[J].
IEEE Transactions on Control Systems Technology, 2014, 22(5): 1892-1898.
DOI: 10.1109/TCST.2013.2291069. |
| [5] |
KWONG R H, YONGEMALLO D L. Fault diagnosis in discrete event systems with incomplete models: learnability and diagnosability[J].
IEEE Transactions on Cybernetics, 2015, 45(7): 1236-1249.
DOI: 10.1109/TCYB.2014.2347801. |
| [6] |
王晓宇, 欧阳丹彤, 赵剑. 不完备模型下的离散事件系 统诊断方法[J].
软件学报, 2012, 23(3): 465-475.
WANG X Y, OUYANG D T, ZHAO J. Discrete-event system diagnosis upon incomplete model[J]. Journal of Software, 2012, 23(3): 465-475. |
| [7] |
ZHANG J, KHALGUI M, LI Z, et al. Reconfigurable coordination of distributed discrete event control systems[J].
IEEE Transactions on Control Systems Technology, 2015, 23(1): 323-330.
DOI: 10.1109/TCST.2014.2313352. |
| [8] |
LIU F, QIU D. Diagnosability of fuzzy discrete-event systems: a fuzzy approach[J].
IEEE Transactions on Fuzzy Systems, 2006, 17(2): 372-384.
|
| [9] |
GENC S, LAFORTUNE S. Predictability of event occurrences in partially-observed discrete-event systems[J].
Automatica, 2009, 45(2): 301-311.
DOI: 10.1016/j.automatica.2008.06.022. |
| [10] |
TAKAI S, KUMAR R. Distributed failure prognosis of discrete event systems with bounded-delay communications[J].
IEEE Transactions on Automatic Control, 2012, 57(5): 1259-1265.
DOI: 10.1109/TAC.2011.2173419. |
| [11] |
KHOUMSI A, CHAKIB H. Conjunctive and disjunctive architectures for decentralized prognosis of failures in discrete-event systems[J].
IEEE Transactions on Automation Science & Engineering, 2012, 9(2): 412-417.
|
| [12] |
NUÑO-SÁNCHEZ S A, RAMÍREZ-TREVIÑO A, RUIZ-LEÓN J. Structural sequence detectability in free choice interpreted petri nets[J].
IEEE Transactions on Automatic Control, 2016, 61(1): 198-203.
DOI: 10.1109/TAC.2015.2426275. |
| [13] |
SHU S, HUANG Z, LIN F. Online sensor activation for detectability of discrete event systems[J].
IEEE Trans- actions on Automation Science & Engineering, 2013, 10(2): 457-461.
|
| [14] |
LIU F. Decentralized predictability of discrete event systems[C]// 2017 29th Chinese Control and Decision Conference. Chongqing: Control and Decision, 2017: 2914-2919.
|
| [15] |
LIU F, YANG P. Verification for the predictability of decentralized discrete event systems with a polynomial complexity[C]// 2017 36th Chinese Control Conference. Dalian: Technical Committee on Control Theory, 2017: 2367-2372.
|
| [16] |
CASSANDRAS C G, LAFORTUNE S. Introduction to discrete event systems[M]. New York: Springer, 2008.
|
| [17] |
THORSLEY D, TENEKETZIS D. Diagnosability of stochastic discrete-event systems[J].
IEEE Transactions on Automatic Control, 2005, 50(4): 476-492.
DOI: 10.1109/TAC.2005.844722. |
| [18] |
LIU F, QIU D, XING H, et al. Decentralized diagnosis of stochastic discrete event systems[J].
IEEE Transactions on Automatic Control, 2008, 53(2): 535-546.
DOI: 10.1109/TAC.2007.915172. |
| [19] |
LIU F, QIU D. Safe diagnosability of stochastic discrete event systems[J].
IEEE Transactions on Automatic Control, 2008, 53(5): 1291-1296.
DOI: 10.1109/TAC.2008.921035. |
| [20] |
常明, 董炜, 吉吟东, 等. 基于随机自动机状态估计的 故障预测[J].
清华大学学报(自然科学版), 2013, 53(11): 1623-1628.
CHANG M, DONG W, JI Y D, et al. State estimation based fault prediction for stochastic automatons[J]. Journal of Tsinghua University (Science and Technology), 2013, 53(11): 1623-1628. |
| [21] |
CHEN J, KUMAR R. Stochastic failure prognosability of discrete event systems[J].
IEEE Transactions on Automatic Control, 2015, 60(6): 1570-1581.
DOI: 10.1109/TAC.2014.2381437. |
 2018, Vol. 35
2018, Vol. 35

