随着桥梁设计理论不断发展以及桥梁施工技术水平的不断提高,大跨度桥梁如雨后春笋般涌现. 钢管混凝土拱桥,一方面借助内填混凝土提高钢管壁受压稳定性,提高钢管的抗腐蚀性和耐久性,另一方面借助管壁对混凝土的套箍作用,提高了混凝土的抗压强度和延性,将钢材和混凝土有机地组合起来可以优势互补,充分发挥两种材料特性[1-2]. 我国第一座钢管混凝土拱桥——四川旺苍东河大桥,于1991年建成通车,主跨为115 m. 目前我国跨度最大的钢管混凝土拱桥为四川合江长江大桥,于2013年建成通车,主跨为518 m[3].
拱肋作为钢管混凝土拱桥的主要受力构件,其受压稳定性是全桥设计的关键环节[4]. 随着桥梁跨度的不断增大,对钢管混凝土拱桥稳定性问题的研究越来越显得重要[5-6]. 此外,桥梁跨度的不断增大,成熟的设计理论及建造技术是前提. 我国在2013和2015相继颁布了钢管混凝土拱桥的相关规范[7-8],不过两种规范在拱肋刚度取值的计算上存在差异,如何确定合理的拱肋刚度也显得尤为关键. 基于此,本文采用我国两种规范给出的拱肋刚度取值方法,对15组不同钢材等级及混凝土标号组合进行截面刚度计算并且进行对比分析. 与此同时,利用大型有限元软件ANSYS按两种拱肋刚度计算方法对陈宝春等提出的试验模型[9]进行模拟,对比分析两种模拟方法,选择一种合理的刚度取值及建模方法. 基于试验验证的合理有限元模拟方法,采用大型有限元软件ANSYS对钢管混凝土拱桥的稳定性影响因素进行分析.
1 我国现行规范拱肋刚度取值分析 1.1 两种规范拱肋刚度取值方法目前现行的两种钢管混凝土拱桥规范分别为GB 50923-2013《钢管混凝土拱桥技术规范》(后文简称2013规范)及JTG/T D65-06-2015《公路钢管混凝土拱桥设计规范》(后文简称2015规范),两种规范内容上大同小异,区别较大的地方在于对钢管混凝土拱桥拱肋刚度取值的规定.
2013规范采用刚度叠加的方法计算拱肋刚度,规范考虑了混凝土开裂而对混凝土的抗弯刚度作了相应的折减,即
| ${(EA)_{{\rm{sc}}}} = {E_s}{A_{s1}} + {E_c}{A_{c1}},$ | (1) |
| ${(EI)_{{\rm{sc}}}} = {E_s}{I_{s1}} + 0.6{E_c}{I_{c1}}.$ | (2) |
式(1)~(2)中,(EA)sc为钢管混凝土拱肋截面整体压缩设计刚度,(EI)sc为钢管混凝土拱肋截面整体弯曲设计刚度,As1为拱肋截面钢材面积,Ac1为拱肋截面混凝土面积,Is1为钢材截面钢材惯性矩,Ic1为混凝土截面惯性矩.
2015规范采用了钟善桐[10]的研究成果——钢管混凝土统一理论:把钢管混凝土视为统一整体,把钢管和混凝土组合成一种新型组合材料. 规范直接列出了组合弹性轴压模量Esc的取值表格,同时给出了相应计算公式. 2015规范的组合弹模计算公式为
| ${E_{{\rm{sc}}}} = f_{{\rm{sc}}}^p/\varepsilon _{{\rm{sc}}}^p,\quad\;\;\;\;\quad\quad\quad\quad\quad\quad\quad$ | (3) |
| $f_{{\rm{sc}}}^p = (0.192{f_y}/235 + 0.448)f_{{\rm{sc}}}^y,$ | (4) |
| $\varepsilon _{{\rm{sc}}}^p = 0.67{f_y}/{E_s},\quad\quad\quad\quad\quad\quad\quad\quad$ | (5) |
| $f_{{\rm{sc}}}^y = (1.212 + B\xi + C{\xi ^2}){f_{{\rm{ck}}}},\quad\quad\quad\quad$ | (6) |
其中,
式(3)~(6)中,Esc为组合弹性模量,
为更直观地比较两种规范对拱肋刚度取值的差别,本节以钢管强度等级、钢管直径、钢管壁厚及混凝土标号为参数,进行15种工况组合,分别按两种规范规定的刚度取值方法进行钢管混凝土截面刚度计算,对比分析按两种规范的规定计算的拱肋刚度计算结果. 详细参数在表1中列出. 计算结果如表1所示.
| 表 1 两本规范刚度取值 Table 1 The stiffness values of the two standards |
由表1可知,依据2013规范和2015规范计算得到的钢管混凝土拱肋刚度的误差前6种组合情况较小,误差值都在10%以内. 第12种组合情况计算出的刚度误差较大,达28.2%. 究其原因,钢管强度等级与混凝土标号出现不匹配的情况,造成按2015规范算出的拱肋刚度值偏大. 实际2015规范也特别规定了钢管与混凝土材料的强度等级必须相匹配,以确保钢管混凝土的力学性能更优良、经济性更好.
此外,通过表1发现,前6种匹配情况依据2013规范计算出的刚度比依据2015规范计算的刚度要大5%~11%,而后面8种情况却出现比依据2015规范计算的刚度小的相反情况. 由此可见,2013规范中基于经验考虑混凝土开裂后给出的刚度折减系数0.6对拱肋刚度的计算结果的影响存在着一定的不准确性.
2 两种规范刚度取值的合理性分析学者们对钢管混凝土拱桥的有限元模拟主要方法为双单元法,即钢管和混凝土分别采用两个单元进行模拟,采用刚度叠加来计算钢管混凝土拱桥. 此外,也有部分学者曾用统一理论法进行模拟,如文献[11],不过该文献仍然采用了双单元法研究脱空对上承式钢管混凝土拱桥整体稳定性能的影响. 对于哪种模拟方法更合理至今无统一定论. 为了便于利用有限元软件模拟钢管混凝土拱桥,本节将采用统一理论法及双单元法对单拱试验[9]进行模拟,并比较两种模拟方法的合理性,最后选择一种合理的模拟方法研究横撑对钢管混凝土拱桥稳定性的影响.
文献[9]中分别做了两组试验:B1拱模型(对称跨中加载)及B2拱模型(非对称1/4跨加载). 试验模型拱的跨径为8.5 m,矢高为1.88 m. 拱轴线采用悬链线,拱轴系数为1.347. 哑铃型截面如图1所示. 试验材料采用的混凝土极限抗压强度为39.38 MPa,轴心抗压强度标准值为26.38 MPa,弹性模量为2.7×104 MPa;钢材屈服强度为378 MPa. 极限抗压强度为567 MPa,弹性模量为2.1×105 MPa,泊松比为0.263.
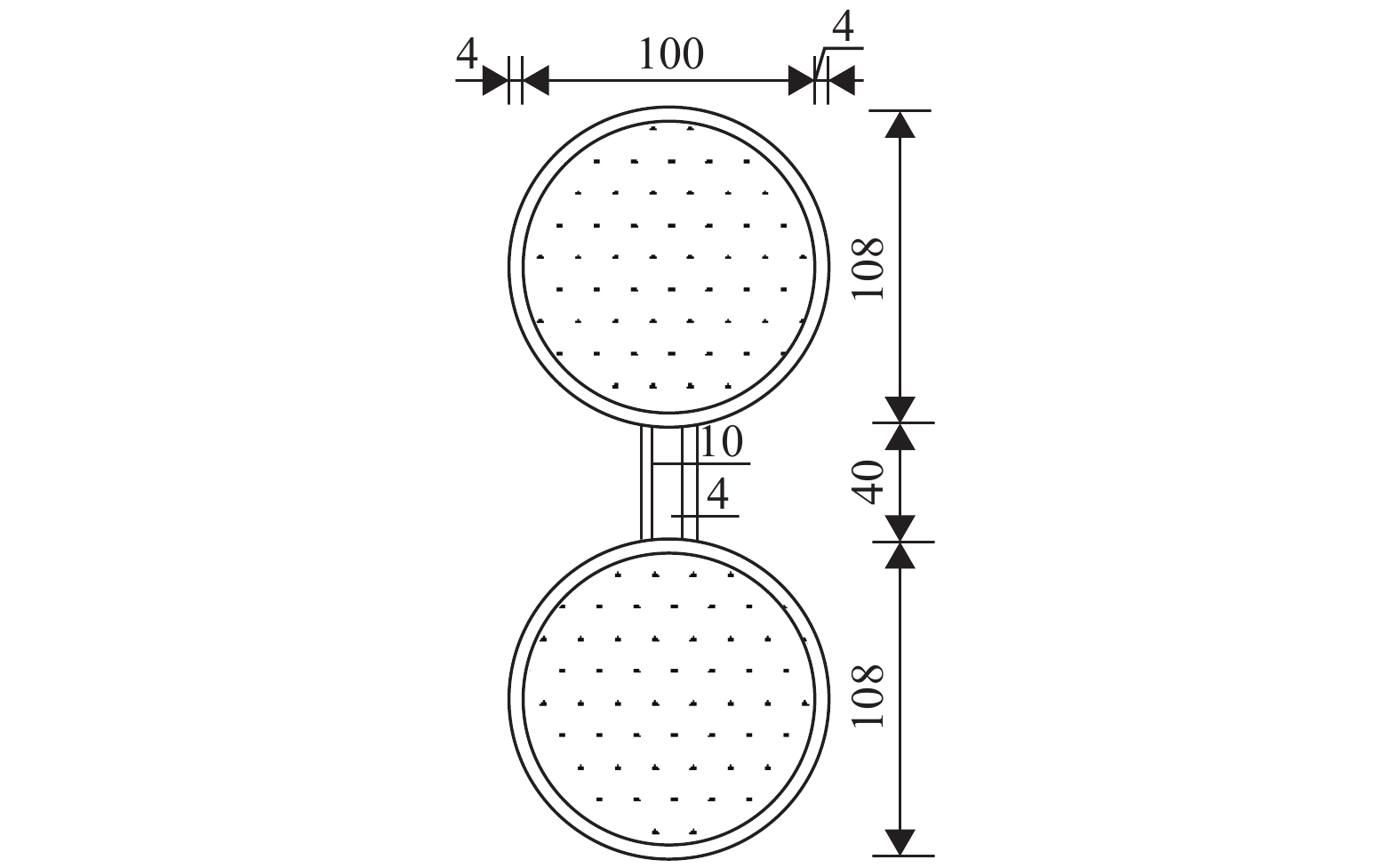
|
图 1 模型拱截面 单位:mm Figure 1 Cross section of model arch |
本节采用大型有限元软件ANSYS基于双单元法及统一理论法对单拱肋试验进行双重非线性分析. 两种模拟方法的拱肋选择空间梁单元BEAM188进行模拟,哑铃型拱肋横截面采用辅助单元PLANE82定义,拱肋共划分为80个单元,两端拱脚节点1和节点81的6个自由度完全约束,加载采用位移加载. 图2和图3分别为统一理论法及双单元法建立的有限元模型的截面,图4为试验单拱肋的有限元模型.
|
图 2 统一理论拱肋截面 Figure 2 Arch section of the unified theory |

|
图 3 双单元法拱肋截面 Figure 3 Arch section of double-element method |

|
图 4 单拱肋试验模型 Figure 4 Model of single arch rib |
其中统一理论模拟的材料本构采用统一理论模型[10]. 双单元模拟中钢管的应力—应变关系采用四折线本构模型[12],混凝土应力—应变曲线采用韩林海[13]提出的充分考虑约束效应的核心混凝土本构模型. 通过有限元计算,得出对称加载B1拱及非对称加载B2拱的荷载—位移曲线如图5所示.
文献[14]也曾采用修正本构关系考虑偏心折减影响模拟B1和B2拱肋试验[9],其计算极限承载力与本文模拟结果对比如表2所示.
| 表 2 极限承载力对比 Table 2 The comparison of ultimate bearing capacity |
由图5可以看出,模拟计算得到的荷载—位移曲线与实测规律基本一致,且统一理论法的计算结果比双单元的计算结果更为接近实测值.
由表2可知,B1拱试验实测拱肋极限承载力为320 kN. 统一理论法的模拟结果比试验值高出了20.1%. 采用双单元法模拟结果比试验值高出26.9%. 而统一理论计算结果与文献[14]计算结果只相差2.5%.
对于B2拱,试验实测值为250 kN. 统一理论法的模拟结果比试验值高出16.3%. 采用双单元法模拟结果比试验值高出27.8%. 而统一理论计算结果与文献[14]计算结果只相差6.3%.
综上所述,采用统一理论法模拟比双单元法更接近实测值,并且与文献[14]考虑偏心影响时的模拟值相差仅6.5%以内. 此外,统一理论法由于所建单元少,在计算效率及计算成本上比双单元法更具有优势. 因此,采用统一理论法模拟钢管混凝土拱桥具有一定合理性.
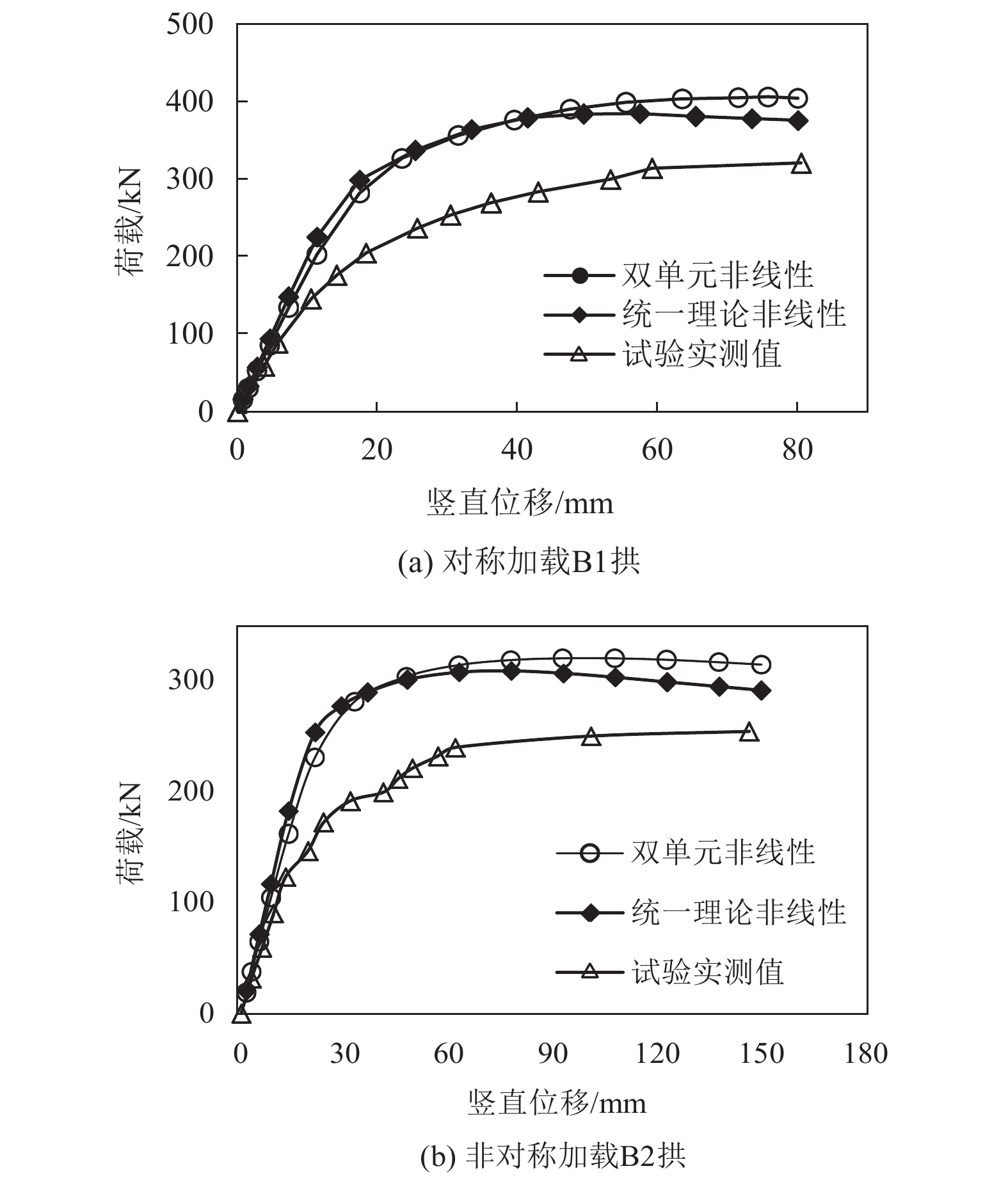
|
图 5 模型拱荷载—位移曲线 Figure 5 Load-vertical displacement curves of model arch |
钢管混凝土拱桥稳定性影响因素主要有横撑、拱肋刚度、吊杆刚度及系梁刚度等. 本文将以文献[15]中所构建的标准钢管混凝土哑铃形拱桥为对象,依据统一理论法建立有限元模型,分析横撑对其稳定性的影响. 其中标准钢管混凝土拱桥跨径为100 m的二次抛物线拱,矢跨比0.2. 具体参数可参见文献[15]. 钢管混凝土拱肋、纵梁、横撑、吊杆横梁、桥面板均采用Timoshenko梁单元模拟,吊杆则采用空间杆单元Link10模拟.
该桥边界为两端拱脚全固结. 该桥横桥向划分四车道,根据最不利布载方式,全桥纵向满布公路一级车道荷载. 全桥有限元模型见图6.
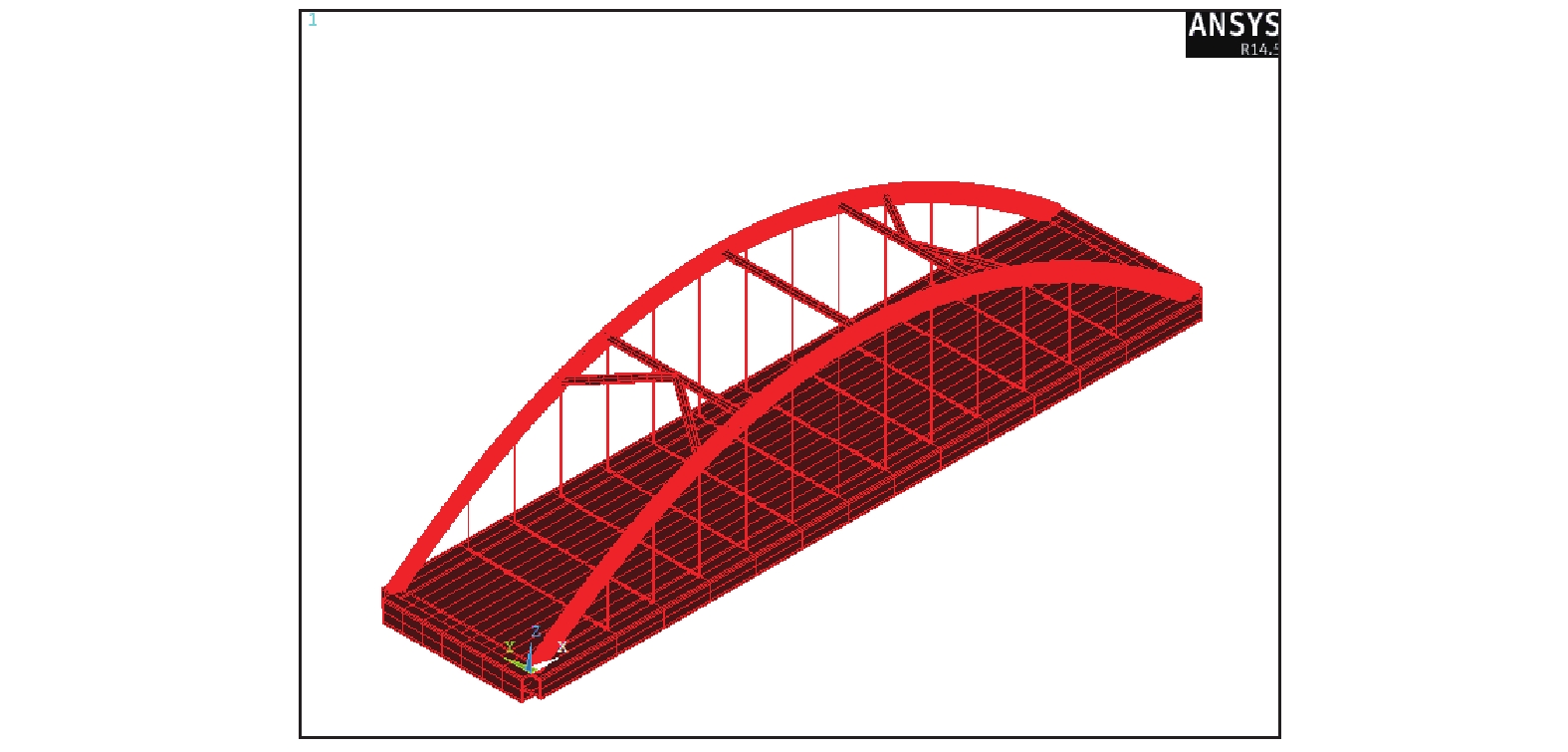
|
图 6 标准钢管混凝土拱桥模型 Figure 6 Model of standard steel tube concrete arch bridge |
在2013规范及2015规范中都明确规定,钢管混凝土拱桥横撑采用构造形式架设,主要形式采用一字撑、K撑、X撑及米字撑. 本节将从横撑的形式、数量及位置这3方面对钢管混凝土拱桥的稳定性进行分析.
(1) 横撑形式. 对于100 m跨的桥横撑形式主要有一字撑、K字撑、X撑等几种,本文采用H撑作为钢管混凝土拱桥的横撑形式. 为了研究不同横撑对钢管混凝土拱桥稳定性的影响,在初始模型的基础上,拆除全部横撑,在拱顶分别单独布置以上4种横撑进行分析. 计算以上几种情况的屈曲稳定系数,结果如表3所示.
| 表 3 不同横撑形式下标准拱稳定系数 Table 3 Variation of stability coefficient of standard arch with different bracing systems |
从表3可以看出,拱顶横撑型式不影响拱桥失稳模态. 拱顶设X撑时稳定系数最大,为11.03,比H撑、K撑及一字撑分别高出4.3%、0.6%及17.8%. 本文采用的H撑对拱桥稳定性比原模型的一字撑有所改善,稳定系数提高了14.1%. 虽然和K 撑效果相差不大且比X撑稍差,但由于施工时K撑和X撑相对比较复杂,选择H撑却比K撑和X撑带来更大的经济效益.
(2) 横撑数量. 合理的横撑数量既能提高钢管混凝土拱桥的稳定性,同时也会带来一定的经济效益. 为研究横撑数量对钢管混凝土拱桥稳定性的影响,将初始模型拱肋拆除所有横撑,通过从拱顶位置到拱脚依次增加对称的一对一字型横撑来分析横撑数量的影响. 计算结果如表4所示.
| 表 4 不同横撑数量下标准拱稳定系数 Table 4 Variation of stability coefficient of standard arch with different number of bracing |
从表4可知,增加横撑数量,拱桥的失稳模态全为面外对称半波失稳. 横撑数量由零增加到2时,拱桥稳定系数提高了41.2%;横撑数量由2增加到4时,稳定系数提高了40.8%;横撑数量由4增加到6时,稳定系数增加了38%;而当横撑数量由6增加到8时,稳定系数提高了27.5%. 横撑数量从零增加到2时,稳定系数提高速率最快;随着横撑数量的继续增加,稳定系数的提高速率开始下降. 并且横撑数量的增多,会造成桥面行车视距有所影响,给司机一种压抑的感觉. 因此,横撑数量并不是越多越好,选择合理的数量,并且稳定系数能保证桥梁稳定安全便为合理.
(3) 横撑位置. 钢管混凝土拱桥横撑的设置不仅需要合理的型式和数量,并且还要在合理的位置上设置,这样才会使横撑发挥最大的作用. 为研究横撑位置对钢管混凝土拱桥稳定性的影响,本节将每次只采用一对对称的一字撑分别设置在拱肋的对称位置,分别计算在拱肋1/4、3/8、5/8、1/2位置设置横撑的稳定系数,从而比较出使钢管混凝土拱桥稳定性最大的横撑位置. 计算结果表5所示.
| 表 5 不同横撑位置下标准拱稳定系数 Table 5 Variation of stability coefficient of standard arch with different position of bracing |
从表5可知,横撑位置对失稳模态有影响,在1/2跨及5/8跨分别设置横撑时,失稳模态为面外对称半波失稳,而在3/8跨及1/4跨单独设置横撑时,失稳模态为面外反对称全波失稳. 在拱肋的1/4跨至1/2跨设置横撑时拱桥稳定系数先增后减,并且在5/8跨设置横撑会使稳定系数达到最大,为19.32. 可以判断,在1/4跨至5/8跨之间设置横撑可以达到稳定性最优的效果.
4 结论本文通过对比我国现行两本钢管混凝土拱桥规范的拱肋刚度取值差异,并采用大型有限元软件ANSYS进行模拟单拱肋试验,分析两种规范对拱肋刚度取值的合理性,采用统一理论模拟横撑对标准钢管混凝土拱桥稳定性的影响.
研究表明,2013规范与2015规范对钢管混凝土拱桥拱肋刚度计算误差在10%以内,并且发现2013规范对开裂后混凝土考虑的刚度折减系数对拱肋钢筋计算结果的影响存在着一定的不准确性;采用ANSYS分别依据两本规范刚度取值方法模拟单拱肋试验,统一理论法模拟更方便快捷,且模拟结果更符合试验结果. 可为今后同类桥梁模拟提供相关依据.
横撑对钢管混凝土拱桥稳定性有一定的影响,X撑的稳定系数最大,K撑和H撑次之,一字撑最小;随着横撑数量的增加,钢管混凝土拱桥的稳定性也随之增加,但稳定系数提高的速率会下降;横撑位置设于1/4跨至5/8跨之间,标准钢管混凝土拱桥稳定性效果最好.
| [1] |
陈宝春. 钢管混凝土拱桥发展综述[J].
桥梁建设, 1997(2): 10-15.
CHEN B C. A summarized account of developments in concrete-filledsteel tube arch bridge[J]. Bridge Construction, 1997(2): 10-15. |
| [2] |
HAN L H, REN Q X, LI W. Tests on inclined, tapered and STS concrete-filled steel tubular (CFST) stub columns[J].
Journal of Constructional Steel Research, 2010, 66(10): 1186-1195.
DOI: 10.1016/j.jcsr.2010.03.014. |
| [3] |
陈宝春. 钢管混凝土拱桥[M]. 3版. 北京: 人民交通出版社, 2016.
|
| [4] |
王卫琴, 陈宇文. 哑铃型钢管混凝土柱的面内弹塑性分析[J].
广东工业大学学报, 2006, 23(3): 62-66.
WANG W Q, CHEN Y W. The elastic-plastic analysis of the surface of the dumbbell steel tubular columns[J]. Journal of Guangdong University of Technology, 2006, 23(3): 62-66. DOI: 10.3969/j.issn.1007-7162.2006.03.012. |
| [5] |
WANG X, ZHOU S. Effect study of initial stress on bearing capacity of dumbbell-shaped CFST bridge[C]// Second International Conference on Mechanic Automation and Control Engineering. Inner Mongolia, China: IEEE, 2011: 6460-6463.
|
| [6] |
SONG F, WU Q. Effects of crossbars on the lateral elastic stability of lift-basket CFST truss rib arch bridge[J].
Journal of Shenyang Jianzhu University, 2014, 30(5): 850-855.
|
| [7] |
中华人民共和国国家标准. 钢管混凝土拱桥技术规范: GB50923-2013[S]. 北京: 中国计划出版社, 2013.
|
| [8] |
中华人民共和国行业推荐性标准. 公路钢管混凝土拱桥设计规范: JTG/T D65-06-2015[S]. 北京: 人民交通出版社, 2015.
|
| [9] |
陈宝春, 盛叶. 钢管混凝土哑铃形拱面内极限承载力研究[J].
工程力学, 2009, 26(9): 94-104.
CHEN B C, SHENG Y. Study on ultimate bearing capacity of steel tube concrete dumbbell shape arch surface[J]. Engineering Mechanics, 2009, 26(9): 94-104. |
| [10] |
钟善桐. 钢管混凝土统一理论——研究与应用[M]. 北京: 清华大学出版社, 2006.
|
| [11] |
李自林, 张德龙, 韦有波, 等. 脱空对上承式钢管混凝土拱桥整体稳定性能的影响[J].
天津城建大学学报, 2017, 23(1): 11-16.
LI Z L, ZHANG D L, WEI Y B et al. Analysis on the influence of disengaging on the global stability of concrete-filledsteel tube deck arch bridge[J]. Journal of Tianjin Chengjian University, 2017, 23(1): 11-16. |
| [12] |
陈宝春, 秦泽豹, 彦坂熙, 等. 钢管混凝土拱(单圆管)面内受力双重非线性有限元分析[J].
铁道学报, 2003, 25(4): 80-84.
CHEN B C, QIN Z B, YAN B X, et al. Analysis of concrete filled steel tubular (single tube) arch subjected to in-plane loads by nonlinear finite element method[J]. Journal of The China Rail Way Society, 2003, 25(4): 80-84. DOI: 10.3321/j.issn:1001-8360.2003.04.017. |
| [13] |
韩林海. 钢管混凝土结构——理论与实践[M]. 北京: 科学出版社, 2004.
|
| [14] |
黄永辉. 钢管混凝土拱桥拱肋病害机理与影响分析及吊杆更换技术研究[D]. 广州: 华南理工大学土木与交通学院, 2010.
|
| [15] |
陈礼榕, 陈宝春. 钢管混凝土哑铃形截面标准拱面外稳定分析[J].
郑州大学学报(工学版), 2015, 36(6): 123-128.
CHEN L R, CHEN B C. Analysis of out-of-plane stability of standard concrete-filled steel tube dumbbell-shaped rib arch[J]. Journal of Zhengzhou University (Engineering Edition), 2015, 36(6): 123-128. DOI: 10.3969/j.issn.1671-6833.2015.06.025. |
 2018, Vol. 35
2018, Vol. 35

