目前,研究人员在边坡的稳定性问题上通常视土体为各向同性介质,即岩土材料在各个方向上表现出相同的物理、力学性质. 然而,土颗粒受重力影响下,长轴趋于水平方向沉积和排列,这种分布会引起土的强度表现出不同程度的各向异性. 此外,在原位条件下,作用于土体上的应力通常也是不等向的,而且在开挖或筑堤过程中土体的主应力轴会发生偏转,这也会使其天然强度随破坏面的方向不同而变化. Koutsoftas和Ladd[1]曾建议,对于二维边坡应采用3种不同类型的试验获得土的抗剪强度指标,即与坡顶、坡中、坡底位置对应,分别采用平面应变压缩试验(PSC)、直剪试验(DSS)和平面应变伸长试验(PSE). 在这些试验中,土试样的应力状态能够更加接近坡体不同位置处的实际受力情况,因而所得结果也更加真实准确. 然而,实际应用中大都按照土体固结方向的抗剪强度指标来评价边坡的稳定性. 如果忽略这种各向异性的影响,在某些情况下可能会使分析结果与实际产生较大偏差.
目前已有诸多学者在边坡稳定性分析中进行相关研究. Lo[2]切取与沉积方向成不同倾角的London黏土试样进行不排水三轴压缩试验,发现其强度随试样倾角的变化与Casagrande公式[3]比较吻合. 按照常规的极限平衡法研究了黏聚力的各向异性对边坡稳定性的影响. Chen等[4]视边坡失稳时的滑动体为一个独立单元,将破坏面采用对数螺旋线表示. 在考虑滑面不同位置处土体强度的差异后,利用极限分析上限定理对黏性土边坡进行研究,并得出稳定系数的表达式. 此后,在边坡稳定分析中考虑强度各向异性的极限平衡法[5-7]、极限分析上限法[8-10]及有限元法[11]大多是在Lo[2]和Chen等[4]的基础上展开.
对试验结果进行回归分析得出的Casagrande公式虽然考虑了各向异性的影响,但却不具有普遍适用性且不能从理论上给出严格的证明. 本文从微观角度出发,在不同主应力方向下借助材料组构张量,建立了各向异性强度参数表达式. 在此基础上,利用加拿大岩土工程软件GeoStudio中的SLOPE/W模块,分析强度各向异性对边坡稳定的影响.
1 各向异性强度参数公式的建立 1.1 组构张量组构是用于描述材料颗粒及其相关孔隙空间分布的专门术语. 对于黏土而言,其颗粒既不是球形也不是椭球形,但每一个颗粒有一个较长的主轴是确定的,当该主轴相对沉积面成不同角度时,其组构也将表现出不同程度的各向异性. 组构张量
| ${{F}}' = \left[ {\begin{array}{*{20}{c}} {{F_{11}}}&0&0 \\ 0&{{F_{22}}}&0 \\ 0&0&{{F_{33}}} \end{array}} \right].$ | (1) |
一般认为土是横观各向同性的材料,所以组构张量中的两个主分量F22和F33相等. 由于组构张量
| ${{F}}' = \frac{1}{{3 + \varDelta }}\left[ {\begin{array}{*{20}{c}} {1 - \varDelta }&0&0 \\ 0&{1{\rm{ + }}\varDelta }&0 \\ 0&0&{1{\rm{ + }}\varDelta } \end{array}} \right].$ | (2) |
式(2)中,
如果材料主方向与参考坐标系不重合,则该组构张量F的各个分量
| ${F_{ij}} = {Q_{ki}}{Q_{lj}}F_{kl}'.$ | (3) |
式(3)中,
由中主应力参数
| ${{n}} = \frac{1}{{{{\left[ {6({b^2} - b + 1)} \right]}^{1/2}}}}\left[ {\begin{array}{*{20}{c}} {2 - b}&0&0 \\ 0&{2b - 1}&0 \\ 0&0&{ - (1 + b)} \end{array}} \right].$ | (4) |
由式(4)可知,单位偏应力张量n为二阶无迹张量,即tr n=0且有tr n2=1,因此单位偏应力张量n只表示偏应力的方向而不包括偏应力数值的大小. 根据Pietruszczak等[13]的研究,可以定义一个组构张量在单位偏应力方向上的投影,记为
| $A = {{{F}}:{{n}}} = {{F}}^\pi :{{{n}}}.$ | (5) |
式中,
将式(2)~(4)代入式(5)中,化简后可得各向异性状态参数A具体为
| $A = \sqrt {\frac{2}{3}} \frac{\varDelta }{{3 + \varDelta }}\frac{{1 + b - 3{{\cos }^2}\alpha }}{{{{({b^2} - b + 1)}^{1/2}}}} = D \times \frac{{1 + b - 3{{\cos }^2}\alpha }}{{{{({b^2} - b + 1)}^{1/2}}}}.$ | (6) |
式(6)中,
参考Yang等[14]、Schweiger等[15]和张玉军等[16]的研究,对于Mohr-Coulomb准则,可以将土的抗剪强度指标c、φ看作为各向异性状态参数A的函数,在横观各向同性条件下,表达为
| $c = {c_0}(1 + F_{ij}^cn_{ij}^c + F_{ijkl}^cn_{ijkl}^c + F_{ijklmn}^cn_{ijklmn}^c + \cdots ).$ | (7) |
| $\varphi \!=\! \arctan [\tan {\varphi _0}(1 \!+\! F_{ij}^\varphi n_{ij}^\varphi \! + \!F_{ijkl}^\varphi n_{ijkl}^\varphi \!+\! F_{ijklmn}^\varphi n_{ijklmn}^\varphi \!+\! \cdots )].$ | (8) |
一般情况下,可写成
| $c = {c_0}[1 + F_{ij}^cn_{ij}^c + {d_1}{(F_{ij}^cn_{ij}^c)^2} + {d_2}{(F_{ij}^cn_{ij}^c)^3} + \cdots ].$ | (9) |
| $\varphi \! =\! \arctan \{ \tan {\varphi _0}[1 \!+\! F_{ij}^\varphi n_{ij}^\varphi \!+\! {b_1}{(F_{ij}^\varphi n_{ij}^\varphi )^2} \!+ \!{b_2}{(F_{ij}^\varphi n_{ij}^\varphi )^3} \!+\! \cdots ]\}. $ | (10) |
根据式(5),可将式(9)与式(10)简化为
| $\left\{\begin{array}{l}c = {c_0}(1 + {A_c} + {d_1}A_c^2 + {d_2}A_c^3 + \cdots );\\\varphi = \arctan [\tan {\varphi _0}(1 + {A_\varphi } + {b_1}A_\varphi ^2 + {b_2}A_\varphi ^3 + \cdots )].\end{array} \right.$ | (11) |
式(11)中,Ac和Aφ分别为黏聚力和内摩擦角的各向异性状态参数,可由式(6)分别确定;c0、φ0、di和bj分别为待定的材料参数.
1.4 参数确定与验证选取赵红华等[17]对上海褐黄色粉质黏土的试验结果. 由于该试验采用与沉积面(水平面)成不同角度切取土样,然后进行直剪试验,经过角度转换后可得大主应力偏离沉积面法线
|
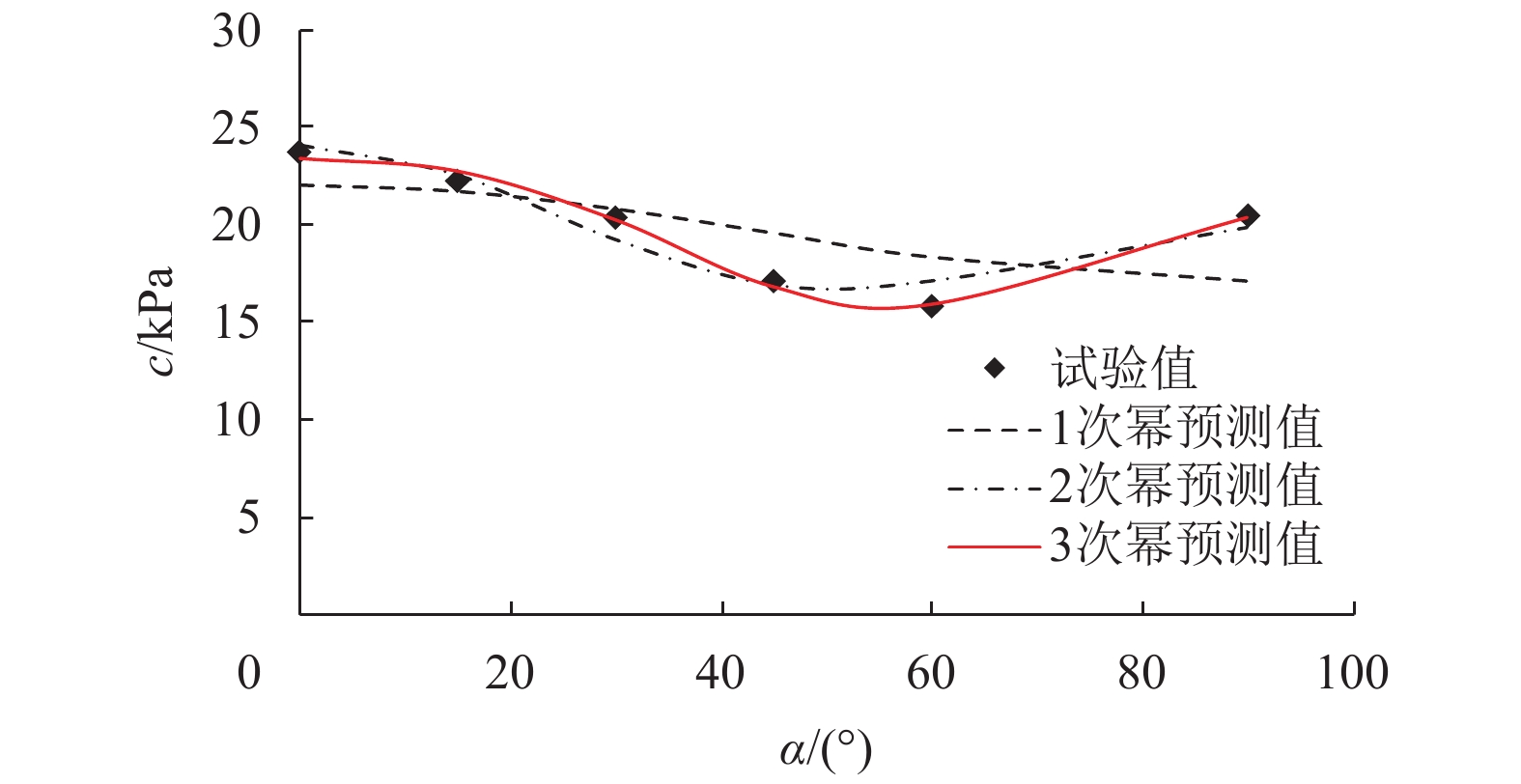
图 1 c 的试验值与预测值之间的比较 Figure 1 Comparison of testing c with predicting c |
|
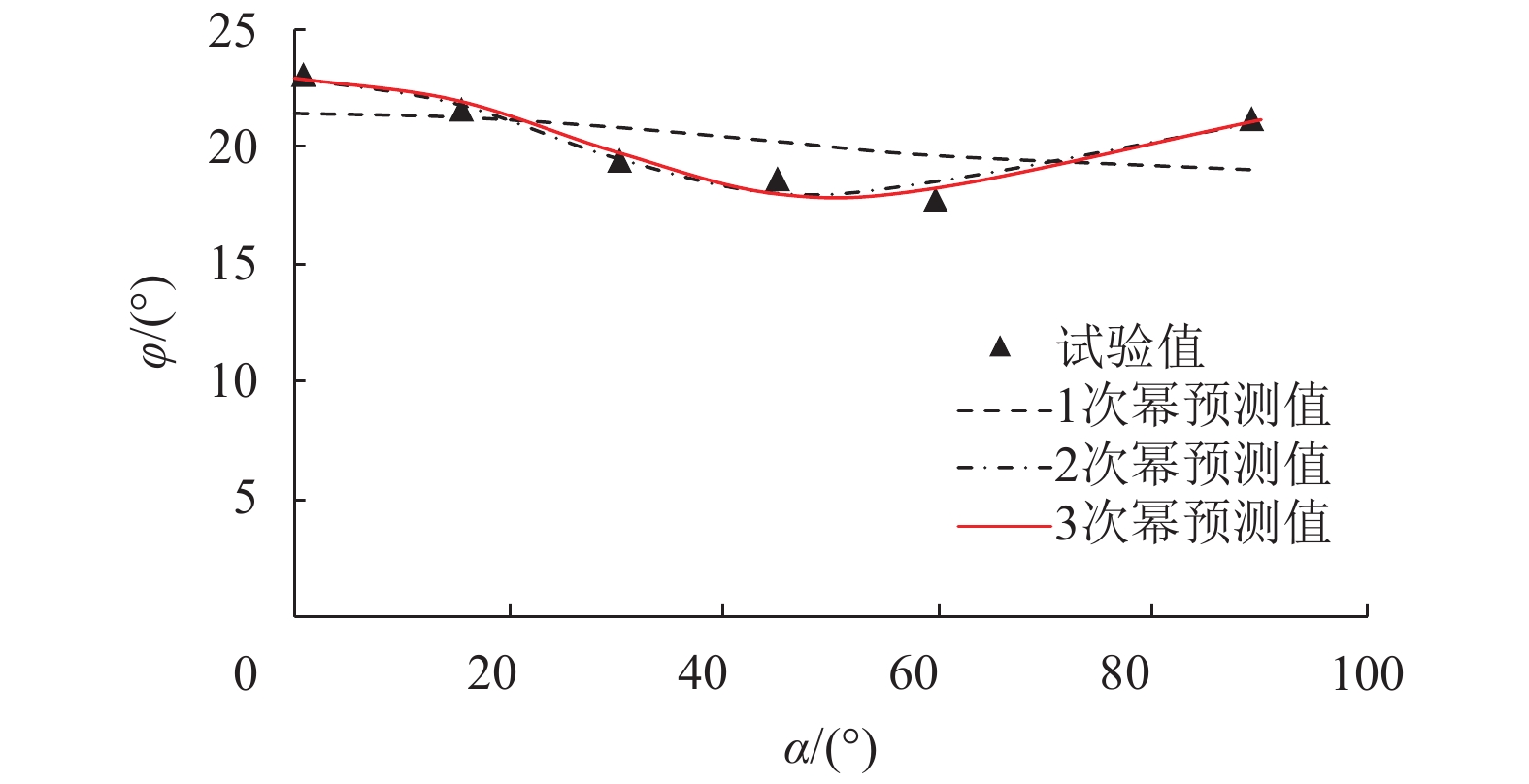
图 2 φ 的试验值与预测值之间的比较 Figure 2 Comparison of testing φ with predicting φ |
直剪试验属于平面应变状态的范畴,而平面应变状态下的罗德角
Ac和Aφ的幂次取至1时,可得
| $\left\{ \begin{array}{l}c = 19.44(1 + {A_c});\\\varphi = \arctan [0.366(1 + {A_\varphi })].\end{array} \right.$ | (12) |
式(12)中,
Ac和Aφ的幂次取至2时,可得
| $\left\{\begin{array}{l}c = 16.77(1 + {A_c} + 46.385A_c^2);\\\varphi = \arctan [0.324(1 + {A_\varphi } + 546.75A_\varphi ^2)].\end{array} \right.$ | (13) |
式(13)中,
Ac和Aφ的幂次取至3时,可得
| $\left\{ \begin{array}{l}c = 16.52(1 + {A_c} + 5.012A_c^2 - 11.865A_c^3);\\\varphi = \arctan [0.323(1 + {A_\varphi } + 62.805A_\varphi ^2 - 181.126A_\varphi ^3)].\end{array} \right.$ | (14) |
式(14)中,
式(12)~(14)对抗剪强度参数的拟合曲线与其试验值之间的对比如图1和图2所示,其中1~3次幂预测值分别与式(12)~(14)对应. 由图可见,在式(11)中随着各向异性状态参数Ac和Aφ最高幂次的增加,式(12)~(14)的计算结果对试验值的拟合效果越来越好. 当Ac和Aφ的幂次取至3时,误差最小,式(14)能够较好地反映大主应力方向对该黏土抗剪强度指标的影响,同时也验证了本文所建各向异性强度参数公式(11)的有效性.
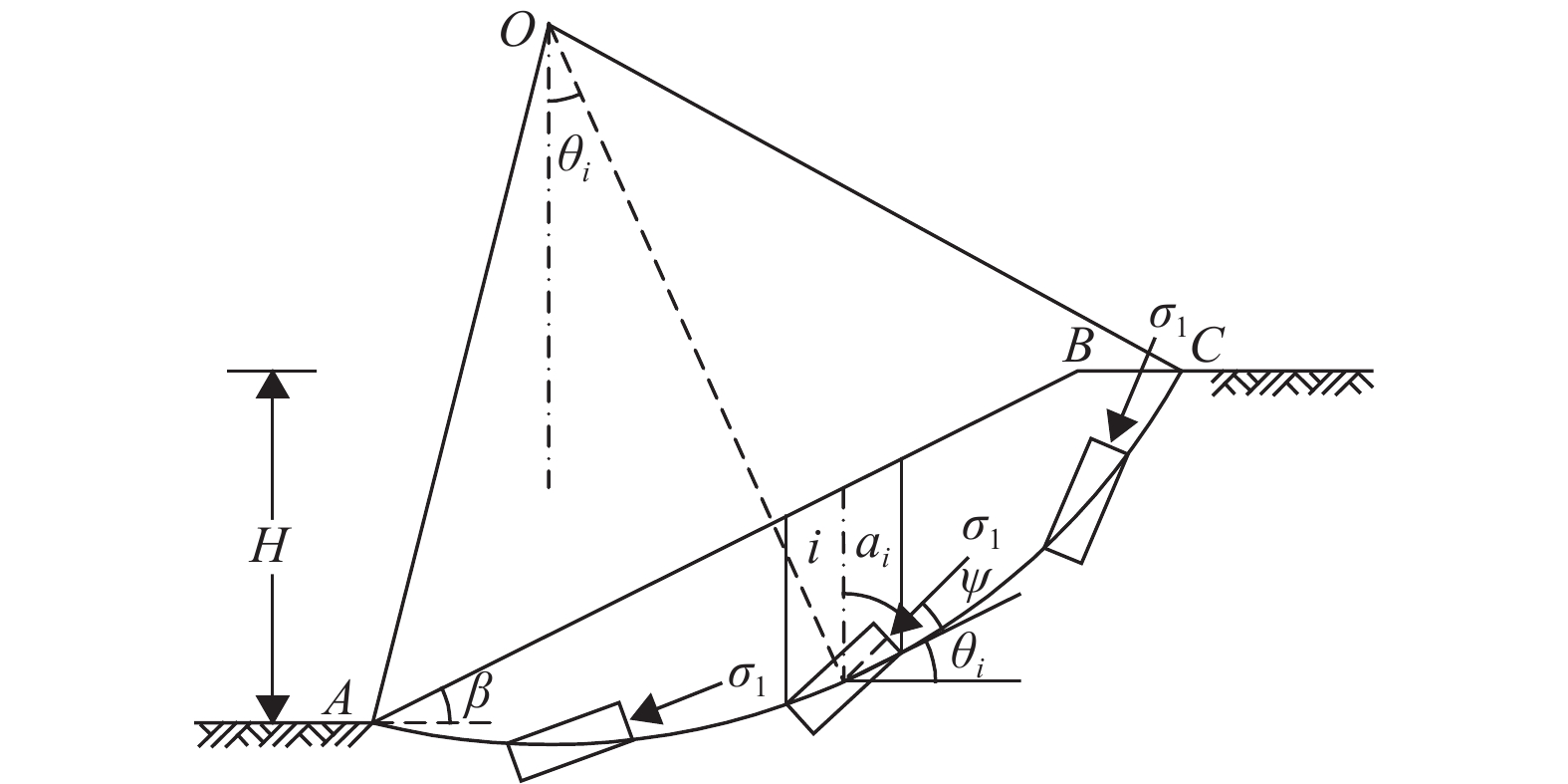
2 边坡稳定性分析 2.1 典型的破坏模式图3给出了边坡典型的圆弧破坏模式及潜在滑动面上土条单元的应力状态变化. 自然条件下,通常可认为土体的沉积面为水平面. 图中折线ABC为边坡坡面线,圆弧AC为潜在滑动面,θi为土条i的滑面底边倾角,αi为土条i底面单元所受大主应力σ1的方向与土层沉积面法线方向(竖直方向)的夹角,ψ为大主应力σ1的方向与土条滑裂面切线的夹角,β为坡角,H为坡高,其他符号见图3.
|
图 3 边坡潜在滑动面的几何参数 Figure 3 Geometrical parameters of potential sliding surface of slope |
某一均质黏土边坡模型几何参数为:坡高H=20 m,坡比(竖直:水平)为1:1.5,即坡角β=33.7°. 土体抗剪强度参数选用赵红华等[17]对上海褐黄色粉质黏土的试验结果,天然重度
各向同性条件下,取α=0°时的抗剪强度参数c=23.8 kPa,φ=23.2°,利用GeoStudio中的SLOPE/W模块通过Spencer法计算得到的安全系数FsI=1.378;各向异性条件下,基于式(14),利用GeoStudio中的SLOPE/W模块搜索出本例边坡模型的临界滑动面,并根据滑面上不同土条的底面倾角θi确定不同的αi角后,代入不同土条的抗剪强度参数,通过Spencer法可求得边坡安全系数FsA=1.158. 比较可知,考虑强度各向异性的影响后,本例边坡的安全系数降低约16.0%.
2.2.2 算例2选取王栋等[11]对某均质土坡的分析计算模型:坡高
对于二维边坡稳定性问题,可认为各向异性黏聚力c为平面应变状态下的结果,与算例1的做法相同,可取中主应力参数
| $c = 16.77(1 + {A_c}).$ | (15) |
式(15)中,

|
图 4 黏聚力c与大主应力方向的关系 Figure 4 Relationship between cohesion c and the direction of major principal stress |
与算例1类似,采用Spencer法时的计算结果如表1所示,相对差值为(各向同性值−各向异性值)/各向同性值. 各向同性情况下,取黏聚力c=20 kPa,内摩擦角φ=20°.
| 表 1 安全系数Fs的对比 Table 1 Comparison of safety factor Fs |
由表1中的结果可见,各向异性情况下,本文解法得到的边坡安全系数与文献[11]采用Casagrande法得到的结果差别较小. 各向同性与各向异性情况下的结果也基本相同,相对差值仅为1.34%. 这是因为对于坡角β=70°的这类陡坡,临界滑动面为靠近坡面的浅层滑动,使得条块底面倾角θi较大,大主应力σ1偏离竖直方向的角度αi = 90° – θi – ψ较小. 由图4可见,当α减小时,黏聚力c的各向异性程度减弱,最终使两种情况下的边坡安全系数差别较小.
3 坡角对各向异性边坡的影响本文前两个算例分别代表了典型的缓坡与陡坡,初步得出如下结论:缓坡角时,各向同性与各向异性情况下的边坡安全系数差别较大;而陡坡角时,两种情况下的边坡安全系数差别较小. 为了不失一般性,本节将建立不同坡角β和坡高H的边坡模型,通过大量计算进一步验证该结论的真实性.
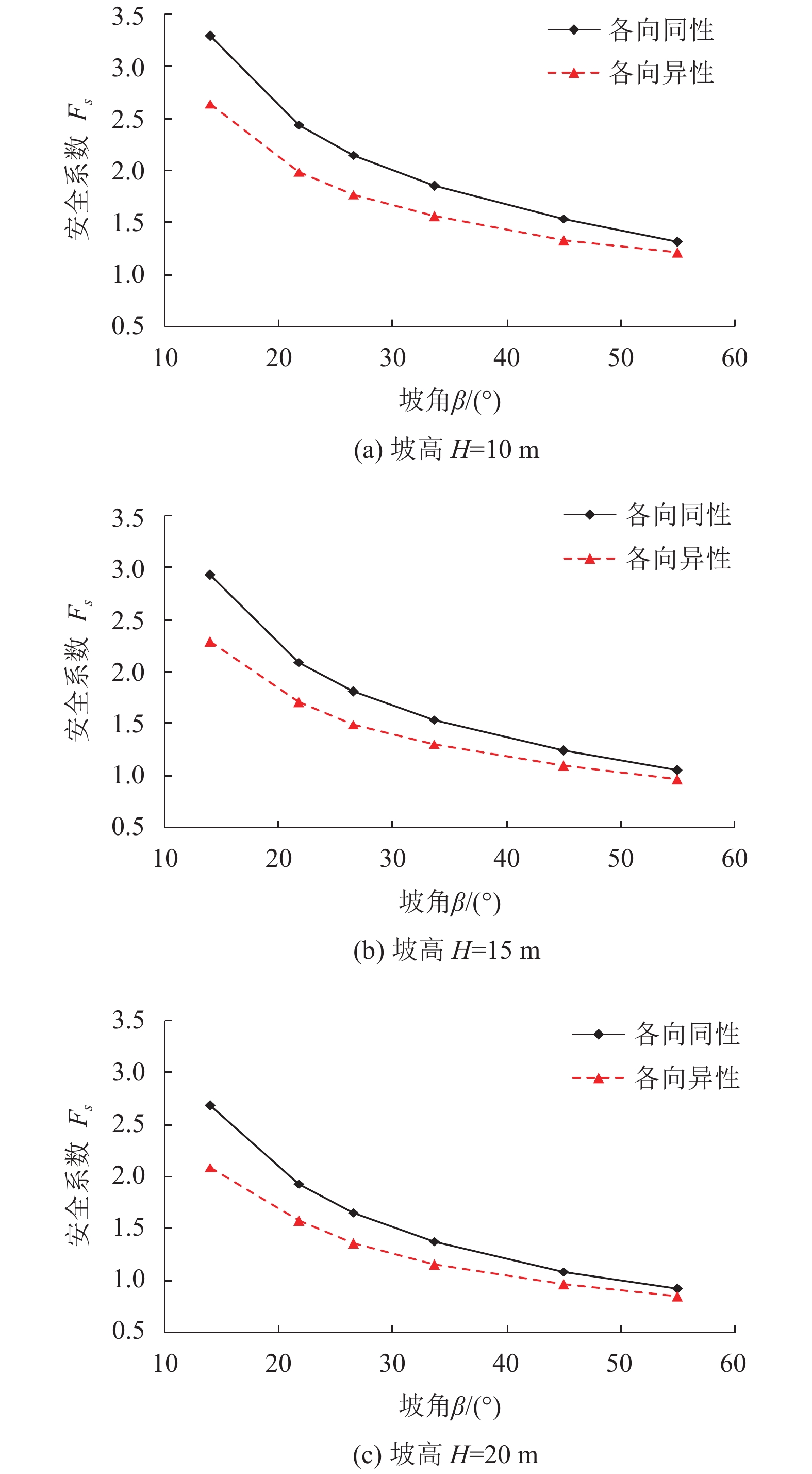
与图3所示的边坡几何形状相似,建立如下不同几何尺寸的边坡模型:坡高H分别取10 m、15 m、20 m;坡角β分别为14°、21.8°、26.6°、33.7°、45°、55°. 边坡土体的物理力学参数与算例1相同,各向同性情况下的抗剪强度参数c=23.8 kPa、φ=23.2°,各向异性情况下的抗剪强度参数采用式(14). 参照算例1的求解方式,利用Spencer法对上述36个边坡模型进行稳定分析,可得边坡安全系数Fs的计算结果如图5和图6所示.
|
图 5 不同坡高时各向同性与各向异性安全系数随坡角的变化 Figure 5 Variation of safety factor of isotropy and anisotropy with slope angle at different slope heights |

|
图 6 安全系数相对差值随坡角的变化 Figure 6 Relative difference of safety factor varies with slope angle |
由图5可见,在不同坡高下,各向同性与各向异性情况下的安全系数均随坡角的增加而减小;且随着坡角的增加,两种情况下的安全系数值越来越接近. 这种变化可由图6更加直观表现:对于坡角为14°的缓坡,考虑强度各向异性的影响后,边坡安全系数降低可达22.0%;随着坡角的增加,各向同性与各向异性安全系数相对差值逐渐减小;当坡角达到55°时,两种情况下的安全系数相对差值略大于8.0%.
4 结论通过以上分析,本文得出的主要结论如下:
(1) 对于黏土材料,将各向异性状态参数定义为材料组构张量与标准化偏应力张量之间的联合不变量,提出了考虑抗剪强度指标
(2) 算例分析表明,不考虑土体强度的各向异性,可能会高估边坡的稳定性,尤其是对于高而平缓的边坡.
(3) 通过对36个边坡模型计算结果的分析,得出结论为:坡角较小时,各向同性与各向异性安全系数相对差值较大;随着坡角的增大,其相对差值逐渐降低,边坡受强度各向异性的影响减弱,即表明土体强度的各向异性对缓坡安全系数的影响比对陡坡的大. 实际应用中,应当重视强度各向异性对高而平缓边坡的影响.
| [1] |
KOUTSOFTAS D C, LADD C C. Design strengths for an offshore clay[J].
Journal of Geotechnical Engineering, 1985, 111(3): 337-355.
DOI: 10.1061/(ASCE)0733-9410(1985)111:3(337). |
| [2] |
LO K Y. Stability of slopes in anisotropic soils[J].
Journal of Soil Mechanics and Foundations Division, 1965, 91(SM4): 85-106.
|
| [3] |
CASAGRANDE A, CARILLO N. Shear failure of anisotropic materials[J].
Journal of the Boston Society of Civil Engineers, 1944, 31(4): 74-87.
|
| [4] |
CHEN W F, SNITBHAN N, FANG H Y. Stability of slopes in anisotropic, nonhomogeneous soils[J].
Canadian Geotechnical Journal, 1975, 12(1): 146-152.
DOI: 10.1139/t75-014. |
| [5] |
AL-KARNI A A, AL-SHAMRANI M A. Study of the effect of soil anisotropy on slope stability using method of slices[J].
Computers and Geotechnics, 2000, 26(2): 83-103.
DOI: 10.1016/S0266-352X(99)00046-4. |
| [6] |
孟庆银. 各向异性土坡稳定性的极限平衡遗传算法[J].
河北工程大学学报(自然科学版), 2003, 20(2): 45-47.
MENG Q Y. Stability analysis of anisotropic soil slope using limit equilibrium genetic algorithm method[J]. Journal of Hebei University of Engineering (Natural Science Edition), 2003, 20(2): 45-47. DOI: 10.3969/j.issn.1673-9469.2003.02.013. |
| [7] |
王建锋, 陈祖煜, 张基泰. 各向异性非线性强度条件下的边坡稳定性[J].
力学与实践, 2004, 26(5): 22-26.
WANG J F, CHEN Z Y, CHANG J T. Slope stability analysis with nonlinear failure envelopes using Janbu’s generalized procedure of slices[J]. Mechanics in Engineering, 2004, 26(5): 22-26. DOI: 10.3969/j.issn.1000-0879.2004.05.005. |
| [8] |
年廷凯, 栾茂田, 杨庆. 考虑各向异性效应的阻滑桩加固土坡稳定性分析[J].
大连理工大学学报, 2005, 45(6): 858-864.
NIAN T K, LUAN M T, YANG Q. Stability analysis of soil slopes stabilized by piles considering effect of soil anisotropy using upper-bound method of limit analysis[J]. Journal of Dalian University of Technology, 2005, 45(6): 858-864. DOI: 10.3321/j.issn:1000-8608.2005.06.017. |
| [9] |
栾茂田, 年廷凯, 杨庆. 考虑非均质各向异性效应的阻滑桩加固土坡稳定性分析[J].
岩土力学, 2006, 27(4): 530-536.
LUAN M T, NIAN T K, YANG Q. Stability analysis of pile-stabilized slopes considering both nonhomogeneity andanisotropy of soil strength using upper bound method of limit analysis[J]. Rock and Soil Mechanics, 2006, 27(4): 530-536. DOI: 10.3969/j.issn.1000-7598.2006.04.005. |
| [10] |
杨雪强, 区兆光, 郑榕明, 等. 坡顶局部荷载下边坡的二维和三维稳定分析(Ⅱ)——极限分析的上限法[J].
广东工业大学学报, 2009, 26(1): 1-8.
YANG X Q, AU S K, CHENG Y M, et al. Two and three-dimensional stability analyses of slopes with local load on top surface (Ⅱ)——Using upper-bound method of limit analysis[J]. Journal of Guangdong University of Technology, 2009, 26(1): 1-8. DOI: 10.3969/j.issn.1007-7162.2009.01.001. |
| [11] |
王栋, 金霞. 考虑强度各向异性的边坡稳定有限元分析[J].
岩土力学, 2008, 29(3): 667-672.
WANG D, JIN X. Slope stability analysis by finite elements considering strength anisotropy[J]. Rock and Soil Mechanics, 2008, 29(3): 667-672. DOI: 10.3969/j.issn.1000-7598.2008.03.018. |
| [12] |
ODA M, NAKAYAMA H. Yield function for soil with anisotropic fabric[J].
Journal of Engineering Mechanics, 1989, 115(1): 89-104.
DOI: 10.1061/(ASCE)0733-9399(1989)115:1(89). |
| [13] |
PIETRUSZCZAK S, MROZ Z. On failure criteria for anisotropic cohesive-frictional materials[J].
International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(5): 509-524.
DOI: 10.1002/(ISSN)1096-9853. |
| [14] |
YANG X Q, ZHANG L J, JI X M. Strength characteristics of transversely isotropic rock materials[J].
Geomechanics and Engineering, 2013, 5(1): 71-86.
DOI: 10.12989/gae.2013.5.1.071. |
| [15] |
SCHWEIGER H F, WILTAFSKY C, SCHARINGER F, et al. A multilaminate framework for modelling induced and inherent anisotropy of soils[J].
Géotechnique, 2009, 59(2): 87-101.
DOI: 10.1680/geot.2008.3770. |
| [16] |
张玉军, 张维庆. 不同的层状岩体抗剪强度表达式计算效果的有限元分析[J].
岩土力学, 2014, 35(S1): 359-364.
ZHANG Y J, ZHANG W Q. Finite element analyses of computational effects with of different shear strength expressions for layered rock mass[J]. Rock and Soil Mechanics, 2014, 35(S1): 359-364. |
| [17] |
赵红华, 袁聚云, 叶志成. 上海褐黄色粉质粘土各向异性的试验研究[J].
勘察科学技术, 2002(4): 21-24.
ZHAO H H, YUAN J Y, YE Z C. Experimental study on the anisotropy of brownish-yellow silty clay in Shanghai[J]. Site Investigation Science and Technology, 2002(4): 21-24. DOI: 10.3969/j.issn.1001-3946.2002.04.005. |
| [18] |
杨雪强, 凌平平, 杨锐, 等. 坡顶局部荷载下边坡的二维和三维稳定分析(Ⅰ)——强度折减的有限元法[J].
广东工业大学学报, 2008, 25(4): 86-93.
YANG X Q, LING P P, YANG R, et al. Two and three-dimensional stability analyses of slopes with local load on top surface (I)—Using strength reduction finite element method[J]. Journal of Guangdong University of Technology, 2008, 25(4): 86-93. DOI: 10.3969/j.issn.1671-623X.2008.04.028. |
| [19] |
杨雪强, 李子生, 梁仕华. 混凝土板的冲切强度[J].
应用力学学报, 2009, 26(4): 731-735.
YANG X Q, LI Z S, LIANG S H. Punching strength of concrete slab[J]. Chinese Journal of Applied Mechanics, 2009, 26(4): 731-735. |
| [20] |
杨雪强, 吴子超, 杨宗轲. 一般应力状态下挡土墙上主动土压力研究[J].
中国公路学报, 2010, 23(2): 25-29.
YANG X Q, WU Z C, YANG Z K. Research on active soil pressure on retaining wall under general stress states[J]. China Journal of Highway and Transport, 2010, 23(2): 25-29. DOI: 10.3969/j.issn.1001-7372.2010.02.005. |
 2018, Vol. 35
2018, Vol. 35

