2. 仲恺农业工程学院 机电工程学院,广东 广州 510225
2. School of Electromechanical Engineering, Zhongkai University of Agriculture and Engineering, Guangzhou 510225, China
少自由度并联机构相对于串联机构,具有高速、高精、大刚度和无累积误差等优势,在搬运、测试、装配等自动化等领域中有着广泛的应用. 其中,常见的一类2自由度(2R,R表示旋转)类型的并联机构以其构型对称和半球内无奇异自由转动等优点,吸引了国内外众多学者的关注和研究[1-5]. 随着新的应用的不断涌现,相应地带来了新的技术难点. 例如电子行业中某些异型件的装配需要将元器件调整空间姿态后迅速插入到指定的位置,这就要求机构至少具备2旋转和1平移3个自由度.
文献[6]采用构型演变法提出了一种可应用于电子装配领域的三自由度(2R1T)类球面并联腕部机构,该机构由上下2个等半径的动、定平台通过3个相同的RSR支链连接而成. 在运动过程中,动平台与定平台始终关于一个中间平面对称,且末端可绕着对称面内的任意轴线连续旋转和沿着两平台中心连线方向连续平移,该机构不仅具有上面2自由度并联机构半球内无奇异自由运动的优点,还能实现单自由度平移(旋转)和三自由度混合运动. Duan等[7]研究了一种具有相同几何特征不同构型的3-RSR并联机构的瞬轴面和瞬时运动特性,为该类机构的运动仿真提供了较为直观的认识. 对于这类3-RSR并联机构的运动控制,如果仅采用运动学方法,虽然可以实现一些既定的运动轨迹,但相对于动力学控制更消耗能量,响应速度更慢. 因此有必要对其进行动力学建模和分析.
目前,进行机器人动力学研究较为成熟的方法有:Newton-Euler法、虚功原理和Lagrange法等[8-9]. DC Carp-Ciocardia等[10]基于虚功原理对Clavel的三自由度Delta并联机器人进行了逆动力学研究;Shiau T N等[11]采用牛顿欧拉法对一种3-PRS并联机构进行了非线性动力学研究,重点分析了机构的关节灵巧性、间隙和摩擦对动力学动态响应的影响;CHEN等[12]基于Lagrange法对一种2-DOF类球面并联转台进行了动力学建模和分析. 通过文献了解到Newton-Euler法易于形成递推形式的动力学方程,但计算量大,容易出错. 虚功原理法在处理受理想约束的力学平衡问题时,其坐标系的选择是有条件的. 相比之下,Lagrange法推导较为简便,并且总能得到形式较为简洁的动力学方程,既能用于并联机构的动力学控制,又可以清楚地表示出各构件之间的耦合关系[13].
本文在文献[7]的基础上,采用Lagrange法建立了机构的动力学模型,结合理论计算和仿真实例,对比分析了机构末端不同运动轨迹下驱动力矩的变化规律,验证了动力学模型的正确性和有效性.
1 机构描述3-RSR并联机构由等半径的动平台和定平台以及3个相同的支链组成. 在初始位形下,机构构型结构简图如图1所示.
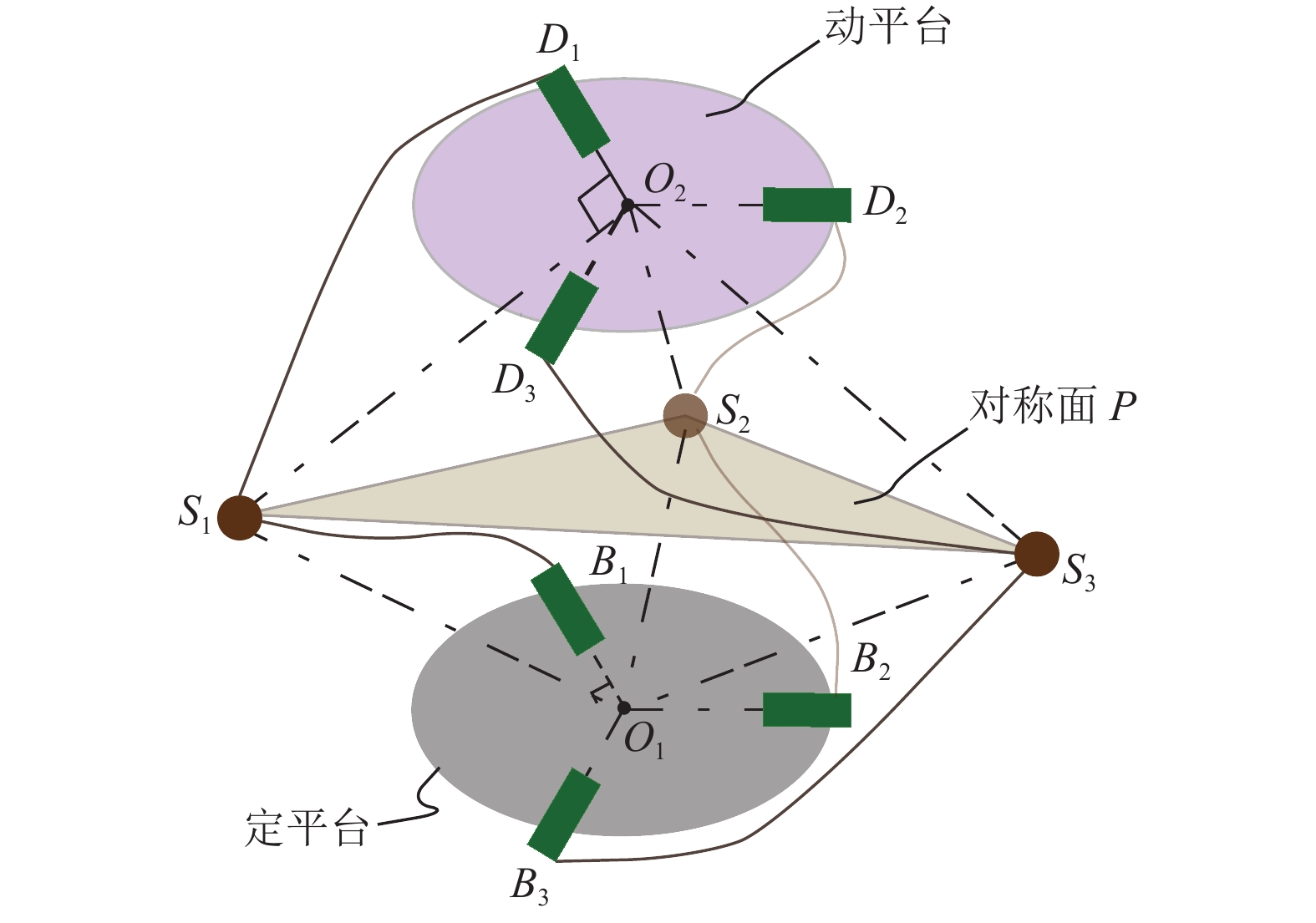
|
图 1 3-RSR结构简图 Figure 1 Schematic diagram of 3-RSR mechanism |
3个支链呈120°均匀分布于基座和动平台之间. 与基座相连的转动副(即驱动副)记为
由于该机构是由Omni-Wrist V演变而来[14],机构的3个支链之所以都采用弯曲结构的杆件,有两方面的原因:(1) 为了装配的需要,弯曲杆件可以实现一种类似Omni-Wrist V的异侧装配. 本文选择了同侧装配的原因请参见文献[15];(2) 为了保证支链上的球关节与两平台中心的连线始终垂直于上下两个转动副的轴线,在设计时需要对球关节的位置做一定的偏移,这个偏移量刚好是动平台或者定平台的半径,因此需要将杆件设计成弯曲的形状,这样的设计对后文运动学等效建模提供了便利.
2 机构运动学分析利用机构几何上的特殊性,可对其作如下等效处理:将各支链中与基座铰链的关节平移至中心
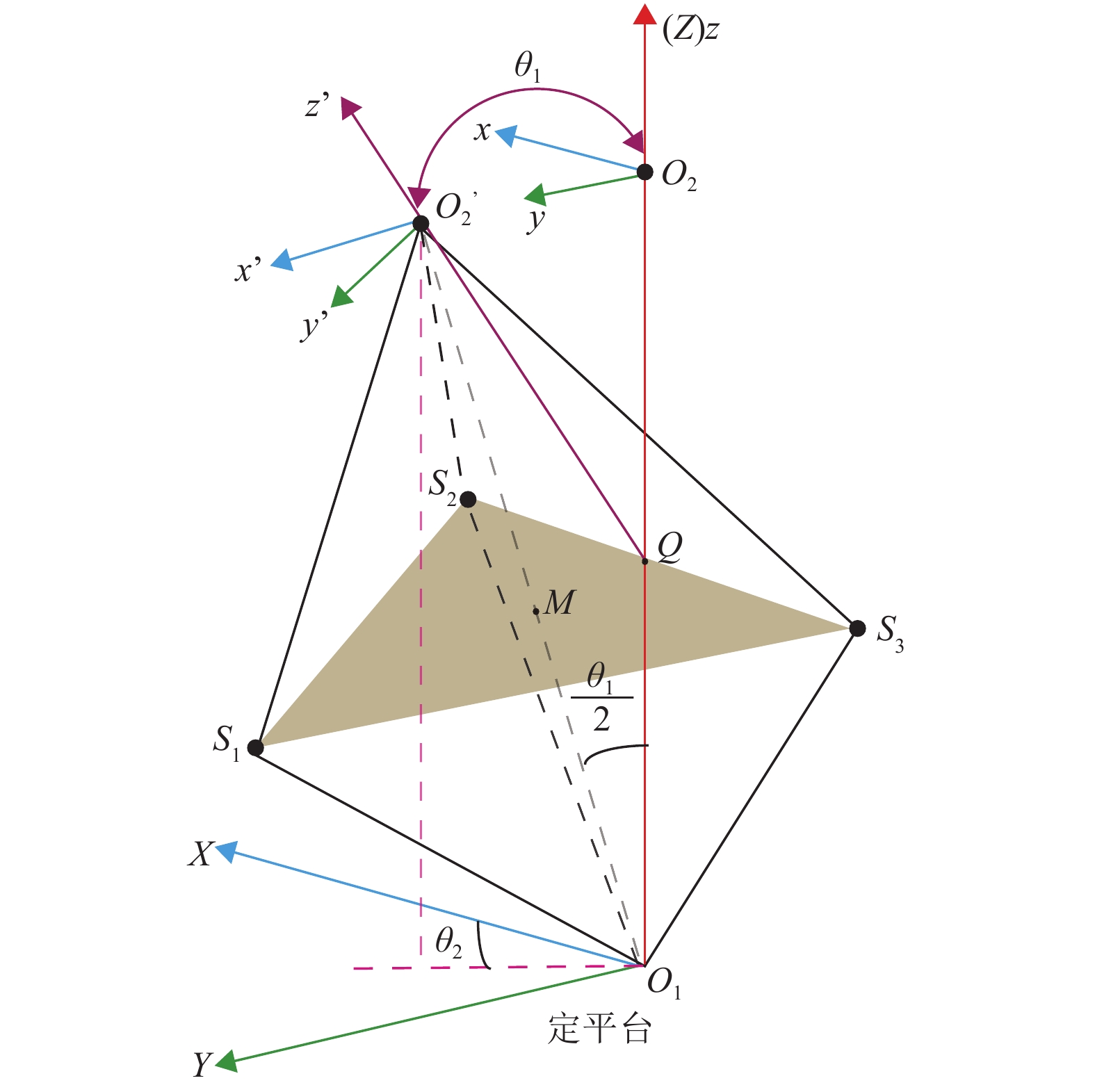
|
图 2 旋转
|
球关节
当动平台绕对称面内过点
对称面方程
| $\left[ {\begin{array}{*{20}{c}} {{S_1}(x)}&{{S_1}(y)}&{{S_1}(z)}&1 \\ {{S_2}(x)}&{{S_2}(y)}&{{S_2}(z)}&1 \\ {{S_3}(x)}&{{S_3}(y)}&{{S_3}(z)}&1 \\ x&y&z&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} a \\ b \\ c \\ d \end{array}} \right] = 0.$ | (1) |
根据点关于平面对称点的求解原理,容易得到
| $\left\{ \begin{array}{l}{X_p} = \displaystyle\frac{{ - 6L{k_1}{k_4}}}{{{k_2}^2 + 3{k_3}^2 + 3{k_4}^2}},\\{Y_p} = \displaystyle\frac{{ - 2\sqrt 3 L{k_1}{k_2}}}{{{k_2}^2 + 3{k_3}^2 + 3{k_4}^2}},\\{Z_p} = \displaystyle\frac{{6L{k_1}{k_3}}}{{{k_2}^2 + 3{k_3}^2 + 3{k_4}^2}},\end{array} \right.$ | (2) |
其中,
| $\left\{\!\! {\begin{array}{*{20}{l}}{{k_1} = {c_1}{c_3}{s_2} + {c_2}{s_{13}},}\\{{k_2} = 2{c_3}\left( {{s_1} - {s_2}} \right) + {c_2}\left( {{s_1} - {s_3}} \right) + {c_1}\left( {{s_3} - {s_2}} \right),}\\{{k_3} = {c_2}{c_3} + {c_1}\left( {{c_2} + {c_3}} \right),}\\{{k_4} = {s_{12}} - {s_3}({c_1} + {c_2}),}\end{array}} \right.$ |
在参考坐标系下很容易推导动平台的位置坐标
动力学建模问题在机器人动力学性能分析和实际运动控制中占有重要的地位. 本文采用拉格朗日法建立3-RSR并联机构的动力学模型,在对模型精度影响较小的情况下对该机构做了如下简化和假设:
(1) 无关节摩擦和间隙;
(2) 将曲形的主、从动杆视为直杆;
(3) 考虑到从动杆对本机构的动力学建模不起主导作用,将每根从动杆的质量平均分为两部分,集中于两点,一个是球关节处,另一个是动平台的中心点.
3.1 系统的动能求解主动杆的动能应为主动杆自身的动能加上从动杆质量分配到主动杆上的动能. 沿用前面的参考系
设从动杆质量被平均分配到主动杆和动平台后,主动杆质心②相对于原质心①偏移的距离为x,如图3所示.
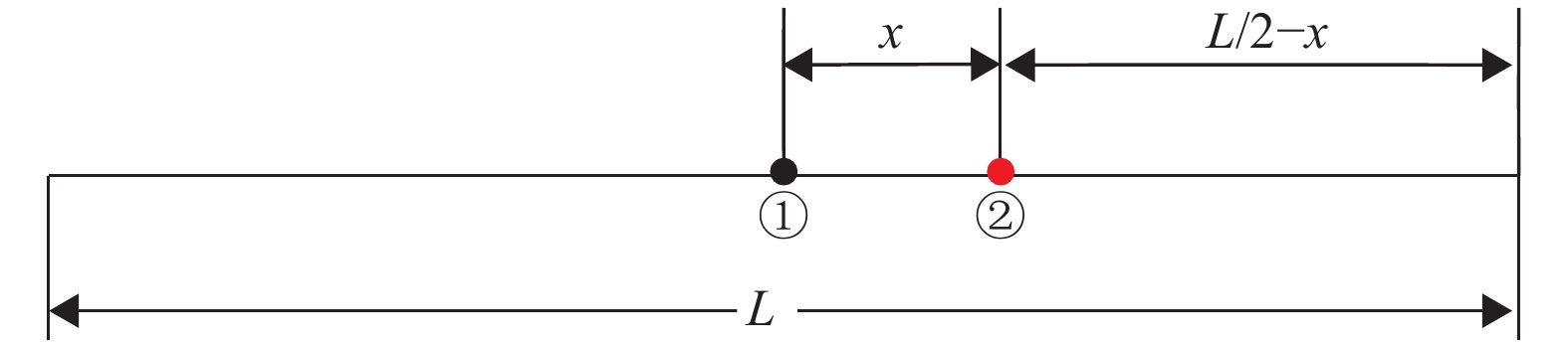
|
图 3 主动杆质心位置 Figure 3 Center-of-mass position for master link |
利用力矩平衡原理:
| ${l_c} = x + \frac{1}{2}L = \frac{{{m_a} + {m_s}}}{{2{m_a} + {m_s}}}L.$ | (3) |
式(3)中,
第
| ${E_{ki}} = \frac{1}{2}{m_i}{v_i}^{\rm{T}}{v_i} + \frac{1}{2}{w_i}^{\rm{T}}{J_i}{w_i},(i = 1,2,3).$ | (4) |
式(4)中,第1项是由杆件质心线速度
| ${E_a} = \sum\limits_{i = 1}^3 {{E_{ki}}} = \sum\limits_{i = 1}^3 {\frac{1}{2}{m_i}{{\dot {\mathbb{C}}}_i}^{\rm{T}}{{\dot {\mathbb{C}}}_i} + \frac{1}{2}{{\dot \theta }_{ia}}^{\rm{T}}{J_i}} {\dot \theta _{ia}}.$ | (5) |
其中
| ${J_i} = \frac{1}{3}{m_a}{L^2} + \frac{1}{2}{m_s}{L^2}.$ | (6) |
下面求解动平台的动能
| ${E_m} = \frac{1}{2}{m_j}{v_m}^2 + \frac{1}{2}{J_m}{w_m^2}.$ | (7) |
式(7)中,
根据运动学分析,很容易得到:
| ${{{v}}_m}{\rm{ = }}\left[ {{{\dot X}_p},{{\dot Y}_p},{{\dot Z}_p}} \right].$ | (8) |
动平台的转动惯量公式为
| ${{{J}}_m} = {{R}}{J_0}{{{R}}^{\rm{T}}},$ | (9) |
其中
| $\left\{ \begin{array}{l}{{V}} = {\rm Unit}\left( {\overrightarrow {{{{O}}_2}{{{D}}_3}} } \right)\\ \quad= \left[ {\displaystyle\frac{{{X_{{D_3}}} - {X_p}}}{r}\;,\displaystyle\frac{{{Y_{{D_3}}} - {Y_p}}}{r}\;,\displaystyle\frac{{{Z_{{D_3}}} - {Z_p}}}{r}} \right];\\{{W}} = \displaystyle\frac{{\overrightarrow {{{{O}}_2}{{{D}}_3}} \times \overrightarrow {{{{O}}_2}{{{D}}_2}} }}{{\left\| {\overrightarrow {{{{O}}_2}{{{D}}_3}} \times \overrightarrow {{{{O}}_2}{{{D}}_2}} } \right\|}};\\{{U}} = {{V}} \times {{W}}.\end{array} \right.$ | (10) |
式(10)中,
| $\left\{ \begin{array}{l}{J_{mx}} = {J_{xx}}{U_x}^2 + {J_{yy}}{V_x}^2 + {J_{zz}}{W_x}^2;\\{J_{my}} = {J_{xx}}{U_y}^2 + {J_{yy}}{V_y}^2 + {J_{zz}}{W_y}^2;\\{J_{mz}} = {J_{xx}}{U_z}^2 + {J_{yy}}{V_z}^2 + {J_{zz}}{W_z}^2;\\{J_{mxy}} = {J_{xx}}{U_x}{U_y} + {J_{yy}}{V_x}{V_y} + {J_{zz}}{W_x}{W_y};\\{J_{mxz}} = {J_{xx}}{U_x}{U_z} + {J_{yy}}{V_x}{V_z} + {J_{zz}}{W_x}{W_z};\\{J_{myz}} = {J_{xx}}{U_y}{U_z} + {J_{yy}}{V_y}{V_z} + {J_{zz}}{W_y}{W_z}.\end{array} \right.$ |
动平台相对于参考系的角速度矩阵可表示为[17]
| ${{\hat{ w}}_m} = {\dot{ R}}{{{R}}^{\rm{T}}},$ | (11) |
其中
| ${E_k} = {E_a} + {E_m}.$ | (12) |
势能的大小与选取的零势能面有关,对于本机构,规定参考系
| ${u_i} = - {m_i}g{\mathbb{C}_i}\left( z \right),\left( {i = 1,2,3} \right),$ | (13) |
其中,
| ${u_a} = \sum\limits_{i = 1}^3 {{u_i}}. $ | (14) |
动平台的势能可表示为
| ${u_m} = - {m_j}g{Z_p}.$ | (15) |
根据所有构件的势能表达式,可得系统的总势能为
| ${E_p} = {u_a} + {u_m}.$ | (16) |
基于Lagrange法的并联机构动力学方程可表示为
| $\frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\text{∂} L}}{{\text{∂} \dot \theta }} - \frac{{\text{∂} L}}{{\text{∂} \theta }} = \tau ,$ | (17) |
式(17)中,
| ${\tau _i} = \frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\text{∂} {E_k}}}{{\text{∂} {{\dot \theta }_i}}} - \frac{{\text{∂} {E_k}}}{{\text{∂} {\theta _i}}} + \frac{{\text{∂} {E_p}}}{{\text{∂} {\theta _i}}},\left( {i = 1,2,3} \right).$ | (18) |
结合并联机构样机(见图4),通过Mathematica软件计算与ADAMS运动仿真对动力学模型进行验证. 机构参数如表1所示.

|
图 4 机构样机图 Figure 4 Prototype of mechanism |
| 表 1 并联机构样机参数表 Table 1 Parameters of prototype of mechanism |
对4种不同的运动情形分别进行计算与仿真:
(1) 单自由度平移. 即沿
| $\left\{ \begin{array}{l}x = 0;\\y = 0;\\z = 0.085 + 0.082t.\end{array} \right.$ |
(2) 单自由度旋转. 如:固定关节
| $\left\{ \begin{array}{l}x = 0.042t - 0.002;\\y = 0;\\z = 0.02t + 0.085.\end{array} \right.$ |
(3) 先单自由度旋转一定角度后再在该姿态下沿两平台中心连线方向做单自由度平移运动. 定义动平台的运动轨迹为
| $\left\{ \begin{array}{l}x = 0.4{t^4} - 0.71{t^3} + 0.28{t^3} + 0.11t - 0.001;\\{{y = }}0;\\z = - 0.23{t^4} + 0.54{t^3} - 0.42{t^2} + 0.15t + 0.085.\end{array} \right.$ |
(4) 多自由度运动(旋转的同时进行平移). 固定关节
| $\left\{ \begin{array}{l}x = - 0.005{t^3} + 0.005{t^2} + 0.002t;\\y = 0.006{t^3} - 0.024{t^2} - 0.022t;\\z = - 0.005{t^3} - 0.02{t^2} + 0.09t + 0.085.\end{array} \right.$ |
上述4种运动轨迹中的时间取值范围为t∈[0,1]。根据式(9)~(18)可计算出机构末端在4种运动情形下力矩

|
图 5 平移时
|
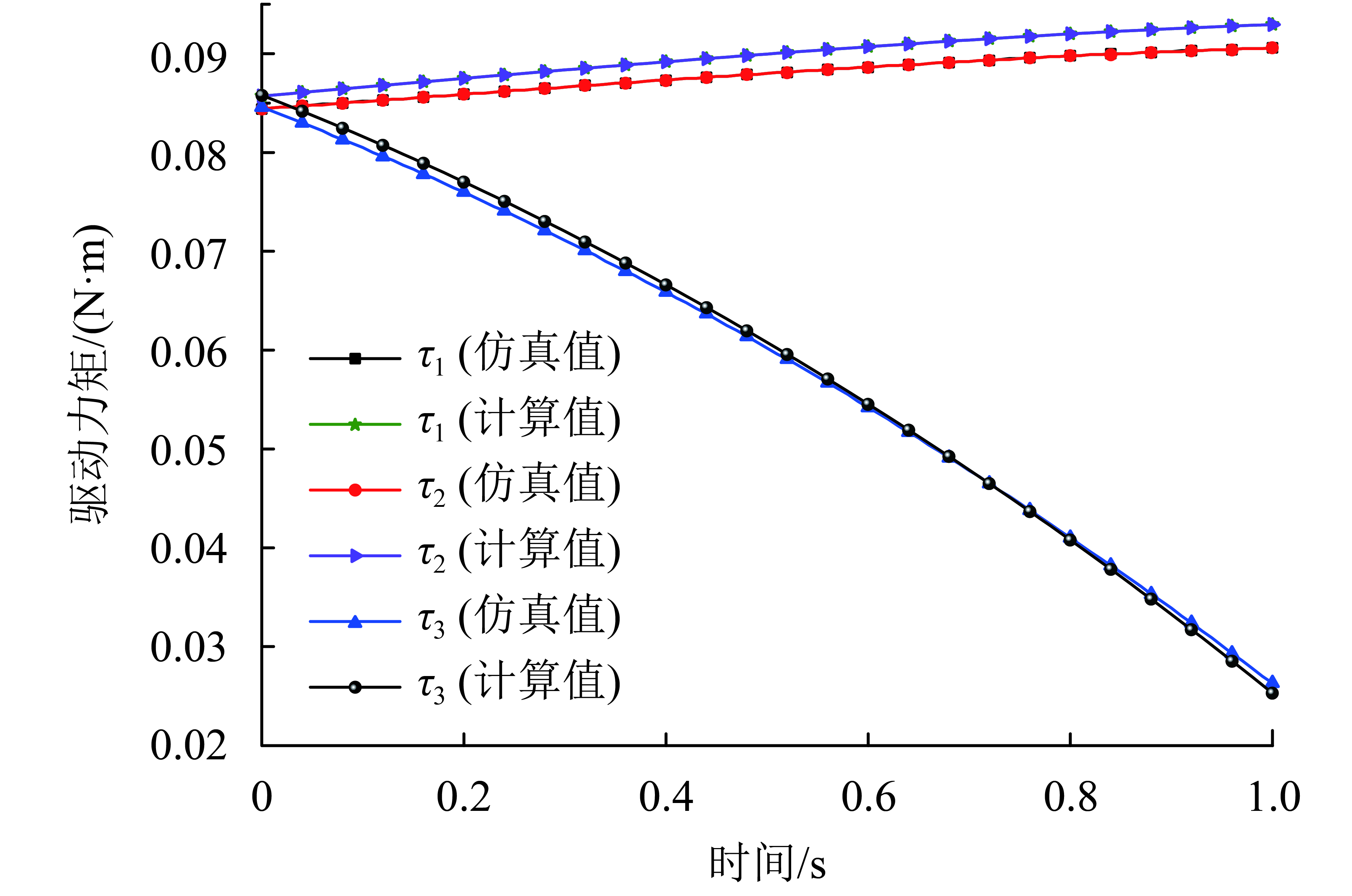
|
图 6 旋转时
|

|
图 7 先旋转后平移时
|
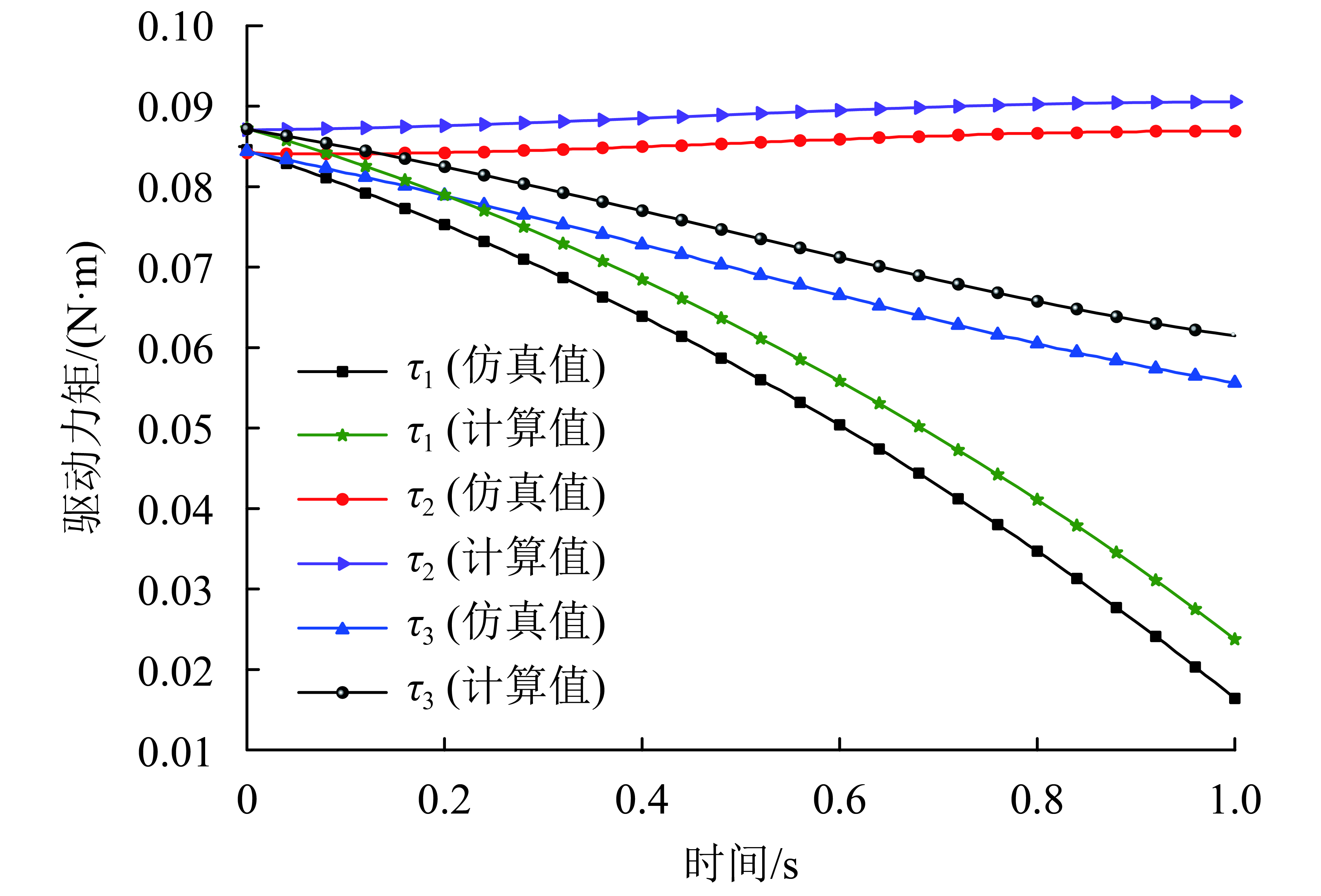
|
图 8 混合运动时
|
4种运动情形下,驱动力矩的理论值与仿真值之间的误差对比如表2所示.
| 表 2 力矩的计算值和仿真值误差比较 Table 2 Comparison of the torque error between calculation and simulation N·m |
综合以上分析知,使用该模型计算和仿真出来的力矩值都有着相同的变化趋势和一定程度上的吻合. 通过表2的误差对比可观察到机构在第(1)、(2)、(4)种运动情形下的力矩仿真值与计算值之间的误差均能控制在0.1%~0.3%以内,只有第(3)种运动情形下的仿真值与计算值的误差在0.7%~6.9%以内,图(7)中很明显地显示出仿真时的启动力矩较大,机构运动到第0.4秒时,机构从转动过渡到平移力矩的变化值也较大,出现这种结果的原因可能与仿真过程中连续运动轨迹的插补步长和电机角度的初始值设定有关,因此后期有必要对此种情形的运动仿真进行优化. 整体而言,通过以上算例仿真与计算,可验证模型的准确性和有效性,还可为电机的选型提供理论依据.
5 结论(1) 利用力矩平衡原理计算了简化模型的质心,推导了3-RSR并联机构系统的动能表达式和势能表达式,角速度矩阵和旋转矩阵之间的关系.
(2) 应用拉法格朗日法建立了并联机构的刚体动力学模型,为并联机构驱动力的求解和整个机构的动力学分析奠定了基础. 结合算例验证了理论模型的准确性和可行性.
| [1] |
WU K, YU J J, ZONG G H, et al. A family of rotational parallel manipulators with equal-diameter spherical pure rotation[J].
Journal of Mechanisms & Robotics, 2014, 6(1): 1-10.
|
| [2] |
YU J J, DONG X, PEI X, et al. Mobility and singularity analysis of a class of 2-DOF rotational parallel mechanisms using a visual graphic approach[J].
American Society of Mechanical Engineers (ASME), 2011, 4(4): 1027-1036.
|
| [3] |
DONG X, YU J J, CHEN B, et al. Geometric approach for kinematic analysis of a class of 2-DOF rotational parallel manipulators[J].
Chinese Journal of Mechanical Engineering, 2012, 25(2): 241-247.
DOI: 10.3901/CJME.2012.02.241. |
| [4] |
陈斌, 于靖军, 宗光华, 等. 一类2自由度n-4R并联指向机构的运动学分析[J].
机械工程学报, 2014, 50(15): 19-27.
CHEN B, YU J J, ZONG G H, et al. Kinematic analysis of a class of 2-dof n-4r parallel pointing mechanism[J]. Journal of Mechanical Engineering, 2014, 50(15): 19-27. |
| [5] |
WU Y Q, LI Z X, SHI J B. Geometric properties of zero-torsion parallel kinematics machines[J].
2010, 6219(1): 2307-2312.
|
| [6] |
张国英, 廖亚军, 梁峰, 等. 一种类球面并联腕部机构及其运动学分析[J].
机器人, 2017, 39(2): 167-175.
ZHANG G Y, LIAO Y J, LIANG F, et al. A spheroid parallel wrist mechanism and its kinematic analysis[J]. Robot, 2017, 39(2): 167-175. |
| [7] |
DUAN Z X, YU J J, QU Y F, et al. Type synthesis and axodes analysis of a class of special 2R1T parallel mechanisms[C]//14th International Federation for the Promotion of Mechanism and Machine Science World Congress.[S.l.]: National Taiwan University, 2015: 299-304.
|
| [8] |
TSAI L W. Robot analysis and design: the mechanics of serial and parallel manipulators[M]. US: John Wiley & Sons, Inc., 1999, 424-455.
|
| [9] |
陈华龙, 梁慧冰, 霍迎辉. 四级倒立摆系统的Lagrange方程建模[J].
广东工业大学学报, 2004, 21(2): 59-63.
CHEN H L, LIANG H B, HUO Y H. Modeling four-stage inverted pendulum system based on lagrange equation[J]. Journal of Guangdong University of Technology, 2004, 21(2): 59-63. DOI: 10.3969/j.issn.1007-7162.2004.02.014. |
| [10] |
CARP-CIOCARDIA D C. Dynamic analysis of clavel's delta parallel robot[C]// 2003 IEEE International Conference on Robotics and Automation, Institute of Electrical and Electronics Engineers Inc. [S.l.]: IEEE, 2003: 4116-4121.
|
| [11] |
SHIAU T N, TSAI Y J, TSAI M S. Nonlinear dynamic analysis of a parallel mechanism with consideration of joint effects[J].
Mechanism & Machine Theory, 2008, 43(4): 491-505.
|
| [12] |
陈斌, 宗光华, 于靖军, 等. 一种2-DOF类球面并联转台的动力学建模及分析[J].
机械工程学报, 2013, 49(13): 24-31.
CHEN B, ZONG G H, YU J J, et al. Dynamic modeling and analysis of 2-DOF quasi-sphere parallel platform[J]. Journal of Mechanical Engineering, 2013, 49(13): 24-31. |
| [13] |
QIU Z C. Current situation of research on parallel robots[J].
Machinery, 2000, 38(428): 27-29.
|
| [14] |
DESIGNS R H. Omni-Wrist V(2002-2016) [2018-6-18]. http://www.anthrobot.com/omni-wrist-v/ [EB/OL].
|
| [15] |
张国英. 基于ADAMS的类球面并联腕部机构的碰撞仿真分析[J].
机械设计与制造, 2017(13): 217-220.
ZHANG G Y. Impact simulation analysis of a spheroid parallel wrist mechanism based on ADAMS[J]. Machinery Design & Manufacture, 2017(13): 217-220. |
| [16] |
卢志辉, 孙志扬, 李祥云, 等. 高精度质心测量方法研究[J].
兵工学报, 2009, 30(12): 1748-1752.
LU Z H, SUN Z Y, LI X Y, et al. Research on high precision measurement of centroid[J]. Acta Armamentarii, 2009, 30(12): 1748-1752. DOI: 10.3321/j.issn:1000-1093.2009.12.034. |
| [17] |
韩建友, 杨通, 于靖军. 高等机构学[M]. 2版. 北京: 机械工业出版社, 2015, 9-18.
|
 2018, Vol. 35
2018, Vol. 35

